Volume 2024, Issue 1 7260336

Research Article

Open Access

On the Use of Taguchi Method in the Analysis of the Dynamic Response of Variable Bearing Design under Impact Load

Corresponding Author

Hazim U. Jamali

[email protected]

orcid.org/0000-0002-2908-3319

Mechanical Engineering Department , College of Engineering , University of Kerbala , Karbala , 56001 , Iraq , uokerbala.edu.iq ,

Search for more papers by this author

M. N. Mohammed,

M. N. Mohammed

orcid.org/0000-0002-1472-8401

Mechanical Engineering Department , College of Engineering , Gulf University , Sanad , 26489 , Bahrain , gust.edu.kw ,

Search for more papers by this author

Muhsin Jaber Jweeg,

Muhsin Jaber Jweeg

orcid.org/0000-0001-7917-9952

College of Technical Engineering , Al-Farahidi University , Baghdad , 00965 , Iraq , uoalfarahidi.edu.iq

Search for more papers by this author

E. Mahdi,

E. Mahdi

Mechanical and Industrial Engineering , Qatar University , Doha , Qatar , qu.edu.qa

Search for more papers by this author

H. S. S. Aljibori,

H. S. S. Aljibori

orcid.org/0000-0002-5815-8148

College of Engineering , University of Warith Al-Anbiyaa , Karbala , 56001 , Iraq

Search for more papers by this author

Oday I. Abdullah,

Oday I. Abdullah

orcid.org/0000-0001-5450-021X

Mechanical Engineering Department , College of Engineering , Gulf University , Sanad , 26489 , Bahrain , gust.edu.kw ,

Department of Energy Engineering , College of Engineering , University of Baghdad , Baghdad , 10071 , Iraq , uobaghdad.edu.iq

Department of Mechanics , Al-Farabi Kazakh National University , Almaty , 050040 , Kazakhstan , kaznu.kz

Search for more papers by this author

Alessandro Ruggiero,

Alessandro Ruggiero

orcid.org/0000-0002-5111-2331

Department of Industrial Engineering , University of Salerno , 84084 , Fisciano , Italy , unisa.it

Search for more papers by this author

M. Alfiras,

M. Alfiras

orcid.org/0000-0001-9398-7737

Electrical and Electronic Engineering Department , College of Engineering , Gulf University , Sanad , 26489 , Bahrain , gust.edu.kw ,

Search for more papers by this author

Josef Schlattmann,

Josef Schlattmann

Institute of Laser and Systems Technologies (iLAS) , Hamburg University of Technology (TUHH) , Harburger Schloßstraße 28, Hamburg , 21079 , Germany , tuhh.de

Search for more papers by this author

Hazim U. Jamali,

Corresponding Author

Hazim U. Jamali

[email protected]

orcid.org/0000-0002-2908-3319

Mechanical Engineering Department , College of Engineering , University of Kerbala , Karbala , 56001 , Iraq , uokerbala.edu.iq ,

Search for more papers by this author

M. N. Mohammed,

M. N. Mohammed

orcid.org/0000-0002-1472-8401

Mechanical Engineering Department , College of Engineering , Gulf University , Sanad , 26489 , Bahrain , gust.edu.kw ,

Search for more papers by this author

Muhsin Jaber Jweeg,

Muhsin Jaber Jweeg

orcid.org/0000-0001-7917-9952

College of Technical Engineering , Al-Farahidi University , Baghdad , 00965 , Iraq , uoalfarahidi.edu.iq

Search for more papers by this author

E. Mahdi,

E. Mahdi

Mechanical and Industrial Engineering , Qatar University , Doha , Qatar , qu.edu.qa

Search for more papers by this author

H. S. S. Aljibori,

H. S. S. Aljibori

orcid.org/0000-0002-5815-8148

College of Engineering , University of Warith Al-Anbiyaa , Karbala , 56001 , Iraq

Search for more papers by this author

Oday I. Abdullah,

Oday I. Abdullah

orcid.org/0000-0001-5450-021X

Mechanical Engineering Department , College of Engineering , Gulf University , Sanad , 26489 , Bahrain , gust.edu.kw ,

Department of Energy Engineering , College of Engineering , University of Baghdad , Baghdad , 10071 , Iraq , uobaghdad.edu.iq

Department of Mechanics , Al-Farabi Kazakh National University , Almaty , 050040 , Kazakhstan , kaznu.kz

Search for more papers by this author

Alessandro Ruggiero,

Alessandro Ruggiero

orcid.org/0000-0002-5111-2331

Department of Industrial Engineering , University of Salerno , 84084 , Fisciano , Italy , unisa.it

Search for more papers by this author

M. Alfiras,

M. Alfiras

orcid.org/0000-0001-9398-7737

Electrical and Electronic Engineering Department , College of Engineering , Gulf University , Sanad , 26489 , Bahrain , gust.edu.kw ,

Search for more papers by this author

Josef Schlattmann,

Josef Schlattmann

Institute of Laser and Systems Technologies (iLAS) , Hamburg University of Technology (TUHH) , Harburger Schloßstraße 28, Hamburg , 21079 , Germany , tuhh.de

Search for more papers by this author

First published: 20 July 2024

https://doi.org/10.1155/2024/7260336

Academic Editor: Michel Fillon

Share a link

Email
Wechat
Bluesky

Abstract

Optimizing the bearing design is an essential step to maintain safe operation and extend the bearing life. Taguchi method is one of the powerful methods in this direction, which can be used to assess the geometrical design parameters under shaft deviation. Shaft deviation is unavoidable in the industrial applications of journal bearing. It results from installation and manufacturing errors, bearing deformation, asymmetric loading, and many other sources. This work investigates the use of three bearing profiles with a wide range of geometrical characteristics to minimize the deviation negative effects. These designs modified the inner bearing surface in a linear, parabolic, or cubic shape. A general 3D deviation representation is considered in the analysis where the deviations in the horizontal and vertical directions are taken into consideration. The analysis is performed for a finite-length journal bearing using the Taguchi method to determine the optimal design characteristics. This analysis is achieved in terms of the rotor critical speed and the film thickness of the lubricant. Furthermore, the system response to an impact load is analyzed. The finite difference method is used in the analysis to solve the governing equations of the hydrodynamic problem, and the 4th-order Range Kutta solution is considered to solve the motion equations of the rotor under the impact load. Results show that using the suggested designs enhances the system’s critical speed, elevates the thickness of the lubricant layer, and extends the safe operation limits under impact load. The parabolic profile gives the most effective outcome where the shaft trajectory under impact excitation is very close to the ideal journal-bearing case. The suggested design reduces the maximum pressure by 17.07%, increases the minimum film thickness by 175.04%, and increases the critical speed by 23.42%.

1. Introduction

Journal bearing is the most common type of hydrodynamic bearing, which is commonly found in equipment and high-speed rotating machineries [1]. In this bearing type, the shaft rotates inside the bearing within a clearance in the order of tens of microns. The axis of the shaft should be paralleled to the bearing longitudinal axis. However, this ideal case is hardly to be achieved in the practical usages. This axis is often subjected to a deviation from a standard designed direction that should be parallel to the axis of the bearings, which is usually called misalignment. It has clear negative influences on the system performance as the deviation takes place within this relatively limited clearance range. Misalignment may result due to installation errors, asymmetric loading, deformation under high levels of load, and manufacturing errors [2, 3, 4]. The presence of misalignment causes uneven distribution of the film thickness along the bearing width, which also results in asymmetric pressure distribution. In such a case, the position of the resulting load point deviates from the bearing mid-plane, in addition to the significant reduction in the film thickness and the increase in the pressure levels [5, 6]. The importance of the misalignment consequences on the general rotor-bearing performance has drawn great attention from researchers for decades. Jang and Khonsari [7] studied the misalignment causes where they investigated their consequences on the bearing performance. Pigott [8] remarkably explained that a misalignment level of only 0.0002 rad decreased the bearing load carrying capacity by 40%. Sun and Changlin [9] and Sun et al. [10] also explained that the misalignment reduced the bearing capacity for load support and reduced the lubricant layer thickness at the bearing edges. The severe level of misalignment reduces significantly the gap between the shaft and the bearing, which may result in metal-to-metal contact that leads to a breakdown of the system [11, 12]. The shaft deviation has also been reported to be one of the most important issues influencing the performance of rotating machinery in terms of friction and wear levels [13, 14, 15].

The misalignment impacts on the shape and levels of pressure, and film thickness is not the same on the critical speed of the rotor bearing system. Misalignment increases the critical speed of the system, which represents a positive effect on the stability of the system [16]. This increase in the critical speed comes at the price of a severe reduction in the minimum film thickness and a significant rise in the pressure values [17, 18]. The reduction in the lubricant layer thickness means, a decrease in the bearing load capacity for the same designed minimum film thickness value. Therefore, a critical balance is required in designing journal bearings between the designed value of the load and the stability limits. One of the methods in this direction is to reduce the misalignment effects by changing the shape of the bearing to increase the clearance at certain locations between the surfaces. Nacy [19] presented an experimental investigation of a chamfered bearing to decrease the lubricant leakage. Bouyer and Fillon [20] used predesigned defects to decrease the misalignment effect in their numerical solution to this problem and reported a 60% increase in the minimum lubricant thickness. Strzelecki [21] changed the whole bearing profile to reduce the misalignment effect. It is also found by [22, 23] that the amplitude of vibration and the stability limit can be improved if a bearing with variable geometry is used. The effect of changing the bearing profiles was also investigated by [24, 25] to minimize the effects of misalignment on the performance of the journal bearing but without considering the system’s stability. On the other hand, the misalignment effect, without considering the change in the bearing profile, has been studied extensively over the last decades [26, 27, 28, 29, 30, 31]. The importance of the stability limits of the rotor-bearing systems comes from the modern applications that operate with high speed and certainly cause stability problems.

Changing the bearing profile is based on some parameters such as the shape of modification (order of the curve), modification height, and the location of the start of modification. The characteristics of the resulting bearing depend on the value of each parameter; therefore, using a traditional method in evaluating the effect of the parameter will not necessarily give the best combination of these parameters. Taguchi method represents one of the efficient statistical methods in this context [32]. Genichi Taguchi proposed this method with the main purpose of reducing the required number of tests in an optimization process. This method was used by Yücel and Saruhan [33] to determine the possible minimum amplitude of vibration of a rotor-bearing system, where it was found to be very efficient in reducing the possibility of operation at the critical speed of the system. Chien et al. [34] adopted the same analysis to optimize the parameters related to the grooving of the bearings. Sharma et al. [35] identified the optimal speed values of the journal in their experimental study based on this method. The performance of journal bearing with the use of asymmetrical herringbone grooves was also investigated using this method by Chen et al. [36]. It is also used as an optimization method by Bhasker et al. [37] to identify the optimal parameters of pressure distribution assessment.

Despite the extensive works presented in the field of enhancing the performance of journal bearing, the shaft deviation problem still causes severe negative effects on this performance. Therefore, the current study presents a novel method to optimize the design of the bearing using three forms of profile based on the Taguchi method. Each form has three levels that are considered to produce the orthogonal array that is used in the optimization procedure. The finite difference method is used in the numerical solution of this problem. The effectiveness of the optimized design is examined based on the combined effect of maximum pressure, minimum film thickness, and the critical speed of the rotor-bearing system. Furthermore, the dynamic response to an impact excitation is also investigated for the optimized design, where the solution of the motion equations is achieved by adopting the 4th-order Range–Kutta analysis.

2. Governing Equations

It is well known that the Reynolds equation solution, together with the film thickness equation, is required to calculate the journal-bearing characteristics. These two equations, under classic hypotheses, are given by the following (Figure 1) [38, 39]:

()

where ρ, η: density and viscosity of the lubricant, respectively (ρ is constant for incompressible fluid).

), U_j, U_b: mean, journal, and bearing velocity, respectively (U_b=0 and U_j = Rω). h: film thickness. p: pressure. C: clearance. ε_r: eccentricity ratio.

It is worth mentioning that, in the steady state case (the squeeze term vanishes).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Section of an ideal aligned case.

The Reynolds boundary conditions are used in solving this hydrodynamic problem, which are given by Hamrock [40], p = 0 at θ = 0, = 0 at θ = θ_cav, where θ_cav is the cavitation angle, and it can be determined in the current research by an iterative solution [40, 41]. Equations (1) and (2) can be given in a dimensionless form considering the following parameters,

where L is bearing length and R is radius.

Using these relations, Equations (1) and (2) in the steady state case becomes,

()

where

()

The load components are given by Chasalevris and Sfyris [38]:

()

And the dimensionless total load is as follows:

()

where

()

The attitude angle, which is the angle between the load line and the line of centers, is given by Feng et al. [42].

()

3. Dynamic Solution

The dynamic coefficients are determined based on the use of the Reynolds equation,

()

The film thickness equation under dynamic conditions is given by Lund and Thomsen [43].

()

The differentiation of Equation (11) with respect to time, substituting the results in Equation (10) and writing the resulting equation in a dimensionless form yield,

()

where

()

The bearing forces are given by Feng et al. [42] and Lund and Thomsen [43].

()

Using these equations, the matrices of stiffness and damping coefficients are given by Someya [44].

()

These coefficients are used in the current work based on the form suggested by Lund and Thomsen [43].

()

Therefore, using the Equations (17) and (18), the dynamic coefficients can be given by the following:

()

where

, and

are the pressure components variations in the neighborhood of a generic equilibrium position.

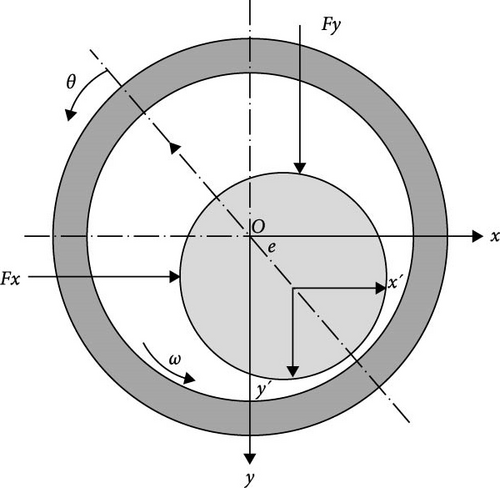
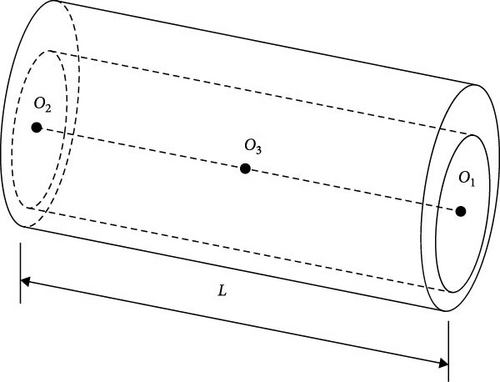
The linearized bearing forces will be written later in terms of the stiffness and damping coefficients in order to determine the critical speed of the rotor bearing system. This can be achieved by solving the equations of motion of the rotor-bearing system [29]. These equations of the rotor bearing system that are shown in Figure 2 are given by Shi et al. [45].

()

where f_x, f_y: bearing forces; f_ex, f_ey: external loads; x′,y′: whirling axes.

Equations (20) and (21) can be given by the following:

()

where

The following function is used in the current work as an impact load [29],

()

The critical speed of the system can be determined by solving the equations of motion, neglecting all the external loads,

()

The linearized bearing forces can be written as follows [29]:

()

The following equations result by substitution of Equations (27) and (28) in Equations (22) and (23),

()

Using the following solution suggested by Nicholas [46], Ruggiero et al. [47], and D’Amato et al. [48] gives, X′ = Ae^iλt and Y′ = Be^iλt

()

where

()

The resulting critical speed (CS) is as follows:

()

4. Deviation Representation

The 3D deviation model is adopted from a previous work [39], where a detailed explanation for this model can be found. Figure 3 shows this model where using a 3D modeling of the deviation results in a more accurate simulation for the journal deviations in the horizontal and vertical directions. These deviations are given by the following:

()

where Z = z/L, Δ = δ/c.

Misalignment in the journal bearing causes a variation in the attitude angle as well as the eccentricity distance along the z-direction. Therefore, these two variables are given in terms of z position as follows [39]:

()

where ∅_n : ∅ at z = L/2; e_n : e at z = L/2.

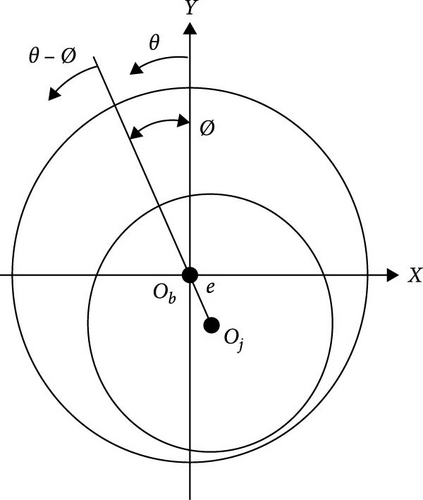
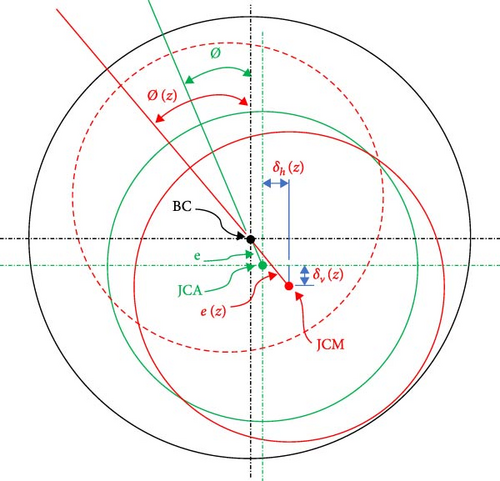
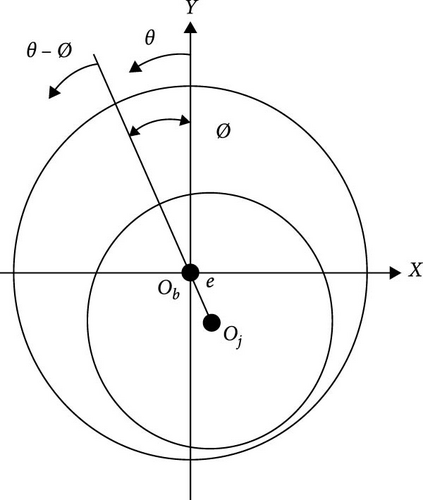
Equation (36) is used to incorporate the misalignment effect in the calculation of the gap at any given θ, Z position that is given by Equation (4). This process can be performed by calculating the eccentricity ratio (e(z)/c) and the attitude angle that is related to the misalignment parameters, as illustrated by Equation (36).

5. Baring Modification

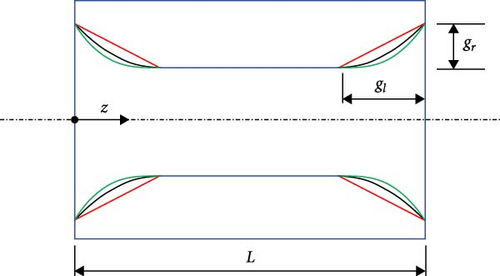
The decrease in the resulting gap due to misalignment can be overcome to an acceptable level by varying the shape of the bush. Figure 4 shows three different designs of the bearing. Figure 4(a) shows a modified bearing, and Figure 4(b) illustrates the three bearing profiles used in the current work, which are linear, parabolic, and cubic profiles. The effect of using these profiles will be investigated in detail in terms of reducing the misalignment negative effects on the maximum pressure, minimum film thickness, and the critical speed of the rotor bearing system.

The three profiles can be expressed mathematically by the following general relation:

()

where ϱ(z): modification amount in the radial direction. c₁ and c₂: constants, which can be easily determined in terms of the boundary conditions of the modification. n: equation order where n = 1, 2, and 3 stands for the linear, parabolic, and cubic modification, respectively.

Figure 5 shows a bearing section (exaggerated scale), which illustrates the modifications. The three designs are shown together for the purpose of illustration. The design parameters are g_r and g_l, representing the modification amount in the radial direction and the length of modification, respectively.

Using the boundary conditions (characteristics of the start and end position of modification) and the following dimensionless relations, the equation of modifications can be given by the following:

()

(1)
Linear profile (n = 1).

()

(2)
Parabolic profile (n = 2).

()

(3)
Cubic profile (n = 3).

()

Scaling the design parameters to the clearance (T = g_r/C) and to the length of the bearing (Γ = g_l/L) provides a clear understanding of the required design changes in terms of the main system parameters. The resulting gap regarding the deviation effect, in addition to the bearing modification effect, is obtained through the coupling of Equations (4), (35), (36), (39), (40), and (41).

5.1. Numerical Solution

The numerical solution starts with discretizing the governing equations using the finite difference method. This discretization involves the misalignment equations and the profile modification equations in addition to the main hydrodynamic equations of the problem. Then, the resulting equation is solved using the successive over-relaxed of the Gauss–Seidel method. At this step, the pressure field and the gap between the bearing and the shaft are known at any θ, Z position. A detailed procedure for the solution procedure was explained in [39]. The convergence criterion used in the current work is as follows:

()

The load convergence criterion is based on the fact that the limit of the load resulting from the integration of a converged pressure solution is ±10⁻⁵ of the applied load. If the integrated load is out of these limits, the eccentricity ratio in the film thickness equation is changed and the whole solution is repeated in order to have a new pressure field.

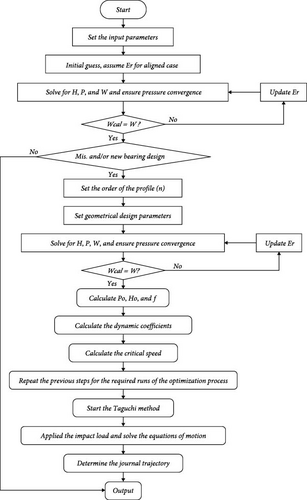
Based on the pressure and film thickness values available at this step, the dynamic coefficients of the journal bearing can now be calculated using a numerical integration method. After that, the critical speed of the rotor-bearing system is calculated. All the data required to perform the Taguchi analysis become available at this step. The Taguchi analysis is performed for three levels to each variable, as will be explained later in Section 5.2. The optimal outcome of the Taguchi method in terms of the bearing design variables will be examined under impact load. This examination is performed to find the journal’s trajectory under such type of excitation and identify the influence of the bearing shape form on the dynamic response of the rotor. Figure 6 illustrates the steps of the solution.

5.2. Results and Discussions

The analysis in the current work is performed for a journal bearing with L/D = 1.5. It is well known that a numerical solution is required in such cases where the pressure gradient in both directions is considered. The first step in this solution is to ensure the independence of the results on the number of nodes used in the discretization of the governing equations. Therefore, a series of tests is performed using different node numbers in the radial (N) and longitudinal (M) sides of the solution space. Using a total number (N × M) of 65,341 is found sufficient enough where any increase in the total number of nodes above 65,341 has a trivial effect on the critical speed, maximum pressure, and minimum film thickness.

All the results are presented in their dimensionless in order to have a general sight of the results in terms of the suggested bearing profile parameters. As the work’s purpose is to identify the effectiveness of the suggested design on the main bearing characteristics under 3D misalignment, it is important to have a clear picture of the misalignment effect at first on these characteristics. Table 1 shows this effect on the dimensionless maximum pressure (P_max), dimensionless minimum film thickness (H_min), and dimensionless critical speed (CS). This table compares these values for the ideal aligned case and the misalignment case. It is clear how the misalignment affects these values where P_max increased by 57.6%, H_min decreased by 78.3%, and the critical speed increased by 45.6%. It is important to notice that the enhancement of the critical speed value comes at the cost of the negative impact on the designed value of the minimum film thickness and the corresponding maximum pressure value. However, it will be shown in the next sections that optimizing the bearing shape design provides a significant compromise between the enhancement of the CS and minimizing the negative effects on P_max and H_min.

Table 1. Effect of 3D deviation on the results.

Parameters	Aligned	3D misalignment	% Change
P_max	0.486397	0.766778	57.64439
H_min	0.5	0.108381	−78.3238
CS	2.452341	3.570661	45.60214

The suggested bearing design is performed on the basis of changing the form of modification (n = 1, n = 2, and n = 3) and the position of the start of modification in the longitudinal direction (Γ) and the modification height (T) in the radial direction. Investigating the effect of each parameter from this wide range of variables on the bearing characteristics is not a practical solution way. Therefore, the Taguchi method is used to have the optimal combination of these parameters, which results in the best possible effect on the bearing performance under 3D misalignment. A nine orthogonal array is adopted in this work for the solution of the Taguchi method, as three levels for each parameter are considered. Using this type of orthogonal array requires results of nine runs. Table 2 shows these results where P_max, H_min, and CS are shown for each run. Each run corresponds to a given combination of n, T, and Γ, and all the considered combinations will be explained later.

Table 2. Bearing characteristics for the nine runs used in Taguchi analysis.

Run no.	P_max	H_min	CS
1	0.69088	0.15826	3.29752
2	0.66579	0.29579	2.99805
3	1.17909	0.19953	4.19292
4	0.62048	0.28692	3.14793
5	0.64802	0.34191	3.00646
6	0.6839	0.15321	3.3018
7	0.61391	0.28599	3.1446
8	0.70415	0.15187	3.35332
9	0.66519	0.26614	3.03415

In order to perform the Taguchi analysis, it is required to normalize the results of the nine runs, as shown in Table 3. The normalization of the results ensures a maximum value of one for each parameter range. This is an essential analysis step to have the weighted sum model for each run, which is given by Fishburn [49].

Table 3. Normalized values of the P_max, H_min, critical speed, and their WSM.

Run no.	P_max (−)	H_min (−)	CS (−)	WSM
1	0.888591	0.46287	0.78645	0.650195
2	0.922078	0.865111	0.715027	0.841831
3	0.520664	0.583575	1	0.671953
4	0.989411	0.839168	0.750773	0.854630
5	0.947363	1	0.717033	0.916099
6	0.89766	0.4481	0.78747	0.645333
7	1	0.836448	0.749979	0.855719
8	0.871845	0.444181	0.799758	0.639991
9	0.922909	0.778392	0.723637	0.800832

()

where w_j: weight of the factor; a_ij: magnitude of the factor.

The relative value of w_j for each factor has an effect on the overall bearing performance, which has to be chosen in accordance with its importance. The value of minimum film thickness under any circumstances is the most important issue in the safe operation of the rotor-bearing system, giving a 50% relative weight. Each of the other two characteristics (P_max and CS) is given a relative weight of 25%. The choice of these relative weight values is performed based on a long experience (more than 15 years) in the field of roto-bearing performance enhancement.

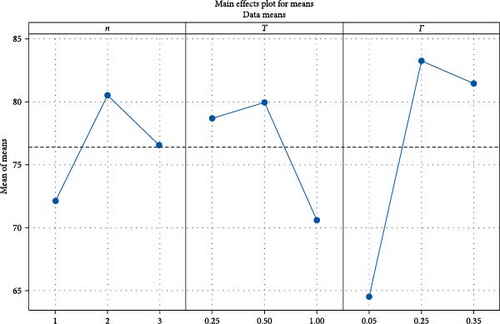
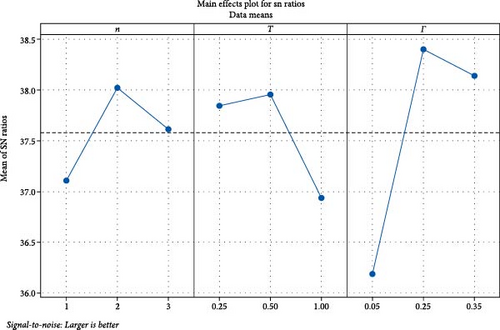
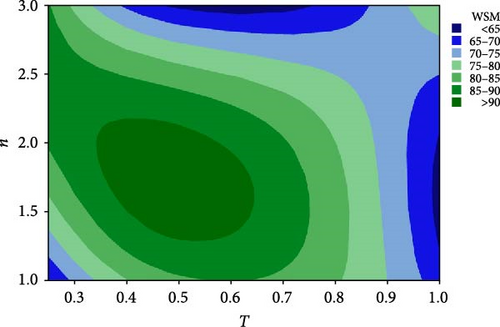
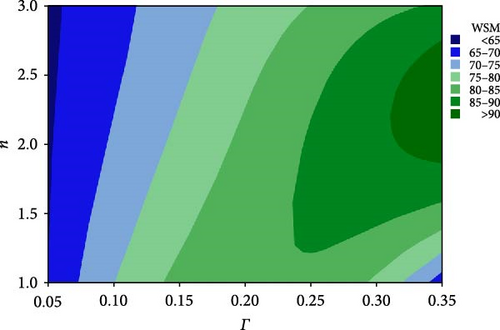
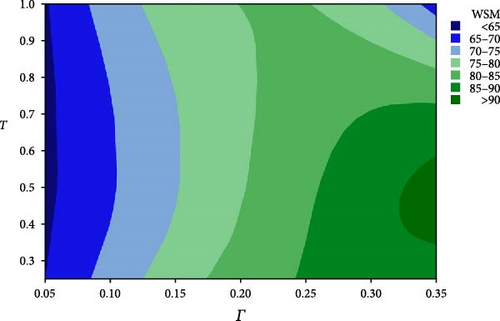
Table 4 shows the values of the designed parameters for the Taguchi orthogonal array and the WSM values for the whole nine runes. The values shown in this table illustrate that the maximum WSM is 91.6099%, which corresponds to run number 5. The bearing design parameters for this run are n = 2 (parabolic profile), T = 0.5, and Γ = 0.35. On the other hand, the worst value of WSM is 63.9991, which corresponds to run number 8. The design parameters of this run are n = 3, T = 0.5, and Γ = 0.05. However, optimizing this whole orthogonal array using the Taguchi method results in the mean effect plots for means and signal-to-noise ratio that are shown in Figures 7 and 8, respectively. The results in these two figures illustrate that the optimal design combination is within the selected ranges of the variables but is out of the selected runs. The optimal values are n = 2, T = 0.5, and Γ = 0.25, where the only difference takes place in φ value. More details about the optimal combination of the design parameters are shown in Figures 9, 10, and 11. These figures show the contour plots of WSM versus (n, T), WSM versus (n, Γ), and WSM versus (T, Γ). It can be seen in these figures that different design combinations affect the WSM values.

Table 4. Modification factors and corresponding orthogonal array.

No. of run	Data of the Taguchi analysis (L/D = 1.5)
	Parameters			WSM (%)
	n	T	Γ	WSM (%)
1	1 (1)	1 (0.25)	1 (0.05)	65.0195
2	1 (1)	2 (0.5)	2 (0.25)	84.1831
3	1 (1)	3 (1.0)	3 (0.35)	67.1953
4	2 (2)	1 (0.25)	2 (0.25)	85.4630
5	2 (2)	2 (0.5)	3 (0.35)	91.6099
6	2 (2)	3 (1.0)	1 (0.05)	64.5333
7	3 (3)	1 (0.25)	3 (0.35)	85.5719
8	3 (3)	2 (0.5)	1 (0.05)	63.9991
9	3 (3)	3 (1.0)	2 (0.25)	80.0832

The optimal combination of the design parameters (n = 2, T = 0.5, and Γ = 0.25) is used to investigate its effect on the considered bearing characteristics in the current work. Table 5 shows the results of the optimized design of the bearing profile. It can be seen that adopting such a profile results in a significant enhancement in the bearing performance in terms of P_max, H_min, and CS. The maximum pressure was reduced by 17.1%, and H_min was increased by 175.0% in comparison with the corresponding values under the 3D misalignment operating conditions. The critical speed is reduced in comparison with the misalignment case, but it is still above the designed value of the ideal case by 23.4%, which represents an improvement in the dynamic characteristic as well. It can be concluded that using the optimal design parameters enhances the general bearing performance under severe levels of 3D misalignment that causes a sharp drop in the levels of the film thickness.

Table 5. Results of the optimized bearing profile: n = 2, T = 0.5, Γ = 0.25.

Parameters	Aligned	Misaligned	Modified	% Change
P_max	0.486397	0.766778	0.635914	−17.07
H_min	0.5	0.108381	0.298093	+175.04
CS	2.452341	3.570661	3.026695	+23.42

Note. The change in the critical speed is calculated compared to the aligned case.

Figures 12 and 13 show the impact of the suggested design on P_max and H_min, respectively, compared with the aligned and misaligned results. It is clear that the 3D deviation results in pressure spikes associated with the reduction of the lubricant thickness at the bush edges in comparison with the uniform distribution (for pressure and film thickness) in the ideal aligned situation. Using the optimized bearing geometry reduces the pressure spike values, elevates the lubricant thickness at the most negative effect area of the misalignment, and reduces the distribution asymmetricity.

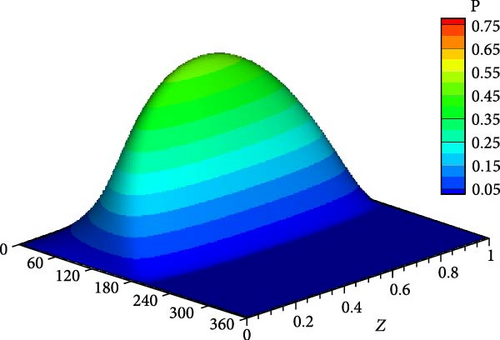
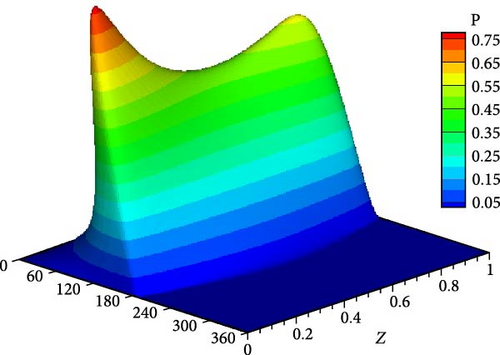
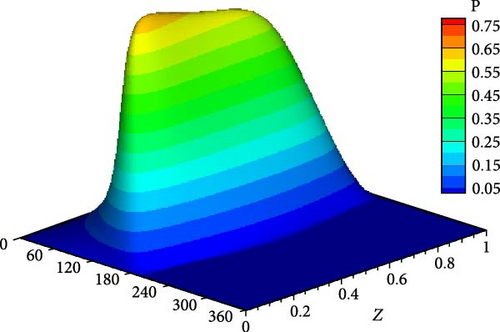
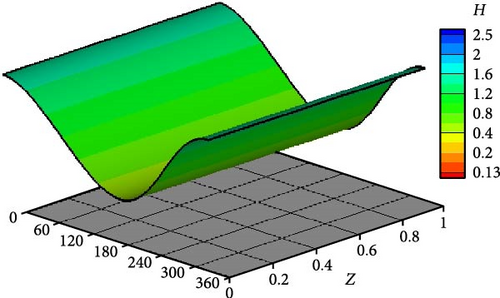
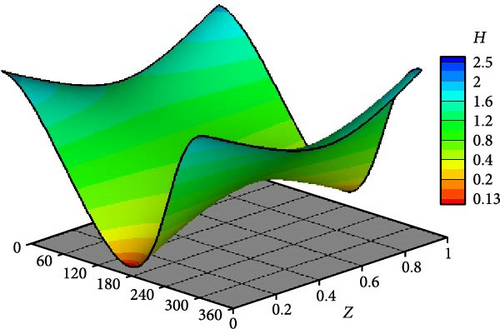
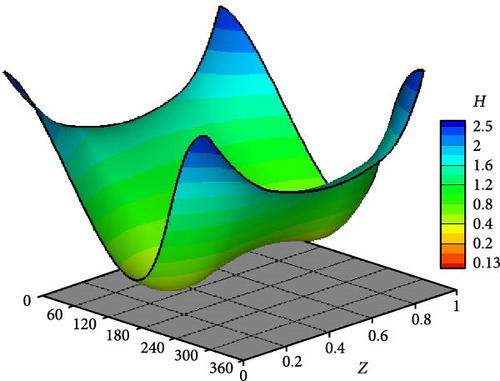
The optimal design is further investigated under the effect of impact load to examine its consequences on the journal trajectory. Figure 14 shows the trajectories at a speed about half the ideal case critical speed when n = 1, 2, and 3. It can be seen that all the trajectories operate in stable conditions without growing up amplitudes. However, when n = 1 (linear profile), the trajectory is relatively far from the corresponding ideal case trajectory. Figure 15 shows the trajectory of the journal center for the ideal case at a speed equal to the critical speed. The journal continues to run over a constant path and never returns to the equilibrium location. Figure 16 compares the trajectories for three profiles with the ideal case shown in Figure 15, i.e., at the aligned case’s critical speed. All shaft trajectories of the variable shape bearings return to equilibrium positions after periods of time. However, the trajectories are not very clear in this figure as the lines are very close to each other; therefore, the results are presented in terms of the variation of eccentricity ratio with time, as shown in Figure 16. The eccentricity ratio curve of the classical design (shown in black) continues to oscillate with time. On the other hand, the eccentricity ratio for all modified cases returns to the steady state positions. The case of n = 1 gives the highest eccentricity ratio, meaning the lowest value of the minimum film thickness. The cases of n = 2 and 3 give very close behaviors to each other. Figure 17 shows the variation of eccentricity ratio with time under impact load at a rotational speed equal to CS of classical design. The result presented in the previous figures emphasizes the effectiveness of the modification even under dynamic load in addition to the previously mentioned advantages in terms of P_max, H_min, and CS.

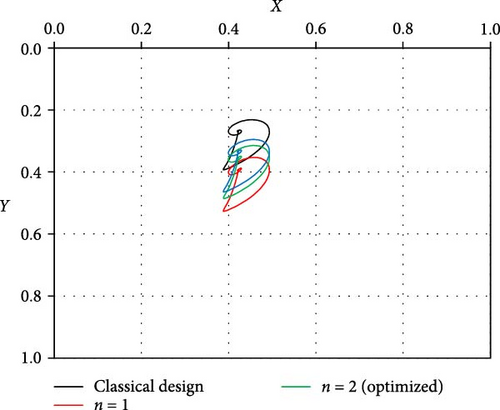
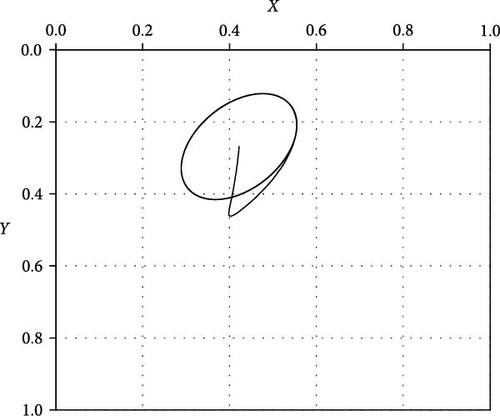
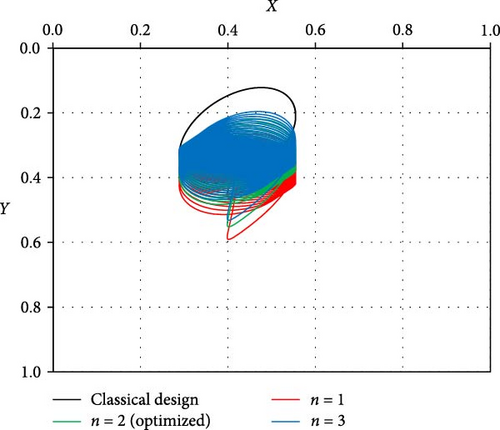
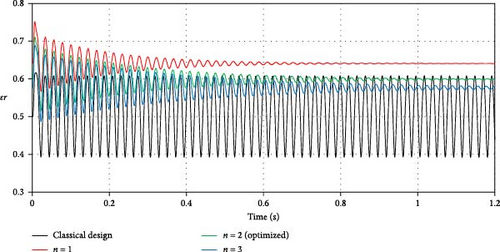
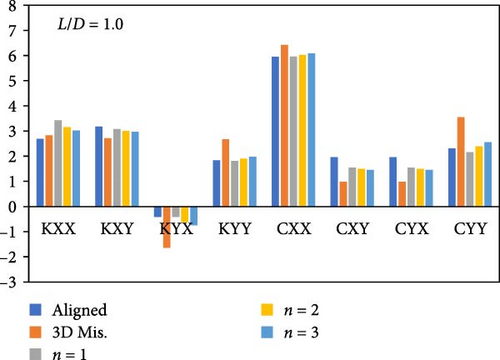
Figure 18 illustrates the effect of the form of modification on the stiffness and damping coefficients. Figure 18(a) shows the results when L/D = 1.0, while Figures 18(b) and 18(c) illustrate the corresponding results when L/D = 1.5 and 2.0, respectively. These figures compare the eight dynamic coefficients for the modified bearing profile (n = 1, 2, and 3) with the corresponding ideal (aligned) and misaligned cases. The misalignment level, as well as the load, are the same in the three cases to study the modification effect precisely. It can be seen that the bearing modifications in the three cases change the coefficient values to become closer to the corresponding values of the aligned case.

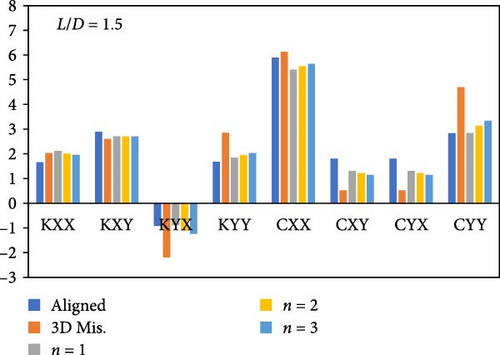
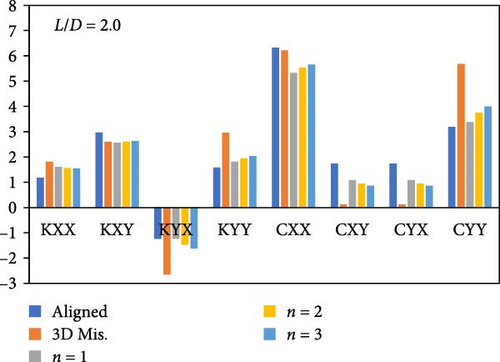
The originality of the results presented in this work is mainly related to the study of the effect of bearing geometry modification using three different profiles and its consequences on the dynamic response of the rotor-bearing system of the modified bearing under impact load.

6. Conclusions

The current study presents a novel optimization solution for bearing design using the Taguchi method under 3D deviation effects. The solution is performed using the finite difference method for a finite-length journal bearing. Three forms of the bearing profile are used, with three levels for each form. The outcomes of the Taguchi solution show that an optimal combination of using a second-order profile with Γ = 0.25 and T = 0.5 results in the best results in terms of the critical speed of the rotor bearing system, minimum film thickness, and maximum pressure values. This design combination is examined under the effect of an impact excitation where the motion equations are solved based on the method of Range-Kutta. The dynamic response shows that the optimized design is stable over a wider range of speeds, which means a further important advantage of the optimized design is obtained in addition to the reduction in H_min and P_max. It can be concluded that using the Taguchi method in optimizing the bearing profile represents a powerful tool in order to identify the optimal profile parameters. These obtained parameters improve the bearing performance in terms of the film thickness, pressure distribution, and critical speed of the system. The solution method presented in this study can be extended in a future work to examine the effect of using different forms of surface texture of the bearing on the system performance under impact as well as unbalanced loads.

Conflicts of Interest

The authors declare no conflicts of interest.

Authors’ Contributions

Hazim U. Jamali and M. N. Mohammed are the co-authors.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Jeon W.-J. and Hong S.-H., A new type of misaligned journal bearing with flexible structure, Lubricants. (2023) 11, no. 6, https://doi.org/10.3390/lubricants11060256, 256.
10.3390/lubricants11060256
Google Scholar
2 Das S., Guha S. K., and Chattopadhyay A. K., On the steady-state performance of misaligned hydrodynamic journal bearings lubricated with micropolar fluids, Tribology International. (2002) 35, no. 4, 201–210, https://doi.org/10.1016/S0301-679X(01)00065-2, 2-s2.0-0036540088.
10.1016/S0301-679X(01)00065-2
Web of Science® Google Scholar
3 Zhang Z. S., Dai X. D., and Xie Y. B., Thermoelastohydrodynamic behavior of misaligned plain journal bearings, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. (2013) 227, no. 11, 2582–2599, https://doi.org/10.1177/0954406213475948, 2-s2.0-84887579945.
10.1177/0954406213475948
Google Scholar
4 Zheng L., Zhu H., Zhu J., and Deng Y., Effects of oil film thickness and viscosity on the performance of misaligned journal bearings with couple stress lubricants, Tribology International. (2020) 146, https://doi.org/10.1016/j.triboint.2020.106229, 106229.
10.1016/j.triboint.2020.106229
Google Scholar
5 Murawski L., Shaft line whirling vibrations: effects of numerical assumptions on analysis results, Marine Technology and SNAME News. (2005) 42, no. 2, 53–60, https://doi.org/10.5957/mt1.2005.42.2.53.
10.5957/mt1.2005.42.2.53
Google Scholar
6 Lv F., Ta N., and Rao Z., Analysis of equivalent supporting point location and carrying capacity of misaligned journal bearing, Tribology International. (2017) 116, 26–38, https://doi.org/10.1016/j.triboint.2017.06.034, 2-s2.0-85021740520.
10.1016/j.triboint.2017.06.034
Google Scholar
7 Jang J. Y. and Khonsari M. M., On the characteristics of misaligned journal bearing, Lubricants. (2015) 3, no. 1, 27–53, https://doi.org/10.3390/lubricants3010027, 2-s2.0-85044744829.
10.3390/lubricants3010027
Google Scholar
8 Pigott R. J. S., Bearings and lubricant-bearing troubles traceable to design can be avoided by engineering study, Mechanical Engineering. (1942) 64, 259–269.
Google Scholar
9 Sun J. and Changlin G., Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation, Tribology International. (2004) 37, no. 10, 841–848, https://doi.org/10.1016/j.triboint.2004.05.007, 2-s2.0-3843083899.
10.1016/j.triboint.2004.05.007
Web of Science® Google Scholar
10 Sun J., Gui C., and Li Z., An experimental study of journal bearing lubrication effected by journal bearing misalignment as a result of shaft deformation under load, Journal of Tribology. (2005) 127, no. 4, 813–819, https://doi.org/10.1115/1.2033007, 2-s2.0-27544465290.
10.1115/1.2033007
Google Scholar
11 Etsion I. and Gommed K., Improved design with noncylindrical profiles of gas-lubricated ringless pistons, Journal of Tribology. (1995) 117, no. 1, 143–147, https://doi.org/10.1115/1.2830590, 2-s2.0-0029104780.
10.1115/1.2830590
Google Scholar
12 Nikolakopoulos P. G. and Papadopoulos C. A., A study of friction in worn misaligned journal bearing under severe hydrodynamic lubrication, Tribology International. (2008) 41, no. 6, 461–472, https://doi.org/10.1016/j.triboint.2007.10.005, 2-s2.0-39749195610.
10.1016/j.triboint.2007.10.005
CAS Web of Science® Google Scholar
13 Shenoy S. B. and Pai R., Theoretical investigations on the performance of an externally adjustable fluid-film bearing including misalignment and turbulence effects, Tribology International. (2009) 42, no. 7, 1088–1100, https://doi.org/10.1016/j.triboint.2009.03.008, 2-s2.0-67349155908.
10.1016/j.triboint.2009.03.008
CAS Web of Science® Google Scholar
14 Ram N. and Sharma S. C., Influence of wear on the performance of hole-entry hybrid misaligned journal bearing in turbulent regime, Industrial Lubrication and Tribology. (2014) 66, no. 4, 509–519, https://doi.org/10.1108/ILT-12-2011-0113, 2-s2.0-84902772970.
10.1108/ILT-12-2011-0113
Google Scholar
15 Ram N. and Sharma S. C., A study of misaligned hole-entry worn journal bearing operating in turbulent regime, Industrial Lubrication and Tribology. (2013) 65, no. 2, 108–118, https://doi.org/10.1108/00368791311303474, 2-s2.0-84874709108.
10.1108/00368791311303474
Google Scholar
16 Rao T. V., Stability characteristics of misaligned journal bearing, Advanced in Vibration Engineering. (2012) 11, 362–369.
Google Scholar
17 Sun J., Gui C., Li Z., and Li Z., Influence of journal misalignment caused by shaft deformation under rotational load on performance of journal bearing, Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology. (2005) 219, no. 4, 275–283, https://doi.org/10.1243/135065005X33937, 2-s2.0-27344456814.
10.1243/135065005X33937
Google Scholar
18 Jamali H. U., Aljibori H. S. S., Al-Tamimi A. N. J., Abdullah O. I., Senatore A., and Mohammed M. N., A new geometrical design to overcome the asymmetric pressure problem and the resulting response of rotor-bearing system to unbalance excitation, Axioms, 2023, 12, no. 9, 812.
Google Scholar
19 Nacy S. M., Effect of chamfering on side-leakage flow rate of journal bearings, Wear. (1997) 212, no. 1, 95–102, https://doi.org/10.1016/S0043-1648(97)00122-1, 2-s2.0-0031260767.
10.1016/S0043-1648(97)00122-1
CAS Google Scholar
20 Bouyer J. and Fillon M., Improvement of the THD performance of a misaligned plain journal bearing, Journal of Tribology. (2003) 125, no. 2, 334–342, https://doi.org/10.1115/1.1510883, 2-s2.0-0037387428.
10.1115/1.1510883
Google Scholar
21 Strzelecki S., Operating characteristics of heavy loaded cylindrical journal bearing with variable axial profile, Materials Research. (2005) 8, no. 4, 481–486, https://doi.org/10.1590/S1516-14392005000400021, 2-s2.0-33644505161.
10.1590/S1516-14392005000400021
Google Scholar
22 Chasalevris A. and Dohnal F., A journal bearing with variable geometry for the suppression of vibrations in rotating shafts: simulation, design, construction and experiment, Mechanical Systems and Signal Processing. (2015) 52-53, 506–528, https://doi.org/10.1016/j.ymssp.2014.07.002, 2-s2.0-84923016332.
10.1016/j.ymssp.2014.07.002
Google Scholar
23 Chasalevris A. and Dohnal F., Enhancing stability of industrial turbines using adjustable partial arc bearings, Journal of Physics: Conference Series. (2016) 744, https://doi.org/10.1088/1742-6596/744/1/012152, 2-s2.0-84994091877, 012152.
10.1088/1742-6596/744/1/012152
Google Scholar
24 Liu C., Zhao B., Li W., and Lu X., Effects of bushing profiles on the elastohydrodynamic lubrication performance of the journal bearing under steady operating conditions, Mechanics & Industry. (2019) 20, no. 2, https://doi.org/10.1051/meca/2019010, 207.
10.1051/meca/2019010
Google Scholar
25 Hamzah A. A., Abbas A. F., Mohammed M. N., Aljibori H. S. S., Jamali H. U., and Abdullah O. I., An evaluation of the design parameters of a variable bearing profile considering journal perturbation in rotor-bearing systems, Designs, 2023, 7, no. 5, 116.
Google Scholar
26 Majumdar B. C. and Brewe D. E., Stability of a rigid rotor supported on oil-film journal bearings under dynamic load, 1987.
Google Scholar
27 Pai R. and Majumdar B. C., Stability of submerged four-lobe oil journal bearings under dynamic load, Wear. (1992) 154, no. 1, 95–108, https://doi.org/10.1016/0043-1648(92)90245-4, 2-s2.0-0026853335.
10.1016/0043-1648(92)90245-4
CAS Web of Science® Google Scholar
28 Qiu Z. L. and Tieu A. K., Misalignment effect on the static and dynamic characteristics of hydrodynamic journal bearings, Journal of Tribology. (1995) 117, no. 4, 717–723, https://doi.org/10.1115/1.2831542, 2-s2.0-0013222666.
10.1115/1.2831542
Google Scholar
29 Tieu A. K. and Qiu Z. L., Stability of finite journal bearings—from linear and nonlinear bearing forces, Tribology Transactions. (1995) 38, no. 3, 627–635, https://doi.org/10.1080/10402009508983452, 2-s2.0-0029328840.
10.1080/10402009508983452
CAS Web of Science® Google Scholar
30 Papadopoulos C. A., Nikolakopoulos P. G., and Gounaris G. D., Identification of clearances and stability analysis for a rotor-journal bearing system, Mechanism and Machine Theory. (2008) 43, no. 4, 411–426, https://doi.org/10.1016/j.mechmachtheory.2007.04.007, 2-s2.0-39749112644.
10.1016/j.mechmachtheory.2007.04.007
Google Scholar
31 Boukhelef D., Bounif A., and Amar Bouzid D., Dynamic characterization and stability analysis of hydrodynamic journal bearing using the FEM, Mechanika. (2011) 17, no. 5, 503–509, https://doi.org/10.5755/j01.mech.17.5.727, 2-s2.0-80855164642.
10.5755/j01.mech.17.5.727
Google Scholar
32 Ganesha A., Joseph A., Pai R., Khader S. M. A., Kumar N., Kumar S., and Girish H., Performance optimization of a multi-groove water lubricated journal bearing with partial slip by Taguchi analysis, Arabian Journal for Science and Engineering. (2024) 49, no. 2, 2249–2267, https://doi.org/10.1007/s13369-023-08191-z.
10.1007/s13369-023-08191-z
Google Scholar
33 Yücel E. and Saruhan H., Design optimization of rotor-bearing system considering critical speed using Taguchi method, Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering. (2017) 231, no. 2, 138–146, https://doi.org/10.1177/0954408915578581, 2-s2.0-85015246894.
10.1177/0954408915578581
PubMed Web of Science® Google Scholar
34 Chen C.-Y., Liu C.-S., Tee C.-K., and Li Y.-C., Application of stabilized term in free boundary problems for optimizing bi-directional-rotation herringbone-grooved journal bearings, Applied Mathematical Modelling. (2017) 47, 826–838, https://doi.org/10.1016/j.apm.2016.11.002, 2-s2.0-85020296726.
10.1016/j.apm.2016.11.002
Google Scholar
35 Sharma V., Singh R., and Chaudhary R., Experimental study of sliding wear behavior of the casted lead bronze journal bearing material, SAE Technical Paper 2019-01-0824, 2019, SAE International, Warrendale, PA, USA, https://doi.org/10.4271/2019-01-0824, 2-s2.0-85064590427.
10.4271/2019-01-0824
Google Scholar
36 Chen C.-Y., Liu C.-S., Li Y.-C., and Mou S., Geometry optimization for asymmetrical herringbone grooves of miniature hydrodynamic journal bearings by using Taguchi technique, Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology. (2015) 229, no. 2, 196–206, https://doi.org/10.1177/1350650114548054, 2-s2.0-84921301550.
10.1177/1350650114548054
Google Scholar
37 Bhasker B., Seetharamaiah N., Babu P. R., and Gugulothu S. K., A novel assessment study on a dynamic analysis of hydrodynamic journal bearing performance: a Taguchi-fuzzy based approach optimization, Transportation Engineering. (2020) 2, https://doi.org/10.1016/j.treng.2020.100033, 100033.
10.1016/j.treng.2020.100033
Google Scholar
38 Chasalevris A. and Sfyris D., Evaluation of the finite journal bearing characteristics, using the exact analytical solution of the reynolds equation, Tribology International. (2013) 57, 216–234, https://doi.org/10.1016/j.triboint.2012.08.011, 2-s2.0-84866268263.
10.1016/j.triboint.2012.08.011
Web of Science® Google Scholar
39 Jamali H. U. and Al-Hamood A., A new method for the analysis of misaligned journal bearing, Tribology in Industry. (2018) 40, no. 2, 213–224, https://doi.org/10.24874/ti.
10.24874/ti.2018.40.02.05
Google Scholar
40 Hamrock B. J., Fundamentals of Fluid Film Lubrication, 1991, McGraw-Hill: Inc, New York.
Google Scholar
41 Harnoy A., Bearing Design in Machinery: Engineering Tribology and Lubrication, 2002, 1st edition, Marcel Dekker Inc, New York – Basel.
10.1201/9780203909072
Google Scholar
42 Feng H., Jiang S., and Ji A., Investigation of the static and dynamic characteristics of water-lubricated hydrodynamic journal bearing considering turbulent, thermo-hydrodynamic and misaligned effects, Tribology International. (2019) 130, 245–260, https://doi.org/10.1016/j.triboint.2018.09.007, 2-s2.0-85054193047.
10.1016/j.triboint.2018.09.007
Web of Science® Google Scholar
43 Lund J. W. and Thomsen K. K., A calculation method and data for the dynamic coefficients of oil-lubricated journal bearings, Topics in Fluid Film Bearing and Rotor Bearing System Design and Optimization, 1978, New York, ASME.
Google Scholar
44 Someya T., Journal Bearing Databook, 1989, Springer-Verlag, Berlin Heidelberg.
10.1007/978-3-642-52509-4
Google Scholar
45 Shi Y., Li M., and Li M., Study on nonlinear dynamics of the marine rotor-bearing system under yawing motion, Journal of Physics: Conference Series. (2020) 1676, no. 1, https://doi.org/10.1088/1742-6596/1676/1/012156, 012156.
10.1088/1742-6596/1676/1/012156
Google Scholar
46 Nicholas J. C., Hydrodynamic Journal Bearings—Types, Characteristics and Applications, 1996, Rotating Machinery Technology, Inc.
Google Scholar
47 Ruggiero A., D’Amato R., Magliano E., and Kozak D., Dynamical simulations of a flexible rotor in cylindrical uncavitated and cavitated lubricated journal bearings, Lubricants, 2018, 6, no. 2.
Google Scholar
48 D’Amato R., Amato G., Wang C., and Ruggiero A., A novel tracking control strategy with adaptive noise cancellation for flexible rotor trajectories in lubricated bearings, IEEE/ASME Transactions on Mechatronics. (2021) 27, no. 2, 753–765.
10.1109/TMECH.2021.3070890
Google Scholar
49 Fishburn P. C., Letter to the editor—additive utilities with incomplete product sets: application to priorities and assignments, Operations Research. (1967) 15, no. 3, 537–542, https://doi.org/10.1287/opre.15.3.537.
10.1287/opre.15.3.537
Web of Science® Google Scholar

All articles

On the Use of Taguchi Method in the Analysis of the Dynamic Response of Variable Bearing Design under Impact Load

Abstract

1. Introduction

2. Governing Equations

3. Dynamic Solution

4. Deviation Representation

5. Baring Modification

5.1. Numerical Solution

5.2. Results and Discussions

6. Conclusions

Conflicts of Interest

Authors’ Contributions

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On the Use of Taguchi Method in the Analysis of the Dynamic Response of Variable Bearing Design under Impact Load

Abstract

1. Introduction

2. Governing Equations

3. Dynamic Solution

4. Deviation Representation

5. Baring Modification

5.1. Numerical Solution

5.2. Results and Discussions

6. Conclusions

Conflicts of Interest

Authors’ Contributions

Open Research

Data Availability

References

Figures

References

Related

Information