This study explores the challenge of tracking control for spacecraft formation flying (SFF) in the presence of dynamic uncertainties and external perturbations. Firstly, sliding mode control combined with backstepping control is used to address saturation issues. Then, neural networks, minimal parameter learning, and adaptive control are integrated to handle dynamic uncertainties and actuator failures. To alleviate the communication load, an event-triggered mechanism is ultimately implemented, which leads to the development of an adaptive sliding mode fault-tolerant control algorithm based on an event-triggered neural network. This control architecture achieves significant advancements over traditional techniques: (1) ensuring system robustness and adaptability in complex scenarios with uncertain system dynamics and external disturbances, effectively counteracting actuator failures and input saturation issues; (2) significantly reducing transmission and computational burdens in resource-limited networked systems through the adoption of event-triggered control (ETC) mechanisms; (3) achieving high-precision tracking performance for SFF without relying on prior knowledge of the system’s inherent dynamics, environmental disturbances, or potential actuator deficiencies. The Lyapunov approach is utilized to confirm the closed-loop system’s boundedness. Finally, the proposed method’s efficacy is confirmed via simulations with a two-satellite formation.

1. Introduction

Spacecraft formation flying (SFF) has garnered significant attention because it offers substantial design cost benefits, increased reliability, and greater flexibility compared to traditional single spacecraft configurations [1]. Innovative formation missions, such as TanDEM-X/TerraSAR-X and PRISMA, have demonstrated their capability in executing a range of tasks, including surveillance, terrain mapping, and high-resolution imaging [2]. The control of formation configurations in operational SFF systems confronts complex challenges, such as task transition management, avoidance of configuration divergence, and space disturbance-induced perturbations like atmospheric drag and solar-lunar gravitational forces [3]. Consequently, formation control has become a pivotal area of aerospace research [3–7].

Addressing the inherent system uncertainties, such as satellite state changes and external disturbances, is crucial for maintaining efficient formation flight. Various control strategies, including robust [8, 9], adaptive [10, 11], sliding mode [12, 13], and optimal control [14, 15], have been developed to navigate these challenges. Notably, sliding mode control (SMC) has been extensively utilized due to its robustness against model uncertainties [10, 12, 13]. Despite SMC’s advantages, limitations such as its slow convergence rate and dependency on accurate disturbance information have spurred research into the integration of intelligent control technologies, including neural networks [16, 17], expert systems [18, 19], and fuzzy logic [20, 21]. This integration has delivered novel solutions to surmount these limitations and significantly enhance control system performance. Recent advancements involve leveraging neural networks to address uncertainties within spacecraft systems [22, 23], with Chebyshev neural networks demonstrating rapid and precise management of uncertainties, actuator faults, and external disturbances in spacecraft attitude control [24, 25]. Addressing the intricate issues posed by space disturbances and thruster malfunctions, a neural network-based control strategy utilizing a prescribed performance function and a novel learning-based approach using a nonsingular terminal SMC law have been developed, ensuring errors in positional tracking remain within predetermined performance bounds [26]. For spacecraft performing autonomous maneuvers [27], RBFNNs have been instrumental in adaptively counteracting model uncertainties. Moreover, Chebyshev neural networks have been employed to manage actuator saturation effectively, enhancing practical system performance [24]. Despite these advances in addressing disturbances, uncertainties, and system performance [25–27], the computational constraints of spacecraft have not been fully accounted for. High computational loads and slow convergence rates may fall short of real mission demands. Therefore, optimization of the neural network models becomes paramount. Research has led to matrix two-norm optimization for weight parameter reduction and enhanced convergence speeds [28], as well as a formula for real-time computation of time-varying matrix square roots, increasing computational efficiency [16]. Specifically, the fast time-varying neural network (FTZNN) manifests superior convergence rates over traditional ZNN models, offering distinct advantages for time-varying matrix square root challenges. Furthermore, fixed-structure RBFNN models have shown promising results for online learning, presenting a robust alternative to adaptive models that rely on instant parameter adjustments [29].

Input saturation in formation flight control, a consequence of the physical constraints on actuator power and response, can result in peak output and energy spikes, severely impacting the reliability of small satellites in particular and increasing the risk of failure [30, 31]. Adaptive control methods informed by neural network approximations have been developed to address attitude control issues arising from input saturation [32]. To improve tracking performance, a dead-zone operator-based model and adaptive techniques have been employed to overcome the challenges posed by the nondifferentiable nature of the saturation model [33]. To guarantee system stability, input saturation has been treated as a disturbance [34]. Extensive research has also been conducted on auxiliary design systems [12, 35–37], with works addressing actuator saturation through non-SMC, antisaturation compensators, and supplementary systems [12]. The backstepping technique has gained attention for its versatile approach to input saturation concerns [38], utilizing the principles of Lyapunov stability to simplify control design [39, 40]. Satellites enduring extended space conditions encounter challenges like space radiation and micrometeoroid strikes, leading to substantial actuator degradation. Developing fault-tolerant control methodologies has thus become a pressing priority to prevent instabilities in spacecraft formations. Actuator anomalies, namely, loss of effectiveness (LOE) and bias faults, have become focal points in formation preservation efforts [41–43]. However, the control solutions offered in [41, 42] depend on detailed knowledge of satellite relative motion models, with an assumed lower threshold for LOE faults as posited in [43]. A new study on fuzzy fault-tolerant control for nontriangular structure nonlinear systems, which bypasses these constraints, was initiated in [44]. Despite previous methodologies adeptly addressing actuator flaws and limitations, they have not adequately tackled the reduction of mechanical wear on actuators, a crucial factor in minimizing failure rates. The event-triggered control (ETC) paradigm offers a conservative actuator operation strategy, activating control only when specific conditions are met [45–48]. ETC has not only optimized actuator efficiency by reducing operational frequency but has also played a key role in stabilizing spacecraft formations [49, 50], reorganizing unmanned aerial vehicle formations [51], and directing maritime surface vessel trajectory control [52].

Inspired by these successes, this study introduces an innovative event-triggered fault-tolerant control approach designed for SFF to tackle dynamic uncertainties, external perturbations, actuator deficiencies, and input saturations using a nonlinear leader-follower dynamic model. It integrates backstepping control, a minimal learning algorithm, and a sliding mode strategy enhanced by neural networks to improve system resilience. Additionally, the ETC framework reduces the communication burden. The main contributions of this article are as follows:

1.
Compared to [41–43], our approach addresses several common issues encountered in actual on-orbit operations, including model uncertainties, external disturbances, actuator malfunctions, input saturation, and restricted Moreover, our method achieves stable tracking performance without relying on prior knowledge of the SFF system dynamics, external disturbances, or actuator failures, demonstrating enhanced adaptability. Additionally, the handling of saturation effects reduces chattering compared to traditional saturation functions.
2.
Unlike [25–27], this study integrates neural networks with a minimal parameter learning algorithm to offer an efficient and practical control solution for SFF configuration. This approach significantly reduces the number of online learning parameters. Additionally, it effectively manages uncertainties without relying on common uncertainty-related assumptions, enhancing overall robustness and performance.
3.
Compared to time-triggered methods [49, 50, 53], this study is the first to propose an event-triggered mechanism-based adaptive neural network backstepping sliding mode fault-tolerant control method for the SFF system. This approach reduces the frequency of control command transmissions and the number of actuator engagements, effectively extending the system’s lifespan. This method significantly optimizes the performance of resource-limited networked systems and provides a robust solution for future SFF missions.

The structure of the paper is as follows: Section 2 introduces the problem formulation and background knowledge. Section 3 covers the controller design and stability analysis. Section 4 demonstrates simulation outcomes to verify the effectiveness of the proposed approach. Lastly, Section 5 wraps up the paper.

2. Preliminary and System Description

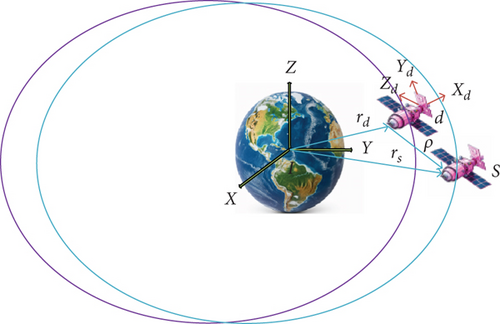
Consider the two spacecrafts depicted in Figure 1, undertaking orbiting flights around the Earth. The tracking spacecraft s and target spacecraft d (passive) are analyzed using two coordinate systems: Earth-centered inertial (ECI) and local vertical local horizontal (LVLH). In the LVLH frame, centered at the target spacecraft, the X_d axis points radially towards the tracking spacecraft, the Z_d axis is perpendicular to the orbital plane along the angular momentum direction, and the Y_d axis is orthogonal to both X_d and Z_d, forming a right-handed Cartesian system.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Diagram of spacecraft relative motion.

The relative kinematics of the spacecraft in the ECI frame are described by a set of differential equations that account for external disturbances

(1)

where r_s denotes the position vector of the tracking spacecraft and r_d denotes that of the target spacecraft. r_s = ‖r_s‖, r_d = ‖r_d‖, μ = 398600 km³/s². Δd represent external disturbances, and u represents the control torque.

To ascertain the relative positioning of the tracking to the target spacecraft, their relative position vector is quantified by the formula

(2)

By substituting Equation (2) into Equation (1), the relative motion dynamics of the spacecraft within the earth’s inertial frame are obtained.

(3)

Taking into account the angular velocity w of the orbital coordinate system relative to the ECI frame, the relative acceleration

can be expressed as follows:

(4)

where ρ = [x y z]^T. The pursuing star and the target spacecraft can be represented in the orbital coordinate system as

(5)

where r_d = a(1 − e²)/(1 + ecosv) and v is a true anomaly.

From Equations (1)–(5), the differential equations can be described as follows

(6)

In the space environment, model uncertainties are also significant and cannot be ignored. To address this challenge, by applying transformation techniques, Equation (6) can be rewritten as follows:

(7)

where

is the sum of model uncertainties.

A set of state variables is defined as X₁ = [x y z]^T and

, through which the relative motion dynamics as per Equation (7) can be reformulated as follows:

(8)

where

, m_s denote the spacecraft’s mass, d = Δd/m_s + Δd_c, u_i is the control torque and is subject to actuator faults.

(9)

where ϱ denotes an LOS fault and ϱ = diag(λ₁, λ₂, λ₃), λ_i > 0, i = 1, 2, 3, while σ refers to constant bias faults. The term sat(u) characterizes the actual control input and can be articulated as follows

(10)

where u_i,max is the maximum control torque.

Substituting Equation (8) into Equation (9) yields

(11)

where g = ϱ/m_s,

, and τ = sat(u).

Remark 1. An LOE fault, also known as a multiplicative fault, and a bias fault, referred to as an additive fault, are both considered. In this paper, ϱ_i = 1 and σ_i = 0 indicate that the SFF is free of faults; 0 < ϱ_i < 1 and σ_i = 0 signifies that the SFF is affected by an LOE fault in the actuator; and ϱ_i = 0 represents a total LOE of the SFF actuator. In this research, we are considering the scenario where ϱ_i ≠ 0. This would render the SFF uncontrollable.

Remark 2. The description of actuator faults in SFF systems, as depicted in Expression (9), draws from references [20, 41–43]. An LOE fault signifies uncertainties in the actuator gain under faulty conditions, while a bias fault accounts for errors in the control input channel. It is important to note that reference [42] focuses solely on the LOE fault ϱ_i, whereas reference [43] addresses bias faults exclusively. Meanwhile, reference [44] examines two fault types—an underlying fault and an LOE fault—yet assumes prior knowledge of the fault ϱ_i. In contrast, in this study, both ϱ_i and σ_i are not predetermined in the control design, enhancing the comprehensiveness and generality of our approach.

In practical scenarios, due to constraints in spacecraft actuator capabilities, prescribed control input commands are subject to saturation limitations.

For the ease of discussing control methodologies for SFF, some assumptions and lemmas are considered.

Assumption 1. The model parameter m_s is unknown.

Assumption 2. The disturbances d_i and bias faults σ_i are constrained by and.

Assumption 3. The reference signals x_d, y_d and z_d as well as and are bounded.

Lemma 1 (see [54].)Consider a dynamic system described by , where and are constants greater than zero and is a function that remains nonnegative. For any t ≥ 0, given that the initial value is both bounded and nonnegative, it follows that will also be nonnegative.

Lemma 2 (see [55].)States that for scalars ς ∈ ℝ and ∅∈ℝ, the inequality ς∅≤(|ς|ⁿνⁿ)/n + (|∅|^m)/mνⁿ holds, where ∅>1 are constants satisfying (n − 1)(m − 1) = 1.

Lemma 3 (see [56].)

, that is

(12)

Lemma 4 (see [57].)For a nonlinear function d(x): Rⁿ⟶R defined over a compact set Ω_x ∈ Rⁿ, there is an NN W^∗Th(x) such that for any given scalar η > 0

(13)

(14)

where

is the basis function vector, W^∗ = [w₁, ⋯, w_l] is the ideal weight, and l (with l > 1) is the selected number of nodes. h(X) are defined using Gaussian functions, described as follows:

(15)

where c_i = [c_i1, ⋯, c_il] and b_i denote the center and the width, respectively.

3. Controller Design and Stability Analysis

3.1. Controller Without ETC

In the subsection, backstepping control is used here, and first, we define

(16)

where λ₁, λ₂ are the state variables, e is the relative position tracking error and is selected as

(17)

Then, we have

; α₁ represents the virtual control and defined as

(18)

A Lyapunov function V₁ is devised as

(19)

Then, the derivative of V₁ is derived as

(20)

The auxiliary system of

are designed as

(21)

where c₁, c₂c₁, c₂ are positive adjustable definite matrices, ϱ is a full-rank, positive definite, symmetric matrix, and Δτ = u − τ is the saturation error.

By substituting Equation (21) into Equation (20), we obtain

(22)

The sliding surface can be described as

(23)

where k represents a positive definite adjustable matrix.

From Equation (16),

can be rewritten as

(24)

(25)

By differentiating Equation (23) and employing Equations (24) and (25), we obtain

(26)

Designing the control law is as follows:

(27)

where μ, η ∈ R⁺.

Theorem 1. For a nonlinear dynamic system with input saturation and dynamic uncertainties, the closed-loop system’s stability is ensured, and the tracking error asymptotically approaches zero when a sliding surface, as defined in Equation (26), is selected, and backstepping SMC is designed according to the specifications in Equation (27).

Proof 1. The Lyapunov function V₂ is defined as

(28)

Upon differentiating Equation (28) and utilizing Equations (21) and (24)–(27), we have

(29)

Upon differentiating Equation (28) and utilizing the relationships provided in Equations (21) and (24)–(27), we obtain the following result under Assumption 1. Provided that the disturbance bound satisfies the inequality , we can deduct from Equation (29) that is nonpositive, that is, . Therefore, this implies the stability of the closed-loop system as ensured by the backstepping SMC methodology.

Furthermore, due to the properties of ϱ, there exists an unknown constant φ > 0 such that

(30)

where ρ = ϱ/m_s.

The RBFNN is applied to approximate the dynamic uncertainties , with the output vector represented as

(31)

The minimum parameter learning approach of the neural network is employed for . Let , ϕ is a positive real number, denotes the online estimated value of ϕ, and the learning error is given by.

The control law is redesigned as

(32)

(33)

(34)

(35)

Theorem 2. In a nonlinear relative dynamics system characterized by input saturation, dynamical uncertainties, and actuator faults, as described in Equation (11), the stability of the closed-loop system can be achieved by selecting an appropriate sliding surface as expressed in Equation (22) and devising a controller in line with Equation (32). The complete dynamic uncertainties of the spacecraft are estimated via Equation (31), while the adaptation laws are established in accordance with Equations (33)–(35). Under this framework, the tracking errors are assured to asymptotically converge to zero.

Proof 2. We propose the subsequent Lyapunov function for the SFF tracking control architecture.

(36)

By differentiating Equation (36) and substituting Equations (23)–(25), we get

(37)

From Lemma 3, we can obtain

(38)

Substituting the adaptation laws (Equations (33)–(35)) into Equation (38) yields leads to

(39)

Using Lemma 2, we have

(40)

(41)

(42)

Substituting Equations (40)–(42) into Equation (39) yields

(43)

where ϒ = min(c_1i + k_i, μ, Γ₁, Γ₂, Γ₃) and Λ = (Γ₁/2)ϕ² + (Γ₂/2)φ² + (Γ₃/2)η² + 1/2.

Solving Equation (43), one obtains

(44)

Thus, V₃ is bounded and . This indicates that are also bounded as per Equation (29), meaning

(45)

For the convenience of subsequent calculations, we assume that Λ is a sufficiently large positive number.

Thus,

(46)

For Equation (18), since c₁ and c₂ are positive definite matrices, and λ₁, λ₂ are as follows:

(47)

From Equations (20), (35), and (36), we obtain

(48)

Considering the bounded nature of , it can readily be deduced that are also bounded. From this, one can infer the boundedness of the term u. Clearly, all signals of the closed-loop control system are bounded.

Remark 3. With the RBFNN approximator, substituting control law Equation (26) into Equation (27) results in Equation (48). However, with the adoption of the RBFNN approximator, the substitution of control law Equation (32) into Equation (24) results in Equation (50). A comparison between Equations (49) and (50) reveals that the uncertainty term of the system has been altered from to upon the employment of the RBFNN approximator. The RBFNN approximator contributes to the compensation of the dynamic uncertainties within the system. When approaches , the RBFNN approximator can reduce the control gain from to , thereby compensating for system uncertainties and reducing the chattering phenomenon.

(49)

(50)

3.2. Controller With ETC

To diminish the frequency of transmission and actuator execution, an event-triggered network control system is introduced, building upon the foundation of the previous section. The architecture of the system is uncomplicated, which simplifies the control scheme design.

In this subsection, building on the previous one, we incorporate a time-triggered mechanism and analyze the system’s stability, while also avoiding Zeno behavior. The design of the event-triggered mechanism is as follows

(51)

where

is the virtual control input.

is the measurement error, χ is the positive parameter, ℏ_i > 0, and 0 < χ < 1.

When the measurement error satisfies the condition , the controller will maintain its current input until transitions to the range , at which point the controller’s input will experience a step change.

Theorem 3. Given the dynamic Equation (11), the adaptive laws (33)–(35), and the event-driven control approach (51), the system exhibits asymptotic stability. Moreover, all signals in the system are guaranteed to be ultimately bounded and consistent, and Zeno behavior is effectively prevented.

Proof 3. From the ETC scheme Equation (51), we can obtain

where ξ₁ and ξ₂ are positive constants with the range [−1, 1].

Considering a Lyapunov equation and differentiating it can yield:

(52)

By substituting control input Equation (51) and the adaptive control law Equations (33)–(35) into the aforementioned expression, it comes to the result that

(53)

Similar to the above proof, the system remains bounded in the end.

The subsequent analysis will demonstrate the existence of a positive minimal time interval between any two successive triggering moments, thus ensuring that Zeno behavior is precluded within the system and .

In the definition of the event-triggering condition, the trigger heavily relies on the control input. A positive interval exists between any two successive instants when the control input changes continuously, given that , and the magnitude of stays within the bounds of ℏ. However, incorporates the discontinuous function sgn(s), leading to a noncontinuous control input, which in turn could result in continuous triggering of the sampling mechanism, precluding the assurance of a positive interval of time between triggers. Consequently, the initial step necessitates the eradication of the discontinuous elements from the control input function. This has been successfully accomplished by substituting the discontinuous function with a continuous counterpart and imposing certain restrictions as additional conditions.

Substitute sgn(s) into the continuous function Θ(s_i) = s_i/(|s_i| + δ), δ > 0 and the setΙ, defined.

as . It can be obtained that

(54)

And we can derive the derivative of as

(55)

The functions are continuous in a compact set Ω_x.

The derivative of Θ(s_i) is given as

(56)

It is clear that . Thus, Θ(s_i) is continuous. Then, is bounded within Ω_x and so is . is designed as

(57)

We can derive that T_k = t_k+1 − t_k ≥ ℏ_i/η from the properties of continuous . Therefore, we can infer the existence of an upper limit that fulfills the condition T = ℏ_i/η between each successive event-triggering moment.

Remark 4. The analysis has shown that the ETC strategy presented in this study successfully guarantees the asymptotic stability of the closed-loop system and substantially decreases the communication frequency between controllers and actuators, as well as decreasing the demand for transmission bandwidth. In the design of control systems, this strategy is particularly suitable for scenarios where there are constraints on resources and where a reduction in the frequency of control execution is necessary to maintain system stability. Through the carefully designed event-triggered mechanism, a more efficient control scheduling can be realized, thereby maximizing the effective utilization of resources.

4. Simulation Results

This section presents simulation results to validate the efficacy of the proposed control method. The initial orbital parameters of the two satellites are shown in Table 1.

Table 1. Initial orbital parameters.

Orbital parameters	Parameter value of satellite d	Parameter value of satellite s
Semi-major axis	7256.14 km	7256.14 km
Eccentricity	0.001	0.001
Orbital inclination	53°	53°
Argument of perigee	120°	120°
Right ascension of ascending node	30°	30°
Mean anomaly	5°	5.004°

The mass of satellite s is 60 kg, which is in the same orbit as satellite d, and the two satellites are in a back-and-forth orbit. To realize the forced circular flying-around of two satellites in the VVLH coordinate system, the flying-around parameters are shown in Table 2.

Table 2. Flying-around parameters.

Flying-around parameters	Value
Flying-around radius	40 m
Angle θ_x of flying-around surface	90°
Angle θ_z of flying-around surface	30°
Initial phase angle	0°
Flying-around period	180 s

During the simulation, the reference trajectory X = [x, y, z]^T is as follows:

(58)

The external disturbance

(59)

The settings for the LOE fault ϱ and the bias fault σ are as follows:

(60)

(61)

To showcase the effectiveness of our proposed control scheme under the combined effects of uncertain dynamics, external disturbances, input saturations, and actuator faults (SFF), we compared our ETC approach with a continuous control strategy. For the continuous control scenario, the control law is defined by Equation (30), with the adaptive laws specified in Equations (31)–(33). The design parameters and initial conditions used were consistent with those in our control law design, as shown in Table 3.

Table 3. Module parameters.

Index	Item	Value
Design parameters	m_s, m_d	60 kg, 60 kg
	c₁	Diag (0.4, 0.4, 0.4)
	c₂	Diag (0.35, 0.35, 0.35)
	μ	Diag (1,1,0,77)
	c_i	(0.2, 0.9, 0.25, 0.245, 0.2, 0.8)
	b_i	8
	k	Diag (1.2, 1.2, 1.2)
	χ	0.1
	ℏ	(0.1; 0.1; 0.1)
	Γ₁γ₁	20, 0.2
	Γ₂γ₂	0.1, 0.1
	Γ₃γ₃	0.5, 0.002
	δ	0.01
	X(0)	(60; −80; 50)
		(1; 2; 1)

	u_i,max, u_1i,max	150 Nm, 150 Nm

Figures 2, 3, 4, 5, 6, 7, 8, and 9 present the simulation results comparing the proposed ETC scheme to the continuous control strategy. As shown in Figures 2 and 3, both the ETC scheme and the continuous control method effectively enable the SFF to track the reference trajectory. This performance is maintained despite challenges such as time-varying uncertainties, input saturations, and actuator faults. However, the stabilization times for the ETC scheme are, respectively, 9, 21, and 11 s, whereas for the continuous control scheme, they are 20 s, 24 s, and 22 s, demonstrating faster stabilization speeds for the ETC scheme.

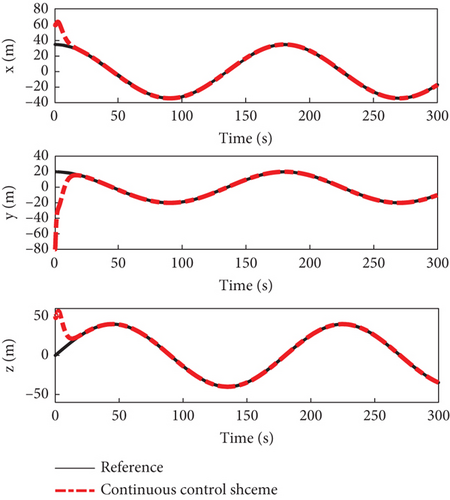
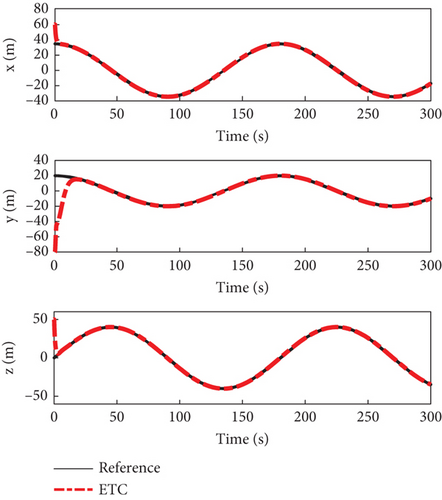
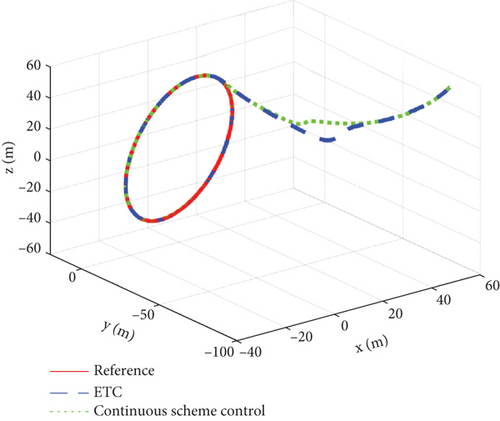
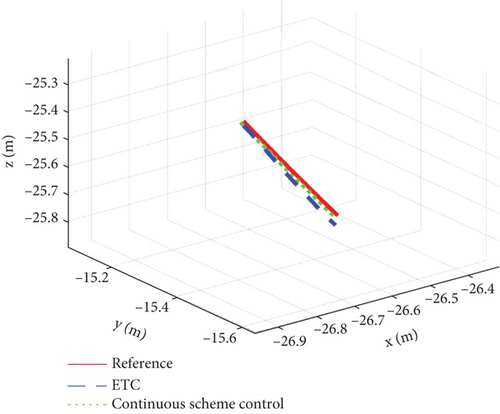
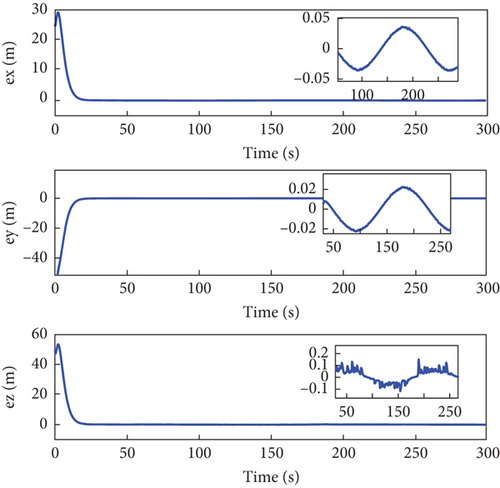
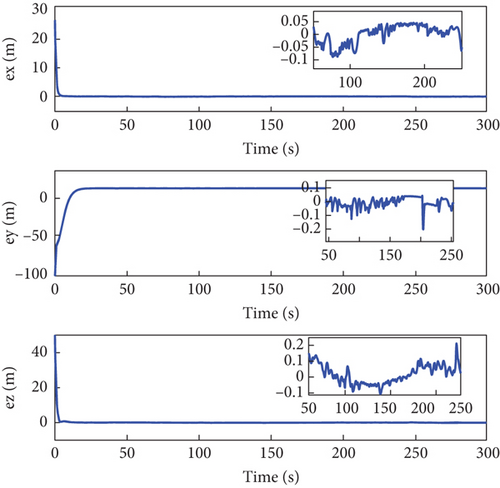
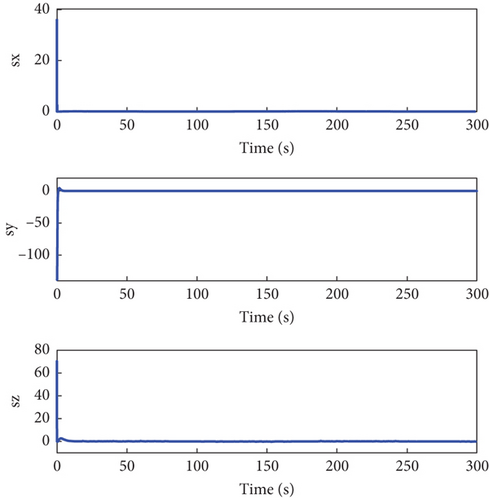
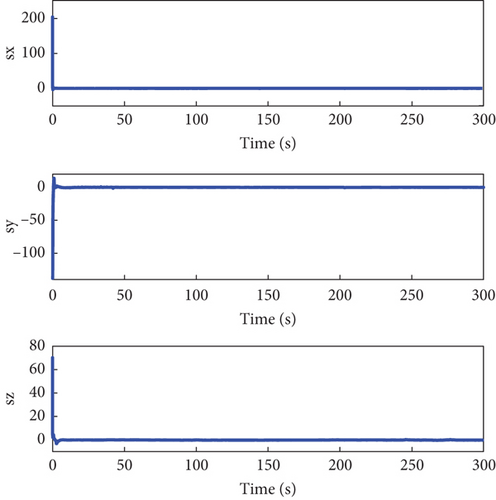
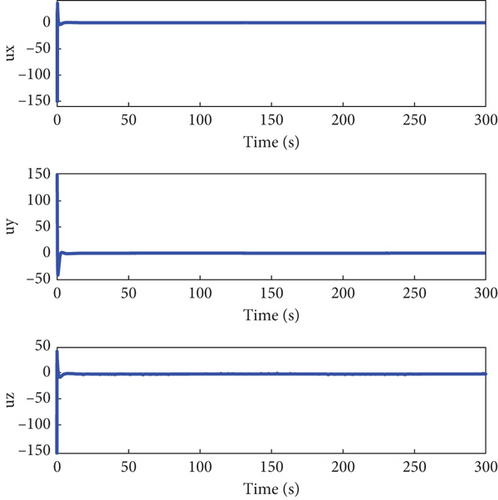
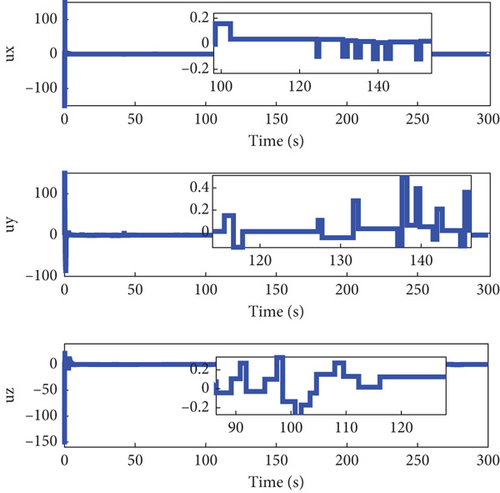
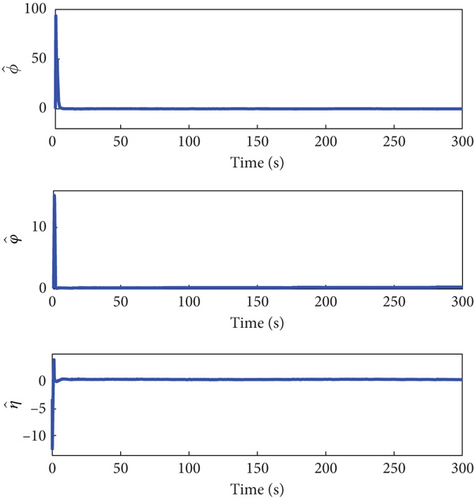
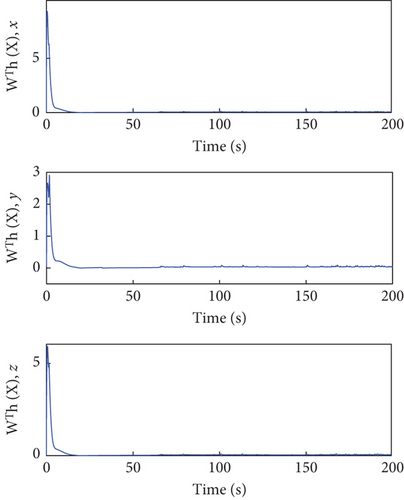
Figures 4 and 5 showcase the historical curves of the relative position error e and the sliding mode surface, showing that the position error e remains bounded under both fault-tolerant control strategies. The accuracy of the two control strategies is approximately the same, each maintaining a precision within the ranges of 10⁻², 10⁻², and 10⁻¹. Figure 6 illustrates the variation of the control force u, u₁ under both methods, demonstrating that both strategies effectively maintain the input u, u₁ within the saturation limit of 150 Nm.

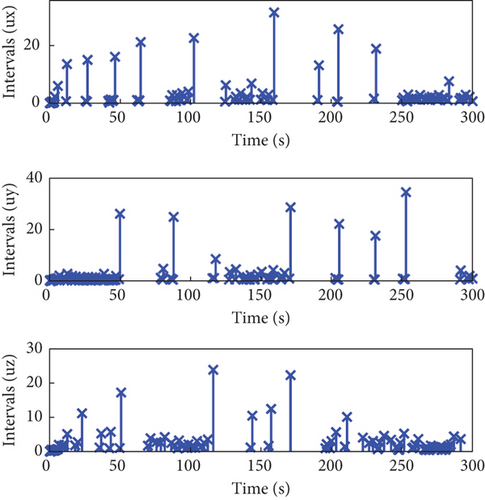
The total number of events in the channel u₁ is 689, 228, and 190, respectively, which stands in stark contrast to the 30,001 events triggered under the continuous control method. This indicates that using our proposed ETC method significantly reduces the number of controller executions. Additionally, Figure 7 illustrates the triggering instances and intervals, showing that control commands u_1i, i = x, y, z are not transmitted indefinitely within a short period. Figures 8 and 9 confirm that u, u₁ remains bounded.

These findings confirm that all signals within the SFF closed-loop tracking control system remain bounded, as demonstrated in Theorem 3. Consequently, it can be inferred that our proposed control scheme effectively manages the SFF, even in the presence of dynamic uncertainties, external disturbances, input limitations, and actuator faults.

5. Conclusions

In the research presented within this paper, an event-triggered neural network adaptive backstepping sliding mode fault-tolerant control scheme, suitable for the challenging conditions of uncertain dynamics and external disturbances affecting SFF, has been proposed. Through the application of model transformation techniques and the implementation of a backstepping control system, issues associated with actuator saturation are aptly addressed. The combination of SMC with a neural network and a minimal parameter learning algorithm significantly enhances the system’s adaptability to uncertain dynamics and its tolerance to external interferences. Actuator usage frequency is thereby reduced, mitigating mechanical wear and obviating the need for prior knowledge of the system’s dynamics to ensure the SFF’s stable tracking. Our theoretical analysis and simulation studies have verified that all closed-loop control signals remain bounded, thus demonstrating the effectiveness of the proposed control strategy.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors received no specific funding for this work.

Open Research

Data Availability Statement

Due to the nature of this research, participants of this study did not agree for their data to be shared publicly, so supporting data is not available.

References

1 Liu G. P. and Zhang S., A survey on formation control of small satellites, Proceedings of the IEEE. (2018) 106, no. 3, 440–457, https://doi.org/10.1109/JPROC.2018.2794879, 2-s2.0-85042186021.
10.1109/JPROC.2018.2794879
Web of Science® Google Scholar
2 Shi Y. and Hu Q., Observer-based spacecraft formation coordinated control via a unified event-triggered communication, IEEE Transactions on Aerospace and Electronic Systems. (2021) 57, no. 5, 3307–3319, https://doi.org/10.1109/TAES.2021.3074201.
10.1109/TAES.2021.3074201
Web of Science® Google Scholar
3 Kristiansen R. and Nicklasson P. J., Spacecraft formation flying: a review and new results on state feedback control, Acta Astronautica. (2009) 65, no. 11-12, 1537–1552, https://doi.org/10.1016/j.actaastro.2009.04.014, 2-s2.0-70349770792.
10.1016/j.actaastro.2009.04.014
Web of Science® Google Scholar
4 Di Mauro G., Lawn M., and Bevilacqua R., Survey on guidance navigation and control requirements for spacecraft formation-flying missions, Journal of Guidance, Control, and Dynamics. (2018) 41, no. 3, 581–602, https://doi.org/10.2514/1.G002868, 2-s2.0-85041963030.
10.2514/1.G002868
Web of Science® Google Scholar
5 Zhang J., Ye D., Biggs J. D., and Sun Z., Finite-time relative orbit-attitude tracking control for multi-spacecraft with collision avoidance and changing network topologies, Advances in Space Research. (2019) 63, no. 3, 1161–1175, https://doi.org/10.1016/j.asr.2018.10.037, 2-s2.0-85056325537.
10.1016/j.asr.2018.10.037
Web of Science® Google Scholar
6 Zou A. M. and Kumar K. D., Distributed attitude coordination control for spacecraft formation flying, IEEE Transactions on Aerospace and Electronic Systems. (2012) 48, no. 2, 1329–1346, https://doi.org/10.1109/TAES.2012.6178065, 2-s2.0-84859815832.
10.1109/TAES.2012.6178065
Web of Science® Google Scholar
7 Zhao L., Yu J., and Shi P., Command filtered backstepping-based attitude containment control for spacecraft formation, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2021) 51, no. 2, 1278–1287, https://doi.org/10.1109/TSMC.2019.2896614.
10.1109/TSMC.2019.2896614
Web of Science® Google Scholar
8 Xing J., Tang G., Cheng W., and Lei Y., Robust nonlinear control of spacecraft formation flying using constraint forces, SCIENCE CHINA Technological Sciences. (2011) 54, no. 9, 2276–2282, https://doi.org/10.1007/s11431-011-4435-8, 2-s2.0-80051687809.
10.1007/s11431-011-4435-8
Google Scholar
9 Liu H., Tian Y., Lewis F. L., Wan Y., and Valavanis K. P., Robust formation flying control for a team of satellites subject to nonlinearities and uncertainties, Aerospace Science and Technology. (2019) 95, https://doi.org/10.1016/j.ast.2019.105455, 2-s2.0-85073123331.
10.1016/j.ast.2019.105455
Google Scholar
10 Zhang K., Duan G., and Ma M., Adaptive sliding-mode control for spacecraft relative position tracking with maneuvering target, International Journal of Robust and Nonlinear Control. (2018) 28, no. 18, 5786–5810, https://doi.org/10.1002/rnc.4346, 2-s2.0-85054341176.
10.1002/rnc.4346
Web of Science® Google Scholar
11 Wang W., Mengali G., Quarta A. A., and Yuan J., Distributed adaptive synchronization for multiple spacecraft formation flying around Lagrange point orbits, Aerospace Science and Technology. (2018) 74, 93–103, https://doi.org/10.1016/j.ast.2018.01.007, 2-s2.0-85041469627.
10.1016/j.ast.2018.01.007
Google Scholar
12 Zhuang M., Tan L., Li K., and Song S., Fixed-time formation control for spacecraft with prescribed performance guarantee under input saturation, Aerospace Science and Technology. (2021) 119, https://doi.org/10.1016/j.ast.2021.107176.
10.1016/j.ast.2021.107176
Google Scholar
13 Cao L., Qiao D., and Xu J., Suboptimal artificial potential function sliding mode control for spacecraft rendezvous with obstacle avoidance, Acta Astronautica. (2018) 143, 133–146, https://doi.org/10.1016/j.actaastro.2017.11.022, 2-s2.0-85035014325.
10.1016/j.actaastro.2017.11.022
Web of Science® Google Scholar
14 Yoshimura Y., Optimal formation reconfiguration of satellites under attitude constraints using only thrusters, Aerospace Science and Technology. (2018) 77, 449–457, https://doi.org/10.1016/j.ast.2018.03.021, 2-s2.0-85044590226.
10.1016/j.ast.2018.03.021
Google Scholar
15 Liu R., Liu M., and Liu Y., Nonlinear optimal tracking control of spacecraft formation flying with collision avoidance, Transactions of the Institute of Measurement and Control. (2019) 41, no. 4, 889–899, https://doi.org/10.1177/0142331218773506, 2-s2.0-85048760787.
10.1177/0142331218773506
Web of Science® Google Scholar
16 Fei J., Wang Z., Lu X., and Deng L., Adaptive RBF neural network control based on sliding mode controller for active power filter, Proceedings of the 32nd Chinese Control Conference, 2013, Xi′an, China, 3288–3293.
Google Scholar
17 Wu D., Long B., and Cheng Y., RBF-NN based upper-bound adaptive learning sliding mode control for grid-connected converter, 2020 IEEE International Conference on Mechatronics and Automation (ICMA), 2020, Beijing, China, 960–965, https://doi.org/10.1109/ICMA49215.2020.9233615.
10.1109/ICMA49215.2020.9233615
Google Scholar
18 Karabatak M. and Ince M. C., An expert system for detection of breast cancer based on association rules and neural network, Expert Systems with Applications. (2009) 36, no. 2, 3465–3469, https://doi.org/10.1016/j.eswa.2008.02.064, 2-s2.0-56349123043.
10.1016/j.eswa.2008.02.064
Web of Science® Google Scholar
19 Gou J., Ma H., Ou W., Zeng S., Rao Y., and Yang H., A generalized mean distance-based k-nearest neighbor classifier, Expert Systems with Applications. (2019) 115, 356–372, https://doi.org/10.1016/j.eswa.2018.08.021, 2-s2.0-85057124353.
10.1016/j.eswa.2018.08.021
Web of Science® Google Scholar
20 Song S., Zhang B., Xia J., and Zhang Z., Adaptive backstepping hybrid fuzzy sliding mode control for uncertain fractional-order nonlinear systems based on finite-time scheme, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2020) 50, no. 4, 1559–1569, https://doi.org/10.1109/TSMC.2018.2877042, 2-s2.0-85058152109.
10.1109/TSMC.2018.2877042
Web of Science® Google Scholar
21 Zheng Y. J., Ling H. F., Chen S. Y., and Xue J. Y., A hybrid neuro-fuzzy network based on differential biogeography-based optimization for online population classification in earthquakes, IEEE Transactions on Fuzzy Systems. (2015) 23, no. 4, 1070–1083, https://doi.org/10.1109/TFUZZ.2014.2337938, 2-s2.0-84938805768.
10.1109/TFUZZ.2014.2337938
Web of Science® Google Scholar
22 Hornik K., Stinchcombe M., and White H., Multilayer feedforward networks are universal approximators, Neural Networks. (1989) 2, no. 5, 359–366, https://doi.org/10.1016/0893-6080(89)90020-8, 2-s2.0-0024880831.
10.1016/0893-6080(89)90020-8
Web of Science® Google Scholar
23 Feng Z., Wang J., Wan N., and Li H., Distributed adaptive NN-based attitude synchronous tracking control with input saturation, Electronics. (2022) 11, no. 24, https://doi.org/10.3390/electronics11244093.
10.3390/electronics11244093
Google Scholar
24 Sun Q. and Jia Y., Attitude-orbit integrated control for spacecraft Fly-Around Mission based on Chebyshev neural network, IEEE Transactions on Aerospace and Electronic Systems. (2024) 60, no. 3, 3177–3191, https://doi.org/10.1109/TAES.2024.3358778.
10.1109/TAES.2024.3358778
Google Scholar
25 Hao Y., He Y., Xie Y., Sun C., and Zhao K., Neural-network based finite-time coordinated formation control for spacecraft Without unwinding, IEEE Access. (2020) 8, 127507–127518, https://doi.org/10.1109/ACCESS.2020.3007530.
10.1109/ACCESS.2020.3007530
Google Scholar
26 Jia Q., Shu R., Yu D., Zhang C., and Tan L., Neural network-based prescribed performance fault-tolerant control for spacecraft formation reconfiguration with collision avoidance, 2023, Research Square.
10.21203/rs.3.rs-3804664/v1
Google Scholar
27 Jia J., Wang Y., and Yue H., Design of sliding mode controller based on radial basis function neural network for spacecraft autonomous proximity, IFAC-PapersOnLine. (2023) 56, no. 2, 2456–2461, https://doi.org/10.1016/j.ifacol.2023.10.1223.
10.1016/j.ifacol.2023.10.1223
Google Scholar
28 Wu X., Zhao H., Huang B., Li J., Song S., and Liu R., Minimum-learning-parameter-based anti-unwinding attitude tracking control for spacecraft with unknown inertia parameters, Acta Astronautica. (2021) 179, 498–508, https://doi.org/10.1016/j.actaastro.2020.11.012.
10.1016/j.actaastro.2020.11.012
Web of Science® Google Scholar
29 Jia Q., Shu R., Ahn C. K., and Zhang C., Learning neural network-based fault-tolerant formation control for elliptical orbit spacecraft, IEEE Transactions on Aerospace and Electronic Systems. (2024) 60, no. 2, 1937–1950, https://doi.org/10.1109/TAES.2023.3344390.
10.1109/TAES.2023.3344390
Google Scholar
30 Fan L. and Huang H., Coordinative coupled attitude and orbit control for satellite formation with multiple uncertainties and actuator saturation, Acta Astronautica. (2021) 181, 325–335, https://doi.org/10.1016/j.actaastro.2021.01.039.
10.1016/j.actaastro.2021.01.039
Web of Science® Google Scholar
31 Shi Y., Hu Q., Li D., and Lv M., Adaptive optimal tracking control for spacecraft formation flying with event-triggered input, IEEE Transactions on Industrial Informatics. (2023) 19, no. 5, 6418–6428, https://doi.org/10.1109/TII.2022.3181067.
10.1109/TII.2022.3181067
Web of Science® Google Scholar
32 Zhou N., Cheng X., Xia Y., and Liu Y., Fully adaptive-gain-based intelligent failure-tolerant control for spacecraft attitude stabilization under actuator saturation, IEEE Transactions on Cybernetics. (2022) 52, no. 1, 344–356, https://doi.org/10.1109/TCYB.2020.2969281, 32149666.
10.1109/TCYB.2020.2969281
PubMed Web of Science® Google Scholar
33 Li Z., Yu G., Zhang Q., Song S., and Cui H., Adaptive sliding mode control for spacecraft rendezvous with unknown system parameters and input saturation, IEEE Access. (2021) 9, 67724–67733, https://doi.org/10.1109/ACCESS.2021.3075564.
10.1109/ACCESS.2021.3075564
Web of Science® Google Scholar
34 Lyu B., Liu C., and Yue X., Hybrid nonfragile intermediate observer-based T-S fuzzy attitude control for flexible spacecraft with input saturation, Aerospace Science and Technology. (2022) 128, article 107753, https://doi.org/10.1016/j.ast.2022.107753.
10.1016/j.ast.2022.107753
Web of Science® Google Scholar
35 Ye D., Zou A. M., and Sun Z., Predefined-time predefined-bounded attitude tracking control for rigid spacecraft, IEEE Transactions on Aerospace and Electronic Systems. (2022) 58, no. 1, 464–472, https://doi.org/10.1109/TAES.2021.3103258.
10.1109/TAES.2021.3103258
Google Scholar
36 Liu E., Yan Y., and Yang Y., Neural network approximation-based backstepping sliding mode control for spacecraft with input saturation and dynamics uncertainty, Acta Astronautica. (2022) 191, 1–10, https://doi.org/10.1016/j.actaastro.2021.10.035.
10.1016/j.actaastro.2021.10.035
Web of Science® Google Scholar
37 Zhu Z. and Guo Y., Adaptive coordinated attitude control for spacecraft formation with saturating actuators and unknown inertia, Journal of the Franklin Institute. (2019) 356, no. 2, 1021–1037, https://doi.org/10.1016/j.jfranklin.2018.02.021, 2-s2.0-85044108296.
10.1016/j.jfranklin.2018.02.021
Web of Science® Google Scholar
38 Huang X. and Yan Y., Saturated backstepping control of underactuated spacecraft hovering for formation flights, IEEE Transactions on Aerospace and Electronic Systems. (2017) 53, no. 4, 1988–2000, https://doi.org/10.1109/TAES.2017.2679838, 2-s2.0-85029520957.
10.1109/TAES.2017.2679838
Web of Science® Google Scholar
39 Yueneng Y. and Ye Y., Backstepping sliding mode control for uncertain strictfeedback nonlinear systems using neural-network-based adaptive gain scheduling, Journal of Systems Engineering and Electronics. (2018) 29, no. 3, 580–586, https://doi.org/10.21629/JSEE.2018.03.15, 2-s2.0-85049730149.
10.21629/JSEE.2018.03.15
Web of Science® Google Scholar
40 Zheng Z. and Zou Y., Adaptive integral LOS path following for an unmanned airship with uncertainties based on robust RBFNN backstepping, ISA Transactions. (2016) 65, 210–219, https://doi.org/10.1016/j.isatra.2016.09.008, 2-s2.0-84994444342, 27665142.
10.1016/j.isatra.2016.09.008
PubMed Web of Science® Google Scholar
41 Zou A.-M. and Kumar K. D., Robust attitude coordination control for spacecraft formation flying under actuator failures, Journal of Guidance, Control, and Dynamics. (2012) 35, no. 4, 1247–1255, https://doi.org/10.2514/1.55218, 2-s2.0-84867045555.
10.2514/1.55218
Web of Science® Google Scholar
42 Gao Z. and Wang S., Fault estimation and fault tolerance control for spacecraft formation systems with actuator fault and saturation, Optimal Control Applications and Methods. (2021) 42, no. 6, 1591–1611, https://doi.org/10.1002/oca.2751.
10.1002/oca.2751
Web of Science® Google Scholar
43 Hu Q., Xiao L., and Wang C., Adaptive fault-tolerant attitude tracking control for spacecraft with time-varying inertia uncertainties, Chinese Journal of Aeronautics. (2019) 32, no. 3, 674–687, https://doi.org/10.1016/j.cja.2018.12.015, 2-s2.0-85061782614.
10.1016/j.cja.2018.12.015
Google Scholar
44 Shen Q., Wang D., Zhu S., and Poh E. K., Integral-type sliding mode fault-tolerant control for attitude stabilization of spacecraft, IEEE Transactions on Control Systems Technology. (2015) 23, no. 3, 1131–1138, https://doi.org/10.1109/TCST.2014.2354260, 2-s2.0-85027947440.
10.1109/TCST.2014.2354260
Web of Science® Google Scholar
45 Li Y., Ma Z., and Tong S., Adaptive fuzzy fault-tolerant control of nontriangular structure nonlinear systems with error constraint, IEEE Transactions on Fuzzy Systems. (2018) 26, no. 4, 2062–2074, https://doi.org/10.1109/TFUZZ.2017.2761323, 2-s2.0-85031793947.
10.1109/TFUZZ.2017.2761323
Web of Science® Google Scholar
46 Yang X., Yuan J., Chen T., and Yang H., Distributed adaptive optimization algorithm for fractional high-order multiagent systems based on event-triggered strategy and input quantization, Fractal and Fractional. (2023) 7, no. 10, https://doi.org/10.3390/fractalfract7100749.
10.3390/fractalfract7100749
Google Scholar
47 Chen T. and Yuan J., Command-filtered adaptive containment control of fractional-order multi-agent systems via event-triggered mechanism, Transactions of the Institute of Measurement and Control. (2023) 45, no. 9, 1646–1660, https://doi.org/10.1177/01423312221137618.
10.1177/01423312221137618
Web of Science® Google Scholar
48 Yang X., Zhao W., Yuan J., Chen T., Zhang C., and Wang L., Distributed optimization for fractional-order multi-agent systems based on adaptive backstepping dynamic surface control technology, Fractal and Fractional. (2022) 6, no. 11, https://doi.org/10.3390/fractalfract6110642.
10.3390/fractalfract6110642
Google Scholar
49 Yang T. and Dong J., Distributed event-triggered fixed-time DSC of multiagent systems, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2024) 54, no. 4, 2484–2494, https://doi.org/10.1109/TSMC.2023.3344269.
10.1109/TSMC.2023.3344269
Web of Science® Google Scholar
50 Li P., Liu Z., He C., Liu Q., and Liu X. Q., Distributed adaptive fault-tolerant control for spacecraft formation with communication delays, IEEE Access. (2020) 8, 118653–118663, https://doi.org/10.1109/ACCESS.2020.3003681.
10.1109/ACCESS.2020.3003681
Google Scholar
51 Wu J., Liu M., Wang Y., and Cao X., Event-trigger-based cluster coordinated control of spacecraft swarm under switching topology, Aerospace Science and Technology. (2023) 135, article 108200, https://doi.org/10.1016/j.ast.2023.108200.
10.1016/j.ast.2023.108200
Google Scholar
52 Zhao Y., Zhu F., and Xu D., Self-triggered bipartite formation-containment control for heterogeneous multi-agent systems with disturbances, Neurocomputing. (2023) 548, article 126382, https://doi.org/10.1016/j.neucom.2023.126382.
10.1016/j.neucom.2023.126382
Google Scholar
53 Deng Y., Zhang X., Im N., Zhang G., and Zhang Q., Model-based event-triggered tracking control of underactuated surface vessels with minimum learning parameters, IEEE Transactions on Neural Networks and Learning Systems. (2020) 31, no. 10, 4001–4014, https://doi.org/10.1109/TNNLS.2019.2951709.
10.1109/TNNLS.2019.2951709
PubMed Google Scholar
54 Wang M., Zhang S., Chen B., and Luo F., Direct adaptive neural control for stabilization of nonlinear time-delay systems, Science China Information Sciences. (2010) 53, no. 4, 800–812, https://doi.org/10.1007/s11432-010-0075-z, 2-s2.0-77952316648.
10.1007/s11432-010-0075-z
Web of Science® Google Scholar
55 Deng H. and Krstić M., Stochastic nonlinear stabilization — I: a backstepping design, Systems & Control Letters. (1997) 32, no. 3, 143–150, https://doi.org/10.1016/S0167-6911(97)00068-6, 2-s2.0-0000422686.
10.1016/S0167-6911(97)00068-6
Web of Science® Google Scholar
56 Sun Y., Xu J., Qiang H., Chen C., and Lin G., Adaptive sliding mode control of maglev system based on RBF neural network minimum parameter learning method, Measurement. (2019) 141, 217–226, https://doi.org/10.1016/j.measurement.2019.03.006, 2-s2.0-85064639883.
10.1016/j.measurement.2019.03.006
Web of Science® Google Scholar
57 Sanner R. M. and Slotine J. J. E., Gaussian networks for direct adaptive control, IEEE Transactions on Neural Networks. (1992) 3, no. 6, 837–863, https://doi.org/10.1109/72.165588, 2-s2.0-0026954302, 18276483.
10.1109/72.165588
CAS PubMed Web of Science® Google Scholar

All articles

Event-Triggered Adaptive Neural Network Backstepping Sliding Fault-Tolerant Control of Spacecraft Formation Flying With Input Saturation

Abstract

1. Introduction

2. Preliminary and System Description

3. Controller Design and Stability Analysis

3.1. Controller Without ETC

3.2. Controller With ETC

4. Simulation Results

5. Conclusions

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Event-Triggered Adaptive Neural Network Backstepping Sliding Fault-Tolerant Control of Spacecraft Formation Flying With Input Saturation

Abstract

1. Introduction

2. Preliminary and System Description

3. Controller Design and Stability Analysis

3.1. Controller Without ETC

3.2. Controller With ETC

4. Simulation Results

5. Conclusions

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information