Department of Chemical and Energy Engineering Faculty of Engineering and Science Curtin University Malaysia, CDT 250 98009 Miri Sarawak Malaysia curtin.edu.my

Search for more papers by this author

Paul Musonge,

Paul Musonge

orcid.org/0000-0001-9049-8655

Faculty of Engineering Mangosuthu University of Technology Durban 4026 South Africa mut.ac.za

Search for more papers by this author

David Olamide Makinde,

David Olamide Makinde

Department of Chemical Engineering Landmark University Omu-Aran Kwara State Nigeria lmu.edu.ng

Search for more papers by this author

Comfort Nneka Okoji,

Comfort Nneka Okoji

Department of Biology and Forensic Admiralty University Ibusa Delta State Nigeria

Search for more papers by this author

Anthony Ikechukwu Okoji,

Anthony Ikechukwu Okoji

orcid.org/0000-0002-5491-2684

Department of Chemical Engineering Covenant University Ota Ogun State Nigeria covenantuniversity.edu.ng

Search for more papers by this author

Abiola Ezekiel Taiwo,

Corresponding Author

Abiola Ezekiel Taiwo

[email protected]

orcid.org/0000-0001-6136-4439

Faculty of Engineering Mangosuthu University of Technology Durban 4026 South Africa mut.ac.za

Search for more papers by this author

John Busayo Adeoye,

John Busayo Adeoye

orcid.org/0000-0002-1212-4030

Department of Chemical and Energy Engineering Faculty of Engineering and Science Curtin University Malaysia, CDT 250 98009 Miri Sarawak Malaysia curtin.edu.my

Search for more papers by this author

Paul Musonge,

Paul Musonge

orcid.org/0000-0001-9049-8655

Faculty of Engineering Mangosuthu University of Technology Durban 4026 South Africa mut.ac.za

Search for more papers by this author

David Olamide Makinde,

David Olamide Makinde

Department of Chemical Engineering Landmark University Omu-Aran Kwara State Nigeria lmu.edu.ng

Search for more papers by this author

Comfort Nneka Okoji,

Comfort Nneka Okoji

Department of Biology and Forensic Admiralty University Ibusa Delta State Nigeria

Search for more papers by this author

First published: 29 May 2024

https://doi.org/10.1155/2024/6843951

Citations: 2

Academic Editor: Geng Chen

Share a link

Email
Wechat
Bluesky

Abstract

An equilibrium-based steady-state simulator model that predicts and optimizes hydrogen production from steam gasification of biomass is developed using ASPEN Plus software and artificial intelligence techniques. Corn cob’s chemical composition was characterized to ensure the biomass used as a gasifier and with potential for production of hydrogen. Artificial intelligence is used to examine the effects of the significant input variables on response variables, such as hydrogen mole fraction and hydrogen energy content. Optimizing the steam-gasification process using response surface methodology (RSM) considering a variety of biomass-steam ratios was carried out to achieve the best results. Hydrogen yield and the impact of main operating parameters were considered. A maximum hydrogen concentration is found in the gasifier and water-gas shift (WGS) reactor at the highest steam-to-biomass (S/B) ratio and the lowest WGS reaction temperature, while the gasification temperature has an optimum value. ANFIS was used to predict hydrogen of mole fraction, 0.5045 with the input parameters of S/B ratio of 2.449 and reactor pressure and temperature of 1 bar and 848°C, respectively. With the steam-gasification model operating at temperature (850°C), pressure (1 bar), and S/B ratio of 2.0, an ASPEN simulator achieved a maximum of 0.5862 mole fraction of hydrogen, while RSM gave an increase of 19.0% optimum hydrogen produced over the ANFIS prediction with the input parameters of S/B ratio of 1.053 and reactor pressure and temperature of 1 bar and 850°C, respectively. Varying the gasifier temperature and S/B ratio have, on the other hand, a crucial effect on the gasification process with artificial intelligence as a unique tool for process evaluation, prediction, and optimization to increase a significant impact on the products especially hydrogen.

1. Introduction

Human development has been challenged by the depletion of energy resources, impacts on the environment, and insecurities around national energy security due to increased energy demand and consumption [1]. Biomass is one of the renewable energy sources that does not involve the emission of greenhouse gases, unlike fossil fuels with many pollutants [2, 3]. Renewable energy is an alternative energy generation that has gained traction for some time, as its sources have a greater presence in the modern world energy market. Human civilization and technological advancement are leading to an increase in global energy demand. The world’s energy security has been threatened by rapidly diminishing fossil fuel reserves [4]. Thus, in response to these problems, continuous efforts have been made to explore clean, renewable alternatives for sustainable development to transition the world from overdependence on fossil fuels gradually [5]. However, alternative energy sources such as hydrogen production, bioethanol, and biogas [6] are proving to be safe and effective means to an extent, addressing the issues mentioned earlier. Global energy consumption was 18.1% fueled by renewable energy sources in 2017, with biomass contributing 12.1% [7], which establishes it as a potentially viable and more advantageous energy source when compared to fossil fuels. It is widely acknowledged that hydrogen serves as an attractive energy source to replace conventional fossil fuels from an economic standpoint as well as from an environmental perspective. Biomass is among the most readily available and abundant renewable energy resources because of its carbon neutrality [8]. In a recent study by Park et al. [9], the authors propose a corn biomass to syngas chemical looping system for a range of downstream applications, with focus on liquid fuel production. The study reported a variable syngas quality with an H₂/CO ratio of approximately 2, and a syngas purity greater than 70% was achieved. A comprehensive comparative study using multicriteria decision analysis was conducted on the gasification of waste polymetric foam at multiobjective optimum conditions using response surface methodology [10]. Another study by Hasanzadeh et al. [11]models and optimizes the performance of the gasification of a rice husk and low-density polyethylene waste composite, and the authors reported an energy efficiency of 77.6%. A high degree of accuracy can be achieved using the ASPEN Plus software model for different gasifiers (air gasification or steam gasification) this simulator could predict high syngas compositions from different biomasses. In a study that assessed the potential for lignocellulosic biomass to be converted to butanol using chemical looping gasification, Li et al. [12] established an ASPEN Plus model, which shows an efficiency of 45.33%. A partial gasification model using ASPEN Plus was developed by Zhang et al. [13]. At the same time, different thermodynamic analyses were performed, such as exergy, energy, and economic analyses. The gasification process that was reported with key input parameters yielded cold gas and energy efficiency of 46.08 and 67.08%, respectively, and a net heat efficiency of 44.25% at a carbon conversion ratio of 0.7. In another study that used the ASPEN Plus model for biomass gasifier, Pala et al. [14] demonstrated that a shift reaction could be used to tune the syngas composition successively and achieved a molar ratio of about 2.15 for H₂ and CO. A 35 kVA downdraft biomass gasifier was modeled using ASPEN Plus simulated by Keche et al. [15], and babul wood was found to produce more H₂ in the syngas than other biomass used as feedstocks. In a model that predicts the result with less error than experimental results in temperatures between 700 and 900°C, Pauls et al. [16] used air and steam as gasifying agents.

The response surface methodology (RSM) is widely used for optimizing new and existing systems [17]. The one factor at a design approach is not cost and time effective. Response surface methodology (RSM) is one of the most applicable designs of experimental methods [18]. RSM helps to present a regression model to predict the response variable based on the considered input parameters [19, 20]. In addition to RSM, genetic algorithms (GA) can be used to optimize any process or system. Nevertheless, RSM offers adequate accuracy for optimizing processes or systems (almost identical to GA). According to a previous study [21], RSM provides better optimization accuracy than GA. Furthermore, GA relies on a heuristic optimization strategy, which does not guarantee optimal solutions.

The optimization of biomass, coal, and waste torrefaction process variables made use of artificial neural networks and RSM by Ozonoh et al. [22]. In comparison with raw fuel, the torrefied product showed 10% higher heating values. Based on RSM, Inayat et al. [23] optimized the catalytic cogasification of palm waste and found that the gasification temperature and the catalytic loading and blending ratio are the most influential. Optimal conditions resulted in 19.96% CH₄ and 38.81% syngas. In a study of hydrothermal gasification (HTG), Fozer et al. [24] used RSM for optimizing microalgae biomass production and sequential biogas generation. In optimum light levels, fermentation of microalgae biomass produces H₂-rich gas without requiring any catalyst, suggesting improvement at the farm stage in downstream processing. As part of the optimization of a design mix of palm oil and diesel fuel introduced into diesel engines, Uslu [25] utilized RSMs and artificial neural networks (ANNs).

Fuzzy inference systems are generated using ANFIS-based methods, such as grid partition, subclustering, and fuzzy c-means. Multiple and individual response variables have been used in this study to optimize the equilibrium gasifier model. To compare BP-ANN and ANFIS models with the ASPEN Plus process model, extensive simulation studies are conducted to determine the best predictive model. Furthermore, synchronized effects among input and response variables determined optimal operating conditions for steam gasification.

Any gasification process requires optimization to achieve high-quality syngas. Thus, no detailed predictive models have been developed using back propagation neural networks (BP-ANN) and ANFIS, statistical analysis, and syngas production optimization for a developed steam-gasification process. This present study combines back propagation artificial neural network BP-ANN and adaptive neuro fuzzy inference system (ANFIS) to develop a prediction model for biomass gasification based on ASPEN Plus simulation. The use of artificial intelligence integrated with process simulations will help provide relevant industrial conditions as a result of energy concerns. The process will provide the opportunity to understand and design an optimal hydrogen production scale-up.

2. Materials and Methods

This study used plant raw materials that are annually renewable in Nigeria and concentrated in growing or processing sites. Corn cob, rice husk, and coconut shell were collected during grain crop harvesting. Plant material was air-dried and crushed to particle sizes (<1 mm) on a disintegrator. Furthermore, some parameters, including the identified biomass’s fixed carbon and volatile matter, were determined using the ASTM standard. Using standard methods established in the literature, the samples’ percentages of moisture and ash were determined [26].

An elemental analysis (proximate and ultimate analysis) was performed on biomass materials such as corn cob and was found to have a moderately higher calorific value, as shown in Table 1. This represents the input parameters in ASPEN Plus for the gasification reaction process for syngas, especially hydrogen. Detailed and comprehensive studies on characterization of corn cob for application in a gasification process for energy production have been reported in literature [27]. The results of the authors are comparable to the current study corn cob analysis.

Table 1. Corn cob elemental analysis.

M	A	VM	FC	HHV	C	H	N	O	S
Proximate analysis, dry basis (%)					Ultimate analysis, dry basis (%)
9.8	8.5	69.2	12.5	17.04	47.2	6.4	0.4	46.0	0

M: moisture; A: ash; VM: volatile matter; FC: fixed carbon; HHV: high heating value (MJ/kg).

3. Model Description

3.1. ASPEN Plus Model, Equation, and Assumptions

A Gibbs free energy minimization equilibrium model was used in this study as represented in Eq. (1). This equilibrium model is computationally economical yet supplies valuable information about gasification at high temperatures [28]. Based on Rupesh et al. [29], the Gibbs free energy can be expressed as the sum of moles (n) and chemical potential (μ) of reacting species (i).

(1)

For the minimization of the Gibbs free energy, it is possible to apply the Lagrange multiplier method, which gives the following equation.

(2)

Thus, L is the Lagrange function, while the Lagrange multiplier is λ_j.

Gibbs free energy and Lagrange multipliers presented in Equations (1) and (2) have been applied in previous studies [30]. The biomass gasification process model flowsheet diagram for the corn cob is displayed in Figure 1. As a result of adopting the Peng-Robinson equation of state [31, 32] in the property method section, excellent precision could be obtained when simulating biomass steam gasification processes. Biomass was classified as a nonconventional input, and its proximate and ultimate analyses were entered in the stream named “Biomass” under “component attributes.” Moreover, steam is supplied at 150°C and 1 bar as a gasifying agent. A Gibbs reactor (RGIBBS) was operated with varying steam mass flow rates and variable biomass inputs to alter the steam-to-biomass ratio (S/B) and temperature in the gasification process (T). The blocks (reactors) used for the ASPEN Plus gasification’s simulations for the corn cob are shown in Table 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

ASPEN Plus process flow diagram for gasification.

Table 2. ASPEN Plus blocks and model representation for biomass steam gasification.

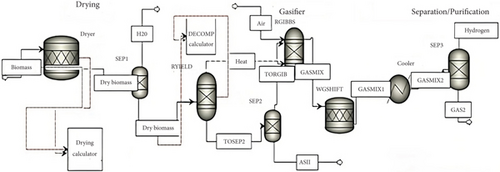
Block	Model	Function
DRYING	RYIELD	Biomass is either dried based on proximate analysis of water content or divided into conventional components and ash
BIOMASS-DECOMPOSE	RSTOIC	For simulation of biomass gasification and combustion, decompose biomass into CO, CO₂, H₂, CH₄, N₂, and ash to easily handle solid reactions
SEP	SEP	Rotation and gravitational forces are used to separate gas and solid impurities
RGIBBS		Gasification reactions occur when the Gibbs free energy minimization is applied to all possible reactions
SSPLIT		A yield reactor creates char, RSTOIC produces H₂S after formation, and dry syngas is obtained by separating H₂O from syngas

This model is simplified by making the following assumptions: (i) Simulating atmospheric conditions and steady-state conditions is carried out; (ii) initially, devolatilization occurs instantaneously; (iii) a negligible amount of heat is lost; (iv) ash is considered an inert substance. In addition, the experimental statistical data range from the ASPEN Plus process model is shown in Table 3.

Table 3. Experimental data range from the ASPEN Plus process model.

Parameters	Unit	Minimum	Mean	Maximum
Input
Steam	kg/h	5500	34952.88	60000
Reactor pressure	Bar	0.1	0.15	1.0
Reactor temperature	°C	360	627.6	850
Biomass	kg/h	10000	20000	30000
Output
Mole fraction
H₂		0.17	0.387	0.5862
CO₂		0.072	0.123	0.145
CO		0.01	0.099	0.332
CH₄		0.00	0.00	0.022

The biomass biodegradation reaction, steam reforming with methanization, and gas-water shift reactions are presented in different conditions. The process for this reaction is presented in [33]

(3)

(4)

(5)

(6)

(7)

3.2. Models Based on BP and ANN

The BP-ANN is one of the most widely used ANNs [34, 35]. This is a multilayer feedforward neural network that uses Rumelhart and McClelland’s error backpropagation algorithm, first proposed in the 1980s [36]. The input, hidden, and output layers of BP-ANN can be divided into three sublayers, with the hidden layer including one or more sublayers as shown in Figure 2. Thus, an ANN with a BP sigmoid function is widely used to activate a neuron as shown in Eq. (8): Equations (8)–(10) have been applied in our previous study [37].

(8)

where s denotes the input variable’s value.

Neurons in the hidden layer and outer layer of a BP-ANN can be expressed as outputs:

(9)

(10)

where s_i, t_i, and u_l represent inputs and outputs, f(net) represents the transfer function, ω and ρ are weight vectors of input layer and hiding layer, and θ is the threshold value of the neuron.

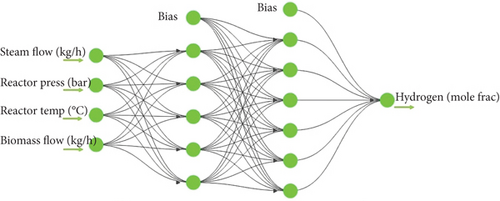
Net = newff (X, Y, ^‘trainfun, ^’‘trainlm) in MATLAB creates the BP model: X is the maximum and minimum value of the input quantity, Y is the number of hidden layer nodes, ^‘trainfun^’ is the transfer function (tansig function was used in this case), and ^‘trainlm^’ is the training function.

In this study, the steam flow (kg/h), reactor pressure (bar), reactor temperature (°C), and biomass flow (kg/h) are considered input data, and the amount of H₂ (mole fraction) and, in the network training, hydrogen energy content (MJ/kg) was considered an output of the process. Training, validation, and test sets of data points for the ANN are divided into three categories, whose percentages are adjustable [36].

3.3. ANFIS Model Building

A model was developed using four (4) parameters which are independent variables, the steam flow (kg/h), reactor pressure (bar), reactor temperature (°C), and biomass flow (kg/h) as input while the output set contains data of the amounts of H₂ (mole fraction) and energy content of the hydrogen produced (MJ/kg). These variables are listed in Table 3 along with their statistical characteristics. All subgroups have quite large ranges of data for each variable.

MATLAB functions linked to ANFIS are used to build model programs; the ANFIS model structure is shown in Figure 3. In general, a subject expert describes the fuzzy rules. The algorithm rather than an expert creates the rules when ANFIS is used. Two strategies were investigated in this study for generating a fuzzy inference system (FIS) structure from ANFIS data [38].

For this study, a first-order Sugeno-type model was built using four input variables and IF-THEN fuzzy logic. Fuzzy rules, assuming two inputs (x, y) and one output (f), are as follows according to equations (11) and (12) of the fuzzy inference method (FIS):

(11)

(12)

Gradient descent and least squares are used to determine contexts and parameters in hybrid learning. For its predictive purposes, ANFIS currently uses an advanced rapid-learning technique called hybrid learning. It has been established by many scientists that hybrid algorithms are effective [39, 40].

3.4. Response Surface Methodology (RSM)

As well as optimizing new systems or processes, RSM is frequently used to optimize existing ones as well [18, 23, 37]. Since RSM uses a partial factorial design, the design of experiments can be improved to perform the minimum number of experiments while reducing costs and time. Model accuracy can be determined by calculating the regression coefficient (R²) and adjusted regression coefficient (R²adj), both of which range from 0 to 1.0. Models with high R² and R²adj values (more than 0.9%) are considered precise [18]. A good model should have a difference between R² and R²adj less than 0.2 for the degree of fit determined by R² [41]. Here is the 2nd-order quadratic equation for the response-variable equation [42].

(13)

Here, “p” represents the response variable; “u” represents input variables; “n” denotes the number of variables; ∂₀, ∂_i, ∂_ii, and ∂_ij indicate constant, linear, square, and interaction terms, respectively.

The following equations define each of the statistical parameters used for model evaluation as mentioned in Table 4 [40, 43].

Table 4. Statistical models for evaluation.

Equations

In this case, R², MAE, MSE, RMSE, and AAE are, respectively, the coefficient of determination, the mean absolute error, the mean square error, the root mean square error, and the average absolute error. Optimal matching of data points occurs when the prediction error approaches zero [1].

4. Results and Discussion

4.1. Model Evaluation for ASPEN plus

Table 5 shows the output and input of the process simulation model used to simulate the gasification of corn cobs. Syngas compositions were predicted using ASPEN Plus software, but certain assumptions were considered, leading to some uncertainty, for instance, an underestimation of CH₄ content. A reliability inspection is therefore required before any further investigations can be conducted. Gasifier models must be validated with different experimental studies to ensure their authenticity and accuracy [44, 45]. As reported in published experimental studies, biomass feeds are validated using the same thermodynamic properties [14].

Table 5. Comparison between the simulated result and the reported data.

Parameters	Unit	Model	Turn et al. [45]	Hu et al. [44]
Input
Steam/biomass	Ratio	2.0	1.84	1.41
Reactor pressure	Bar	1.0	1.0	1.0
Reactor temperature	°C	850	800	800
Output
H₂	Mol/mol	0.5862	0.513	0.4701
Energy	MJ/kg	138.7

4.2. Model Evaluation for Predictive Potential

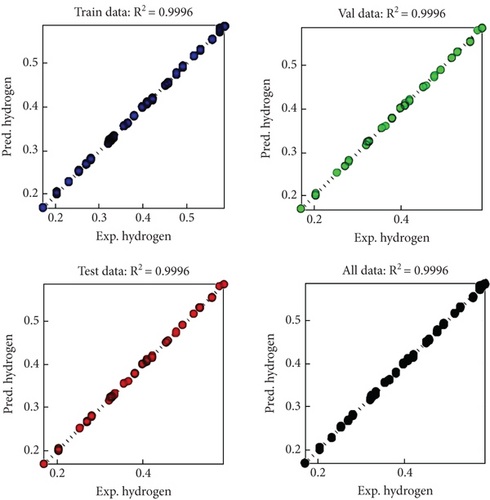
The model capability was evaluated using the following statistical parameters: R², MAE, MSE, RMSE, and AAE which are the coefficient of determination, the mean absolute error, the mean square error, the root mean square error, and the average absolute error, respectively. ASPEN Plus, backpropagation neural networks, and ANFIS models were evaluated to predict hydrogen production. For various models, results are shown in Tables 6, 7, and 8. Figures 4 and 5 represent parity plots between experimental data and predicted values; in addition, Tables 6 and 7 show different trial results of the three models involved in this study. However, R² should be close to unity (1) to achieve a strong correlation between experimental and expected values. In all three models, R² was close to one, indicating strong compatibility [37]. Furthermore, for each model, the RMSE and MSE square root were calculated. All of the values obtained for MSE and RMSE were low, confirming that all of the models used are within range. AAE and MAE calculate a model’s precision and accuracy as displayed in Tables 6 and 7; however, Table 8 expresses the summary of the best results of the two predictive models for comparison. The model of ANFIS-grid partitioning (GP) was able to predict hydrogen production more closely than the best of BP-ANN with two hidden layers (4-4-5-2), based on statistical index results.

Table 6. ANN prediction model error analysis with different hidden neurons for hydrogen.

Error analysis indicators	3	4	5
R²	0.9355	0.9397	0.935
MAE	0.0153	0.0147	0.0151
MSE	0.0006	0.0005	0.0006
RMSE	0.0236	0.0232	0.0237
AAE	0.0475	0.0428	0.0422

Table 7. ANFIS prediction model error analysis with ANFIS type for hydrogen production.

Error analysis indicators	ANFIS-grid partitioning (ANFIS-GP)	ANFIS-subtractive clustering (ANFIS-SC)	ANFIS-fuzzy c-means (ANFIS-FCM)
R²	0.9993	0.9993	0.9977
MAE	0.0013	0.0014	0.0023
MSE	0.0000	0.0000	0.0000
RMSE	0.0023	0.0025	0.0044
AAE	0.0040	0.0041	0.0063

Table 8. Summary of the different best models for the prediction of hydrogen production.

Error analysis indicators	ANN	ANFIS-grid partitioning (GP)
R²	0.9397	0.9993
MAE	0.0147	0.0013
MSE	0.0005	0.0000
RMSE	0.0232	0.0023
AAE	0.0428	0.0040

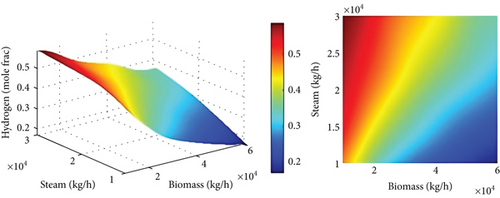
4.3. Relationship of Gasification with Steam-to-Biomass Ratio (S/B)

The gasification of biomass is characterized by the following main reactions. The results of steam gasification of corn cob feedstock at 850°C with different steam-to-biomass (S/B) ratios are shown in Figure 6(a). H₂ increased with an increase in S/B from 0.8 to 2.0, while CO and CH₄ content decreased. Gas composition could change with a change in S/B for two reasons. Exothermic water-gas shift reactions occur when steam is added to the gasification system (Eq. (10)), and steam reforming of methane being endothermic methods (Eqs. (6)–(9)) consumed CO and CH₄, increasing [44] H₂ and CO₂ content while decreasing CO and CH₄. Le Chatelier’s principle could explain the second reason. By adding steam (reactant) to the gasification system, reactions shift toward products, increasing H₂ production. According to Hu et al. [44], the same trend could be explained by an increase in steam reforming and shifting reactions because of the increased S/B. With an increase in S/B from 0.8 to 2.0, Figure 6(a) shows a slight increase in H₂ content. Steam can limit cracking and endothermic reactions like water-gas (equations (6)–(8)) and Boudouard reactions (equation (9)) caused by the addition of a significant increase in steam quantity. Low S/Bs, however, had less effect since the composition of the gas remained the same. For the production of syngas, it seems reasonable to use higher S/B values (>1.4). While keeping the gasification temperature constant at 850°C, S/B varied from 0.8 to 1.2. It defines the further use of the syngas produced by biomass gasification by measuring H₂/CO. As S/B increased, H₂/CO trended upwards. Gas quality was shown to be affected in two opposite ways by steam addition. A higher S/B results in a higher dry gas yield and char yield [46].

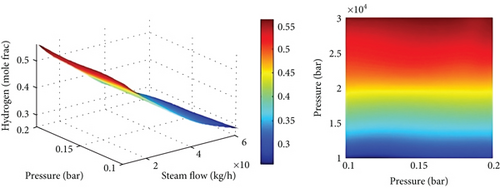
4.4. Gasification Temperature and Gasification Control Variables

Figures 6(b) and 6(c) show the composition of gas at various temperatures with S/B at a constant value. By steam-gasifying biomass at 650 to 850°C, 22% of CO was produced, while CH₄ and CO₂ contents were decreased. The CO₂ generated by shifting, cracking, and reactions (eqn. (10) and eqns. (6)–(9)) and consumed by the Boudouard reaction were similar to Mazumder and de Lasa [47], however taking these trends into account. Increasing gasification temperature led to an increase in CO₂ consumption rate, which decreased CO concentration. Due to the enhanced endothermic water-gas reaction (eqn. (10)) as the temperature increased, H₂ content increased slightly. Enhanced water-gas reactions (equation (10)) and Boudouard reactions (eqn. (4)) result in a rise in CO content as a result of a rise in gasification temperature. As a result, increasing gasification temperature leads to a greater rate of methane-steam reforming reaction (equation (10)) and decreases the amount of CH₄. The products in endothermic reactions such as 1 and 2 are favored by Le Chatelier’s principle when the temperature is higher.

4.5. Model Optimization and Validation

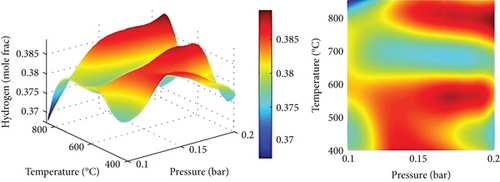
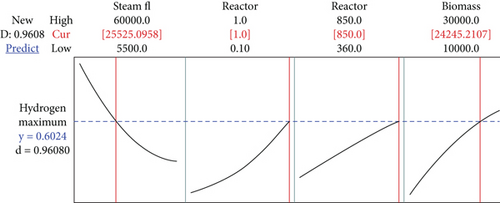
The maximum hydrogen value obtained using ASPEN Plus for the gasification of the biomass, corn cob with the input parameters such as steam flow of 60000 kg/h, the reactor pressure of 1 bar, the reactor temperature of 850°C, and the biomass flow of 30000 kg/h is 0.5862 mole fraction. Minitab 17 software (RSM) was used to estimate the optimum hydrogen produced from the process simulator in mole fraction, which was 0.6024 as shown in Figure 7. The input parameters were estimated to be a steam flow of 25525.1 kg/h, the reactor pressure was 1 bar, the reactor temperature was 850°C, and the biomass flow was 24245.2 kg/h. While ANFIS was also used to predict the mole fraction of hydrogen produced to be 0.5045, with the input parameters of steam flow, 60000 kg/h, the reactor pressure was 1 bar, the reactor temperature was 848°C, and the biomass flow was 24500 kg/h. The average hydrogen produced of 0.5085 (mole fraction) was obtained using the ASPEN Plus to validate the predicted optimal value with the experimental data. Predictive optimal model value and operational plant value were in good agreement.

5. Conclusion

The feasibility of producing syngas using corn cobs as biomass of choice was evaluated. The study performed a process simulation of steam gasification using the ASPEN Plus simulator. Using experimental data from the literature, the simulated results were validated. In addition to the gasification temperature, the steam-to-biomass ratio results in various effects on gas composition, gas yield, char yield, and H₂/CO. Based on the simulated results, the yield of the gas was positively influenced by an increase in steam-to-biomass ratio from 0.8 to 2.0. The simulations show that an acceptable level of H₂/CO gas could be produced under certain conditions such as steam flow of 23854.6 kg/h, the reactor pressure was 1 bar, the reactor temperature was 847.9°C, and the biomass flow was 23141.8 kg/h. Compared to the combustion of corn cobs (biomass) and without pretreatment, steam gasification significantly increased gas yield but decreased char yield. Due to the need to address the energy concerns, research in this direction using artificial intelligence integrated with process simulation will help provide relevant industrial condition that will give appropriate opportunity for understanding and constructing the optimum design for large-scale production of hydrogen.

5.1. Limitations of the Study

By coupling several gasification technologies, it is possible to overcome the limitations of each technology individually. In spite of this, hydrogen production is expected to incur higher operating costs.

5.2. Future Perspectives and Directions of the Study

The biomass gasification and catalytic gasification mechanisms must be determined in order to optimize H₂ yield and control product composition. Moreover, integrating multiple gasification technologies will produce more hydrogen, as well as lower cost of production.

Conflicts of Interest

The authors declare that they have no conflicts of interest

Authors’ Contributions

Conceptualization, review, simulation, supervision, and modeling were conducted by Anthony I. Okoji; cosupervision, analysis, interpretation, review, and editing were conducted by Abiola E. Taiwo; analysis and interpretation were conducted by John Busayo Adeoye; review and editing were conducted by Paul Musonge; writing of the first draft preparation was conducted by David Olamide Makinde; review and editing were conducted by Comfort Nneka Okoji.

Acknowledgments

Open access funding is enabled and organized by SANLiC Gold.

Open Research

Data Availability

Data is available on reasonable request from the corresponding author.

References

1 Nhuchhen D. R. and Salam P. A., Estimation of higher heating value of biomass from proximate analysis: a new approach, Fuel. (2012) 99, 55–63, https://doi.org/10.1016/j.fuel.2012.04.015, 2-s2.0-84862170995.
10.1016/j.fuel.2012.04.015
CAS Web of Science® Google Scholar
2 Özyuğuran A. and Yaman S., Prediction of calorific value of biomass from proximate analysis, Energy Procedia. (2017) 107, 130–136, https://doi.org/10.1016/j.egypro.2016.12.149, 2-s2.0-85015436555.
10.1016/j.egypro.2016.12.149
Google Scholar
3 Taiwo A. E., Madzimbamuto T. F., and Ojumu T. V., M. Daramola and A. Ayeni, Development of an Integrated Process for the Production and Recovery of Some Selected Bioproducts From Lignocellulosic Materials, Valorization of Biomass to Value-Added Commodities, 2020, Springer, Cham, Green Energy and Technology, https://doi.org/10.1007/978-3-030-38032-8_21.
10.1007/978-3-030-38032-8_21
Google Scholar
4 Amran Y. A., Amran Y. M., Alyousef R., and Alabduljabbar H., Renewable and sustainable energy production in Saudi Arabia according to Saudi Vision 2030; current status and future prospects, Journal of Cleaner Production. (2020) 247, article 119602, https://doi.org/10.1016/j.jclepro.2019.119602.
10.1016/j.jclepro.2019.119602
Web of Science® Google Scholar
5 Betiku E. and Taiwo A. E., Modeling and optimization of bioethanol production from breadfruit starch hydrolyzate vis-à-vis response surface methodology and artificial neural network, Renewable Energy. (2015) 74, 87–94, https://doi.org/10.1016/j.renene.2014.07.054, 2-s2.0-84906234025.
10.1016/j.renene.2014.07.054
CAS Web of Science® Google Scholar
6 Oloko-Oba M. I., Taiwo A. E., Ajala S. O., Solomon B. O., and Betiku E., Performance evaluation of three different-shaped bio-digesters for biogas production and optimization by artificial neural network integrated with genetic algorithm, Sustainable Energy Technologies and Assessments. (2018) 26, 116–124, https://doi.org/10.1016/j.seta.2017.10.006, 2-s2.0-85032576196.
10.1016/j.seta.2017.10.006
Web of Science® Google Scholar
7 Quarton C. J., Tlili O., Welder L., Mansilla C., Blanco H., Heinrichs H., Leaver J., Samsatli N. J., Lucchese P., Robinius M., and Samsatli S., The curious case of the conflicting roles of hydrogen in global energy scenarios, Sustainable Energy & Fuels. (2020) 4, no. 1, 80–95, https://doi.org/10.1039/C9SE00833K.
10.1039/C9SE00833K
CAS Web of Science® Google Scholar
8 Rasheed T., Anwar M. T., Ahmad N., Sher F., Khan S. U.-D., Ahmad A., Khan R., and Wazeer I., Valorisation and emerging perspective of biomass based waste-to-energy technologies and their socio-environmental impact: a review, Journal of Environmental Management. (2021) 287, article 112257, https://doi.org/10.1016/j.jenvman.2021.112257.
10.1016/j.jenvman.2021.112257
Web of Science® Google Scholar
9 Park C., Joshi R. K., Falascino E., Pottimurthy Y., Xu D., Wang D., Sunny A., Hwang S., Joshi A. S., Mohapatra P., Kumar S., Zhang Q., Meng Q., Shah V., Tong A., and Fan L. S., Biomass gasification: sub-pilot operation of >600 h with extensive tar cracking property and high purity syngas production at H2: CO ratio∼2 using moving bed redox looping technology, Fuel Processing Technology. (2023) 252, article 107966, https://doi.org/10.1016/j.fuproc.2023.107966.
10.1016/j.fuproc.2023.107966
Web of Science® Google Scholar
10 Hasanzadeh R., Azdast T., Mojaver M., and Park C. B., High-efficiency and low-pollutant waste polystyrene and waste polystyrene foam gasification: comprehensive comparison analysis, multi-objective optimization and multi-criteria decision analysis, Fuel. (2022) 316, article 123362, https://doi.org/10.1016/j.fuel.2022.123362.
10.1016/j.fuel.2022.123362
Web of Science® Google Scholar
11 Hasanzadeh R., Mojaver P., Chitsaz A., Mojaver M., Jalili M., and Rosen M. A., Biomass and low-density polyethylene waste composites gasification: orthogonal array design of Taguchi technique for analysis and optimization, International Journal of Hydrogen Energy. (2022) 47, no. 67, 28819–28832, https://doi.org/10.1016/j.ijhydene.2022.06.244.
10.1016/j.ijhydene.2022.06.244
CAS Web of Science® Google Scholar
12 Li G., Chang Y., Chen L., Liu F., Ma S., Wang F., and Zhang Y., Process design and economic assessment of butanol production from lignocellulosic biomass via chemical looping gasification, Bioresource Technology. (2020) 316, article 123906, https://doi.org/10.1016/j.biortech.2020.123906, 32739580.
10.1016/j.biortech.2020.123906
PubMed Web of Science® Google Scholar
13 Zhang X., Li H., Liu L., Bai C., Wang S., Zeng J., Liu X., Li N., and Zhang G., Thermodynamic and economic analysis of biomass partial gasification process, Applied Thermal Engineering. (2018) 129, 410–420, https://doi.org/10.1016/j.applthermaleng.2017.10.069, 2-s2.0-85031107720.
10.1016/j.applthermaleng.2017.10.069
CAS Web of Science® Google Scholar
14 Pala L. P. R., Wang Q., Kolb G., and Hessel V., Steam gasification of biomass with subsequent syngas adjustment using shift reaction for syngas production: an Aspen Plus model, Renewable Energy. (2017) 101, 484–492, https://doi.org/10.1016/j.renene.2016.08.069, 2-s2.0-84987985221.
10.1016/j.renene.2016.08.069
CAS Web of Science® Google Scholar
15 Keche A. J., Gaddale A. P. R., and Tated R. G., Simulation of biomass gasification in downdraft gasifier for different biomass fuels using ASPEN PLUS, Clean Technologies and Environmental Policy. (2015) 17, no. 2, 465–473, https://doi.org/10.1007/s10098-014-0804-x, 2-s2.0-84957877837.
10.1007/s10098-014-0804-x
CAS Web of Science® Google Scholar
16 Pauls J. H., Mahinpey N., and Mostafavi E., Simulation of air-steam gasification of woody biomass in a bubbling fluidized bed using Aspen Plus: a comprehensive model including pyrolysis, hydrodynamics and tar production, Biomass and Bioenergy. (2016) 95, 157–166, https://doi.org/10.1016/j.biombioe.2016.10.002, 2-s2.0-84992397235.
10.1016/j.biombioe.2016.10.002
CAS Web of Science® Google Scholar
17 Hasanzadeh R., Mojaver P., Azdast T., Khalilarya S., and Chitsaz A., Developing gasification process of polyethylene waste by utilization of response surface methodology as a machine learning technique and multi-objective optimizer approach, International Journal of Hydrogen Energy. (2023) 48, no. 15, 5873–5886, https://doi.org/10.1016/j.ijhydene.2022.11.067.
10.1016/j.ijhydene.2022.11.067
CAS Web of Science® Google Scholar
18 Mojaver P., Khalilarya S., and Chitsaz A., Multi-objective optimization using response surface methodology and exergy analysis of a novel integrated biomass gasification, solid oxide fuel cell and high-temperature sodium heat pipe system, Applied Thermal Engineering. (2019) 156, 627–639, https://doi.org/10.1016/j.applthermaleng.2019.04.104, 2-s2.0-85064738125.
10.1016/j.applthermaleng.2019.04.104
CAS Web of Science® Google Scholar
19 Chalermsinsuwan B., Li Y.-H., and Manatura K., Optimization of gasification process parameters for COVID-19 medical masks using response surface methodology, Alexandria Engineering Journal. (2023) 62, 335–347, https://doi.org/10.1016/j.aej.2022.07.037.
10.1016/j.aej.2022.07.037
Web of Science® Google Scholar
20 Mojaver P., Hasanzadeh R., Chitsaz A., Azdast T., and Mojaver M., Tri-objective central composite design optimization of co-gasification of eucalyptus biomass and polypropylene waste, Biomass Conversion and Biorefinery. (2022) 14, no. 4, 4829–4841.
10.1007/s13399-022-02597-9
Web of Science® Google Scholar
21 Amiri M., Najafi A. A., and Gheshlaghi K., Response surface methodology and genetic algorithm in optimization of cement clinkering process, Journal of Applied Sciences. (2008) 8, no. 15, 2732–2738, https://doi.org/10.3923/jas.2008.2732.2738, 2-s2.0-67649276934.
10.3923/jas.2008.2732.2738
CAS Google Scholar
22 Ozonoh M., Oboirien B., and Daramola M., Optimization of process variables during torrefaction of coal/biomass/waste tyre blends: application of artificial neural network & response surface methodology, Biomass and Bioenergy. (2020) 143, article 105808, https://doi.org/10.1016/j.biombioe.2020.105808.
10.1016/j.biombioe.2020.105808
Web of Science® Google Scholar
23 Inayat M., Sulaiman S. A., Shahbaz M., and Bhayo B. A., Application of response surface methodology in catalytic co-gasification of palm wastes for bioenergy conversion using mineral catalysts, Biomass and Bioenergy. (2020) 132, article 105418, https://doi.org/10.1016/j.biombioe.2019.105418.
10.1016/j.biombioe.2019.105418
Web of Science® Google Scholar
24 Fozer D., Kiss B., Lorincz L., Szekely E., Mizsey P., and Nemeth A., Improvement of microalgae biomass productivity and subsequent biogas yield of hydrothermal gasification via optimization of illumination, Renewable Energy. (2019) 138, 1262–1272, https://doi.org/10.1016/j.renene.2018.12.122, 2-s2.0-85062110654.
10.1016/j.renene.2018.12.122
CAS Web of Science® Google Scholar
25 Uslu S., Optimization of diesel engine operating parameters fueled with palm oil-diesel blend: comparative evaluation between response surface methodology (RSM) and artificial neural network (ANN), Fuel. (2020) 276, https://doi.org/10.1016/j.fuel.2020.117990.
10.1016/j.fuel.2020.117990
Web of Science® Google Scholar
26 Wróbel M., Mudryk K., Jewiarz M., Głowacki S., and Tulej W., Characterization of selected plant species in terms of energetic use. Renewable Energy Sources: Engineering, Technology, Innovation: ICORES 2017, 2018, Springer, 671–681.
Google Scholar
27 Anukam A., Goso B. P., Okoh O. O., and Mamphweli S. N., Studies on characterization of corn cob for application in a gasification process for energy production, Journal of Chemistry. (2017) 2017, 9, https://doi.org/10.1155/2017/6478389, 2-s2.0-85021648163, 6478389.
10.1155/2017/6478389
Web of Science® Google Scholar
28 Formica M., Frigo S., and Gabbrielli R., Development of a new steady state zero-dimensional simulation model for woody biomass gasification in a full scale plant, Energy Conversion and Management. (2016) 120, 358–369, https://doi.org/10.1016/j.enconman.2016.05.009, 2-s2.0-84965049874.
10.1016/j.enconman.2016.05.009
CAS Web of Science® Google Scholar
29 Rupesh S., Muraleedharan C., and Arun P., ASPEN Plus modelling of air–steam gasification of biomass with sorbent enabled CO2 capture, Resource-Efficient Technologies. (2016) 2, no. 2, 94–103, https://doi.org/10.1016/j.reffit.2016.07.002.
10.1016/j.reffit.2016.07.002
Google Scholar
30 Hasanzadeh R., Mojaver P., Khalilarya S., and Azdast T., Air co-gasification process of LDPE/HDPE waste based on thermodynamic modeling: hybrid multi-criteria decision-making techniques with sensitivity analysis, International Journal of Hydrogen Energy. (2023) 48, no. 6, 2145–2160, https://doi.org/10.1016/j.ijhydene.2022.10.101.
10.1016/j.ijhydene.2022.10.101
CAS Web of Science® Google Scholar
31 Adnan M. A. and Hossain M. M., Gasification performance of various microalgae biomass–a thermodynamic study by considering tar formation using Aspen Plus, Energy Conversion and Management. (2018) 165, 783–793, https://doi.org/10.1016/j.enconman.2018.03.078, 2-s2.0-85044965443.
10.1016/j.enconman.2018.03.078
CAS Web of Science® Google Scholar
32 Chen Y., Yu G., Long Y., Teng J., You X., Liao B.-Q., and Lin H., Application of radial basis function artificial neural network to quantify interfacial energies related to membrane fouling in a membrane bioreactor, Bioresource Technology. (2019) 293, article 122103, https://doi.org/10.1016/j.biortech.2019.122103, 2-s2.0-85071878624.
10.1016/j.biortech.2019.122103
Web of Science® Google Scholar
33 Shahbaz M., Yusup S., Inayat A., Patrick D. O., Pratama A., and Ammar M., Optimization of hydrogen and syngas production from PKS gasification by using coal bottom ash, Bioresource Technology. (2017) 241, 284–295, https://doi.org/10.1016/j.biortech.2017.05.119, 2-s2.0-85019659464, 28575792.
10.1016/j.biortech.2017.05.119
CAS PubMed Web of Science® Google Scholar
34 Wu D., Zhang D., Liu S., Jin Z., Chowwanonthapunya T., Gao J., and Li X., Prediction of polycarbonate degradation in natural atmospheric environment of China based on BP-ANN model with screened environmental factors, Chemical Engineering Journal. (2020) 399, article 125878, https://doi.org/10.1016/j.cej.2020.125878.
10.1016/j.cej.2020.125878
Web of Science® Google Scholar
35 Zhang X., Lee S.-Y., Luo H., and Liu H., A prediction model of sleep disturbances among female nurses by using the BP-ANN, Journal of Nursing Management. (2019) 27, no. 6, 1123–1130, https://doi.org/10.1111/jonm.12782, 2-s2.0-85066077284, 31006161.
10.1111/jonm.12782
CAS PubMed Web of Science® Google Scholar
36 Demuth H. and Beale M., Neural Network Toolbox for Use with MATLAB: User′s Guide; Computation, Visualization, Programming, 2000, MathWorks Incorporated.
Google Scholar
37 Okoji A., Anozie A., and Omoleye J., Evaluation of optimization techniques for predicting exergy efficiency of the cement raw meal production process, Cogent Engineering. (2021) 8, no. 1, article 1930493, https://doi.org/10.1080/23311916.2021.1930493.
10.1080/23311916.2021.1930493
Web of Science® Google Scholar
38 Okoji A. I., Anozie A. N., Omoleye J. A., Taiwo A. E., and Babatunde D. E., Evaluation of adaptive neuro-fuzzy inference system-genetic algorithm in the prediction and optimization of NOx emission in cement precalcining kiln, Environmental Science and Pollution Research. (2023) 30, no. 19, 54835–54845, https://doi.org/10.1007/s11356-023-26282-0, 36882651.
10.1007/s11356-023-26282-0
CAS PubMed Web of Science® Google Scholar
39 Okoji C., Okoji A. I., Ibrahim M. S., and Obinna O., Comparative analysis of adaptive neuro-fuzzy inference system (ANFIS) and RSRM models to predict DBP (trihalomethanes) levels in the water treatment plant, Arabian Journal of Chemistry. (2022) 15, no. 6, article 103794, https://doi.org/10.1016/j.arabjc.2022.103794.
10.1016/j.arabjc.2022.103794
Web of Science® Google Scholar
40 VU-Bac N., Lahmer T., Zhang Y., Zhuang X., and Rabczuk T., Stochastic predictions of interfacial characteristic of polymeric nanocomposites (PNCs), Composites Part B: Engineering. (2014) 59, 80–95, https://doi.org/10.1016/j.compositesb.2013.11.014, 2-s2.0-84890447496.
10.1016/j.compositesb.2013.11.014
CAS Web of Science® Google Scholar
41 Çelebican Ö., İnci İ., and Baylan N., Modeling and optimization of formic acid adsorption by multiwall carbon nanotube using response surface methodology, Journal of Molecular Structure. (2020) 1203, article 127312, https://doi.org/10.1016/j.molstruc.2019.127312.
10.1016/j.molstruc.2019.127312
Web of Science® Google Scholar
42 Detchusananard T., Im-Orb K., Maréchal F., and Arpornwichanop A., Analysis of the sorption-enhanced chemical looping biomass gasification process: performance assessment and optimization through design of experiment approach, Energy. (2020) 207, article 118190, https://doi.org/10.1016/j.energy.2020.118190.
10.1016/j.energy.2020.118190
Web of Science® Google Scholar
43 Jian M., Hongdong Z., and Jingjing Y., Development and application of artificial neural networks, Electronic Design Engineering. (2011) 24.
Google Scholar
44 Hu Y., Cheng Q., Wang Y., Guo P., Wang Z., Liu H., and Akbari A., Investigation of biomass gasification potential in syngas production: characteristics of dried biomass gasification using steam as the gasification agent, Energy & Fuels. (2019) 34, 1033–1040.
10.1021/acs.energyfuels.9b02701
Web of Science® Google Scholar
45 Turn S., Kinoshita C., Zhang Z., Ishimura D., and Zhou J., An experimental investigation of hydrogen production from biomass gasification, Hydrogen Energy. (1998) 23, no. 8, 641–648, https://doi.org/10.1016/S0360-3199(97)00118-3.
10.1016/S0360-3199(97)00118-3
CAS Web of Science® Google Scholar
46 Kartal F. and Özveren U., A comparative study for biomass gasification in bubbling bed gasifier using Aspen HYSYS, Bioresource Technology Reports. (2021) 13, article 100615, https://doi.org/10.1016/j.biteb.2020.100615.
10.1016/j.biteb.2020.100615
Google Scholar
47 Mazumder J. and De Lasa H. I., Catalytic steam gasification of biomass surrogates: thermodynamics and effect of operating conditions, Chemical Engineering Journal. (2016) 293, 232–242, https://doi.org/10.1016/j.cej.2016.02.034, 2-s2.0-84959261962.
10.1016/j.cej.2016.02.034
CAS Web of Science® Google Scholar

Citing Literature

All articles

Process Integration of Hydrogen Production Using Steam Gasification and Water-Gas Shift Reactions: A Case of Response Surface Method and Machine Learning Techniques

Abstract

1. Introduction

2. Materials and Methods

3. Model Description