This paper presents a modification of the Differential Transform Method (ModDTM) formulated so that the search direction of the solution is along a spatial axis (x). It is shown that the method is applicable to a wide spectrum of (1 + 1) partial differential equations, integro partial differential equations, and integral equations. The solutions obtained are in the form of a Taylor series, the coefficients of which are determined by recursively operating a differential transform of the equation. These solutions are either exact and in closed form, or are good approximations. To illustrate the application of the method, as well as to show its versatility, examples are chosen from all the categories mentioned earlier. These include equations such as the nonlinear Fisher, combined KdV-mKdV, Hunter–Saxton (H-S), Fornberg–Whitham (FW), coupled systems such as the Whitham–Broer–Kaup (WBK) and the sine-Gordon (s-G) equations, integral equations, Volterra partial integro-differential equations (PIDE), and linear and nonlinear versions of the (complex) Schröedinger equation. The Tables and 3D-plots show the good rate of convergence of the obtained solutions with the exact ones. It is thus found that the new scheme is successful in producing satisfactory results as any other method in which the conventional approach of searching for solutions along the temporal axis is followed. Further, the procedures involved are simple, and hence may be operated with great ease.

1. Introduction

Finding analytical solutions of partial differential equations (PDE) is of vital importance because of their wide range of applications in engineering, medicine and other sciences. Various methods have been devised for this purpose such as the classical methods, which are particularly applicable to linear PDEs, and semianalytical methods such as the Adomian Decomposition Method (ADM), the Homotopy Perturbation Method (HPM), and the Differential Transformation Method (DTM), among several others, and their improvements and adaptations. The main advantage of semianalytical methods such as those mentioned here is that they are applicable to a wider category of differential equations (DE), including nonlinear PDEs (NLPDE), integro-differential equations, fractional PDEs, and fuzzy PDEs. In [1], Lu and Zheng applied the ADM, as well as ADM with integrating factor (ADMIF), to symbolically solve PDEs without specifically prescribed initial data. The Elzaki transform was combined with the projected DTM to solve the Schrödinger equation in [2]. Sivasundaram, Kumar, and Singh [3] applied the sine-Gordon Expansion Method (SGEM) and its rational form (RSGEM), which are procedures derived from the solution of the sine-Gordon (s-G) equation, to determine waveform solutions of the first of the Kadomtsev–Petviashvili hierarchy. In another modification, the DTM was coupled with the techniques of Laplace transformation and Padé approximation for solving Volterra IDE and pantograph type DEs with proportional delays [4]. In recent years, there have been devised a multitude of adaptations of the standard methods to cater to fractional PDE (FPDEs). These equations are significant since several phenomena in the fields of electrodynamics, random walk, biotechnology, signal and image processing, and nanotechnology, to name just a few, are modeled using FPDEs. Alaje et al. [5] applied a modified form of the HPM for solving a fractional version of the Korteweg de-Vries equation with Caputo fractional derivatives. The modification involves the application of a power series of arbitrary order as the initial correctional function. A revised form of the Extended Direct Algebraic Method, called the r + mEDAM, was used by Yasmin et al. [6] to extract stochastic soliton solutions of the fractional stochastic Kraenkel–Manna–Merle system. The solitons generated were in the form of trigonometric, hyperbolic, and rational functions. The Iterative Transform Method (ITM), another reliable tool suitable for PDEs, has been effectively applied for solving the fuzzy fractional Degasperis–Procesi and Camassa–Holm equations in [7]. This type of FPDEs are used as models of systems with uncertain or imprecise information, and as such have fuzzy initial conditions. By the application of the ITM, the equations were first converted into a series of ordinary differential equations (ODE), which were then solved iteratively using a recursive algorithm.

Of the different semianalytical methods in existence, the DTM is a powerful and versatile method that is applicable to a variety of equations such as ODEs, PDEs, fractional PDEs, delay DE, and fuzzy PDEs [8–11]. It was first applied in 1986 by Zhou to find solutions of electric circuit problems [11]. The method is built upon a differential transform (DT) that defines the (k, h) transform of a function, say u(x, t), as follows:

Definition 1. Let u(x, t) be a function that is continuously differentiable with respect to x. Then, the differential transform of u(x, t), denoted by U(k, h), is defined as

()

for positive integers k and h.

It is to be noted that U(k, h) is the coefficient of x^kt^h in the Taylor series of the function developed about the origin. When applied to a DE, it gets converted to an algebraic recurrence relation, which in turn generates the Taylor series coefficients of the solution u(x, t). The inverse DT given by Definition 2 is then applied to determine u(x, t). As is known, the Taylor series is convergent only in narrow neighborhoods of (0, 0), which is about which the DT above is defined. Thus, in order to obtain a good approximation of the exact solution to a given problem, a large number of terms is required in the series representation. This makes the computations involved in the DTM, voluminous. Additionally, the complexity of the transform is expected to increase with the complexity of the equation. These are aspects of the DTM that will be addressed by the new modification.

Definition 2.

()

More often than not, the existing classical and semianalytical methods, including the DTM, use procedures that are directed along the time-axis. The rationale behind such a practice might be the fact that the problems modeled by the equations solved are deemed to be evolving with time. Moreover, they are mostly of order two in the time variable t, and hence require fewer initial conditions. Nevertheless, the other independent variable in the equation, which is most often a spatial variable, has the same theoretical significance as the temporal one. Hence, it is equally possible to consider the PDE to be evolving with respect to this variable, and so may be solved as a space-dependent equation. This idea was examined in [12] by the formulation of a new modification of the DTM, called the ModDTM, which is short for modified DTM. In this modification, the differential transform (1) is refined in such a way that a function u(x, t) gets represented as an infinite series containing powers of x with functions of t as coefficients, as opposed to the procedure of the DTM which generates series solutions involving powers of both x and t. Thus, in the application of the ModDTM a PDE will be transformed to an ODE in t, creating a recurrence relation that will be applied recursively to find the unknown coefficients in the series solution, thereby simplifying the procedures comparatively. It is also expected that the new procedure will require a lesser volume of computations to generate solutions with convergence properties similar to that of the DTM generated solution, even when applied to NLPDEs of high complexity, as well as to other types of DEs.

Boundary value problems (BVP) form a significant class of DEs due to their applications in fluid mechanics and other engineering problems, as well as in the modeling of tumor and its treatment. Even though the DTM is applicable to BVPs of ODEs [13, 14], the method is not well suited to be applied to such problems of PDEs. Since the ModDTM focuses on finding solutions in the x-direction, the prescribed initial data correspond to x. This feature of the method may facilitate using the ModDTM with a suitable adaptation for solving BVPs of PDEs, thereby creating a way forward to deal with such problems.

In this paper, the ModDTM is re-introduced as a method for solving not only NLPDEs, but also other types of equations, such as coupled systems of nonlinear PDEs, integral equations, partial integro-differential equations, and equations involving the complex variable i. The remaining part of the paper contains the following sections. Section 2 discusses the methodology of the ModDTM in detail. In this section the properties of the method and the symbolic derivation of the recurrence relation that determines the coefficients occurring in the power series solution are included. Convergence of the solutions is also proved theoretically. Illustrative examples are found in Section 3. They include NLPDEs such as the Fishers, the combined KdV-mKdV, the Hunter–Saxton (H-S) and the Fornberg–Whitham equations. These equations are of high complexity since they contain several nonlinear terms. The last two involve cross-derivatives as well, the presence of which is usually dealt with a suitable variable change in order to remove the cross derivatives. This is to avoid spurious solutions and other instabilities that arise due to their presence [15]. Coupled (1 + 1) systems like the Whitham–Broer–Kaup (WBK) equations and the sine-Gordon equations (s-G) are also included. Such systems are used to model problems of physical and engineering sciences such as fluid flow, reaction-diffusion systems, spread of epidemics and population growth/decay, which cannot be represented completely by single PDEs as they involve the simultaneous occurrence of several processes. Integral equations (IE) form the next category of equations solved. These equations contain the integral of the function that is to be determined, instead of its derivatives. An IE is equivalent to a corresponding differential equation combined with suitable initial or boundary conditions. Large-scale control-volume analyses, such as those required in fluid flow problems, are possible with solutions of integral equations rather than with those obtained by solving the corresponding differential equations. This is so because the domain of application of the former is much larger than that of the latter [16]. IE are followed by partial integro-differential equations (PIDE). This type of equations finds applications in areas of probability theory, fluid mechanics, and epidemiology [17, 18]. They contain both the derivatives as well as the integral of the unknown function. The section ends with the Schröedinger equation, the most important equation in quantum wave theory [19] as it describes different types of microscopic phenomena in the best possible manner. The Schröedinger equation serves as a model for problems in optics, plasma physics, superconductivity, in addition to those in quantum mechanics [20]. In Section 4, the ModDTM is compared with the DTM and the Elzaki Homotopy Transformation Perturbation method obtained by coupling the HPM with Elzaki Transformation. Discussion of results is included in Section 5. Finally, conclusions about the work are drawn in Section 6.

2. Methodology of the Modified Differential Transform Method

The modified differential transform method (ModDTM) [12] is a variation of the DTM. The difference is mainly to do with the way in which a function is transformed in the two methods. While in the DTM, the transform of a function u(x, t) is a constant as seen in (1), its (modified) differential transform (ModDT) is a function of t, as defined below [12].

Definition 3. Let u(x, t) be a function that is continuously differentiable with respect to x. Then, the differential transform (ModDT) of u(x, t), denoted by U_k(t), is defined as

()

for every positive integer k.

Thus, the k th transform of u(x, t) is determined by differentiating the function partially with respect to x, k times, and then evaluating the resulting function at x = 0. Since the ModDT of u(x, t) is a function of t, the inverse ModDT is defined in such a way that the function will be represented as an infinite series in x, in which the coefficients of the terms are functions of t, as represented below [12].

Definition 4. Suppose U_k(t) is the k^th transform of the function u(x, t). Then its inverse transform is defined as

()

2.1. Properties of the Modified Differential Transform

The properties stated below may be deduced from definition (3) of ModDT [12].

Theorem 1. If w(x, t) = u(x, t) ± v(x, t), W_k(t) = U_k(t) ± V_k(t).

Theorem 2. If w(x, t) = αu(x, t), α ∈ R, W_k(t) = αU_k(t).

Theorem 3. If w(x, t) = u_x, W_k(t) = (k + 1)U_k+1(t).

Theorem 4. If w(x, t) = u_t, W_k(t) = ∂/∂t[U_k(t)].

Theorem 5. If w(x, t) = (∂^ru/∂x^r), W_k(t) = (k + 1)(k + 2) … (k + r)U_k+r(t).

Theorem 6. If w(x, t) = (∂^hu/∂t^h), W_k(t) = ∂^h/∂t^h[U_k(t)].

Theorem 7. If w(x, t) = u(x, t)v(x, t),

()

Theorem 8. If w(x, t) = uu_x,

()

Theorem 9. If w(x, t) = u_xu_xx,

()

Theorem 10. If w(x, t) = uu_xxx,

()

Theorem 11. If w(x, t) = u³,

()

Theorem 12. If w(x, t) = x^mf(t), then

()

where δ is the kronecker δ function.

Theorem 13. If w(x, t) = c, where c is a constant, then

()

Theorem 14. If w(x, t) = e^x, then

()

Theorem 15. If w(x, t) = e^x+t, then

()

Theorem 16. If , then,

()

Theorem 17. If U_k(t), V_k(t), H_k(t), and W_k(t) denote the transforms of u(x, t), v(x, t), h(x, t), and w(x, t), respectively, then

(a)
given that
()
(b)
given that
()

2.2. Derivation of the Recurrence Relation

When presented with a PDE, the first procedure of the ModDTM is to determine the transform of the equation by applying the definitions and properties stated above. The transformed equation can generally be operated algebraically, even though it will turn out to be a first order differential equation in t. By its recursive operation, the coefficients of the power series representation of the solution function are determined, the first few of which are obtained from the initial conditions. The final step is to determine the solution by using the inverse transform. In this section, the symbolic form of the said recurrence relation is derived theoretically.

Consider the representation of a PDE given by L(u) + R(u) + N(u) = f(x, t), where L is the linear operator in the equation denoting the highest order partial derivative with respect to x, N is the nonlinear operator (if present), while R denotes the remaining terms. f(x, t) is a forcing term, which is zero if the equation is homogeneous. Rewriting the equation by removing all terms except L(u) to the right-hand side, one obtains

()

Applying the inverse L⁻¹ on both sides,

()

where g₀(t) = u(0, t), g₁(t) = u_x(0, t), etc. represent the initial values of u(x, t). If the differential transforms of f(x, t), R(u), and N(u) are given by

()

Equation (18) becomes

()

For the sake of illustration, assume that L ≡ ∂²/∂x², so that L⁻¹ ≡ ∬(.)dx dx. Thus,

()

Equating like powers of x on both sides of the equation, it is seen that U₀(t) = g₀(t), U₁(t) = g₁(t), and for k ≥ 2,

()

If the order of L(u) is different from two, the equation above will be modified correspondingly.

2.3. Convergence of the ModDTM

The Banach fixed point theorem [21, 22] is applied to prove the convergence of the ModDTM.

Theorem 18. Let C(Ω, ‖⋅‖_∞) be the Banach space of continuous functions on . The series converges to S ∈ C(Ω, ‖⋅‖_∞) if there exists an α given by 0 ≤ α < 1 such that ∀k ≥ 0

()

Proof 1. If the sequence of partial sums of the given series is , then S_n is given by

()

The metric induced by the norm is

()

Since each S_n belongs to C, we show that the sequence is Cauchy so as to ensure its convergence, as C is a complete space. Define a mapping T : C⟶C such that S_n = T(S_n−1), with S₀ = U₀(t). It is easy to verify that T is a contraction mapping. Also,

()

For positive integers m, n such that m > n, the following is obtained with the application of the triangle inequality.

()

Since (1 − α^m−n) < 1. As ‖U₀(t)‖ is fixed, the right-hand side of the above inequality can be made as small as required by choosing sufficiently large values of n, as 0 ≤ α < 1. Hence, given ϵ > 0, there exists a large positive integer N such that, ∀m, n > N,

()

This shows that {S_n} is a Cauchy sequence. Hence, the sequence converges to some S in C. All that is needed now is to prove that S is a fixed point of T, that is, T(S) = S. Applying the triangle inequality once again,

()

Since {S_n} is convergent, for a given ϵ > 0, and for suitably large values of m, each quantity on the right hand side of the inequality can be made smaller than ϵ/2, implying that d(S, T(S)) = 0, proving that T(S) = S. Finally, it is to be shown that S is unique. Assume, to the contrary, that there exists a such that . Then, , which is possible if, and only if, , as α < 1. Thus, S is uniquely determined as the fixed point of the mapping, completing the proof of the theorem.

Note: Alternatively, it is established that convergence occurs in Ω = [a, b] × [c, d] if, for each k ≥ 0, α_k, as defined below, is less than one.

Definition 5.

()

by reference to Theorem 18. (α_k represents the ratio of two adjacent terms in the series).

3. Numerical Examples

3.1. The Fishers Equation

The Fishers equation is a NLPDE with one nonlinear term of quadratic nonlinearity. It has wide range of applications in engineering and other sciences, and is given by [23, 24]:

()

The two initial conditions (I.C.) required for solving (31) are assumed as

()

The differential transform of (31) is found to be:

()

From the initial conditions (32):

()

Setting k = 0, 1, 2 in (33) one obtains

()

Applying inverse transform (4), the solution of the Fishers equation is

()

The exact solution of the PDE is

[23, 24]. The absolute error of the five − term truncated series solution is given in Table 1. To determine the convergence-behavior, α_k are determined as shown below.

()

Table 1. Absolute error between exact and ModDTM solutions for Fishers equation.

x	t = 0.0	t = 0.25	t = 0.5	t = 0.75	t = 1.0
0.0	0.00	0.00	0.00	0.00	0.00
0.1	1.934e − 8	3.613e − 9	1.037e − 8	3.897e − 10	7.915e − 10
0.2	5.700e − 7	1.493e − 7	3.396e − 7	1.113e − 8	2.557e − 8
0.3	3.953e − 6	1.396e − 6	2.639e − 6	7.353e − 8	1.960e − 7
0.4	1.507e − 5	7.016e − 6	1.137e − 5	2.600e − 7	8.337e − 7
0.5	4.117e − 5	2.491e − 5	3.544e − 5	6.298e − 7	2.567e − 6

The plots in Figure 1 show both the exact and the ModDTM solutions of the Fishers equation.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Graphs of exact and ModDTM solutions for Fishers equation. (a) Fishers equation: exact solution. (b) Fishers equation: ModDTM solution.

3.2. The Combined KdV-mKdV Equation

The combined KdV-mKdV or the Gardner’s equation that models internal solitary waves in shallow seas is given by [25, 26]:

()

The PDE is nonlinear with two nonlinear terms, of which 6u²u_x has a third degree nonlinearity. The differential transform of the equation is found to be

()

Three initial conditions are assumed as given below:

()

from which:

()

Set k = 0, 1, 2 in (39) to obtain:

()

and

()

The solution of the combined KdV-mKdV equation by the ModDTM is determined as

()

The absolute error of the six-term truncated series solution when compared with the exact solution u(x, t) = −1/2 + sech(x + t/2) [25, 26] is presented in Table 2. Figure 2 shows the good rate of convergence of the exact and the ModDTM solutions. The α values are found to be

()

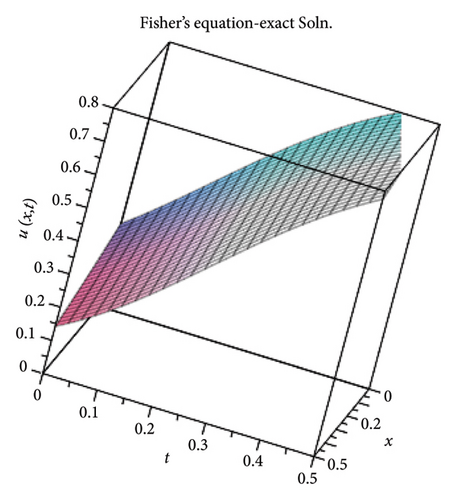
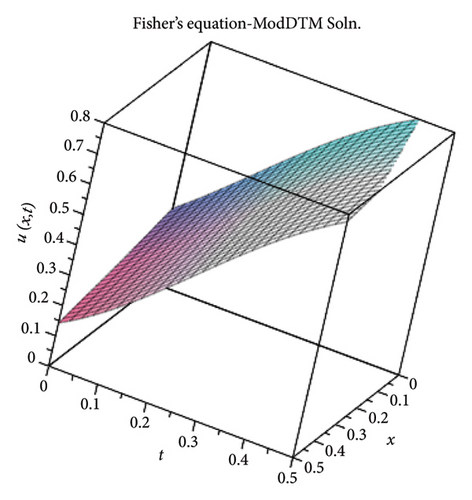
Table 2. Absolute error of ModDTM solution of combined KdV-mKdV equation.

x	t = 0.0	t = 0.1	t = 0.2	t = 0.3	t = 0.4	t = 0.5
0.0	0.00	0.00	0.00	0.00	0.00	0.00
0.1	8.438e − 8	7.941e − 8	6.270e − 8	2.854e − 8	2.684e − 8	1.048e − 7
0.2	5.336e − 6	4.977e − 6	4.114e − 6	2.593e − 6	3.279e − 7	2.687e − 6
0.3	5.959e − 5	5.481e − 5	4.536e − 5	3.029e − 5	9.259e − 6	1.752e − 5
0.4	3.259e − 4	2.952e − 4	2.419e − 4	1.631e − 4	5.839e − 5	7.012e − 5
0.5	1.202e − 3	1.072e − 3	8.661e − 4	5.784e − 4	2.113e − 4	2.257e − 4

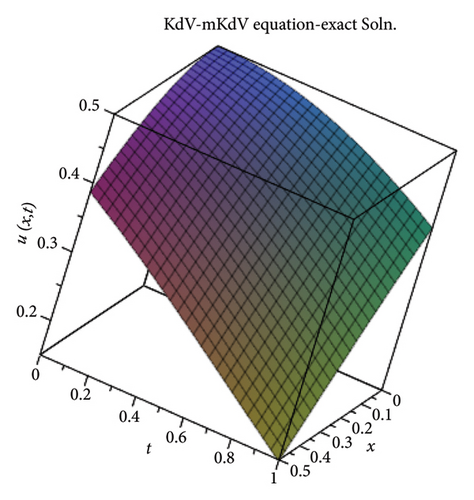
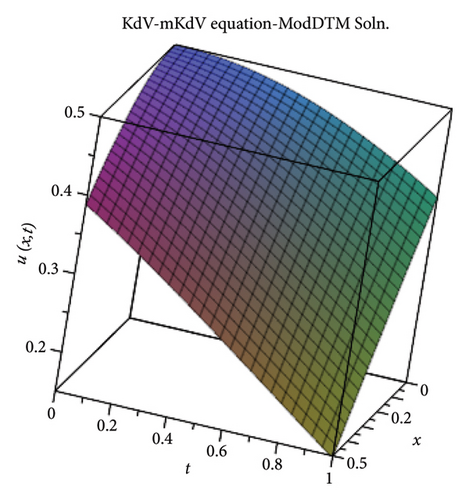
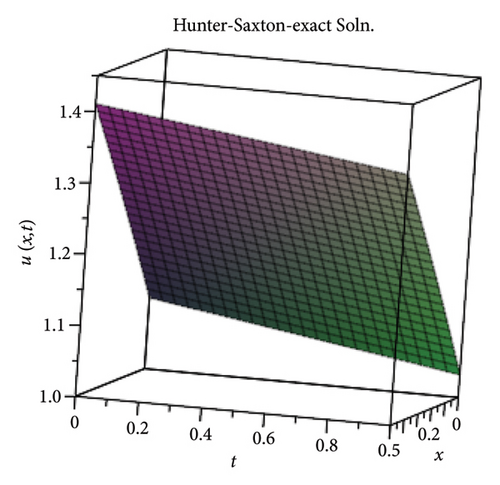
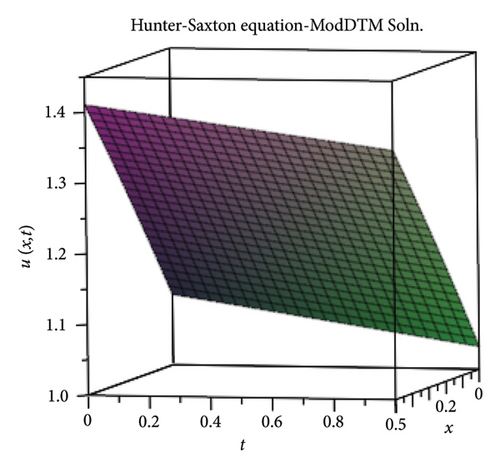
3.3. The H-S Equation

The H-S equation, originally devised as a model of the dynamics of nematic liquid crystals, describes geodesic flow on the diffeomorphism group of the circle and pseudo-spherical surfaces [24]. The equation has a mixed third order partial derivative and two nonlinear terms, and is given by [24]:

()

The differential transform of (46) is obtained as

()

The initial conditions are chosen to be

()

The transforms of (48) are:

()

Set k = 0, 1, 2 in relation (47) to obtain:

()

The solution u(x, t) by the ModDTM is thereby found to be:

()

To verify if the ModDTM solution converges to the exact solution, u(x, t) = (x − ct + 1)^(2/3) + c [24], α_k are found for k = 0, 1, …4.

()

The absolute errors of the six-term ModDTM solution are given in Table 3, and the graphs of the exact and ModDTM solution are given in Figure 3.

Table 3. Absolute error of ModDTM solution of Hunter–Saxton equation.

x	t = 0.0	t = 0.25	t = 0.5	t = 0.75	t = 1.0
0.0	0.00	0.00	0.00	0.00	0.00
0.1	1.289e − 8	2.601e − 8	5.842e − 8	1.517e − 7	4.856e − 7
0.2	7.708e − 7	1.542e − 6	3.426e − 6	8.766e − 6	2.749e − 5
0.3	8.241e − 6	1.637e − 5	3.602e − 5	9.107e − 5	2.809e − 4
0.4	4.364e − 5	8.612e − 5	1.880e − 4	4.704e − 4	1.432e − 3

3.4. The FW Equation

The FW equation determined in 1974 by Whitham [27] is a NLPDE with three nonlinear terms, and one cross-derivative. It has the form

()

For the I.C.s:

()

the solution of (53) is [28, 29].

()

The differential transform of PDE (53) is

()

From (54),

()

Setting k = 0, 1, 2 in recurrence relation (56) and solving the equations it is seen that

()

Thus, the solution of FW equation (53) with initial conditions (54) is obtained as

()

which is the exact solution of the equation. This is the same solution obtained for the equation when solved by the application of the DTM in [30].

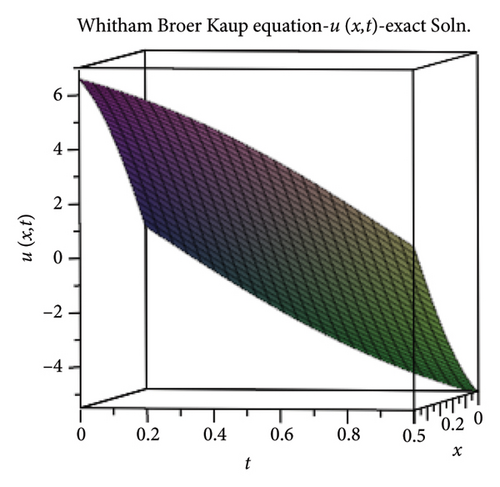
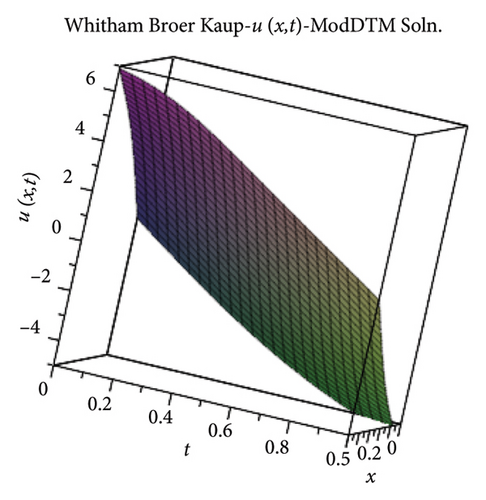
3.5. The WBK Equations

The WBK system of equations is one among several models that describe the propagation of shallow water waves that exhibit differing dispersion relations [31–35]. In particular, the system models the dynamics of tsunami water waves under gravity [34]. The general form of WBK equations is given by the coupled system [32–36]:

()

where u(x, t) represents the horizontal velocity of the waves, v(x, t) represents the height of the waves from the equilibrium position, and α and β are constants. By choosing α = 3 and β = 1 the system becomes [33]:

()

The exact solutions of (62) and (63) are [28]:

()

To solve the system by the ModDTM, initial conditions are chosen to be:

()

The differential transforms of the WBK equations are found to be:

()

From equations (65) and (66),

()

Setting k = 0 up to k = 4 in equations (67) and (68), and solving the pair of transformed equations simultaneously for each k, one obtains

()

The inverse differential transform is applied to obtain

()

To verify convergence of the ModDTM solution with the exact u, the α_k ratios of successive terms are determined as shown in the following

()

Similarly, for the 6-term truncated series (72):

()

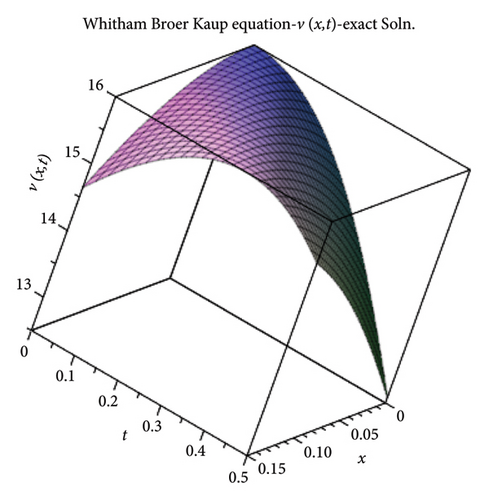
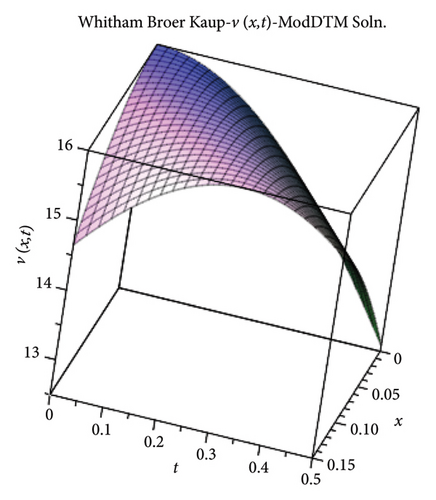
Tables 4 and 5 provide the absolute errors of the seven-term truncated series (71) and the six-term (72). Figures 4 and 5 show the exact solutions and the ModDTM solutions for u(x, t) and v(x, t).

Table 4. Absolute error of ModDTM solution of WBK equations: u(x, t).

x	t = 0.0	t = 0.1	t = 0.2	t = 0.3	t = 0.4	t = 0.5
0.00	0.00	0.00	0.00	0.00	0.00	0.00
0.05	4.300e − 8	3.830e − 8	2.340e − 8	4.000e − 9	1.100e − 8	2.300e − 8
0.10	5.438e − 6	5.046e − 6	3.302e − 6	9.011e − 7	1.304e − 6	2.707e − 6
0.15	9.110e − 5	8.771e − 5	6.058e − 5	2.060e − 5	1.783e − 5	4.369e − 5
0.20	6.643e − 4	6.627e − 4	4.809e − 4	1.921e − 4	9.854e − 5	3.046e − 4

Table 5. Absolute error of ModDTM solution of WBK equations: v(x, t).

x	t = 0.0	t = 0.1	t = 0.2	t = 0.3	t = 0.4	t = 0.5
0.00	0.00	0.00	0.00	0.00	0.00	0.00
0.05	6.020e − 6	5.400e − 6	3.370e − 6	7.000e − 7	1.660e − 6	3.080e − 6
0.10	3.789e − 4	3.554e − 4	2.363e − 4	6.924e − 5	8.628e − 5	1.868e − 4
0.15	4.209e − 3	4.115e − 3	2.905e − 3	1.064e − 3	7.404e − 4	1.983e − 3
0.20	2.285e − 2	2.325e − 2	1.733e − 2	7.457e − 3	2.737e − 3	1.018e − 2

3.6. The Coupled s-G Equations

The coupled nonlinear s-G equations is a reduced form of the Klein–Gordon equations with a potential function given by f(u, w) = cos(u − w) − 1. Both systems represent one dimensional nonlinear wave processes in bi-layer media such as hydrogen-bonded chains and molecular crystals (Frenkel–Contorova dislocation model) [37]. Other applications of the s-G equations include the representation of fluxon phenomena of stacked intrinsic Josephson junction in high temperature superconductors, and the description of open states in DNA [37, 38].

The (1 + 1) dimensional coupled s-G equations are given by [39]:

()

Functions f(x, t) and g(x, t) are source terms represented by:

()

To solve the s-G equations the following initial conditions are assumed:

()

If it is assumed that v = sin(u − w), the differential transform V_k for k = 0 to k = 4 are determined to be:

()

The transforms F_k and G_k of the source terms are

()

The differential transforms of the coupled s-G equations and the I.C.s represented by equation (79) are

()

As in the case of the WBK equations, set k = 0 up to k = 4 in the recurrence relations, and solve them in pairs to get

()

The general form of U_k and W_k are thereby:

()

Thus solutions u(x, t) and v(x, t) of the coupled s-G equations are:

()

These are the exact solutions of system (75) and (76) [39].

3.7. Volterra Integral Equation 1

The Volterra integral equation contains the integral of the function that is to be determined, instead of its derivatives. The (1 + 1) dimensional Volterra integral equation [40]

()

involves a double integral, and the kernel is a product of two functions. From the initial condition u(0, t) = sin t, U₀(t) = sin t. The differential transforms of w(x, t) = sin(x + t)(e^x−t + 1) are

()

and for k ≥ 1,

()

The transform of e^−t sin t is (δ_k,0)e^−t sin t. Finally, if w(x, t) = e^x sin x,

()

The given PIDE transforms to

()

For k = 1,

()

Solving the above equation for U₁(t), it is found that

()

Next, set k = 2 in (97) to get

()

Solving which U₂(t) = −1/2 sin t. In a similar way, setting k = 3 and four in the transform, U₃(t) = −(1/6)cos t and U₄(t) = 1/24 sin t. Hence, the solution is obtained as

()

which converges to the solution sin(x + t) [40].

3.8. Volterra Integral Equation 2

In this example of the Volterra integral equation the double integral of u(x, t) is multiplied by e^t−x [41].

()

Multiplying the equation by e^x−t:

()

The transforms of e^x−tu(x, t), e^x−t sinh(t − x), sinh(t − x),

, and sinh x − sinh t are, respectively,

()

and

()

Thereby, the transform of (103) is obtained as

()

where W_1,k, W_2,k, and W_3,k represent the transforms of e^x−t sinh(t − x), sinh(t − x), and sinh x − sinh t, respectively. To initialize the solution process, it is assumed that u(0, t) = sinh t, from which U₀(t) = sinh t. Setting k = 1 up to five in (106):

()

The solution of IE (102) is, therefore,

()

The sum on the right-hand-side converges to the exact solution of the integral equation given by sinh(t − x) [40].

3.9. First Order PIDE

The PIDE that is given below is nonhomogeneous and of first order in x [41]:

()

The differential transform of (109) is

()

The initial condition is assumed to be u(0, t) = cos t, from which U₀(t) = cos t. For k = 0, 1, 2, 3 in (110):

()

The solution of PIDE (109) is thereby

()

The series on the right-hand-side converges to u(x, t) = e^x cos t, which is the exact and closed form solution of PIDE (109) [41].

3.10. Second Order PIDE

For the second order PIDE given by [42]:

()

the following initial conditions are assumed: u(0, t) = 0 and u_x(0, t) = t. The differential transform of (113) is

()

Setting k = 0, 1, 2, 3 in (114) one obtains

()

The solution of PIDE (113) is therefore

()

which forms the exact and closed form solution [42], that may be verified by substitution.

3.11. Volterra PIDE

The third example is that of a linear and nonhomogeneous Volterra PIDE [43]:

()

The equation is solved assuming that u(0, t) = e^t, from which U₀(t) = e^t. The transform of (117) is found to be:

()

Setting k = 0, 1, 3, 4 in (118),

()

Thus,

()

This is the same solution of (117) in [43].

3.12. Linear Schröedinger Equation

In the linear Schröedinger equation [19]

()

u(x, t) is a complex function and

. To solve the equation by the ModDTM it is assumed that

()

(121) is simplified by multiplying it by i to obtain:

()

The transform of (123) is

()

From initial conditions (122):

()

Setting k = 0, 1, 2, 3, 4 in (123) gives

()

The solution of the linear Schrodinger (121) is therefore:

()

which is the exact solution [19].

3.13. Nonlinear Schröedinger Equation

In the nonlinear Schröedinger equation [19] given by

()

|u| represents the modulus of u. The two initial conditions assumed are

()

For the convenience of applying the method (128) is rewritten as

()

where

represents the conjugate of u. The differential transform of (130) is

()

From the initial conditions,

()

Following the procedure of the ModDTM, set k = 0, 1, 2 in (131) to obtain:

()

The solution of nonlinear Schröedinger (128) is therefore

()

This is the same solution obtained in [19], and is the exact solution.

4. Comparison of the ModDTM With Other Methods

While the ModDTM generates solutions in the form of a power series of x with functions of t as coefficients, other methods, with the exception of DTM, generally provide solutions that are power series of t with functions of x as coefficients. In all of these cases, good approximations of the exact solutions will be obtained with very few terms, but, this will happen only in small neighborhoods of the variable in which the series is represented: in the vicinity of x = 0 for the ModDTM, and t = 0 in the other cases. Comparatively larger values of the remaining variable will not affect the convergence considerably. As an exception comes the case of the DTM for which convergence occurs in small neighborhoods of the point about which the series has been determined, which is usually the origin (0, 0), since the solutions are in the form of a Taylor series. Besides, a larger number of terms may be needed to get the same level of accuracy.

To illustrate these aspects of the methods the case of the Fishers (31) is considered. The exact solution of the equation is

, while the ModDTM solution has been determined to be

()

The DTM solution is found to be

()

and the EHTPM solution [23] is

()

The tables that follow verify what have been stated above. In Table 6 the Exact, ModDTM, DTM and EHTPM solutions in the immediate neighborhood of (0, 0) are displayed. The good agreement of the values is evident on examination of the table.

Table 6. Comparison of exact, ModDTM, DTM, and EHTPM at points close to (0, 0).

(x, t)	Exact	ModDTM	DTM	EHTPM
(0.0, 0.0)	0.25	0.25	0.25	0.25
(0.0, 0.1)	0.3874,556,189	0.3874,556,189	0.3874,348,958	0.3874,556,206
(0.0, 0.2)	0.5344,466,455	0.5344,466,455	0.5333,333,333	0.5344,511,614
(0.1, 0.0)	0.2256,447,723	0.2256,447,916	0.2256,447,708	0.2256,447,723
(0.1, 0.1)	0.3584,269,144	0.3584,269,582	0.3584,213,332	0.3584,269,144
(0.1, 0.2)	0.5054,491,951	0.5054,492,160	0.5048,333,125	0.5054,506,464
(0.2, 0.0)	0.2026,494,300	0.2026,500,000	0.2026,493,333	0.2026,494,300
(0.2, 0.1)	0.3299,842,050	0.3299,856,093	0.3099,831,875	0.3299,842,035
(0.2, 0.2)	0.4760,647,847	0.4760,654,792	0.4757,493,320	0.4760,629,844

Table 7 exhibits the solution of the Fishers equation for values of t that are comparatively larger than that of x. It is seen that the ModDTM solution compares favorably with the exact solution, while the others deviate considerably. This property is reversed when it is x that is large, as seen in Table 8.

Table 7. Comparison of exact, ModDTM, DTM, and EHTPM for large t.

(x, t)	Exact	ModDTM	DTM	EHTPM
(0.1, 1.0)	0.9852,715,523	0.9852,715,530	0.404,504,145	170.94,775,160
(0.1, 2.0)	0.9998,996,575	0.9998,996,581	86.69,690,510	220,719.69240
(0.1, 3.0)	0.9999,993,240	0.9999,993,236	965.5,090,979	13,376,912.170
(0.1, 4.0)	0.9999,999,960	0.9999,999,956	4733.872,333	241,919,574.50
(0.1, 5.0)	1.0000000000	1.0000000000	15,660.69285	2,272,864,165.0

Table 8. Comparison of exact, ModDTM, DTM, and EHTPM for large x.

(x, t)	Exact	ModDTM	DTM	EHTPM
(1.0, 0.1)	0.14253,695,660	0.1465,278,638	0.1425,130,207	0.14253,695,660
(2.0, 0.1)	0.03327,907,174	0.1275,086,155	0.0173,828,125	0.03327,907,174
(3.0, 0.1)	0.00575,446,348	0.4852,141,971	−0.269,205,729	0.00575,446,348
(4.0, 0.1)	0.00085,920,687	1.3435,966,890	−1.623,502,605	0.00085,920,688
(5.0, 0.1)	0.00012,071,291	2.7957,439,310	−5.826,757,813	0.00012,071,291

The ModDTM-solution was truncated with 5 terms, the DTM solution with 21 terms, and the EHTPM solution with 11 terms, to determine the values presented in the tables above. Additionally, it can be verified that the transform of the Fishers equation in the application of the DTM is more complex than the one in the ModDTM, by comparing (33) with

()

which is the transform of the equation in the DTM.

5. Results and Discussion

This study was intended to examine if the ModDTM, which is a method in which the search direction of the solution is along the x axis, would yield satisfactory results as any other traditional method that solves initial value problems of the time variable. The other aim was to establish the versatility of the method, by showing that it could be applied to a wide variety of equations including, differential, integral, and PIDE.

To examine the viability of the new approach, and the adaptability of the ModDTM to various types of equations, the method was applied to four nonlinear PDE such as the Fishers, the KdV-mKdV, the H-S, and the FW equations, two systems of NLPDEs, viz., the WBK and the sine − Gordon equations, two integral equations, three PIDE, and linear and nonlinear versions of the complex Schröedinger equation. Except for the Fishers, the KdV-mKdV, the H-S, and the WBK equations, it was possible to identify the closed form of the ModDTM solutions, which coincided with the exact solutions. Even though the same cannot be claimed for the remaining equations, the truncated solutions, with only a few numbers of terms, showed a very high rate of convergence with the exact ones. For example, for the five-term truncated series solution of the Fishers equation the absolute error deviated from 7.915 × 10⁻¹⁰ to 4.117 × 10⁻⁵. The 3D graphs also showed the good agreement existing between the exact and the ModDTM solutions. Convergence was also verified by observing that the α_k were less than one. Similar analyses for the KdV-mKdV, H-S, and the WBK equations provide matching results. In the case of the WBK system, it was found that the window of convergence of the ModDTM solutions was comparatively smaller. This drawback may be improved by including more terms in the truncated series. The analysis is that the errors occurring for each function affect the other function as well, as they are interdependent. Again, v is seen to deviate more from the corresponding exact solution than u. The reason behind this rests in the fact that the series for the former had 6 terms, whereas for the latter it had 7. This happened because, to determine each U_k, V_k−1 had to be computed first symbolically.

It is also to be noted that no change of variable was needed to solve the H-S and FW equations which had cross derivatives.

6. Conclusion

This paper presents a modification of the Differential Transform Method (ModDTM) formulated so that the search direction of the solution is along a spatial axis (x). This means that solutions are sought for given initial values at x = 0, instead of at t = 0. To achieve this, a given equation is transformed to an ODE in t by using the ModDT and its properties, which are then applied recursively to find the solution. The recurrence relations used in the application of the ModDTM are less complex than their corresponding counterparts in the DTM, and as such the former method is simpler and easier to apply than the latter. Moreover, the fact that only a few number of terms is needed in the approximate truncated ModDTM-solution to produce good levels of convergence, shows that the volume of computations required for satisfactory results is low as well. The method has been well illustrated by solving a wide spectrum of equations including nonlinear PDE, integral equations, PIDE, and complex equations.

One of the aspects of the ModDTM that may be improved is that in its present form the method is applicable only to (1 + 1) PDEs. This situation may be changed by adapting the method for solving equations of higher dimensions. Suitable adaptations of the method may also make it good for fractional PDEs, especially space-fractional equations. Another possibility for future development is to adapt the ModDTM to suit boundary value problems of PDEs, since the method focuses on finding solutions in the x-direction, being prescribed initial data corresponding to the spatial variable.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors declare that funding of any kind was not received for this research or for the publication of this paper.

Open Research

Data Availability Statement

No underlying data were collected or produced in this study.

References

1 Lu T.-T. and Zheng W.-Q., Adomian Decomposition Method for First Order PDEs With Unprescribed Data, Alexandria Engineering Journal. (2021) 60, no. 2, 2563–2572, https://doi.org/10.1016/j.aej.2020.12.021.
10.1016/j.aej.2020.12.021
Google Scholar
2 Akinfe K. T. and Loyinmi A. C., The Implementation of an Improved Differential Transform Scheme on the Schrodinger Equation Governing Wave-Particle Duality in Quantum Physics and Optics, Results in Physics. (2022) 40, https://doi.org/10.1016/j.rinp.2022.105806.
10.1016/j.rinp.2022.105806
PubMed Google Scholar
3 Sivasundaram S., Kumar A., and Singh R. K., On the Complex Properties of the First Equation of the Kadomtsev-Petviashvili Hierarchy, International Journal of Mathematics and Computer in Engineering. (2024) 2, no. 1, 71–84, https://doi.org/10.2478/ijmce-2024-0006.
10.2478/ijmce-2024-0006
Google Scholar
4 Noori M., Roodabeh S., and Taghizadeh N., Modified Differential Transform Method for Solving Linear and Nonlinear Pantograph Type of Differential and Volterra Integro-Differential Equations With Proportional Delays, Advances in Difference Equations 2020. (2020) 1–25.
Google Scholar
5 Alaje A. I., Olayiwola M. O., Adedokun K. A., Adedeji J. A., and Oladapo A. O., Modified Homotopy Perturbation Method and Its Application to Analytical Solitons of Fractional-Order Korteweg–De Vries Equation, Beni-Suef University Journal of Basic and Applied Sciences. (2022) 11, no. 1, https://doi.org/10.1186/s43088-022-00317-w.
10.1186/s43088-022-00317-w
PubMed Google Scholar
6 Yasmin H., Alshehry A. S., Ganie A. H., Shafee A., and Shah R., Noise Effect on Soliton Phenomena in Fractional Stochastic Kraenkel-Manna-Merle System Arising in Ferromagnetic Materials, Scientific Reports. (2024) 14, no. 1, https://doi.org/10.1038/s41598-024-52211-3.
10.1038/s41598-024-52211-3
Google Scholar
7 Alshehry A. S., Yasmin H., Shah M. A., and Shah R., Analyzing Fuzzy Fractional Degasperis–Procesi and Camassa–Holm Equations With the Atangana–Baleanu Operator, Open Physics. (2024) 22, no. 1, https://doi.org/10.1515/phys-2023-0191.
10.1515/phys-2023-0191
Google Scholar
8 Madi F. A. M. and Abdelwahid F., Using the Differential Transform Method to Solve Non-Linear Partial Differential Equations, Journal of Advances in Mathematics and Computer Science. (2020) 35, no. 8, 34–43, https://doi.org/10.9734/jamcs/2020/v35i830311.
10.9734/jamcs/2020/v35i830311
Google Scholar
9 Abdallah H. A. and Shama A. M., Applications of Differential Transform Method to Integral Equations, American journal of Engineering Research (AJER). (2018) 7, no. 1, 71–276.
Google Scholar
10 Yavuz M. T. and Ozkol İ., Solution of Integro-Differential Difference Equations via Differential Transform Method, University Journal of Science and Engineering. (2021) 18, no. 1, 33–46.
Google Scholar
11 George S. and Sivakumar T. R., Application of Differential Transform Method to Integral and Integro-Differential Equations, Asian Journal of Applied Sciences (ISSN: 2321–0893). (2019) 7, no. 6, https://doi.org/10.24203/ajas.v7i6.6028.
10.24203/ajas.v7i6.6028
Google Scholar
12 Nayar H. and Phiri P. A., A New Modification of the Differential Transform Method, Asian Journal of Mathematics and Computer Research. (2020) 27, no. 3, 38–51.
Google Scholar
13 Ogunrinde R. B. and Ojo O. M., Application of Differential Transformation Method to Boundary Value Problems of Order Seven and Eight, American Journal of Computational Mathematics. (2018) 8, no. 03.
10.4236/ajcm.2018.83022
Google Scholar
14 Opanuga A. A., Edeki S. O., Okagbue H. I., and Akinlabi G. O., Numerical Solution of Two-Point Boundary Value Problems via Differential Transform Method, Global Journal of Pure and Applied Mathematics. (2015) 11, no. 2, 801–806.
Google Scholar
15 Company R., Egorova V. N., Jódar L., and Soleymani F., A Mixed Derivative Terms Removing Method in Multi-Asset Option Pricing Problems, Applied Mathematics Letters. (2016) 60, 108–114, https://doi.org/10.1016/j.aml.2016.04.011, 2-s2.0-84967214561.
10.1016/j.aml.2016.04.011
Web of Science® Google Scholar
16 Rahman M., Integral Equations and Their Applications, 2007, WIT Press.
Google Scholar
17 Fahim A., Araghi M. A. F., Rashidinia J., and Jalalvand M., Numerical Solution of Volterra Partial Integro-Differential Equations Based on Sinc-Collocation Method, Advances in Difference Equations 2017. (2017) 1–21.
Google Scholar
18 Gusu D. M. and Bulo C., Research Article Solutions of Nonlinear Integro-Partial Differential Equations by the Method of (G′/G, 1/G), Nonlinear Optics. (2022) 12.
Google Scholar
19 Schleich W. P., Greenberger D. M., Kobe D. H., and Scully M. O., Schrödinger Equation Revisited, Proceedings of the National Academy of Sciences. (2013) 110, no. 14, 5374–5379, https://doi.org/10.1073/pnas.1302475110, 2-s2.0-84875822268.
10.1073/pnas.1302475110
CAS PubMed Web of Science® Google Scholar
20 Ayati Z., Biazar J., and Ebrahimi S., A New Homotopy Perturbation Method for Solving Linear and Nonlinear Schroedinger Equations, Journal of Interpolation and Approximation in Scientific Computing. (2014) 2014, 1–8, https://doi.org/10.5899/2014/jiasc-00062.
10.5899/2014/jiasc-00062
Google Scholar
21 Simmons G. F., Introduction to Topology and Modern Analysis, 1963, McGraw-Hill, Inc, Singapore.
Google Scholar
22 Limaye B. V., Functional Analysis, 2006, New Age International, Delhi, India.
Google Scholar
23 Loyinmi A. C. and Akinfe T. K., Exact Solutions to the Family of Fisher’s Reaction-Diffusion Equation Using Elzaki Homotopy Transformation Perturbation Method, Engineering Reports. (2020) 2, no. 2, https://doi.org/10.1002/eng2.12084.
10.1002/eng2.12084
Google Scholar
24 Saha D. and Sengupta S., A Comparative Analysis of DTM and HAM Solutions for Hunter-Saxton Equation and Fisher Equation, International Journal of Mathematics Trends and Technology. (2018) 56, no. 4, 236–243, https://doi.org/10.14445/22315373/ijmtt-v56p534.
10.14445/22315373/IJMTT-V56P534
Google Scholar
25 Manafianheris J. and Aghdaei M. F., Application of the Exp-Function Method for Solving the Combined KdV-mKdV and Gardner-KP Equations, Mathematical Sciences. (2012) 6, 68–8, https://doi.org/10.1186/2251-7456-6-68.
10.1186/2251-7456-6-68
Google Scholar
26 Günerhan H., Exact Traveling Wave Solutions of the Gardner Equation by the Improved Tanθϑ-Expansion Method and the Wave Ansatz Method, Mathematical Problems in Engineering. (2020) .
10.1155/2020/5926836
Google Scholar
27 Whitham G. B., Variational Methods and Applications to Water Waves, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. (1967) 299, no. 1456, 6–25.
10.1098/rspa.1967.0119
Web of Science® Google Scholar
28 Abidi F. and Omrani K., The Homotopy Analysis Method for Solving the Fornberg–Whitham Equation and Comparison With Adomian’s Decomposition Method, Computers and Mathematics with Applications. (2010) 59, no. 8, 2743–2750, https://doi.org/10.1016/j.camwa.2010.01.042, 2-s2.0-77950187598.
10.1016/j.camwa.2010.01.042
Web of Science® Google Scholar
29 Karbalaie A., Muhammed H. H., Shabani M., and Mohammad M. M., Exact Solution of Partial Differential Equation Using Homo-Separation of Variables, International Journal of Nonlinear Science. (2014) 17, no. 1, 84–90.
Google Scholar
30 Nayar H. and Phiri P. A., The Fornberg-Whitham Equation Solved by the Differential Transform Method, Journal of Advances in Mathematics and Computer Science. (2020) 35, no. 7, 85–95, https://doi.org/10.9734/jamcs/2020/v35i730306.
10.9734/jamcs/2020/v35i730306
Google Scholar
31 Mohamed M. A. and Mohamed S. T., Numerical Solution of Nonlinear System of Partial Differential Equations by the Laplace Decomposition Method and the Pade Approximation, American Journal of Computational Mathematics. (2013) 3, no. 03, 175–184.
10.4236/ajcm.2013.33026
Google Scholar
32 Ahmad J., Mushtaq M., and Sajjad N., Exact Solution of Whitham Broer-Kaup Shallow Water Wave Equations, Journal of Science and Arts. (2015) 15, no. 1.
Google Scholar
33 Nikkar A. and Ahmadihasil R., A Novel Method for Solving Nonlinear Whitham-Broer-Kaup Equation System, International Journal of Advances in Science, Engineering and Technology. (2016) 4, no. 1, 100–103.
Google Scholar
34 Wang Y., Xu H., and Sun Q., New Groups of Solutions to the Whitham-Broer-Kaup Equation, Applied Mathematics and Mechanics. (2020) 41, no. 11, 1735–1746, https://doi.org/10.1007/s10483-020-2683-7.
10.1007/s10483-020-2683-7
Google Scholar
35 Rafei M. and Daniali H., Application of the Variational Iteration Method to the Whitham–Broer–Kaup Equations, Computers and Mathematics With Applications. (2007) 54, no. 7-8, 1079–1085, https://doi.org/10.1016/j.camwa.2006.12.054, 2-s2.0-34748889861.
10.1016/j.camwa.2006.12.054
Web of Science® Google Scholar
36 Abdulkareem H. H., Ismael H. F., Panakhov E. S., and Bulut H., Some Novel Solutions of the Coupled Whitham-Broer-Kaup Equations, 4th International Conference On Computational Mathematics and Engineering Sciences (CMES-2019) 4, 2020, Springer International Publishing, Berlin, Germany, 200–208.
10.1007/978-3-030-39112-6_14
Google Scholar
37 Khusnutdinova K. R. and Pelinovsky D. E., On the Exchange of Energy in Coupled Klein–Gordon Equations, Wave Motion. (2003) 38, no. 1, 1–10, https://doi.org/10.1016/s0165-2125(03)00022-2, 2-s2.0-0038543060.
10.1016/S0165-2125(03)00022-2
Google Scholar
38 Li D., Lai H., and Lin C., Mesoscopic Simulation of the Two-Component System of Coupled Sine-Gordon Equations With Lattice Boltzmann Method, Entropy. (2019) 21, no. 6, https://doi.org/10.3390/e21060542, 2-s2.0-85068044093.
10.3390/e21060542
Google Scholar
39 Hashemi M. S., Numerical Study of the One-Dimensional Coupled Nonlinear Sine-Gordon Equations by a Novel Geometric Meshless Method, Engineering With Computers. (2021) 37, no. 4, 3397–3407, https://doi.org/10.1007/s00366-020-01001-2.
10.1007/s00366-020-01001-2
Web of Science® Google Scholar
40 Abazari R. and Kılıçman A., Numerical Study of Two-Dimensional Volterra Integral Equations by RDTM and Comparison With DTM, Abstract and Applied Analysis 2013, 2013, Hindawi, London, UK.
10.1155/2013/929478
Google Scholar
41 Dhunde R. R. and Waghmare G. L., Solving Partial Integro-Differential Equations Using Double Laplace Transform Method, American Journal of Computational and Applied Mathematics. (2015) 5, no. 1, 7–10.
Google Scholar
42 Soliman A. F., Approximate Solution of Partial Integro-Differential Equation via Modified Adomian Decomposition Method, Numerical and Computational Methods in Sciences and Engineering. (2020) 2, no. 3, 89–95.
Google Scholar
43 Moosavi Noori S. R. and Taghizadeh N., Study on Solving Two-Dimensional Linear and Nonlinear Volterra Partial Integro-Differential Equations by Reduced Differential Transform Method, Applications and Applied Mathematics: International Journal. (2020) 15, no. 1.
Google Scholar

Citing Literature

All articles

Modification of the Differential Transform Method With Search Direction Along the Spatial Axis

Abstract

1. Introduction

2. Methodology of the Modified Differential Transform Method

2.1. Properties of the Modified Differential Transform

2.2. Derivation of the Recurrence Relation

2.3. Convergence of the ModDTM

3. Numerical Examples

3.1. The Fishers Equation

3.2. The Combined KdV-mKdV Equation

3.3. The H-S Equation

3.4. The FW Equation

3.5. The WBK Equations

3.6. The Coupled s-G Equations

3.7. Volterra Integral Equation 1

3.8. Volterra Integral Equation 2

3.9. First Order PIDE

3.10. Second Order PIDE

3.11. Volterra PIDE

3.12. Linear Schröedinger Equation

3.13. Nonlinear Schröedinger Equation

4. Comparison of the ModDTM With Other Methods

5. Results and Discussion

6. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Modification of the Differential Transform Method With Search Direction Along the Spatial Axis

Abstract

1. Introduction

2. Methodology of the Modified Differential Transform Method

2.1. Properties of the Modified Differential Transform

2.2. Derivation of the Recurrence Relation

2.3. Convergence of the ModDTM

3. Numerical Examples

3.1. The Fishers Equation

3.2. The Combined KdV-mKdV Equation

3.3. The H-S Equation

3.4. The FW Equation

3.5. The WBK Equations

3.6. The Coupled s-G Equations

3.7. Volterra Integral Equation 1

3.8. Volterra Integral Equation 2

3.9. First Order PIDE

3.10. Second Order PIDE

3.11. Volterra PIDE

3.12. Linear Schröedinger Equation

3.13. Nonlinear Schröedinger Equation

4. Comparison of the ModDTM With Other Methods

5. Results and Discussion

6. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Related

Information