A novel standard trajectory design and tracking guidance used in the multiple active leap maneuver mode for hypersonic glide vehicles (HGVs) is proposed in this paper. First, the dynamic equation and multiconstraint model are first established in the flight path coordinate system. Second, the reference drag acceleration-normalized energy (D-e) profile of the multiple active leap maneuver mode is quickly determined by the Newton iterative algorithm with a single design parameter. The range to go error is corrected by the drag acceleration profile update algorithm, and the drag acceleration error of the gliding terminal is corrected by the aerodynamic parameter estimation algorithm. Then, the reference drag acceleration tracking guidance law is designed based on the prescribed performance control method. Finally, the CAV-L vehicle model is used for numerical simulation. The results show that the proposed method can satisfy the design requirements of drag acceleration under multiple active leap maneuver modes, and the reference drag acceleration can be tracked precisely. The adaptability and robustness of the proposed method are verified by the Monte Carlo simulations under various combined deviation conditions.

1. Introduction

An HGV is a kind of vehicle that achieves long-range nonballistic re-entry by performing unpowered gliding motion in near space. HGVs possess many characteristics, such as high flight speeds, strong breakthrough maneuver abilities, and wide coverage of airspaces, making them a popular topic in the current research and development of new equipment [1, 2]. However, with the rapid development of relevant technologies in air and missile defense systems and the gradual improvement of equipment systems, there have been certain breakthroughs in trajectory tracking and prediction methods for the gliding phase of HGVs [3–7], as well as defensive interception technologies [8, 9]. These advancements pose a certain threat and challenge to the survivability of HGVs. Therefore, researching the utilization of the high lift-to-drag ratio characteristics of HGVs to achieve multiple extended range maneuver within the atmosphere can reduce the tracking and prediction accuracy of defense systems as well as interception probabilities [10]. This is important for enhancing the survivability and breakthrough capability of HGVs.

Regarding the trajectory design for the gliding phase of HGVs, existing trajectory design methods include standard trajectory guidance, predictive correction guidance, and closed-loop optimal guidance [11]. The standard trajectory guidance law is more developed and widely used. It is typically implemented by selecting specific flight profiles, such as the drag acceleration-velocity (D-V) [12], drag acceleration-normalized energy (D-e) [13], and altitude-velocity (H-V) [14]. Regarding the drag acceleration-energy profile, Gifty et al. [15] designed a drag acceleration curve with an analytical range form by using a multi-segment-modulated cubic polynomial. Sagliano and Mooij [16] designed the drag acceleration curve by the convex optimization method, and Zhang et al. [17] designed the quadratic polynomial and linear drag acceleration curve. The aforementioned trajectory design methods have low computational complexities but do not account for the requirements for gliding phase leap maneuver.

Aiming at the problem of leap maneuver trajectory design for the gliding phase of HGVs, Li et al. [18] used a stochastic gradient particle swarm optimization algorithm to design the drag acceleration curve. However, their method has high computational complexity. Regarding the glide maneuver trajectory design problem, Zhang et al. [19] divided the glide phase maneuver into two strategies, longitudinal maneuver and lateral maneuver. They used sequential quadratic programming methods to design five different maneuver trajectory modes, including longitudinal serpentine maneuvers. In relation to lateral maneuver strategy, Zhu et al. [20] incorporated lateral maneuver paths into the trajectory model and optimized the trajectory. Liang et al. [21] introduced the concept of maneuver coefficient and designed a three-dimensional trajectory planning method for decoupling the longitudinal and lateral planes by using the maneuver coefficient to describe the strength of lateral maneuver. For the longitudinal maneuver strategy, Tan et al. [22] used the adaptive pseudospectral method to obtain the optimal dive trajectory considering the path constraints. An et al. [23] applied predictive correction guidance methods to longitudinal trajectory design and obtained the gliding phase ballistic trajectory form through offline calculations. Zhu et al. [24] obtained the optimal maneuver form for the dive section based on the optimal control method with minimum energy consumption and line-of-sight angular velocity as the performance index in the dive stage. Aiming at the planar tripartite pursuit problem model, Hu et al. [25] solved the optimal breakout strategy based on differential countermeasure theory, which realized the breakout strike mission requirements to a certain extent. For the case of antidefense of two interceptors, Shen et al. [26] solved the surprise ballistic design problem by the second-order cone planning method and obtained an antidefense strategy based on the initial line-of-sight angle of the interceptors. Jiang et al. [27] studied a hypersonic gliding vehicle antidefense method based on deep reinforcement learning, which abstracts the confrontation process into a generalized three-body confrontation optimization problem and generates a breakout guidance law and the corresponding breakout trajectory through data training. From the perspective of escaping the KKV maneuver interception range, Liu et al. [28] first analysed the feasibility of anti-head-on interception for hypersonic glide vehicle and then designed a maneuver strategy in resolved form based on the state of the KKV at the moment of its separation from the booster stage. However, the abovementioned maneuver trajectory design method has insufficient adaptability to online trajectory design due to the real-time performance of the optimization algorithm and the difficulty of adjusting the maneuver state.

To address the design issues of the gliding phase guidance method for vehicle and to achieve controllable active leap maneuver during the gliding flight process, it is necessary to track the reference standard states designed based on optimization conditions considering process and terminal constraints. This involves generating high-precision tracking guidance commands to eliminate deviations between the actual trajectory and the standard trajectory. Mease and Kremer applied the differential geometric feedback linearization theory [29] and the evolved acceleration guidance logic for entry (EAGLE) [30] method for tracking the drag acceleration standard profile of spaceplanes, achieving excellent control results. The traditional proportional-differential guidance law [31] has limited adaptability, and the guidance parameters need to be reset for different tasks. To improve the guidance parameter sensitivity, Liang et al. [32] used the incremental nonlinear dynamic inversion method to track the design reference state, only calculating the needed guidance command increments at a given time. However, since the dynamic inversion method requires an accurate mathematical model of the object, it is sensitive to deviations. To improve the robustness of the guidance law, the sliding mode control method has been introduced into the design of the gliding tracking guidance law. An et al. [23] designed a finite-time convergent sliding mode guidance law according to the tracking error, and Li et al. [33] designed a sliding mode guidance law combining the global integral sliding mode surface and the exponential form reaching law. The above method can achieve good state tracking ability through reasonable parameter design under standard conditions, but there are some shortcomings, such as repeated formulation of guidance parameters and the inability to constrain dynamic performance. To solve the above problems, Bechlioulis and Rovithakis [34] and Chandramohan and Calise [35] studied the prescribed performance control method. This method introduces the prescribed performance function and the error conversion function to constrain the transient performance and steady-state performance of the system at the same time. This method transforms the tracking error problem into a uniformly bounded problem of the prescribed performance function, which reduces the sensitivity of the actual system to the control parameters. In addition, linear quadratic regulator (LQR) [36], optimal control, adaptive control, and other methods are also widely used in the study of standard trajectory tracking laws.

In this paper, an analytical design method of drag accelerations and a robust gliding guidance law that can realize multiple active leap maneuver are studied. First, in the drag acceleration-normalized energy (D-e) profile, the maneuver acceleration in the form of a polyline is rapidly designed by single-parameter iteration. Under the premise of satisfying the terminal and path constraints, the longitudinal leap maneuver is realized by using the change in drag acceleration in the form of a polyline. Second, to ensure that the standard reference drag acceleration meets the requirements of the terminal state constraint under the condition of deviations, the drag acceleration profile update algorithm is used for rapid correction. Afterward, the reference drag acceleration tracking guidance law is designed based on the sliding mode and prescribed performance control method. The tracking error convergence problem is transformed into a uniformly bounded problem, which improves the robustness of the gliding guidance law. Finally, through numerical simulation and the Monte Carlo calculations, the proposed method is verified under nominal conditions and disturbance conditions.

2. Gliding Phase Formulation

2.1. Coordinate System

Since the descriptions of the state parameters such as the force, position, and velocity of an HGV are usually in different coordinate systems, the dynamic model is established in the flight path coordinate system o-x₂y₂z₂ to ensure that analyses and calculations are conducted under the same space-time reference.

The earth-centered inertial coordinate system O_E-XYZ is a geocentric coordinate system with its origin O_E at the center of the earth. The O_EX axis is the intersection of equatorial and ecliptic planes. The O_EZ axis is the rotation direction of the earth. The O_EY axis satisfies the right-hand rule. The origin o of the o-x₂y₂z₂ coordinate system is the center of the vehicle mass. The ox₂ axis is the direction of the flight velocity. The axis oy₂ is located in the plane formed by the velocity vector and the vector from the center of the earth to the vehicle, perpendicular to the axis ox₂, and positive in the upward direction. The oz₂ axis satisfies the right-hand rule, as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Definition of flight path coordinate system.

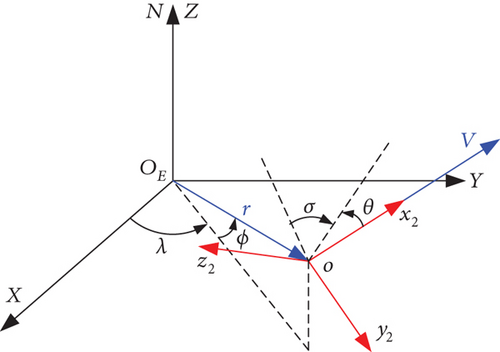
2.2. Dynamic Equations

It is assumed that the vehicle has no power, and the mass is constant during the gliding phase. The sideslip angle is zero. The earth is assumed to be a uniform sphere rotating around its own axis, without considering the nonspherical perturbation caused by the earth’s oblateness. The atmosphere is assumed to be stationary relative to the earth and uniform at the same altitude. The 3DOF dynamic equation of the vehicle is established in the flight path coordinate system as follows:

()

The following six state variables are included in the above dynamic equations: r, λ, ϕ, V, θ, σ. r denotes the distance from the center of the earth to the center of mass of the vehicle. λ is the longitude. ϕ is the latitude. V is the earth-relative velocity. θ and σ are the flight path angle and velocity heading angle measured from the north in a clockwise direction, respectively. ν is the bank angle, which is one of the two control variables. g is the gravitational acceleration with a value of 9.8 m/s². C_V, C_θ, C_σ are the additional terms caused by the rotation of the earth, and their sizes are represented as follows:

()

where ω_e is the rotational angular velocity of the earth with a value of 7.27 × 10⁻⁷ rad/s⁻¹.

The terms D and L are the aerodynamic drag and lift, respectively, and they are expressed as follows:

()

where C_D and C_L are drag and lift coefficients that are functions of α and the Mach number Ma. ρ is the atmospheric density and can be calculated by

, where ρ₀ is the atmospheric density at sea level and h_s is the scale altitude. h = r − R_e is the altitude, and R_e is the radius of the earth. S_ref is the reference area, and m is the vehicle mass. Since C_D and C_L are directly related to the angle of attack α of the vehicle and the bank angle ν can control the component of the lift in the longitudinal plane, it can be seen from Eq. (1) that α and ν can be used as the control variables of the glide trajectory design.

2.3. Constraint Analysis

During the gliding phase of vehicle flight, due to the long-term flight in the thin atmosphere, energy dissipation will be caused due to aerodynamic forces, which will produce strong mechanical and thermal effects, such as heat flow, overload, and dynamic pressure. At the same time, to meet the wide range of maneuver of the vehicle within the atmosphere, quasiequilibrium gliding should also be considered in the design of the profile to ensure flight capabilities during the maneuver process [37]. Therefore, a variety of path constraints must be satisfied in the trajectory design of the vehicle to achieve the relevant state variables within the acceptable envelope range. In summary, the constraint conditions are as follows:

()

where C₁ is a constant, R_N is the radius of the vehicle nose, V_c is the reference velocity,

is the maximum heating rate, n_max is the maximum load factor, and q_max is the maximum dynamic pressure.

In addition, the trajectory design for the gliding phase also needs to satisfy the terminal constraints, including the terminal altitude h_f, terminal velocity V_f, and terminal remaining flight range S_togo,f.

()

3. Multiple Leap Maneuver Flight Profile Design

In this paper, to achieve the goal of an active leap maneuver within the longitudinal flight profile during the gliding phase, the standard maneuver reference drag acceleration curve is designed in the drag acceleration-normalized energy ratio (D-e) profile. First, the gliding corridor is determined in the angle of attack α flight profile. Then, the reference standard maneuver drag acceleration is determined based on the analytic form of the single-parameter mapping of the range to go. Finally, the algorithm for updating and preprocessing the standard reference maneuver drag acceleration is provided.

3.1. Profile Design of the Angle of Attack α

The gliding corridor needs to be determined to obtain the α profile in advance. The design of α needs to account for both the aerodynamic heating and range. In the initial stage of the gliding phase, the heating flow is the main constraint condition. At this time, a larger magnitude of α should be adopted to reduce aerodynamic heating. When the heating flow is no longer the main constraint, α should be reduced, and the range is increased near α corresponding to the maximum lift-drag ratio. In engineering implementation, the α envelope can be designed as a piecewise linear function of velocity [38] as follows:

()

where α₁ and α₂ are the maximum angle of α and the corresponding α of the maximum lift-to-drag ratio, respectively, and V₁ and V₂ are two given velocities.

3.2. Determination of the Gliding Flight Corridor

During the gliding phase, the vehicle can achieve changes in the altitude by altering the magnitude of drag. Since the energy that can characterize the change in the flight state during the gliding phase decreases monotonically, the energy is a more appropriate trajectory design-independent variable than time. Therefore, in this paper, the glide trajectory is designed in the D-e profile. The energy E of the vehicle during flight is expressed as follows:

()

To improve the computational efficiency, the energy E is normalized as follows:

()

where e is the normalized energy of the vehicle, E₀ is the initial energy of the gliding phase, and E_f is the terminal energy of the gliding phase.

Based on the determination of α in Section 3.1, the gliding flight corridor of the drag acceleration-normalized energy (D-e) profile can be obtained according to the maximum dynamic pressure q_max, maximum overload n_max, maximum heating flow

, and quasiequilibrium glide constraints given in Eq. (4) [39]:

()

where

is the geocentric distance, which can be taken as a function of the linear change with the normalized energy e as follows:

()

where r₀ is the initial geocentric distance of the gliding phase and r_f is the terminal geocentric distance of the gliding phase.

Combining the above constraints, the upper and lower boundaries of the drag acceleration-normalized energy (D-e) profile can be obtained as follows:

()

D_max and D_min represent the upper and lower boundaries of the D-e profile gliding corridor, respectively.

3.3. Drag Acceleration Profile Design of Multiple Leap Maneuver Mode

3.3.1. Reference Drag Acceleration Profile Planning Algorithm

To enhance the longitudinal maneuver flexibility of the vehicle and achieve multiple leap maneuver, the form of the single-stage maneuver drag acceleration is designed as follows:

()

where e_m0 and e_m3 are the normalized energy parameters corresponding to the design nodes of the initial and end drag acceleration, respectively. D_m0 is the base drag acceleration corresponding to the design node e_m0. D_add is the additional drag acceleration. The drag acceleration form of a single-segment maneuver is composed of an oblique straight segment, a horizontal segment, and an oblique straight segment. It changes the original drag acceleration D_m0 through additional drag acceleration D_add to meet the longitudinal maneuver of vehicle. The single-stage maneuver drag acceleration profile is shown in Figure 2.

A flexible maneuver configuration can be achieved by introducing multiple single-stage maneuvers during the gliding flight phase. The design nodes of the multistage maneuver drag acceleration profile can be expressed in the form of a set as follows:

()

In the design of multistage maneuver acceleration profiles, the base drag acceleration and the additional drag acceleration of the ith maneuver are expressed as

and

. When

, and

are known, the distribution design of the multisegment maneuver drag acceleration profile can be further carried out. In this paper,

takes the three-segment drag acceleration profile form as the value basis as follows:

()

where D₀ and D_f are the drag acceleration of the initial and terminal of the gliding phase, respectively. D₂ is the drag acceleration that satisfies the constraint of the remaining flight range S_togo,f. The multistage maneuver process is limited to the horizontal segment of drag acceleration in Eq. (14). The elements in the design node set m_i satisfy the following constraint:

()

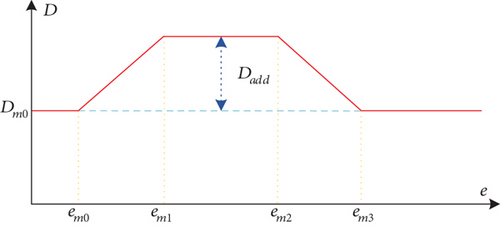
The preset maneuver corridor is [e₁, e₂], and the drag acceleration is taken as D₂, which is the benchmark. The estimated range to go based on the single-stage maneuver drag acceleration mode is calculated as follows:

According to the drag acceleration profile analytical predictive correction method,

in the form of single-segment maneuver drag acceleration has analytical solution [40]:

()

The estimated range to go S_pre based on the multistage maneuver drag acceleration mode is calculated as follows:

()

In Eq. (17), a total of n stages of maneuver drag acceleration are introduced in the design, and the preset range to go requirement S_pre is realized through a single-parameter D₂ iterative search [41]. In this paper, the Newton iterative method [42] is applied to solve for the profile design parameter D₂ as follows:

()

3.3.2. Reference Drag Acceleration Profile Update Algorithm

Due to the influence of the aerodynamic uncertainty during the gliding phase, the drag coefficient of the vehicle needs to be corrected. The corrected terminal drag acceleration at the gliding terminal time D_f is as follows [43]:

()

where

is the drag acceleration coefficient deviation and

is the predetermined drag acceleration at the gliding terminal time before updating.

In the process of gliding maneuver, due to the simplified calculation of the estimated range to go and the assumption of the large arc of the expected flight range, the drag acceleration profile needs to be updated to correct the range deviation in the actual flight process. In the multistage maneuver acceleration profile, based on the maneuver drag acceleration form designed in Eq. (17), the profile update nodes are chosen as follows to minimize the impact on the maneuver process:

()

where Δ_e is the update node additional item and satisfies Δ_e > 0.

The profile is updated in the form of three segment broken lines represented by Eq. (14). It is known that the remaining design nodes

, and

are not updated. The normalized energy nodes of the updated drag acceleration profile are reselected as follows:

()

where

avoids large changes in drag acceleration after profile updating due to the small energy interval by increasing the scaling factor of the energy interval about the additional drag acceleration.

The updated reference drag acceleration profile maintains the form of Eq. (14).

3.3.3. Reference Drag Acceleration Profile Preprocessing Algorithm

Using a piecewise linear drag acceleration form, Eq. (14) may lead to first-order discontinuity in the design profile, which could lead to significant abrupt changes in the guidance command. Therefore, it is necessary to implement a smooth transition process near the segment endpoints or the profile design nodes to address this issue.

The set of preset values can be expressed as follows:

()

The smooth transition profile is expressed as follows:

()

where q_d is the design node and q_d ∈ m. The value of ε is small. The value of ε requires that the smoothed profile has little effect on the estimated range to go and satisfies the following constraints:

()

Eq. (24) ensures that the smooth transition trajectory does not exceed other design nodes and maintains the main characteristics of the broken line reference drag acceleration curve.

4. Maneuver Drag Acceleration Tracking Guidance Law

When the drag acceleration profile design is obtained, it is necessary to design the tracking guidance law to track the design profile. In this paper, the bank angle ν is chosen as the control variable to ensure that the actual drag acceleration D equals the corresponding standard reference drag acceleration of the profile. In this section, the method based on the sliding mode and preset performance control is used to design the standard reference drag acceleration tracking guidance law to ensure that the vehicle satisfies multiple constraints at the gliding terminal time.

The error conversion function is defined as follows:

()

where ρ_d and ρ_u are the convergence error envelopes. Moreover, ρ_d and ρ_u represent the actual error convergence boundaries, which are designed to be in an exponential convergence form as follows:

()

where

and

are the initial and final values of the error envelope, respectively, and k_ρ is the convergence rate factor.

In Eq. (25), s is the sliding mode variable, which can be expressed as follows:

()

where k_e is a sliding mode design parameter greater than zero. The reference drag acceleration tracking error e_D and its derivative

are expressed as follows:

()

Reference [44] has demonstrated that when the sliding mode variable s tends to zero, e_D will converge to zero. Taking further derivative of the drag acceleration tracking error

yields

as follows:

()

where u is the virtual control variable, u = cosν, and d₁ is the uncertainty. Additionally, A and B can be determined by the following equations:

()

The derivative of the conversion error Z_u defined in Eq. (25) can be obtained as follows:

()

where A_z, B_z, and

are expressed as follows:

()

Substituting Eq. (29) and Eq. (33) into Eq. (31) yields the following expression:

()

Considering the uncertain disturbance term, u is designed as follows:

()

where u₁ is the balance term, which is used to counteract the known term in Eq. (34). The construction form of u₁ is as follows:

()

By substituting Eq. (35) and Eq. (36) into Eq. (34), the following simplification can be obtained:

()

The uncertain disturbance d_z is passed through a first-order low-pass filter to obtain the following equation:

()

where τ_f is the time constant term and satisfies 0 < τ_f ≤ 1 [45]. From the first-order low-pass filter, the error estimation

can be obtained as follows:

()

The variable u₂ is designed as follows:

()

where k_z is the design parameter and satisfies k_z > 0.5 [45]. By substituting Eq. (40) into Eq. (39), the following expression can be obtained:

()

Both sides of the above equation can be integrated to obtain the following expression:

()

where

is the initial value of estimation error. By substituting Eq. (42) into Eq. (39), u₂ can be simplified as follows:

()

According to Eq. (35) and considering the amplitude constraint, the magnitude of the control variable ν can be obtained as follows:

()

It is proved in Reference [45] and Reference [46] that the conversion error function is uniformly bounded by the guidance law (Eq. (44)) under the condition that the interference error is bounded, the sliding mode surface s is guaranteed to be within the error envelope, and the tracking error e approaches zero.

5. Simulation Verification and Analysis

The CAV-L vehicle model is taken as the simulation object. Its mass is 816.48 kg, and the reference area is 0.32258 m². The lift-drag coefficient is provided in Reference [43]. The design parameters of the angle of attack α profile are as follows: α₁ = 20^°, α₂ = 10^°, V₁ = V₀ − (V₀ − V_f)/4, and V₂ = V₀ − 3(V₀ − V_f)/4. The design parameters of the drag acceleration profile of the two-stage longitudinal leap maneuver are selected to be

and

. The design nodes are set as follows:

()

The guidance parameters are set to k_e = 0.5, k_z = 0.52, τ_f = 0.2, , , and k_ρ = 0.02. The constraints for the dynamic pressure, load factor, and heat flux during the gliding phase are q_max = 200 kPa, n_max = 3 g₀, and , respectively. The target location is 115°E and 32°N.

5.1. Nominal Mission Simulation

To verify the effectiveness of the designed reference drag acceleration profile and the tracking guidance law under multiple active leap maneuver modes, two sets of different initial conditions are selected for simulation analysis in this section. The initial state and the terminal constraints of the gliding phase are shown in Tables 1 and 2, respectively.

Table 1. Initial state of the nominal gliding missions.

Mission	h₀ (m)	λ₀ (°)	ϕ₀ (°)	V₀ (m/s)	θ₀ (°)	σ₀ (°)
1	39000	118	18	5440	0	-10.4
2	41000	100	23	5120	0	52.6

Table 2. Terminal expected state of the gliding phase.

h_f (m)	S_togo,f (m)	V_f (m/s)
18000	20000	1280

Simulations were conducted using the drag acceleration profile design method and tracking guidance algorithm proposed in this article. The results are as follows. Figure 3 is the reference drag acceleration and actual drag acceleration curve under the two-stage longitudinal leap maneuver modes in the D-e profile. It can be seen from the figure that the turning point of the reference drag acceleration profile is smooth and the tracking error of the actual drag acceleration is very small. This indicates that the vehicle can effectively control drag acceleration and maintain a stable flight state during the gliding phase.

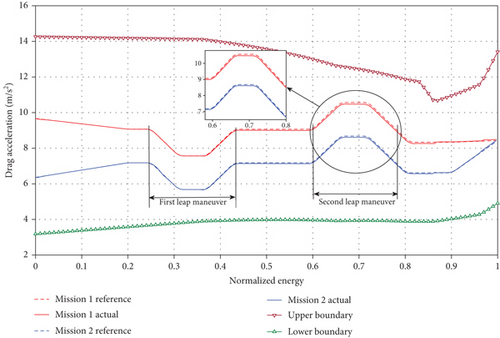
The variations in the vehicle angle of attack α and command bank angle ν are shown in Figures 4 and 5, respectively. Figures 6 and 7 present the three-dimensional trajectories and velocity-altitude curve during the gliding phase, respectively. It can be concluded that the algorithm studied in this paper can guide the vehicle to the terminal expected state and satisfy the multiple constraint conditions. The guidance algorithms exhibit strong adaptability. Further analysis reveals that the variation in the reference drag acceleration designed in Figure 3 can achieve the longitudinal leap maneuver shown in Figure 6. When the drag acceleration significantly changes, the high-precision tracking of the drag acceleration can be realized by implementing the rapid large-scale bank angle.

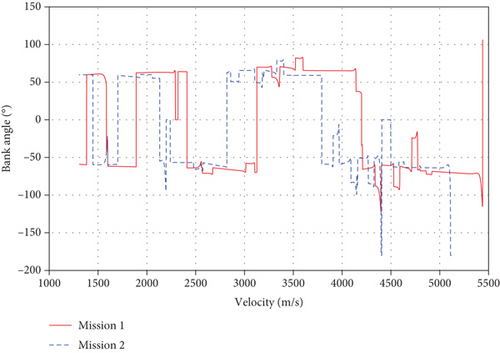
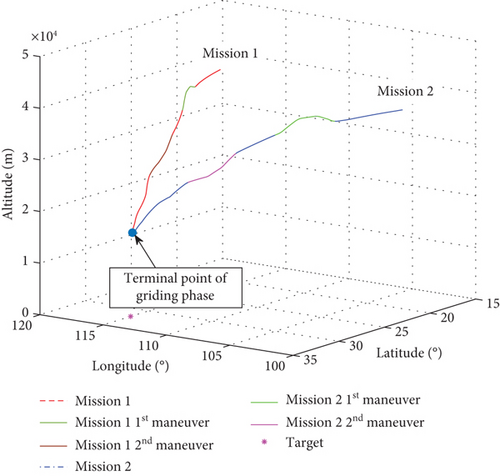
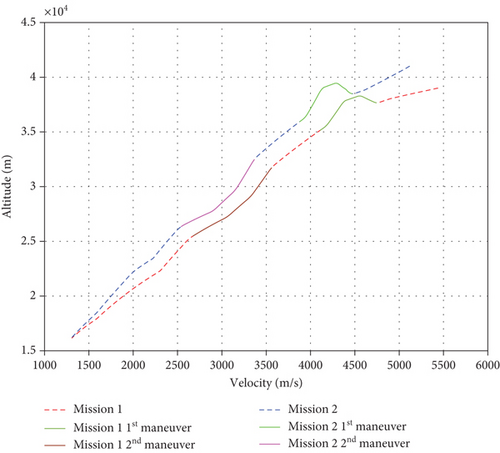
Table 3 shows the terminal actual state of the gliding phase. The terminal altitude error is less than 220 m, the terminal range to go error is less than 100 m, and the velocity error is less than 10 m/s, which can accurately satisfy the constraints of the gliding handover.

Table 3. Terminal actual state of the gliding phase.

Mission	h_f (m)	S_togo,f (m)	V_f (m/s)
1	18135	20040	1304
2	18217	20080	1308

5.2. Monte Carlo Simulation

To verify the robustness of the design method to the initial state deviation and aerodynamic parameter uncertainties, the Monte Carlo simulations are carried out. The initial state of the gliding phase simulation of the vehicle is based on the mission 1 state in Table 1, and the range of disturbance deviations is selected based on the 3σ principles, as shown in Table 4.

Table 4. Dispersions in the Monte Carlo simulations.

h₀	V₀	θ₀	σ₀	C_L	C_D
±2000 m	±300 m/s	±0.5°	±10°	±20%	±20%

The Monte Carlo simulation results of 200 dispersed cases are shown in Figures 8–11.

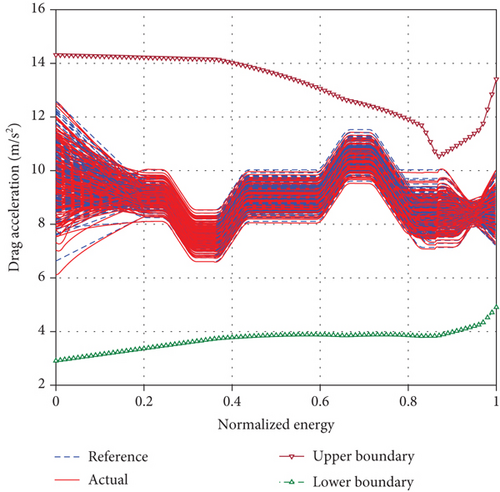
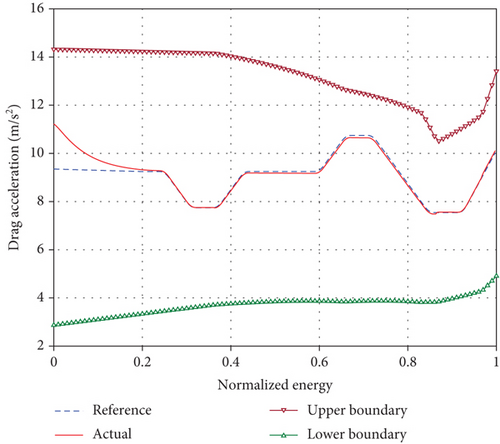
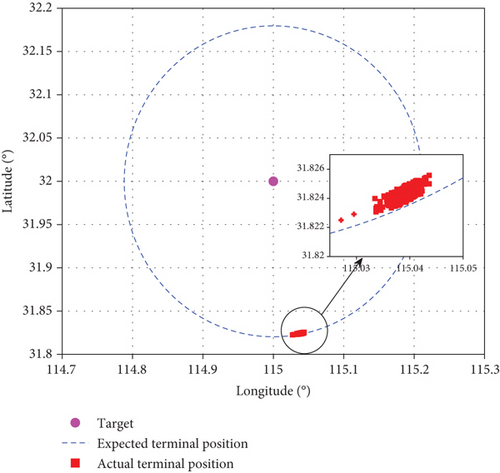
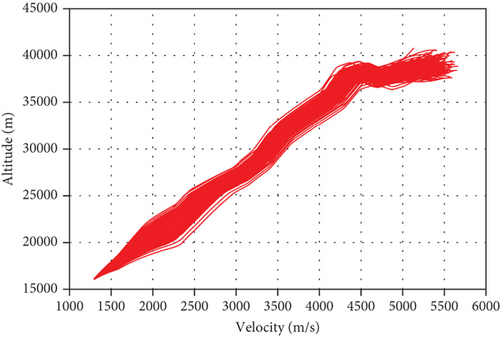
From the calculation results of Figures 8 and 9, it can be seen that due to the influence of aerodynamic parameter deviations, there is a certain deviation between the actual drag acceleration and the reference resistance acceleration in the initial stage of gliding. The gliding guidance law studied in this paper can quickly converge to the design profile of the reference drag acceleration in finite time and maintain high-precision tracking. The drag acceleration state of the reference terminal is corrected by the online estimation of the aerodynamic coefficient to ensure that the vehicle meets the terminal state handover constraint requirements. The terminal positions during the gliding phase under comprehensive deviation conditions are shown in Figure 10. The actual positions are all located on the circle that satisfies the remaining gliding terminal range constraints. The statistical simulation results show that the mean and variance of S_togo,f are 19986.8 m and 75.3 m, respectively, and the mean and variance of h_f are 18032.4 m and 169.6 m, respectively. The Monte Carlo simulation results demonstrate that the design method of the drag acceleration profile and the gliding guidance algorithm for the multiple leap maneuver mode proposed in this paper are reliable and effective, with strong adaptability.

6. Conclusions

In this paper, a fast design algorithm of drag accelerations that can be used to achieve multiple maneuvers in the gliding phase and a gliding guidance algorithm with a strong anti-interference ability are proposed. Through single-parameter analytical iterations, the reference drag acceleration profile of multiple leap maneuvers satisfying process and terminal constraints can be quickly obtained, which has the potential for online planning applications. The drag acceleration tracking algorithm based on the sliding mode and prescribed performance control has a strong anti-interference ability. The simulation results show that the drag acceleration profile design method and tracking guidance algorithm in this paper have good adaptability and robustness based on different missions and disturbance deviation conditions and have great engineering application potential.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This study was funded by the National Natural Science Foundation of China (grant no.: 62101579).

Open Research

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Zhang Y. L. and Xie Y., Review of trajectory planning and guidance methods for gliding vehicles, Acta Aeronautica et Astronautica Sinica. (2021) 41, no. 1, article 023377.
Google Scholar
2 Law Y. W., Gliponeo J. J., Singh D., McGuire J., Liang J., Ho S. Y., and Slay J., Detecting and tracking hypersonic glide vehicles: a cybersecurity-engineering analysis of academic literature, International Conference on Cyber Warfare and Security. (2023) 18, no. 1, https://doi.org/10.34190/iccws.18.1.950.
10.34190/iccws.18.1.950
Google Scholar
3 Hu Y., Gao C., Li J., and Jing W., Maneuver mode analysis and parametric modeling for hypersonic glide vehicles, Aerospace Science and Technology. (2021) 119, article 107166, https://doi.org/10.1016/j.ast.2021.107166.
10.1016/j.ast.2021.107166
Web of Science® Google Scholar
4 Hu Y., Gao C., Li J., Jing W., and Li Z., Novel trajectory prediction algorithms for hypersonic gliding vehicles based on maneuver mode on-line identification and intent inference, Measurement Science and Technology. (2021) 32, no. 11, article 115012, https://doi.org/10.1088/1361-6501/ac1284.
10.1088/1361-6501/ac1284
PubMed Web of Science® Google Scholar
5 Cheng Y. P., Tang S., Lyu S., Wu M. Q., and Qiao H., Aerodynamic statistics-based trajectory estimation of hypersonic: maneuvering target, IEEE Access. (2020) 8, no. 1, 227642–227656, https://doi.org/10.1109/ACCESS.2020.3044589.
10.1109/ACCESS.2020.3044589
Web of Science® Google Scholar
6 Li F., Xiong J. J., Qu Z. G., and Lan X. H., A damped oscillation model for tracking near space hypersonic gliding targets, IEEE Transactions on Aerospace and Electronic Systems. (2019) 55, no. 6, 2871–2890, https://doi.org/10.1109/TAES.2019.2897517.
10.1109/TAES.2019.2897517
Web of Science® Google Scholar
7 Huang J. S., Zhang H. B., Tang G. J., and Bao W. M., Robust UKF-based filtering for tracking a maneuvering hypersonic glide vehicle, Journal of Aerospace Engineering. (2022) 236, no. 11, 2162–2178, https://doi.org/10.1177/09544100211051106.
10.1177/09544100211051106
Web of Science® Google Scholar
8 Sun L. H., Yang B. Q., and Ma J., Trajectory prediction in pipeline form for intercepting hypersonic gliding vehicles based on LSTM, Chinese Journal of Aeronautics. (2023) 36, no. 5, 421–433, https://doi.org/10.1016/j.cja.2023.02.017.
10.1016/j.cja.2023.02.017
Web of Science® Google Scholar
9 Liu S. X., Yan B. B., Huang W., Zhang X., and Yan J., Current status and prospects of terminal guidance laws for intercepting hypersonic vehicles in near space: a review, Journal of Zhejiang University-SCIENCE A. (2023) 24, no. 5, 387–403, https://doi.org/10.1631/jzus.A2200423.
10.1631/jzus.A2200423
Web of Science® Google Scholar
10 Li G. H., Zhang H. B., and Tang G. J., Maneuver characteristics analysis for hypersonic glide vehicles, Aerospace Science and Technology. (2015) 43, 321–328, https://doi.org/10.1016/j.ast.2015.03.016, 2-s2.0-84926229258.
10.1016/j.ast.2015.03.016
Web of Science® Google Scholar
11 Zhang Y. L., Chen K. J., Liu L. H., Tang G. J., and Bao W. M., Entry trajectory planning based on three-dimensional acceleration profile guidance, Aerospace Science and Technology. (2016) 48, 131–139, https://doi.org/10.1016/j.ast.2015.11.009, 2-s2.0-84948138988.
10.1016/j.ast.2015.11.009
CAS Web of Science® Google Scholar
12 Harpold J. C. and Gravert D. E., Space shuttle entry guidance performance results, Journal of Guidance, Control, and Dynamics. (1983) 6, no. 6, 442–447, https://doi.org/10.2514/3.8523, 2-s2.0-0020843782.
10.2514/3.8523
Web of Science® Google Scholar
13 Roenneke A. J. and Markl A., Re-entry control to a drag-vs-energy profile, Journal of Guidance Control, and Dynamics. (1994) 17, no. 5, 916–920, https://doi.org/10.2514/3.21290, 2-s2.0-85003301415.
10.2514/3.21290
Web of Science® Google Scholar
14 Shen Z. and Lu P., Onboard generation of three-dimensional constrained entry trajectories, Journal of Guidance, Control, and Dynamics. (2003) 26, no. 1, 111–121, https://doi.org/10.2514/2.5021, 2-s2.0-0037265934.
10.2514/2.5021
Web of Science® Google Scholar
15 Gifty R., Rajeev U. P., Lalithambika V. R., and Dhekane M. V., Entry guidance with smooth drag planning and non-linear tracking, Control Engineering Practice. (2017) 63, 24–33, https://doi.org/10.1016/j.conengprac.2017.03.014, 2-s2.0-85017150895.
10.1016/j.conengprac.2017.03.014
Web of Science® Google Scholar
16 Sagliano M. and Mooij E., Optimal drag-energy entry guidance via pseudospectral convex optimization, Aerospace Science and Technology. (2021) 117, article 106946, https://doi.org/10.1016/j.ast.2021.106946.
10.1016/j.ast.2021.106946
Web of Science® Google Scholar
17 Zhang W., Chen W., and Yu W., Entry guidance for high-L/D hypersonic vehicle based on drag-vs-energy profile, ISA Transactions. (2018) 83, 176–188, https://doi.org/10.1016/j.isatra.2018.08.012, 2-s2.0-85051720122.
10.1016/j.isatra.2018.08.012
PubMed Web of Science® Google Scholar
18 Li Z. H., Hu C., Ding C. B., Liu G., and He B., Stochastic gradient particle swarm optimization based entry trajectory rapid planning for hypersonic glide vehicles, Aerospace Science and Technology. (2018) 76, 176–186, https://doi.org/10.1016/j.ast.2018.01.033, 2-s2.0-85042186598.
10.1016/j.ast.2018.01.033
Web of Science® Google Scholar
19 Zhang K. N., Zhou H., and Chen W. C., Trajectory planning for hypersonic vehicle with multiple constraints and multiple maneuvering penetration strategies, Journal of Ballistics. (2012) 24, no. 3, 85–90.
Google Scholar
20 Zhu J. W., He R. Z., Tang G. J., and Bao W. M., Pendulum maneuvering strategy for hypersonic glide vehicles, Aerospace Science and Technology. (2018) 78, 62–70, https://doi.org/10.1016/j.ast.2018.03.038, 2-s2.0-85044944715.
10.1016/j.ast.2018.03.038
Web of Science® Google Scholar
21 Liang Z. X., Ren Z., Li Q. D., and Chen J., Decoupled three-dimensional entry trajectory planning based on maneuver coefficient, Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering. (2017) 231, no. 7, 1281–1292, https://doi.org/10.1177/0954410016650906, 2-s2.0-85017544535.
10.1177/0954410016650906
Web of Science® Google Scholar
22 Tan S., Lei H., and Liu T., Optimal maneuver trajectory for hypersonic missiles in dive phase using inverted flight, IEEE Access. (2019) 7, 63493–63503, https://doi.org/10.1109/ACCESS.2019.2916464, 2-s2.0-85066444065.
10.1109/ACCESS.2019.2916464
Web of Science® Google Scholar
23 An K., Guo Z. Y., Huang W., and Xu X. P., Leap trajectory tracking control based on sliding mode theory for hypersonic gliding vehicle, Journal of Zhejiang University-SCIENCE A. (2022) 23, no. 3, 188–207, https://doi.org/10.1631/jzus.A2100362.
10.1631/jzus.A2100362
Web of Science® Google Scholar
24 Zhu J. W., Liu L. H., Tang G. J., and Bao W. M., Optimal diving maneuver strategy considering guidance accuracy for hypersonic vehicle, Acta Astronautica. (2014) 104, no. 1, 231–242, https://doi.org/10.1016/j.actaastro.2014.07.026, 2-s2.0-84906833974.
10.1016/j.actaastro.2014.07.026
Web of Science® Google Scholar
25 Hu Y. A., Zhang X. L., Li X. D., and Fan Z. E., Missile optimal penetration method based on differential games, Journal of Naval Aeronautical Engineering Institute. (2007) 22, no. 1, 169–172.
Google Scholar
26 Shen Z. P., Yu J. L., Dong X. W., Hua Y. Z., and Ren Z., Penetration trajectory optimization for the hypersonic gliding vehicle encountering two interceptors, Aerospace Science and Technology. (2022) 121, article 107363, https://doi.org/10.1016/j.ast.2022.107363.
10.1016/j.ast.2022.107363
Web of Science® Google Scholar
27 Jiang L., Nan Y., Zhang Y., and Li Z. H., Anti-interception guidance for hypersonic glide vehicle: a deep reinforcement learning approach, Aerospace. (2022) 9, no. 8, https://doi.org/10.3390/aerospace9080424.
10.3390/aerospace9080424
Web of Science® Google Scholar
28 Liu K. F., Meng H. D., Wang C. J., Li J. Y., and Chen Y., Anti-head-on interception penetration guidance law for slide vehicle, Modern Defence Technology. (2018) 46, no. 5, 39–45, https://doi.org/10.3969/j.issn.1009-086x.2018.05.07.
10.3969/j.issn.1009-086x.2018.05.07
CAS Google Scholar
29 Mease K. D. and Kremer J., Shuttle entry guidance revisited using nonlinear geometric methods, Journal of Guidance, Control, and Dynamics. (1994) 17, no. 6, 1350–1356, https://doi.org/10.2514/3.21355, 2-s2.0-0028550587.
10.2514/3.21355
Web of Science® Google Scholar
30 Saraf A., Leavitt J. A., Chen D. T., and Mease K. D., Design and evaluation of an acceleration guidance algorithm for entry, Journal of Spacecraft and Rockets. (2004) 41, no. 6, 986–996, https://doi.org/10.2514/1.11015, 2-s2.0-11044232552.
10.2514/1.11015
Web of Science® Google Scholar
31 Qiao H., Li X. G., and Chang W. Q., Reentry guidance method considering maneuver coefficient, Journal of Astronautic. (2020) 41, no. 2, 206–214.
Google Scholar
32 Liang Z., Duan G., and Ren Z., Mars entry guidance based on an adaptive reference drag profile, Advances in Space Research. (2017) 60, no. 3, 692–701, https://doi.org/10.1016/j.asr.2017.04.027, 2-s2.0-85019950518.
10.1016/j.asr.2017.04.027
Web of Science® Google Scholar
33 Li S. C., He R. Z., Tang G. J., and Ao P., Profile tracking guidance law based on sliding mode control, Acta Aeronautica et Astronautica Sinica. (2020) 41, no. S2, article 724578.
Google Scholar
34 Bechlioulis C. P. and Rovithakis G. A., Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance, IEEE Transactions on Automatic Control. (2008) 53, no. 9, 2090–2099, https://doi.org/10.1109/TAC.2008.929402, 2-s2.0-54349115224.
10.1109/TAC.2008.929402
Web of Science® Google Scholar
35 Chandramohan R. and Calise A. J., Output feedback adaptive control of plants with unmodeled dynamics and input uncertainties, Journal of Guidance, Control, and Dynamics. (2019) 42, no. 10, 2143–2156, https://doi.org/10.2514/1.G003548, 2-s2.0-85073150568.
10.2514/1.G003548
Web of Science® Google Scholar
36 Webb K. D. and Lu P., Entry guidance by onboard trajectory planning and tracking, AIAA Atmospheric Flight Mechanics Conference, 2016, San Diego, California.
Google Scholar
37 Zheng Z., Wang C., Sun X., Yan L., and Chen W., Entry guidance with no-fly zone avoidance for hypersonic glide vehicle, Proceedings of the International Conference on Autonomous Unmanned Systems, 2022, Chang Sha, China, 1358–1366.
Google Scholar
38 Wang Z. Y., Tang S. J., and Guo J., Entry guidance command generation for hypersonic glide vehicles under threats and multiple constraints, IEEE Access. (2022) 10, no. 10, 1–15, https://doi.org/10.1109/ACCESS.2021.3137641.
10.1109/ACCESS.2021.3137641
Web of Science® Google Scholar
39 Zhou H. Y., Wang X. G., Zhao Y. L., and Cui N. G., Online guidance for aerospace vehicle in return-gliding phase, Journal of Astronautics. (2021) 42, no. 2, 175–184.
Google Scholar
40 Yan X. D. and Wang Z., Three-dimensional trajectory planning method for hypersonic glide vehicles, Transactions of Beijing institute of Technology. (2013) 33, no. 7, 669–674.
Google Scholar
41 Xu H., Cai G., Fan Y., Wei H., Li X., and Wang Y., Analytic time reentry cooperative guidance for multi-hypersonic glide vehicles, Applied Sciences. (2023) 13, no. 8, https://doi.org/10.3390/app13084987.
10.3390/app13084987
Google Scholar
42 Xue S. and Lu P., Constrained predictor-corrector entry guidance, Journal of Guidance, Control, and Dynamics. (2010) 33, no. 4, 1273–1281, https://doi.org/10.2514/1.49557, 2-s2.0-77956377901.
10.2514/1.49557
Web of Science® Google Scholar
43 Zhang K., Shi G. X., and Wang P., Predictor-corrector reentry guidance with cross range dynamic constraint, Journal of Astronautic. (2020) 41, no. 4, 429–437.
Google Scholar
44 Yu X. and Man Z., Fast terminal sliding-mode control design for nonlinear dynamical systems, IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. (2002) 49, no. 2, 261–264, https://doi.org/10.1109/81.983876, 2-s2.0-0036475055.
10.1109/81.983876
Web of Science® Google Scholar
45 Yan X. and Lyu S., Robust intercept guidance law with predesigned zero-effort miss distance convergence for capturing maneuvering targets, Journal of the Franklin Institute. (2020) 357, no. 2, 1118–1136, https://doi.org/10.1016/j.jfranklin.2019.10.021.
10.1016/j.jfranklin.2019.10.021
Web of Science® Google Scholar
46 Bechlioulis C. P. and Rovithakis G. A., Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems, Automatica. (2009) 45, no. 2, 532–538, https://doi.org/10.1016/j.automatica.2008.08.012, 2-s2.0-58349111549.
10.1016/j.automatica.2008.08.012
Web of Science® Google Scholar

All articles

Multiple Leap Maneuver Trajectory Design and Tracking Method Based on Prescribed Performance Control during the Gliding Phase of Vehicles

Abstract

1. Introduction

2. Gliding Phase Formulation

2.1. Coordinate System

2.2. Dynamic Equations

2.3. Constraint Analysis

3. Multiple Leap Maneuver Flight Profile Design

3.1. Profile Design of the Angle of Attack α

3.2. Determination of the Gliding Flight Corridor

3.3. Drag Acceleration Profile Design of Multiple Leap Maneuver Mode

3.3.1. Reference Drag Acceleration Profile Planning Algorithm

3.3.2. Reference Drag Acceleration Profile Update Algorithm

3.3.3. Reference Drag Acceleration Profile Preprocessing Algorithm

4. Maneuver Drag Acceleration Tracking Guidance Law

5. Simulation Verification and Analysis

5.1. Nominal Mission Simulation

5.2. Monte Carlo Simulation

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Multiple Leap Maneuver Trajectory Design and Tracking Method Based on Prescribed Performance Control during the Gliding Phase of Vehicles

Abstract

1. Introduction

2. Gliding Phase Formulation

2.1. Coordinate System

2.2. Dynamic Equations

2.3. Constraint Analysis

3. Multiple Leap Maneuver Flight Profile Design

3.1. Profile Design of the Angle of Attack α

3.2. Determination of the Gliding Flight Corridor

3.3. Drag Acceleration Profile Design of Multiple Leap Maneuver Mode

3.3.1. Reference Drag Acceleration Profile Planning Algorithm

3.3.2. Reference Drag Acceleration Profile Update Algorithm

3.3.3. Reference Drag Acceleration Profile Preprocessing Algorithm

4. Maneuver Drag Acceleration Tracking Guidance Law

5. Simulation Verification and Analysis

5.1. Nominal Mission Simulation

5.2. Monte Carlo Simulation

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information