International Transactions on Electrical Energy Systems

Volume 2024, Issue 1 6484369

Research Article

Open Access

ANFIS-Controlled Boost and Bidirectional Buck-Boost DC-DC Converters for Solar PV, Fuel Cell, and BESS-Based Microgrid Application

Dessalegn Bitew Aeggegn,

Corresponding Author

Dessalegn Bitew Aeggegn

[email protected]

orcid.org/0000-0002-7253-1287

Pan African University Institute for Basic Sciences, Technology and Innovation (PAUSTI) , Nairobi , 62000 , Kenya

Debre Markos University , Debre Markos , 26900 , Ethiopia , dmu.edu.et

Search for more papers by this author

George Nyauma Nyakoe,

George Nyauma Nyakoe

orcid.org/0000-0002-0402-4048

Pan African University Institute for Basic Sciences, Technology and Innovation (PAUSTI) , Nairobi , 62000 , Kenya

Jomo Kenyatta University of Agriculture and Technology , Nairobi , 62000 , Kenya , jkuat.ac.ke

Search for more papers by this author

Cyrus Wekesa,

Cyrus Wekesa

orcid.org/0000-0001-8827-1005

Pan African University Institute for Basic Sciences, Technology and Innovation (PAUSTI) , Nairobi , 62000 , Kenya

University of Eldoret , Eldoret , 30100 , Kenya , uoeld.ac.ke

Search for more papers by this author

Dessalegn Bitew Aeggegn,

Corresponding Author

Dessalegn Bitew Aeggegn

[email protected]

orcid.org/0000-0002-7253-1287

Pan African University Institute for Basic Sciences, Technology and Innovation (PAUSTI) , Nairobi , 62000 , Kenya

Debre Markos University , Debre Markos , 26900 , Ethiopia , dmu.edu.et

Search for more papers by this author

George Nyauma Nyakoe,

George Nyauma Nyakoe

orcid.org/0000-0002-0402-4048

Pan African University Institute for Basic Sciences, Technology and Innovation (PAUSTI) , Nairobi , 62000 , Kenya

Jomo Kenyatta University of Agriculture and Technology , Nairobi , 62000 , Kenya , jkuat.ac.ke

Search for more papers by this author

Cyrus Wekesa,

Cyrus Wekesa

orcid.org/0000-0001-8827-1005

Pan African University Institute for Basic Sciences, Technology and Innovation (PAUSTI) , Nairobi , 62000 , Kenya

University of Eldoret , Eldoret , 30100 , Kenya , uoeld.ac.ke

Search for more papers by this author

First published: 20 July 2024

https://doi.org/10.1155/2024/6484369

Citations: 4

Academic Editor: Julio C. Rosas-Caro

Share a link

Email
Wechat
Bluesky

Abstract

DC-DC converters are essential for integrating distributed energy resources into microgrid (MG) systems. These converters are designed to incorporate intermittent renewable energy sources such as solar photovoltaic (PV) panels, fuel cells (FCs), and battery energy storage systems (BESSs) into the grid. However, conventional DC-DC converters have limitations including lower efficiency, voltage ripple, insufficient voltage regulation, and compatibility issues. This article presents boost and bidirectional buck-boost converters for direct current microgrid (DCMG) applications, employing an adaptive neuro-fuzzy inference system (ANFIS) for control. These proposed converter configurations adeptly manage wide input voltage fluctuations from intermittent sources, consistently supplying power to the DC bus at 500 V and 120 V for boost and buck operations, respectively, with an efficiency of 98.8%. The output voltage result shows that the ANFIS-based boost converter has 10% overshoot as compared to 41% and 50% overshoot in proportional integral (PI) and fuzzy logic controller (FLC), respectively. In both buck and boost modes, the converters’ voltage gain is influenced by duty ratio adjustments only, not sensitive to dynamic input voltage and flexible manipulation of the output voltage for BESS charging. Moreover, the designed converters accommodate load variations within the MG. To assess the converters’ ability to regulate output voltage effectively, PI, FLC, and ANFIS controllers are implemented and compared. And the ANFIS controller demonstrates superior performance, offering faster response times and enhanced stability. Evaluations are conducted through simulations in the MATLAB/Simulink environment.

1. Introduction

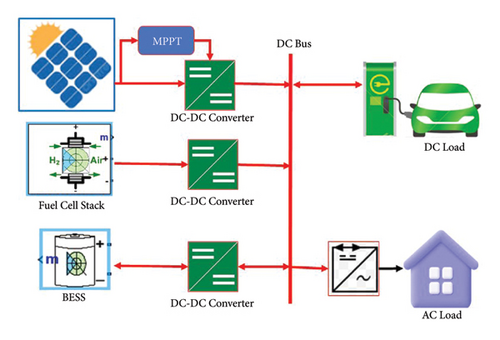
An MG is a self-contained power system that combines distributed energy resources (DERs) and different controllers within a defined location. It operates as a single controllable unit, able to function in either grid-connected mode or independently in islanded mode. An MG can be DC, AC, or hybrid sourced to accommodate both AC and DC loads. DCMG is the most proposed architectures due to inherently experiencing lower energy losses compared to AC systems, leading to more efficient power utilization, and also DC microgrids (DCMGs) has reduced costs, improved power quality, and are suitable to integrate DERs [1–3]. For instance, as depicted in Figure 1, DERs such as solar PV, FC stacks, and battery energy storage systems (BESSs) are linked to a shared DC node through relevant DC-DC converters. The solar PV system employs its own maximum power point tracker (MPPT) and connects to a DC-DC boost converter. Similarly, the FC stack plant utilizes a DC-DC boost converter to ensure a consistent output voltage at the common DC bus [4]. The BESS is interfaced with a bidirectional buck-boost converter, facilitating the charging of the battery from the DC bus during surplus power from the MG. During the buck mode operation of the buck-boost converter, the common DC bus voltage needs to be decreased to charge the BESS to its nominal voltage [5]. Significantly, the BESS plays a crucial role in mitigating peak demands, thereby reducing operational costs and enhancing system reliability [6].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Boost and buck-boost converter-based microgrid.

1.1. Motivation

Amid the growing global energy crisis, microgrids are seen as a crucial strategy for tackling energy issues. This research study focuses on improving the smooth operation of DC microgrids by utilizing an efficient DC-DC boost converter for solar PV and FC plants, along with a bidirectional buck-boost converter for integrating BESS into the microgrid. This paper evaluates the efficiency and speed of these converters by employing an ANFIS controller, which minimizes voltage fluctuations and maintains the output voltage at the desired level.

1.2. Related Works

Numerous DC-DC converters have been developed and studied to tackle the previously mentioned challenges. Various topologies and controllers, from classical to intelligent approaches, are explored in this context. For instance, Liu et al. [2] employed supertwisting high-order sliding-mode control to reduce converter output voltage overshoot in a photovoltaic-based DC microgrid (MG). This method resulted in a 33% reduction in system overshoot, significantly enhancing response speed, with stability confirmed via Lyapunov theory control [7].

In another study, Ullah et al. [8] introduced a bidirectional buck-boost converter regulated by a sliding-mode controller (SMC) to ensure system stability despite variations in the energy storage device (ESD) voltage. Lai et al. [9] implemented a two-phase, interleaved, bidirectional DC-DC converter topology for electric vehicles and DC microgrids. The results indicated that this design effectively minimized output ripple, achieving efficiencies of 98.4% in buck mode and 97.7% in boost mode for a small-scale prototype MG model.

A fractional-order PID controller approximation was proposed for voltage regulation in a buck-boost converter in [10]. The results demonstrated that signal stability remained consistent for low-voltage applications using operational amplifiers, validated with commercial parameters. In another study [11], a bidirectional DC-DC converter controlled through a PI controller processed and triggered the converter switch, resulting in stable output voltage with some input current ripples under variable PV-sourced MG. Yfoulis et al. [12] employed a PID-controlled boost and buck-boost DC-DC converter in a DCMG under uncertain mixed load conditions. The output voltage was governed by a PID as the primary controller and model predictive control (MPC) based on specialized current and power estimators [13].

AI methods have proven effective in managing nonlinear systems, such as those found in DERs modeling and interfacing converters [14]. Unlike classical techniques, AI approaches excel in extracting maximum power from PV arrays, optimizing hydrogen fuels, and managing BESS for improved performance. These methods are efficient with nonlinear systems, offering speed, flexibility, and reliability [15]. Among soft-computing AI techniques, artificial neural networks (ANNs), fuzzy logic controllers (FLCs), and ANFIS are used for DER generation control and converter design, ensuring fast response and stable output in intermittently sourced MGs and interfacing DC-DC converters. Rouzbehi et al. [16] proposed a data-driven voltage control strategy for DC-DC converters, utilizing a local model network (LMN) to identify a dynamic model for the converter across its operating regime. This strategy processes the generated control signal (duty ratio, D) to enable efficient operation in buck and boost modes for MG applications. Liu et al. [17–20] introduced a droop control method for multiple DC-DC converters, demonstrating effective power sharing in an MG by balancing the load. Koundi et al. [21] applied closed-loop Lyapunov stability control to a fuel cell-fed interleaved buck-boost converter, ensuring the DC voltage tracks and its desired value despite load uncertainties, and facilitating adequate current sharing between the fuel cell and IBBC. However, this study did not address response speed or input and output ripples [22].

The reviewed literature emphasizes that the effectiveness of a microgrid (MG) control system relies heavily on the accuracy and reliability of both the MG model and its controller. Traditional control methods, such as the PI controller, require precise mathematical models of the MG to manage voltage and frequency [23]. Conversely, AI-based control strategies, such as ANN and FLC methods, operate without needing exact mathematical models and can adeptly handle the system’s nonlinear dynamics [24]. Fuzzy-based dynamic control of DCMG has proposed in [25] to improve the power management control of renewable energy-integrated MG. ANFIS-PID- and FA-PSO-based DCMG has proposed by considering electric vehicle charging ecosystems for assuring stability of DC microgrids [26].

Regarding high-power DC-DC boost and bidirectional buck-boost converter interleaving techniques, some existing models lack DER self-interleaving or AI-based control. For instance, Aditama et al. [27] proposed a multilevel modular buck-boost converter without considering MPPT for interleaving or powerful controllers. Lv et al. [28] used three control loops for a high-voltage-gain boost converter without interleaving, resulting in high sensitivity of the output voltage to input variations [29, 30]. Some models neither used the interleaving technique nor AI-based control. This study explores the design and modeling of high-power DC-DC converters using an ANFIS controller, integrating solar PV arrays, FC stacks, and BESS to create a robust DCMG configuration [31, 32]. The proposed model incorporates the interleaving technique for DC-DC converters and employs an ANFIS controller for DERs, such as in PV array MPPT, FC closed-loop control, and BESS management as the primary control. Modifications to the DC-DC converters include using high-power IGBT devices for high-frequency switching and fast response, and replacing the RC circuit in parallel with the output capacitor [33, 34]. FLC-based MPPT has been implemented to respond instantly to changes in PV array resources and environmental conditions, remaining unaffected by circuit parameter changes [35]. An FLC/ANFIS/ANN-based MPPT technique for a buck-boost converter is presented by Guerra et al. [15], considering ambient conditions (solar irradiance and temperature) as input variables. Results show that the ANN outperforms in tracking speed, accuracy, and reducing oscillation around the maximum power point (MPP) [36]. Khan et al. [37] introduced a voltage control strategy for the DC-DC boost converter using an ANN-based approach, where MPC acts as an expert providing data to train the ANN [38]. The ANN control strategy outperforms the PI controller across various loading conditions, achieving about 97% accuracy during model training [4]. This design assumes that the values of the inductor and capacitor in both the boost and bidirectional buck-boost converters remain constant and do not deviate from their nominal values.

However, the preceding discussion highlights a significant gap in the use of ANFIS techniques for designing controllers for DC-DC converters to address issues such as voltage ripple, inefficiency, inadequate voltage regulation, and compatibility problems. The proposed ANFIS-controlled DC-DC converters, powered by intermittently sourced DERs, effectively manage ripple current and single-stage control issues while maintaining a constant DC bus voltage despite wide-ranging input voltage and load demand variations. Simulation tests confirm that the implementation of the ANFIS controller on interleaved DC-DC converters is highly efficient for high-power converter applications in MGs.

1.3. Major Contributions

This paper has the following major contributions:

(i)
It introduces high-voltage-gain DC-DC boost and bidirectional buck-boost converters using ANFIS-based control to obtain high efficiency and fast response by considering nonideal dynamic input voltage from distributed energy resources (DERs), and at the same time, ANFIS is also used to model solar PV, FC, and BESS systems to reduce the influence of uncertainties.
(ii)
It demonstrates how the proposed converters are capable of accommodating a wide range of input voltages from variable DERs and applying different loads, yielding nearly constant output voltages at the common DC bus.
(iii)
While traditional droop control effectively distributes power between the BESS and DC, it tends to result in higher voltage deviations, consequently hastening BESS capacity degradation. In this paper, the BESS incorporates its own ANFIS controller for managing state of charge (SoC) during charging and discharging operations, ensuring a consistent nominal voltage for the bidirectional buck-boost converter input.

1.4. Paper Organization

The reminder of this work is organized as follows: Section 2 presents MG component modeling with detail description. Section 3 discusses the DC-DC converter controller ANFIS with detail explanation and definition to apply on the proposed system. Section 4 discusses the design of DC-DC high-power boost and bidirectional buck-boost converters for MG applications. Section 5 summarizes the simulation results and discussion. Finally, in Section 6, conclusion is drawn along with suggested future works.

2. System Component Modeling

2.1. Mathematical Model of Solar PV Module

A solar cell functions as a semiconductor device converting photons into renewable and clean electricity. By connecting solar cells in both series and parallel configurations, a solar module is created, and the assembly of these solar modules in series and parallel arrangements forms a photovoltaic (PV) array. The modeling of a solar cell involves representing it as a p-n junction, which is depicted as a diode, a current source, and two resistors—one in series and another in parallel with the diode, along with a current generator, as illustrated in Figure 2 [39]. The key variables influencing the modeling of a solar cell are solar irradiance and temperature, as indicated in the following equation:

(1)

where I_ph and I_sc are the photon current and short circuit current, K_i is the temperature coefficient, and T_o and T_r are standard and ambient cell temperatures.

Hence, the output power of a PV array depends on the size and efficiency of solar modules and can be expressed as a function of the main parameter irradiance, G with assumed electronic maximum power point tracker (MPPT) operation. Then, the PV array power can be calculated as the following equation [40]:

(2)

where A, η_PV, and P_PV are area, efficiency, and output power of the PV array.

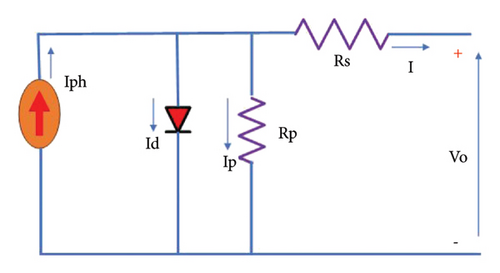
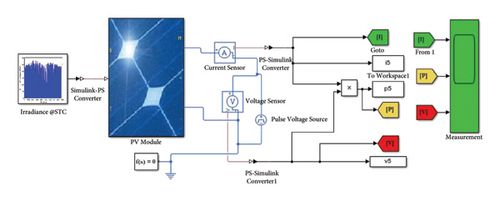
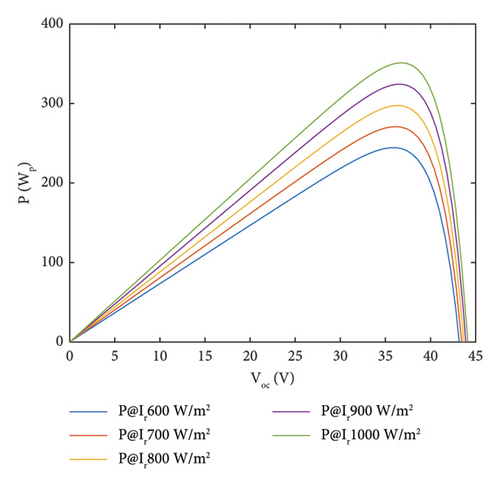
In this paper, a standard PV module has been simulated to evaluate the characteristics of the module based on the influencing parameters such as irradiance and temperature. Figure 3 shows the Simulink module of a standard PV module of 360 Wp rated power to demonstrate characteristic curves based on intermittent resources. Figure 4 shows the P-V and I-V characteristic curves to show the relationship between the open circuit voltage, short circuit current, and output power of the module by considering the irradiance and temperature. The PV system parameter of the selected module specification is shown in Table 1.

Table 1. Polycrystalline module: 200 × 110 mm, 350 Wp, 72 cells (12 × 6) [41].

Parameter	Quantity
Solar irradiance (test irradiance)	1000 W/m²
Maximum power (Pmax)	350 Wp
Voltage at Pmax (Vmp)	37.0 V
Current at Pmax (Imp)	9.71 A
Open circuit voltage (Voc)	43.2 V
Short circuit current (Isc)	10.1 A
Maximum system voltage	100 V DC
Cell efficiency	20.06%
Number of by-pass diodes	6
Maximum series fuse	15 A
Nominal operating cell temperature	47 ± 2^°C

2.2. Fuel Cell Modeling

Fuel cells are clean energy sources employed to convert chemical energy to DC electrical energy using electrolyzers. Its operation is like battery, but no need of recharging, and it has more advantages such high efficiency, simplicity, needs low maintenance, and carbon neutral as compared to the battery [42]. Once the excess power is used to feed the electrolyzer to produce hydrogen by separating water into oxygen (air) which is fed to the cathode and hydrogen is fed to the positive electrode (anode) by supplying DC power via two electrodes.

(3)

Then, the output power delivered from the electrolyzer to the hydrogen tank can be expressed as follows:

(4)

where

and P_in−ele are the output and input power of the electrolyzer and η_ele is the electrolyzer efficiency. Finally, the total generated power from the fuel cell plant can be determined using the following equation:

(5)

The FC and BESS parameters are illustrated in Table 2 that are used in the modeling of the unit FC stack and BESS. Figure 5 shows the ANFIS-controlled MATLAB/Simulink model of a standard 45 V, 6 kW fuel cell stack where the hydrogen flow rate is controlled by the ANFIS to optimize the accumulated hydrogen gas in the hydrogen tank. The V-I and P-I characteristic curve of the given FC stack is shown in Figure 6 that shows the relationship of the stack voltage and power versus the current. As the V-I curve shows, as the stack current increases, the voltage will decrease, and the P-I curve depicts that the output power of the FC stack increases as the stack current or the the hydrogen utilization rate increases. Hence, it is compulsory to optimize and control the flow rate of the gases in the stack.

Table 2. FC stack and BESS specifications.

Parameter	Quantity
Stack power	6 kW
Stack voltage	45 V
Nominal hydrogen utilization	99.56%
Nominal oxidant utilization	59.3%
Hydrogen fuel flow rate	50.06 lpm
Air (oxygen) flow rate	300 lpm
System temperature	338 Kelvin
Fuel supply pressure	1.5 bar
Air supply pressure	1.0 bar
Battery type	Lithium ion
Nominal voltage	187 V
Rated capacity	30 A
Initial state of charge	80%

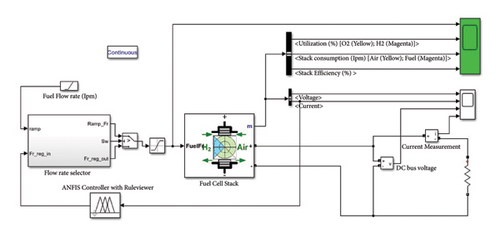
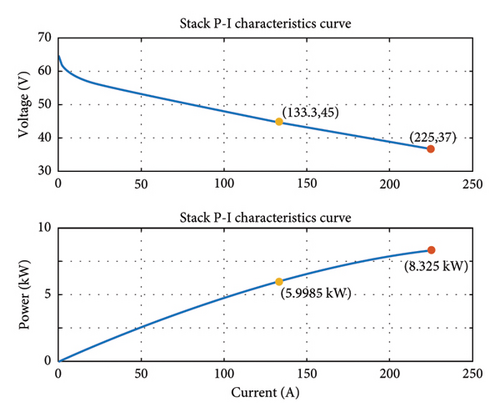
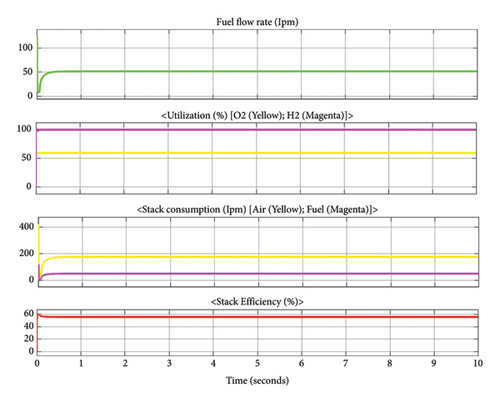
Figure 7 depicts the FC stack parametric values which show the FC flow rate in liters/minute (lpm) resulted around 55 lpm and the utilization of oxygen (labeled yellow) and hydrogen (labeled red) are 60% and 100%, respectively. And the stack consumption of air (labeled green) and fuel consumption are 180 lpm and 50 lpm, respectively, and as shown in the Figure 7, the FC stack efficiency is around 56%.

2.3. BESS and SoC Modeling

BESS helps in smoothing the intermittent power generation from RES and also it can support in shaving the peak demands. The modeling of its capacity can be determined as follows:

(6)

where AD and DoD are autonomy day and depth of discharge, respectively, and η_inv and η_BESS are efficiency of inverter and the battery itself, respectively.

When power generated from each microgrid exceeds the demand, the excess power is used to charge the BESS and the battery power can be expressed as follows:

(7)

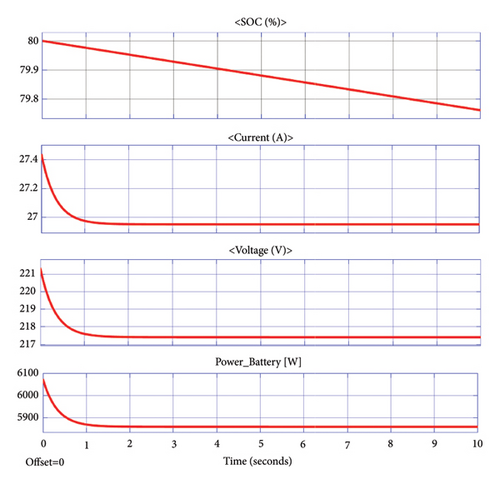
Figure 8 shows the MATLAB/Simulink model of a unit BESS system with measurement features to see the BESS state-of-charge (SoC), current, voltage and power during the simulation. And Figure 9 shows the SoC which represents the energy stored in the battery expressed as percentage between 0% and 100%, current which is dependent on the load connected, system voltage, and output power of the BESS. In this case, the SoC is depleted from 80% to 79.96% for 10 seconds.

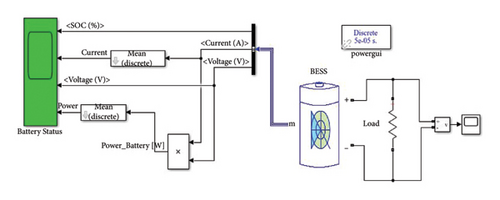
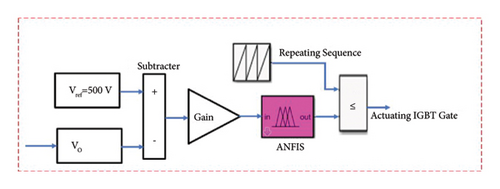
3. Proposed Real-Time Controller: ANFIS

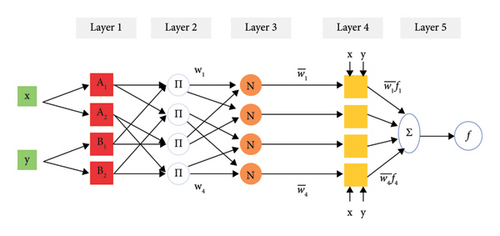
ANFIS attracts a worldwide attention due to its robust control and improves the dynamic behavior of the system. The ANFIS controller, which combines the benefits of ANNs and FLCs, is now regarded as one of the most effective tools for system identification, pattern recognition, and building precise models of systems [43]. Figure 10 shows the architecture of the ANFIS model with five layers. At the first layer, inputs (errors and error changes) will be sent to the second layer without processing. The second layer, each membership function is represented in a fuzzy cluster [44]. At the third layer, minimization of input sets will be applied at each node. The fourth layer is a defuzzification stage which extracts the fuzzy sets of each node. At the fifth layer, output of each node at the fourth layer will be accumulated for the final value of the ANFIS controller. ANFIS uses Sugeno-type inference system that provides a structured method for generating if-then rules by formalizing the input-output relationship in a systematic manner. As Figure 10 illustrates ANFIS two inputs and one output structure where x and y are crisp inputs, and f is the crisp output. Referring to Figure 10, two rules are articulated for the first-order Sugeno fuzzy inference system as follows [45–47]: rule 1: if x is A₁ and y is B₁, then f₁ = p₁x + q₁y + r₁, rule 2: if x is A₂ and y is B₂, then f₂ = p₂x + q₂y + r₂, where x and y denote inputs, A_i and B_i are fuzzy variables, f_i represents outputs within fuzzy sets, and p_i, q_i, and r_i are design parameters established through the training process of the ANFIS system. Figure 10 illustrates the architecture of ANFIS. In this depiction, a fixed node is denoted by a circle, while an adaptive node is represented by a square. ANFIS features a five-layer structure, with nodes in each layer serving comparable functions. Detailed explanations for each layer are given as follows.

3.1. Layer 1

The results produced by layer 1 consist of the fuzzy membership grades assigned to the inputs, as determined by the following equations:

(8)

(9)

where x and y represent the inputs to node i and A_i and B_i are linguistic labels (such as high or low) associated with the functions of this node. μ_Ai(x) and μ_Bi(y) can take on any fuzzy membership function. For instance, if a bell-shaped membership function is utilized, μAi(x) can be expressed as follows:

(10)

where a_i, b_i, and c_i are parameters of the membership function.

3.2. Layer 2

Layer 2 comprises fixed nodes utilizing fuzzy operators, specifically employing the AND operator for the fuzzification of inputs. These nodes, labeled with π, function as simple multipliers. The outcome of this layer can be expressed as follows:

(11)

These are the so-called firing strength of the rules.

3.3. Layer 3

Layer 3 consists of fixed nodes labeled as N, signifying their role in normalizing the firing strengths from the preceding layer. The result of this layer can be denoted as follows:

(12)

Outputs of this layer are called normalized firing strengths.

3.4. Layer 4

In layer 4, adaptive nodes are featured. Each node’s output is the product of the normalized firing strength and a first-order polynomial, specifically for a first-order Sugeno model. The expression for the output of this layer is as follows:

(13)

3.5. Layer 5

In layer 5, there is only one single-fixed node labeled with ∑x. This node performs the summation of all incoming signals. The overall output of the model is given as follows:

(14)

4. Design of DC-DC Boost and Buck-Boost Converters

4.1. Mathematical of Buck and Boost Converters

As shown in Figure 11, the equivalent circuit of the booster circuit can be analyzed by applying the KVL as follows:

(15)

(16)

The switch states, S, is defined as u(t) in which switch S is ON, when S = 1, and switch S is OFF, when S = 0, as shown in the following equation:

(17)

From the circuit, the duty cycle and voltage gain of the converter can be calculated according to the following equation:

(18)

And then, output voltage of the converter can be evaluated as follows:

(19)

Then, the voltage gain can be estimated as follows:

(20)

For bidirectional buck-boost converter, there are two operation modes called buck operation mode: in this mode, the voltage is going to reduce from the input by a factor of its duty ration, D_Buck, as given in the following:

(21)

The operation is optimized by the action of ANFIS that actuates S₁ as shown in Figure 12. Boost operation mode: during this operation mode, the voltage from the BESS can be setup using the booster section of the converter to normalize the DC bus voltage. Hence, the voltage gain in the case of the boost mode can be estimated as follows:

(22)

where is the actuating signal S₂. When the two converters are cascaded, the network can be synchronized to the main DC bus.

4.2. DC-DC Boost Converter Model

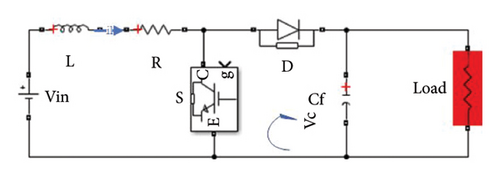
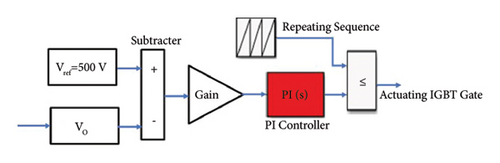
DC-DC boost converter for microgrid application is similar to a conventional boost converter; it increases the DC voltage from its input (sourced from renewable energy sources, batteries, or other microgrid elements) to the microgrid’s DC bus. The proposed converter as shown in Figure 13 is designed to accommodate wide range of input voltages from different renewable DC voltage sourced such as solar PV, FC, and BESS with high transient response during the generation and demand changes and high-power efficiency. The booster is controlled through the application of adaptive PI controller, fuzzy logic controller, and ANFIS to compare and choose the suitable controller with fast response and high accuracy. The designed converter desired output voltage is 500 V and the input sources are designed for 300 V with variable and intermittent nature in the solar PV and FC stacks which has to be further optimized through electronic maximum power point tracker (MPPT).

The solar array voltage is set to 300 V by embedding the MPPT internally, and the FC stack is also designed for 300 V by increasing the number of cells in the stack and optimizing the hydrogen and air flow rate. Then, the DC-DC boost converter is implemented to step-up the 300 V to a constant 500 V DC for the DC subgrid.

4.3. DC-DC Buck-Boost Converter Model

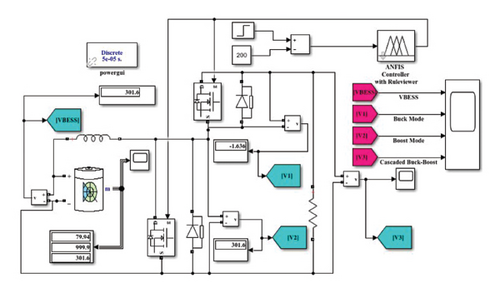
Unlike a buck converter (step-down) or a boost converter (step-up), a buck-boost converter can both increase and decrease the DC voltage, depending on the operating mode. This allows for flexible power flow management within the MG. The designed buck-boost converter is implemented on BESS-based DC subgrid to charge the battery from the DC bus through the buck converter side when there is surplus energy from the renewable energy sources and to utilize the BESS power when there is a power deficiency to shave the peak demand of the MG trough the boost side of the converter so that the overall operating cost will be minimized. IGBT switch, S₁, is used to optimize/actuating the buck mode operation of the converter where the input voltage is V_BESS and the output voltage is V₁ through PI, FLC, and ANFIS controllers for comparison. And S₂ is triggered by the proposed controllers to optimize the boost side converter by keeping the input voltage, V_BESS, and the output voltage is V₂. By summing both converter output voltages, the converter can be a cascaded converter which can act as a bidirectional buck-boost converter and a cascaded converter that can synchronize the main system DC bus at a constant voltage of 500 V of the DCMG as shown in Figure 12. The proposed ANFIS closed-loop controller was used to optimize and actuate the IGBT PWM signal for voltage regulation in both buck and boost modes of operation by keeping the DC bus voltage 500 V as a reference.

Table 3 illustrates the boost converter design parameters that is assumed and calculated based on trial and error for the desired DC bus voltage output in the DCMG application. By having the aforementioned parameters in the boost converter, the buck and cascaded converters are also formulated from the boost converter design parameters by amending the values by assumption and trial and error method until the target point reaches the desired voltage values of each converters. Figure 14 highlights the subsystem diagram of the controllers.

Table 3. Boost converter design parameter.

No.	Parameter	Designed value
1	Input voltage	300 V
2	Output voltage	500 V
3	Input current	252 A
4	Output current	123.6 A
5	Load resistance	200 Ω
6	System test load	61.5 kW
7	Duty cycle	0.5 p.u.
8	Switching frequency	250 kHz
9	Inductor	76.8∗10⁻⁶ H
10	Capacitor	400∗10⁻⁶ F

5. Simulation Results and Discussion

The proposed soft-computing algorithms and methodology are executed in the MATLAB R2022b academic version Simulink environment using a machine with processor speed of 2.4 GHz Intel Core i7 and 16 GB RAM.

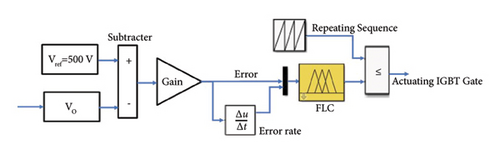
Figure 15 shows the output voltages of PI/FLC/ANFIS-controlled DC-DC boost converter for the DCMG application by accommodating intermittent voltage sourced renewable energy resources such as solar PV, FC stacks, and BESS in the MG. As the result depicts the ANFIS-based control is more accurate and faster than PI and FLC. Since the ANFIS has the advantages of both the ANN and FLC, it is clear that the efficiency of the converter is higher than the adaptive PI and FLC. The output voltage result shows that the ANFIS-based boost converter has 10% overshoot as compared to 41% and 50% overshoot in PI and FLC, respectively. And the settling time in ANFIS is 0.01 seconds which is fastest as compared to 0.015 seconds and 0.05 seconds in FLC and PI controllers, respectively.

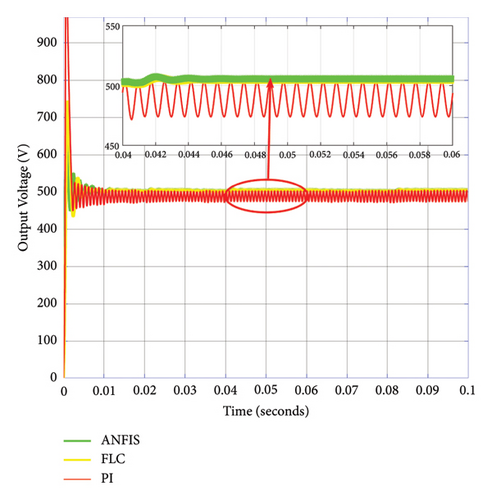
Figure 16 shows the ANFIS-based boost converter parameter simulation results. As the scope depicts, the input PV array, FC, and BESS voltage is set to 300 V by implementing an implicit ANFIS controller for each plants such as MPPT booster in the PV array, fuel flow rate optimization in the FC stack, and state-of-charge (SoC) controller in the BESS. Then, by using the converter ANFIS controller, the voltage is further stepped-up to 500 V which is assumed as the output voltage of the DC bus. Hence, the ANFIS controller effectively handles the regulation task in the boost converter for the proposed MG application. Furthermore, as the scope shows the input current in the PV array and FC was 238.6 A, but the boost converter effectively reduced the input current to 121.5 A in the output port. The variation in the buffering DC link capacitor voltage is measured at 1.14%. This fluctuation is minimized on the capacitor side, ensuring that the output voltage remains stable. With a permissible limit of 5%, the proposed ANFIS has effectively reduced the DC link voltage variation to a significantly lower value within this limit.

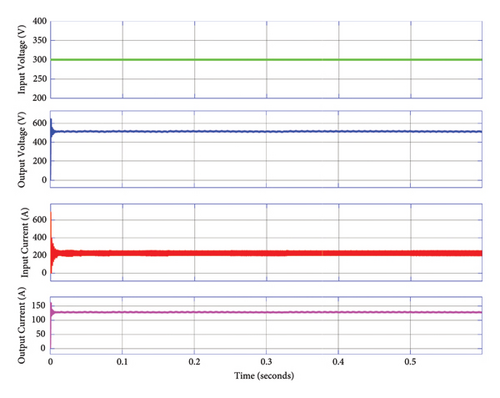
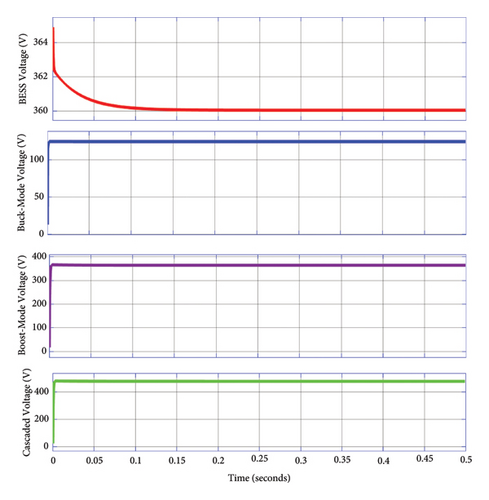
Figure 17 depicts the bidirectional buck-boost converter simulation result. When the bidirectional buck-boost converter is applied on the BESS for the charging and discharging applications, the BESS voltage is around 360 V under the initial SoC of 80% then under the buck mode operation, the output buck voltage is 120 V which can charge the BESS effectively with the help of embedded charge controller. The booster side has stepped-up the input BESS voltage to 360 V, and by cascading the two converters, the DC bus will receive 500 V from the BESS through the bidirectional buck-boost converter.

The operation of buck and boost converters are actuating by the pulse width modulation (PWM) through the ANFIS controller. In the simulation, it has also observed that the duty ratio during the ANFIS operation to ON and OFF the IGBT switch has been stepped-up or stepped-down with a certain voltage gain from the pulse that triggered the gate of the IGBT. The measurement showed that the mean value is around 0.48 p.u. and ranges from 0 to 1. For bidirectional buck-boost converter, the duty ration for buck mode and boost mode operations is different which is directly proportional to the voltage gains in each mode of operation.

Table 4 illustrates the voltage gain sensitivity in buck and boost modes of operation. As the load resistance/demand in the MG increases, the output voltage of the converter is consistent in both modes of operations. Even if there is a slight voltage drop as the load change is getting bigger, the converters are effective to handle reasonable load changes in the MG for practical applications since the simulation is set up with the real renewable energy-sourced voltage supplies. Hence, it can be concluded that the voltage gain is not sensitive to the load change in both converter operations.

Table 4. ANFIS-controlled gain sensitivity in buck and boost modes at different load.

No.	Load resistance (Ω)	Boost mode output voltage (V)	Buck mode output voltage (V)
1	50	500.5	119.9
2	100	500.09	119.8
3	150	500.05	119.6
4	200	500.01	120.0
5	250	500.00	120.05
6	300	500.00	120.06
7	350	500.0	120.09
8	400	499.96	120.09

Table 5 depicts the voltage gain sensitivity in buck and boost operation modes by varying the input voltage. As the input voltage is from the intermittent energy sources such as solar PV, FC stacks, wind power, and energy storage systems (ESSs), the output voltage of these sources are variable. The designed buck and boost converters are receiving a variable input voltage from 200 V − 320 V, then regulates the output voltage to a consistent and constant voltage of 500 V and 120 V for boost and buck converters, respectively. As the input voltage ranges from 200 V to 320 V and the output voltages are then regulated by the ANFIS controller to a constant voltage of 500 V and 120 V for the converter. Hence, both converters have 98.8% efficiency at the optimum duty ratio and can accommodate variable input voltages from dynamic energy sources. The ANFIS is working on the pulse width modulation operation where the actuating signal is a square wave that controls the IGBT gate. Consequently, the duty cycle can be adjusted within the range of 0 to 1 p.u., as depicted in Figure 18.

Table 5. ANFIS-controlled gain sensitivity in buck and boost modes at different input voltages.

No.	Input voltage (V)	Boost mode output voltage (V)	Buck mode output voltage (V)
1	200	499.15	119.2
2	220	499.69	119.9
3	250	499.98	119.99
4	270	500.00	120.00
5	290	500.00	120.00
6	300	500.00	120.00
7	310	500.04	120.02
8	320	500.06	120.03

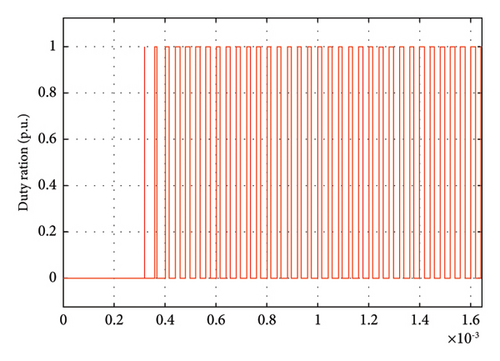
Table 6 demonstrates the output voltage at different duty cycle values ranging from 5% to 50%. As the duty ratio increases, the buck and boost converters output voltage increases. Therefore, the duty ratio is the key factor to vary the output voltage of the converters.

Table 6. ANFIS-controlled output voltage at fixed load (200(Ω)) for different cycle ratios.

No.	Duty ratio (%)	Boost mode output voltage (V)	Buck mode output voltage (V)
1	5	25.95	5.24
2	10	45.23	7.45
3	15	72.49	7.99
4	20	94.56	8.78
5	25	121.97	9.92
6	30	150.29	1025
7	35	182.54	12.96
8	40	205.74	25.20
9	45	235.10	70.67
10	50	493.30	89.90

The comparison between different approaches in the literature is presented in Table 7. Although in the literature, few researchers focused on conventional boost and bidirectional buck-boost converters, there are some works on the MG applications. Few research studies utilize sole energy storage such as flywheel or ultracapacitor to minimize the fluctuations caused by intermittent renewable energy resources such as solar PV systems, FC, and wind energy, but these ESS devices can smooth or mitigate short-term fluctuations only and also shave the peak demand so that the operating cost is getting minimized. Most of the authors utilize conventional and soft-computing algorithms for optimizing the converter control gates using PWM. The proposed approach in this study utilizes PI, FLC, and ANFIS controllers for comparison and on the output voltage stability which mainly focused on nonideal input voltage sources. As stated in the conventional circuit, efficiency can be calculated using the following equation:

(23)

Table 7. Comparison between different MG input sources and converter efficiency.

Ref.	MG sources	ESS	Techniques	Converter efficiency
[48]	WT + PV	Capacitor	FA-PSO	96.5
[49]	WT + PV	EV + BESS	MPC	96.6
[50]	DG + PV	BESS	PFM	97.7
[51]	PV + Grid	BESS + EV	PID	98.2
[52]	WT + PV	BESS + EV	FLC	98.39
[53]	WT + PV	FC	PSO-PID	98.5
Proposed method	PV + FC	BESS	PI, FLC, ANFIS	98.8

Since the proposed circuit is a simplified form of the conventional model of the boost converter, diodes and other passive elements are reduced and replaced with a controllable IGBT and maintained using the ANFIS controller that tries to reduce the error and always follow the desired DC voltage. Hence, the designed converter efficiency is almost 99.5% as calculated from Table 5.

6. Conclusion

This article presents DC-DC boost and bidirectional buck-boost converter configurations designed for DC microgrid applications. It compares the performance of these converters using PI, FLC, and ANFIS controllers. The ANFIS controller demonstrated the highest efficiency, approximately 98.8%, for the proposed converter designs. Compared to traditional boost and buck-boost converters, the ANFIS-controlled converter models effectively handle variable input voltages from intermittent renewable energy sources such as solar PV, fuel cell stacks, wind power, and BESS. Simulations with real-time PV arrays, fuel cell stacks, and BESS showed the converters achieving voltage outputs of 500 V and 120 V at the boost and buck converter ports, respectively. Despite significant input voltage variations and load fluctuations, both converters maintained stable output voltages after a 10% overshoot lasting only 0.05 seconds.

Furthermore, this study suggests that future work could involve validating the performance of the proposed converters in a nonideal DER-sourced laboratory, aiming for a scalable design and enabling seamless expansion to support multiple ports for EV charging infrastructure or higher power requirements in hybrid microgrids.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the Pan African University Institute for Basic Sciences, Technology and Innovation (PAUSTI).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author on request.

References

1 Frivaldsky M., Kascak S., Morgos J., and Prazenica M., From non-modular to modular concept of bidirectional buck/boost converter for microgrid applications, Energies. (2020) 13, no. 12, https://doi.org/10.3390/en13123287.
10.3390/en13123287
Google Scholar
2 Liu S., Liu X., Jiang S., Zhao Z., Wang N., Liang X., Zhang M., and Wang L., Application of an improved stsmc method to the bidirectional dc–dc converter in photovoltaic dc microgrid, Energies. (2022) 15, no. 5, https://doi.org/10.3390/en15051636.
10.3390/en15051636
Google Scholar
3 Broday G. R., Damm G., Pasillas-Lépine W., and Lopes L. A., A unified controller for multi-state operation of the bi-directional buck–boost dc-dc converter, Energies. (2021) 14, no. 23, https://doi.org/10.3390/en14237921.
10.3390/en14237921
Google Scholar
4 Aljafari B., Devarajan G., Subramani S., and Vairavasundaram S., Intelligent rbf-fuzzy controller based non-isolated dc-dc multi-port converter for renewable energy applications, Sustainability. (2023) 15, no. 12, https://doi.org/10.3390/su15129425.
10.3390/su15129425
Google Scholar
5 Kulshreshtha A. and Saxena A. R., Generalized game-theoretic approach for the design of energy storage elements of higher-order dc-dc converters, International Transactions on Electrical Energy Systems. (2021) 31, no. 11, https://doi.org/10.1002/2050-7038.13085, e13085.
10.1002/2050-7038.13085
Google Scholar
6 Raj Kafle Y., Hossain M. J., and Kashif M., Quasi-z-source-based bidirectional dc-dc converters for renewable energy applications, International Transactions on Electrical Energy Systems. (2021) 31, no. 4, https://doi.org/10.1002/2050-7038.12823, e12823.
10.1002/2050-7038.12823
Web of Science® Google Scholar
7 Gebru Y., Bitew D., Aberie H., and Gizaw K., Performance enhancement of radial distribution system using simultaneous network reconfiguration and switched capacitor bank placement, Cogent Engineering. (2021) 8, no. 1, https://doi.org/10.1080/23311916.2021.1897929, 1897929.
10.1080/23311916.2021.1897929
Google Scholar
8 Ullah Q., Busarello T. D. C., Brandao D. I., and Simões M. G., Design and performance evaluation of smc-based dc–dc converters for microgrid applications, Energies. (2023) 16, no. 10, https://doi.org/10.3390/en16104212.
10.3390/en16104212
PubMed Google Scholar
9 Lai C.-M., Lin Y.-C., and Lee D., Study and implementation of a two-phase interleaved bidirectional dc/dc converter for vehicle and dc-microgrid systems, Energies. (2015) 8, no. 9, 9969–9991, https://doi.org/10.3390/en8099969, 2-s2.0-84945293594.
10.3390/en8099969
Web of Science® Google Scholar
10 Sánchez A. G. S., Soto-Vega J., Tlelo-Cuautle E., and Rodríguez-Licea M. A., Fractional-order approximation of pid controller for buck–boost converters, Micromachines. (2021) 12, no. 6, https://doi.org/10.3390/mi12060591.
10.3390/mi12060591
PubMed Google Scholar
11 Bharath K., Choutapalli H., and Kanakasabapathy P., Control of bidirectional dc-dc converter in renewable based dc microgrid with improved voltage stability, International Journal of Renewable Energy Research (IJRER). (2018) 8, no. 2, 871–877.
Google Scholar
12 Yfoulis C., Papadopoulou S., and Voutetakis S., Robust linear control of boost and buck-boost dc-dc converters in micro-grids with constant power loads, Energies. (2020) 13, no. 18, https://doi.org/10.3390/en13184829.
10.3390/en13184829
Google Scholar
13 Liu L., Li D., and Yao L., A family of non-isolated transformerless high step-up dc-dc converters, International Transactions on Electrical Energy Systems. (2019) 29, no. 4, https://doi.org/10.1002/etep.2794, 2-s2.0-85059059165.
10.1002/etep.2794
Google Scholar
14 Rong X., Shek J. K., and Macpherson D. E., The study of different unidirectional input parallel output series connected dc-dc converters for wind farm based multi-connected dc system, International Transactions on Electrical Energy Systems. (2021) 31, no. 5, https://doi.org/10.1002/2050-7038.12855, e12855.
10.1002/2050-7038.12855
Web of Science® Google Scholar
15 Guerra M. I., Ugulino de Araújo F. M., Dhimish M., and Vieira R. G., Assessing maximum power point tracking intelligent techniques on a pv system with a buck–boost converter, Energies. (2021) 14, no. 22, https://doi.org/10.3390/en14227453.
10.3390/en14227453
Google Scholar
16 Rouzbehi K., Miranian A., Escaño J. M., Rakhshani E., Shariati N., and Pouresmaeil E., A data-driven based voltage control strategy for dc-dc converters: Application to dc microgrid, Electronics. (2019) 8, no. 5, https://doi.org/10.3390/electronics8050493, 2-s2.0-85067081285.
10.3390/electronics8050493
Google Scholar
17 Liu Y., Han Y., Lin C., Yang P., and Wang C., Design and implementation of droop control strategy for dc microgrid based on multiple dc/dc converters, 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), 2019, IEEE, Piscataway, NJ, USA, 3896–3901.
10.1109/ISGT-Asia.2019.8881129
Google Scholar
18 Aeggegn D. B., Nyakoe G. N., and Wekesa C., A state of the art review on energy management techniques and optimal sizing of ders in grid-connected multi-microgrids, Cogent Engineering. (2024) 11, no. 1, https://doi.org/10.1080/23311916.2024.2340306, 2340306.
10.1080/23311916.2024.2340306
Google Scholar
19 Aeggegn D. B., Agajie T. F., Workie Y. G., Khan B., and Fopah-Lele A., Feasibility and techno-economic analysis of pv-battery priority grid tie system with diesel resilience: a case study, Heliyon. (2023) 9, no. 9, e19387, https://doi.org/10.1016/j.heliyon.2023.e19387.
10.1016/j.heliyon.2023.e19387
PubMed Google Scholar
20 Aeggegn D. B., Salau A. O., Gebru Y. W., and Agajie T., Mitigation of reactive power and harmonics in a case of industrial customer, International Journal of Engineering Research in Africa. (2022) 60, 107–124, https://doi.org/10.4028/p-j716jb.
10.4028/p-j716jb
Google Scholar
21 Koundi M., El Idrissi Z., El Fadil H., Belhaj F. Z., Lassioui A., Gaouzi K., Rachid A., and Giri F., State-feedback control of interleaved buck–boost dc–dc power converter with continuous input current for fuel cell energy sources: theoretical design and experimental validation, World Electric Vehicle Journal. (2022) 13, no. 7, https://doi.org/10.3390/wevj13070124.
10.3390/wevj13070124
Google Scholar
22 Mostaan A., Zeinali H., Asghari S., and Baghramian A., Novel high step up dc/dc converters with reduced switch voltage stress, The 5th Annual International Power Electronics, Drive Systems and Technologies Conference (PEDSTC 2014), 2014, IEEE, Piscataway, NJ, USA, 379–384.
10.1109/PEDSTC.2014.6799404
Google Scholar
23 Senapati M. K., Pradhan C., Nayak P. K., Padmanaban S., and Gjengedal T., Modified demagnetisation control strategy for low-voltage ride-through enhancement in dfig-based wind systems, IET Renewable Power Generation. (2020) 14, no. 17, 3487–3499, https://doi.org/10.1049/iet-rpg.2019.1128.
10.1049/iet-rpg.2019.1128
Web of Science® Google Scholar
24 Aeggegn D. B., Gebru Y. W., Agajie T. F., Salau A. O., and Akindadelo A. T., Alleviation of voltage quality-related issues: a case study of bahir dar textile share distribution system, Smart Trends in Computing and Communications: Proceedings of SmartCom 2022, 2022, Springer, Berlin, Germany, 369–379.
Google Scholar
25 Senapati M. K., Pradhan C., Samantaray S. R., and Nayak P. K., Improved power management control strategy for renewable energy-based dc micro-grid with energy storage integration, IET Generation, Transmission & Distribution. (2019) 13, no. 6, 838–849, https://doi.org/10.1049/iet-gtd.2018.5019, 2-s2.0-85065146188.
10.1049/iet-gtd.2018.5019
Web of Science® Google Scholar
26 Senapati M. K., Al Zaabi O., Al Hosani K., Al Jaafari K., Pradhan C., and Muduli U. R., Advancing electric vehicle charging ecosystems with intelligent control of dc microgrid stability, IEEE Transactions on Industry Applications. (2024) 1–14, https://doi.org/10.1109/tia.2024.3413052.
10.1109/TIA.2024.3413052
Google Scholar
27 Aditama R. D., Ramadhani N., Ardriani T., Furqani J., Rizqiawan A., and Dahono P. A., New modular multilevel dc–dc converter derived from modified buck–boost dc–dc converter, Energies. (2023) 16, no. 19, https://doi.org/10.3390/en16196950.
10.3390/en16196950
PubMed Google Scholar
28 Lv M., Wang P., Wei Y., Wen C., Li J., Jia P., and Wei Q., An input-series-output-parallel cascaded converter system applied to dc microgrids, Symmetry. (2023) 15, no. 6, https://doi.org/10.3390/sym15061174.
10.3390/sym15061174
PubMed Google Scholar
29 Salau A. O., Gebru Y. W., and Bitew D., Optimal network reconfiguration for power loss minimization and voltage profile enhancement in distribution systems, Heliyon. (2020) 6, no. 6, e04233, https://doi.org/10.1016/j.heliyon.2020.e04233.
10.1016/j.heliyon.2020.e04233
PubMed Web of Science® Google Scholar
30 Aeggegn D. B., Salau A. O., and Gebru Y., Load flow and contingency analysis for transmission line outage, Archives of Electrical Engineering. (2020) 581–594.
Google Scholar
31 Aeggegn D. B., Nyakoe G. N., and Wekesa C., Optimal sizing of grid connected multi-microgrid system using grey wolf optimization, Results in Engineering. (2024) 23, 102421.
10.1016/j.rineng.2024.102421
Google Scholar
32 Agajie T. F., Awoke Y. A., and Aeggegn D. B., Optimal expansion planning of distribution system in smart grid environment, Active Electrical Distribution Network, 2022, Elsevier, Amsterdam, Netherlands, 381–400.
10.1016/B978-0-323-85169-5.00021-6
Google Scholar
33 Ertekin D., Arvin converter: a bidirectional dc/dc converter for grid-connected g2v/v2g energy storage and electrification approaches, Electrical Engineering. (2024) 1–21, https://doi.org/10.1007/s00202-024-02295-x.
10.1007/s00202-024-02295-x
Google Scholar
34 Senapati M. K., Pradhan C., Nayak P. K., and Samantaray S. R., Lagrange interpolating polynomial–based deloading control scheme for variable speed wind turbines, International Transactions on Electrical Energy Systems. (2019) 29, no. 5, https://doi.org/10.1002/2050-7038.2824, 2-s2.0-85059852689.
10.1002/2050-7038.2824
Google Scholar
35 Subramanian V., Indragandhi V., Kuppusamy R., and Teekaraman Y., Modeling and analysis of pv system with fuzzy logic mppt technique for a dc microgrid under variable atmospheric conditions, Electronics. (2021) 10, no. 20, https://doi.org/10.3390/electronics10202541.
10.3390/electronics10202541
Google Scholar
36 Khan M., Raza M. A., Jumani T. A., Mirsaeidi S., Abbas G., Touti E.-D., Alshahir A., and Alshahir A., Modeling of intelligent controllers for solar photovoltaic system under varying irradiation conditions, Frontiers in Energy Research. (2023) 11, https://doi.org/10.3389/fenrg.2023.1288486, 1288486.
10.3389/fenrg.2023.1288486
Google Scholar
37 Khan H. S., Mohamed I. S., Kauhaniemi K., and Liu L., Artificial neural network-based voltage control of dc/dc converter for dc microgrid applications, 2021 6th IEEE Workshop on the Electronic Grid (eGRID), 2021, IEEE, Piscataway, NJ, USA, 1–6.
10.1109/eGRID52793.2021.9662132
Google Scholar
38 Shahid M. A., Abbas G., Hussain M. R., Asad M. U., Farooq U., Gu J., Balas V. E., Uzair M., Awan A. B., and Yazdan T., Artificial intelligence-based controller for dc-dc flyback converter, Applied Sciences. (2019) 9, no. 23, https://doi.org/10.3390/app9235108.
10.3390/app9235108
Google Scholar
39 Kumar R., Singh S., and Singh S., Solar photovoltaic modeling and simulation: as a renewable energy solution, Energy Reports. (2018) 4, 701–712, https://doi.org/10.1016/j.egyr.2018.09.008, 2-s2.0-85056150296.
10.1016/j.egyr.2018.09.008
Web of Science® Google Scholar
40 Hossain M. A., Pota H. R., Squartini S., and Abdou A. F., Modified pso algorithm for real-time energy management in grid-connected microgrids, Renewable Energy. (2019) 136, 746–757, https://doi.org/10.1016/j.renene.2019.01.005, 2-s2.0-85060317723.
10.1016/j.renene.2019.01.005
Web of Science® Google Scholar
41 Vasantharaj S., Indragandhi V., Subramaniyaswamy V., Teekaraman Y., Kuppusamy R., and Nikolovski S., Efficient control of dc microgrid with hybrid pv—fuel cell and energy storage systems, Energies. (2021) 14, no. 11, https://doi.org/10.3390/en14113234.
10.3390/en14113234
Google Scholar
42 Mahmoud F. S., Abdelhamid A. M., Al Sumaiti A., El-Sayed A.-H. M., and Diab A. A. Z., Sizing and design of a pv-wind-fuel cell storage system integrated into a grid considering the uncertainty of load demand using the marine predators algorithm, Mathematics. (2022) 10, no. 19, https://doi.org/10.3390/math10193708.
10.3390/math10193708
Google Scholar
43 Kaur S., Kaur T., and Khanna R., Anfis based smart control of electric vehicles integrated with solar powered hybrid ac-dc microgrid, Electric Power Components and Systems. (2020) 48, no. 12-13, 1282–1295, https://doi.org/10.1080/15325008.2020.1854386.
10.1080/15325008.2020.1854386
Web of Science® Google Scholar
44 Osheba D. S., Osheba S., Nazih A., and Mansour A. S., Performance enhancement of pv system using vsg with anfis controller, Electrical Engineering. (2023) 105, no. 5, 2523–2537, https://doi.org/10.1007/s00202-023-01824-4.
10.1007/s00202-023-01824-4
Google Scholar
45 Mlakić D., Baghaee H. R., and Nikolovski S., A novel anfis-based islanding detection for inverter-interfaced microgrids, IEEE Transactions on Smart Grid. (2019) 10, no. 4, 4411–4424, https://doi.org/10.1109/tsg.2018.2859360, 2-s2.0-85050611845.
10.1109/TSG.2018.2859360
Web of Science® Google Scholar
46 Moyo R. T., Tabakov P. Y., and Moyo S., Design and modeling of the anfis-based mppt controller for a solar photovoltaic system, Journal of Solar Energy Engineering. (2021) 143, no. 4, https://doi.org/10.1115/1.4048882, 041002.
10.1115/1.4048882
Google Scholar
47 Guerra M. I., de Araújo F. M., de Carvalho Neto J. T., and Vieira R. G., Survey on adaptative neural fuzzy inference system (anfis) architecture applied to photovoltaic systems, Energy Systems. (2022) 15, no. 2, 505–541, https://doi.org/10.1007/s12667-022-00513-8.
10.1007/s12667-022-00513-8
Google Scholar
48 Hasanpour S., Siwakoti Y. P., and Blaabjerg F., A new high efficiency high step-up dc/dc converter for renewable energy applications, IEEE Transactions on Industrial Electronics. (2023) 70, no. 2, 1489–1500, https://doi.org/10.1109/tie.2022.3161798.
10.1109/TIE.2022.3161798
Web of Science® Google Scholar
49 Andrade A. M. S. S., Schuch L., and da Silva Martins M. L., Analysis and design of high-efficiency hybrid high step-up dc–dc converter for distributed pv generation systems, IEEE Transactions on Industrial Electronics. (2019) 66, no. 5, 3860–3868, https://doi.org/10.1109/tie.2018.2840496, 2-s2.0-85048000701.
10.1109/TIE.2018.2840496
Web of Science® Google Scholar
50 Jin F., Nabih A., Chen C., Chen X., Li Q., and Lee F. C., A high efficiency high density dc/dc converter for battery charger applications, 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), 2021, IEEE, Piscataway, NJ, USA, 1767–1774.
10.1109/APEC42165.2021.9487108
Google Scholar
51 Ye H., Jin G., Fei W., and Ghadimi N., High step-up interleaved dc/dc converter with high efficiency, Energy Sources, Part A: Recovery, Utilization, and Environmental Effects. (2020) 1–20, https://doi.org/10.1080/15567036.2020.1716111.
10.1080/15567036.2020.1716111
Google Scholar
52 Li R. and Shi F., Control and optimization of residential photovoltaic power generation system with high efficiency isolated bidirectional dc–dc converter, IEEE Access. (2019) 7, 116107–116122, https://doi.org/10.1109/access.2019.2935344.
10.1109/ACCESS.2019.2935344
Web of Science® Google Scholar
53 Samanta S., Mishra J. P., and Roy B. K., Virtual dc machine: an inertia emulation and control technique for a bidirectional dc–dc converter in a dc microgrid, IET Electric Power Applications. (2018) 12, no. 6, 874–884, https://doi.org/10.1049/iet-epa.2017.0770, 2-s2.0-85049249263.
10.1049/iet-epa.2017.0770
Web of Science® Google Scholar

Citing Literature

All articles

ANFIS-Controlled Boost and Bidirectional Buck-Boost DC-DC Converters for Solar PV, Fuel Cell, and BESS-Based Microgrid Application

Abstract

1. Introduction

1.1. Motivation

1.2. Related Works

1.3. Major Contributions

1.4. Paper Organization

2. System Component Modeling

2.1. Mathematical Model of Solar PV Module

2.2. Fuel Cell Modeling

2.3. BESS and SoC Modeling

3. Proposed Real-Time Controller: ANFIS

3.1. Layer 1

3.2. Layer 2

3.3. Layer 3

3.4. Layer 4

3.5. Layer 5

4. Design of DC-DC Boost and Buck-Boost Converters

4.1. Mathematical of Buck and Boost Converters

4.2. DC-DC Boost Converter Model

4.3. DC-DC Buck-Boost Converter Model

5. Simulation Results and Discussion

6. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley