With the increasing demands of ultra-large space antennas, on-orbit assembly stands out as a promising solution. However, this achievement necessitates the reconfiguration design of the whole antenna structure to maintain structural integrity and stability. In light of this challenge, a novel rapid design method is proposed for the unit configuration of modular-assembled antennas in this paper. The method utilizes an inscribed regular hexagon, which is positioned within a horizontal topological circle. The hexagon is subsequently projected onto a spinning paraboloid, resulting in the creation of unit nodes that conform to the shape of the paraboloid. The configuration of the unit topology is then determined based on the arrangement of these nodes. By using the method, two units of space-assembled antennas are designed. The topology design of the cable network is carried out for the modular unit. The pretensions of the cables are calculated. The results of the case study reveal that the developed modular units fulfill the requirements of the on-orbit-assembly antenna structure and can solve the engineering application difficulties of this type of antenna.

1. Introduction

With the continuous development of space technology and the increasing number of space activities, space structures are constantly developed in the direction of large scale and lightweight [1–4]. Large-scale space solar power stations of kilometer size, ultra-large space payloads, and ultra-large space science probes would play an increasingly important role in space activities such as the utilization of space resources, high-resolution earth observation, and exploration of the mysteries of the universe in the future. Constrained by launch size and weight, ultra-large space structures have to be constructed by on-orbit deployment and assembly.

The space on-orbit assembly technology has gradually changed from concept to reality since 1984. In 1985, the testing of the on-orbit assembly of the EASE/ACCESS truss structure was completed by NASA and ESA in the STS-61-B mission [5], which fully demonstrated the feasibility of the concept. After that, many on-orbit assemblies have been put forward by domestic and foreign scholars, most of which are in the phase of scheme research or experimental verification of key technologies [6–10].

In the design of on-orbit-assembled space structures, modularity and deployability are crucial. For space antennas, to assemble ultra-large structures effectively, it is essential to cleverly design modular trusses and cable network structures that can be efficiently assembled and deployed in orbit. ETS-VIII type modules have been extensively researched and applied [11–13]. Tian et al. conducted research on the hexagonal prism modular deployable antenna, which includes the topological design, the assembly of the modular units, and dynamics of hexagonal prism modules, and then developed a prototype to demonstrate the principles [14–19]. Wang et al. proposed a tension multilayer design method for the hexagonal prism modular deployable antenna, which improved the structural stiffness of the antenna [20]. Shi et al. designed a brand-new assembly interface for large space structures and analyzed its performance in detail according to the requirements of on-orbit assembly [21]. Dong et al. proposed a method for calculating assembly errors of assembly antennas considering assembly gaps [22]. Tang et al. analyzed the influences of systematic surface error by three factors including errors of faceted paraboloids, fabrication imperfections, and random thermal strains on orbit [23]. Fan et al. put forward a coordinate iteration algorithm for form-finding of cable network structure with equal tension; the uniformity of cable tension obtained by the algorithm is better than that by the minimum norm method or the equal force density method [24]. She et al. investigated the planning problem of the on-orbit assembling mission of a large space antenna structure [25]. Tibert presented a design method of a rigid prestressed tension truss antenna, which combines the basic rules of rigid truss structure with the effective form-finding method of cable network structure [26]. By establishing a structural mechanical model, Li et al. proposed a method of force-thermal matching design for cable network structures, which can improve surface accuracy to a certain extent in a temperature-varying environment [27].

In the aforementioned study, the modular antenna employed identical modules to approximate the parabolic surface, which proved to be challenging due to the inability to achieve precise fitting. Additionally, it is worth noticing that while the antenna employs modular units, it does not fall within the realm of on-orbit assembly. To meet the growing demand for ultra-large space antennas in space activities, it is necessary to conduct research on space antennas for on-orbit assembly, including the design of novel modules, precisely fitting antenna reflectors, and achieving the desired antenna size via on-orbit assembly.

In this paper, a configuration design method of a modular unit of large space-assembled antenna is proposed, which can generate configuration information of the modular unit efficiently, and solve the topology design problem of on-orbit-assembled antenna. Since the traditional division method of mesh surface has limitations in solving the cable relaxation problem in the proposed modular unit, a novel mesh surface topology is developed to solve the division problem of the cable network. This method effectively fills the challenging issue of mesh design for assembled antenna module units and avoids the cable relaxation problem caused by traditional mesh partitioning as well as develop hardware for a single module.

The rest of the paper is organized as follows. In Section 2, a fast configuration generation method of the modular unit is proposed for the modular-assembled antenna. In Section 3, a division method of cable network topology for modular units is proposed; the pretension design is carried out. Section 4 verifies the validity of the pretension calculation for the modular unit. Section 5 is a summary of the overall findings and conclusions.

2. Configuration Design of the Modular Units

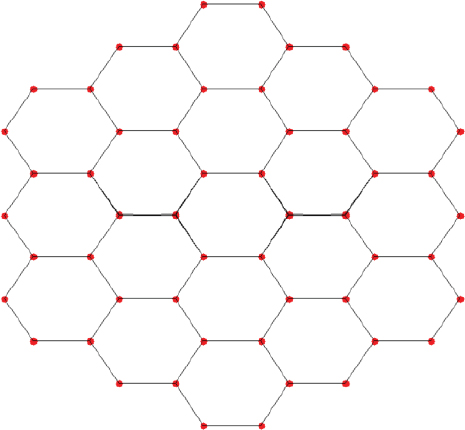
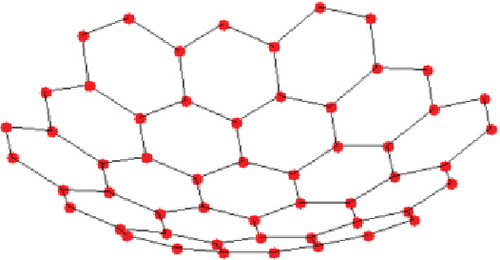
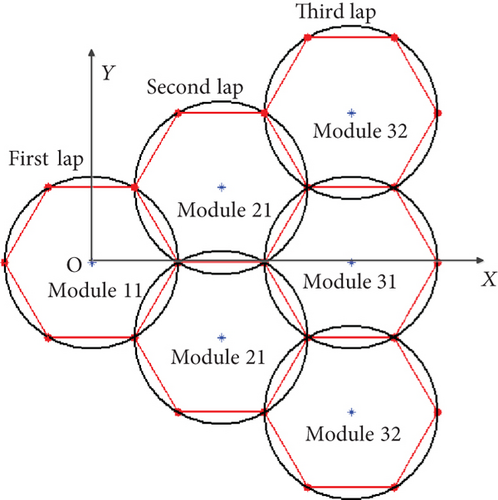
The consensus among scholars suggests that on-orbit assembly is a viable and effective approach for constructing super-large space structures. It is also a necessary means to realize the super large size of the space structure. In order to obtain the parabolic reflective surface of the super-large on-orbit-antenna assembly, the design idea of modularity is adopted. Figure 1 shows the schematic diagram of an assembled paraboloidal antenna which consists of 19 modules. The antenna is constructed by hexagonal modules, which are composed of hexagonal trusses, tension cable networks, and metal reflective meshes, with different specifications.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram of the antenna assembly.

The configuration of the modular unit determines the reflecting surface and the assembling sequence of the on-orbit-assembled antenna. The paraboloidal antenna is constructed by utilizing the metal mesh of the module to conform to the shape of a paraboloid reflecting surface. To achieve optimal reflection performance of an antenna, all boundary points of the units must match the theoretical paraboloid. For maintaining the consistency of the assembly module units, all assembly units are projected on the horizontal plane inside a specified topological circle, and the assembly hexagon is designed to be an inscribed hexagon of the circle. As a result, a module unit structure design method based on topological circles is proposed.

Figure 2 shows the topological circle and the boundary point of a modular unit. All topological circles are located in the OXY plane. The regular hexagon is an inscribed hexagon of the circle, as shown in Figure 2(a). The topological circle can be placed at any position in the OXY plane. Its size is determined by the diameter of the assembly antenna, the fitting accuracy, the number of modules, etc. On the theoretical paraboloid, the boundary points of each module can be obtained by projecting the regular hexagon onto the surface, as shown in Figure 2(b). Assuming the center of the central topological circle is at (0,0), through projection, the coordinates of the hexagonal boundary point of the module on the paraboloid can be obtained as follows:

()

where x_ij, y_ij, and z_ij the boundary points of the modular unit and ij (i = 1, 2, ⋯N, j = 1, ⋯, 6) represents the jth vertex of the ith topological circle; θ_j is the included angle between the boundary point and the horizontal direction; f is the focal length of the paraboloid; and R is the radius of the topological circle.

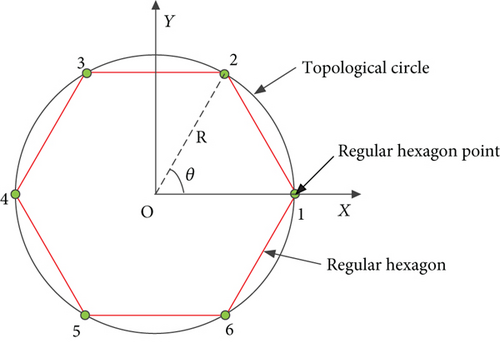
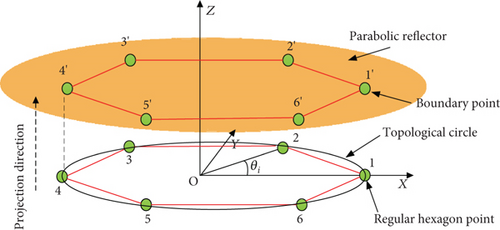
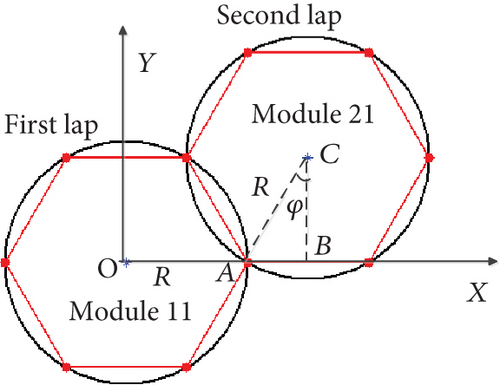
After calculating the location of boundary points, we proceed to determine the center of each topological circle for on-orbit assembly. Without loss of generality, the distribution of the 19 modular units of an assembled antenna is shown in Figure 3.

Since the assembled antenna is symmetrical about the centerline, one-sixth of the total modules is chosen to simplify the calculation. The selected modular units and the center of the corresponding topological circle are shown in Figure 4.

The one-sixth of the structure is also symmetrical about the OXY plane. Hence, in Figure 4(a), the modules labeled with the same number are identical, the module type is indicated by the second number, and the number of laps is represented by the first. For a standard paraboloid, Module 11 is located at the center of the paraboloid; the coordinates of the center of its corresponding topological circle are (0,0). As can be seen from Figure 4, the center of the topological circle of Module 21 can be solved by

()

where φ is the angle between AC and CB and φ = 30^° for the regular hexagon. The center of the other topological circle in Figure 4(a) can be calculated as

()

where i indicates the number of laps, j is the number of modules in the positive direction of the y-axis of the i lap, and y_ij = −y_ij for the negative direction of the y-axis. The center of all topological circles of the one-sixth modules can be obtained from Equations (3) and (4). Combining with Equation (1), the boundary points of any hexagon of the one-sixth modules can be calculated. According to the symmetry of the distribution of modular elements, the boundary points of all hexagons on the paraboloidal surface can be obtained.

The calculated coordinates of the hexagonal units are adopted in the design of the modular unit. Each unit has two layers. It is required that all the vertices on the upper layer are located exactly at the obtained coordinates. Two modular units have been designed, as shown in Figures 5 and 6.

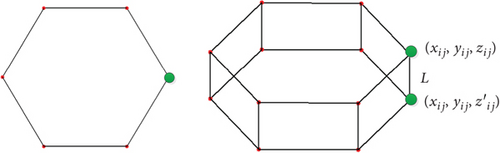
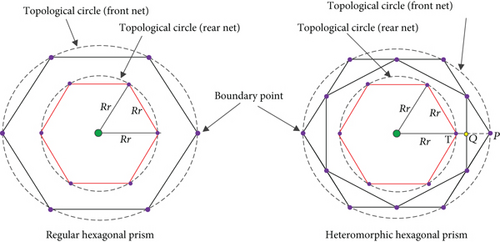
The module, which is shown in Figure 5, has the structure of a regular hexagonal prism with identical upper and lower layers. (x_ij, y_ij, z_ij) is the boundary node of the upper layer of the hexagonal prism, which can be solved by Equations (1)–(4). (x_ij, y_ij, z′_ij) indicates the boundary nodes of the lower layer. The projection of the upper and lower surfaces along the axis of the prism coincides, that is, z′_ij = z_ij − L, L is a given constant value.

There is an angular offset between the projections of the upper and lower layers of the heteromorphic hexagonal prism unit in Figure 6. (x_i1, y_i1, z_i1) and (x_i2, y_i2, z_i2) are two boundary nodes of the upper layer of the heteromorphic hexagonal prism, which can be solved by Equations (1)–(4). (x′_i1, y′_i1, z′_i1) is a node on the lower layer of the heteromorphic hexagonal prism. It can be calculated as

()

Once L is prescribed, the coordinates of all nodes on the lower layer of the heteromorphic hexagonal prism unit can be obtained from Equation (5). Figure 7 shows the topological structure of the assembly antenna constructed by the two proposed units.

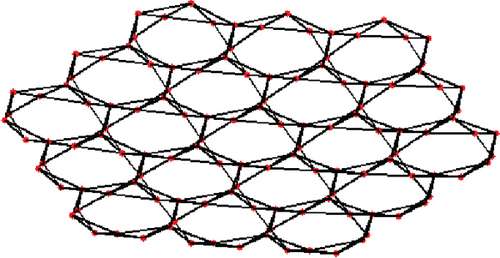
3. Design of the Cable Network System

Currently, in the realm of on-orbit applications, large space mesh antennas utilize metal mesh as the primary medium for reflecting electromagnetic waves. The metal mesh is positioned atop the tension cable mesh, thus making the topological configuration of the tension cable mesh critical in determining the surface accuracy of the antenna. In the case of super-large on-orbit modular-assembled antennas, the modular units need to be folded during launching and deployed after entering orbit; the reflective surface of the modular unit adopts the cable network system. The conventional cable network is designed for structures with symmetry, whereas the modular units in the assembly antenna only have six boundary points, rendering them incapable of maintaining the balance required by the cable network. Consequently, the traditional cable network division is unsuitable for the two types of module units proposed in this paper, particularly the heteromorphic hexagonal prism unit. As a result, a novel cable network system has been developed in this section.

In Section 3.1, the cable network topologies are developed for the two units, respectively. In Section 3.2, the pretension of the proposed cable network is calculated.

3.1. Division of the Cable Network Topology

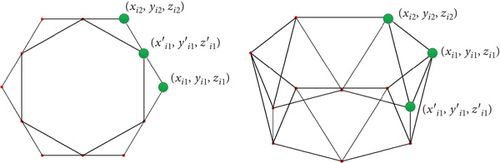
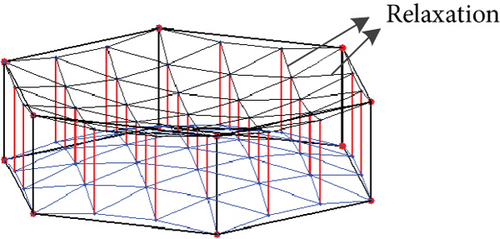
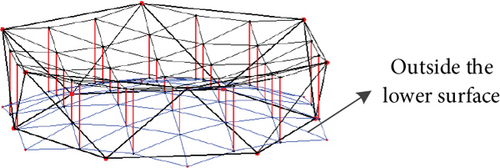
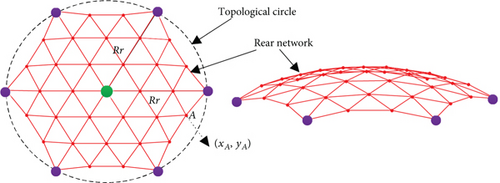
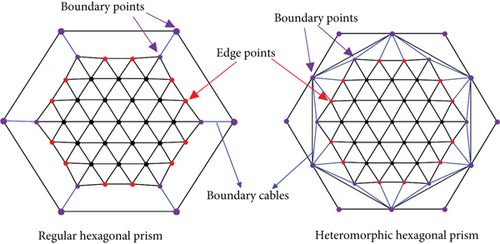
The regular hexagonal prism unit is comparable to the conventional loop antenna. The difference is mainly reflected in the considerably fewer boundary connection points the regular hexagonal assembly has than the loop antenna. The use of the three-dimensional grid, quasigeodesic grid, and other divisions cannot guarantee uniform stress on the cable network; cable relaxation might occur (Figure 8(a), [28]). Projections of the upper and lower surfaces of the heteromorphic hexagonal prism are misaligned, resulting in the fact that the symmetric triangle meshing cannot allow all networks to lie inside the lower surface of the unit, as shown in Figure 8. Therefore, a novel network topology scheme, which is adapted to the proposed units, is developed.

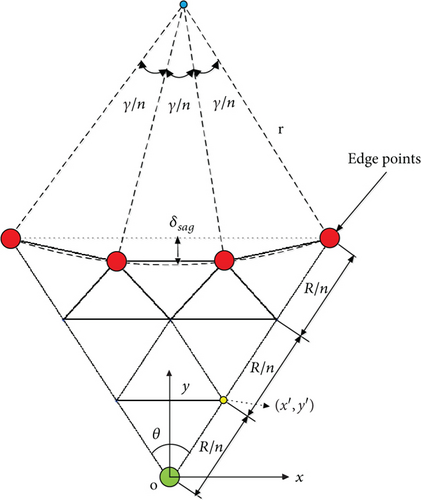
For properly tensioning the cables, the sag (δ_sag)is adopted in the network surface design [29]. Sag describes the sag of the edge cable, as shown in Figure 9.

The edge points are equidistantly positioned on an arc with radius r and opening angle γ,

()

where θ = π/3, R is the radius of the topological circle, n is the number of triangles along the R direction, and n ≥ 2. δ_sag is the given, sag/R ratio of 8%~12% is common, and

. The coordinates of the edge points can be calculated from geometric relationships.

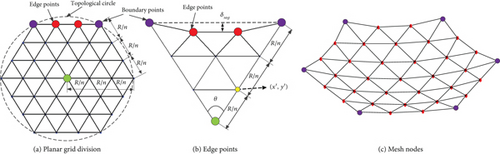
With the given δ_sag, the front network of the two module units has been designed as shown in Figure 10. First, the hexagons in the planar topological circle are meshed, where R is the radius of the topological circle and also the edge of the hexagon. The edges of the hexagon are then partitioned into n segments, where n ≥ 2. Subsequently, calculating the (x^′, y^′) coordinates of all triangle nodes is based on the geometric relationships with the given R and n. Then, substitute the edge points in Figure 10(a) with the calculated edge points that take into account δ_sag, as shown in Figure 10(b). Finally, by projecting all the triangular nodes inside the topological circle onto the parabolic surface, for instance , all the coordinates on the parabolic surface can be obtained as shown in Figure 10(c).

The design of the front net has been illustrated in Figure 10. As the rear network needs to meet the requirements of two different types of prism units, a similar method is used to determine the hexagonal shape of the rear network, as shown in Figure 11. To ensure that the ropes of the rear network of the heteromorphic hexagonal prism units do not exceed the prism constraint on the bottom surface of the truss, it is required that the rear network nodes must all lie within the topology circle, and the radius of the topology circle of the rear network meets

()

where PQ_max is the maximum distance from the boundary point of the front network to the rear network hexagonal edge of the heteromorphic hexagonal prism, QT > 0. The rear network has a hexagonal form and is placed in the oxy plane; its boundary points are calculated using the same manner as the front network.

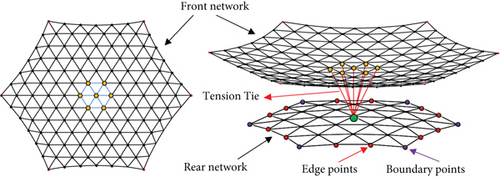
Considering the characteristics that regular triangles can form regular hexagons, a “many-to-one” cable network design method is proposed. The design procedure is shown in Figure 12.

Figure 12(a) shows the generation mapping of the rear network, where the number of front network segments n = 7, and the radius Rr of the rear network topology circle is related to the topology circle of the front network. The calculation can be performed using Equation (8). After determining the radius Rr of the rear network topology circle, the number of segments inside the rear network can be calculated as

()

where Nn is the number of segment rear net. When n ≤ 3, the number of rear network segments being 1, the rear network edge points are independent of sag. For any point A(x_A, y_A, z_A) in the rear network, its corresponding equilateral triangle side length is Rr/Nn, and its x_A and y_A coordinates can be solved based on the trigonometric function. The z_A coordinate can be determined by

()

Using Figure 12(b), the tension ties can be constructed. The front network segments and rear network segments are in accordance with Equation (9), indicating that the number of front network segment is approximately double that of the rear network segments. Therefore, besides the boundary points and edge points in the rear network, each node in the rear network can be associated with seven nodes in the front network. The correspondence between the boundary nodes is related to the amount of front network segments:

•
When the number of segments n = 2, no edge points exist in the rear network, and each rear network boundary point corresponds to three front nodes.
•
When n = 3, there is no edge point in the rear network, and each rear network boundary point corresponds to six front nodes.
•
When n is odd and n > 3, each rear network boundary point is associated with six front nodes, whereas each edge point is associated with seven front nodes.
•
When n is even and n > 3, each rear network boundary point is associated with three front nodes, whereas the edge point is associated with five front nodes.

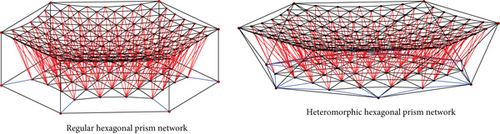
Figure 12(c) illustrates the distribution of the boundary cables of the rear network. In the case of regular hexagonal prisms, the rear network can be generated by connecting the boundary points of the rear network with the corresponding boundary points on the lower surface of the module unit. The rear network of the heteromorphic hexagonal prism units can be formed by connecting the boundary point and edge point of the rear network to the nearest boundary point on the bottom surface of the module unit. The comprehensive network design of the two prisms is shown in Figure 12(d).

The aforementioned design is capable of achieving the cable network topology configuration that meets the requirements of the assembled antenna module units. When all cables exhibit positive tension, it indicates that the entire cable network system is in a condition of pretension, hence preventing any relaxation.

3.2. Pretension of the Cable Network

The electrical performance of a large mesh antenna depends upon the specific geometry of its mesh reflector. The uniformity and stability of the mesh tension is the key to achieve the desired on-orbit profile. Hence, the form finding of the cable network is an essential step in designing the overall network structure. Applying a certain pretension on each cable is necessary to establish the position of each node within a theoretically stable configuration, while also ensuring a desired level of structural stiffness.

The division of the cable network topology proposed in this paper belongs to the problem of solving the pretension of the cable network with known node coordinates, which is called “finding the state by shape.” Due to the asymmetry of the network surface of the heteromorphic hexagonal prism and the difference in the number and position of the front and rear network cables, the force density optimization method is utilized to solve the pretension in this study [30]. The approach utilized in this study is grounded in the traditional force density method, which aims to enhance the performance of the cable network through the optimization of the force density values. For the cable network of the module units, the nodal force equilibrium equations are

()

where F_ij is the pretension of the cable between nodes i and j; l_ij is the length of the cable between nodes i and j; q_ij is the force density; C_s is the m × n incidence matrix for the structure; and m and n are the numbers of cables and nodes. C_s can be partitioned as C_s = [C_fC_g], where C_f and C_g are the free and fixed node matrices; Q is a diagonal matrix containing the force densities; and x is a column vector of the x-coordinates.

The optimizing model of the force density optimization method is as follows:

()

where q_i is the force density, q^L and q^U are the lower and upper bounds of force density; X_f, Y_f, Z_f and X_g, Y_g, Z_g are the coordinates of free and fixed nodes, respectively; L_f is the length of the cable between nodes i and j,

; F is the force of cable; fun(Q) is an objective function with force density; and fun(Q) = max(F)/min(F).

According to the optimization model of the force density in Equation (12), the pretension of cables of the above two units can be calculated, which is subsequently verified through Ansys analysis.

4. Case Studies

To support the validity of the proposed approach for generating modular unit meshes and to demonstrate its utility in practical engineering applications, a numerical example is performed. The specifications of the assembly antenna reflector are given as Table 1.

Table 1. Geometric parameters of an assembled antenna.

Item	Aperture (mm)	Force length (mm)	Height (L ) (mm)	No. of modular units
Parameters	200,000	80,000	1,000	7

The design of the two modular units and the cable networks is shown in Figure 13.

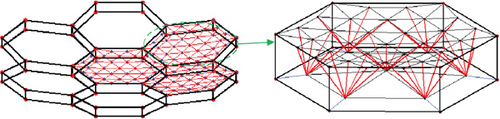
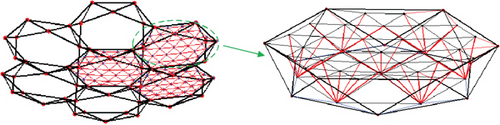
Utilizing the force density optimization method, the pretension of the two units is calculated. The results are presented in Tables 2 and 3, respectively. All cable tensions are positive, indicating that the cables are in a state of tension and not experiencing any relaxation or slackness.

Table 2. Cable pretension of the regular hexagonal prism (N).

Item	Maximum	Minimum	Mean
Front net	31.08	0.12	13.32
Rear net	61.97	13.86	24.51
Tension tie	2.83	0.44	1.85

Table 3. Cable pretension of the heteromorphic hexagonal prism (N).

Item	Maximum	Minimum	Mean
Front net	26.33	0.2	10.26
Rear net	74.29	1.9	26.29
Tension tie	2.36	0.26	1.36

The finite element model is established without including the truss element. The boundary nodes are fixed and constrained. The material parameters for the model are shown in Table 4.

Table 4. Material parameters of cables.

Item	Material	Diameter (mm)	Density (g/mm³)	Elastic modulus (GPa)	Poisson ratio
Cables	Carbon fiber	1.4	1.8 × 10³	230	0.3

The finite element models and analysis results of the two modular units are shown in Figure 14.

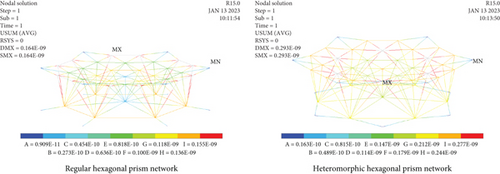
The finite element analysis adopts the static analysis in Ansys, and the link10 element is used to simulate the characteristics of the rope. The form of the internal stress of the rope tension analyzed above is assigned to the rope element. According to the result of finite element analysis, the deformations of the two types of cable networks are 0.164 × 10⁻⁹ and 0.293 × 10⁻⁹ m, respectively. Hence, the utilization of the initial force density method effectively addresses the tension in both types of modular units. This approach guarantees the uniform distribution of stress in cables, thereby maintaining the structural integrity and stability of the modular units. Furthermore, these advantages persist even under challenging environmental conditions in space.

Based on the proposed method for topology design of module unit, a prototype of the antenna assembly module was developed. The unfolded size of the prototype is 4.8 m, the folded size is 0.38 × 2.2 m, and the mass of a single module is 29.6 kg. The folding and unfolding function of the module is normal and consistent with the design, as shown in Figure 15.

A module unit prototype for large space modular-assembled antennas has been developed. The prototype consists of a deployable module structure and a cable network system, and the successful development of the prototype proves the feasibility of the design method.

5. Conclusion

In this paper, the modular element design, mesh division, and mesh pretension computation of large space modular-assembled antenna are studied. A rapid design approach of modular unit configuration based on topological circles is proposed. The method enables the efficient generation of comprehensive module unit information of the whole assembled antenna. Furthermore, it facilitates the generation of all modules of the assembled antenna based on the predetermined unit information. A novel mesh division method is developed for the proposed unit structure. The network division approach effectively fulfills the requirements of prism units without the need for relaxation. The calculation of pretension is accomplished by using the force density optimization method. The finite element simulation provides empirical evidence that the proposed method ensures uniform and stable tension across the network.

Through an examination of the assembled antenna module units and module cable networks, this study confirms the effectiveness of the design strategy employed in the modular antenna system. The design approach successfully achieves the essential structural stability and stiffness necessary for on-orbit assembly, thereby establishing a solid basis for future engineering applications.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research has been supported by the National Natural Science Foundation of China (Grant Nos. 52222501 and 52192632).

Acknowledgments

This research has been supported by the National Natural Science Foundation of China (Grant Nos. 52222501 and 52192632).

Open Research

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author, Ma Xiaofei, upon reasonable request.

References

1 Ma X., Li T., Ma J., Wang Z., Shi C., Zheng S., Cui Q., Li X., Liu F., Guo H., Liu L., Wang Z., and Li Y., Recent advances in space-deployable structures in China, Engineering. (2022) 17, 207–219, https://doi.org/10.1016/j.eng.2022.04.013.
10.1016/j.eng.2022.04.013
Web of Science® Google Scholar
2 Liu R., Shi C., Guo H., Li B., Tian D., and Deng Z., Review of space deployable antenna mechanisms, Journal of Mechanical Engineering. (2020) 56, no. 5, 1–12, https://doi.org/10.3901/JME.2020.05.001.
10.3901/JME.2020.05.001
Google Scholar
3 Meguro A., Harada S., and Watanabe M., Key technologies for high-accuracy large mesh antenna reflectors, Acta Astronautica. (2003) 53, no. 11, 899–908, https://doi.org/10.1016/S0094-5765(02)00211-4, 2-s2.0-0037716290.
10.1016/S0094-5765(02)00211-4
Web of Science® Google Scholar
4 Cherniavsky A., Gulyayev V., Gaidaichuk V., and Fedoseev A. I., Large deployable space antennas based on usage of polygonal pantograph, Journal of Aerospace Engineering. (2005) 18, no. 3, 139–145, https://doi.org/10.1061/(ASCE)0893-1321(2005)18:3(139), 2-s2.0-22944441937.
10.1061/(ASCE)0893-1321(2005)18:3(139)
Web of Science® Google Scholar
5 Cousins D. and Akin D. L., Moments applied in the manual assembly of space structures: ease biomechanics results from STS-61B, Acta Astronautica. (1989) 19, no. 12, 973–979, https://doi.org/10.1016/0094-5765(89)90092-1, 2-s2.0-0024857464, 11541162.
10.1016/0094-5765(89)90092-1
CAS PubMed Google Scholar
6 Seboldt W., Klimke M., Leipold M., and Hanowski N., European sail tower SPS concept, Acta Astronautica. (2001) 48, no. 5-12, 785–792, https://doi.org/10.1016/S0094-5765(01)00046-7, 2-s2.0-0035264789.
10.1016/S0094-5765(01)00046-7
Google Scholar
7 Mankins J. C., New directions for space solar power, Acta Astronautica. (2009) 65, no. 1-2, 146–156, https://doi.org/10.1016/j.actaastro.2009.01.032, 2-s2.0-65549109747.
10.1016/j.actaastro.2009.01.032
CAS Web of Science® Google Scholar
8 Suzuki Y., Tsuchiya S., Okuyama T., Takahashi T., Nagai Y., and Kimura S., Mechanism for assembling antenna in space, IEEE Transactions on Aerospace and Electronic Systems. (2001) 37, no. 1, 254–265, https://doi.org/10.1109/7.913683, 2-s2.0-0035039955.
10.1109/7.913683
Google Scholar
9 Oda M., Kibe K., and Yamagata F., ETS-VII, space robot in-orbit experiment satellite, Proceedings of IEEE International Conference on Robotics and Automation, 1996, Minneapolis, MN, USA, 739–744, https://doi.org/10.1109/ROBOT.1996.503862.
10.1109/ROBOT.1996.503862
Google Scholar
10 Kawano I., Mokuno M., Kasai T., and Suzuki T., Result and evaluation of autonomous rendezvous docking experiment of ETS-VII, Guidance, Navigation, and Control Conference and Exhibit, 1999, Portland, OR, USA, https://doi.org/10.2514/6.1999-4073.
10.2514/6.1999-4073
Google Scholar
11 Nakamura K., Tsutsumi Y., Uchimaru K., Tsujihata A., and Meguro A., Large deployable reflector on ETS-VIII, 17th AIAA International Communications Satellite Systems Conference and Exhibit, 1998, Yokohama, Japan, https://doi.org/10.2514/6.1998-1229, 2-s2.0-84977073834.
10.2514/6.1998-1229
Google Scholar
12 Meguro A., Tsujihata A., and Hamamoto N., The 13 m aperture space antenna reflectors for Engineering Test Satellite VIII, IEEE Antennas and Propagation Society International Symposium. 1999 Digest. Held in conjunction with: USNC/URSI National Radio Science Meeting (Cat. No.99CH37010), 1999, Orlando, FL, USA, 1520–1523, https://doi.org/10.1109/APS.1999.788231, 2-s2.0-84894500101.
10.1109/APS.1999.788231
Google Scholar
13 Yamada K., Tsutsumi Y., Yoshihara M., Homma M., Tsujihata A., Miyasaka A., Shintate K., and Meguro A., Integration and testing of large deployable reflector on ETS-VIII, 21st International Communications Satellite Systems Conference and Exhibit, 2003, Yokohama, Japan, https://doi.org/10.2514/6.2003-2217.
10.2514/6.2003-2217
Google Scholar
14 Tian D., Fan X., Jin L., Guo Z., Gao H., and Chen H., Design and kinematics analysis of support structure for multi-configuration rigid-flexible coupled modular deployable antenna, Aerospace China. (2021) 3, 46–53.
Google Scholar
15 Tian D., Guo Z., Liu R., Gao H., Fan X., Liu Z., and Deng Z., Design of supporting mechanism for space modular deployable truss antenna, Spacecraft Engineering. (2021) 30, no. 4, 39–47.
Google Scholar
16 Tian D., Liu R., Xie Y., and Zongquan D., Deployment accuracy measurement and analysis of truss structure for modular space deployable truss antenna, Journal of Mechanical Engineering. (2020) 56, no. 5, 63–71, https://doi.org/10.3901/JME.2020.05.063.
10.3901/JME.2020.05.063
Google Scholar
17 Tian D., Fan X., Zhang J., Jin L., Liu R., and Zhang Y., Networking method for the structure of a large modular deployable space antenna, International Journal of Aerospace Engineering. (2022) 2022, no. Part 5, 13, https://doi.org/10.1155/2022/4583374, 4583374.
10.1155/2022/4583374
Web of Science® Google Scholar
18 Jin L., Zhang F., Tian D., Wang Q., and Cao Q., Thermal-structural analysis of the support structure for a modular space deployable antenna, International Journal of Aerospace Engineering. (2022) 2022, 13, https://doi.org/10.1155/2022/2164485, 2164485.
10.1155/2022/2164485
Google Scholar
19 Tian D., Shi Z., Jin L., Yang X., Liu R., and Shi C., Pre-tension design and research of cable net structure for space modular deployable antenna, Advances in Engineering Software. (2024) 195, article 103685, https://doi.org/10.1016/j.advengsoft.2024.103685.
10.1016/j.advengsoft.2024.103685
Google Scholar
20 Wang H., He T., Du X., and Wang C., Multi-layer design method of tension rope for paraboloid antenna, Journal of Beijing University of Aeronautics and Astronautics. (2022) 48, no. 4, 657–664.
Google Scholar
21 Shi C., Guo H., Wang H., Tao L., Liu R., and Deng Z., Design and assembly performance analysis of large space structure assembly interface, Journal of Astronautics. (2021) 42, no. 12.
Google Scholar
22 Dong H. J., Li T. J., Zheng S. K., Wang Z. W., Tang Y. Q., Ma X. F., and Li Y., Analytical method for computing assembly errors in modular antenna during on-orbit assembly, The Aeronautical Journal. (2023) 127, no. 1315, 1505–1522, https://doi.org/10.1017/aer.2023.5.
10.1017/aer.2023.5
Google Scholar
23 Tang Y., Li T., Wang Z., and Deng H., Surface accuracy analysis of large deployable antennas, Acta Astronautica. (2014) 104, no. 1, 125–133, https://doi.org/10.1016/j.actaastro.2014.07.029, 2-s2.0-84906318627.
10.1016/j.actaastro.2014.07.029
Web of Science® Google Scholar
24 Fan Y., Li T., Ma X., and Li Z., Form-finding method of equal tension cable networks for space mesh antennas, Journal of Xidian University. (2015) 42, no. 1, 49–55.
Google Scholar
25 She Y., Li S., Du B., and Cao K., On-orbit assembly mission planning considering topological constraint and attitude disturbance, Acta Astronautica. (2018) 152, 692–704, https://doi.org/10.1016/j.actaastro.2018.09.014, 2-s2.0-85054008387.
10.1016/j.actaastro.2018.09.014
Google Scholar
26 Tibert G., Optimal design of tension truss antennas, 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2003, Norfolk, Virginia, https://doi.org/10.2514/6.2003-1629.
10.2514/6.2003-1629
Google Scholar
27 Li T., Yang L., Li Y., and Ma X., Mechanical-thermal matching design for the rope-wire mesh composite structure, Journal of Xidian University. (2018) 45, no. 2, 48–53.
Google Scholar
28 Chen C., Li T., and Tang Y., Faceting deviation calculation of cable-net reflector antenna, Journal of Mechanical Engineering. (2022) 58, no. 7, 176–182, https://doi.org/10.3901/JME.2022.07.176.
10.3901/JME.2022.07.176
Google Scholar
29 Tibert A. G. and Pellegrino S., Deployable tensegrity reflectors for small satellites, Journal of Spacecraft and Rockets. (2002) 39, no. 5, 701–709, https://doi.org/10.2514/2.3867, 2-s2.0-0036756947.
10.2514/2.3867
Web of Science® Google Scholar
30 Li T., Deng H., Tang Y., Jiang J., and Ma X., Accuracy analysis and form-finding design of uncertain mesh reflectors based on interval force density method, Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering. (2017) 231, no. 11, 2163–2173, https://doi.org/10.1177/0954410016662061, 2-s2.0-85026799996.
10.1177/0954410016662061
Web of Science® Google Scholar

Citing Literature

All articles

Topology Design of Modular Unit and Cable Network of On-Orbit Modular-Assembled Antenna

Abstract

1. Introduction

2. Configuration Design of the Modular Units

3. Design of the Cable Network System

3.1. Division of the Cable Network Topology

3.2. Pretension of the Cable Network

4. Case Studies

5. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Topology Design of Modular Unit and Cable Network of On-Orbit Modular-Assembled Antenna

Abstract

1. Introduction

2. Configuration Design of the Modular Units

3. Design of the Cable Network System

3.1. Division of the Cable Network Topology

3.2. Pretension of the Cable Network

4. Case Studies

5. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Related

Information