1. Introduction

THz technology is one of the most promising research areas of the 21st century for transformational advances in defense technology, spectroscopy, biomedical, sensing, image processing, and communication technology [1–4]. THz waves belong to the frequency bandwidth 0.1–10 ∗ 10¹² Hz and exist between long wavelength of the microwave radiation and short wavelength of the infrared radiation in the EM spectrum [5]. The controlling and manipulation of the THz radiations is one of the major challenges for the experimental implementation of THz based-optoelectronic devices. Many researchers and scientific communities have proposed the different techniques as well as materials to control and manipulate the propagation characteristics of THz radiation [6, 7]. Besides the natural materials, the man-made THz metamaterials have been proposed for their extraordinary control over the THz radiations [8, 9]. In recent works, graphene has been realized as a natural THz metamaterial due to its unconventional control over the THz radiations such as phase controlling, wave shaping, wave guiding, imaging, and sensing in the THz range [10–13]. Graphene is realized as the honeycomb structure of a single layer of carbon atoms. The high thermal stability, high mechanical strength, ultra-high mobility, and zero band gap are the remarkable physical properties of graphene [14]. The electrostatic and magnetic biasing schemes have been used for the active tuning of the optical conductivity of graphene [15, 16].

Graphene-based structures have potential advantages in the designing the plasmonic nanoantennas, absorbers, sensors, broadband polarizers, filters, tunable and switchable THz-metamaterials, and optoelectronic devices in the THz-IR region [17–21]. To manipulate and control, the electromagnetic properties by Vakil and Engheta reported that the graphene can be used to get unprecedented control on propagation, polarization, and phase modulation of THz radiations [22]. In addition to these potential applications, graphene plasmonics can be used to design the near surface communication and sensing devices. Graphene’s high conductivity and impressive tuning capabilities allow it to effectively mitigate scattering effects. The moderately sized conducting objects cannot be cloaked by a graphene monolayer because a graphene monolayer possesses an intrinsically inductive nature in the low terahertz range but this problem can be overcome by a patterned graphene metasurface. The researchers made the use of graphene to control the THz waves in different ways, i.e., Naserpour et al. introduced the phenomenon of invisibility in graphene -wrapped nanowires and dimers for the THz region and reported that the control on the modification of graphene’s chemical potential may lead to the invisibility or cloaking in the THz region. [23]. Velichko studied the THz radiation interaction with a graphene-coated dielectric cylinder and computed the absorption scattering cross section (ACS) and the total scattering cross section (TSCS). The excitation of surface plasmon resonance (SPR) modes and whispering-gallery (WG) modes has been reported [24]. Riso et al. studied electromagnetic scattering from graphene-coated subwavelength dielectric nano wires and reported that when the electromagnetic wave causes the excitation of localized surface plasmons, dramatical increase can be seen in the extinction cross sections and scattering cross sections. Tunable plasmon-based enhancement of light scattering and absorption in graphene-wrapped subwavelength wires can be obtained with the change in the chemical potential of graphene. Pashaeiadl et al. studied electromagnetic scattering from graphene-encapsulated left-handed metamaterial (LHM) and studied the scattering efficiency (Q_sca) by computing the scattering coefficients [25]. Ghaffar et al. studied electromagnetic scattering from graphene-coated DPS/DNG metamaterial cylinders and computed the scattering efficiency, absorption efficiency, extinction efficiency, and the bistatic radar cross section (RCS). The numerical results for micro- and nanoregime have been computed and reported that the proposed geometry supports the localized surface plasmons under perpendicularly polarized wave for nano regime [26]. In addition to these works, graphene coatings have been applied on the dielectric cylindrical structures and discussed the tunable excitations of Fano resonances [27–29].

In the present work, to optimize the radiative response of the plasmonic antenna designs, the THz scattering and tunable plasmonic features of the graphene-coated metallic nanowire under oblique incidence has been studied. As a case study, the tunable plasmonic resonances excited by the oblique THz scattering from the graphene-coated gold nanowire has been presented. The major objective of the present work is to design the metal-based plasmonic structures for antenna applications in THz and IR regions. The metals behave as perfect electric conductors in the THz region which is the major challenge of the present work. To overcome this issue, the graphene encapsulation/coating has been used for the controlling and manipulating the radiative response of the metals in THz and IR regions. Meanwhile, the plasmonic resonances can be actively tuned by varying the graphene parameters, the core size of the gold nanowire, and the angle of incidence of the THz waves. The second feature of the proposed work is to develop a generalized methodology for such graphene-based plasmonic antenna structures. The organization of the manuscript is followed as the analytical modeling for oblique scattering of the graphene-coated gold nanowire is presented in section 2 and the numerical results regarding the tunability of plasmonic resonances and scattering response of the graphene-coated metallic nanowire is depicted in section 3. The exp(−iωt) time dependence has been considered for all mathematical expressions.

2. Analytical Formulations

The analytical formulation for the scattering of THz waves from graphene-coated metallic nanowires has been presented in this section. The geometry of the problem is given in Figure 1. The three regions of space have been considered with respect to electromagnetic characteristics and wavenumbers, i.e., free space, graphene, and metallic nanowire. All the electromagnetic fields are expressed in cylindrical coordinates to develop the symmetry in the calculations as well as in formulation of the required scattering problem.J_n and $$ are the special functions introduced in all expressions. J_n depicts the Bessel function of the 1st kind to model physically the incoming cylindrical waves. On the other hand, $$ shows the Henkel function of the 2nd kind to model physically the outgoing cylindrical waves. The incidence of the THz wave on graphene-coated metallic nanowires has been considered for two orientations, i.e., parallel and perpendicular polarization states of electromagnetic fields with respect to the cylindrical axis.

In subsequent sections, the analytical formulation and the results of both parallel polarization and perpendicular polarization have been presented.

3. Numerical Results and Discussion

3.1. Scattering Characteristics

3.1.1. Extinction Efficiency

The extinction efficiency (Q_ext) is the sum of absorption efficiency (Q_abs) and scattering efficiency (Q_sca) and is mathematically defined as [30]

$$ (25)

Equation (25) states that more physical information can be obtained through the extinction efficiency instead of both scattering efficiency and absorption efficiency. Therefore, the interaction of the THz wave with the graphene-coated metallic nanowire has been studied by computing the Q_ext. For both parallel polarization and perpendicular polarization, the scattering coefficients are determined. Therefore, the Q_ext is computed for TE polarization and for TM polarization.

3.1.2. Graphene-Coated Gold Nanowire under Perpendicular Polarization

The Q_ext for perpendicular polarization has been computed by following Equation [30]

$$ (26)

where k₀ represents wave vectors in free space, R represents size of the graphene-coated gold nanowire, and a_n represents the scattering coefficients of perpendicular polarization. By taking various values of chemical potential, scattering rate of graphene, and angle of incidence, the variations in the Q_ext have been computed.

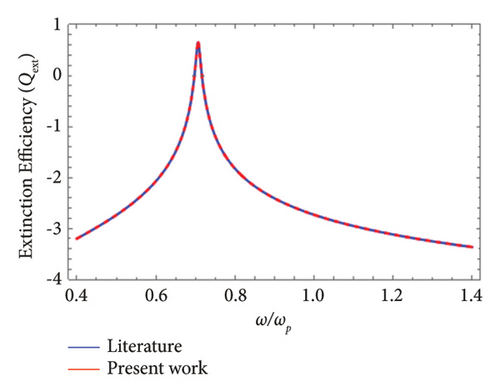
To check the correctness of the kernel developed for the graphene-coated gold nanowire, the comparison has been made for Q_ext of the sodium (Na) bare nanowire under special conditions, i.e., $$, ω_p = 8.65 × 10¹⁵ (1/s), and ζ = 0.01ω_p. It is clear from Figure 2 that under special conditions, our result converges to the Ruppin work [31], which confirms the accuracy of the presented work.

After the comparison, in the subsequent section, the influence of chemical potential ( μ_c) on the Q_ext has been presented. The chemical potential ( μ_c) is also called Fermi energy for graphene layers and is determined by the formula, i.e., $$.  v_F represents the Fermi velocity.  n_2D represents the charge carrier concentration. Chemical potential ( μ_c) is not only influenced by Fermi velocity of electrons but also by the charge carrier concentration. The external gate voltage or the doping can change the charge concentration and as a result chemical potential of graphene is tuned. Figure 3 shows the influence of chemical potential on the Q_ext of graphene-coated Au nanorods brightened with the perpendicular polarization in nanoregime. The Q_ext is expressed in terms of frequency. In this case, the electromagnetic wave strikes graphene-coated Au nanorods by making an angle of 30^°,  45^°,  60^°,  and 90^° with the cylindrical axis of graphene-coated Au nanorods. At dissimilar values of chemical potential ( μ_c), i.e.,  μ_c = 0.2 eV,  μ_c = 0.4 eV,  μ_c = 0.6 eV,  and μ_c = 0.8 eV, the magnitude of Q_ext is different. It can be seen that as the value of chemical potential increases, the plasmonic peaks start shifting toward the high THz frequency. However, such peaks are localized surface plasmon resonance (LSPR) modes which are different from whispering-gallery (WG) modes. At a high THz frequency range, the localized surface plasmon resonance (LSPR) is only supported by graphene-coated Au nanorods, in case of perpendicular polarization.

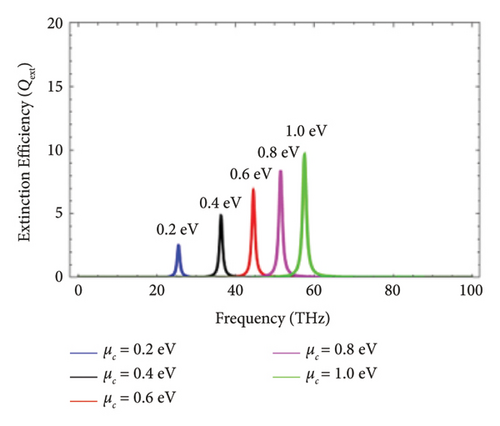
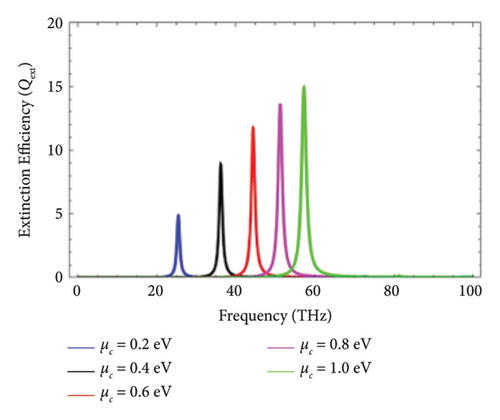
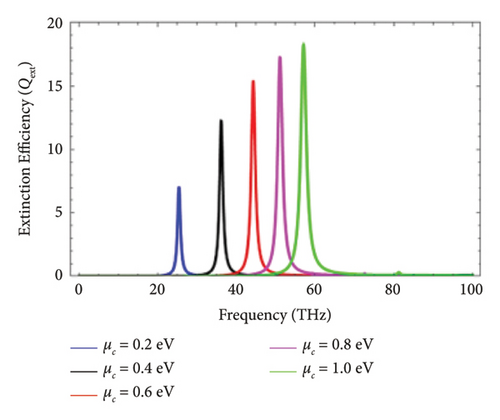
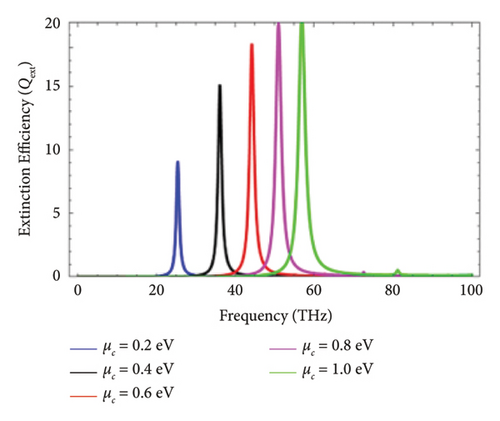
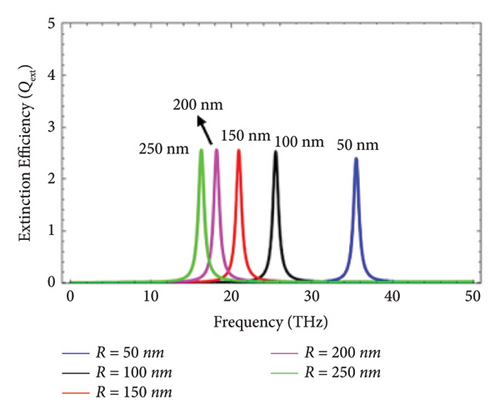
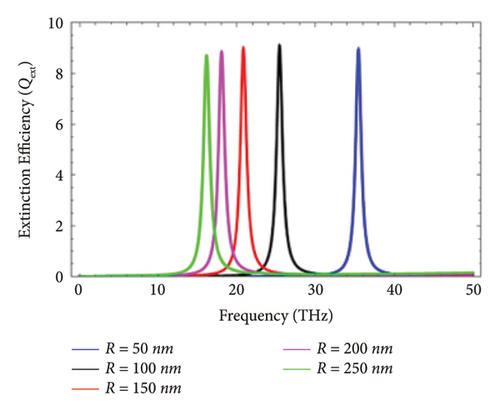
Figure 4 deals with the variation in Q_ext of graphene-coated Au nanowires illuminated with the perpendicular polarization in the nanoregime under different values of the core size, i.e, R = 50 nm,  R = 100nm,  R = 150nm,  R = 200nm,  and R = 250nm. By making an angle of 30^°,  45^°, 60^°,  and 90^° with the cylindrical axis of graphene-coated Au-nanorods, the electromagnetic wave hits the graphene coated Au nanorods. This result depicted that the magnitude of the core size influences the LSPR modes and also the magnitude of Q_ext. It is obvious that the tresonance frequency is sensitive to the size he of diameter of nanowires. Another thing is the correspondence that is present between the high THz resonance frequency and the larger core size.

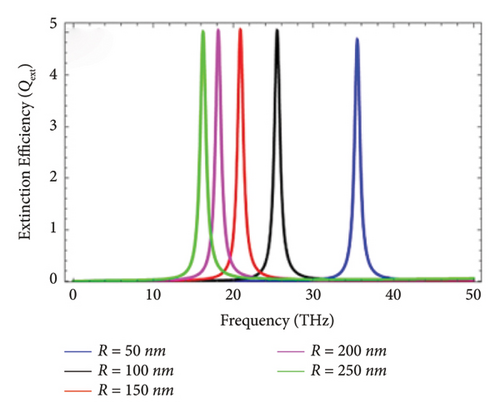
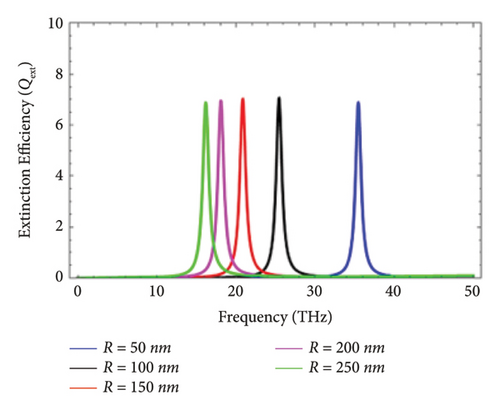
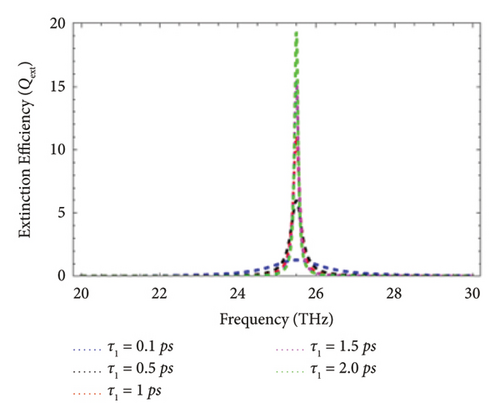
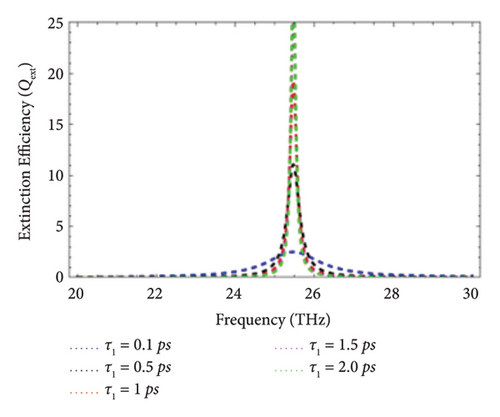
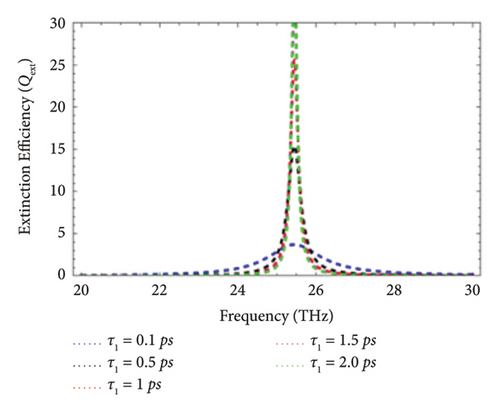
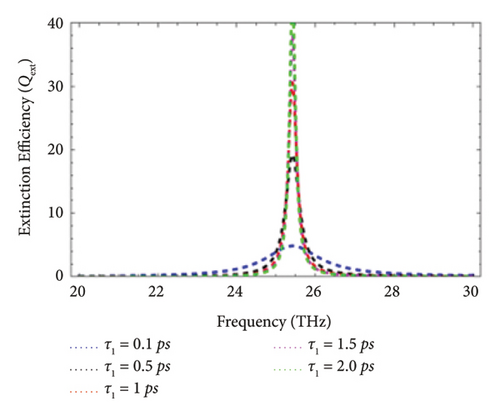
The phonon electron relaxation time is another name of the scattering rate τ₁ and is associated with the quality of the graphene layer. It is mathematically defined as τ₁ = (μ_e∗μ_c/ev_F), where μ_e is the mobility of electrons, μ_c is the chemical potential, e is the electronic charge, and v_F is the Fermi velocity of electrons (∼10⁶ m/s) [20, 21]. The effect of the scattering rate on the Q_ext has been illustrated in this subsection. Figure 5 represents the effect of the scattering rate on the Q_ext of graphene-coated Au wires excited with the THz wave under perpendicular polarization. In this case, the electromagnetic wave strikes graphene-coated Au nanorods by making an angle of 30^°,  45^°, 60^°,  and 90^° with the cylindrical axis of graphene-coated Au nanorods. The comparison between the Q_ext as a function of the incident frequency for values of the scattering rate, i.e., τ₁ = 0.1 ps,  τ₁ = 0.5 ps,  τ₁ = 1 ps,  τ₁ = 1.5 ps,  and τ₁ = 2.0 ps, is presented. It is observed that peaks of the LSPR upshifts with the increase of the scattering rate. In other words, it can be stated that the rise of the scattering rate enhances the magnitude of Q_ext.

3.1.3. Graphene-Coated Gold Nanowires under Parallel Polarization

The Q_ext for parallel polarization has been computed by following equation [30]

$$ (27)

where, k₀ represents wave vectors in free space, R represents size of the graphene-coated gold nanowire, and c_n is the scattering coefficient. By taking various values of chemical potential, scattering rate of graphene, and angle of incidence, the variation in the Q_ext has been studied.

The effect of chemical potential on the Q_ext has been studied in this subsection. Figure 6 represents the effect of chemical potential on the Q_ext of graphene-coated Au nanorods illuminated with the parallel polarization in the nanoregime. The pattern presented in Figure 6 shows that the Q_ext decreases with the increase of chemical potential as elaborated in the inset graph of Figure 6. In the previous section, it is clear that the change in the angle provides the change in the Q_ext not in the resonance frequency; therefore, the analysis has been made for θ_i = 45^° for all the subsequent results. The behavior of Q_ext of graphene-coated Au nanorods under TE polarization and TM polarization is entirely different for the same values of chemical potential, i.e., $$ and graphene-coated Au nanorods can support (LSPR), in the regime of the nanorange at a high THz frequency range for both polarizations. On contrary, the change in chemical potential for the TM polarization does not change the plasmonic frequency as for the TE polarization.

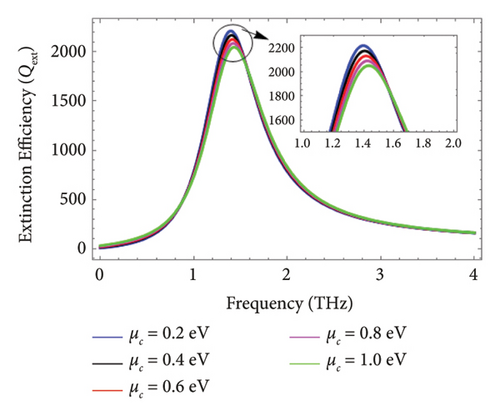
Figure 7 illustrates the effect of the size of the diameter of nanorods on the Q_ext for graphenecoated Au nanorods under TM polarization for different values, i.e., R = 10 nm,  R = 20nm,  R = 30nm,  R = 40nm,  and R = 50nm. The variation in the core size highly affects Q_ext under TM polarization. It is obvious from Figure 7 that with the increase of the core size, the plasmonics peak becomes sharper and starts shifting towards the low THz frequency range. However, the size dependence behavior of Q_ext of graphene-coated Au nanorods under TM polarization and TE polarization is found similar.

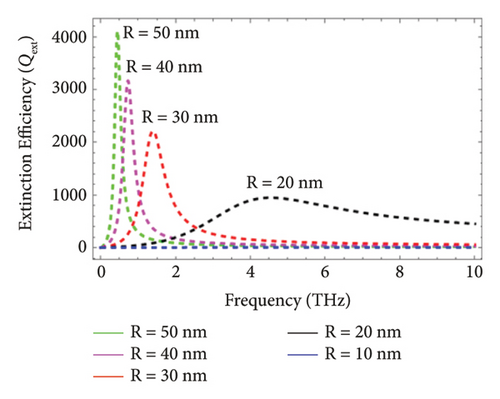
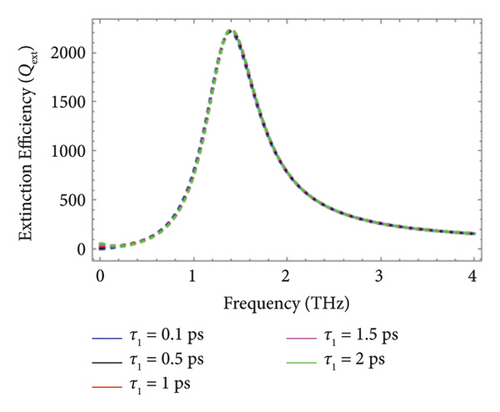
Figure 8 represents the effect of the scattering rate on the Q_ext for graphene-coated Au nanorods under TM polarization in the nanoregime. The Q_ext is plotted in terms of frequency under five various values of the scattering rate, i.e., τ₁ = 0.1 ps,  τ₁ = 0.5 ps,  τ₁ = 1 ps,  τ₁ = 1.5 ps,  and τ₁ = 2.0 ps. With the increase of the scattering rate, the Q_ext and plasmonic frequency do not show any variation, which is different from the TE polarization case. For the case of TM polarization, the graphene parameters, i.e., chemical potential and scattering rate, do not affect the plasmonic characteristics (resonance frequency) of graphene-coated Au nanorods. A major physical reason for such behavior could be the dominating behavior of the metallic plasmons in TM polarization which was absent in the TE polarization case.

4. Concluding Remarks

The subsequent conclusions have been drawn from the numerical simulations carried out for the THz scattering from graphene-coated Au nanowires under oblique incidence, i.e., the graphene-coated Au nanowires show a distinct response under parallel polarization and perpendicular polarization. The plasmonic resonances highly depend upon the state of polarization, graphene parameters, core size, and angle of incidence. The Q_ext has been computed as a function of the THz frequency under different values of graphene parameters, core size, and angle of incidence. The localized surface plasmon resonance (LSPR) on the graphene-coated Au nanowire is sensitive to the type of polarization and exits for the both polarization states. The Q_ext increases with the increase of the angle of incidence under both polarization states. The tunable and controlled radiative responses of graphene-coated metallic nanorods can be used in designing in the graphene-assisted plasmonic devices, active plasmonic antennas, and plasmonic sensors in the THz to IR region.

Conflicts of Interest

The authors declared that they have no conflicts of interest.

Authors’ Contributions

M.N. Akram wrote the main manuscript and derived analytical expressions. Faroq Razzaz edited the manuscript and reviewed the numerical analysis. M. Z. Yaqoob developed the methodology in the given study. All authors reviewed the manuscript before submission.