Evolutionary Game Analysis of Queue-Jumping and Yielding Behaviours of Drivers With Type A and Type B Personality Traits
Abstract
Although Type A personality traits have been confirmed to be more frequently engaged in risky driving behaviours, the existing research on the decision-making of queue-jumping behaviours has not considered this personality trait. This study aimed to explore the decision-making processes of the subject driver’s queue-jumping and the follower vehicle driver’s yielding behaviours with Type A and Type B personalities. First, the decision-making utility variables for both players were selected, and a payoff matrix considering utility variable weights was constructed. Next, a decision-making utility evaluation questionnaire was designed, and this questionnaire and the existing Type A behaviour pattern scale were investigated simultaneously. Then, the weight coefficients of the decision-making utility variables were calculated; the replicated dynamic equations of four game combinations were constructed and the local stability principle of a dynamic system was used to determine the evolutionarily stable strategy for each game combination. Finally, the evolutionary process in which subject vehicle drivers select jumping the queue strategy and follower vehicle drivers select giving way strategy was simulated using MATLAB software based on empirical data to verify the validity of the constructed evolutionary game model. The results indicated some differences in the weight coefficients of decision utility variables between Type A and Type B personalities. The constructed game model can effectively reflect the decision-making processes of subject and follower vehicle drivers of different personality types. The dynamic evolution processes of strategy selection were different for the four game combinations. This study revealed the evolutionary game process between subject and follower vehicle drivers, laying a theoretical foundation for traffic management departments to manage queue-jumping behaviours.
1. Introduction
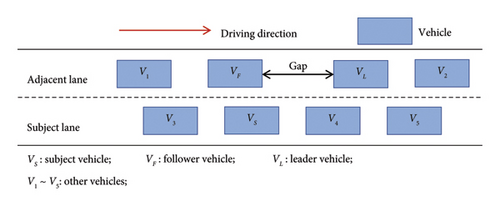
Recently, traffic congestion has become a common problem faced in various cities. In heavy traffic, drivers are commonly required to queue for passage, which will inevitably lead to increased travel times. In this situation, some drivers will attempt to change lanes to minimize their travel delays when there is a gap in the adjacent lane, as shown in Figure 1. However, the gap between the leader and follower vehicles is usually not sufficient to allow the subject vehicle to complete the lane change, which implies that the lane-changing of subject vehicle is bound to force the deceleration of the follower vehicle. Because of this type of lane changing behaviour occupies the driving space originally belonging to the follower vehicle; thus, it is usually called queue-jumping behaviour [1]. Queue-jumping behaviours not only will increase collision risks with adjacent vehicles and easily cause traffic accidents but also will disrupt the order of road traffic operations and reduce the capacity of the road. Thus, they should be given more attention in driving behaviour studies.
Personality traits have always been regarded as important factors affecting driving behaviours, and in particular, some previous studies have confirmed that personality traits are closely related to dangerous driving behaviours and traffic accidents [2–8]. Type A personality is one of the most important personality traits that scholars focus on. This type of personality originated from the clinical observations of Friedman and Rosenman, who found that patients with heart diseases have certain typical characteristics in behaviours and emotions that are different from those without, such as competitiveness, impatience and an exaggerated sense of time urgency. These behavioural traits were defined as the Type A behaviour pattern (TABP), while those opposite behavioural traits, such as serenity, patience and no sense of time urgency [9, 10], were defined as the Type B behaviour pattern (TBBP).
Considering the differences in personality traits between Types A and B individuals, some scholars have explored the characteristics dangerous driving behaviours and accident involvements of the two personality types. Results show that Type A drivers have a higher accident rate and more frequently engage in illegal and risky driving behaviours [11–19]. During actual driving, drivers need to be patient and calm in some situations in which traffic is not moving smoothly (such as traffic jams and rush hour); however, Type A drivers easily become irritable in these situations due to impatience. Driven by emotional edginess, Type A drivers are more prone to exhibit dangerous driving behaviours and be involved in more traffic accidents. However, existing studies have mainly attempted to explore the differences in behavioural performance between Type A and Type B drivers, while few studies focused on behavioural decision-making between the two types of drivers. In fact, a driver’s decision-making directly affects driving behaviour, and exploring the driver’s decision-making process is conducive to identifying the formation mechanism of driving behaviour. Thus, this study focused on exploring the decision-making process underlying drivers’ queue-jumping behaviours. Moreover, given the significant effects of personality types on driving behaviours, the drivers’ personality types (Type A and Type B) were also considered in this study of queue-jumping decision-makings.
Queue-jumping behaviour is a kind of lane-changing behaviour that occurs when the gap between the leader and follower vehicles is insufficient in a queued traffic flow. Because the gap is usually not sufficient to allow the subject vehicle driver to complete a lane change, the queue-jumping completion usually requires the deceleration cooperation of follower vehicle driver. However, such deceleration cooperation means that the follower vehicle driver gives up his or her own driving space to the subject vehicle driver, which will affect the driving smoothness of the follower vehicle; thus, the follower vehicle driver may not cooperate. In this situation, the driver will adjust the strategy from queue-jumping to queueing. It is obvious that the decision-making of the subject vehicle driver and that of the follower vehicle driver clearly depend on and influence each other. Both the subject and follower vehicle drivers will choose the strategy that will bring them greater gain based on their perceived traffic environment and accumulated driving experience, which corresponds to typical game behaviour.
Game theory is a framework for studying how individuals make the most reasonable decisions in complex and interactive situations [20]. It studies the interactions between action subjects from the perspective of strategy selection and has been used in many studies in the field of transportation, such as travel choice, traffic control, interaction behaviour and road congestion pricing [21–23]. However, traditional game theory assumes that all players are completely rational, which does not conform to the reality that human knowledge is bounded. As a further development of game theory, Maynard [24] presented evolutionary game theory by combining classical game theory with biological evolutionary theory. The distinctive characteristics of the evolutionary game theory are that it is based on the premise that players act with bounded rationality and that it can describe the dynamic game process between players; thus, the evolutionary game theory has also been widely used in some studies related to traffic management and control, such as speeding, signal timing optimization, carpooling and commuting mode selection [25–28]. Some scholars are also researching lane-changing or queue-jumping behaviours based on the game theory or evolutionary game theory. For example, Wang, Lyu and Wen [29] proposed a mandatory lane change model in intelligent connected vehicles environment based on the game theory. Reference [30] formulated the lane-changing process as a multiplayer nonzero-sum noncooperative game in a connected environment. Li, Qian, and Liu [31] proposed a decision-making model of queueing and queue-jumping of drivers at intersections based on the evolutionary game theory. Yang and Jia [32] analysed the psychological game process of small and large vehicles’ drivers in the formation of queue-jumping behaviour and proposed the decision-making model of queueing and queue-jumping of drivers at traffic bottleneck based on the evolutionary game theory. In addition, some studies on lane-changing behaviour also consider driving style. Yao and Du [33] analysed the interactions between passenger car drivers in target lanes and bus drivers with different driving styles (e.g., aggressive or conservative style) based on the game theory. Another study explored the evolutionary game mechanism of lane-changing and targeted lane-following vehicles with different driving styles (aggressive, ordinary and cautious) [34]. These studies have enhanced the understanding of lane-changing or queue-jumping behaviours, laying a solid theoretical foundation for related research.
The abovementioned research indicated that the game theory had been widely used in studying traffic behaviours, but the existing research on queue-jumping behaviours has not yet considered the effects of Type A personality traits, resulting in a lack of systematic understanding of the decision-making process of Type A and Type B subject and follower vehicle drivers. Therefore, this study used the evolutionary game theory to explore the dynamic evolution processes of strategy selection by subject and follower vehicle driver combinations with different personality types. The following work has been carried out to achieve the research objective. First, the decision-making utility variables of both players were selected, and a payoff matrix considering utility variable weights was constructed. Next, a decision-making utility evaluation questionnaire was designed, and this questionnaire and the existing TABP scale were investigated together. Then, the weight coefficients of the decision-making utility variables were calculated; the replicated dynamic equations of four game combinations were constructed, and the local stability principle of a dynamic system was used to determine the evolutionarily stable strategy for each game combination. Finally, the evolutionary process in which subject vehicle drivers select jumping the queue strategy and follower vehicle drivers select the giving way strategy was simulated using MATLAB software based on empirical data to verify the validity of the constructed evolutionary game model.
2. Materials and Methods
2.1. Payoff Matrix
In game theory, the payoff matrix is used to describe the strategy set of game players and the utility of each strategy. The game players of queue-jumping are the subject and follower vehicle drivers in the adjacent lane. According to the personality types, the subject and follower vehicle drivers were further divided into Type A and Type B drivers, and the pairwise combinations of different types of drivers form four game combinations in total.
In a queued traffic flow, when there is a possible insertion gap in the adjacent lane, the subject vehicle driver has two strategic choices: jumping the queue and queueing up. The follower vehicle driver has also two strategic choices: giving way and accelerating for prevention. The decision-making utility variables were chosen from two aspects of profits and losses of each strategy. The existing studies have shown that emotions can change cognitive processes and further affect decision-making behaviours [35, 36]. Thus, the profits and losses related to emotions were also considered. According to the profits and losses for each strategy of both players, a payoff matrix considering the personality types of drivers was constructed. As shown in Table 1, both objective and emotional profit and loss variables were included in the payment matrix, which is helpful in identifying the effects of different types of variables on driving decisions. In addition, given that the effects of various utility variables on the total utility may be different, the constructed payoff matrix incorporates weight coefficients of the utility variables.
| Strategy | Type k follower vehicle driver (k = 1, 2) | ||
|---|---|---|---|
| Giving way | Accelerating for prevention | ||
| Type i subject vehicle driver (i = 1, 2) | Jumping the queue | α1iTi + α2iDi − α3iR1i, β1kSk − β2kVk − β3kH1k | α1iTi + α2iDi − α4iR2i − α5iAi, −β4kH2k − β5kFk |
| Queueing up | 0, −β2kVk | 0, 0 | |
- Note: i = 1 and 2 denote subject vehicle drivers of Type A and Type B, respectively. k = 1 and 2 denote follower vehicle drivers of Type A and Type B, respectively. Ti: the time profit for a Type i driver when jumping the queue. Di: the mental profit (such as joy) for a Type i driver when jumping the queue. R1i: the collision risk suffered by a Type i driver when jumping the queue under the condition that the follower vehicle driver gives way. R2i: the collision risk suffered by a Type i driver when jumping the queue under the condition that the follower vehicle driver accelerates to prevent queue-jumping. Ai: the anger of a Type i driver caused by the follower vehicle driver accelerating to prevent queue-jumping. Sk: the safety profit for a Type k driver when giving way under the condition that the subject vehicle driver jumps the queue. Vk: the speed loss for a Type k driver when giving way. H1k: the collision risk suffered by a Type k driver when giving way under the condition that the subject vehicle driver jumps the queue. H2k: the collision risk suffered by a Type k driver when accelerating for prevention under the condition that the subject vehicle driver jumps the queue. Fk: the anger of a Type k driver caused by the subject vehicle driver still insisting on jumping the queue regardless of the prevention behaviour. αri (r = 1, 2, 3, 4, 5): the weight coefficients of the utility variables for a subject vehicle driver with a Type i personality. βrk (r = 1, 2, 3, 4, 5): the weight coefficients of the utility variables for a follower vehicle driver with a Type k personality.
2.2. Measures
2.2.1. TABP
TABP scale developed by Zhang [37] was used to measure the personality types of drivers. There are 60 items on the TABP scale, including 10 lie detection items. The other items are divided into two dimensions and each dimension corresponds to 25 items. Each item has two possible responses: yes and no. Participants are required to choose the more appropriate responses based on the conformity between the item descriptions and their individual characteristics. When the score on the lie detection items is higher than 7, the results of the questionnaire are considered to be true and effective; otherwise, they are regarded as invalid. Drivers can be classified in accordance with their self-reported scores on the TABP scale.
2.2.2. Decision-Making Utility Evaluation Questionnaire
To determine the weight coefficients of the decision-making utility variables in the payoff matrix, i.e., the values of αri and βrk(i, k = 1, 2; r = 1, 2, 3, 4, 5), a decision-making utility evaluation questionnaire was designed in this study with the aim of collecting evaluation data on the utility variables and the total utility of each strategy for both players.
As shown in the payoff matrix, for the subject vehicle driver, there are 5 utility variables (T, D, R1, R2 and A) when not considering the personality type. For the two conditions in which the follower vehicle driver selects giving way and accelerating for prevention, the total utility that the subject vehicle driver earns by jumping the queue is denoted by Y1 and Y2, respectively. For the follower vehicle driver, there are also 5 utility variables (S, V, H1, H2 and F) when not considering the personality type. Under the condition that the subject vehicle driver selects jumping the queue, the total utility that the follower vehicle driver earns by selecting giving way or accelerating for prevention is denoted by Z1 or Z2, respectively. Thus, there were 14 items in total in the decision-making utility evaluation questionnaire. The detailed contents of the items are shown in Table 2.
| No. | Item description | Measured utility variable |
|---|---|---|
| 1 | How much do you think the travel time can be shortened when you jump the queue? | T |
| 2 | How joyful are you when the driving conditions are improved after queue-jumping? | D |
| 3 | How likely do you think it is that queue-jumping will still cause a collision accident when the follower vehicle driver selects giving way? | R1 |
| 4 | How likely do you think it is that queue-jumping will cause a collision accident when the follower vehicle driver selects accelerating for prevention? | R2 |
| 5 | How angry are you when your queue-jumping is prevented by the follower vehicle driver? | A |
| 6 | How much do you think the total utility of queue-jumping is when the follower vehicle driver selects giving way? | Y1 |
| 7 | How much do you think the total utility of queue-jumping is when the follower vehicle driver selects accelerating for prevention? | Y2 |
| 8 | How much do you think the driving safety can be improved by giving way when the subject vehicle driver jumps the queue? | S |
| 9 | How much do you think the driving speed can be reduced caused by giving way when the subject vehicle driver jumps the queue? | V |
| 10 | How likely do you think it is that a collision accident will still be caused by queue-jumping when you select giving way? | H1 |
| 11 | How likely do you think it is that a collision accident will be caused by queue-jumping when you select accelerating for prevention? | H2 |
| 12 | How angry are you when the subject vehicle driver still insists on jumping the queue regardless of your prevention behaviour? | F |
| 13 | How much do you think the total utility of giving way is when the subject vehicle driver jumps the queue? | Z1 |
| 14 | How much do you think the total utility of accelerating for prevention is when the subject vehicle driver jumps the queue? | Z2 |
To eliminate the effects of different variable attributes and measurement magnitudes on the results, the responses for all decision-making utility variables were set to 5 levels with integer values between 1 and 5, with a higher value indicating higher profit or loss. The values for the total utility of a strategy were defined as integers between −2 and 2.
2.2.3. Field Survey
The TABP scale and decision-making utility evaluation questionnaire were distributed at shopping malls and automobile 4S shops. The participants were required to be drivers with valid driving licences and driving experience. Participants were informed that this was an anonymous survey to allay potential concerns about responding honestly. After obtaining the informed consent of each participant, the investigation was distributed. Each questionnaire took approximately 10 min to complete, and the participant was given RMB10 or a key chain as a reward after completing the questionnaire. It should be noted that the investigation has been reviewed and approved by the Biomedical Ethics Committee of Hefei University of Technology, and it is stated that the investigation plan complies with national laws and regulations, is scientifically reasonable and feasible and is agreed to conduct.
According to the self-reported scores on the TABP scale, the collected samples were divided into three groups: 96 samples were Type A drivers, 10 samples were Intermediate drivers and 101 samples were Type B drivers. However, the intermediate driver samples were eliminated for two reasons: on the one hand, the size of this sample was too small to be representative, and on the other hand, this study focused on Type A drivers and Type B drivers with significant differences in personality traits. Thus, 96 samples of Type A drivers and 101 samples of Type B drivers were ultimately used for subsequent analysis and modelling.
2.3. Weight Coefficients
The designed decision-making utility questionnaire could obtain evaluation data from each participant on the total decision-making utility and the utility variables under the two conditions in which the participant was the subject vehicle driver and the follower vehicle driver. The data were randomly divided into two parts, the first part was used to determine the weight coefficients of the utility variables for both players and the other part was used to determine the strategy payoff relationship of the four game combinations and conduct the simulation of dynamic evolutionary process of strategy selection of both players.
This study used the multivariable linear regression model to determine the weight coefficients of decision-making utility variables. As shown in Table 1, four game combinations of both players corresponded to four models, and the number of independent variables in these models was between two and three. The sample size for linear regression should be at least 10 times that of the independent variables. Thus, 60 samples were randomly selected from all samples of each personality type to determine the weight coefficients of utility variables for both players. Specifically, for each game combination, the perceived total utility of the subject or follower vehicle driver on each strategy was regarded as the dependent variable, and the corresponding utility variables of each strategy were regarded as the independent variables. The results of weight coefficients are shown in Tables 3 and 4.
| Personality type | Type A driver | Type B driver | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α11 | α21 | α31 | α41 | α51 | α12 | α22 | α32 | α42 | α52 | |
| Values | 0.22 | 0.35 | −0.33 | −0.56 | −0.25 | 0.15 | 0.26 | −0.36 | −0.61 | −0.15 |
| Standard error | 0.037 | 0.027 | 0.031 | 0.034 | 0.037 | 0.0376 | 0.037 | 0.03 | 0.040 | 0.039 |
| Sig. | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Lower limit of confidence interval | 0.146 | 0.297 | −0.396 | −0.624 | −0.323 | 0.074 | 0.186 | −0.416 | −0.694 | −0.223 |
| Upper limit of confidence interval | 0.294 | 0.406 | −0.272 | −0.487 | −0.175 | 0.217 | 0.333 | −0.298 | −0.534 | −0.067 |
| Personality type | Type A driver | Type B driver | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β11 | β21 | β31 | β41 | β51 | β12 | β22 | β32 | β42 | β52 | |
| Values | 0.26 | −0.22 | −0.31 | −0.52 | −0.45 | 0.35 | −0.17 | −0.32 | −0.65 | −0.34 |
| Standard error | 0.03 | 0.041 | 0.038 | 0.049 | 0.047 | 0.029 | 0.040 | 0.036 | 0.035 | 0.029 |
| Sig. | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Lower limit of confidence interval | 0.198 | −0.303 | −0.389 | −0.619 | −0.546 | 0.292 | −0.251 | −0.396 | −0.719 | −0.398 |
| Upper limit of confidence interval | 0.371 | −0.139 | −0.236 | −0.422 | −0.358 | 0.407 | −0.090 | −0.251 | −0.579 | −0.281 |
2.4. Construction of the Evolutionary Game Model
2.4.1. The Replicated Dynamic Equation
The evolutionary game theory holds that an individual is not an optimal actor in reality; instead, individual decision-making is realized through a dynamic process, including imitation, learning and mutation between individuals. The replicated dynamic equation is the dynamic differential equation describing the adoption ratio of a particular strategy in a population and is used to study the strategy adjustment processes of both players [38]. The replicated dynamic equations for the jumping the queue strategy and the giving way strategy represent the rate of change in the subject vehicle driver’s proportion of selecting the jumping the queue strategy over time and the rate of change in the follower vehicle driver’s proportion of selecting the giving way strategy over time, respectively.
The definition of each variable is as follows:
Ui,1: the expected payoff of the jumping the queue strategy for Type A or Type B subject vehicle drivers.
Ui,2: the expected payoff of the queueing up strategy for Type A or Type B subject vehicle drivers.
Bi,1: the expected payoff of the giving way strategy for Type A or Type B follower vehicle drivers.
- •
: the average expected payoff of the two strategies for Type A or Type B subject vehicle drivers.
- •
: the average expected payoff of the two strategies for Type A or Type B follower vehicle drivers.
In accordance with the expected payoff of each strategy and the average payoff of the two strategies for Type A and Type B drivers, the replicated dynamic equations for the jumping the queue strategy of subject vehicle drivers with different personality types and the giving way strategy of follower vehicle drivers with different personality types were obtained.
2.4.2. Evolutionarily Stable Strategy
The evolutionarily stable strategy refers to the case in which there is no mutational strategy that can invade this population under the effects of natural selection if all members of a population adopt this strategy [39]. In actual driving, both subject and follower vehicle drivers will usually adjust their strategic choices dynamically based on their perceived road environment and accumulated driving decision experience until they have all selected the strategy with the maximal payoff, i.e., the evolutionarily stable strategy.
The key to determining the evolutionarily stable strategy is to find the strategic equilibrium points for both game players and further use the local stability principle of a dynamic system to analyse the state of each equilibrium point. The point at which the replicated dynamic equations are equal to zero is the equilibrium point, which means that the game populations are no longer evolving [38]. The local stability principle of a dynamic system allows the stability of an equilibrium point to be judged based on the sign of the determinant and the trace of the Jacobian matrix [38]. Equilibrium points can be divided into saddle points, unstable points and stable points in accordance with their directions of change; a saddle point is stable along one direction and unstable along the other, an unstable point is unstable along each direction and a stable point is stable along both directions and represents the endpoint of the evolutionary game [38].
In the Jacobian matrix, the values of i and k represent different types of drivers. Please see Table 1 for detailed meanings. Because of the different weight coefficients of the utility variables for different types of drivers, the strategy payoff relationship and the evolutionarily stable strategy for each game combination should be explored individually. For the collected decision-making utility questionnaire data, some were used to determine the weight coefficients of utility variables, and the remaining were used to determine the strategy payoff relationship of the four game combinations and conduct the simulation of dynamic evolutionary process of strategy selection of both players.
When the drivers of both the subject and follower vehicles are of the Type A personality type, the relationships between the decision-making utility variables are as follows: 0.22T1 + 0.35D1 > 0.56R12 + 0.25A1 and 0.35S2 + 0.65H22 + 0.34F2 < 0.17V2 + 0.32H12. This relationship implies that the payoff of the jumping the queue strategy is greater than that of the queueing up strategy for the subject vehicle driver, while the payoff of the accelerating for prevention strategy is greater than that of the giving way strategy for the follower vehicle driver.
When the drivers of the subject and the follower vehicles are of the Type A and Type B personality types, respectively, the relationships between the decision-making utility variables of the different strategies are as follows: 0.22T1 + 0.35D1 > 0.56R21 + 0.25A1 and 0.35S2 + 0.65H22 + 0.34F2 > 0.17V2 + 0.32H12. This relationship implies that the payoff of the jumping the queue strategy is greater than that of the queueing up strategy for the subject vehicle driver, while the strategy with the greater payoff for the follower vehicle driver depends on the strategy selected by the subject vehicle driver.
When the drivers of the subject and follower vehicles are of the Type B and Type A personality types, respectively, the relationships between the decision-making utility variables of the different strategies are as follows: 0.33R11 < 0.22T1 + 0.35D1 < 0.56R21 + 0.25A1 and 0.35S2 + 0.65H22 + 0.34F2 < 0.17V2 + 0.32H12. This relationship implies that the strategy with the greater payoff for the subject vehicle driver depends on the strategy selected by the follower vehicle driver, while for the follower vehicle driver, the payoff of accelerating for prevention is greater than that of the giving way strategy.
When the drivers of both the subject and follower vehicles are of the Type B personality type, the relationships between the decision-making utility variables of the different strategies are as follows: 0.33R11 < 0.22T1 + 0.35D1 < 0.56R21 + 0.25A1 and 0.35S2 + 0.65H22 + 0.34F2 > 0.17V2+0.32H12. This relationship implies that the strategy with the greater payoff for the subject vehicle driver depends on the strategy selected by the follower vehicle driver; similarly, the strategy with the greater payoff for the follower vehicle driver depends on the strategy selected by the subject vehicle driver.
By solving the equations Type (2.7) = 0 and Type (2.8) = 0, Type (2.9) = 0 and Type (2.10) = 0, Type (2.11) = 0 and Type (2.12) = 0 and Type (2.13) = 0 and Type (2.14) = 0, the evolutionary equilibrium points of each game are obtained, as shown in Table 5. The results indicated that for the evolutionarily stable strategy, the game combination of Type A subject and follower vehicle drivers was (1, 0), the game combination of Type A subject and Type B follower vehicle drivers was (1, 1), the game combination of Type B subject and Type A follower vehicle drivers was (0, 0) and the game combination of Type B subject and follower vehicle drivers was (1, 1).
| Game combination | Equilibrium points | Sign [det(J)] | Sign [Tr(J)] | Results |
|---|---|---|---|---|
| Type A and Type A drivers | (0, 0) | − | Saddle point | |
| (0, 1) | + | + | Unstable point | |
| (1, 0) | − | + | Stable point | |
| (1, 1) | − | Saddle point | ||
| Type A and Type B drivers | (0, 0) | − | Saddle point | |
| (0, 1) | + | + | Unstable point | |
| (1, 0) | − | Saddle point | ||
| (1, 1) | + | − | Stable point | |
| Type B and Type A drivers | (0, 0) | + | − | Stable point |
| (0, 1) | + | + | Unstable point | |
| (1, 0) | − | Saddle point | ||
| (1, 1) | − | Saddle point | ||
| Type B and Type B drivers | (0, 0) | + | + | Unstable point |
| (0, 1) | + | + | Unstable point | |
| (1, 0) | + | + | Unstable point | |
| (1, 1) | + | − | Stable point | |
| (−0.17V2/0.35S2 + 0.32H12 − 0.65H22 − 0.34F2, −0.15T2 − 0.26D2 − 0.61R22 − 0.15A2/−0.61R22 − 0.15A2 + 0.36R12) | − | 0 | Saddle point | |
3. Game Model Verification
To clearly illustrate the dynamic process of strategy selection by the subject and follower vehicle drivers, the values of the decision-making utility variables for each game combination were substituted into their corresponding dynamic replication equations, and MATLAB 17.0 was used to simulate the evolutionary process. The results are shown in Figures 2, 3, 4 and 5.
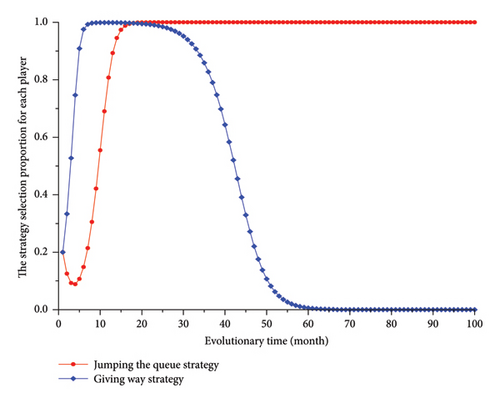
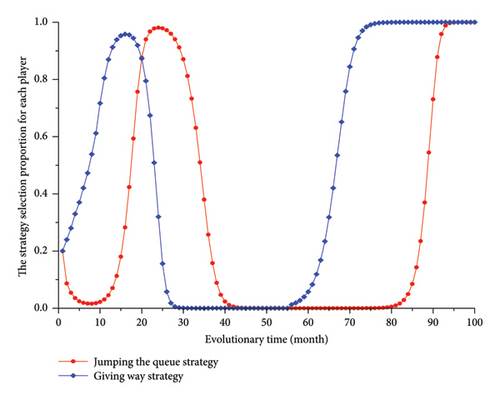
As shown in Figure 2, for the game combination of Type A subject and follower vehicle drivers, at the beginning, the selection proportion of jumping the queue strategy shows a downward trend, while the selection proportion of giving way strategy shows an increasing trend. Clearly, both game sides initially tend to choose the strategy that will lead to fewer conflicts with each other, which may be attributed to their lack of understanding of each other’s strategy selection at this stage. However, after initially decreasing to approximately 0.1, the selection proportion of jumping the queue strategy then begins to increase; this change may be caused by the subject vehicle drivers realizing that an increasing number of follower vehicle drivers are tending to select the giving way strategy. A change in the strategy selection on both sides appears once the drivers’ selection proportions for the jumping the queue and giving way strategies both reach their maximum value of 1. Specifically, the proportion of Type A subject vehicle drivers selecting jumping the queue strategy remains constant, while the proportion of Type A follower vehicle drivers selecting giving way strategy begins to decrease and eventually drops to 0. Afterwards, the strategy selection of the players on both sides of the game no longer changes. The strategies selected by the Type A subject and follower vehicle drivers are jumping the queue and accelerating for prevention, respectively, once the game reaches a stable state.
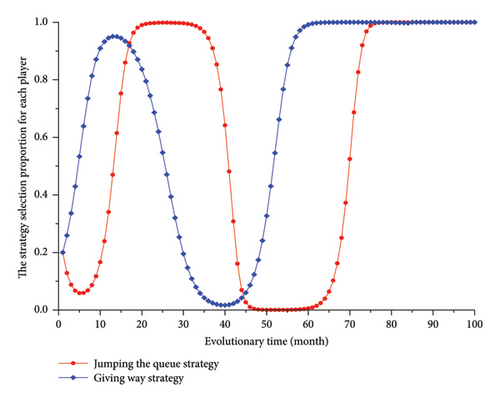
As shown in Figure 3, for the game combination of Type A subject and Type B follower vehicle drivers, at the beginning, the selection proportion of jumping the queue strategy shows a downward trend, while the selection proportion of giving way strategy shows an increasing trend. However, the selection proportion of jumping the queue strategy begins to increase once it has decreased to approximately 0.05, while the selection proportion of giving way strategy continues to increase. Then, once the selection proportion of jumping the queue strategy has increased to approximately 0.55, the selection proportion of giving way strategy begins to decrease and eventually drops to approximately 0. This decrease in the selection proportion of giving way strategy indicates that an increasing number of follower vehicle drivers tend to act to prevent subject vehicle drivers from jumping the queue. Faced with this hindrance from follower vehicle drivers, the selection proportion of jumping the queue strategy initially increases, then remains constant and finally decreases; however, once it has decreased to 0.65, the selection proportion of giving way strategy begins to gradually increase again until it reaches 1, which may be attributed to follower vehicle drivers observing a gradual decrease in the number of subject vehicle drivers selecting jumping the queue strategy. As an increasing number of follower vehicle drivers make the giving way decision, the proportion of subject vehicle drivers selecting jumping the queue strategy initially decreases, then remains constant and finally increases to 1. Afterwards, the strategy selection of the subject and follower vehicle drivers no longer changes. The strategies selected by the Type A subject vehicle drivers and Type B follower vehicle drivers are jumping the queue and giving way, respectively, once the game reaches a stable state.
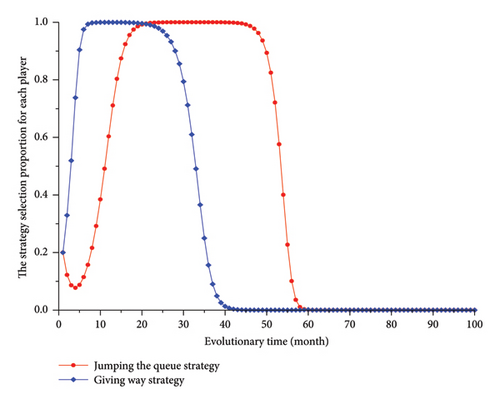
As shown in Figure 4, for the game combination of Type B subject and Type A follower vehicle drivers, at the beginning, the selection proportion of jumping the queue strategy shows a downward trend, while the selection proportion of giving way strategy shows an increasing trend. However, this begins to change when the selection proportion of jumping the queue strategy drops to approximately 0.1. The main change is that an increasing number of subject vehicle drivers begin to select jumping the queue strategy, possibly because subject vehicle drivers have observed that most follower vehicle drivers tend to select the giving way strategy. Once the selection proportion of jumping the queue strategy has increased to its maximum value of 1, the follower vehicle drivers realize that continuing to select the giving way strategy would encourage queue-jumping behaviours by subject vehicle drivers; thus, they begin to adjust their strategy selection, and the selection proportion of giving way strategy gradually decreases from the maximum to the minimum. As an increasing number of follower vehicle drivers act to prevent subject vehicle drivers from jumping the queue, the proportion of subject vehicle drivers selecting jumping the queue strategy first remains unchanged and then gradually decreases. Afterwards, the strategy selection of subject and follower vehicle drivers no longer changes. The strategies selected by Type B subject and Type A follower vehicle drivers are queueing up and accelerating for prevention, respectively, once the game reaches a stable state.
As shown in Figure 5, for the game combination of Type B subject and follower vehicle drivers, at the beginning, the selection proportion of jumping the queue strategy shows a downward trend, while the selection proportion of giving way strategy shows an increasing trend. As an increasing number of follower vehicle drivers select giving way strategy, the proportion of subject vehicle drivers selecting jumping the queue strategy eventually begins to increase after first decreasing to near 0. Subsequently, as an increasing number of subject vehicle drivers select jumping the queue strategy, the proportion of follower vehicle drivers selecting giving way strategy initially increases and then decreases until it drops to 0, meaning that an increasing number of follower vehicle drivers are acting to prevent subject vehicle drivers from jumping the queue. Faced with this hindrance from the follower vehicle drivers, the proportion of subject vehicle drivers selecting the jumping the queue strategy begins to decrease until no subject vehicle drivers select this strategy. At this stage, although subject vehicle drivers all select the queueing up strategy, follower vehicle drivers start to adjust their strategies after a while, which may be affected by the conservative strategy selection of subject vehicle drivers. As an increasing number of follower vehicle drivers select the give way strategy, the selection proportion of jumping the queue strategy also increases correspondingly until all subject vehicle drivers select this strategy. Afterwards, the strategy selection of subject and follower vehicle drivers no longer changes. The strategies selected by Type B subject and follower vehicle drivers are jumping the queue and giving way, respectively, once the game reaches a stable state.
4. Discussion
The results of weight coefficients indicate that both subject and follower vehicle drivers are concerned about the collision risk in the case that jumping the queue strategy and accelerating for prevention strategy are simultaneously selected, which may be because a collision accident caused by competing with each other will directly lead to losses of both time and money on both sides and even lead to casualties. In addition, comparing the weight coefficients of decision-making utility variables for Type A and Type B subject vehicle drivers, it can be found that Type A subject vehicle drivers give more attention to the benefits of a shorter travel time and a more joyful mood gained by jumping the queue, while Type B subject vehicle drivers are more concerned about the potential collision risks caused by jumping the queue, consistent with the personality traits of Type A and Type B drivers. More specifically, Type A drivers are less patient and feel greater time urgency, and these traits cause these drivers to dislike queueing up while driving; while queue-jumping makes travel times shorter and makes the driver’s mood more joyful, so it has a greater appeal to Type A drivers. In contrast, Type B drivers are patient and have little sense of urgency; these characteristics make these drivers more cautious while driving, and thus, the potential risks of queue-jumping are more important to Type B drivers. These findings further confirm the existence of differences in behaviour decisions between Type A and Type B drivers [12,14,17,40].
This study found that the strategy payoff relationships for subject and follower vehicle driver combinations with different personality types are different. Pan et al. [41] have proposed that it is necessary to explore decision-making differences between Type A and Type B drivers in practice to provide a psychological basis for the improvement and cultivation of drivers’ decision-making. Differences in the strategy utility evaluations between Type A and Type B drivers were found in this study; this lays a foundation for preliminarily identifying the decision-making characteristics of these two types of drivers. In addition, the equilibrium points and evolutionarily stable strategies for different personality type combinations are also different, which is expected because the differences in the strategy utility evaluations among drivers with different personality types will inevitably affect their strategy selections. The evolutionarily stable strategy for the Type A subject and follower vehicle drivers means that neither player accedes to the other; this situation is prone to cause collision accidents and thus is not conducive to driving safety. The evolutionarily stable strategy for the Type A subject and Type B follower vehicle drivers implies that the follower vehicle driver will always make way for the subject vehicle driver. The active yielding of the follower vehicle driver can greatly reduce the collision risks between the subject and follower vehicles, but this coping strategy will exacerbate the queue-jumping behaviours of the subject vehicle driver and may even form the habit of queue-jumping. The evolutionarily stable strategy for the Type B subject and Type A follower vehicle drivers means that both sides of the game engage in orderly driving in their own road space, and there is little collision risk between them. The evolutionarily stable strategy for the Type B subject and follower vehicle drivers means that the interactive process between two sides is relatively safe, but the constant yielding of the follower vehicle driver will cause queue-jumping behaviours of subject vehicle drivers to occur more frequently.
The simulation results show that the evolutionarily stable strategies for the four driver combinations are consistent with the results of the local stability analyses, which indicates that the constructed game model can effectively reflect the decision-making processes of subject and follower vehicle drivers of different personality types. From the decision-making process of both game sides, it can be seen that the decision-makings of Type A drivers are offensive in nature whether they are driving the subject vehicle or the follower vehicle. Furthermore, no matter which strategy the other player selects, they always tend to select the strategy allowing them to occupy the driving space of the other player or avoiding allowing their own driving space to be occupied. In contrast, the decision-makings of Type B drivers are more cautious. They usually select their strategy by observing the strategy selection preference of the other player and deliberately avoid the strategy combination of jumping the queue and accelerating for prevention to reduce potential conflicts and improve driving safety. This finding implies that traffic management departments should consider the personality differences of drivers when formulating improvement measures for queue-jumping behaviours and should direct more attention towards drivers with Type A personality traits. In addition, traffic management departments can compare the queue-jumping decision-making processes of Type A and Type B drivers to make Type A drivers more clearly aware of the potential safety risks arising in their decision-making process and further guide the decision-making of Type A drivers towards a safer state.
5. Conclusions
- 1.
Type A subject vehicle drivers pay more attention to the benefits of shorter travel time and a more joyful mood gained by jumping the queue than Type B subject vehicle drivers. In contrast, Type B subject vehicle drivers are more concerned about the potential collision risks caused by queue-jumping than Type A subject vehicle drivers.
- 2.
The simulation results of evolutionarily stable strategies for the four game combinations are consistent with the results of the local stability analyses, which indicates that the constructed game model can effectively reflect the decision-making processes of subject and follower vehicle drivers of different personality types
- 3.
The dynamic evolution processes of strategy selection were different for the four game combinations. The evolutionarily stable strategy of Type A subject and follower vehicle drivers was jumping the queue and accelerating for prevention, Type A subject and Type B follower vehicle drivers was jumping the queue and giving way, Type B subject and Type A follower vehicle drivers was queueing up and accelerating for prevention and Type B subject and follower vehicle drivers was jumping the queue and giving way.
This study has significant theoretical and practical implications. From a theoretical perspective, on the one hand, this study revealed the game process in which subject vehicle drivers select jumping the queue strategy and follower vehicle drivers select the giving way strategy with different personality traits, which enhanced the understanding of the decision-making differences and interactive progress between drivers with Type A and Type B personality traits. On the other hand, this study formed an integrated research framework on the dynamic decision-making progress of drivers based on the evolutionary game theory, which provided references for modelling the interaction behaviours between drivers. From a practical perspective, on the one hand, this study identified the difference in the effect of profit and loss variables on drivers with Types A and B personalities, which is conducive to developing targeted intervention measures for queue-jumping behaviours for the traffic management department based on the decision-making characteristics of drivers with different personalities. On the other hand, this study proposed an interaction behaviour model of queue-jumping and giving way considering personality traits, which enriched the existing microdriving behaviour models and provided new ideas and theoretical support for more refined traffic flow simulations. In addition, it should be noted that this study obtained the strategy utility evaluation data through questionnaire. Although some mitigation measures were taken in the questionnaire design and survey, such as avoiding tendentiousness items and providing notification of anonymity, the common weaknesses of self-reported questionnaires, such as the social desirability, were still unavoidable. In future research, we will consider collecting data on various decision-making utility variables by means of a driving simulator and psychological testing instruments to reduce the impacts of potential individual response bias on the research results.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This paper was supported by the Innovative Team Project of Ji’nan Government (no. 202333036), Jinan City’s Self-Developed Innovative Team Project for Higher Educational Institutions (no. 20233040).
Open Research
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.




