Volume 2024, Issue 1 5550897

Research Article

Open Access

Optimum Allocation of Microgrid and D-STATCOM in Radial Distribution System for Voltage Profile Enhancement Using Particle Swarm Optimization

Corresponding Author

Mezigebu Getinet Yenealem

[email protected]

orcid.org/0000-0001-6450-0125

Faculty of Electrical and Computer Engineering , Bahir Dar Institute of Technology , Bahir Dar University , P.O. Box 26, Bahir Dar , Ethiopia , bdu.edu.et

Search for more papers by this author

Mezigebu Getinet Yenealem,

Corresponding Author

Mezigebu Getinet Yenealem

[email protected]

orcid.org/0000-0001-6450-0125

Faculty of Electrical and Computer Engineering , Bahir Dar Institute of Technology , Bahir Dar University , P.O. Box 26, Bahir Dar , Ethiopia , bdu.edu.et

Search for more papers by this author

First published: 28 June 2024

https://doi.org/10.1155/2024/5550897

Academic Editor: Alberto Álvarez-Gallegos

Share a link

Email
Wechat
Bluesky

Abstract

The integration of microgrid (MG) and distribution static synchronous compensator (D-STATCOM) controller in power system has become crucial for enhancing voltage profiles, improving system reliability, and minimizing power losses in radial distribution networks. This study presents an innovative approach for the optimal allocation of MG and D-STATCOM within a radial distribution system (RDS), aimed at significantly improving voltage profiles. Particle swarm optimization (PSO), a powerful and efficient metaheuristic algorithm, is utilized to determine the optimal sizing of MG and D-STATCOM controllers. The loss sensitivity factor (LSF) technique is employed to find the optimal position for D-STATCOM, and the voltage stability index (VSI) is used to determine the optimal location for MG. To validate the effectiveness of the PSO-based approach, simulations are conducted on a standard IEEE 30 bus RDS. The results indicate that the strategic placement of MGs and D-STATCOMs markedly enhances the voltage profile across the distribution network, leading to improved power quality and reduced technical losses.

1. Introduction

Currently, electrical consumption of energy is growing, yet investments in conventional transmission and distribution systems and the usage of fossil fuels are steadily declining [1]. The power supply companies are then encouraged to face unprecedented problems in terms of meeting load requirements, consumer satisfaction, and environmental considerations. Numerous investigations have shown that 13% of power generation is ineffective in the entire power system because of the higher energy loss values [2]. Due to variations in radial topologies and voltage levels, distribution systems have higher losses than transmission networks [3]. The electrical energy distribution in the range of 10–15 KV is average in the Ethiopian context; however, lower voltage levels are utilized for operational purposes [3]. Radial topology is used in distribution networks to lower investment costs in conductors and protection elements. One significant issue is that it results in a large proportion of energy losses [4].

In the Ethiopian distribution system, energy losses from the electric system range between 1.5% and 2.5% of the net energy produced. However, the energy loss in networks with average voltage varies from 5% to 18% [5, 6]. Less than 10% of networks experience loss, which is partially attributed to legal regulations and the fact that maintenance is performed. Many approaches to reducing technical loss in distribution networks are demonstrated in the literature. Hence, the integration of microgrid (MG) [7], reconfigurations of primary feeders [8], connections of shunt capacitors, and Flexible Alternating Current Transmission System (FACTS) devices [9, 10] are considered.

In particular, distribution systems with a long power supply distance and a weak network structure benefit greatly from the use of MGs. These benefits include shifting peak loads, lowering network losses, boosting system reliability, improving voltage profiles, and so on [11]. However, a few factors need to be taken into account, including the number and size of MG units, the best location, and the bus configuration [3]. The optimal location and size of MG in distribution networks have been investigated in the literature from different perspectives.

First, from the viewpoint of MG modelling, most of the research studies consider nondispatchable MG such as photovoltaic (PV) and wind turbines (WTs), whose outputs are indeterminate and hard to designate due to the volatility and intermittency of environmental influences (e.g., solar insolation and wind speed) [12]. This causes a variation in voltage profiles and an increment in power losses which can increase power quality issues [13].

The uncertain outputs of MG which impact power quality issue are modelled using artificial intelligence algorithms and stochastic theory [6]. To solve the power quality issues, fixed capacitor banks and synchronous condensers have been in use for several years [14]. Nevertheless, such compensation of reactive power has certain disadvantages that comprise high losses, slow response time, rigidity, high cost, and large dimensions. In addition, they may cause overvoltage or resonance problems and introduce harmonics into the system, and they may not be effective for long-distributed loads. To confront the operational challenges associated with monitoring, processing, and control of power systems, FACTS devices were habituated and established [15]. The most regularly used converter in the FACTS family due to its fastest response in reactive power compensation is the distribution static synchronous compensator (D-STATCOM). Using D-STATCOM, power quality problems are compensated [16]. D-STATCOM is used for reactive power compensation, which in turn minimizes power losses and voltage disturbances [17]. The optimal solution is obtained after solving several power flow solutions corresponding to a specified set of consumer demands [18]. The importance of the optimum size and location of MG in the radial distribution system (RDS) is described in [19]. Power loss and voltage disruption in a distribution system are the main important factors for RDS [20].

Second, regarding optimization objectives, previous investigations have concentrated on distinct targets based on different planning circumstances. In [11], the objective function for determining the most suitable MG and D-STATCOM allocation scheme and the entire investment cost, operational cost, and maintenance (O & M) costs, as well as network losses, are fully taken into consideration in [14]. A power outage has been converted into a reliability cost and added to the objective function [21]. In [22], MG and D-STATCOM allocation in a RDS for mitigation of overloading of lines, quality, reliability, and power losses have been presented. However, optimal MG and D-STATCOM allocation (i.e., location and sizing) are the stimulating issues to advance system efficiency by decreasing power losses and by enhancing the voltage reliability and security of the network [23].

Third, the optimization models of both MG and D-STATCOM management are always solved using mathematical techniques, intelligence search methods, and review from the perspective of solution algorithms. Mathematical approaches are extra reliable in catching universal optimal solutions; however, they are always not directly pertinent for MG and D-STATCOM development problems due to the complexity and nonconvexity of optimization models. To simplify the model and facilitate its mathematical solution, a piecewise linear approximation is employed [24].

Intelligence search methods are easy to use and constantly proficient for solving upsetting optimization models, but they are time-consuming and easily lead to locally optimal solutions instead of globally optimal solutions. Genetic algorithm (GA), particle swarm optimization (PSO), GA-PSO hybrid algorithm, honey bee mating optimization (HBMO), and ant colony optimization (ACO) are, respectively, utilized in [23–26].

Almost all the reviewed studies focused on modelling MG and D-STATCOM for integration in the network for the optimum operation of the system. However, additional techniques to increase system accuracy were not utilized. In this study, the PSO algorithm is developed with supplementary techniques such as voltage stability index (VSI) and loss sensitivity factor (LSF) for solving the optimal location and sizing of D-STATCOM and MG in the distribution networks. The most suitable location for installing MG in the distribution system is determined by VSI, and the optimal location of D-STATCOM is determined by the LSF method. The framework of this document is as follows. The research methodology is described in depth in Section 2, the simulation findings and discussions are presented in Section 3, and the study’s conclusion is presented in Section 4.

2. Methodology

2.1. Power Flow Analysis

The current and voltage measurements of the network in each bus and the active and reactive power flows in each line are analyzed using the power flow analysis method. The power flow equations derived depend on the conventional power flow algorithm, which is essentially significant in transmission networks yet irrelevant for RDSs because of its inherent characteristics (low reactance to resistance ratios (X/R)) [14]. Thus, the conventional power flow strategies, for example, Gauss–Seidel, Newton–Raphson, and so forth, are not effective for the distribution system. The single-line diagram of simple RDS is depicted in Figure 1 [15].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Single-line diagram of simple RDS.

From Figure 1, i is the sending end and i + 1 is the receiving end. The active and reactive power flows in the first section are expressed in Equations (1) and (2) [16].

()

The voltage at the bus (i + 1)_th is calculated using Equation (3) [17].

()

The active and reactive power losses in the first section at i are calculated using Equations (4) and (5) [17].

()

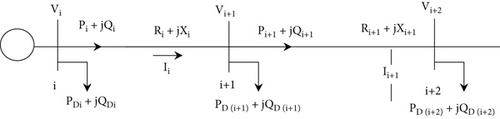
2.2. Direct Load Flow (DLF) Analysis in RDS

A feeder carries power from the substation to load in the RDS. To govern the total power loss of the system or each feeder branch, the maximum voltage deviation (VD) is resoluted by performing load flow. Hence, a DLF technique is used to find the voltage profile and the total power loss of RDS. In this distribution power flow algorithm, bus injection to branch current (BIBC) matrix and branch current to bus voltage (BCBV) matrix power flow techniques are developed. Based on the DLF analysis, the complex power flow (Si) of bus i can be expressed in [27].

The BIBC and BCBV relationship expression in matrix form is derived as follows based on the 30-bus RDS as developed in [28]. The correlation between branch current and bus current injections can be found by applying Kirchhoff’s current law (KCL) in Equation (6).

()

Branch injection currents and bus currents are related in matrix form given by Equation (7).

()

The association between bus current injection and branch current can be expressed in Equation (8).

()

where BIBC is the bus injection branch current matrix.

The general expression of branch currents and bus voltages can also be represented by Equation (9).

()

The BIBC matrix provides an easy relationship between node current injections and branch currents.

This relationship provides a clear solution to the variance of branch currents, which arises due to the variation of the current injection nodes, and can be obtained directly using the BIBC matrix. The BCBV matrix constructs a convincing relationship between the branch current flows and node voltages. The concern variation of the node voltage is created by the variation of the branch currents by using the BCBV. The correlation between bus voltage and bus current injections can be communicated in Equation (10) [29].

()

For RDSs, power flow can be solved using Equation (11) iteratively.

()

where k is the iteration count and V_o is the initial voltage. The new definition as delineated uses only the DLF network to deal with load flow. Hence, this technique is very time-productive.

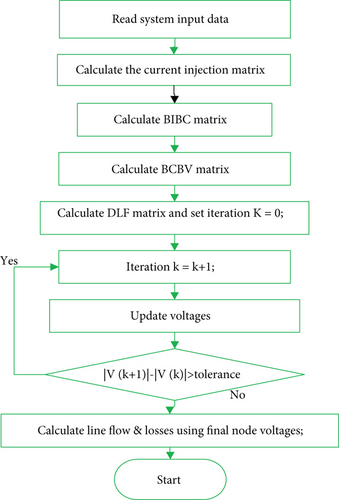
The RDS power flow algorithm flow chart is given in Figure 2.

2.3. D-STATCOM

D-STATCOM is a shunt system capable of injecting and absorbing real or reactive power on the bus, thereby eliminating the sag in bus voltages [30]. It is a voltage-source inverter with a DC energy storage unit or a DC link capacitor for constant DC voltage delivery [31]. The bus voltage and power factor are regulated and corrected by D-STATCOM since it acts as a synchronous source of voltage. The modelling, working principle, and block diagram of D-STATCOM are detailed in [32].

2.4. MG Configuration and Modelling

2.4.1. MG Configuration

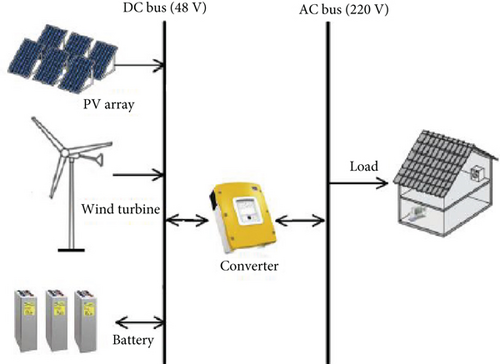
The MG uses PV and wind energy sources to provide power during regular operation and to operate it in grid-connected mode. A storage device is required to provide electric power to the load during lean times since solar radiation and wind speed are erratic and seasonally dependent. The whole MG setup for this study is illustrated in Figure 3.

2.4.2. Component-Wise Modelling

2.4.2.1. Modelling of Solar PV

PV cells can convert photons of light into electrical energy. PV cells are connected in parallel to increase the current and in series to increase the voltage. In this system, a PV cell is typically modelled for its forward-biased characteristics using a one-diode model, and its equivalent circuit diagram consisting of photo lights (I_ph), series (R_s), and shunt (R_sh) resistors is detailed in [33, 34]. The equation demonstrating the output current of a PV cell is determined using Equation (12).

()

2.4.2.2. Modelling of WTs

Fixed-speed and variable-speed WT generators (WTGs) are the two main types of WTGs utilized as DERs in MGs. A squirrel cage induction generator operating in the fixed speed category is the most basic type of WT [35]. Another important type is the permanent magnet synchronous generator (PMSG) [36]. Even though double-fed induction generators (DFIGs) are the most often utilized WTGs, their variable-speed operation is in sync with the grid frequency [37]. The multitude of events that are involved in induction/asynchronous generator modulating, such as the dynamics of the stator and rotor flux, core losses, magnetic saturation, and skin effect, contribute to the modulation’s extreme complexity.

The WT model presents the rotor power by calculating the mechanical torque determined by airflow on the blades. The wind passes over the blades of the WT. The kinetic energy generated by dynamic-wind entry and the mechanical energy were mathematically developed in [38]. The total mechanical power extracted from a WT is computed using Equation (13) [39].

()

where

()

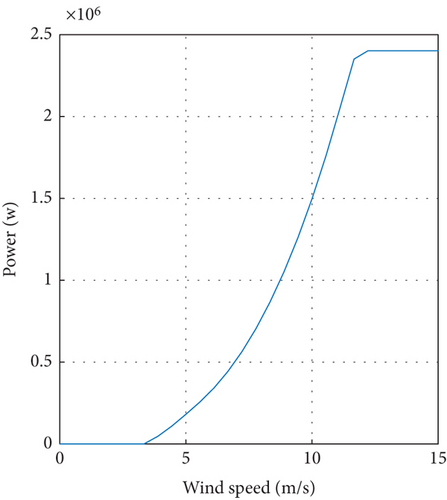
C_p is a power coefficient, which varies with the tip speed ratio of the WT (λ), pitch angle (β), and air density (ρ = 1.225 kg/m³). Based on the equations driven above, the MATLAB-simulated characteristics of a WT are given in Figure 4. Figure 4(a) shows the characteristics of a WT as a function of lambda and power coefficient, and Figure 4(b) illustrates the wind speed and extracted mechanical power relationships. From Figure 4, the extracted mechanical power depends on wind speed. When the wind speed is 10 m/s, the output power reaches 1.5 MW, while 2 MW is generated at the wind speed of 12 m/s.

2.5. VSI

A variety of voltage and power stability indices, including the VSI, power stability index (PSI), and LSF, are available in the literature and can be used to identify the power system security level. VSI, as described in [24], can be used in this investigation to identify the voltage-collapsed nodes. Equation (12) has been used to determine the VSI at each node.

A low VSI bus value increases the likelihood of locating MG. The VSI value needs to be maximized to stop the voltage collapse in the RDS.

()

By using the PSO algorithm, the optimal size of the MG at RDS buses is estimated.

2.6. LSF

The LSF technique is an analytical method for figuring out where D-STATCOM should be placed in a power system network. LSF is one technique for making an optimization algorithm’s work easier; as a result, it is calculated to minimize the search space for solutions [40]. Equation (13) [25] can be utilized to obtain the LSF equation concerning reactive power.

()

LSFs are determined at each bus based on Equation (13), and the buses are ordered in descending order. Higher bus LSF values increase the likelihood of placing D-STATCOM. The PSO algorithm is used to estimate the D-STATCOM size of candidate buses.

2.7. Real Power Loss Equation

By considering MG and D-STATCOM in the RDS, the power losses with the following constraints can be computed as follows [41]. The total real power loss in the system without MG penetration is expressed using Equation (14).

()

The power losses are reduced by penetrating the MG system in the distribution system. The ratio of total power losses with a MG to total power losses without a MG is the power loss index (PLoss_MG) which is expressed using Equation (15).

()

2.8. VD

A trivial variation in the voltage disturbs the whole system and possibly results in a block-out condition. From the calculations, it can be observed that the minimum value of VD indicates a good improvement in the voltage profile of the RDS.

()

where N is the total number of buses, V_t is the voltage magnitude at bus t, and V_ref is the reference voltage (i.e., 1.0 p.u.). Therefore, sizing and connecting MG and D-STATCOM for voltage profile improvement and power loss reduction using PSO optimization then requires minimizing the objective functions under different constraints.

2.9. Objective Function

Minimizing the total real power losses in the system while meeting equality and inequality constraints is the objective of the optimal placement and sizing of MG and D-STATCOM in RDS using Equation (17) [42].

()

where β₁ and β₂ are the weighting factors related to power loss and VD minimization, respectively. The weighting factors are intended to give each impact index for the MG or D-STATCOM connection. The appropriate priority for each impact index is selected based on the required analysis, such as planning and operation [26, 27]. The selection of the weighting criteria also took into consideration the expertise of the researchers and the problems associated with distribution-side utilities for effective performance. The coordinated placement of MG and D-STATCOM in the RDS has a substantial impact on the reduction of power loss and enhancement of the voltage profile. Power loss reduction is currently one of the most important priorities at the RDS level since it has a greater influence on utilities’ profits than voltage profile improvement. Because of this, the authors’ weighting factors for the voltage profile of power loss minimization in this work are 0.3 and 0.2, respectively.

2.9.1. Power Balance Constraint

()

where P_Loss is the real power losses from the bus k to bus k + 1, P_D(t) is the real power demand, P_MG(t) is the real power MG system, P_MGk is the real generation power of MG, and P_D-STATCOM is the D-STATCOM generated power.

2.9.2. Voltage Limit Constraint

()

where V_k,min and V_k,max are the minimum and maximum permissible bus voltage at bus K.

2.9.3. Real Power Limits of Generation

()

where P_k,min and P_Dk,max are the minimum and maximum power limits of the compensated bus.

2.9.4. Reactive Power Limits of Generation

()

where P_Dk,min and Q_DK,max are the minimum and maximum reactive power limits compensated by bus k, respectively.

2.9.5. Reactive Power Compensation Constraint

()

2.10. PSO

The PSO algorithm keeps a population of particles, where each particle characterizes a potential solution to an optimization problem. Each possible solution in PSO is allied with a randomized velocity, and the potential solutions, termed particles, are then flowing through the problem space [43]. Each particle keeps track of its coordinates in the tricky space, which is associated with the best fitness. This individual best value is termed P_best. Each particle has its own memory, which updates the velocity and position in searching for particles and individual bests iteratively based on Equations ((23)) and ((24)) [44].

()

The inertia weight (w) that facilitates the global and local parameters is given in Equation (25).

()

where w_min and w_max are the minimum and maximum weights, commonly 0.4 and 0.9; k and k_max are the current and maximum iteration; Xi is the position of each particle; P_best (i) is the best position of each particle; G_best (i) is the global best of all particles, usually less than unity; V_i is the velocity of particle; c₁ and c₂ are the acceleration constant, commonly ranges between 1 and 2; and the rand is random variable ranging from 0 to1.

2.11. Step by Step Algorithm

The optimal placement and sizing of MG and D-STATCOM in an RDS using PSO for reduction of power losses along with voltage profile improvement takes the following steps.

Step1: Get the input data (i.e., bus data, line data, real, and reactive powers).

Step 2: Compute total power losses and bus voltage using distribution load flow based on the DLF method.

Step 3: Set the bus count C = 2.

Step 4: Set the generation count j = 0.

Step 5: Generate an initial population randomly with random positions and velocities.

Step 6: Calculate the total power loss for each particle using Equation (26).

()

Step 7: Check the bus voltage whether it lies within the limits or not. If the bus voltage does not lie on the limit, then the particle is infeasible.

Step 8: Compare the objective value with the individual P_best value of the particle.

Step 9: Choose the particle associated with the lowest individual P_best of the entire particles and set the value of P_best as the present overall best “G_best.”

Step 10: Update the position and velocity of the particle using Equations (23) and (24).

Step 11: Go to Step 12 if the generation number reaches the maximum limit or set the generation index to j = j + 1, and go back to Step 5 if the generation number has not reached the maximum limit.

Step 12: If the bus counts the maximum limit, go to Step 13, otherwise set the bus count to C = C + 1 and go back to Step 4.

Step 13: Print out the optimal solutions.

3. Result and Discussion

The simulation results include a comparison with the base case and integration of MG and D-STATCOM in the IEEE test system. Each scenario taken into consideration for this study is presented below.

i.
Scenario 1: Base caseload flow results.
ii.
Scenario 2: Base case with MG and D-STATCOM.

In this test system, the distribution system is connected to a 12.66 KV voltage at the secondary side of the transformer. The active and reactive power loaded in the system are 3.75 MW and 2.33 MVAR, respectively. The bus and line data for the IEEE 30 bus system have been taken in [45].

3.1. Scenario 1: Base Case Power Flow Results in RDS

The base-case power flow analysis is performed using the DLF analysis algorithm without integrating MG and D-STATCOM in the distribution network. The voltage profile results of all buses, as well as active and reactive losses in the distribution system, are computed and presented in Table 1.

Table 1. Voltage profile and power losses of all buses at base case.

Bus number	Voltage profile (p.u.)	Active power losses in (p.u.)	Reactive power losses in (p.u.)
1	1	1	0.65571
2	0.9974	0.652	0.4896
3	0.9852	0.361	0.266
4	0.9791	0.2807	0.17678
5	0.9731	0.1507	0.1248
6	0.9683	0.232	0.15771
7	0.9583	0.2275	0.1269
8	0.9500	0.212	0.1253
9	0.9438	0.2042	0.0749
10	0.9382	0.2009	0.1209
11	0.9373	0.20071	0.1056
12	0.9359	0.14205	0.0849
13	0.9298	0.13741	0.06494
14	0.9276	0.1219	0.0538
15	0.9262	0.1004	0.03241
16	0.9248	0.1028	0.03829
17	0.9228	0.066	0.0142
18	0.9222	0.0529	0.0265
19	0.9969	0.0497	0.00818
20	0.9933	0.0288	0.01783
21	0.9926	0.02765	0.0197
22	0.9919	0.2112	0.11894
23	0.9816	0.2011	0.10774
24	0.9749	0.013947	0.01526
25	0.9716	0.1325	0.1125
26	0.9571	0.2159	0.21685
27	0.9556	0.2553	0.2115
28	0.9486	0.2549	0.2115
29	0.9438	0.2591	0.21327
30	0.9436	0.2231	0.2109

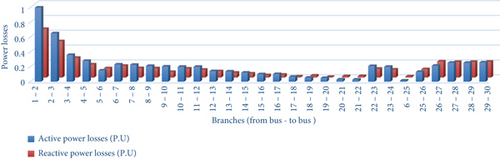
As it can be noted in the table, the voltage profile of buses from Bus 9 to Bus 18 and from Bus 28 to Bus 30 is below the standard voltage limits (0.95–1.05 p.u.), and this infers that the far-end customers frequently suffer from under-voltage problems. The base-case active and reactive power losses of the system are also calculated and presented in Figure 5. In general, the power losses are significant in magnitude, as shown in Table 1 and Figure 5. Also, the voltage profile of the system is tremendously poor, which in turn marks the performance of the distribution system very weak.

3.2. Scenario 2: Optimal MG and D-STATCOM Integration

The IEEE 30 bus test system is used in this study to verify the applicability of the suggested optimal allocation technique. In the base-case simulation, the optimal real and reactive power losses are 0.209814 MW and 0.12464 MVAr, respectively, as shown in Table 2. The minimum voltage is 0.9222 p.u. in Bus Number 18, and the VSI in this bus is 0.7864 p.u.

Table 2. Obtained results for IEEE 30 bus RDs.

	Case 1	Case 2
Optimal size and location of MG	—	3.2 MW at Bus 18
Optimal size and location of D-STATCOM	—	1.5 MW at Bus 17
V_in (p.u.)	0.9222	0.9680
VSI_min (p.u.)	0.7864	0.9108
Optimum real power loss (MW)	0.209814	0.063532
Optimum reactive power loss (MVAR)	0.12464	0.052341
Real power loss reduction (%)	—	69.72
Reactive power loss reduction (%)	—	58

In Scenario 2, MG and D-STATCOM are sized and integrated at optimal places in the distribution network using LSF and VSI-based PSO algorithms. Hence, the simulation is conducted, and the results are presented in Table 2. 3.2 MW MG and 1.5 MVAr D-STATCOM are placed at Bus 18 and Bus 17, respectively. The optimal active power loss of the system is 0.063532 MW. In this scenario, the minimum voltage is 0.9680 p.u., which has been improved compared to the base-case value (0.9222 p.u.). Similarly, the minimum VSI is 0.9108 p.u., which is also improved as compared to the base-case value (0.7864 p.u.). Figure 6 shows the comparison of voltage profiles before and after MG and D-STATCOM integrations using PSO.

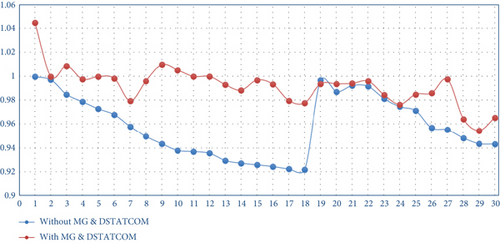
As shown in Table 2, the voltage profile of the system is boosted while the real power losses are decreased after the integration of MG and D-STATCOM. It is also observed that all bus voltages are within the IEEE standard acceptable limit (0.95–1.05 per unit). Figure 7 shows the comparison of voltage profiles before and after MG and D-STATCOM integrations. Before the integration of the MG and D-STATCOM, the lowest voltage was 0.9222 p.u. at Bus 18 which is below the acceptable limit, whereas all the voltage profiles at each bus were above the limit bus voltage standards after integration of the MG and DSATCOM.

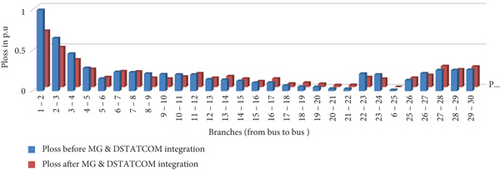
Figure 7 presents the real power loss comparison before and after the placement of the MG and D-STATCOM at their respective optimal locations. It can be inferred that the real power losses before and after the placement of the MG and D-STATCOM are different. The change in real power loss is mainly due to the placement of the MG and D-STATCOM which increased real power and decreased reactive power, respectively.

4. Conclusion

This paper presents the best size and optimal placement of MG and D-STATCOM using the PSO technique to boost the voltage profile and reduce the real power losses. The LSF method is utilized to find a suitable location for D-STATCOM, and the VSI is utilized to determine the suitable location for MG. The PSO algorithm is mainly employed to find the optimal sizing of MG and D-STATCOM in RDSs. A constrained nonlinear problem was applied to the IEEE 30 bus RDS to authenticate its validity. Finally, the results proved that both the MG and D-STATCOM sizes, as well as placement using the PSO algorithm, have a critical inspiration in reducing real power losses and boosting the voltage profile of the network.

Conflicts of Interest

The author declares no conflicts of interest.

Funding

The author received no specific funding for this work.

Open Research

Data Availability Statement

The data used to provision the findings of this work are accessible from the corresponding author upon request.

References

1 Moghbel M., Member S., Masoum M. A. S., Member S., and Deilami S., Optimal placement and sizing of multiple STATCOM in distribution system to improve voltage profile, 2016 Australasian Universities Power Engineering Conference (AUPEC), 2016, Brisbane, QLD, Australia, https://doi.org/10.1109/AUPEC.2016.7749327.
10.1109/AUPEC.2016.7749327
Google Scholar
2 Note R., Microgrids – a review of modeling, control, protection, simulation and future potential, 2012 IEEE Power and Energy Society General Meeting. (2012) 9, no. 12, 1–4.
Google Scholar
3 Luo L., Gu W., Zhang X. P., Cao G., Wang W., Zhu G., You D., and Wu Z., Optimal siting and sizing of distributed generation in distribution systems with PV solar farm utilized as STATCOM (PV-STATCOM), Applied Energy. (2017) 210, 1092–1100, https://doi.org/10.1016/j.apenergy.2017.08.165, 2-s2.0-85028306883.
10.1016/j.apenergy.2017.08.165
Web of Science® Google Scholar
4 Khasanov M., Kamel S., Xie K., Zhou P., and Li B., Allocation of distributed generation in radial distribution networks using an efficient hybrid optimization algorithm, IEEE PES Innovative Smart Grid Technologies, Europe. (2019) 15, 1300–1305.
Google Scholar
5 Rukmani D. K., Thangaraj Y., and Subramaniam U., A new approach to optimal location and sizing of DSTATCOM in radial distribution networks using Bio-Inspired Cuckoo Search Algorithm, Energies. (2020) 13, no. 18, https://doi.org/10.3390/en13184615.
10.3390/en13184615
Web of Science® Google Scholar
6 Saw B. K., Bohre A. K., Jobanputra J. H., and Kolhe M. L., Solar-DG and DSTATCOM Concurrent Planning in Reconfigured distribution system using APSO and GWO-PSO based on novel objective function, Energies. (2023) 16, no. 1, https://doi.org/10.3390/en16010263.
10.3390/en16010263
PubMed Web of Science® Google Scholar
7 Yeshaneh G. and Yeshaneh G., Rapid power restoration and network reconfiguration for power distribution system reliability enhancement : a case study on Bahir Dar power distribution systems, International Journal for Modern Trends in Science and Technology. (2023) 12, no. 2, 916–928, https://doi.org/10.62226/ijarst20230247.
10.62226/ijarst20230247
Google Scholar
8 Lakshmi M., Kurapati P., and Jain A., Optimal reconfiguration of radial distribution system having photovoltaic distributed generation with controlled voltage, 2015 International Conference on Circuits, Power and Computing Technologies. (2015) 20, https://doi.org/10.1109/ICCPCT.2015.7159518, 2-s2.0-84945981187.
10.1109/ICCPCT.2015.7159518
Google Scholar
9 Hosseinzadeh N., Aziz A., Mahmud A., Gargoom A., and Rabbani M., Voltage stability of power systems with renewable-energy inverter-based generators: a review, Electronics. (2021) 10, no. 2, 115–127, https://doi.org/10.3390/electronics10020115.
10.3390/electronics10020115
Web of Science® Google Scholar
10 Kazemtabrizi B. and Acha E., An advanced STATCOM model for optimal power flows using Newton’s method, IEEE Transactions on Power Apparatus and Systems. (2014) 29, no. 2, 514–525, https://doi.org/10.1109/TPWRS.2013.2287914, 2-s2.0-84897599790.
10.1109/TPWRS.2013.2287914
Web of Science® Google Scholar
11 Systems C. and Methods C., Review on the microgrid concept, structures, components, communication systems, and control methods, Energies. (2023) 16, https://doi.org/10.3390/en16010484.
10.3390/en16010484
PubMed Web of Science® Google Scholar
12 Placement O., Networks using MLPSO algorithm, Energies. (2020) 13, https://doi.org/10.3390/en13236185.
10.3390/en13236185
Web of Science® Google Scholar
13 Ullah W., Tareen K., Aamir M., Id S. M., and Nakaoka M., Mitigation of power quality issues due to high grid systems using three-phase APF/STATCOM technologies: a review, Energies. (2018) 12, no. 218, https://doi.org/10.3390/en11061491, 2-s2.0-85049635299.
10.3390/en11061491
Google Scholar
14 Yuvaraj T. and Ravi K., Multi-objective simultaneous DG and DSTATCOM allocation in radial distribution networks using cuckoo searching algorithm, Alexandria Engineering Journal. (2018) 57, no. 4, 2729–2742, https://doi.org/10.1016/j.aej.2018.01.001, 2-s2.0-85057056436.
10.1016/j.aej.2018.01.001
Web of Science® Google Scholar
15 Yenealem M. G., Ngoo L. M. H., Shiferaw D., and Hinga P., Management of voltage profile and power loss minimization in a grid-connected microgrid system using fuzzy-based STATCOM controller, Journal of Electrical and Computer Engineering. (2020) 2020, 13, https://doi.org/10.1155/2020/2040139, 2040139.
10.1155/2020/2040139
Web of Science® Google Scholar
16 Molderink A., Bakker V., Bosman M. G. C., Hurink J. L., and Smit G. J. M., Management and control of domestic smart grid technology, IEEE Transactions on Energy Conversion. (2010) 1, no. 2, 109–119, https://doi.org/10.1109/TSG.2010.2055904, 2-s2.0-77956060622.
10.1109/TSG.2010.2055904
Google Scholar
17 Adetunji K. E. and Hofsajer I., Allocation and sizing in power system networks using swarm-based algorithms arXiv : 2002. 08089v1 [cs. NE] 19 Feb 2020, Proceedings of International Joint Conference on Neural Networks. (2020) 20, 1–20.
Google Scholar
18 Zanib N., Batool M., Riaz S., Afzal F., Munawar S., Daqqa I., and Saleem N., Analysis and power quality improvement in hybrid distributed generation system with utilization of unified power quality conditioner, Communication. (2022) 19, https://doi.org/10.32604/cmes.2022.021676.
10.32604/cmes.2022.021676
Google Scholar
19 Parisio A., Rikos E., Glielmo L., and Member S., A model predictive control approach to microgrid operation optimization, IEEE Transactions on Control Systems Technology. (2014) 22, no. 5, 1813–1827, https://doi.org/10.1109/TCST.2013.2295737, 2-s2.0-84905244928.
10.1109/TCST.2013.2295737
Web of Science® Google Scholar
20 Hernández-hernández C., Rodríguez F., Moreno J. C., Renato P., and Normey-Rico J. E., The use of model predictive control (MPC) in the optimal distribution of electrical energy in a microgrid located in southeastern of Spain: a case study simulation keywords, International Energy Journal. (2017) 1, no. 15, https://doi.org/10.24084/repqj15.278, 2-s2.0-85072230966.
10.24084/repqj15.278
Google Scholar
21 Milano F., Frequency control of distributed energy resources in distribution networks, IFAC-PapersOnLine. (2018) 51, no. 28, 37–42, https://doi.org/10.1016/j.ifacol.2018.11.674, 2-s2.0-85058217147.
10.1016/j.ifacol.2018.11.674
Google Scholar
22 Asghar F., Talha M., and Kim S. H., Fuzzy logic-based intelligent frequency and voltage stability control system for standalone microgrid, ResearchGate. (2018) 28, no. 4, https://doi.org/10.1002/etep.2510, 2-s2.0-85038845286.
10.1002/etep.2510
Google Scholar
23 Das S. R., Mishra D. P., Ray P. K., and Salkuti S. R., Power quality improvement using fuzzy logic-based compensation in a hybrid power system, International Journal of Power Electronics and Drive Systems. (2021) 12, no. 1, 576–584, https://doi.org/10.11591/ijpeds.v12.i1.pp576-584.
10.11591/ijpeds.v12.i1.pp576-584
Google Scholar
24 Luo A., Tang C., Shuai Z., Tang J., Xu X. Y., and Chen D., Fuzzy-PI-based direct-output-voltage control strategy for the STATCOM used in utility distribution systems, IEEE Transactions on Industrial Electronics. (2009) 56, no. 7, 2401–2411, https://doi.org/10.1109/TIE.2009.2021172, 2-s2.0-67651154681.
10.1109/TIE.2009.2021172
Web of Science® Google Scholar
25 Alhattab A. S., Alsammak A. N., and Mohammed H. A., A review on D-STATCOM for power quality enhancement, Al-Rafidain Engineering Journal. (2023) 28, no. 1, 207–218, https://doi.org/10.33899/rengj.2022.136635.1210.
10.33899/rengj.2022.136635.1210
Google Scholar
26 Mohagheghi S. and Harley R. G., Modified Takagi-Sugeno fuzzy logic based controllers for a static compensator in a multimachine power system, IEEE. (2018) 12, no. 3, 2637–2642.
Google Scholar
27 Yuvaraj T., Ravi K., and Devabalaji K. R., Electrical engineering D-STATCOM allocation in distribution networks considering load variations using bat algorithm, Ain Shams Engineering Journal. (2015) 20, no. 2015, 1–13.
Google Scholar
28 Gupta A. R. and Kumar A., Optimal placement of D-STATCOM using sensitivity approaches in mesh distribution system with time variant load models under load growth, Ain Shams Engineering Journal. (2016) 30, https://doi.org/10.1016/j.asej.2016.05.009, 2-s2.0-85006356196.
10.1016/j.asej.2016.05.009
Google Scholar
29 Eswari J. and Jeyadevi S., An evolutionary approach for optimal citing and sizing of micro-grid in radial distribution systems, International Journal of Engineering Trends and Technology. (2014) 11, no. 9, 429–433, https://doi.org/10.14445/22315381/IJETT-V11P286.
10.14445/22315381/IJETT-V11P286
Google Scholar
30 Salkuti S. R., Optimal location and sizing of DG and D-STATCOM in distribution networks, Indonesian Journal of Electrical Engineering and Computer Science. (2019) 16, no. 3, 1107–1114.
10.11591/ijeecs.v16.i3.pp1107-1114
Google Scholar
31 Jain M. L. P. K. A. and Kr J., Electrical & electronic systems particle swarm optimization application for optimal location of multiple distributed generators in power distribution network, Electronic Systems. (2017) 6, no. 4, 4–7.
Google Scholar
32 Iqbal F., Khan M. T., and Siddiqui A. S., Optimal placement of DG and DSTATCOM for loss reduction and voltage profile improvement, Alexandria Engineering Journal. (2018) 57, no. 2, 755–765, https://doi.org/10.1016/j.aej.2017.03.002, 2-s2.0-85016032807.
10.1016/j.aej.2017.03.002
Web of Science® Google Scholar
33 Sen S. and Kumar V., Microgrid modelling: a comprehensive survey, Annual Reviews in Control. (2018) 46, no. xxxx, 216–250, https://doi.org/10.1016/j.arcontrol.2018.10.010, 2-s2.0-85055530317.
10.1016/j.arcontrol.2018.10.010
Web of Science® Google Scholar
34 Apateka S. and Mallareddy C., Mathematical modeling of photovoltaic cell, International Journal of Science and Research. (2013) 4, no. 4, 2950–2953.
Google Scholar
35 Ekanayake U. N. and Navaratne U. S., A survey on microgrid control techniques in islanded mode, Journal of Electrical and Computer Engineering. (2020) 2020, no. 1, 6275460, https://doi.org/10.1155/2020/6275460.
10.1155/2020/6275460
Web of Science® Google Scholar
36 Fernández L. M., Saenz J. R., and Jurado F., Dynamic models of wind farms with fixed speed wind turbines, Renewable Energy. (2006) 31, no. 8, 1203–1230, https://doi.org/10.1016/j.renene.2005.06.011, 2-s2.0-32044467173.
10.1016/j.renene.2005.06.011
Web of Science® Google Scholar
37 Alzahrani A., Ferdowsi M., Shamsi P., and Dagli C. H., Modeling and simulation of microgrid, Procedia Computer Science. (2017) 114, 392–400, https://doi.org/10.1016/j.procs.2017.09.053, 2-s2.0-85040016323.
10.1016/j.procs.2017.09.053
Google Scholar
38 Al-Quraan A., Al-Masri H., Al-Mahmodi M., and Radaideh A., Power curve modelling of wind turbines- a comparison study, IET Renewable Power Generation. (2022) 16, no. 2, 362–374, https://doi.org/10.1049/rpg2.12329.
10.1049/rpg2.12329
Web of Science® Google Scholar
39 Gonzalo A., Lopez J., Rodriguez M. A., Marroyo L., and Lwanski G., Doubly Fed Induction Machine, 2011, 1st edition, John Wiley & Sons, Inc, New Jersey, Canada, https://doi.org/10.1002/9781118104965, 2-s2.0-84874750199.
Google Scholar
40 Abebe A., Pushparaghavan A., and Gedefaye E., A study on optimal design feasibility of microgrid power system for rural electrification: Amhara region in Ethiopia, Asian Journal of Electrical Sciences. (2019) 8, no. 3, 26–30, https://doi.org/10.51983/ajes-2019.8.3.2064.
10.51983/ajes-2019.8.3.2064
Google Scholar
41 Singh S., Optimization technique optimal allocation of, International Journal for Modern Trends in Science and Technology. (2021) 4, no. 5, 14–19.
Google Scholar
42 Salmani M., Pasupuleti J., and Ramachandaramurthy V. K., Optimal placement and sizing of multiple DG in microgrid systems, International Journal of Recent Technology and Engineering. (2019) 3878, no. 4, 6230–6235, https://doi.org/10.35940/ijrte.D5145.118419.
10.35940/ijrte.D5145.118419
Google Scholar
43 Nageswari D., Kalaiarasi N., and Geethamahalakshmi G., Optimal placement and sizing of distributed generation using metaheuristic algorithm, Computer Systems Science and Engineering. (2022) 14, no. 2022, https://doi.org/10.32604/csse.2022.020539.
10.32604/csse.2022.020539
Google Scholar
44 Al-tameemi Z. H., Neda O. M., Jumaa F. A., and Dalya H., Optimal sizing and location of DG units for enhancing voltage profile and minimizing real power losses in the radial power systems based on PSO technique, IOP Conference Series: Materials Science and Engineering. (2019) 518, no. 4, https://doi.org/10.1088/1757-899X/518/4/042021, 2-s2.0-85067897327.
10.1088/1757-899X/518/4/042021
Google Scholar
45 Yuvaraj T., Ravi K., and Devabalaji K. R., D-STATCOM allocation in the radial distribution networks with different stability indices u sing bat algorithm, Gazi University Journal of Science. (2017) 30, no. 4, 314–328.
Google Scholar

All articles

Optimum Allocation of Microgrid and D-STATCOM in Radial Distribution System for Voltage Profile Enhancement Using Particle Swarm Optimization

Abstract

1. Introduction