Twirling Operations to Produce Energy Eigenstates of a Hamiltonian by Classically Emulated Quantum Simulation
Abstract
We propose a simple procedure to produce energy eigenstates of a Hamiltonian with discrete eigenvalues. We use ancilla qubits and quantum entanglement to separate an energy eigenstate from the other energy eigenstates. We exhibit a few examples derived from the (1 + 1)-dimensional massless Schwinger model. Our procedure in principle will be applicable for a Hamiltonian with a finite-dimensional Hilbert space. Choosing an initial state properly, we can in principle produce any energy eigenstate of the Hamiltonian.
1. Introduction
In quantum physics and quantum chemistry, it is an important task to find energy eigenstates of a quantum system. For a large quantum system, however, it will be desperately difficult to find energy eigenstates by the exact diagonalization of the Hamiltonian. Since the publication of the universal type of quantum computer by IBM in 2016, quantum systems have been actively analyzed by quantum computers [1] and quantum simulators [2–4]. A ground state is especially important among the energy eigenstates and has been investigated actively. To prepare a ground state of a quantum system in quantum computer, there are two representative methods: the adiabatic quantum computation [5, 6] and the variational quantum eigensolver (VQE) [7, 8]. We can easily prepare an approximate ground state by the adiabatic quantum computation, but we need relatively long computation time. Moreover, the approximate ground state is a superposition of a true ground state and excited states with tiny but non-negligible amplitudes [2, 9, 10]. As for the VQE, we can find a ground state rather well with a few iterations. Recently, (1 + 1)-dimensional Schwinger model [11] has been studied with the IBM Eagle processor by VQE [12].
In this paper, we propose a procedure to produce the energy eigenstate of a Hamiltonian not only the ground state by the classically emulated quantum simulation. We can easily carry out the procedure only using the Hamiltonian and the ancilla qubits [13]. Concatenating ancilla qubits, we can in principle produce energy eigenstate precisely. We operate controlled Hamiltonian between the quantum system and the ancilla qubits. The entropy of quantum entanglement between the quantum system and the ancilla qubits increases, and a certain energy eigenstate and the other energy eigenstates are separated. In the previous paper [9, 10], we have started from an approximate ground state prepared by the adiabatic quantum computation. This time we start from a state that is properly selected. By choosing one initial state properly, we can produce one energy eigenstate. We do not use the adiabatic quantum computation. Therefore, the computation time is very short. We simulate a one-qubit system, a two-qubit system, and a three-qubit system based on the (1 + 1)-dimensional massless Schwinger mode [14].
2. One-Qubit System
The expectation values of Z are .
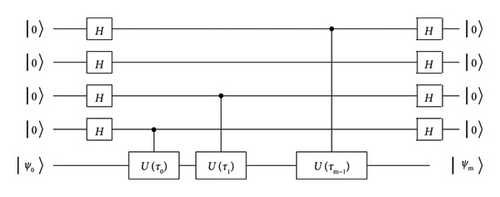
Using the Hamiltonian and ancilla qubits, we produce the two eigenstates by the classically emulated quantum simulation. First, we start from the initial state . Note that the state |0〉 does not mean a vacuum |vac〉 of the system. We apply the first twirling operation in Figure 1 on |ψ0〉; the quantum system time develops from |ψ0〉 to |ψ1〉 by the Hamiltonian controlled by the first ancilla qubit during a definite time period τ0. This time period τ0 is prescribed by τ0 = π/2E0, where . Next, we compute the expectation value . We apply the second twirling operation on |ψ1〉 controlled by the second ancilla qubits. This time the time period is τ1 = π/2E1. We repeat this process for adequate times. After some rounds of the twirling operations the total state is |Ψ〉 = |ψk〉|0〉|0〉 ⋯ |0〉 + |ϕk〉‖1〉〉, where ‖1〉〉 means that at least one of the ancilla qubits is in the state |1〉. We call the state |ψk〉|0〉|0〉 ⋯ |0〉 active state. In Table 1, we show our simulation result by IBM qiskit qasm simulator for J = 1. We have used the second-order Suzuki-Trotter formula [15, 16]. We see that each eigenstate is produced depending on the initial state |ψ0〉. In addition to the energy, we have measured Z which does not commute with the Hamiltonian and gives a character of goodness of the produced state.
| n = 0 | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | Theoretical | ||
|---|---|---|---|---|---|---|---|---|
| |ψ0〉 = |0〉 | 〈Z〉 | 1.0000000 | 0.7972744 | 0.7022552 | 0.7072281 | 0.7073355 | 0.7073265 | 0.707107 |
| 0.9999628 | 1.3596955 | 1.4143788 | 1.4145616 | 1.4145079 | 1.4144442 | 1.414214 | ||
| Active state | 107 | 7,813,952 | 7,656,759 | 7,655,162 | 7,656,563 | 7,657,168 | — | |
| |ψ0〉 = |1〉 | 〈Z〉 | 1.0000000 | −0.7968211 | −0.7020439 | −0.7069365 | −0.7067735 | −0.7072803 | −0.707107 |
| −1.0001038 | −1.3594381 | −1.4140652 | −1.4134110 | −1.4141577 | −1.4146414 | −1.414214 | ||
| Active state | 107 | 6,894,003 | 6,882,968 | 6,880,064 | 6,881,986 | 6,878,468 | — | |
- Note: The “active state” means the number of states that all the ancilla qubits are measured to be in the state |0〉. The number n = 0 means only measurements of Z and have been done without twirling operations. The numbers n = 1, 2, …, 5 indicate the number of times that we have acted the twirling operation. We have used n = 107 shots. We exhibit the results for the initial state |ψ0〉 = |0〉 and for the initial state |ψ0〉 = |1〉.
In the following, we explain why an energy eigenstate is produced. A quantum state |ψ〉 is expanded as |ψ〉 = α|ui〉 + Σj≠iβj|uj〉. If we know the energy ϵi, by applying the corresponding twirling operation controlled by the ancilla qubit, the total state is changed as , where θj is an angle derived from the energy difference ϵj − ϵi. By the Hadamard transformation on the ancilla qubit, we have the following total state . If we exclude the ancilla qubit in the state |1〉, the amplitude of the state |ui〉 is relatively amplified. Even when we only know an approximate value of ϵi, the above situation will hold under the condition that the angle θi is small.
3. Two-Qubit System
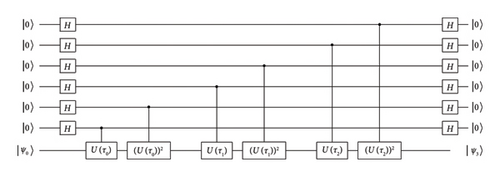
In the same way as the one-qubit case, using the Hamiltonian and ancilla qubits, we produce the four eigenstates by the classically emulated quantum simulation. The quantum circuit for the two-qubit system is shown in Figure 2. We use two ancilla qubits for one twirling operation. As the initial state of the simulation, we choose four states |0〉0|0〉1, |0〉0|0〉1, |1〉0|0〉1, and |1〉0|1〉1. In terms of the (1 + 1)-dimensional Schwinger model, the states |0〉0|1〉1 and |1〉0|0〉1 correspond to the state that neither electrons nor no positrons exist and the state that a pair of an electron and a positron bounded by the electric field is created, respectively. The states |0〉0|0〉1 and |1〉0|1〉1 correspond to the state in that one positron exists and the state that one electron exists, respectively. The latter two states undergo no changes under the charge preserving Hamiltonian. In Table 2, we show our simulation result for J = 1. We see that each eigenstate is produced depending on the initial state |ψ0〉. In addition to the energy, we have measured Z0 which does not commutes with the Hamiltonian .
| n = 0 | 1 | 2 | 3 | 4 | 5 | Theoretical | ||
|---|---|---|---|---|---|---|---|---|
| |0〉0|1〉1 | 〈Z0〉 | 1.0000000 | 0.6863952 | 0.7073591 | 0.7068051 | 0.7073355 | 0.7068394 | 0.707107 |
| 0.9997964 | 1.4084719 | 1.4146696 | 1.4143585 | 1.4139457 | 1.4146494 | 1.414214 | ||
| Active state | 107 | 6,891,253 | 6,876,931 | 6,877,308 | 6,879,307 | 6,878,882 | — | |
| |1〉0|0〉1 | 〈Z0〉 | 1.0000000 | −0.6863618 | −0.7070429 | −0.7069414 | −0.7069884 | −0.7073392 | −0.707107 |
| −0.999909 | −1.40843695 | −1.4142024 | −1.4138955 | −1.4143327 | −1.4151875 | −1.414214 | ||
| Active state | 107 | 6,893,632 | 6,880,351 | 6,881,961 | 6,878,923 | 6,875,563 | — | |
- Note: We have used n = 107 shots. We exhibit the results for the initial state |ψ0〉 = |0〉0|1〉1 and for the initial state |ψ0〉 = |1〉0|0〉0. The trivial cases |ψ0〉 = |0〉0|0〉1 and |ψ0〉 = |1〉0|1〉0 are omitted.
4. Three-Qubit System
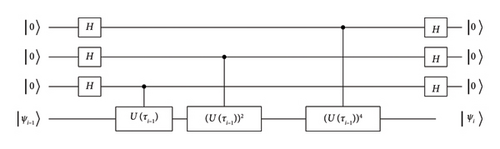
In the same way as in the two-qubit case, starting from an adequate initial state, we can produce a corresponding energy eigenstate. For a three-qubit Hamiltonian, we need three ancilla bits for one twirling operation (see Figure 3).
Starting from the initial state |0〉0|0〉1|1〉2, we can produce the state |E7〉. We show a simulation result in Table 3. The state |E7〉 is a superposition of the initial state |0〉0|0〉1|1〉2 and other states.
| |0〉0|0〉1|1〉2 | n = 0 | 1 | 2 | 3 | 4 | Theoretical |
|---|---|---|---|---|---|---|
| −0.33333 | −0.111,612 | −0.11114 | −0.11124 | −0.11109 | −0.11111 | |
| 2.00040 | 2.44939 | 2.45003 | 2.44933 | 2.44949 | 2.44895 | |
| Active states | 107 | 4,083,826 | 4,080,271 | 4,083,011 | 4,082,364 | — |
- Note: An example of average values of and the number of active states for each round of the twirling operation for J = 1 is shown. We have used n = 107 shots. The initial state is |ψ0〉 = |0〉0|0〉1|1〉2.
Starting from the initial state |0〉0|0〉1|0〉2, we can produce the state |E6〉. We show a simulation result in Table 4. Since |0〉0|0〉1|0〉2 is |E6〉 itself, we have a trivial result.
| |0〉0|0〉1|0〉2 | n = 0 | n = 1 | Theoretical |
|---|---|---|---|
| 0.33333 | 0.33333 | 0.33333 | |
| 2.00045 | 2.00037 | 2 | |
| Active states | 107 | 9,999,991 | — |
- Note: Under the twirling operation, no meaningful changes occur.
Starting from the initial state |0〉0|1〉1|1〉2, we intend to produce the state |E5〉. In this case, since the expectation value of the Hamiltonian is almost zero, we are in a delicate situation. We cannot use the time τ0 = π/2E0. We explore a suitable value of τ0 by experience. We show a simulation result in Table 5 that we have replaced the value of E0 by E = 0.5 artificially. We see that the state |E5〉 seems to be produced. Since the number of active state is very small, the expectation values of and correspondingly sift from the theoretical values.We show in Table 6 another simulation result for the initial state |0〉0|1〉1|1〉2. In this case, the ground state |E0〉 is produced, which will be attributed that the two states |E5〉 and |E0〉 are akin in the sense that the two states are linear combinations of |0〉0|1〉1|1〉2, |1〉0|0〉1|1〉2, and |1〉0|1〉1|0〉2.
| |0〉0|1〉1|1〉2 | n = 0 | 1 (E = 0.5) | 2 | 3 | 4 | Theoretical |
|---|---|---|---|---|---|---|
| 0.33333 | −0.17105 | 0.05702 | 0.0548 | 0.04729 | 0.05157 | |
| 0.00034 | 0.60887 | 0.72180 | 0.72684 | 0.72715 | 0.73205 | |
| Active states | 107 | 25,930 | 1,431,771 | 14,142 | 14,070 | — |
- Note: For the initial state, since the expectation value of the Hamiltonian is almost zero, in the first twirling operation, we set E = 0.5 by the hands.
| |0〉0|1〉1|1〉2 | n = 0 | 1 (E = 0.4) | 2 | 3 | 4 | Theoretical |
|---|---|---|---|---|---|---|
| 0.33333 | −0.25223 | −0.79754 | −0.72597 | −0.72016 | 0.05157 | |
| 0.00030 | −2.19846 | −2.71408 | −2.73546 | −2.72963 | 0.73205 | |
| Active states | 107 | 843,541 | 311,532 | 309,589 | 310,191 | — |
- Note: In the first twirling operation, we set E = 0.4 by the hands. In this case, the ground state |E0〉 seems to be produced. For the value E = 0.4, the state |E5〉 is not produced.
Next, we will treat the three zero energy states. For the nonzero energy states, we have adopted the twirling time period τ = π/2E and have used the relation e−iπ/2 = 1. If as in the case |E5〉, we cannot directly adopt the relation τ = π/2E. Note that, if , we have for any τ. Under this situation, to produce the zero energy states, we adopt the twirling time period τ = 2π/E for some artificial nonzero value E and use the simple relation e−2πi = 1 not the relation ie−iπ/2 = 1.
We produce the state |E4〉. We examine the initial state |0〉0|1〉1|0〉2. The expectation value of the Hamiltonian for this state is 0. In the following, we see that this value 0 is not violated by the twirling operations. We perform the twirling operations four times by setting the value of E as E = −0.2 or E = 0.2 at will. We show a result in Table 7. The value varies violently, and it seems that the state |E4〉 may not be produced by the four times twirling operations.
| |0〉0|1〉1|0〉2 | n = 0 | 1 (E = −0.2) | 2 (E = 0.2) | 3 (E = 0.2) | 4 (E = −0.2) | Theoretical |
|---|---|---|---|---|---|---|
| 1.00000 | 0.51226 | 0.86966 | 0.57704 | 0.56051 | 0.55556 | |
| 0.00014 | 0.00062 | −0.00015 | 0.00087 | 0.00020 | 0 | |
| Active state | 107 | 8,110,010 | 7,288,765 | 6,929,521 | 6,669,713 | — |
- Note: We cannot be convinced that the state |E4〉 is produced.
This time, we set E = −1, E = 2, E = −3, and E = 4 in the four twirling operations. We show a result in Table 8. We see that the state |E4〉 is produced almost exactly.
| |0〉0|1〉1|0〉2 | n = 0 | 1 (E = −1) | 2 (E = 2) | 3 (E = 3) | 4 (E = −4) | Theoretical |
|---|---|---|---|---|---|---|
| 1.00000 | 0.57776 | 0.56048 | 0.55591 | 0.55560 | 0.55556 | |
| 〈Z0〉 | 1.00000 | 0.68331 | 0.67084 | 0.66684 | 0.66678 | 0.66667 |
| 〈Z1〉 | −1.00000 | −0.36665 | −0.34071 | −0.33387 | −0.33394 | −0.33333 |
| 〈Z2〉 | 1.00000 | 0.68333 | 0.66988 | 0.66703 | 0.66615 | 0.66667 |
| 0.00007 | −0.00003 | 0.00135 | −0.00018 | 0.00052 | 0 | |
| Active state | 107 | 6,671,011 | 6,666,402 | 6,665,359 | 666,450 | — |
- Note: In addition to and , Z0, Z1, and Z2 are measured.
Starting from the initial state |1〉0|1〉1|0〉2, we produce the state |E3〉. Our simulation result is in Table 9. Since the expectation value of is almost zero for |1〉0|1〉1|0〉2, we simulate by setting E = −0.2 for the first twirling operation. We also take E = 0.2 for the third twirling operation and take E = −0.2 for the fourth twirling operation. We see that the state |E3〉 is produced with high accuracy.
| |1〉0|1〉1|0〉2 | n = 0 | 1 (E = −0.2) | 2 | 3 (E = 0.2) | 4 (E = −0.2) | Theoretical |
|---|---|---|---|---|---|---|
| 0.33333 | 0.29169 | 0.33292 | 0.33332 | 0.33333 | 0.33333 | |
| 〈Z0〉 | −1.00000 | 0.10780 | 0.02292 | −0.01136 | 0.00524 | 0 |
| 〈Z1〉 | −1.00000 | −0.93754 | −0.99938 | −0.99998 | −0.99999 | −1 |
| 〈Z2〉 | 1.00000 | −0.17026 | −0.02354 | 0.01134 | −0.00524 | 0 |
| 0.00003 | 0.06916 | 0.00008 | 0.00005 | 0.00001 | 0 | |
| Active state | 107 | 5,588,131 | 5,002,241 | 5,001,886 | 5,001,862 | — |
- Note: In the second twirling operation, the nonzero value E1 = 0.06916 has been used.
We start from |1〉0|1〉1|1〉2 which is |E2〉 itself. This time, the expectation value of the Hamiltonian is almost 0, and we cannot set the twirling time period as τ0 = 2π/E. Therefore, we perform the first twirling operation by setting E = −0.2, which is a suitable value other than 0. We show a simulation result in Table 10. We see that the state |1〉0|1〉1|1〉2 is almost not changed by the twirling operation and is a zero energy eigenstate of .
| |1〉0|1〉1|1〉2 | n = 0 | 1 (E = −0.2) | Theoretical |
|---|---|---|---|
| −0.33333 | −0.33333 | −0.33333 | |
| −0.00011 | −0.00016 | 0 | |
| Active states | 107 | 9,999,999 | — |
- Note: We have assumed the artificial value E = −0.2 in the first twirling operation.
Starting from the initial state |1〉0|0〉1|0〉2, we can produce the first exited state |E1〉. We show a simulation result in Table 11.
| |1〉0|0〉1|0〉2 | n = 0 | 1 | 2 | 3 | 4 | Theoretical |
|---|---|---|---|---|---|---|
| −0.33333 | −0.11613 | −0.11092 | −0.11123 | −0.11107 | −0.11117 | |
| −2.00046 | −2.44702 | −2.454,908 | −2.44884 | 2.44984 | −2.44949 | |
| Active states | 107 | 4,083,447 | 4,083,541 | 4,083,922 | 4,082,517 | — |
- Note: The time period τ = π/2E and the relation ie−i(π/2) = 1 are used.
Starting from the initial state |1〉0|0〉1|1〉2, we can produce the ground state |E0〉. We show a simulation result in Table 12.
| |1〉0|0〉1|1〉2 | n = 0 | 1 | 2 | 3 | 4 | Theoretical |
|---|---|---|---|---|---|---|
| −1.00000 | −0.520,733 | −0.70065 | −0.71411 | −0.71856 | −0.71823 | |
| −1.99963 | −2.63677 | −2.73484 | −2.73240 | −2.73279 | −2.73205 | |
| Active states | 107 | 874,150 | 834,283 | 834,484 | 835,523 | — |
- Note: The adiabatic quantum computation is not used to produce the ground state |E0〉.
To produce a ground state we can use the adiabatic quantum computation. We adopt the initial trivial Hamiltonian as , and we start from the initial ground state |1〉0|0〉1|1〉2. After the adiabatic quantum computation, we have almost ground state, which is a superposition of a ground state with excited states with small amplitudes. We show a simulation result in Table 13. After the three or four twirling operations, the results in Table 12 and in Table 13 are almost indistinguishable.
| |1〉0|0〉1|1〉2 | Adiabatic | n = 1 | 2 | 3 | 4 | Theoretical |
|---|---|---|---|---|---|---|
| −0.71256 | −0.71863 | −0.71817 | −0.71824 | −0.71859 | −0.71823 | |
| −2.73169 | −2.73227 | −2.73221 | −2.73246 | −2.73281 | −2.73205 | |
| Active states | 107 | 9,998,684 | 9,998,546 | 9,998,621 | 9,998,620 | — |
- Note: Before the twirling operations, we have used the adiabatic quantum computation.
5. N-Qubits Hamiltonian
6. Summary and Discussions
We have proposed a procedure to produce the energy eigenstate of a quantum Hamiltonian without algebraic calculation. We have performed classically emulated quantum simulation for the one-qubit system, the two-qubit system, and the three-qubit system based on the (1 + 1)-dimensional massless Schwinger model. Choosing an initial state properly, we have produced the corresponding energy eigenstate. We have concatenated the ancilla qubits to rectify one energy eigenstate. Our procedure is in principle applicable to a Hamiltonian represented by the Pauli matrices. Our procedure will work well for a Hamiltonian with discrete eigenvalues. An n-qubits Hamiltonian has 2n energy eigenstates. In our procedure, choosing 2n orthogonal initial states properly, the 2n energy eigenstates will be produced. Without using the adiabatic quantum computation, we can produce a ground state precisely by the twirling operation. Since we do not use the adiabatic quantum computation, each computation time is very short. As for the three-qubit case, the four states |E7〉, |E6〉, |E1〉, and |E0〉 are produced or certified straightforwardly in our procedure. The rest four states |E5〉, |E4〉, |E3〉, and |E2〉 are produced or certified by setting some artificial values of twirling period τ.
Conflicts of Interest
The author declares no conflicts of interest.
Funding
This study was funded by the National Institute of Technology, Gunma College.
Open Research
Data Availability Statement
The simulation data used to support the findings of this study are included within the article.