Volume 2024, Issue 1 3763892

Research Article

Open Access

Formula of Cylindrical Spring Stiffness for Nonlinear Large Deformation and Its FEM Verification

Zhi Huang,

Zhi Huang

Jiangxi Gandong Road and Bridge Construction Group Ltd. , 1288 Yingbin Avenue, Fuzhou , 344000 , China

Search for more papers by this author

Fengying Xiao,

Fengying Xiao

orcid.org/0009-0008-0940-0330

Department of Engineering , Mechanics , Nanchang University , 999 Xuefu Avenue, Nanchang , 330031 , China , ncu.edu.cn

Search for more papers by this author

Risheng Zhu,

Risheng Zhu

Project Management Office of Shanghai-Kunming Expressway , Liyuan to Dongxiang Section Reconstruction and Expansion , 13 Xingye Avenue, Shangrao , 334100 , China

Search for more papers by this author

Chunhua Rao,

Chunhua Rao

Department of Engineering , Mechanics , Nanchang University , 999 Xuefu Avenue, Nanchang , 330031 , China , ncu.edu.cn

Jiangxi Transportation Design and Research Institute Co.Ltd. , 575 Dongxin 1st Road, Nanchang , 330209 , China

Search for more papers by this author

Mojia Huang,

Corresponding Author

Mojia Huang

[email protected]

orcid.org/0009-0005-6812-7686

Department of Engineering , Mechanics , Nanchang University , 999 Xuefu Avenue, Nanchang , 330031 , China , ncu.edu.cn

Search for more papers by this author

Tengfei Zhao,

Tengfei Zhao

orcid.org/0000-0001-5030-3286

College of City Construction , Jiangxi Normal University , 99 Ziyang Avenue, Nanchang , 330022 , China , jxnu.edu.cn

Search for more papers by this author

Huajie Yin,

Corresponding Author

Huajie Yin

[email protected]

orcid.org/0009-0008-9286-1751

Jiangxi Province Traffic Construction Engineering Quality Supervision Administration , 218 Gaoxin Third Road, Nanchang , 330069 , China

Search for more papers by this author

Zhi Huang,

Zhi Huang

Jiangxi Gandong Road and Bridge Construction Group Ltd. , 1288 Yingbin Avenue, Fuzhou , 344000 , China

Search for more papers by this author

Fengying Xiao,

Fengying Xiao

orcid.org/0009-0008-0940-0330

Department of Engineering , Mechanics , Nanchang University , 999 Xuefu Avenue, Nanchang , 330031 , China , ncu.edu.cn

Search for more papers by this author

Risheng Zhu,

Risheng Zhu

Project Management Office of Shanghai-Kunming Expressway , Liyuan to Dongxiang Section Reconstruction and Expansion , 13 Xingye Avenue, Shangrao , 334100 , China

Search for more papers by this author

Chunhua Rao,

Chunhua Rao

Department of Engineering , Mechanics , Nanchang University , 999 Xuefu Avenue, Nanchang , 330031 , China , ncu.edu.cn

Jiangxi Transportation Design and Research Institute Co.Ltd. , 575 Dongxin 1st Road, Nanchang , 330209 , China

Search for more papers by this author

Mojia Huang,

Corresponding Author

Mojia Huang

[email protected]

orcid.org/0009-0005-6812-7686

Department of Engineering , Mechanics , Nanchang University , 999 Xuefu Avenue, Nanchang , 330031 , China , ncu.edu.cn

Search for more papers by this author

Tengfei Zhao,

Tengfei Zhao

orcid.org/0000-0001-5030-3286

College of City Construction , Jiangxi Normal University , 99 Ziyang Avenue, Nanchang , 330022 , China , jxnu.edu.cn

Search for more papers by this author

Huajie Yin,

Corresponding Author

Huajie Yin

[email protected]

orcid.org/0009-0008-9286-1751

Jiangxi Province Traffic Construction Engineering Quality Supervision Administration , 218 Gaoxin Third Road, Nanchang , 330069 , China

Search for more papers by this author

First published: 26 September 2024

https://doi.org/10.1155/2024/3763892

Academic Editor: Ivan Giorgio

Share a link

Email
Wechat
Bluesky

Abstract

Springs are fundamental components in mechanical systems, crucial for ensuring the safety and functionality of mechanisms. Timoshenko’s stiffness formula accounts for both bending and torsional energy effects, providing accurate results for small deformations. However, when the deformation becomes large, the spring stiffness becomes a nonlinear problem due to the changing inclination angle and radius during deformation. In this study, we derive a formula for the cylindrical spring stiffness under nonlinear large deformation by considering two assumptions: the invariability of the polar angle at any point and spring wire length during deformation. This formula incorporates the effects of inclination and radius changes on the spring wire. We analyze the stiffness of the cylindrical spring with different initial inclinations using the finite element method (FEM). FEM results were compared with those obtained from Timoshenko’s formula, Hiroyuki’s formula, and the derived formula. For small deformations, the FEM results matched well with all three formulas. However, for nonlinear large deformations, the calculated results from Timoshenko’s formula showed a discrepancy of up to 32.58% compared to the FEM results. The modified Hiroyuki formula also exhibited slightly poorer agreement with the FEM results than the formula proposed in this paper. On the other hand, our derived formula demonstrated excellent agreement with the FEM results for nonlinear large deformations. Therefore, our stiffness formula for cylindrical springs is recommended for mechanical engineering spring design applications involving nonlinear large deformations.

1. Introduction

Springs are often used in mechanical systems such as automotive engines and suspension systems [1, 2]. The stiffness, strength, and stability of springs play an important role in the safety of mechanism [3–5]. The springs are often classified as cylindrical spring, leaf spring, and torsion bar spring. However, because of the good performance of the cylindrical spring, the cylindrical spring is widely used in engineering [6, 7]. The spring stiffness of the cylindrical spring is one of the important parameters on the spring properties [8]. In engineering, people use the formula to compute the cylindrical spring stiffness [9], where G is the shear modulus of the spring, d is the diameter of the spring wire, n is the number of coils in the spring, and R₀ is the initial radius of the spring. The spring stiffness can be optimized by adjusting these parameters (d, n, R₀) [10]. The spring stiffness in this equation includes only the effect of torsional energy on the spring wire.

Timoshenko gave the stiffness formula of the cylindrical spring with the effect of the initial helix angle α₀ in Figure 1b [11]:

(1)

where the spring stiffness includes the effect of both the bending energy and the torsion energy on the spring wire; I_p and I_z are the polar moment and the moment of inertia on the spring wire’s section, respectively; and E is the elastic modulus of the spring material. Formula (1) is suitable for the calculation of the cylindrical spring stiffness for the small deformation. Formula (1) can be degenerated to K₀ if α₀ = 0. To consider the influence of the shear energy in the spring wire, Mohazzabi [12] modified K₀. While Ancker and Goodier [13] obtained the spring stiffness with the effect of helix angle and curvature on the spring wire. In [9, 11–13], there are the theoretical derivations of spring stiffness. But their formulas of the spring stiffness are only applicable in the case of small deformations.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) Initial height H₀ and initial radius R₀. (b) Length L₀, helix angle α₀, and horizontal projection 2πnR₀.

Nowadays, helical springs with nonlinear geometrical parameters show great advantages over classical linear springs, especially due to their superior performance in reducing the dynamic response at high speeds [14–16]. Nonlinear theories for helical springs are also increasing annually. Previously, Whal [17] gave a method for calculating the stiffness of cylindrical springs under large deformations, but his expression is not in closed form and is very complicated and not applicable to spring design in engineering. Ivchenko [18] and Andrey, Babak, and Pouyan [19] gave a detailed derivation of the equations for the elastic properties of coil springs in the case of large deflections, which culminated in a formula for the spring strain. Radaelli and Herder [20], Crescenzo and Salvini [21], and Baran, Michalczyk, and Warzecha [22] specifically analyzed the torsional, tangential, and transverse stiffnesses of helical springs under large deformations, respectively, in which the torsional and tangential stiffnesses are nonlinear, which provide important references for the derivation of the deflection equations at a later stage. Kato and Suzuki [23] established the material mechanics theory of nonlinear deflection of coil springs inside and outside the elastic limit and corrected on the basis of K₀ to obtain the following:

(2)

where α is the pitch angle of the spring after deformation. Formula (2) shows the comprehensive consideration of the torsion and bending deformation energy on the spring stiffness, but the expression is only applicable to the pulling condition; the compression state of the stiffness calculation results with Formula (2) is not consistent. Zhang, Qi, and Zhuo [24] and Qi, Cao, and Wang [25] used the Bernoulli beam theory to improve the expression of the spring stiffness. Qaiser and Johnson [26] and Zhuo et al. [27] analyzed the generalized helical springs based on virtual work and curved beam theory, showing that the computational efficiency can be improved by using using beam elements to analyze the stiffness characteristics of cylindrical springs.

Researchers often use SolidWorks [28, 29] or Pro/E to establish the model of the spring; import the model into Ansys [27, 30], Abaqus [31], or other finite element software; and calculate the stiffness and strength of the spring by these FEM programs. For the case of small deformation, the spring stiffness is almost invariable during deformation. But the large deformation of the spring belongs to the geometric nonlinear problems [23, 26, 27, 32–34]. Therefore, it is very meaningful to study the change of the cylindrical spring stiffness during the large deformation.

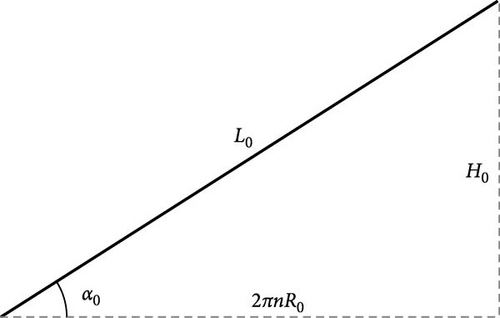
In this paper, the stiffness expression of the cylindrical spring with free rotation (one end fixed, one end free) is given. The structure of this paper is as follows: In Section 2, the two assumptions are given. The geometric parameters of the cylindrical spring are defined. The two assumptions are in good agreement with the FEM results. In Section 3, the nonlinear relation between the load and the spring deformation is established. The formula of the spring stiffness includes the nonlinear effect of spring deformation up to quadratic terms of the deformation h. The torsional and bending deformation energy of the spring wire is given during the deformation. The nonlinear formula of the spring stiffness is obtained by the energy method. To derive the formula of the spring stiffness, we consider the influence of the inclination change and the radius change. In Section 4, we compare the FEM results with those of Formulas (1) and (2) and our Formula (27). Our Formula (27) is reliable and useful to the design and calculation of the cylindrical spring in the case of the nonlinear large deformation.

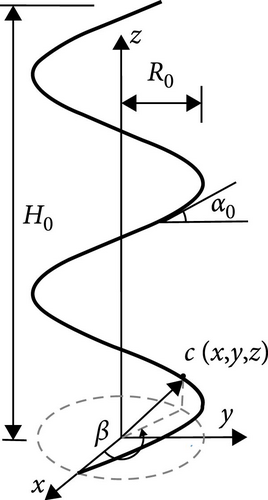
2. Geometrical Parameters and Their Description of Cylindrical Spring

2.1. Geometrical Description of Cylindrical Spring

The initial height of the cylindrical spring is H₀, the initial radius is R₀, and the number of coils is n. Choose a three-dimensional coordinate system as shown in Figure 1a, where the z-axis coincides with the central axis of the cylindrical spring. Any point c (x,y,z) at the sectional centroid of the spring wire is given by the following:

(3)

where β is the polar angle of the spring. The initial length of the spring wire is L₀, the horizontal projection value of the spring wire L₀ is 2πnR₀, and the helix angle of the cylindrical spring is α₀. The geometric parameters are defined in Figure 1a, b.

In Figure 1b, there are the relations

(4)

among the initial inclination κ₀, L₀, H₀, R₀ and n of the cylindrical spring.

2.2. Two Assumptions of Spring on Deformation

If the central axis of the spring coil always coincides with the z-axis in Figure 1 during the nonlinear large deformation of the spring, the two assumptions are proposed:

Assumption 1. Compared with the torsion and bending deformation energy, the axial deformation energy of the spring wire is very small. Hence, the length is almost invariable during the large deformation, i.e., L ≈ L₀.

Assumption 2. It is assumed that the spring is stable during the whole large deformation process and will not destabilize; the polar angle β of any point at the spring wire is invariable during the large deformation; therefore, the number n of the spring coils of at any time is always invariable.

The above two basic assumptions are consistent with empirical evidence and our FEM simulations.

When the spring is subjected to external force, the initial helix angle α₀ becomes to α. From Assumption 1 and Assumption 2 and Formula (4), we always have the following:

(5)

(6)

where h is the change of the spring height and Δκ is the change of the spring wire inclination. Equations (5) and (6) give the change relation between the spring radius R and the helix angle α.

3. Nonlinear Formula of Spring Stiffness for Large Deformation

3.1. Form of Nonlinear Relation Between Load and Deformation on Spring Stiffness

For the small deformation, the spring stiffness K, the deformation h, and the vertical load P of the cylindrical spring exist the relation P = Kh. However, because the spring radius R and the helix angle α are changing during the large deformation, the stiffness of the cylindrical spring is also changing. Formula (1) is no longer applicable to the computation of the cylindrical spring stiffness. Hence, for the large deformation problems of the cylindrical spring, the relation between the vertical load P and the spring deformation h is assumed to have the following form:

(7)

where K(h) is the form of the cylindrical spring stiffness. Only the third term (K₃h²) is taken into account in Formula (7) to derive a simple expression, enhancing the ease of designing and applying springs in mechanical engineering. By focusing on the third term, the resulting expression maintains a high level of accuracy that meets the precision standards necessary for engineering applications.

3.2. Torque and Bending Moment of Spring Wire Under Load P

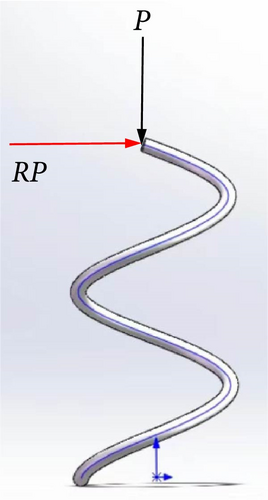
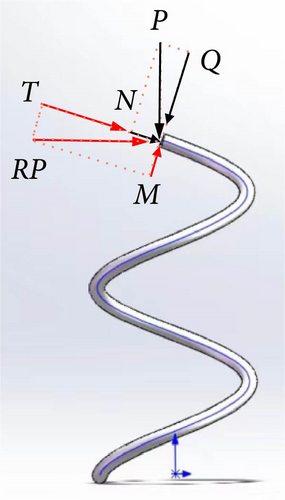
The vertical load P in Figure 2a can be equivalent to the moment RP and the force P acting on the spring wire as shown in Figure 2b. The moment RP in Figure 2b can be decomposed into the torque T and the bending moment M acting on the spring wire as shown in Figure 2c. The principal vector P can be decomposed into the shear force Q and the axial force N acting on the spring wire.

From Formula (5), the moment RP can be expressed as follows:

(8)

From Formulas (6) and (8), torque T and the bending moment M in Figure 2c are, respectively, as follows:

(9)

The torsion angle dϕ and the bending angle dθ of the spring wire end with respect to the other end are generated by the torque dT and the bending moment dM, respectively:

(10)

where dT and dM are obtained:

(11)

by Formula (9). Because P and κ are the function of h in Formulas (5)–(7), dκ and dP can be given via the following:

(12)

The torque deformation energy U_T and the bending deformation energy U_M of the cylindrical spring due to the deformation h of the spring from 0 to h₁ under load P are as follows:

(13)

(14)

from Formulas (9)–(12), where E = 2G(1 + ν). Substituting Formulas (6)–(12) into Formulas (13) and (14), we obtain the deformation energy U_T and U_M of the spring wire as follows:

(15)

(16)

in which

(17)

(18)

The work of the load P on the cylindrical spring due to deformation h from 0 to h₁ is as follows:

(19)

which should be equal to the deformation energy of U_T and U_M,

(20)

where we do not consider the effect of the axial and shear deformation energy on the spring wire because it is small compared to the torsion and bending deformation energy.

Putting Formulas (15)–(19) into Formula (20), we have the following three formulas:

(21)

(22)

(23)

for terms

and

because h₁ is arbitrary. The solutions of Equations (21)–(23) on K₁, K₂ and K₃ are as follows:

(24)

(25)

(26)

From Formulas (4) and (6), substituting Formulas (24)–(26) into Formula (7), we give the formulas of the spring stiffness for the nonlinear large deformation:

(27)

where η(κ₀, Δκ) is called the nonlinear factor of the spring stiffness:

(28)

(29)

The nonlinear factor η(κ₀, Δκ) in Formula (27) is the quadratic polynomial of Δκ. η₂ and η₃ are related to the initial inclination κ₀.

4. Discussion and FEM Simulations of Cylindrical Spring Stiffness for Nonlinear Large Deformation

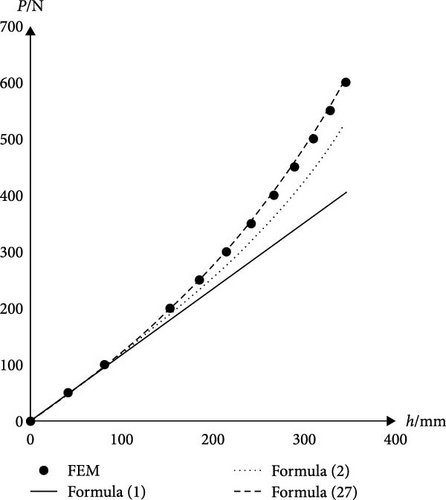
4.1. Nonlinear Stiffness Formula (27) and Its Reduced Result: Timoshenko Formula for the Small Deformation

For the small deformation problem, if O(|Δκ|) can be discarded, the nonlinear stiffness Formula (27) of the cylindrical spring can be reduced to the Timoshenko Formula (1) as follows:

(30)

where the relations

, and

in Formula (4) are employed; i.e., when η(κ₀, Δκ) = 1 + O(|Δκ|) for the small deformation, the nonlinear Formula (27) of the spring stiffness becomes the Timoshenko Formula (1).

4.2. Verification of Experimental Result: Verification of Assumption 1 and Assumption 2

Based on Assumption 1 and Assumption 2, the nonlinear Formula (27) of the spring stiffness is derived by the energy method. To verify the two basic assumptions, we establish the model of the cylindrical spring whose structure and material properties are given by the following:

(31)

4.2.1. Verification of Assumption 1

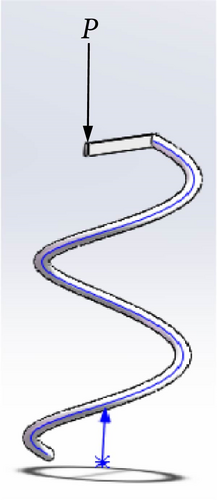
For this verification, we take H₀ = 250 mm cylindrical spring in Formula (31). Then the length L₀ of the spring wire is 533.447 mm from Formulas (4) and (31) and H₀ = 250 mm. The FEM model of the cylindrical spring is shown in Figure 3. We find the maximum axial force F_N = (P sinα)_max = 31.51 N in the calculation process of the FEM model for the nonlinear large deformation. The length of the spring wire is deformed to by the maximum axial force F_N, where is the cross-sectional area of spring wire. The deformation 0.023 mm of the spring length is small compared to the initial length L₀ = 533.447 mm. The feasibility of Assumption 1 is verified.

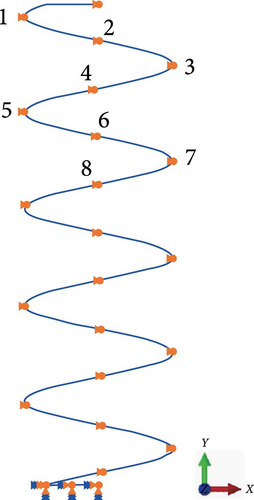
4.2.2. The FEM Verification of Assumption 2

Employing the spring data in Formula (31) with H₀ = 250 mm, we establish the FEA model by Abaqus software as shown in Figure 3.

In Figure 3, each end of the coil spring is connected to two wires of high stiffness. The lower wire is fully fixed, while one end of the upper wire is linked to the spring, and the other end applies load P while constraining the displacement of the point in both the x and y directions. This constraint ensures that the load remains centrally located throughout the loading process, thereby preventing eccentric instability. The FEM spring model is meshed by the three-node quadratic spatial beam element. The displacement of the spring is computed utilizing the geometric nonlinear iterative method. Within the FEM simulation, we monitor the changes in the polar angles of the eight specified points as depicted in Figure 3. The computational results indicate that the polar angles of these eight points remain constant throughout the nonlinear large deformation, thereby validating the second assumption’s accuracy.

4.3. Consistence of Computational Results Between Formula (27) and FEM Under Tensional Load

To show the consistence of computational results between Formula (27) and FEM, we establish the FEM model of the cylindrical spring whose structure and material properties are given in Formula (31). Take the initial heights of the spring which are H₀ = 20 mm, 50 mm, and 100 mm, respectively. The correspondence initial inclinations of them are

(32)

respectively. We calculate the spring stiffness K_FEM by the geometric nonlinear iterative method of FEM. Putting Formulas (31) and (32) into Formulas (1), (2), and (27), we can obtain the cylindrical spring stiffness K_Tim, K_Hi, and K. For the finite element calculations, we extracted the deformation cloud for each step of the cylindrical spring (κ₀ = 0.042) to organize it and obtain Figures 4 and 5. These figures show the large deformation process and the displacement–load curve of the cylindrical spring under tensional load. From Figure 5, our Formula (27) displacement–load curve agrees well with the finite element results. However, Formula (1) displacement–load relationship only agrees with the finite element results for small deformations. Although Formula (2) results are better than Formula (1) after modifications, our Formula (27) consistently outperforms Formula (2) as the cylindrical spring deformation increases.

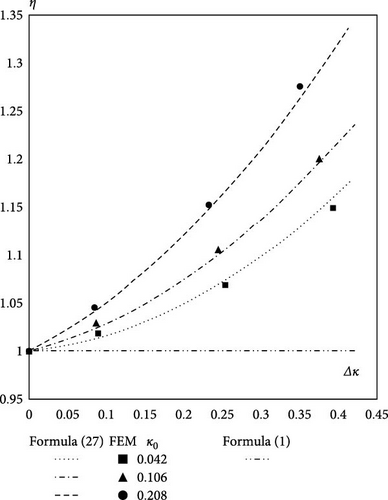
Similar to the results in Figure 5 and Table 1 for κ₀ = 0.042, we also compute the stiffness results (K_FEMK_TimK_HiK) of the cylindrical spring based on the FEM, the Timoshenko Formula (1), and our Formula (27) for κ₀ = 0.106 and 0.208, respectively. Then we put the computed stiffness results (K_FEMK_TimK) into η(κ₀, Δκ) = 1 + η₂Δκ + η₃Δκ² in Formula (27), and we plot the nonlinear factor of the spring stiffness η(κ₀, Δκ) as shown in Figure 6.

Table 1. Comparison of FEM results with Formulas (1), (2) and (27) at κ₀ = 0.391 and κ₀ = 0.469.

P_FEM/ (N)	h/ mm	K_FEM/ (N/mm)	K_Tim/ (N/mm)	K_Hi/ (N/mm)	K/ (N/mm)	h/ mm	K_FEM/ (N/mm)	K_Tim/ (N/mm)	K_Hi/ (N/mm)	K/ (N/mm)
	κ₀ = 0.391					κ₀ = 0.469
0	0	—	—	—	—	0	—	—	—	—
−30	−26.62	1.13	1.12	1.29	1.08	−28.11	1.07	1.09	1.36	1.03
−50	−46.77	0.99	1.12	1.26	1.01	−49.60	0.93	1.09	1.32	0.97
−70	−67.13	0.98	1.12	1.24	0.98	−71.24	0.92	1.09	1.29	0.92
−90	−88.43	0.94	1.12	1.22	0.96	−93.55	0.90	1.09	1.26	0.90
−110	−109.71	0.93	1.12	1.20	0.95	−116.51	0.87	1.09	1.23	0.88

In Figure 6, Δκ has a great influence on the nonlinear factor η(κ₀, Δκ) of the spring stiffness. Formula (27) agrees with the results of the FEM. The results in Figure 6 show that Formula (27) is important and necessary for the large deformation computation of the cylindrical spring.

4.4. Consistence of Computational Results Between Formula (27) and FEM Under Compression Load

Take the initial heights of the spring which are H₀ = 200 mm and 250 mm, respectively. Their correspondence initial inclinations are

(33)

respectively. We calculate the spring stiffness K_FEM by the geometric nonlinear iterative method of FEM. Putting Formulas (31) and (33) into Formulas (2) and (27), we can obtain the cylindrical spring stiffness K_Tim, K_Hi, and K. The stiffness results (K_FEM K_Tim K_Hi and K) of the cylindrical spring are shown in Table 1. From Table 1, we know that the finite element calculation results of these two springs are in good agreement with Formula (27). On the contrary, the displacement–load relationships of Formulas (1) and (2) do not agree with the finite element calculation results. Under compressive loading conditions, our Formula (27) gives much better results than both Formulas (1) and (2).

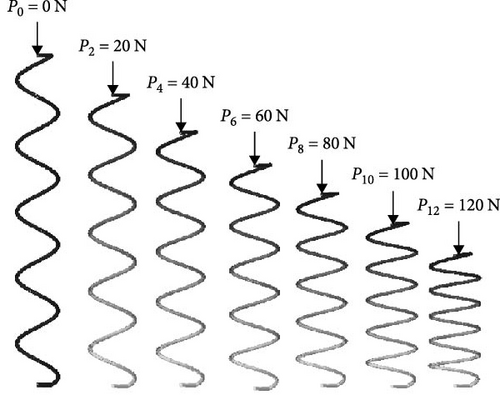
In Figure 7, we present the deformation processes of the cylindrical spring (κ₀ = 0.469) under compression load. Then we put the computed stiffness results (K_FEM K_Tim K) into η(κ₀, Δκ) = 1 + η₂Δκ + η₃Δκ² in Formula (27), and we plot the nonlinear factor of the spring stiffness η(κ₀, Δκ) as shown in Figure 8.

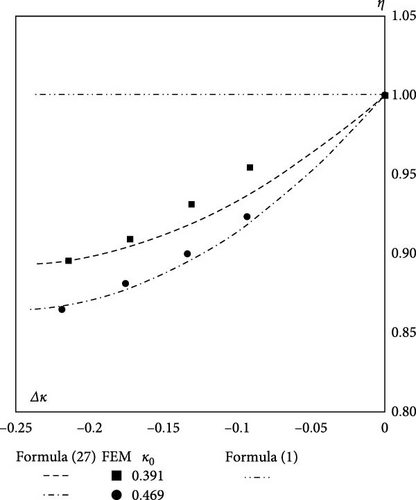
In Figure 8, Δκ also has a great influence on the nonlinear factor η(κ₀, Δκ) of the spring stiffness under compression conditions. At the same time, it can be found that the greater the κ₀ of spring, the more obvious the nonlinear effect of spring stiffness. Formula (27) agrees with the results of the FEM. The results in Figure 8 show again that Formula (27) is important and necessary for the large deformation computation of the cylindrical spring.

Comparing Figures 8 and 6, we can find that the finite element results for the tensile condition are in better agreement with the theoretical results than the compressive condition with the theoretical results. This is due to the fact that the spring does not destabilize and bend laterally in tension. During compression, even if it is ensured that the load always acts on the positive center of the spring, it is still difficult to prevent a little transverse bending of the spring during large deformations of the spring, which can lead to slight errors.

5. Conclusion

This study delves into the formulation of cylindrical spring stiffness under nonlinear large deformations and its verification through FEM. The proposed Formula (27) takes into account the combined effect of torsional and bending deformation energies, as well as the effect of pitch angle and radius variations on stiffness, which provides a comprehensive approach to stiffness calculations in nonlinear situations.

By verifying two fundamental assumptions and conducting FEM simulations, we compared the results obtained from Timoshenko’s formula, Hiroyuki’s formula, and our derived formula. For small deformations, all three formulas showed good agreement with the FEM results. While the modified Hiroyuki formula also exhibited some discrepancies, our derived formula demonstrated excellent alignment with the FEM results for nonlinear large deformations. Comparative analyses with existing formulas reveal significant discrepancies under large deformations, emphasizing the necessity of accurate stiffness formulations for practical engineering applications. FEM simulations under tensional and compressive loads demonstrate the efficacy of Formula (27) in capturing the nonlinear behavior of cylindrical springs. The formula’s reliability and consistency with FEM results highlight its suitability for designing and analyzing cylindrical springs experiencing nonlinear large deformations in mechanical engineering applications.

In conclusion, the derived Formula (27) offers a robust and accurate tool for engineers to predict and optimize cylindrical spring properties under nonlinear large deformations, facilitating enhanced design efficiency and performance in mechanical systems.

Disclosure

The authors have no relevant financial or nonfinancial interests to disclose.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Conceptualization, Z.H.; software, C.R. and R.Z.; formal analysis, T.Z. and F.X.; investigation, M.H. and T.Z.; resources, Z.H.; data curation, F.X. and C.R.; writing, original draft preparation, H.Y., and Z.H.; writing, review and editing, H.Y. and T.Z.; project administration, H.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Jiangxi Provincial Natural Science Foundation (Award No. 20224BAB214072) and the Jiangxi Province Education Science “14th Five-Year Plan” Project (Award No. 22QN007).

Open Research

Data Availability Statement

The data of this study are available from the corresponding author upon request.

References

1 Ke J., Xu J., and Wu Z., et al.A Theoretical Model Used for Stiffness Matching Design and Structure Optimization of Composite Helical Spring with Nonlinear Stiffness, Journal of the Brazilian Society of Mechanical Sciences and Engineering. (2022) 44, no. 4, 142.
10.1007/s40430-022-03444-8
Google Scholar
2 Dumitriu M., A Nonlinear Model of Mix Coil Spring—Rubber for Vertical Suspension of Railway Vehicle, Archive of Mechanical Engineering. (2016) 63, no. 1, 25–44, https://doi.org/10.1515/meceng-2016-0002, 2-s2.0-84967332842.
10.1515/meceng-2016-0002
Google Scholar
3 Fakhreddine D., Mohamed T., Said A., Abderrazek D., and Mohamed H., Finite Element Method for the Stress Analysis of Isotropic Cylindrical Helical Spring, European Journal of Mechanics—A/Solids. (2005) 24, no. 6, 1068–1078, https://doi.org/10.1016/j.euromechsol.2005.07.002, 2-s2.0-27144457669.
10.1016/j.euromechsol.2005.07.002
Web of Science® Google Scholar
4 Bartolozzi R. and Frendo F., Stiffness and Strength Aspects in the Design of Automotive Coil Springs for McPherson Front Suspensions: A Case Study, Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering. (2011) 225, no. 10, 1377–1391, https://doi.org/10.1177/0954407011403853, 2-s2.0-80054793762.
10.1177/0954407011403853
Google Scholar
5 Liu H. and Kim D., Estimation of Valve Spring Surge Amplitude Using the Variable Natural Frequency and the Damping Ratio, International Journal of Automotive Technology. (2011) 12, no. 5, 631–638, https://doi.org/10.1007/s12239-011-0073-1, 2-s2.0-80051951747.
10.1007/s12239-011-0073-1
CAS Web of Science® Google Scholar
6 Hu Z. Z., Ma L. H., and Cao S. S., A Study of Shear Fatigue Crack Mechanisms, Fatigue & Fracture of Engineering Materials & Structures. (1992) 15, no. 6, 563–572, https://doi.org/10.1111/j.1460-2695.1992.tb01295.x, 2-s2.0-0026881160.
10.1111/j.1460-2695.1992.tb01295.x
CAS Web of Science® Google Scholar
7 Xiong Z. Y., Song R. X., and Kang Z. X., et al.Analysis of Composite Spiral Spring Stiffness and Its Influencing Factors, Engineering Mechanics. (2015) 32, no. 9, 216–221.
Google Scholar
8 Hong Z., Gang C., and Jun Z. Z., The Robust Optimization Design for Cylindrical Helical Compression Spring, Advanced Materials Research. (2012) 1566, no. 433–440, 2201–2205.
Google Scholar
9 Love A. E. H., A Treatise on the Mathematical Theory of Elasticity, 1944, Dover Publications, New York.
Google Scholar
10 Taktak M., Omheni K., Aloui A., Dammak F., and Haddar M., Dynamic Optimization Design of a Cylindrical Helical Spring, Applied Acoustics. (2014) 77, 178–183, https://doi.org/10.1016/j.apacoust.2013.08.001, 2-s2.0-84890098101.
10.1016/j.apacoust.2013.08.001
Web of Science® Google Scholar
11 Timoshenko S., Strength of Materials Part Ⅱ, 1963, Advanced Mechanics, New York.
Google Scholar
12 Mohazzabi P., On the Spring Constant of a Close-Coiled Helical Spring, American Journal of Physics. (1989) 57, no. 7, 639–641, https://doi.org/10.1119/1.15962.
10.1119/1.15962
Google Scholar
13 AnckerC. J.Jr. and Goodier J. N., Theory of Pitch and Curvature Corrections for the Helical Spring—I (Tension), Journal of Applied Mechanics. (1958) 25, no. 4, 471–483, https://doi.org/10.1115/1.4011860.
10.1115/1.4011860
Google Scholar
14 Jianwei Z., Zewen G., and Quan Y., et al.Dynamic Finite Element Model Based on Timoshenko Beam Theory for Simulating High-Speed Nonlinear Helical Springs, Sensors. (2023) 23, no. 7, 3737.
10.3390/s23073737
Google Scholar
15 Chandravanshi M. L. and Mukhopadhyay A. K., Analysis of Variations in Vibration Behavior of Vibratory Feeder due to Change in Stiffness of Helical Springs Using FEM and EMA Methods, Journal of the Brazilian Society of Mechanical Sciences and Engineering. (2017) 39, no. 9, 3343–3362, https://doi.org/10.1007/s40430-017-0767-z, 2-s2.0-85028025513.
10.1007/s40430-017-0767-z
Web of Science® Google Scholar
16 Zewen G., Xiaonan H., and Jianqiao Y., Design and Analysis Method of Nonlinear Helical Springs Using a Combining Technique: Finite Element Analysis, Constrained Latin Hypercube Sampling and Genetic Programming, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. (2021) 235, no. 22, 5917–5930.
10.1177/09544062211010210
Google Scholar
17 Wahl A. M., Mechanical Spring, 1963, McGraw-Hill Book Company, New York.
Google Scholar
18 Ivchenko V. V., Theoretical Study of the Geometrical Non-Linearity of the Elastic Properties of Helical Springs, American Journal of Physics. (2020) 88, no. 11, 958–961, https://doi.org/10.1119/10.0001696.
10.1119/10.0001696
Google Scholar
19 Andrey B. Y., Babak S., and Pouyan M. S., Solving Geometrically Nonlinear Problem on Deformation of a Helical Spring through Variational Methods, International Journal of Mechanics and Applications. (2018) 8, no. 1, 4.
Google Scholar
20 Radaelli G. and Herder J. L., Study on the Large-Displacement Behaviour of a Spiral Spring with Variations of Cross-Section, Orthotropy and Prestress, Mechanical Sciences. (2018) 9, no. 2, 337–348, https://doi.org/10.5194/ms-9-337-2018, 2-s2.0-85054693392.
10.5194/ms-9-337-2018
Google Scholar
21 Crescenzo F. D. and Salvini P., Two-Dimensional Discrete Model for Buckling of Helical Springs, Procedia Structural Integrity. (2019) 24, 28–39, https://doi.org/10.1016/j.prostr.2020.02.003.
10.1016/j.prostr.2020.02.003
Google Scholar
22 Baran R., Michalczyk K., and Warzecha M., Experimental Analysis of Transverse Stiffness Distribution of Helical Compression Springs, Acta Mechanica et Automatica. (2023) 17, no. 1, 95–103, https://doi.org/10.2478/ama-2023-0011.
10.2478/ama-2023-0011
Google Scholar
23 Kato H. and Suzuki H., Nonlinear Deflection Analysis of Helical Spring in Elastic-Perfect Plastic Material: Application to the Plastic Extension of Piano Wire Spring, Mechanics of Materials. (2021) 160, https://doi.org/10.1016/j.mechmat.2021.103971, 103971.
10.1016/j.mechmat.2021.103971
Google Scholar
24 Zhang J., Qi Z. H., and Zhuo Y. P., Coil Spring Stiffness Analysis Based on Beam Element of Precise Geometric Model, Engineering Mechanics. (2020) 37, no. 2, 16–22.
Google Scholar
25 Qi Z. H., Cao Y., and Wang G., Model Noise Reduction Method for Numerical Analysis of Flexible Multi-Body Systems, Journal of Mechanics. (2018) 4, 863–870.
Google Scholar
26 Qaiser Z. and Johnson S., Generalized Spiral Spring (GSS: A Bioinspired Tunable Stiffness Mechanism (TSM) for Linear Response with High Resolution, Journal of Mechanisms and Robotics. (2021) 13, no. 1, https://doi.org/10.1115/1.4045654, 011007.
10.1115/1.4045654
Google Scholar
27 Zhuo Y., Qi Z., Zhang J., and Wang G., A Geometrically Nonlinear Spring Element for Structural Analysis of Helical Springs, Archive of Applied Mechanics. (2022) 92, no. 6, 1789–1821, https://doi.org/10.1007/s00419-022-02147-9.
10.1007/s00419-022-02147-9
Google Scholar
28 Tian S. T., Du Y. X., and Guo J., Analysis of Stiffness Characteristics of Cylindrical Coil Springs Based on Different Loads, Mechanical Engineering and Automation. (2014) 2, 46–47.
Google Scholar
29 Gong Q. and Chen B. Z., Analysis of the Influence of Light Material round Spring on Vehicle Dynamic Performance, Mechanical Design and Manufacturing Engineering. (2020) 49, no. 10, 97–101.
Google Scholar
30 Zhao T., Wang X., Liu G., Zhu J., and Yin S., The Thermal Conductivity of Graphite Composite Insulation Boards: A Theoretical and Experimental Study, Composites Science and Technology. (2024) 256, https://doi.org/10.1016/j.compscitech.2024.110760, 110760.
10.1016/j.compscitech.2024.110760
CAS Google Scholar
31 Zhou K. L. and Xiao F. X., Contact Simulation Research of Cylindrical Coil Spring Based on ANSYS, Mechanical Engineering and Automation. (2019) 1, 60–61.
Google Scholar
32 Zhu X., Lu K. Y., and Song C. L., Analyzed the Influence of Geometric Parameters of Cylindrical Coil Spring on Spring Stiffness Based on ABAQUS, Mechanical Design and Research. (2015) 31, no. 4, 95–98.
Google Scholar
33 Yang C. J., Zhang W. H., Ren G. X., and Liu X. Y., Modeling and Dynamics Analysis of Helical Spring under Compression Using a Curved Beam Element with Consideration on Contact between Its Coils, Meccanica. (2014) 49, no. 4, 907–917, https://doi.org/10.1007/s11012-013-9837-1, 2-s2.0-84897025965.
10.1007/s11012-013-9837-1
Google Scholar
34 De C. F. and Salvini P., Influence of Coil Contact on Static Behavior of Helical Compression Springs, IOP Conference Series: Materials Science and Engineering. (2021) 1038, no. 1, 012064.
10.1088/1757-899X/1038/1/012064
Google Scholar

All articles

Formula of Cylindrical Spring Stiffness for Nonlinear Large Deformation and Its FEM Verification

Abstract

1. Introduction

2. Geometrical Parameters and Their Description of Cylindrical Spring

2.1. Geometrical Description of Cylindrical Spring

2.2. Two Assumptions of Spring on Deformation

3. Nonlinear Formula of Spring Stiffness for Large Deformation

3.1. Form of Nonlinear Relation Between Load and Deformation on Spring Stiffness

3.2. Torque and Bending Moment of Spring Wire Under Load P

4. Discussion and FEM Simulations of Cylindrical Spring Stiffness for Nonlinear Large Deformation

4.1. Nonlinear Stiffness Formula (27) and Its Reduced Result: Timoshenko Formula for the Small Deformation

4.2. Verification of Experimental Result: Verification of Assumption 1 and Assumption 2

4.2.1. Verification of Assumption 1

4.2.2. The FEM Verification of Assumption 2

4.3. Consistence of Computational Results Between Formula (27) and FEM Under Tensional Load

4.4. Consistence of Computational Results Between Formula (27) and FEM Under Compression Load

5. Conclusion

Disclosure

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Formula of Cylindrical Spring Stiffness for Nonlinear Large Deformation and Its FEM Verification

Abstract

1. Introduction

2. Geometrical Parameters and Their Description of Cylindrical Spring

2.1. Geometrical Description of Cylindrical Spring

2.2. Two Assumptions of Spring on Deformation

3. Nonlinear Formula of Spring Stiffness for Large Deformation

3.1. Form of Nonlinear Relation Between Load and Deformation on Spring Stiffness

3.2. Torque and Bending Moment of Spring Wire Under Load P

4. Discussion and FEM Simulations of Cylindrical Spring Stiffness for Nonlinear Large Deformation

4.1. Nonlinear Stiffness Formula (27) and Its Reduced Result: Timoshenko Formula for the Small Deformation

4.2. Verification of Experimental Result: Verification of Assumption 1 and Assumption 2

4.2.1. Verification of Assumption 1

4.2.2. The FEM Verification of Assumption 2

4.3. Consistence of Computational Results Between Formula (27) and FEM Under Tensional Load

4.4. Consistence of Computational Results Between Formula (27) and FEM Under Compression Load

5. Conclusion

Disclosure

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information