Electronic Study of Rare Earth Intermetallics in CsCl Phase
Abstract
In this study, we utilize density functional theory (DFT) calculations to investigate the structural and electronic properties of YAg-B2(CsCl) and YCu-B2(CsCl) intermetallic compounds (IMCs). Our enthalpy calculations confirm that these compounds crystallize in a CsCl-type structure, highlighting their stability in this phase. The lattice constants provide insights into the atomic arrangement and bonding strength within the crystal, influencing the material’s density and overall structural integrity. The bulk modulus reflects the material’s resistance to uniform compression, indicative of its incompressibility, and rigidity, which are essential for applications requiring high strength and durability. By analyzing the density of states (DOSs) and electronic band structure (BS), we further discuss the electronic stability and metallic nature of these materials. Additionally, the electronic properties derived from the DOS and BS analysis suggest good electrical conductivity, making these materials suitable for use in electronic and optoelectronic devices. The calculated equilibrium structural parameters, including bulk modulus, lattice constants, and their derivatives, are found to be in good agreement with available experimental and theoretical data. Understanding these properties is crucial for optimizing the performance of YAg and YCu intermetallics in practical applications, from structural components to advanced electronic systems.
1. Introduction
The most significant artificial materials that inorganic chemists, physicists, and material scientists are interested in are intermetallic compounds (IMCs) [1]. Chemistry requires a grasp of systematic trends pertaining to the phase stability of IMCs. When compared to ordinary metals, these compounds have better qualities. The growing research into advanced materials with vast compositional and structural diversity makes identifying and discovering new materials for specific applications a challenging task. The structural, optoelectronic, and mechanical properties of germanium-based AGeF3 (A = Ga and In) halide perovskites have been studied using density functional theory (DFT) computational methods by Pasha et al. [2]. Theoretical investigation of the physical properties of synthesized SrMO3 (M = Hf and Pt) oxide perovskites using DFT has been reported by Rahman et al. [3]. The WIEN2k software was used to simulate and analyze their physical properties. The structural stability of SrHfO3 and SrPtO3 was confirmed through optimization with the Birch–Murnaghan equation of state. Intriguing insights into the structural, electronic, elastic, and optical properties of LiRCl3 (R = Be and Mg) halide perovskites have been investigated by a DFT study [4]. In this study, the WIEN2K simulation code was employed using the plane wave and self-consistent field (PWSCF) approach. The cutoff energy for distinguishing core and valence states was set at −6.0 Ry. First principles calculations have been performed to investigate the structural, electrical, elastic, and optical properties of BWF3 (W = S and Si) fluoro-perovskites [5]. With the aid of the WIEN2K code, recent computations solely relied on DFT. The equation of state by Birch–Murnaghan was used for optimization. The elastic factors were figured out and used to compute elastic characteristics, revealing that both composites are structurally and elastically stable. These substances exhibit strong resistance to plastic strain and show ductility, scratch resistance, and anisotropic behavior. Calculations made using the Tb-mBJ potential approach indicate that BSF3 and BSiF3 are metal-like substances. A computational first principles examination of the elastic, optical, structural, and electronic properties of AlRF3 (R = N and P) fluoro-perovskites compounds has been reported [6]. This work describes an ab initio computational examination of the optical, structural, elastic, electronic, and mechanical characteristics of aluminum-based compounds AlRF3 (R = N and P) halideperovskites. For optimization purposes, the Birch–Murnaghan equation of state was used, revealing that the compounds AlNF3 and AlPF3 are structurally stable. The IRelast software was used to compute elastic constants (ECs) of the elastic properties. The aforementioned compounds are mechanically stable, exhibiting strong resistance to plastic strain, possessing ductile nature, anisotropic behavior, and scratch resistance.
Research on the electrical and elastic properties of Y-based intermetallics in the CsCl phase has revealed significant findings that underscore their potential for various technological applications. To investigate the impact of filling the d shell of atom B, IMCs of the CsCl structure, ScB (where B is Ag, Cu, Pd, Rh, Ir, and Ru), YRh, and LaAg have had their susceptibility, specific heat, and Knight shift measurements performed in addition to band structure (BS) computations [7]. A quantitative examination of the local susceptibilities, as characterized for the various angular moment and locations of origin, is presented. One member of the B2 rare earth IMC family with strong ductilities is YAg, a rare earth-precious metal “line compound.” Polycrystalline YAg specimens have shown elongations of up to 27% before failing in tensile tests. Tensile tests were conducted at room temperature on single crystal specimens of YAg with the B2, CsCl-type crystal structure in the current study [8]. Using the combustion process, yttrium doped cobalt zinc nanoferrites were created. X-ray diffraction is utilized to form and confirm the single phase cubic spinel structure [9]. We originally projected that YAg alloy undergoes a first-order phase transition from CsCl phase to Fd-3m phase at roughly 25 GPa with a volume collapse of 7.47% using the particle swarm optimization approach on crystal structure prediction. It was found that the phase changeover was accompanied by a sudden change in electrical resistance [10]. Conduction electrons and localized rare earth magnetic moments interact, offering a viable substrate for emerging magnetotransport characteristics in frustrated rare earth–based intermetallics [11]. Using a first principles approach, we give the temperature-dependent ECs of two ductile rare earth IMCs, YAg and YCu, with CsCl-type B2 structure [12]. The combination of the thermal expansion obtained by the first principles phonon calculations with density-functional perturbation theory (DFPT) and the static volume-dependent ECs obtained by the first principles total energy method with density-functional theory yields the elastic moduli as a function of temperature. Single crystal specimens of YCu with the B2-type crystal structure were evaluated in both tension and compression. Before breaking, the YCu tensile specimens lengthened by several percent [13]. The lattice constants, ECs, and mechanical characteristics of gold–copper (Au─Cu) IMCs, such as AuCu3, AuCu, and Au3Cu, were examined in this work using first principles calculations [14]. YAg and YCu, two ductile rare earth IMCs with CsCl-type B2 structure, have their temperature-dependent ECs shown here, derived from basic principles [12]. Within the generalized gradient approximation (GGA), the full-potential linearized augmented plane wave (FLAPW) method has been used to study the structural and elastic properties of compounds such as YAg, CeAg, HoCu, LaAg, LaZn, and LaMg [15]. These studies collectively highlight the dual nature of Y-based intermetallics in the CsCl phase while promising electrical properties suitable for advanced applications are exhibited, their elastic properties, characterized by high stiffness and brittleness, present challenges that require further research and optimization.
However, certain characteristics of them, such as brittleness, room temperature, and low fracture toughness, severely limit their application. Interest has been garnered by YCu and YAg within this particular set of compounds owing to their unique electrical, mechanical, physical, and chemical characteristics. FLAPW based computations using YAg and YCu were focused on by Morris et al. [16]. A change from the B2 phase to the orthorhombic B27 phase at roughly 140 K was noted by Ritter, Ibarra, and Ibberson [17]. The room temperature fracture toughness of YAg was studied by Zhang et al. [18]. The mechanical characteristics of single crystal YAg were explored experimentally by Russell et al. [19]. The perfect dislocation and ductility mechanism in YAg and YCu were also explored by Chen and Biner [20].
Previous studies on Y-based intermetallics in the CsCl phase have primarily focused on their electrical and elastic properties. It has been demonstrated that notable conductivity and unique electronic structures are exhibited by these materials, making them promising candidates for various applications. The potential of YCu and YAg intermetallics in electronic device engineering due to their distinct electrical characteristics has been revealed by studies. In terms of elastic properties, significant mechanical strength and rigidity have been shown by investigations on Y-based intermetallics in the CsCl phase. However, brittleness at room temperature is also exhibited by these materials, which limits their practical applications. Further research is necessitated by the combination of high elastic moduli and brittleness to enhance their mechanical performance while maintaining their advantageous electrical properties.
The research that is now available makes it abundantly evident that incredibly little attention has been given to the electrical and elastic properties of Y-intermetallics. A systematic examination of these intermetallics’ elastic characteristics and electrical structure is presented in this research. The structural and electrical features of current intermetallics have been studied using first principles DFT in this research. These calculations have been performed within DFT using the GGA for YAg and YCu molecules with B2 structure. The bulk modulus and fundamental ground state characteristics have been provided. Additionally, the density of states (DOSs), various elastic characteristics, and the electronic BS have been studied.
2. Method of Computation
Quantum ESPRESSO is an open-source software suite designed for the first principles calculations of materials properties using DFT. The software employs plane wave basis sets and pseudopotentials to solve the Kohn–Sham equations, which are at the heart of DFT. The process begins with the creation of input files that describe the system under study. These files include the lattice parameters, atomic positions, types of pseudopotentials, and the specific computational parameters such as energy cutoffs for the plane wave basis set and k-point sampling of the Brillouin zone. The accuracy of the results largely depends on the careful selection of these parameters.
The computational workflow typically starts with a self-consistent field (SCF) calculation. This step aims to find the ground state electron density by iteratively solving the Kohn–Sham equations until convergence is achieved, that is, the total energy and electron density do not change significantly between iterations. The SCF calculation involves setting a cutoff energy for the plane waves, which determines the precision of the wave function representation and a mixing scheme to efficiently reach convergence. The outputs from this step include the total energy, electronic density, and potential energy surface of the system.
Following the SCF calculation, non-self-consistent field (non-SCF) calculations can be performed to obtain properties such as the DOSs and electronic BS. These calculations use the converged electron density from the SCF step and compute the electronic states at various points in the Brillouin zone. The DOS provides information about the number of electronic states available at each energy level, while the BS reveals the dispersion relation of electrons and can indicate metallic or insulating behavior.
Additionally, Quantum ESPRESSO can perform geometry optimizations and phonon calculations. Geometry optimization adjusts the atomic positions to minimize the total energy, thereby finding the most stable structure of the material. Phonon calculations, using DFPT, provide insights into the vibrational properties of the material, which are essential for understanding thermal properties and electron–phonon interactions. Postprocessing tools available within Quantum ESPRESSO can further analyze ECs, optical properties, and various other material characteristics, making it a versatile tool for materials science research.
Espresso quantum for both insulators and metals, it computes the ground state energy, the Kohn–Sham orbital, and other kinds of structural optimizations. You can utilize quantum espresso to examine semiconductors, insulators, and metals. PWSCF, Car–Parinello (CP), and first principle molecular dynamics (FPMD) are the three primary components of the approach. Irreducible k-points for quantum espresso are produced using the Monkhorst–Pack technique [21]. With a kinetic energy cutoff of 32 Ry, the Kohn–Sham single-particle functions were enlarged on a plane wave set basis. To obtain well-converged ground state energy, a 12 × 12 × 12 k-point mesh was used to sample the Brilliouin zone. Within the GGA, the exchange and correlation effects have been addressed. Using the conventional method of calculating the total energy for various volumes, the lattice parameter, bulk modulus, and pressure derivative of the bulk modulus were calculated and fitted to Murnaghan’s equation of state [22].
Quantum ESPRESSO is a comprehensive suite of codes designed for electronic-structure calculations and materials modeling using DFT, plane wave basis sets, and pseudopotentials. The process begins with defining the system’s crystal structure and computational parameters in input files. These include lattice vectors, atomic coordinates, and types of pseudopotentials, which represent the interaction between the valence electrons and the ion cores. The choice of pseudopotentials (norm-conserving, ultrasoft, or PAW) and the cutoff energy for the plane wave basis set are crucial as they affect the accuracy and computational cost.
3. Results and Discussion
The study of the electronic, structural, and mechanical properties of YAg and YCu in the CsCl structure using quantum ESPRESSO begins with preparing the necessary input files. These files include details about the crystal structure, atomic positions, pseudopotentials, and computational parameters. The lattice parameters for the CsCl structure, which is characterized by a simple cubic lattice with each atom at the body center of the other’s cubic cell, are specified.
The CsCl crystal structure is based on a simple cubic unit cell presented in Figure 1. Each corner of the cube has a lattice point occupied by one type of atom (usually the anion) and the center of the cube has a lattice point occupied by the other type of atom (usually the cation). Each cesium (Cs) atom is surrounded by eight chlorine (Cl) atoms, and each Cl atom is surrounded by eight Cs atoms. This high coordination number (8) is a distinctive feature of the CsCl structure. The structure can be visualized as a body-centered cubic arrangement, where one type of atom (Cs) is at the body center and the other type (Cl) is at the corners of the cube, or vice versa. The edge length of the cubic unit cell, denoted as aaa, is related to the sum of the ionic radii of the two atoms forming the compound. For the CsCl structure, this edge length is typically larger than that of NaCl due to the larger size of Cs and Cl ions compared to Na and Cl ions. The CsCl structure possesses high symmetry with the space group Pm3m (No. 221).
The next step is the SCF calculation, which involves solving the Kohn–Sham equations iteratively to achieve the ground state electron density. This is done using a plane wave basis set and pseudopotentials to describe the electron–ion interactions. The SCF input file specifies the kinetic energy cutoff for the plane waves, the type of exchange-correlation functional (typically PBE-GGA for GGA) and the k-point grid for Brillouin zone sampling.
After the SCF calculation converges, non-SCF calculations are performed to obtain the DOSs and electronic BS. The DOS calculation involves sampling the electron states over a dense k-point mesh (12,12,12,0,0,0) to provide detailed information about the energy levels. The BS calculation maps the energy dispersion relation ɛ (k) along high-symmetry paths in the Brillouin zone.
| Solid | Approach | a (Å) | B (GPa) | B′ | C11 | C12 | C44 |
|---|---|---|---|---|---|---|---|
| YAg |
|
|
|
|
|
|
|
| YCu |
|
|
|
|
|
|
|
The lattice constant indicates the equilibrium spacing between atoms in the crystal structure. It provides insights into the material’s geometric structure and bonding characteristics. A larger lattice constant typically suggests weaker bonding forces, while a smaller lattice constant indicates stronger atomic interactions. The calculated values of lattice constant for YAg is 3.615 Å and YCu is 3.476 Å; hence, YAg has weak atomic interactions than YCu. It also affects the material’s density and can influence its electronic and mechanical properties.
GV is the Voigt shear modulus and GR is the Reuss shear modulus.
The calculated values of shear modulus G, Young modulus Y, anisotropic parameter A, and Poisson ratio σ of YAg and YCu have been depicted in Table 2.
| Solid | Approach | G | Y | A | σ | C12–C44 | B/G |
|---|---|---|---|---|---|---|---|
| YAg | Present | 31.74 | 82.6710 | 1.5238 | 0.2240 | 65.1 | 2.195 |
| YCu | Present | 31.86 | 82.7990 | 1.0034 | 0.2994 | 79.9 | 2.159 |
The bulk modulus measures the material’s resistance to uniform compression. It is a key indicator of the material’s incompressibility. A high bulk modulus means the material is less compressible and generally more resistant to pressure-induced volume changes, indicating strong bonding and rigidity. The calculated values of bulk modulus for YAg is 69.7 GPa and YCu is 68.8 GPa, hence YAg is less compressible and generally more resistant to pressure-induced volume changes as compared to YAg. This property is crucial for applications requiring materials that can withstand high pressures without deforming. The shear modulus represents the material’s resistance to shear deformation. It provides insights into the rigidity of the material when subjected to shear stress. A higher shear modulus indicates a material that can better resist shape changes under shear forces, suggesting higher mechanical strength and stability, which is important for structural applications. The calculated values of shear modulus of both the materials are almost similar, for YAg is 31.74 and YCu is 31.86.
Young’s modulus measures the stiffness of a material or its ability to resist deformation under tensile stress. A high Young’s modulus means the material is very stiff and will deform less when subjected to a tensile load. The calculated values of shear modulus of both the materials are almost similar, for YAg is 82.6710 and YCu is 82.7990. This property is essential for applications where maintaining shape under load is critical, such as in beams and structural components. Poisson’s ratio describes the ratio of transverse strain to axial strain when a material is stretched or compressed. A Poisson’s ratio (σ) close to 0.5 indicates a highly incompressible material, while values closer to 0 suggest more brittle behavior. The calculated values of Poisson’s ratio (σ) for YAg is 0.2240 and YCu is 0.2994; hence, YAg is more brittle than YCu. This ratio helps in understanding the material’s deformation characteristics under mechanical loads.
Any compound must have a positive strain energy in order to be mechanically stable, which places further restrictions on the values of ECs like C11 > C12, C44 > 0, and C11 + 2C12 > 0. Both the materials under investigation have estimated ECs that fulfill these specifications for mechanical stability. These requirements are met by our reported values of the ECs C11, C12, and C44, which are shown in Table 1. These results are comparable with available results. Present results are more close to experimental results as compared to other theoretical results. Table 2 presents the calculated values of the anisotropy parameter (A), Poisson’s ratio, C12–C44 value, isotropic shear modulus (G), Young’s modulus (Y), and B/G ratio under the framework of the CsCl structure. These values were obtained using the PWSCF–GGA approximations. There are no results available for comparison of these data.
The experiments are performed at ambient conditions or specified temperatures. Theoretical calculations, often performed using DFT, predict lattice parameters by minimizing the total energy of the system. Generally, these calculations assume a perfect crystal at absolute zero temperature unless finite temperature methods are used. Real crystals expand upon heating, which affects lattice parameters. Experimental values measured at higher temperatures are generally larger than those predicted at 0 K by DFT. This discrepancy can be addressed by comparing experimental data at low temperatures (close to 0 K) with DFT results or by incorporating thermal expansion coefficients in theoretical models. At finite temperatures, lattice vibrations (phonons) contribute to the overall energy and affect atomic positions. Finite temperature DFT calculations, which include phonon effects, can provide better agreement with experimental data taken at nonzero temperatures. The choice of exchange-correlation functional in DFT (e.g., LDA, GGA, or hybrid functionals) significantly impacts the predicted lattice parameters. Some functionals systematically overestimate or underestimate bond lengths, leading to discrepancies with experimental data. Approximations in pseudopotentials, which simplify the treatment of core electrons, and the choice of basis sets can introduce errors. For instance, more accurate all-electron calculations or improved pseudopotentials can reduce discrepancies. The accuracy of DFT calculations also depends on the thoroughness of structural relaxation and the convergence criteria used. Incomplete relaxation or insufficient convergence can lead to errors in the predicted lattice parameters.
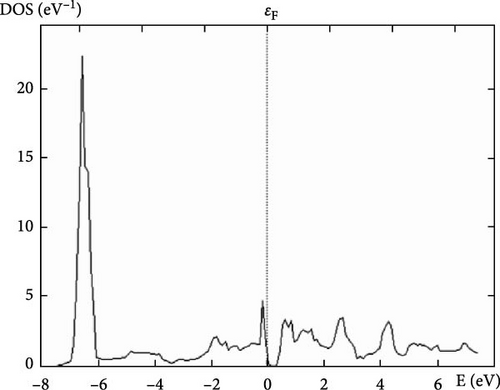
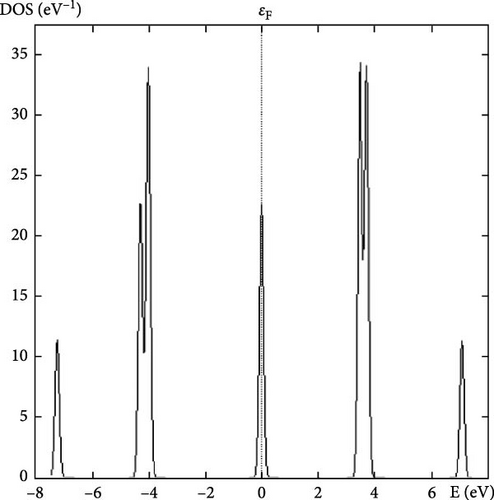
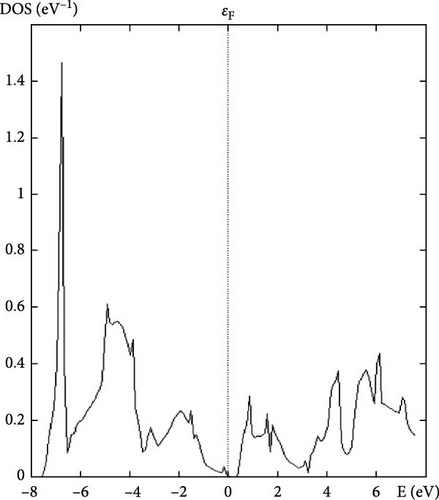
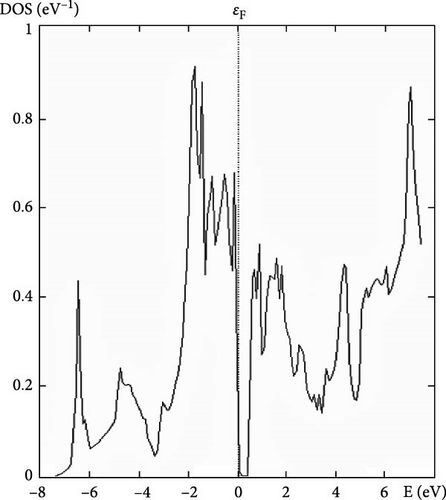
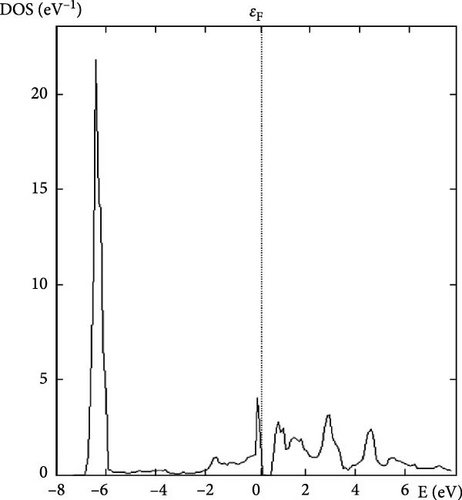
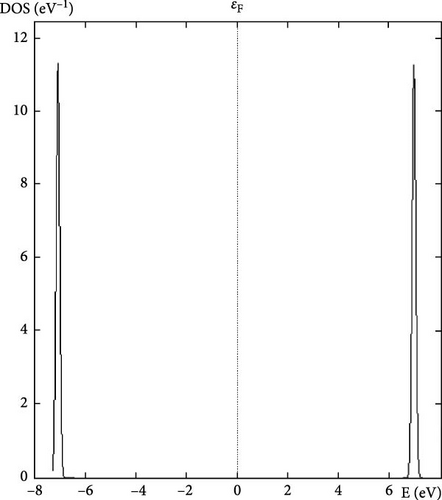
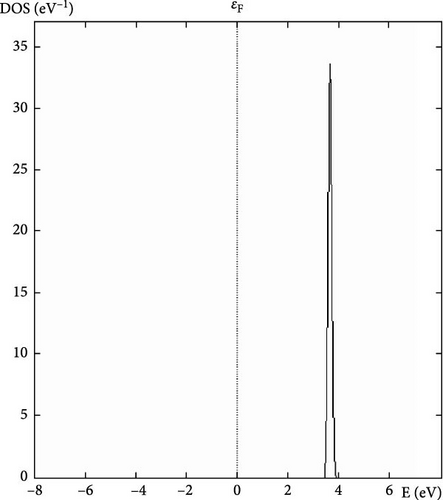
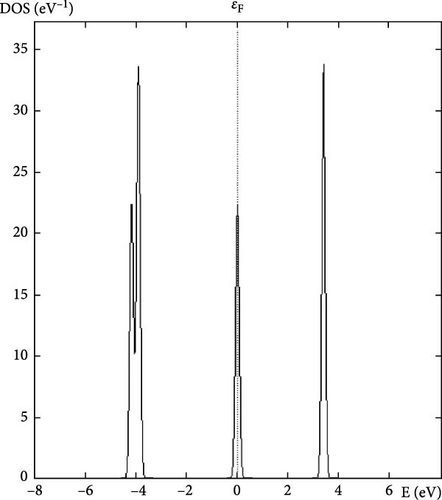
The DOS at the Fermi level indicates the number of electronic states available for conduction at the Fermi energy. A high DOS at the Fermi level suggests good metallic conductivity, as more states are available for electron movement. This property is crucial for assessing the material’s potential for electronic applications. Each calculated property of YAg and YCu provides valuable information about the material’s structural, mechanical, and electronic characteristics. Understanding these properties helps in determining the suitability of these materials for various applications, such as in electronics, structural components, and high-pressure environments.
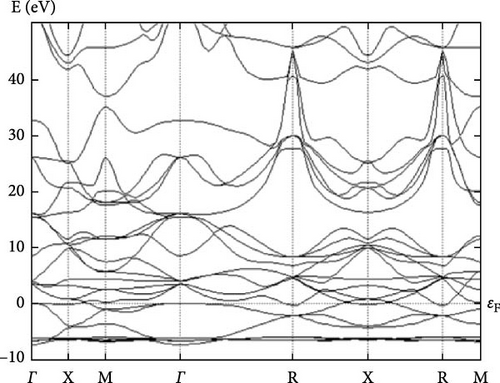
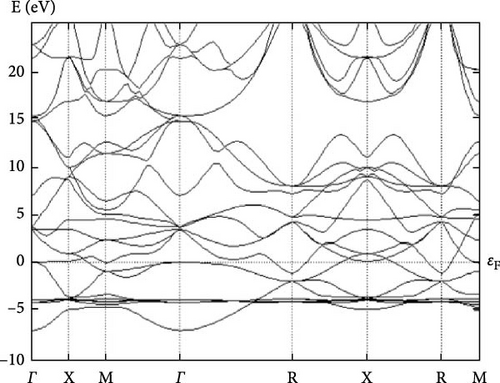
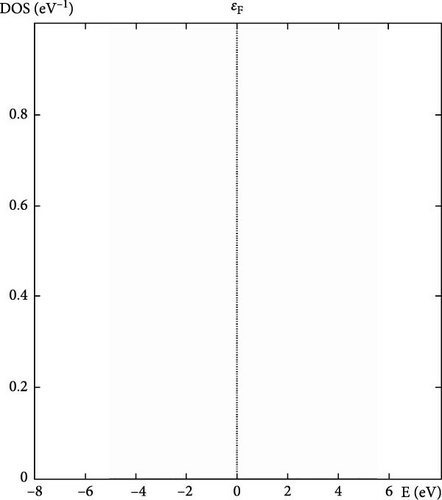
Further research examines the electronic characteristics of current intermetallic, including their electronic BS, DOSs, and partial density of states (PDOS). The matching electrical characteristics are displayed in Figures 2–7. These numbers validate that the current IMCs are metallic. In analyzing the DOS plot for YCu in the CsCl structure, we can gain insights into the electronic structure and identify specific contributions from the Y and Cu atoms, as well as from their electronic orbital. Near the Fermi level (EF), a high DOS at EF indicates metallic behavior. Check for contributions from Cu 3d and Y 4d states near EF. Below the Fermi level, Cu 3d states: Peaks around 1–2 eV below EF might be due to Cu 3d states. Y 4d states: Peaks in the range of 2–4 eV below EF might be attributed to Y 4d states. Above the Fermi level, peaks just above EF can indicate available states for conduction. Look for both Y and Cu contributions here.
4. Conclusions
By analyzing these features in the DOS plot, we can gain a detailed understanding of the electronic structure of YCu in the CsCl phase. The peaks and dips in the DOS, along with the PDOS, help identify the specific contributions of Y and Cu atoms and their electronic orbital, revealing insights into the material’s metallic character and potential applications. A calculation based on first principles has been carried out to examine the electrical properties of current compounds in the CsCl phase. Reports and comparisons with experimental data are made regarding the lattice parameter and other basic features. The metallic quality of YAg and YCu is evident in the electronic BS.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
No funding was received for this manuscript.
Open Research
Data Availability Statement
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.




