Aerial manipulators, integrating a quadrotor base and a multifaceted manipulator, represent a frontier in robotic innovation. This study introduces an identification methodology for the comprehensive dynamics of a cable-driven aerial manipulator, incorporating both rigidity and flexibility. The initial section delineates the conception of an inventive cable-driven aerial manipulator. Subsequent to the design, separate dynamics models for the quadrotor and the cable system are formulated using the Newton–Euler approach. The manipulator’s dynamics incorporate joint flexibility, resulting in a hybrid rigid-flexible dynamics model. A synthesized dynamics model emerges upon the integration of the quadrotor and manipulator models. For the system’s identification, a backpropagation neural network is utilized. Enhancement of the neural network’s performance is achieved through an augmented butterfly optimization algorithm (BOA), which fine-tunes thresholds and weights. This algorithm operates effectively owing to a clustering-based competitive learning and a chaotic elite learning strategy, demonstrating adeptness in data extraction. Experimental validation confirms the superior accuracy and precision of the model derived from the algorithm herein, in comparison to two alternative methodologies. The findings underscore the algorithm’s exceptional accuracy, robustness, and stability, providing an accurate dynamic representation of the aerial manipulator.

1. Introduction

Operational aerial manipulators are intelligent systems composed of rotorcrafts equipped with robotic arms, which can replace people to accomplish some tasks such as information collection, emergency rescue, and remote control in high-risk environments, and are triggering extensive and in-depth research in academia and industry [1–3]. The European Union has also been supporting research on operational aerial manipulators for a long time through programs such as ARCAS, AIROBOTS, and AROWORKS, which shows that the application of aerial robots to environmental interaction has become a global research focal point [4, 5]. In recent years, many scholars [6–9] have attempted to mount kinds of manipulators with different configurations onto aircraft to perform low-altitude operation tasks such as grasping, handling, hanging, and inspection. Restricted by the load capacity of the flight platform, the design of aerial manipulators generally focuses on lightweight, integration, and fewer degrees of freedom. In practice, the coupling effect between the aircraft and manipulator leads to the system dynamical uncertainty [10, 11], which can increase the difficulty of model analysis, motion planning, and controller design. From a dynamical modeling perspective, obtaining relatively accurate dynamic performance of aerial manipulators faces several significant challenges, as follows:

i.
Traditional aerial manipulators typically mount the electric drive module directly at the joints. This approach not only elevates the robotic arm’s inertia but also magnifies the coupling effect between the aircraft and the manipulator.
ii.
An aerial manipulator represents a complex nonlinear system characterized by multiple inputs and outputs, robust coupling, and underactuation. Due to these features, obtaining an accurate model of its dynamics is challenging. If there are flexible elements in the system structure, the traditional rigid-body dynamics theory does not accurately characterize the system dynamics.
iii.
If the system identification method is used to infer the dynamic behavior of the aerial manipulator, how to enhance the computational efficiency of the identification process and the confidence level of the identified model is another challenge.

Restricted by the load capacity and endurance of the aircraft platform, the design of the aerial manipulators is generally based on lightweight, integration, and fewer degrees of freedom, and the high inertia ratio and mass ratio between the aircraft and the robotic arm need to be considered. Usually, aerial manipulators place the drive unit at the joints, which not only increases the inertia and stiffness of the arm [12–14] but also limits the increase in the degrees of freedom of the robotic arm, which in turn leads to high operational energy consumption and low interaction safety. To address the above issues, several novel drive types for the aerial manipulators have been explored. Kim et al. [15] skillfully utilized an origami mechanism to design an aerial manipulator, relying on a single motor to drive seven folding modules. Inspired by the perching behavior of birds, Zhang et al. [16] retrofitted a finger-palm synergistic flexible robotic claw to a six-rotor vehicle and developed an aerial manipulator that can rapidly capture dynamic targets. Although the above new drive methods realize the lightweight design of the aerial manipulators and increase the operational flexibility, these complex mechanical structure will bring difficulties to the design of the controller. In addition, these types of aerial manipulators are characterized by extremely complex nonlinearities that do not lend themselves easily to system modeling.

There are two general forms of modeling the dynamics of an aerial manipulator [17, 18]; one approach is to consider the coupling effect between the aircraft and the robotic arm as an intrinsic factor and model the entire system under this assumption. The other is to treat the coupling effect as an external perturbation and model the aircraft and robotic arm independently, respectively [19, 20]. Due to the special characteristics of aerial operations, the aerial manipulator is required to have a light body mass, fast operating speed, low energy consumption, and thin connecting rods [21]. However, these characteristics can lead to a large flexible deformation of the arm, which reduces the working precision of the aerial manipulator. In addition, the strong vibration generated by the aircraft due to the interference of airflow and gusts will further aggravate the flexible deformation of the robotic arm. Most of the existing researches adopt the multirigid body dynamics modeling theory [22, 23], and the established models are too idealized to accurately describe the dynamic performance of the aerial manipulators with low confidence. Therefore, modeling the dynamics of aerial manipulators considering the rigid-flexible coupling characteristics has become a major trend.

For the third challenge, the dynamical behavior of a complex robotic system can usually be described by means of parameter identification and system identification. Among them, parameter identification involves linearizing the nonlinear dynamics model of the system at its equilibrium point and then employing an identification algorithm to derive certain dynamic parameters of the linearized model [24]. The accuracy of parameter identification heavily relies on the choice of the identification algorithm. Commonly used algorithms encompass the least square method [25], genetic algorithm [26], artificial bee colony algorithm [27], cuckoo algorithm [28], and so on. Nonetheless, the dynamics models obtained through these approaches can only describe the manipulator’s behavior in specific states, leading to certain limitations. As system identification technology continues to advance; various artificial neural network types are now being employed for robot system identification [29–31]. Among these, the BP neural network has gained widespread adoption due to its strong nonlinear mapping capabilities and flexible network structure [32]. However, it is worth noting that while the BP neural network exhibits excellent local search abilities, it may suffer from limited global search capabilities, slow convergence, and less-than-optimal convergence accuracy, especially when input interference is present. The butterfly optimization algorithm (BOA) offers a metaheuristic intelligence approach with several advantages, such as minimal adaptive parameters, a well-balanced exploration-exploitation trade-off, and the ability to escape local optima [33, 34]. These characteristics have made it a popular choice for solving optimization problems.

This paper is aimed at harnessing the benefits of both the BOA and BP neural network to achieve system identification for cable-driven aerial manipulators, enabling the accurate representation of the system’s dynamic behavior. The primary contributions of this work include the following:

i.
Compared to [35, 36] and [37], a novel aerial manipulator featuring a cable-driven robotic arm is designed. This innovative design positions the drive motor at the robotic arm’s base, enabling remote transmission of joint torque through the cable. This approach effectively minimizes the inertia ratio within the linkage and reduces the impact of the robotic arm on the quadrotor’s operation.
ii.
Compared to [2, 38] and [39], the cable-driven robotic arm’s rigid-flexible coupling characteristics are taken into account, incorporating factors such as link deformation, cable flexibility, and other nonlinear elements into the joint flexibility. These aspects are then integrated into the manipulator’s rigid-body dynamics model, resulting in the establishment of a rigid-flexible coupling dynamics model alongside the quadrotor dynamics model.
iii.
To address the challenges encountered with cable-driven aerial manipulators, including issues related to mechanism modeling, accurate parameter identification, the complexity of the identification process, and system fitting limitations, a system identification strategy grounded in neural networks is introduced. Recognizing that the traditional BP neural network faces difficulties like slow convergence and local optimization, an enhanced BOA is incorporated to determine the optimal values for its weights and thresholds.

The subsequent sections of this paper are organized as follows: Section 2 details the system modeling of the aerial manipulator, encompassing both the quadrotor and manipulator models. Section 3 delves into BP neural networks, the improved BOA, and the mathematical mechanisms aimed at enhancing algorithm performance. Section 3.5 outlines the implementation process of identification, covering system overview, software and hardware architectures, data acquisition, preprocessing methods, data normalization, and data back-normalization. Section 4 presents the experimental data and simulation comparisons. Finally, Section 5 concludes this study and outlines our team’s future plans.

2. Dynamics Modeling

A prototype of the designed aerial manipulator is shown in Figure 1, consisting of a quadrotor and a cable-driven manipulator. The design concept can be found in our previous work [40]. In the system, an X450 quadrotor is selected as the aerial platform. The device is outfitted with a suite of avionics, including magnetometers, barometric altitude sensors, a flight controller, and a global position system. The flight data containing attitude and position is measured by these sensors. The 2-DOF manipulator below the quadrotor has two joints, two links, and an end-effector. It adopts a rope-driven mechanism, which remotely transfers the motor torque at the base to the joints via flexible cables. Next, the dynamics model of these two subsystems will be established separately.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Prototype of the aerial manipulator.

The quadrotor has two coordinate frames, that is, inertial coordinate system O_IX_IY_IZ_I and fuselage coordinate system O_BX_BY_BZ_B, as depicted in Figure 2 [41]. In the coordinate frames, the attitude of the quadrotor is described by the Euler angles, ϕ, θ, and ψ. The position of the quadrotor is denoted as X, Y, and Z. The force and moment produced by each propeller are denoted as F_i(i = 1, 2, 3, 4) and M_i(i = 1, 2, 3, 4). The dynamics model of the quadrotor can be deduced by the Newton–Euler equation:

()

where m_A is the mass of the quadrotor, K_i(i = x, y, z, ϕ, θ, ψ) is the atmospheric drag coefficient, J_i(i = x, y, z) is the moment of inertia of the fuselage, J_m is the moment of inertia of the motor, and f_i(i = ϕ, θ, ψ) is the air friction torque. s and c are the abbreviations of sin and cos, respectively. T and τ_i(i = ϕ, θ, ψ) are the thrust and moments, which can be calculated by

()

where Ω_i(i = 1, 2, 3, 4) denotes the motor speed,

, C_T is the rotor tension coefficient, C_Q is the rotor moment coefficient, and L is the distance between the rotation axes and the center of the quadrotor.

Compared to conventional gearing, cable exhibits significant flexible deformation during force/torque transfer, leading to difficulty of establishing flexible dynamics. In the paper, the nonlinear factors such as the flexibility effect of the cable and the deformation of the link are considered as the joint flexibility. According to the study of literature [42], the flexible characteristics of a complex robotic joint can be simplified to a spring for analysis, as shown in Figure 3.

()

where q(t),

, and

are the position vector, velocity vector, and acceleration vector of the joint, respectively. θ(t),

, and

are the position vector, velocity vector, and acceleration vector of the motor, respectively. I_m and D_m are the moment of inertia and damping matrix of the motor, respectively. τ_m(t) and τ_l(t) are the motor torque and joint torque, respectively. K_s and K_d are the stiffness and damping matrix of the spring, respectively. M(q),

, G(q), and

are mass matrix, centrifugal and Coriolis forces, gravity, and friction, respectively. τ_dl(t) is the disturbance torque.

Substituting Equations (3) and (4) into Equation (5) gives

()

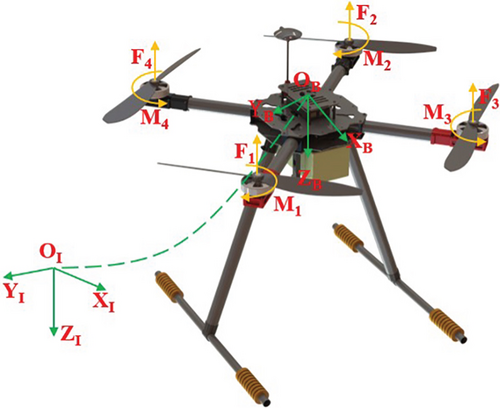
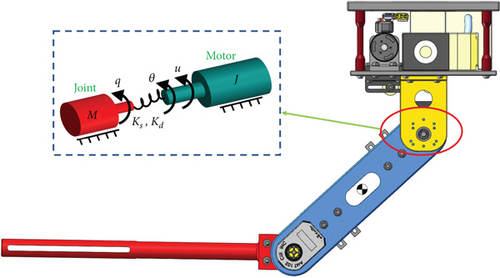
Remark 1. There are uncertainties in the dynamics of the manipulator. According to our precious works [40, 43, 44], a diagonal matrix is used to estimate the above uncertainty.

With Remark 1, Equation (6) can be rewritten as

()

where

denotes the set containing the internal unmodeled characteristics and the external disturbances.

When the inertia of the manipulator is relatively small with respect to the quadrotor, it is possible to treat the manipulator as an extra mass attached to the quadrotor, and the coupled dynamics are simplified and compensated. Since the quadrotor has a symmetric structure, its inertia matrix can be simplified to the diagonal principal moment of inertia, and the simplified quadrotor dynamics model can be expressed as follows:

()

where

is the perturbation force on the three axes of the inertial coordinate system and

is the perturbation moment in the three axes of the body coordinate system.

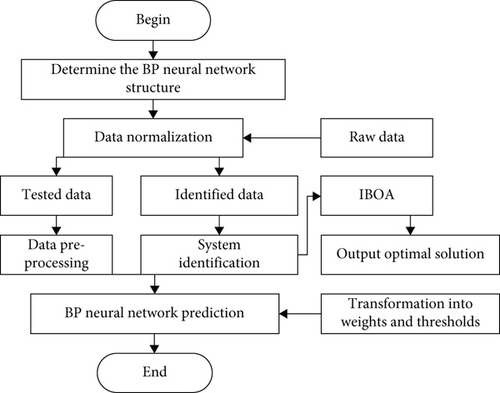
3. System Identification Methodology

Remark 2. The models obtained by system identification are mainly used to describe and predict the dynamic behavior of the system, thus playing a key role in the fields of control system design, performance optimization, fault diagnosis, and decision support. With these models, the mechanisms of complex systems can be better understood and system efficiency and reliability can be improved.

3.1. BP Neural Network

The BP neural network is an error backpropagation multilayer feed-forward neural network [45, 46], composed of an input layer, a hidden layer, and an output layer, as illustrated in Figure 4. The network is continuously and iteratively trained using signal forward propagation and error backpropagation to minimize the error function. This process ultimately establishes the relationship between the system’s input and output, achieving system identification.

Define the error function as

()

where Z is the number of training sample set and m is the output layer node.

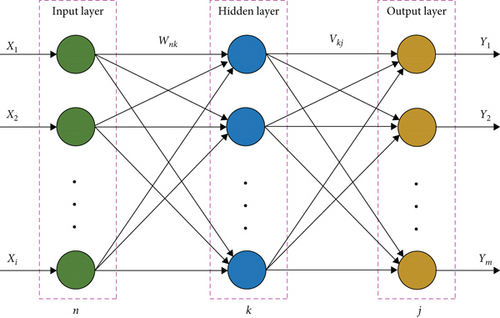
The training steps for the BP neural network are as follows.

Step 1. Initialize the network weights w_nk and v_kj, and the thresholds a and b.

Step 2. Calculate the output value of the hidden layer neuron q_k.

()

where k = 1, 2, ⋯, h, f is the implicit layer activation function, and x_n is the nth input signal.

Step 3. Calculate the output of the neurons in the output layer o_j.

()

Step 4. Update the weights.

()

where η is the parameter of learning rate with a value between zero and one.

Step 5. Update the thresholds.

()

Step 6. Determine whether the algorithm completes the iteration, and return to Step 2 if it does not.

BP neural network prediction necessitates establishing the number of hidden layers and their nodes. Hecht-Nielson has theoretically proven that a single hidden layer in a BP neural network can approximate a continuous function within any interval [47]. As a result, this paper adopts a neural network structure with a single hidden layer. The number of nodes within the hidden layer is determined using the empirical Equation (9), and it is defined based on achieving the minimum mean square error after normalizing the training set.

()

where h represents the number of nodes in the hidden layer, i denotes the number of nodes in the input layer, m corresponds to the number of nodes in the output layer, and a is an integer ranging from 1 to 10. In this paper, i, m, and a are selected as five, four, and one, respectively. Then, h is calculated as four.

BP neural networks are prone to fall into local optimal solutions during training, especially when dealing with complex, high-dimensional data. In addition, the performance of BP neural networks depends greatly on the initial settings of their parameters. Metaheuristic algorithms can assist BP neural networks to better address their inherent shortcomings by providing an efficient and flexible way to explore the solution space.

3.2. Improved BOA

BOA is a heuristic swarm intelligence optimization algorithm whose core strategy is to simulate butterfly foraging and mating behaviors. Compared to other metaheuristics, BOA achieves a good balance between efficient exploration (global search) and utilization (local search) of the solution space in the algorithm. This helps to find the global optimal solution while avoiding premature convergence to the local optimal solution. It is assumed that all butterflies can emit some kind of scent to make them attract and approach each other, and the scent concentration is related to the fitness function. In this paper, the BOA will be used to optimize the weights and threshold of BP neural network. Here are the steps:

Step 1. Each individual butterfly in the algorithm represents a possible solution, and the initial butterfly population X_id is randomly generated as follows:

()

where i = 1, 2, ⋯, g is the number of butterfly populations. d is the dimension of the problem, that is, the number of variables.

and

are the upper and lower limit if the search space. r_id is the random number between zero and one. X_id is the d-dimensional vector of BP neural network weights and threshold mappings. The parameter d satisfies the following equation:

()

Step 2. BOA is characterized by a scent modulation mechanism whereby when the butterfly changes position, its fitness function changes accordingly. The scent information emitted by the butterfly is calculated as

()

where c is the sensitivity factor and α is the power index. fit(X_i) is the value of the ith fitness function, which is described as

()

where RY_n denotes the nth output of the BP neural network training sample and Y_n denotes the actual output data.

Step 3. In BOA, the random movement of individuals and the movement towards the optimal individual correspond to the global and local search of the algorithm. The movements are described as

()

where

and

are the ith individual at G + 1 iteration and G iteration, respectively. r is a uniformly distributed random number between zero and one.

is the optimal solution for the current iteration.

and

are two different individuals randomly selected at the Gth iteration.

Step 4. Individual butterflies can search for food or mating objects in both global and local search phases. BOA introduces switch probability (SP) to maintain the balance between the two search phases. SP takes the value in the range of [0,1]. For each individual butterfly, if r > SP, end the optimization and assign the optimal solution to the threshold and weights of the BP neural network. Otherwise, a local search is executed according to Equation (22).

3.3. Clustering Competitive Learning Mechanism

Clustering technology can divide a large amount of data into several categories based on certain characteristics, so that data within the same category have the same characteristics. Hence, clustering techniques are an effective way to discover the intrinsic characteristics of data. The overall data information within a certain category can be represented by the clustering center, so that the cluster information can be fully and efficiently utilized to increase the convergence speed of the algorithm. K-mean clustering is one of the typical clustering techniques. It is an unsupervised learning algorithm with a clear structure and simple operation. It mainly includes the following three steps.

Step 1. Randomly select PX₁, X₂, ⋯, X_m, ⋯, X_g individuals from the current population as initial clustering centers .

Step 2. The distance between the one individual X_m of the population and the clustering center c_j(j = 1, 2, ⋯, k) satisfies the condition ‖X_m − c_j‖ ⩽ ‖X_m − c_p‖; it can be calculated using Euclidean distance:

()

where d represents the count of unknown parameters.

Step 3. Calculating the new clustering center :

()

where X_j and n_j are the sample and quantity belongs to category C_j.

This paper proposed clustering competitive mechanisms based on K-mean clustering. Perform K-mean clustering on butterfly populations PX₁, X₂, ⋯, X_m, ⋯, X_g, and they will become k category P₁, P₂, ⋯, P_k, according to Equations (23) and (24) to obtain the clustering centers.

Assume that butterfly individuals within the same category compete with each other. In the Gth competition, the butterfly individual with the smallest objective function value becomes the winner of the competition, and other individuals within the category become the losers of the competition. The winner of the competition can directly enter the G + 1th generation, and the loser of the competition learns from the winner and the clustering center according to the following formula:

()

where

and

are the winners and the loser is j category Gth generation and

is clustering center.

Competitive winners and clustering centers represent the local optimum and mean values in a category, respectively. The second item in Equation (25), where the loser learns from the winner, can make other individuals move towards the local optimal solution, improve their local search capabilities, and speed up the convergence of the algorithm. Those who fail the third item in Equation (25) learn from the clustering center, which can effectively use population information, increase population diversity, and help achieve a balance between global search and local search.

3.4. Chaos Elite Learning Mechanism

The optimal solution plays an important role in the search process, guiding and attracting other individuals towards the optimal solution. When solving a multipeak problem, the optimal individual may be located in a local optimum, where other individuals are easily attracted to the region, leading to a local optimum and premature convergence. This paper introduces the learning mechanism of chaotic sequences to update the optimal solution. Chaotic sequences have randomness and traversal, which is conducive to improve the quality of the optimal solution. Hence, the logistic operator has been selected to produce the chaos sequence through Equation (26). The optimal solution is updated by Equation (27). The process is governed by

()

where Z_t and Z_t+1 are the chaos iteration value at t generation and t + 1 generation, respectively. The initial vale Z₀ is randomly generated in the interval [0,1].

is the updated value of the nth variable of the optimal solution of the Gth iteration.

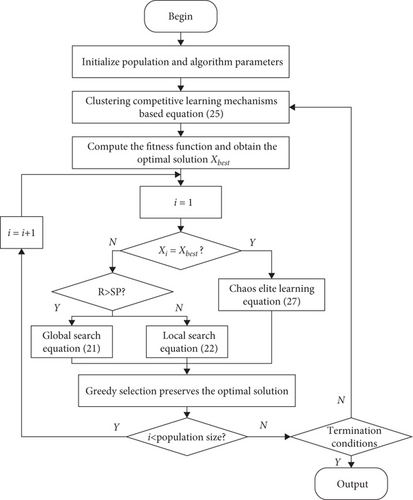
The flow of the proposed IBOA is illustrated in Figure 5.

3.5. System Identification Process

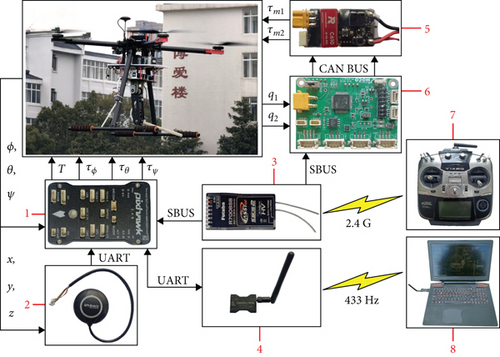
The control system of the experimental platform contains a set of avionics, such as flight controller (1), GPS (Global Positioning System) (2), receiver (3), digital radio (4), C610 driver (5), STM32 control board (6), Futaba remote controller (7), and QGC ground station (8), as shown in Figure 6. The C610 driver and the STM32 control board communicate with each other via the CAN bus. The GPS and the digital radio communicate with the Pixhawk flight control via the UART serial port. The Futaba remote control sends remote control signals to the receiver via a 2.4 G signal. The ground station is wirelessly connected to the Pixhawk flight control via a 433 Hz digital radio. The receiver transmits remote control commands to the Pix flight control and the STM32 control board via the SBUS bus. For the motion control, the Pixhawk flight controller sends PWM (pulse-width modulation) signals o the ESC (electronic speed controller) of the quadrotor to control the flight maneuvers. The STM32 control board sends current commands to the C610 driver according to the collected joint signals, and the C610 outputs current to drive the motor according to the current commands, which in turn completes the driving of the manipulator.

Recall Equations (1), (2), and (7), and the input of the aerial manipulator is , and the output of the aerial manipulator is . The above input and output signals are also the inputs and outputs of the BP neural network model. The process of the IBOA-BP for system identification of the aerial manipulator is given as follows.

3.5.1. Data Collected

The flight operation experiment is divided into two parts: (i) The joints of the cable-driven manipulator are in the original position, and the operator excites the pitch, roll, yaw, and altitude channels of the quadrotor, respectively. (ii) When the quadrotor is hovering, the two joints of the cable-driven manipulator are excited. All the input and output signals are collected by the sensors equipped in the aerial manipulator. More specially, the four control inputs to the vehicle as well as the pose signals are obtained by Pixhawk flight controller with 1 kHz sampling frequency. The joint position and control torque signals are obtained by the STM32 with 1 kHz sampling frequency.

Remark 3. The joint velocity and acceleration cannot be measured directly, if the direct differentiation of the joint position will amplify the noise existing in the measurement, so the analytical method in the literature [48] is used to obtain the angular velocity and angular acceleration, and the specific steps will not be repeated here.

3.5.2. Data Preprocessing

Due to the presence of unmodeled characteristics, external disturbances, and measurement noise in aerial manipulator motion control, the collected flight data are inevitably subject to raw errors. Hence, we adopt the five-spot triple smoothing method to process the raw flight data. The principle of the five-spot triple smoothing method originates from the least square method, which can perform three least squares polynomial smoothing of discrete data. When processing discrete data in the time domain, the five-spot triple smoothing can filter the high frequency part of the collected signal to make the time-domain curve smoother. The formula for the five-spot triple smoothing method is shown below:

()

where [y₁, y₂, ⋯, y_m] is the raw data and

is the filtered data.

Remark 4. Excessive use of five-point cubic filtering on the raw data can lead to distortion of the data, thus losing the characterization of the raw data. Therefore, the filtering was repeated five times in this experiment.

3.5.3. Data Normalization

Due to the different units and value ranges of different variables in the system, the neural network training will be more biased towards variables with larger values, resulting in a huge difference in the fitting effect of variables with different scales. Normalization is to map the data of different variables into the interval [−1,1], and the formula for normalization is as follows:

()

where ξ₀ is the raw data and ξ_max and ξ_min are the maximum and minimum values of the data. It should be noted here that all input and output data of the system need to be normalized.

3.5.4. Data Back-Normalization

In order to observe and apply the identification data, it is also necessary to back-normalize the data after the identification is completed, and the formula for back-normalization is shown below:

()

The flow of the proposed cable-driven aerial manipulator system identification algorithm based on BP-IBOA is shown in Figure 7.

4. Result Analysis

4.1. Identification Results

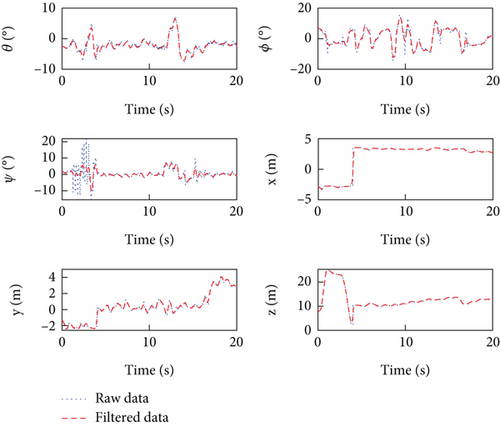
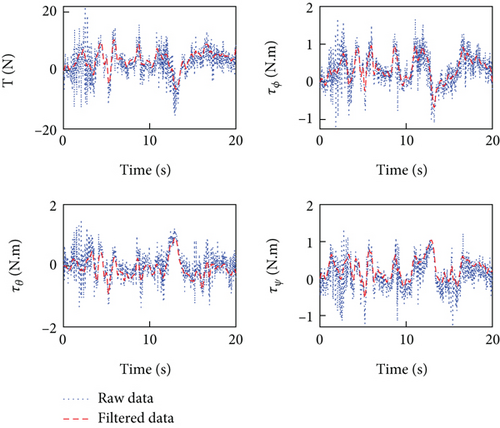
Figures 8, 9, and 10 provide the input and output data of the aerial manipulator system, as well as the raw data after undergoing the five-spot triple smoothing method. The data was sampled over a 20-s period with a sampling frequency of 1 kHz. Notably, the figures clearly illustrate the transformation of the system’s input and output data into a smoother and more consistent form after filtering, which enhances the effectiveness of the system identification algorithm. It is important to emphasize that excessive application of the five-point cubic filtering method can distort the raw data and lead to the loss of essential information. Therefore, in this experiment, a filtering frequency of 10 is selected.

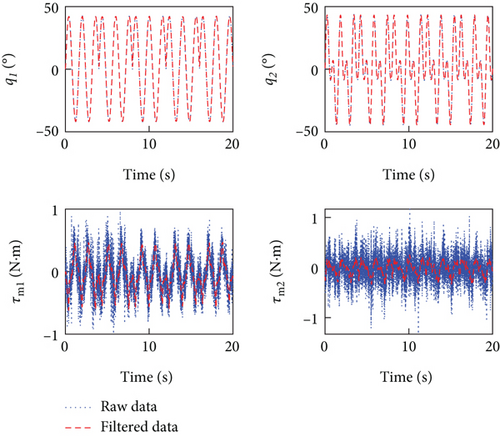
The BP neural network employs the S-type activation function, with 20 nodes in the hidden layer. Training is performed using the Trainlm function, with a maximum of 50 training iterations. The training target is set at 0.003, and the learning rate is 0.01. The weights and thresholds of the BP neural network model are optimized using the IBOA proposed in this paper. To assess the IBOA’s performance, it is compared with the BOA and the chaotic artificial bee colony (CABC) algorithm, with their execution conditions outlined in Table 1. It is important to note that the parameters for CABC are defined in [49, 50].

Remark 5. The proposed system identification method, utilizing the BP neural network with the IBOA, is denoted as Algorithm 1. Similarly, the BP neural network with the BOA is referred to as Algorithm 2, and the one with the CABC algorithm is designated as Algorithm 3.

Table 1. Parameters of the three algorithms.

Algorithm	Parameters
1	c = 2, r_id = 0.5, r = 0.5, g = 20, SP = 0.8, T_max = 50
2	c = 2, r_id = 0.5, r = 0.5, g = 20, SP = 0.8, T_max = 50
3	N_p = 20, limit = 20, T_max = 50

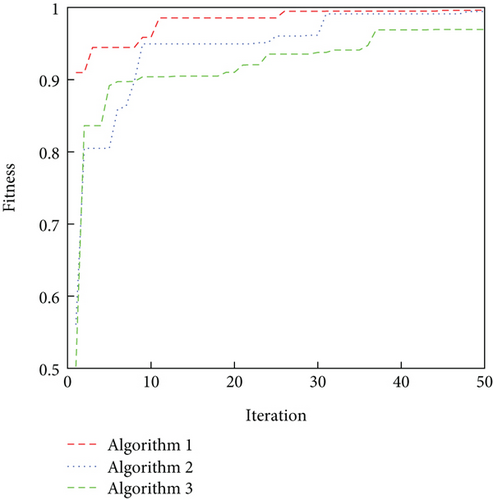
The iteration curves of the three algorithms are shown in Figure 11. As can be seen from the figure, all three algorithms begin to converge at around 10 generations, although Algorithm 1 has the fastest convergence rate. Meanwhile, Algorithm 1 finally obtains an adaptation value of 0.9962, Algorithm 2 is 0.9844, and Algorithm 3 is 0.9684. Furthermore, Algorithm 1 runs for 2.4 s, Algorithm 2 for 3.7 s, and Algorithm 3 for 1.8 s. This shows that compared to the other two algorithms, the IBOA can help the BP neural network to obtain optimal thresholds and weights by fully mining the data. Due to the addition of improved operators, the operational efficiency of IBOA is lower than BOA, but it is still 35.14% higher than CABC. This also proves that IBOA has a better operational framework.

In the system identification process, the first 10s of filtered input and output data are selected as the excitation signal, and three algorithms are used to fit the dynamics model of the aerial manipulator, respectively. Then, the filtered input data of the latter 10s is utilized as the excitation signal to activate the identified dynamics model. The output signal produced by the model is compared with the filtered input data of the latter 10s output data. Figures 12 and 13 show the identified results by the three algorithms. It can be seen that the predicted values from all three identification algorithms track the actual data, but it is clear that the predictions from Algorithm 1 track the actual data the best.

The correlation coefficient quantifies the strength of the relationship between two variables, helping to determine whether they exhibit a linear association and the extent of this association. Hence, a correlation coefficient is introduced to evaluate the identification accuracy of the model to the actual data. The formula is given as

()

where

is the mean of the identified data, y_mi is the identified data,

is the mean of the actual data, and y_i is the actual data. If Δ_c is closer to one, the higher the identification accuracy. Conversely, if Δ_c is closer to zero, the worse the identification accuracy.

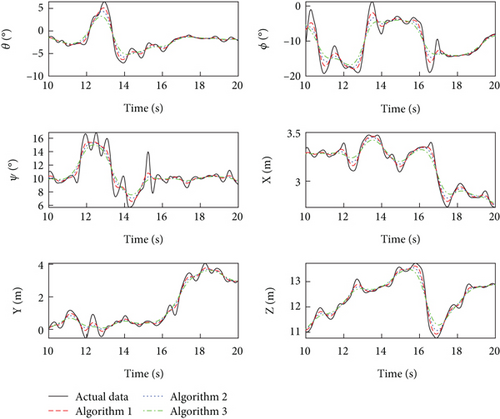
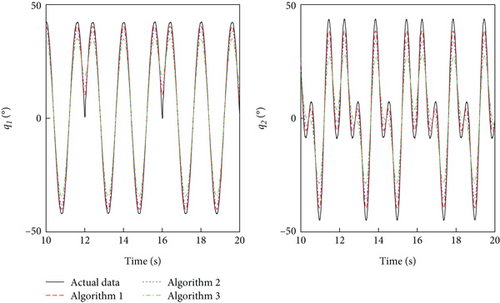
Table 2 shows the correlation coefficient of the three identified algorithms. It can be seen that the three algorithms can all obtain good correlation coefficient. The correlation coefficient of IBOA-BP is higher than that of BOA-BP and CABC-BP. For example, the correlation coefficient of output θ of IBOA-BP is 3.86% and 9.96% higher CABC-BP and BOA-BP, respectively. The correlation of output X of IBOA-BP is 4.25% and 11.87% higher CABC-BP and BOA-BP, respectively. The correlation of output q₁ of IBOA-BP is 0.11% and 0.51% higher CABC-BP and BOA-BP, respectively. The results show that IBOA-BP has a stronger system identification capability and is able to obtain more accurate dynamics models using input and output data. In addition, the correlation coefficient of the robotic arm output is significantly better than that of the quadrotor output. This is due to the fact that the manipulator uses joint space control and is not subjected to as much perturbation as the quadrotor.

Table 2. Correlation coefficient of the three identified algorithms.

Output	Algorithm 1	Algorithm 2	Algorithm 3
θ	0.9661	0.9288	0.8699
ϕ	0.9671	0.9199	0.8671
ψ	0.8706	0.8023	0.7327
X	0.9526	0.9121	0.8515
Y	0.9769	0.9562	0.9199
Z	0.9922	0.9815	0.9600
q₁	0.9991	0.9980	0.9940
q₂	0.9914	0.9678	0.9024

4.2. Model Validation

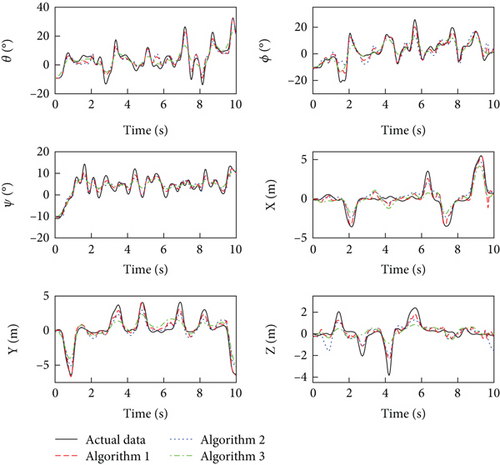
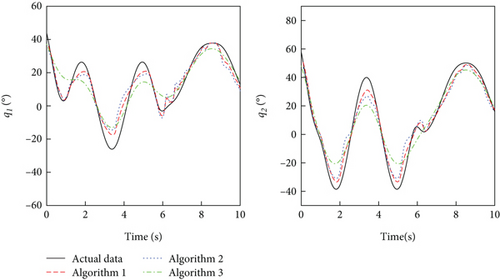
For system identification, model validation is also required to verify the validity of the identified model. Another set of experimental data will be used to validate the effectiveness of the identified model. We collected 10s of flight data, which are also preprocessed using the five-point triple filtering method. Then, the processed input data are used as excitation signals to stimulate the identified model, and the predicted output data are compared with the actual output data. As shown in Figures 14 and 15, the predicted output data by three algorithms are in better agreement with the experimental data and basically match up. Furthermore, the correlation coefficient between the predicted output and actual output is listed in Table 3. It is evident that the correlation coefficients of the output state quantities are worse than those in Table 2, especially for the Z channel. However, the dynamics models obtained by the three algorithms still provide a good description of the dynamic response of the cable-driven aerial manipulator. More specially, the dynamics model obtained by the IBOA-BP algorithm is still by superior to the models obtained by the other two algorithms. This indicates the robustness and accuracy of the dynamics model obtained through IBOA-BP algorithm.

Table 3. Correlation coefficient of the three identified algorithms in model validation.

Output	Algorithm 1	Algorithm 2	Algorithm 3
θ	0.9157	0.8520	0.8946
ϕ	0.9685	0.8874	0.9239
ψ	0.9755	0.8955	0.8497
X	0.8630	0.8252	0.7643
Y	0.9288	0.9210	0.8436
Z	0.7977	0.7993	0.5959
q₁	0.9696	0.9359	0.8874
q₂	0.9913	0.9785	0.9735

In addition, the identified models of an aerial manipulator generated by data analysis and mathematical modeling are often a simplified approximate description. Such models usually fail to fully capture the dynamic behavior of real and complex systems because they may not account for nonlinearities, coupling effects, and unmodeled dynamic properties. Therefore, model uncertainties need to be fully considered in control and decision-making strategy development, and appropriate control strategies need to be employed to cope with these discrepancies to ensure the reliability and performance of the aerial manipulator.

Remark 6. The dynamics model of the cable-driven aerial manipulator in this paper should include the dynamic response of the controller. The controller used in this paper is a PID (proportion integration differentiation) controller, which is a commonly used controller for robotic systems. In order to exclude the influence of controllers on the identification results, the same set of controllers and the same set of controller parameters were used for the two previous and two previous identifications.

5. Conclusions

This paper presents a new method combining BP neural network technique and improved BOA for system identification of an aerial manipulator equipped with a cable-driven manipulator. It is found that the algorithm proposed in this paper outperforms BOA-BP and CABC-BP in terms of identified accuracy, robustness, and stability. Thanks to IBOA, the BP neural network is able to describe the dynamic behavior of the aerial manipulator faster and better. Meanwhile, the designed cable-driven aerial manipulator prototype is also proved to be effective and controllable through the identified experiments.

In the future, another advanced methods will be developed for the system identification of the robotic systems. The identified objects will also be extended from aerial manipulators to other types of robots, such as space manipulators, underwater manipulators, and ground mobile manipulators. In addition, we will explore novel controllers to achieve stable control of these identified models.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This paper was supported by the National Natural Science Foundation of China (Nos. 52375101 and 52005231).

Open Research

Data Availability Statement

The data of simulation can be provided if necessary.

References

1 Roderick W. R. T., Cutkosky M. R., and Lentink D., Bird-inspired dynamic grasping and perching in arboreal environments, Science Robotics. (2021) 6, no. 61, article eabj7562, https://doi.org/10.1126/scirobotics.abj7562, 34851710.
10.1126/scirobotics.abj7562
PubMed Web of Science® Google Scholar
2 Xu M., Hu A., and Wang H., Image-based visual impedance force control for contact aerial manipulation, IEEE Transactions on Automation Science and Engineering. (2023) 20, no. 1, 518–527.
10.1109/TASE.2022.3162207
Web of Science® Google Scholar
3 Xilun D., Pin G., Kun X., and Yushu Y., A review of aerial manipulation of small-scale rotorcraft unmanned robotic systems, Chinese Journal of Aeronautics. (2019) 32, no. 1, 200–214, https://doi.org/10.1016/j.cja.2018.05.012, 2-s2.0-85049875132.
10.1016/j.cja.2018.05.012
Web of Science® Google Scholar
4 Ollero A., Tognon M., Suarez A., Lee D., and Franchi A., Past, present, and future of aerial robotic manipulators, IEEE Transactions on Robotics. (2022) 38, no. 1, 626–645, https://doi.org/10.1109/TRO.2021.3084395.
10.1109/TRO.2021.3084395
Web of Science® Google Scholar
5 Meng J., Buzzatto J., Liu Y., and Liarokapis M., On aerial robots with grasping and perching capabilities: a comprehensive review, Frontiers in Robotics and AI. (2022) 8, article 739173, https://doi.org/10.3389/frobt.2021.739173.
10.3389/frobt.2021.739173
Web of Science® Google Scholar
6 Danko T. W., Chaney K. P., and Oh P. Y., A parallel manipulator for mobile manipulating UAVs, 2015 IEEE International Conference on Technologies for Practical Robot Applications (TePRA), 2015, Woburn, MA, USA, https://doi.org/10.1109/TePRA.2015.7219682, 2-s2.0-84949946305.
10.1109/TePRA.2015.7219682
Google Scholar
7 Laiacker M., Huber F., and Kondak K., High accuracy visual servoing for aerial manipulation using a 7 degrees of freedom industrial manipulator, 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2016, Daejeon, Korea (South), 1631–1636, https://doi.org/10.1109/IROS.2016.7759263, 2-s2.0-85006336220.
10.1109/IROS.2016.7759263
Google Scholar
8 Orsag M., Korpela C., Oh P., and Bogdan S., Aerial Manipulation, 2018, Springer, https://doi.org/10.1007/978-3-319-61022-1.
10.1007/978-3-319-61022-1
Google Scholar
9 Paul H., Miyazaki R., Ladig R., and Shimonomura K., Tams: development of a multipurpose threearm aerial manipulator system, Advanced Robotics. (2021) 35, no. 1, 31–47, https://doi.org/10.1080/01691864.2020.1845237.
10.1080/01691864.2020.1845237
Web of Science® Google Scholar
10 Khamseh H. B., Janabi-Sharifi F., and Abdessameud A., Aerial manipulation—a literature survey, Robotics and Autonomous Systems. (2018) 107, 221–235, https://doi.org/10.1016/j.robot.2018.06.012, 2-s2.0-85049508777.
10.1016/j.robot.2018.06.012
Web of Science® Google Scholar
11 Meng X., He Y., and Han J., Survey on aerial manipulator: system, modeling, and control, Robotica. (2020) 38, no. 7, 1288–1317, https://doi.org/10.1017/S0263574719001450.
10.1017/S0263574719001450
Web of Science® Google Scholar
12 Ladig R., Paul H., Miyazaki R., Shimonomura K., and Ritsumeikan University 1-1-1 Nojihigashi, Kusatsu, Shiga 525-8577, Japan, Aerial manipulation using multirotor UAV: a review from the aspect of operating space and force, Journal of Robotics and Mechatronics. (2021) 33, no. 2, 196–204, https://doi.org/10.20965/jrm.2021.p0196.
10.20965/jrm.2021.p0196
Web of Science® Google Scholar
13 Bartelds T., Capra A., Hamaza S., Stramigioli S., and Fumagalli M., Compliant aerial manipulators: toward a new generation of aerial robotic workers, IEEE Robotics and Automation Letters. (2016) 1, no. 1, 477–483, https://doi.org/10.1109/LRA.2016.2519948, 2-s2.0-85058585417.
10.1109/LRA.2016.2519948
Google Scholar
14 Ruggiero F., Lippiello V., and Ollero A., Aerial manipulation: a literature review, IEEE Robotics and Automation Letters. (2018) 3, no. 3, 1957–1964, https://doi.org/10.1109/LRA.2018.2808541, 2-s2.0-85063306131.
10.1109/LRA.2018.2808541
Google Scholar
15 Kim S.-J., Lee D.-Y., Jung G.-P., and Cho K.-J., An origami-inspired, self-locking robotic arm that can be folded flat, Science Robotics. (2018) 3, no. 16, article eaar2915, https://doi.org/10.1126/scirobotics.aar2915, 2-s2.0-85048200805, 33141746.
10.1126/scirobotics.aar2915
PubMed Web of Science® Google Scholar
16 Zhang Y., Zhang W., Gao P., Zhong X., and Pu W., Finger-palm synergistic soft gripper for dynamic capture via energy harvesting and dissipation, Nature Communications. (2022) 13, no. 1, https://doi.org/10.1038/s41467-022-35479-9, 36513668.
10.1038/s41467-022-35479-9
PubMed Web of Science® Google Scholar
17 Kuci’nski T., Rybus T., Seweryn K., Banaszkiewicz M., Buratowski T., Chmaj G., Grygorczuk J., and Uhl T., Deployable manipulator technology with application for UAVs, Aerospace Robotics II. (2015) 93–103, https://doi.org/10.1007/978-3-319-13853-4_9.
10.1007/978-3-319-13853-4_9
Google Scholar
18 Abaunza H., Castillo P., Victorino A., and Lozano R., Dual quaternion modeling and control of a quad-rotor aerial manipulator, Journal of Intelligent & Robotic Systems. (2017) 88, no. 2-4, 267–283, https://doi.org/10.1007/s10846-017-0519-4, 2-s2.0-85014732507.
10.1007/s10846-017-0519-4
Web of Science® Google Scholar
19 Pounds P. E. and Dollar A. M., Aerial grasping from a helicopter UAV platform, Experimental Robotics: The 12th International Symposium on Experimental Robotics, 2014, Springer, 269–283.
10.1007/978-3-642-28572-1_19
Google Scholar
20 Orsag M., Korpela C. M., Bogdan S., and Oh P. Y., Hybrid adaptive control for aerial manipulation, Journal of Intelligent & Robotic Systems. (2014) 73, no. 1-4, 693–707, https://doi.org/10.1007/s10846-013-9936-1, 2-s2.0-84899437988.
10.1007/s10846-013-9936-1
Web of Science® Google Scholar
21 Zhang G., He Y., Dai B., Feng G., Han J., and Liu G., Robust control of an aerial manipulator based on a variable inertia parameters model, IEEE Transactions on Industrial Electronics. (2020) 67, no. 11, 9515–9525, https://doi.org/10.1109/TIE.2019.2956414.
10.1109/TIE.2019.2956414
Web of Science® Google Scholar
22 Nikou A., Gavridis G. C., and Kyriakopoulos K. J., Mechanical design, modelling and control of a novel aerial manipulator, 2015 IEEE International Conference on Robotics and Automation (ICRA), 2015, Seattle, WA, USA, IEEE, 4698–4703, https://doi.org/10.1109/ICRA.2015.7139851, 2-s2.0-84938279791.
10.1109/ICRA.2015.7139851
Google Scholar
23 Tognon M., Yüksel B., Buondonno G., and Franchi A., Dynamic decentralized control for protocentric aerial manipulators, 2017 IEEE International Conference on Robotics and Automation (ICRA), 2017, Singapore, IEEE, 6375–6380, https://doi.org/10.1109/ICRA.2017.7989753, 2-s2.0-85027967268.
10.1109/ICRA.2017.7989753
Google Scholar
24 Chovancová A., Fico T., Chovanec L.’u., and Hubinsk P., Mathematical modelling and parameter identification of quadrotor (a survey), Procedia Engineering. (2014) 96, 172–181, https://doi.org/10.1016/j.proeng.2014.12.139, 2-s2.0-84923700207.
10.1016/j.proeng.2014.12.139
Google Scholar
25 Sumantri B., Uchiyama N., and Sano S., Least square based sliding mode control for a quadrotor helicopter and energy saving by chattering reduction, Mechanical Systems and Signal Processing. (2016) 66-67, 769–784, https://doi.org/10.1016/j.ymssp.2015.05.013, 2-s2.0-84955721210.
10.1016/j.ymssp.2015.05.013
Web of Science® Google Scholar
26 West C., Montazeri A., Monk S. D., and Taylor C. J., A genetic algorithm approach for parameter optimization of a 7dof robotic manipulator, IFACPapersOnLine. (2016) 49, no. 12, 1261–1266, https://doi.org/10.1016/j.ifacol.2016.07.688, 2-s2.0-84992337688.
10.1016/j.ifacol.2016.07.688
Google Scholar
27 Zhang L. and Xiao N., A novel artificial bee colony algorithm for inverse kinematics calculation of 7-dof serial manipulators, Soft Computing. (2019) 23, no. 10, 3269–3277, https://doi.org/10.1007/s00500-017-2975-y, 2-s2.0-85037710435.
10.1007/s00500-017-2975-y
Web of Science® Google Scholar
28 Ding L., Li X., Li Q., and Chao Y., Nonlinear friction and dynamical identification for a robot manipulator with improved cuckoo search algorithm, Journal of Robotics. (2018) 2018, 10, https://doi.org/10.1155/2018/8219123, 2-s2.0-85042652260, 8219123.
10.1155/2018/8219123
Google Scholar
29 Zhao G., Zhang P., Ma G., and Xiao W., System identification of the nonlinear residual errors of an industrial robot using massive measurements, Robotics and Computer-Integrated Manufacturing. (2019) 59, 104–114, https://doi.org/10.1016/j.rcim.2019.03.007, 2-s2.0-85063904909.
10.1016/j.rcim.2019.03.007
Web of Science® Google Scholar
30 Horvath S. and Neuner H., System identification of a robot arm with extended Kalman filter and artificial neural networks, Journal of Applied Geodesy. (2019) 13, no. 2, 135–150, https://doi.org/10.1515/jag-2018-0045, 2-s2.0-85061156493.
10.1515/jag-2018-0045
Web of Science® Google Scholar
31 Allevato A. D., Short E. S., Pryor M., and Thomaz A. L., Iterative residual tuning for system identification and sim-to-real robot learning, Autonomous Robots. (2020) 44, no. 7, 1167–1182, https://doi.org/10.1007/s10514-020-09925-w.
10.1007/s10514-020-09925-w
Web of Science® Google Scholar
32 Wu R.-T. and Mohammad R., Deep convolutional neural network for structural dynamic response estimation and system identification, Journal of Engineering Mechanics. (2019) 145, no. 1, article 04018125, https://doi.org/10.1061/(ASCE)EM.1943-7889.0001556.
10.1061/(ASCE)EM.1943-7889.0001556
Web of Science® Google Scholar
33 Tubishat M., Alswaitti M., Mirjalili S., Al-Garadi M. A., and Rana T. A., Dynamic butterfly optimization algorithm for feature selection, IEEE Access. (2020) 8, 194303–194314, https://doi.org/10.1109/ACCESS.2020.3033757.
10.1109/ACCESS.2020.3033757
Web of Science® Google Scholar
34 Sharma T. K., Enhanced butterfly optimization algorithm for reliability optimization problems, Journal of Ambient Intelligence and Humanized Computing. (2021) 12, no. 7, 7595–7619, https://doi.org/10.1007/s12652-020-02481-2.
10.1007/s12652-020-02481-2
Web of Science® Google Scholar
35 Liang J., Chen Y., Wu Y., Miao Z., Zhang H., and Wang Y., Adaptive prescribed performance control of unmanned aerial manipulator with disturbances, IEEE Transactions on Automation Science and Engineering. (2023) 20, no. 3, 1804–1814, https://doi.org/10.1109/TASE.2022.3186315.
10.1109/TASE.2022.3186315
Web of Science® Google Scholar
36 Brunner M., Rizzi G., Studiger M., Siegwart R., and Tognon M., A planning-and-control framework for aerial manipulation of articulated objects, IEEE Robotics and Automation Letters. (2022) 7, no. 4, 10689–10696, https://doi.org/10.1109/LRA.2022.3191178.
10.1109/LRA.2022.3191178
Web of Science® Google Scholar
37 Chen Y., Liang J., Wu Y., Miao Z., Zhang H., and Wang Y., Adaptive sliding-mode disturbance observer-based finite-time control for unmanned aerial manipulator with prescribed performance, IEEE Transactions on Cybernetics. (2023) 53, no. 5, 3263–3276, https://doi.org/10.1109/TCYB.2022.3168030, 35507614.
10.1109/TCYB.2022.3168030
PubMed Web of Science® Google Scholar
38 Imanberdiyev N., Sood S., Kircali D., and Kayacan E., Design, development and experimental validation of a lightweight dual-arm aerial manipulator with a COG balancing mechanism, Mechatronics. (2022) 82, article 102719, https://doi.org/10.1016/j.mechatronics.2021.102719.
10.1016/j.mechatronics.2021.102719
Web of Science® Google Scholar
39 Zeng J., Zhong H., Wang Y., Fan S., and Zhang H., Autonomous control design of an unmanned aerial manipulator for contact inspection, Robotica. (2023) 41, no. 4, 1145–1158, https://doi.org/10.1017/S0263574722001588.
10.1017/S0263574722001588
Web of Science® Google Scholar
40 Ding L., Zhu G., Li Y., and Wang Y., Cable-driven unmanned aerial manipulator systems for water sampling: design, modeling, and control, Drones. (2023) 7, no. 7, 450–477, https://doi.org/10.3390/drones7070450.
10.3390/drones7070450
Google Scholar
41 Wang Y., Wang Y., and Ren B., Energy saving quadrotor control for field inspections, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2022) 52, no. 3, 1768–1777.
10.1109/TSMC.2020.3037071
Web of Science® Google Scholar
42 Jin M., Lee J., and Tsagarakis N. G., Modelfree robust adaptive control of humanoid robots with flexible joints, IEEE Transactions on Industrial Electronics. (2017) 64, no. 2, 1706–1715, https://doi.org/10.1109/TIE.2016.2588461, 2-s2.0-85015240161.
10.1109/TIE.2016.2588461
Web of Science® Google Scholar
43 Wang Y., Zhang R., Feng J., Zhao J., Chen B., and Wu H., A light cable-driven manipulator developed for aerial robots: structure design and control research, International Journal of Advanced Robotic Systems. (2020) 17, no. 3, article 172988142092642, https://doi.org/10.1177/1729881420926425.
10.1177/1729881420926425
Web of Science® Google Scholar
44 Ding L., Yao Y., and Ma R., Observer-based control for a cable-driven aerial manipulator under lumped disturbances, CMES-Computer Modeling in Engineering & Sciences. (2023) 135, no. 2, 1539–1558.
10.32604/cmes.2022.023003
Web of Science® Google Scholar
45 Ruan X., Zhu Y., Li J., and Cheng Y., Predicting the citation counts of individual papers via a BP neural network, Journal of Informetrics. (2020) 14, no. 3, article 101039, https://doi.org/10.1016/j.joi.2020.101039.
10.1016/j.joi.2020.101039
PubMed Web of Science® Google Scholar
46 Song S., Xiong X., Wu X., and Xue Z., Modeling the SOFC by BP neural network algorithm, International Journal of Hydrogen Energy. (2021) 46, no. 38, 20065–20077, https://doi.org/10.1016/j.ijhydene.2021.03.132.
10.1016/j.ijhydene.2021.03.132
CAS Web of Science® Google Scholar
47 Zhang Y.-g., Tang J., Liao R.-p., Zhang M.-f., Zhang Y., Wang X.-m., and Zheng-yang S., Application of an enhanced BP neural network model with water cycle algorithm on landslide prediction, Stochastic Environmental Research and Risk Assessment. (2021) 35, no. 6, 1273–1291, https://doi.org/10.1007/s00477-020-01920-y.
10.1007/s00477-020-01920-y
Web of Science® Google Scholar
48 Kinsheel A., Taha Z., Deboucha A., and Ya T. M. Y. S. T., Robust least square estimation of the CRS A465 robot arm’s dynamic model parameters, Journal of Mechanical Engineering Research. (2012) 4, no. 3, 88–89, https://doi.org/10.5897/JMER11.061.
10.5897/JMER11.061
Google Scholar
49 Ding L., Wu H., and Yu Y., Chaotic artificial bee colony algorithm for system identification of a small-scale unmanned helicopter, International Journal of Aerospace Engineering. (2015) 2015, 11, https://doi.org/10.1155/2015/801874, 2-s2.0-84938651783, 801874.
10.1155/2015/801874
Web of Science® Google Scholar
50 Ma R., Ding L., Liu K., and Wu H., Dynamical model identification for a small-scale unmanned helicopter using an integrated approach, International Journal of Aerospace Engineering. (2019) 2019, 11, https://doi.org/10.1155/2019/8407013, 2-s2.0-85065716773, 8407013.
10.1155/2019/8407013
Web of Science® Google Scholar

All articles

System Identification for Rigid-Flexible Coupled Dynamics Model of a Cable-Driven Aerial Manipulator

Abstract

1. Introduction

2. Dynamics Modeling