1. Introduction

Currently, with the continuous development of aviation technology and artificial intelligence [1], unmanned aerial vehicles (UAVs) have been widely used in target reconnaissance [2], communication relay [3], geographic surveying and mapping [4], logistics, and distribution [5]. However, as application environments become more complex, traditional single UAV performs poorly in terms of adapting to the environment and achieving low mission success rates for complex operational tasks [6]. Fortunately, the collaborative work of multiple UAVs effectively mitigates many drawbacks of a single UAV in complex environments and significantly improves the success rate of mission execution. Multi-UAV cooperative work has the characteristics of low cost, good scalability, and strong adaptability, which has become the mainstream direction of UAV application [7].

The basis of multi-UAV cooperative work is the multi-UAV path planning problem [8], which generates an optimal path for each UAV to reach its destination, taking into account various constraints, such that the total path planned is the shortest [9]. Especially in dynamic environments with partial or no prior knowledge, collaborative path planning of multiple UAVs requires real-time adjustment of planned paths based on environmental changes to avoid collisions with other flying objects, which is a highly complex and challenging problem. Path planning for multiple UAVs is essentially a multiconstraint combinatorial optimization problem [10], and the nature of combinatorial optimization makes it become a strongly NP-hard complexity problem [11]. Moreover, the presence of multiple environmental constraints and the varying performance capabilities of the UAVs contribute to the increased complexity in achieving optimal solutions.

The performance limitations of a single UAV must be taken into account during the actual path planning process, in addition to the limitations of objective conditions like the job task and its environment [12]. As demonstrated in Figure 1, path planning for UAVs entails getting the group job specifications and quickly computing a workable path for every UAV. This process takes into full consideration the significant influencing factors, including both static and dynamic factors. The static factors encompass UAV capabilities, region scope, and fixed obstacles. On the other hand, the dynamic factors involve cooperative relationships, communication networks, and moving obstacles. The cooperative path planning of UAVs is aimed at efficiently generating feasible pathways for each UAV while ensuring that the UAVs can efficiently accomplish the cluster mission.

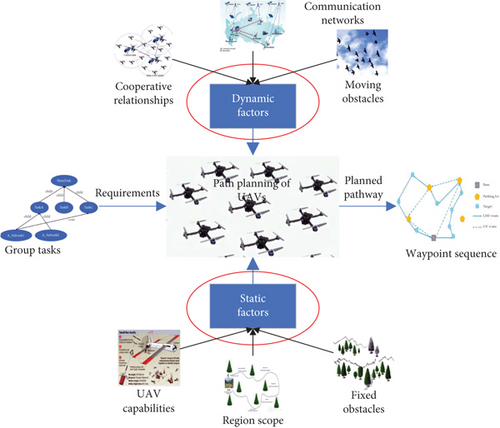
With the extensive application of large-scale UAV collaborative work, multi-UAV path planning has gained widespread attention and has become a hot topic in the current research field of UAV technology. Researchers with diverse backgrounds have studied and investigated multi-UAV path planning issues with various restrictions and objectives in recent years. However, due to the multitude of constraints, immense computational requirements, and the complexity of UAV motion models, most previous studies have simplified the UAV constraints and applied them to relatively simple static environments. As a result, they have been unable to generate optimal solutions for path planning in real-time complex environments. Luckily, deep reinforcement learning techniques based on trial-and-error learning mechanisms have been widely applied to address multi-UAV path planning problems. These techniques adapt to dynamically changing environments and generate optimal paths for each UAV, thanks to the rapid advancements in artificial intelligence technology. Compared to traditional methods, deep reinforcement learning approaches have significant advantages in complex environments, demonstrating stronger robustness and enabling true collective intelligence [13].

However, despite the potential of deep reinforcement learning algorithms in addressing multi-UAV path planning problems, they face several challenges. One of these challenges is how to effectively utilize valuable experiences [14]. During the training process, deep reinforcement learning algorithms need to interact with the environment and extract useful knowledge from experiences. However, due to the complexity and diversity of path planning problems, effectively leveraging experiences becomes quite difficult. Furthermore, deep reinforcement learning algorithms are prone to instability during the training process [15]. This means that the algorithm may experience fluctuations and inconsistencies, leading to slower convergence speeds.

The remainder of this work is organized as follows. Section 2 reviews related work of path planning. In Section 3, the cooperative path planning of multiple UAVs is abstracted as a multiconstraint combinatorial optimization problem, and its Markov model is established. Section 4 presents the PERDE-MADDPG algorithm. In Section 5, simulation experiments are carried out, and the proposed algorithm’s efficacy is confirmed. Section 6 summarizes the work of this paper and future research directions.

2. Related Work

Path planning is aimed at designing the optimal path for each drone to follow during its flight [16], which is the main key reason why multiple UAVs can be successfully deployed in different domains [17]. Path planning algorithms can generally be categorized into three main groups: sampling-based methods, heuristic algorithms, and deep reinforcement learning algorithms.

Probabilistic Roadmap Method (PRM) [18] and Rapid-exploration Random Tree (RRT) [19] are the main sampling methods. The sampling method avoids the need to model the entire environmental space and instead reconstructs the environment using sampled points, resulting in relatively lower computational intensity. For instance, Yan, Zhuang, and Xiao [20] proposed a real-time path planning technique for UAV in intricate 3D environments. A modified PRM is introduced in this work by random sampling in a bounding box array. Song et al. [21] proposed an improved Rapid-exploration Random Tree (RRT) path planning algorithm for the application of automated land vehicles (ALVs), which combines the no logic constraints of the vehicle and the double extended RRT to not only improve the searching efficiency but also ensure the feasibility of the paths. Although sampling methods can handle path planning problems in high-dimensional environments, they rely on random sampling within the problem space, which makes it impossible to guarantee the quality of the obtained paths. As a result, the outcomes are frequently less than ideal.

Heuristic-based methods include genetic algorithm (GA) [22], particle swarm algorithm (PSO) [23], ant colony algorithm (ACO) [24], and others. Most heuristic algorithms search for spatially optimal solutions by mimicking group organisms’ behavior, such as foraging or roundup capture. These algorithms can solve high-dimensional, multiconstraint optimization problems. To address the issue of the traditional PSO algorithm easily falling into local optima, Huang et al. [25] proposed a novel PSO algorithm called ACVDEPSO. In this algorithm, the velocity of particles is transformed into cylinder vectors for the convenience of path searching. To overcome the main drawbacks of low search efficiency in solving path planning problems using the traditional ACO algorithm, Li, Xiong, and She [26] introduced variable pheromone enhancement factors and variable pheromone evaporation coefficients into the ACO algorithm, proposing a new algorithm called ACO-VP. Despite the capability of heuristic algorithms to find approximate optimal solutions in large-scale problems and effectively explore complex search spaces, they often suffer from slow convergence, complex operations, long computation time, and sensitivity to parameters.

Sampling methods and heuristic algorithms mostly deal with UAV cluster task allocation and path planning problems separately, ignoring the coupling between the two. Deep reinforcement learning algorithms are more task-oriented and guided by reward functions to accomplish task allocation, path planning, collision avoidance, and obstacle avoidance under the premise of satisfying various constraints. For the problem of slow convergence due to the low reward of training samples, Jun, Yunxiao, and Li [27] combined HER with DQN to increase the sample validity of the experience pool, thus improving the convergence speed. Han et al. [28] employed the artificial potential field approach to influence the DDPG algorithm’s action selection, which ultimately improved the path smoothness and shortened the path length. The benefits of using reinforcement learning algorithms to solve path planning problems include their capacity to adapt to complex environments and their adaptive and generalization abilities.

However, despite the various advantages of deep reinforcement learning algorithms in solving multi-UAV path planning problems, they still face some problems. Two significant challenges are how to efficiently utilize experience, as well as the instability and slow convergence speed during the training process. To address the challenge of effectively utilizing experience, we propose a PER mechanism based on TD-error. This mechanism assigns priority based on the TD-error of experience, reflecting the importance of each experience in learning and decision-making. In addition, we address the issues of instability and slow convergence during the training process by introducing a delayed update strategy. By using this delayed update strategy, the frequency of parameter updates during the training process can be reduced, thereby increasing the stability of the training.

3. Problem Formulation and System Model

In this section, we define and model the path planning problem of multiple UAVs. Firstly, the path planning problem is described as an optimization problem subject to multiple constraints. Then, in order to satisfy the optimization conditions, we construct a multiagent system based on the MADDPG framework.

3.1. Formulation of the Multi-UAV Path Planning Problem

In our work, a fleet of N homogeneous UAVs navigates from their respective starting points to predefined destinations by communicating and coordinating in the air, which need to navigate around M obstacles. Like most research studies, we assume that all UAVs fly at the same altitude, focusing primarily on horizontal control and ignoring the UAVs’ lift control. And we use P_i(t) = (x_i(t), y_i(t)), i ∈ [1, N] to represent the position of the UAV i at time t. Since the UAVs are homogeneous, their radii are all the same and can be represented by r. In addition, we use P_i = (x_i, y_i), i ∈ [1, N] to represent the destination position of UAV i, and $$, j ∈ [1, M] is used to represent the position of obstacle j. Meanwhile, we employ r_j, j ∈ [1, M] to denote the radius of obstacle j.

As shown in Figure 2, D_i(t) is the distance at time t from the current position of UAV i to the predefined destination; D_arrived represents the arrival threshold, where UAV i is considered to have reached its destination when D_i(t) is less than D_arrived and u_i(t) indicates its linear velocity at time t, ψ_i(t) denotes its heading angle which means the angle between the linear velocity and the x-axis direction at time t, the angle between the target line vector at time t and the velocity vector of UAV i is represented by α_i(t), which stands for the target velocity angle, respectively. ψ_i(t) and α_i(t) are within the range of (−π, π], and the angular velocity of UAV i at time t is denoted by w_i(t). And the following is a definition of its motion model:

$$ ()

The collaborative path planning problem in this work is aimed at creating an uninterrupted flight path for each UAV connecting its starting position and destination while avoiding collisions with other obstacles and UAVs. Each UAV should arrive at its specified position at a given time point. Therefore, a time-sensitive series of waypoints can be used to characterize the flight route of a specific UAV. The time-sensitive waypoint sequence for UAV i is represented by φ_i, which has the following representation:

$$ ()

where $$ represents the k-th time-sensitive waypoint, indicating that at time point $$, UAV i should arrive at position $$. And when UAV i reaches its destination at the arrival time T_i, $$ denotes the last waypoint. This study focuses on multi-UAV collaborative path planning, with the primary goal being the effective search for an ideal time-sensitive waypoint sequence φ_i for UAV i. The following three restrictions must be followed while creating the flight routes for UAVs:

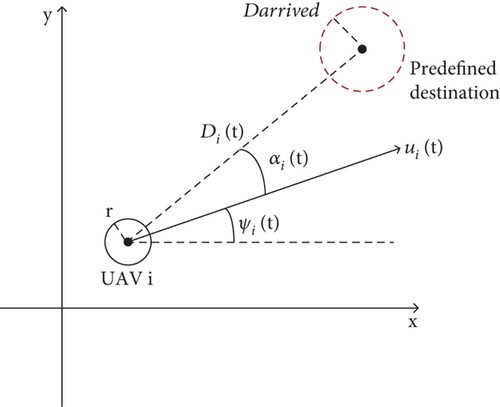
• 1.

  Collision avoidance constraint: Each UAV should avoid collisions with other UAVs or obstacles. We define the safety distance d_s between two UAVs as the sum of their radius, which is equal to d_s = 2r. The safety distance $$ between UAV i and obstacle j is defined as the sum of the radius of UAV i and obstacle j, which is equal to $$. Specifically, at any time, the distance between UAVs should be not less than d_s, and the distance between UAV i and obstacle j should be not less than $$. Therefore, this constraint can be expressed as follows:

$$ ()

• 2.

  Motion state update constraint: Each UAV motion state needs to be periodically updated by applying a new control vector through iterative steps. The UAV motion over short durations Δt can be considered as uniform linear motion. Based on the dynamic model shown in Equation (1), the following is an expression for this constraint:

$$ ()

• 3.

  Destination arrival constraint: We consider a UAV to have reached its destination when the distance between the UAV and the endpoint is less than D_arrived. Moreover we use T_i to represent the time at which UAV i reaches its destination. This constraint can be expressed as follows:

$$ ()

The collaborative path planning problem can be described as the minimization of the total flight distance for all UAVs, as its primary objective is to find collision-free routes for each UAV to efficiently reach their respective targets. According to the waypoint sequence φ_i in Equation (2), L(φ_i) is a representation of the flight length of UAV i from its starting point to its endpoint.

It can be calculated using the following formula:

$$ ()

The collaborative path planning problem addressed in this paper is to find the optimal path for each UAV without collision, aiming to minimize the total path length of all UAVs. It can be expressed as follows:

$$ ()

4. The PERDE-MADDPG Approach

In this section, we propose the PERDE-MADDPG algorithm to solve the path planning problem of multiple UAVs. The PERDE-MADDPG algorithm builds upon the MADDPG algorithm and introduces a PER mechanism based on sample priority, which replaces the traditional empirical playback mechanism. And this algorithm incorporates delayed update skills to reduce the update frequency of the actor network and target network parameters, which helps mitigate the impact of parameter instability.

In this approach, each UAV is considered as an autonomous agent that intelligently learns a reasonable path selection strategy and executes optimal actions based on its current local observations. Similar to the MADDPG algorithm, the proposed approach employs a system with centralized training and distributed execution. In the decentralized execution phase, agents have the capability to share their experiences and iteratively optimize their policies through interactions with the environment and other agents. During the phase of decentralized execution, each agent independently takes actions according to its observations based on its policy.

The PERDE-MADDPG algorithmic architecture is shown in Figure 3, which can be divided into three main parts: environment, UAVs, and replay buffer D. Below, a detailed explanation will be provided for each section.

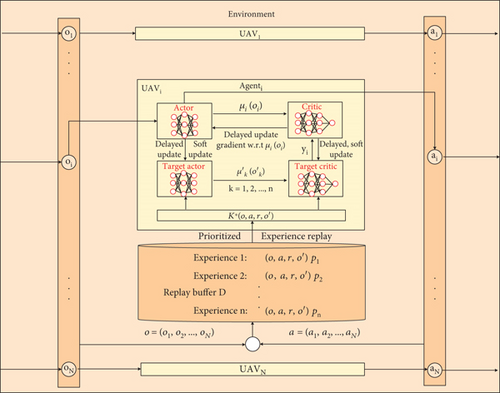
First, the environment module serves as a simulation environment for the path planning problem. It encompasses all the elements that the UAVs need to perceive and interact with. The environment provides state information, such as the current position and velocity, to the UAVs. Through interactions with the environment, the UAVs execute actions and receive reward signals, enabling them to learn adaptive path planning strategies. The environment module plays the role of facilitating the interaction between the UAVs and provides necessary information and feedback.

Next, the UAV module is the core of the system, where each UAV is represented by an intelligent agent responsible for generating optimal paths for each UAV. The agent utilizes deep reinforcement learning to select actions based on the environment and experiences stored in the pool. Each agent consists of four networks: actor, critic, target actor, and target critic. The actor network chooses actions based on the environment state. The critic network scores the state-action pairs for path planning. The target networks stabilize the training process. During network updates, we employ a delayed update strategy on top of soft updates, where the critic network is updated multiple times while the actor and target networks are updated once. This reduces the update frequency of the actor and target networks, making the training more stable. During the training process, the agents update their parameters based on reward signals and environmental feedback, continuously improving their path planning strategies.

Finally, the replay buffer module is used to store the UAVs’ experiences in the environment and provide samples for the UAV module during training. The replay buffer adopts the PER method, assigning priorities to experiences and sampling and updating them based on these priorities. As a result, experiences that have a greater impact on path planning are selected more frequently for training, thereby improving the efficiency and performance of the path planning algorithm. Through PER, UAVs can better leverage their previous experiences to optimize their path planning strategies.

And the following can be used to characterize each agent’s training process: (1) By interacting with the environment, each agent obtains its local observation o_i and uses the actor network to determine its optimal action a_i. (2) All agents execute their optimal actions, and the environment transitions to the next state S^′. (3) Experience transitions, defined as tuples {o, a, r, o^′}, are stored in an experience replay buffer D. (4) From the replay buffer D, K experiences are sampled based on sample priorities to update the network parameters. (5) The critic network is updated by minimizing the loss. (6) After multiple updates to the critic network, the actor network is updated once using gradient ascent, while the target actor network and target critic network are updated once using a soft update method.

5. Experiments and Results

In this section, we conduct experiments in the MPE (multiagent particle environment) simulation environment to validate the effectiveness of the proposed PERDE-MADDPG algorithm. We evaluate our method’s performance by contrasting it with three widely used reinforcement learning algorithms: MATD3 [30], MADDPG [31], and SAC [32]. In the following sections, we first explore the settings of parameters in our proposed algorithm and then test the performance gains of our method based on average reward, arrival rate, and path length.

5.1. Parameter Setting

The four approaches’ parameters correspond to the configurations found in [33, 34], as shown in Table 1. The effectiveness of the reinforcement learning algorithms is strongly influenced by the number of neurons in the neural networks’ hidden layers as well as the learning rate of each network. Thus, in order to figure out the ideal values for later trials, we first carry out tests to assess the effects of the number of neurons n and the learning rate ρ.

Table 1. Parameter configuration in the algorithm.

Parameters	Value
Batch size K	1024
Replay buffer D	1e6
Update interval φ	50
Soft update rate τ	1e − 2
Priority parameter α	0.6
Reward discount factor γ	0.95
Delayed update interval ω	100
Number of steps in each episode T	100
The total number of episodes Emax	50,000

In the experiments shown in Figures 4 and 5, there are 4 UAVs and 12 obstacles, and their positions are randomly generated. Each UAV flies towards its destination while avoiding collisions with obstacles and other UAVs. Figures 4 and 5 display the mean episode reward (every 1000 episodes) in the training process of the PERDE-MADDPG method.

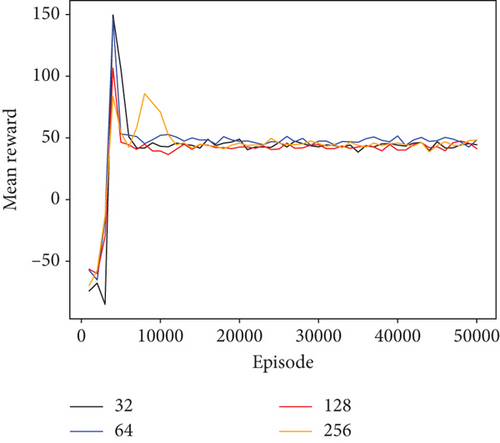
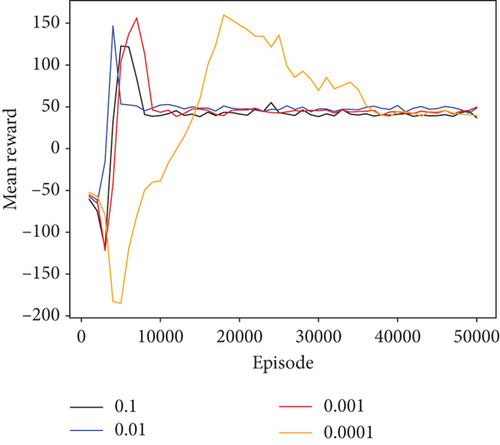
As shown in Figure 4, the number of neurons in the hidden layers changes from 32 to 256. From Figure 4, it can be observed that our method achieves the shortest convergence time and highest reward when the number of neurons is set to 64. As a result, setting the neuron number n to 64 is advised. Similarly, Figure 5 shows the average reward when the learning rate ρ increases. It can be seen that when the learning rate is set to 0.01, the algorithm converges faster and achieves a higher reward. Therefore, we set the learning rate ρ to 0.01.

5.2. Mean Reward Evaluation

Under the parameter settings mentioned earlier, we evaluate the performance of our method based on mean reward, which is the mean value of the rewards obtained per episode during the evaluation process. The average reward is a significant indicator of reinforcement learning algorithms’ learning efficiency and optimization capability. Algorithms that achieve higher mean reward are considered more efficient and accurate. In this subsection, we sum up the rewards of the agents over 100 evaluate episodes, calculate the mean reward by dividing the sum by 100, and evaluate the performance of different methods by comparing their average rewards.

Figure 6 displays the average rewards obtained by the four reinforcement learning methods under different scenarios, where the number of obstacles is fixed at 12, and the number of UAVs ranges from 2 to 6. From the graph, it can be observed that as the number of UAVs increases, the average rewards for each method also increase. This is because, with an increasing number of UAVs, although the number of times each UAV reaches its destination decreases, the overall number of successful UAV arrivals increases, resulting in higher rewards. Furthermore, we can also observe that regardless of the number of UAVs, our proposed PERDE-MADDPG algorithm achieves higher mean reward than the other three algorithms. For instance, when the number of UAVs is 5, our algorithm obtains a reward of 52.70, which is an improvement of 10.43% compared to MATD3, 17.27% compared to MADDPG, and 26.74% compared to SAC.

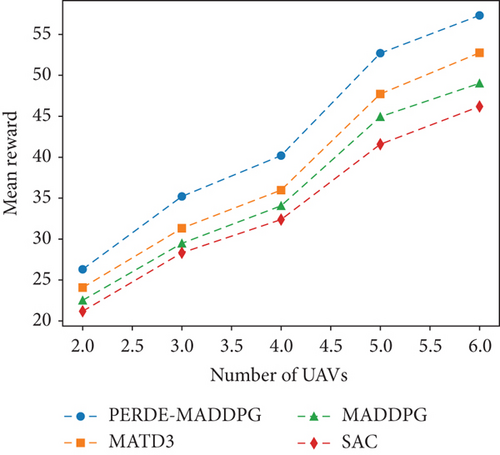
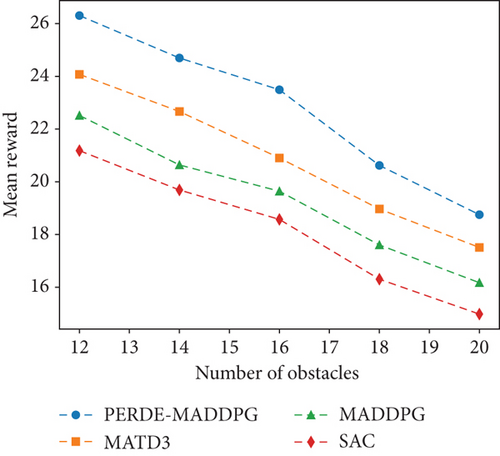
Figure 7 illustrates the average rewards obtained by the four reinforcement learning methods under different scenarios, where the number of UAVs is fixed at 2 and the number of obstacles ranges from 12 to 20. From the graph, it can be observed that as the number of obstacles increases, the average rewards for each method decrease. This is because, with more obstacles, the likelihood of collisions between UAVs increases, making it more challenging to reach their destinations and resulting in lower rewards. Additionally, we can also observe that regardless of the number of obstacles, our proposed PERDE-MADDPG algorithm achieves higher mean reward than the other three algorithms. For instance, when the number of obstacles is 20 and the number of UAVs is 6, our algorithm obtains a reward of 18.75, which is an improvement of 7.10% compared to MATD3, 15.96% compared to MADDPG, and 25.18% compared to SAC.

5.3. Arrival Rate Evaluation

The arrival rate is an important metric for evaluating path planning algorithms. We evaluate the trained algorithm in different scenarios for 100 episodes. Each time all UAVs reach their destinations, we increment the counter for successful episodes. Therefore, the arrival rate of the algorithm in a particular scenario is defined as the number of successful episodes divided by 100.

Figure 8 shows the arrival rate of four different methods in various scenarios where the number of obstacles is fixed at 12 and the number of UAVs ranges from 2 to 6. Based on the graph, it is evident that as the number of UAVs increases, the success rates of all four algorithms demonstrate a comparable pattern. This is because, with more UAVs, the likelihood of collisions between them increases, resulting in a decrease in the number of successful episodes. Additionally, the graph also indicates that our algorithm outperforms the other three methods when the number of UAVs is fixed. For instance, when the number of UAVs is five, the success rate of the PERDE-MADDPG algorithm is 40.00%, which is 10.00%, 13.00%, and 16.00% higher than that of MATD3, MADDPG, and SAC, respectively.

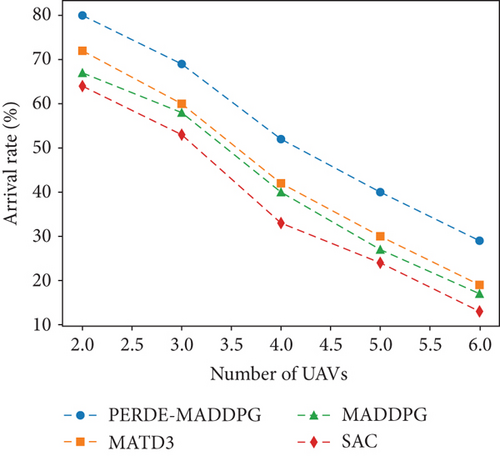
Figure 9 illustrates the arrival rate of four different methods in various scenarios where the number of UAVs is 2 and the number of obstacles ranges from 12 to 20. From the graph, it is clear that the arrival rate of all four algorithms falls as the number of obstacles rises. This is because with more obstacles, the scenarios become more complex, and the likelihood of collisions between UAVs and obstacles increases, resulting in a decrease in the success rate. Additionally, the graph also demonstrates that regardless of the number of obstacles, our algorithm outperforms the other three methods. For instance, when the number of obstacles is 20, the success rate of the PERDE-MADDPG algorithm is 70.00%, which is 9.00%, 14.00%, and 17.00% higher than that of MATD3, MADDPG, and SAC, respectively.

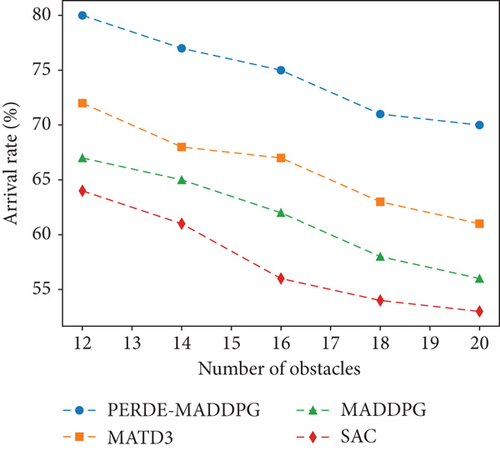
5.4. Path Length Evaluation

In this section, we will validate the performance of our method by evaluating the total length of the planned paths. As stated in Equation (7), the objective of multi-UAV path planning is to minimize the total length of the planned paths. Therefore, a direct evaluation of path planning methods is to compare the total lengths of the planned paths. A more accurate method will generate shorter path lengths for the UAVs.

We will evaluate the trained algorithm in different scenarios for 100 episodes. If, in an evaluating episode, all UAVs reach their destinations, we will record their total path length. The path length of the planned paths in different scenarios is then defined as the total path length of all UAVs in successful episodes divided by the total number of successful episodes.

Figure 10 shows the path lengths of four methods in the experiment with 12 obstacles and a varying number of UAVs from 2 to 6. It can be seen that as the number of UAVs increases, the path lengths of all methods also increase. This is because the total flying distance of UAVs increases with the number of UAVs. Additionally, as the number of UAVs increases, the probability of collisions between UAVs also increases. To avoid collisions, UAVs tend to choose longer paths, thus increasing the flying distance. From Figure 10, it can be observed that regardless of the number of UAVs used in the experiment, our PERDE-MADDPG method consistently plans paths with shorter lengths compared to the other methods. When the number of UAVs is five, our method achieves a path length of 89.78 km, which is 7.64%, 10.13%, and 13.76% shorter than the path lengths produced by the MATD3, MADDPG, and DDPG algorithms, respectively.

Figure 11 displays the path lengths of four methods in the experiment with a fixed number of 2 UAVs and a varying number of obstacles from 12 to 20. It is evident that as the number of obstacles increases, the path lengths of all methods also increase. This is because as the number of obstacles increases, the likelihood of collisions between UAVs and obstacles also increases. UAVs need to navigate through more complex paths to avoid collisions with obstacles. From Figure 11, it can be observed that our PERDE-MADDPG method consistently plans paths with shorter lengths compared to the other methods, regardless of the number of obstacles. When the number of obstacles is 16, our method achieves a path length of 35.2 km, which is 5.98%, 10.19%, and 14.62% shorter than the path lengths produced by the MATD3, MADDPG, and SAC algorithms, respectively.

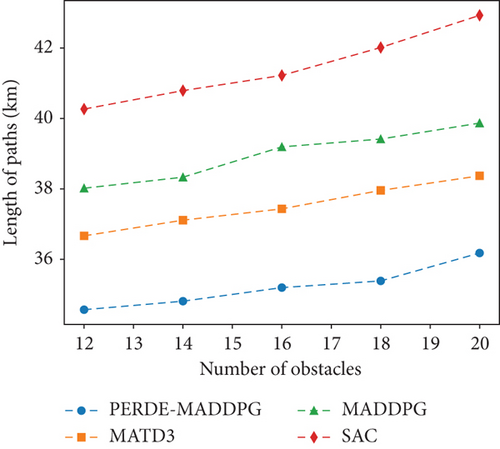
6. Conclusions

This paper proposed a path planning algorithm: PERDE-MADDPG based on PER and delayed update skills. When selecting experiences from the experience pool, we employed a PER mechanism to utilize valuable experiences efficiently. On this basis, we have adopted a delayed update strategy to address the issue of unstable updates during the agents’ training process. Experimental results show that our proposed PERDE-MADDPG algorithm outperforms better than the MATD3, MADDPG, and SAC algorithms in terms of mean reward, arrival rate, and planned path lengths under different environments. However, when the number of drones becomes too large, the PERDE-MADDPG algorithm also suffers from difficulties in convergence and poor training performance. So, we intend to further incorporate attention mechanisms in the future to boost the PERDE-MADDPG algorithm’s performance.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the National Natural Science Foundation of China (No. 62106202), the Key Research and Development Program of Shaanxi (No. 2024GX-YBXM-118), the Aeronautical Science Foundation of China (No. 2023M073053003), and the Fundamental Research Funds for the Central Universities.