International Journal of Aerospace Engineering

Volume 2024, Issue 1 1263459

Research Article

Open Access

Fixed-Time Sliding Mode Control for Robotic Manipulators Based on Disturbance Observer

Tianli Li,

Tianli Li

School of Intelligent Manufacturing , Anhui Wenda University of Information Engineering , Hefei , 230000 , China

Search for more papers by this author

Gang Zhang,

Corresponding Author

Gang Zhang

[email protected]

orcid.org/0000-0001-6534-2018

Anhui Undergrowth Crop Intelligent Equipment Engineering Research Center , Lu’an , 237012 , China

Search for more papers by this author

Tan Zhang,

Tan Zhang

Anhui Undergrowth Crop Intelligent Equipment Engineering Research Center , Lu’an , 237012 , China

Search for more papers by this author

Jing Pan,

Jing Pan

Anhui Undergrowth Crop Intelligent Equipment Engineering Research Center , Lu’an , 237012 , China

Search for more papers by this author

Tianli Li,

Tianli Li

School of Intelligent Manufacturing , Anhui Wenda University of Information Engineering , Hefei , 230000 , China

Search for more papers by this author

Gang Zhang,

Corresponding Author

Gang Zhang

[email protected]

orcid.org/0000-0001-6534-2018

Anhui Undergrowth Crop Intelligent Equipment Engineering Research Center , Lu’an , 237012 , China

Search for more papers by this author

Tan Zhang,

Tan Zhang

Anhui Undergrowth Crop Intelligent Equipment Engineering Research Center , Lu’an , 237012 , China

Search for more papers by this author

Jing Pan,

Jing Pan

Anhui Undergrowth Crop Intelligent Equipment Engineering Research Center , Lu’an , 237012 , China

Search for more papers by this author

First published: 16 August 2024

https://doi.org/10.1155/2024/1263459

Academic Editor: Jinchao Chen

Share a link

Email
Wechat
Bluesky

Abstract

A novel controller using fixed-time sliding mode (FTSM) and fixed-time disturbance observer (FTDO) is proposed to achieve trajectory tracking control of robotic manipulators. First, the mathematical model is established for robots with dynamic model uncertainties and external disturbances. An FTSM control strategy is presented where the integral terms of position errors are introduced into the existing sliding mode surface (SMS) to reduce the steady-state error of the system. The exponential form in the integral terms can provide an appropriate control force for tracking systems when the position errors are far from the sliding surface for a long time. Then, an FTDO is designed to obtain a precise estimation of lumped disturbances which can be used to weaken the impact of disturbances on the control accuracy. Finally, the fixed-time convergence properties of the tracking control system are demonstrated using Lyapunov stability theory. Simulation research is carried out to illustrate that the proposed control strategy has strong robustness and fast-tracking speed.

1. Introduction

With the expansion of the application range of robotics technology, the performance requirements for robotic manipulators are constantly improving. Consequently, the trajectory tracking accuracy of robots has important research significance [1–3]. In this regard, researchers have put forth an array of control algorithms, including fuzzy control [4], proportional integral differential (PID) control [5], sliding mode control (SMC) [6, 7], robust control [8], and backstepping control [9].

A learning algorithm controller based on the SMC theory was designed in [10], which achieves good tracking performance without considering the dynamic model of aerial manipulators. A variable universe fuzzy controller whose universe can be adjusted by contraction-expansion factor in real-time was presented to optimize the trajectory tracking effect of the system [11]. The dynamic model of mobile manipulators was adjusted, and the control laws of two subsystems were obtained based on the decentralized control method [12]. It is worth noting that these studies of tracking control for robotic manipulators did not adequately consider model parameter perturbations. However, SMC has a switching term, and its sliding mode dynamics can be designed, which has strong robustness to model uncertainties and external disturbances, so it is widely used in robot control. A terminal SMC is devised for flexible joint robots to eliminate the effects of lumped disturbances and estimation errors while ensuring system convergence within a finite time [13], and it is possible to suppress lumped disturbances and enhance the system’s robustness by modifying the control parameters. To enhance the flexibility of human-robot interaction, a finite time control method combined with super-twisted terminal SMC was employed to eliminate the problem of chatter in the system [14]. A continuous terminal SMC algorithm was proposed for servo systems in [15], which avoids the problem of replacing switch functions based on boundary layer methods and overcomes the disadvantage of high-order derivative discontinuity in high-order SMC. In [16], a nonsingular terminal SMC was proposed for the cable-driven manipulator, and the designed control scheme is model-free, which can avoid the uncertainty of the system model. In these three studies, the finite time control methods were introduced, and Lyapunov’s stability theorem was used to prove closed-loop stability and finite time convergence characteristics. A composite controller combining model tracking control strategy and robust adaptive terminal SMC was constructed in [7], which enables the robot to achieve high-precision tracking control of both directed curved-trajectory and undirected polyline-trajectory. In [17–19], variable structure control was proposed for tracking control of a six-degree-of-freedom robotic arm. Control laws were formulated based on their kinematic and dynamic equations, and experiments were conducted on a pseudoindustrial autonomous articulated robot to verify the feasibility of the proposed method. To improve the accuracy of the task, [18] also discussed the coupling effect between the joints of the robotic manipulator. An embedded controller for robot platforms is introduced in [19], which can analyze its transient performance and achieve stable state signal feedback in trajectory tracking control tasks.

The above control method can only ensure the asymptotic or finite time convergence of the robot system. The disadvantage is that the stability time depends on the initial conditions of the system and cannot be obtained in advance. On this basis, a SMC strategy combining fixed time control was considered. In contrast to typical finite-time control, regardless of whether the original condition of the system is near or far from the balance point, fixed-time control can ensure that the tracking error quickly approaches zero within a fixed time [20]. Non-singular fixed-time sliding mode (FTSM) control strategies for robotic manipulators were studied in [21, 22], and adaptive control was cited to estimate and compensate for disturbances, The closed-loop system’s error signals all converge in a fixed time, and the convergence time does not require any prior knowledge about the initial state. This scheme does not require coupling of uncertain boundary information and can avoid singular points, effectively reducing the phenomenon of chatter in the system. A FTSM control was proposed for robots with dynamic uncertainties and external disturbances in [23], which can completely eliminate singularity. The benefits of the planned control strategy’s quick convergence time and excellent tracking accuracy are confirmed by the simulation results. A control scheme combining inverse trigonometric function, adaptive control algorithm, and FTSM was proposed for manipulator systems with uncertain disturbances [24], and the designed controller can achieve faster convergence speed and higher accuracy.

The trajectory-tracking effect of the robotic manipulator is susceptible to interference from the external environment and unmodeled dynamics within the system. Therefore, the disturbance observer technology is introduced into the control law to form composite control, which estimates and compensates for the lumped disturbance. It can effectively improve tracking accuracy and ensure system stability. The fixed-time tracking design and the use of observers for interference estimates were studied in [25], and numerical simulations were used to confirm the effectiveness of the proposed method. An FTDO-based control scheme combining fixed-time control and an adaptive neural network was designed to address the dynamics and internal disturbance uncertainties of aerial robots [26]. A new form of composite controller combining fixed time disturbance observer and SMC was developed in [7], which can solve the problem of chattering and is suitable for nonlinear systems, such as robot systems and surface unmanned ship control systems. A disturbance observer was presented in [27] to estimate and compensate for joint position errors generated in robot milling. In [28, 29], An FTSM control method combining FTDO has been proposed, which can accurately estimate the lumped disturbance. In this research, a disturbance observer was constructed based on fixed-time theory to estimate uncertainties in the system. The designed FTDO ensures that the observation error converges within a fixed time, which does not require prior knowledge of the initial observation errors.

In actual operation, robotic manipulators are easily affected by parameter perturbations and external disturbances. At present, fixed-time control theory is rarely applied to robot control. Therefore, this article attempts to combine the fixed-time algorithm, observer, and sliding mode methods for trajectory tracking control of manipulators. Based on the above discussion, this article considers an n-link robot model with dynamic model uncertainty. An FTSM control based on the FTDO is employed to guarantee rapid convergence of the tracking control system and avoid the chattering phenomenon. The main contributions of this article include the following:

1.
In contrast to the method developed in [30], the integral terms with respect to the position error are introduced into the FTSM, which can reduce the steady-state error of the system. The integral terms of the sign function are added into the sliding mode surface (SMS) instead of directly using the sign function, which eliminates the problem of chattering in the error tracking. Further combining the fixed-time theory ensures that all tracking errors in the system converge to zero within a fixed time.
2.
The FTDO proposed in this paper can accurately estimate and compensate for lumped disturbances, effectively improving the tracking performance of the system. Meanwhile, the sig(⋅) function is introduced to avoid the problem of observation chattering.

The remaining work tasks are arranged as follows: Section 2 introduces the preliminaries and problem description. Section 3 presents the controller design without lumped disturbances and conducts stability analysis. The design of control algorithms and system stability analysis under bounded lumped disturbances are introduced in Section 4. Section 5 presents the numerical simulation results on a robotic arm with two degrees of freedom. Finally, the conclusion of the article is given in Section 6.

2. Preliminaries and Problem Description

2.1. Preliminaries

Notation 1. (⋅)^T is the transpose matrix, |⋅| represents the absolute value, and ‖⋅‖ means the Euclidean norm. sig^a(x) = |x|^asign(x), a > 0, x ∈ R, and sign(x) denotes the standard sign function shown as

()

Lemma 1 (see [31].)Consider continuous radial unbounded functions V : Rⁿ⟶R₊ ∪ {0}, and meet the following conditions:

()

1.
If any x(t) satisfies the inequality:

()

then there exists a positive number θ, and θ ∈ (0, 1), so that the convergence time Tsatisfies

()

where ι₁, ι₂, p, q, and ϑ are positive numbers, and 0 < p < 1, q > 1.

2.
If any x(t) satisfies the inequality:

()

where c₁, c₂, d₁, and d₂ are positive numbers and 0 < d₁ < 1, d₂ > 1. The system converges within a fixed time, and its convergence time satisfies the following inequality:

()

2.2. Problem Description

Consider the dynamic description of an n-link rigid robot system as follows [32]:

()

where M(⋅) ∈ R^n×n represents the symmetric positive definite inertia matrix, C(⋅) ∈ Rⁿ denotes the Coriolis-centripetal matrix, G(⋅) ∈ Rⁿ is the gravitational matrix, q,

, and

are the position, velocity, and acceleration vectors, τ(t) ∈ Rⁿ is the control input torque, and J(q) describes the Jacobian matrix. The nonlinear term f(t) ∈ Rⁿ represents the vector of constrained force exerted by humans and the environment. τ_e ∈ Rⁿ means the model error of the robotic system.

To facilitate control design, we define

()

According to (6) and (7), robot dynamics can be expressed as follows:

()

where ϖ_i = −M⁻¹[J^T(x)f(t) + τ_e] is the lumped unknown disturbance of the robot system. The control objective is to design a controller that enables the system variable q to accurately track the given desired trajectory

, ensuring that the tracking error converges to a small neighborhood near zero. In the following, we abbreviate M(x) as M, C(x, v) as C, and G(x) as G.

Assumption 1. The nonlinear term f(t) is supposed to be constrained and bounded. The constrained force ϖ_i is bounded and satisfies , where is a positive constant.

Remark 1. In practical work, the forces that interact between the robot and its surroundings are mostly responsible for the external disturbance of the model. It has no effect on the system’s overall convergence; rather, it solely influences the estimated value or tracking error of the lumped interference during the operating time. In addition, the force f(t) is time-varying and bounded because of the constraints imposed by the robot’s physical structure. Then, we are aware that the robot’s joint position and joint velocity are related to the lumped disturbance ϖ_i = −M⁻¹[J^T(x)f(t) + τ_e]. We reasonably assume that the model error and disturbance are bounded because the system’s joint angles and velocities are bounded. Therefore, the above Assumption 1 is reasonable.

3. Controller Design Without Lumped Disturbances

For the convenience of controller design, the position and velocity errors between the tracking trajectory and the expected trajectory can be defined as

()

Differentiating (9) with respect to time yields, we have

()

We design the FTSM surface for e₁ and e₂ as follows:

()

where α₀ = α₁/α₂, β₀ = β₁/β₂, α₀ > 1, 0 < β₀ < 1, and α₃ > 0. α₁, α₂, β₁, and β₂ are positive odd numbers; k₁, k₂, k₃, and k₄ are positive real numbers; the value of k₄ will directly affect the speed at which the system reaches a steady state.

Remark 2. The SMS used in [30] is . However, the SMS is altered in this article where the integration term is introduced into (11), which avoids oscillation caused by the direct use of the sign function on the sliding surface. Moreover, the integral terms are used to provide the necessary control force to enable the tracking system to rapidly approach when the position error is distant from the sliding surface for a long time; conversely, when the position error is close to the sliding surface, it slows down to reduce chattering.

The derivative of S(t) is

()

The control law is defined as

()

where

()

where λ_i > 0(i = 1, 2, 3), m, n, a, and b are positive odd numbers and m > n, a < b.

Theorem 1. The designed tracking control law (13) enables the system to accurately track the desired trajectory x_d within a fixed time T₁.

Proof 1. Choosing the Lyapunov function V₁as

()

Differentiating V₁ leads to

()

From Lemma 1, the fixed time controller (13) can drive the tracking control subsystem to accurately track the desired trajectory and calculate the maximum convergence time T₁.

()

Within the maximum set time T₁, the sliding surface S can reach, i.e., S(t) = 0, . Furthermore, the tracking errors e₁ and e₂ will converge to zero along the SMS within a finite time. Based on the above analysis, the controller (13) can ensure that the robotic manipulator accurately tracks the given desired trajectory, namely, x = x_d and . The proof is completed.

4. Control Design With Lumped Disturbances

4.1. Disturbance Observer Design

The actual robot system ((6)) has external disturbances and system uncertainties, which can affect tracking accuracy and reduce system control performance. Therefore, in this section, a disturbance observer is introduced to estimate the lumped disturbance and compare it with the actual disturbance. The system corrects the disturbance estimation value to achieve the goal of disturbance error approaching zero. The detailed design steps are provided below.

Step 1. To facilitate the design of the observer, we can design an auxiliary variable ξ ∈ Rⁿ as follows:

()

where μ₁, μ₂, μ₃ and μ₄ are positive.

According to (8) and (19), the derivative of ξ is

()

Then, we design the fixed-time disturbance observer (FTDO) as

()

Step 2. Define the observation error as , we can obtain

()

According to (22), it is evident that if ξ converges, then also converges.

In the case of Assumption 1, to prove that the designed FTDO is fixed-time stable, we select the following Lyapunov function

()

The derivative of time for V₂ is

()

where

. According to Lemma 1, the state of the system ξ reaches stability within a fixed time.

4.2. Controller Design

According to (8) and (9), we can get

()

Similarly to (11), we have

()

The derivative of S(t) is

()

Then, the control law (13) becomes

()

where

()

Theorem 2. In the presence of lumped unknown disturbances, the system error can be guaranteed to converge to zero within a fixed time T by the designed observer (21), SMS (26), and control law (28).

Proof 2. We consider the following Lyapunov function V₃as

()

Differentiating V₃ yields

()

Next, we conduct stability analysis on the closed-loop system and construct the following Lyapunov function V:

()

Taking the derivative of V yields

()

where ι₁ = 2^{(m + n)/2n}min{μ₂, λ₂} and ι₂ = 2^{(a + b)/2b}min{μ₃, λ₃}.

Remark 3. After the sliding stage, , combining (27), it can be concluded that . Within the maximum set time, the designed control strategy can ensure that the system can quickly track the desired trajectory within a fixed time during both the arrival and sliding stages. According to the above operation, we know that within the convergence time, the system can observe lumped disturbances. Within a fixed time T, the system can reach the FTSM surface S, and the tracking errors e₁ and e₂ will eventually approach zero. Therefore, the convergence time for the control system to reach stability from the initial state satisfies

()

5. Simulations

To demonstrate the effectiveness of the proposed control, simulation experiments were conducted on a robotic manipulator with two rotating joints in the vertical plane, as shown in Figure 1 [32]. m_i and l_i are the weight and length of the link i, and l_ci is the distance from link i − 1 to the center of mass of joint i, i = 1, 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic of the manipulator with a two-joint robot.

We let

. According to Reference [32], the dynamics of robot manipulators can be described as (6), where

()

with

()

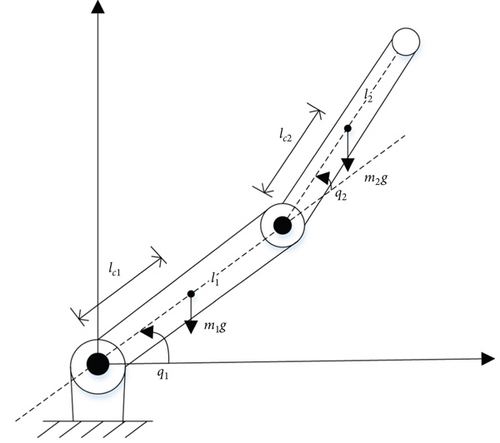
The parameter selection for the robot is m₁ = 2.00 kg, m₂ = 0.85 kg, l₁ = 0.35 m, l₂ = 0.31 m, I₁ = 6.1 × 10⁻⁴ kgm², and I₂ = 2.0 × 10⁻⁴ kgm².

The initial conditions of the system are determined by

()

The selection of the desired trajectory is the same as [32], x_d1 = 0.14sin(0.5t), x_d2 = 0.14cos(0.5t). We choose f(t) = [0.3sin(t); 0.3cos(t)] and τ_e = [0.1sin(t); 0.1cos(t)]. The simulation time is set to 40 s. The parameter values of the disturbance observer, SMC surface, and controller are shown in Table 1.

Table 1. The values of each parameter.

Variable	Value
μ₁	30
μ₃	5
α₁	7
β₁	5
k₁	100
k₃	2
α₃	5/3
n	5
b	9
λ₂	0.8
μ₂	4
μ₄	7
α₂	3
β₂	7
k₂	16
k₄	10
m	9
a	7
λ₁	1.2
λ₃	5

In this section, by contrasting the suggested control technique with the procedure in [30], the efficacy of the proposed strategy is confirmed. The sliding surface is designed in the following form:

()

The derivative of S is

()

The control law design in [30] is as follows:

()

where ε = λ₁S + λ₂S^m/n + λ₃S^a/b.

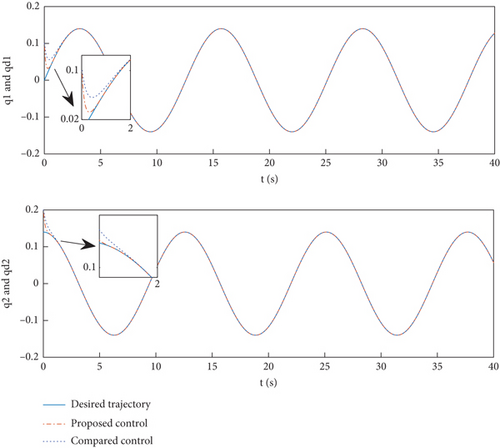
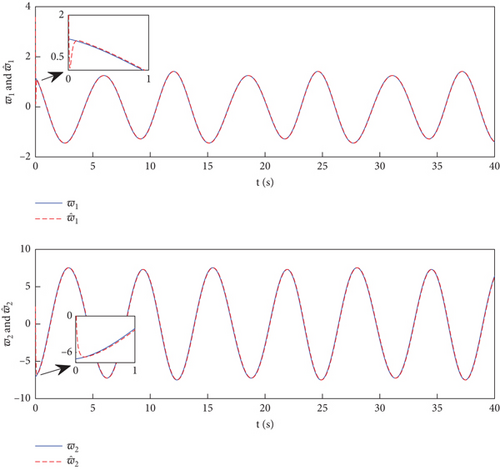
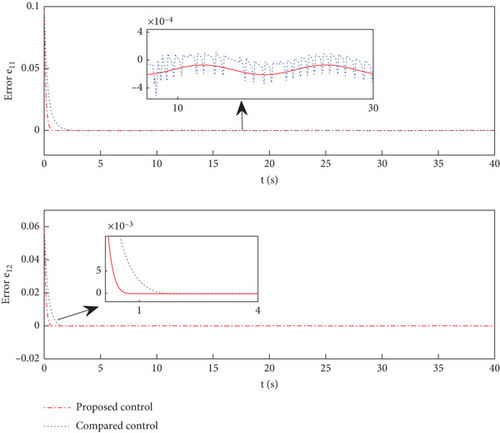
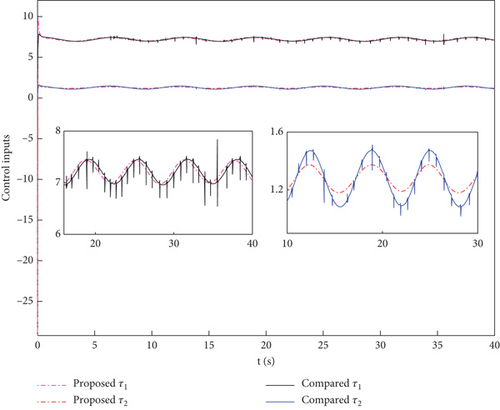
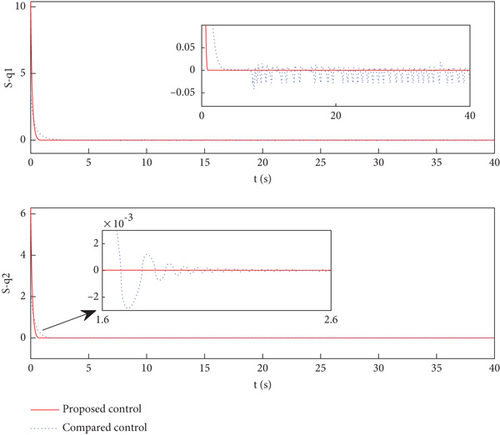
The results of the simulation are shown in Figures 2 and 3. Figures 2 and 4 illustrate the trajectory tracking and errors for two joints. From these two figures, we can see that both control design methods can effectively track the set desired trajectory. In Figure 4, it is evident that the tracking errors of e₁ and e₂ caused by the designed controller have higher accuracy than the control presented in [30], which proves that the added integral terms significantly reduce the steady-state errors of the system. The tracking errors can converge to zero within approximately 0.7 s with the proposed method, which is 58.8% faster than the comparative control. Additionally, the tracking error can be as small as 10⁻⁴ rad. The control inputs are shown in Figure 5. The proposed control input is smoother and without chatter, and this is because the integral terms of position errors are introduced into the sliding surface, which is a part of the control input. Figure 6 shows the response of variables S to the control scheme. The FTSM method was compared with the method developed in [30]. This reveals that the SMS in this article is smoother, and this is due to the SMS using the integral terms of the sign function, rather than directly using the sign function, which avoids system chattering. The disturbance true value ϖ_i and the observation value under the action of the observer are given in Figure 3, which demonstrates that the designed FTDO can achieve an accurate estimation of lumped disturbances.

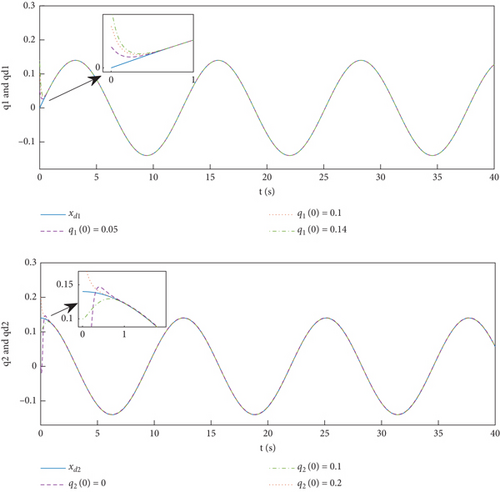
To prove that the time for the system to reach a stable state is independent of the initial state, we set the initial state as [q₁(0); q₂(0)] = [0.05; 0.1], [q₁(0); q₂(0)] = [0.1; 0.2], and [q₁(0); q₂(0)] = [0.14; 0]. The numerical simulation results are shown in Figure 7. It can be seen that under different initial conditions, the developed control algorithm can ensure the tracking of the desired trajectory within a fixed time, and the effectiveness of the designed control law is verified.

6. Conclusions

An FTSM control method based on FTDO was designed for trajectory tracking control of robot manipulators while considering the nonlinearity and uncertainty of the system. The stability of the designed controller and the fixed-time convergence of the observer were proven using the Lyapunov stability theorem. The comparison of simulation studies illustrates that the proposed strategy has a faster convergence speed and higher control accuracy. Then, the integral terms of the position error are applied to reduce steady-state errors, which benefit from providing an appropriate control force when the tracking error deviates or approaches the SMS. Moreover, the phenomena of chattering are lessened by adding the integral terms of the sign function to the sliding surface as opposed to employing the sign function directly. The designed FTSO can accurately estimate the lumped disturbance in the system and provide real-time compensation for the controller, effectively improving the robustness of the system. One of our future researches is to use optimization algorithms to adjust control parameters to improve control performance. Another task is to study the trajectory tracking control of dual-arm or multiarm robots and extend the proposed scheme to the aforementioned projects.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research was funded by the University Synergy Innovation Program of Anhui Province under Grant No. GXXT-2021-026, the Startup Fund for Distinguished Scholars of West Anhui University under Grant No. WGKQ2022050, the Smart Agriculture and Forestry and Smart Equipment Scientific Research and Innovation Team (Anhui Undergrowth Crop Intelligent Equipment Engineering Research Center) under Grant No. 2022AH010091.

Acknowledgments

Open Research

Data Availability Statement

All data utilized to support the findings of this paper are contained in the paper.

References

1 Cruz-ortiz D., Chairez I., and Poznyak A., Adaptive sliding-mode trajectory tracking control for state constraint master–slave manipulator systems, ISA Transactions. (2022) 127, 273–282, https://doi.org/10.1016/j.isatra.2021.08.023, 34517982.
10.1016/j.isatra.2021.08.023
PubMed Google Scholar
2 Spyrakos-Papastavridis E. and Dai J. S., Minimally model-based trajectory tracking and variable impedance control of flexible-joint robots, IEEE Transactions on Industrial Electronics. (2021) 68, no. 7, 6031–6041, https://doi.org/10.1109/TIE.2020.2994886.
10.1109/TIE.2020.2994886
Web of Science® Google Scholar
3 Zhu P. and Ren W., Fully distributed joint localization and target tracking with mobile robot networks, IEEE Transactions on Control Systems Technology. (2021) 29, no. 4, 1519–1532, https://doi.org/10.1109/TCST.2020.2991126.
10.1109/TCST.2020.2991126
Google Scholar
4 Fan Y. Q., Xing K. Y., and Jiang X. K., Fuzzy adaptation algorithms’ control for robot manipulators with uncertainty modelling errors, Complexity. (2018) 2018, 8, https://doi.org/10.1155/2018/5468090, 2-s2.0-85047506498, 5468090.
10.1155/2018/5468090
Google Scholar
5 Ma R. Y., Li Z. H., Jiang D., Yun J., Liu Y., Liu Y., Bai D., and Li G., Simulation research on trajectory tracking control system of manipulator based on fuzzy PID control, International Journal of Innovative Computing and Applications. (2022) 13, no. 5/6, 269–277, https://doi.org/10.1504/IJICA.2022.128434.
10.1504/IJICA.2022.128434
Google Scholar
6 Zhang L. Y., Su Y. X., Wang Z., and Wang H., Fixed-Time Terminal Sliding Mode Control for Uncertain Robot Manipulators, 2023, ISA Transactions, https://doi.org/10.1016/j.isatra.2023.10.011.
Google Scholar
7 Alinaghi Hosseinabadi P., Ordys A., Abadi A. S. S., Mekhilef S., and Pota H. R., State and disturbance observers-based chattering-free fixed-time sliding mode control for a class of high-order nonlinear systems, Advanced Control for Applications: Engineering and Industrial Systems. (2021) 3, no. 3, https://doi.org/10.1002/adc2.81.
10.1002/adc2.81
Google Scholar
8 Ramirez-Neria M., Ochoa-Ortega G., Lozada-Castillo N., Trujano-Cabrera M. A., Campos-Lopez J. P., and Luviano-Juarez A., On the robust trajectory tracking task for flexible-joint robotic arm with unmodeled dynamics, IEEE Access. (2016) 4, 7816–7827, https://doi.org/10.1109/ACCESS.2016.2618373, 2-s2.0-85012888599.
10.1109/ACCESS.2016.2618373
Google Scholar
9 Nikdel N., Badamchizadeh M., Azimirad V., and Nazari M. A., Fractional-order adaptive backstepping control of robotic manipulators in the presence of model uncertainties and external disturbances, IEEE Transactions on Industrial Electronics. (2016) 63, no. 10, 6249–6256, https://doi.org/10.1109/TIE.2016.2577624, 2-s2.0-84987755484.
10.1109/TIE.2016.2577624
Web of Science® Google Scholar
10 Andaluz G. M., Morales L., Leica P., Andaluz V. H., and Palacios-Navarro G., LAMDA controller applied to the trajectory tracking of an aerial manipulator, Applied Sciences. (2021) 11, no. 13, https://doi.org/10.3390/app11135885.
10.3390/app11135885
Google Scholar
11 Wang H. T., Jiang W. S., Jiang Q. Z., Zhang Q., and Dai N., Error analysis of optimizing manipulator trajectory tracking controller based on contraction-expansion factor, Acta Metrologica Sinica. (2020) 41, no. 10, 1177–1183.
Google Scholar
12 Fareh R., Saad R. M., Saad M., Brahmi A., and Bettayeb M., Trajectory tracking and stability analysis for mobile manipulators based on decentralized control, Robotica. (2019) 37, no. 10, 1732–1749, https://doi.org/10.1017/S0263574719000225, 2-s2.0-85062679581.
10.1017/S0263574719000225
Google Scholar
13 Rsetam K., Cao Z., and Man Z., Design of robust terminal sliding mode control for underactuated flexible joint robot, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2022) 52, no. 7, 4272–4285, https://doi.org/10.1109/TSMC.2021.3096835.
10.1109/TSMC.2021.3096835
Web of Science® Google Scholar
14 Wang Y. X., Sun T. R., and Yang J. T., Super-twisting nonsingular terminal sliding mode-based robust impedance control of robots, Complexity. (2022) 2022, 6, 9263699, https://doi.org/10.1155/2022/9263699.
10.1155/2022/9263699
Google Scholar
15 Hou H., Yu X., Xu L., Rsetam K., and Cao Z., Finite-time continuous terminal sliding mode control of servo motor systems, IEEE Transactions on Industrial Electronics. (2020) 67, no. 7, 5647–5656, https://doi.org/10.1109/TIE.2019.2931517.
10.1109/TIE.2019.2931517
Web of Science® Google Scholar
16 Wang Y. Y., Jiang S. R., Chen B., and Wu H. T., A new continuous fractional-order nonsingular terminal sliding mode control for cable-driven manipulators, Advances in Engineering Software. (2018) 119, no. 21, 21–29, https://doi.org/10.1016/j.advengsoft.2018.01.011, 2-s2.0-85041402647.
10.1016/j.advengsoft.2018.01.011
Web of Science® Google Scholar
17 Iqbal J., Ullah M. I., Khan A. A., and Irfan M., Towards sophisticated control of robotic manipulators: an experimental study on a pseudo-industrial arm, Strojniski Vestnik-Journal of Mechanical Engineering. (2015) 61, no. 7-8, 465–470, https://doi.org/10.5545/sv-jme.2015.2511, 2-s2.0-84947549947.
10.5545/sv-jme.2015.2511
Google Scholar
18 Ullah M. I., Ajwad S. A., Irfan M., and Iqbal J., Non-linear control law for articulated serial manipulators: simulation augmented with hardware implementation, Elektronika ir Elektrotechnika. (2016) 22, no. 1, 3–7.
10.5755/j01.eee.22.1.14094
Google Scholar
19 Iqbal U., Samad A., Nissa Z., and Iqbal J., Embedded control system for AUTAREP-A novel autonomous articulated robotic educational platform, Tehnicki vjesnik - Technical Gazette. (2014) 21, no. 6, 1255–1261.
Google Scholar
20 Wang D., Ge S. S., Liang X., and Li D., Time-synchronized formation control of unmanned surface vehicles, IEEE Transactions on Intelligent Vehicles. (2024) 1–9, https://doi.org/10.1109/TIV.2024.3371431.
10.1109/TIV.2024.3371431
Google Scholar
21 Zhang X., Shi R., Zhu Z., and Quan Y., Adaptive nonsingular fixed-time sliding mode control for manipulator systems’ trajectory tracking, Complex & Intelligent Systems. (2023) 9, no. 2, 1605–1616, https://doi.org/10.1007/s40747-022-00864-w.
10.1007/s40747-022-00864-w
Google Scholar
22 Sai H. Y., Xu Z. B., He S., Zhang E., and Zhu L., Adaptive nonsingular fixed-time sliding mode control for uncertain robotic manipulators under actuator saturation, ISA Transactions. (2022) 123, 46–60, https://doi.org/10.1016/j.isatra.2021.05.011, 34238519.
10.1016/j.isatra.2021.05.011
PubMed Web of Science® Google Scholar
23 Zhang L., Wang Y., Hou Y., and Li H., Fixed-time sliding mode control for uncertain robot manipulators, IEEE Access. (2019) 7, 149750–149763, https://doi.org/10.1109/ACCESS.2019.2946866.
10.1109/ACCESS.2019.2946866
Web of Science® Google Scholar
24 Zhang X. and Shi R., Novel fast fixed-time sliding mode trajectory tracking control for manipulator, Chaos, Solitons & Fractals. (2022) 162, article 112469, https://doi.org/10.1016/j.chaos.2022.112469.
10.1016/j.chaos.2022.112469
Google Scholar
25 Gao H. L. and Chen M., Fixed-time tracking control for two-link rigid manipulator based on disturbance observer, Transactions of the Institute of Measurement and Control. (2021) 43, no. 9, 1924–1935, https://doi.org/10.1177/0142331220983637.
10.1177/0142331220983637
Google Scholar
26 Li T., Li S., Sun H., and Lv D. C., The fixed-time observer-based adaptive tracking control for aerial flexible-joint robot with input saturation and output constraint, Drones. (2023) 7, no. 6, https://doi.org/10.3390/drones7060348.
10.3390/drones7060348
Google Scholar
27 Khishtan A., Wang Z. H., Kim S. H., Park S. S., and Lee J., Nonlinear disturbance observer-based compliance error compensation in robotic milling, Manufacturing Letters. (2022) 33, 117–122, https://doi.org/10.1016/j.mfglet.2022.07.017.
10.1016/j.mfglet.2022.07.017
Google Scholar
28 Ullah I. and Pei H. L., Fixed time disturbance observer based sliding mode control for a miniature unmanned helicopter hover operations in presence of external disturbances, IEEE Access. (2020) 8, no. 2020, 73173–73181, https://doi.org/10.1109/ACCESS.2020.2987960.
10.1109/ACCESS.2020.2987960
Web of Science® Google Scholar
29 Wang Y. and Chen M. S., Fixed-time disturbance observer-based sliding mode control for mismatched uncertain systems, International Journal of Control, Automation and Systems. (2022) 20, no. 9, 2792–2804, https://doi.org/10.1007/s12555-021-0097-x.
10.1007/s12555-021-0097-x
Web of Science® Google Scholar
30 Yu M. Y., Li Z. K., and Wang B. H., Fixed-time disturbance observer-based accurate formation control of unmanned surface vehicles, Control and Decision. (2023) 38, no. 2, 379–387.
Google Scholar
31 Polyakov A., Nonlinear feedback design for fixed-time stabilization of linear control systems, IEEE Transactions on Automatic Control. (2012) 57, no. 8, 2106–2110, https://doi.org/10.1109/TAC.2011.2179869, 2-s2.0-84864747003.
10.1109/TAC.2011.2179869
Web of Science® Google Scholar
32 Liu Y. J., Lu S. M., and Tong S. C., Neural network controller design for an uncertain robot with time-varying output constraint, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2017) 47, no. 8, 2060–2068, https://doi.org/10.1109/TSMC.2016.2606159, 2-s2.0-85028734602.
10.1109/TSMC.2016.2606159
Web of Science® Google Scholar

All articles

Fixed-Time Sliding Mode Control for Robotic Manipulators Based on Disturbance Observer

Abstract

1. Introduction