In this paper, a stochastic multi-objective (MO) modeling for the optimal reconfiguration and placement of photovoltaic (PV) systems in distribution networks (DNs) is presented. The main objectives are to jointly maximize the profit of generating companies (GenCos) as well as to minimize the distribution company’s (DisCo) costs and the expected interruption cost (ECOST). This approach can provide numerous economic and technical advantages for all players in the restructured power system, including GenCos, DisCos, and customers. To attain more practical and accurate results in the simultaneous placement of PVs and reconfiguration, uncertainties are considered in the problem formulation. To cope with the stochastic behavior of PV systems, electricity prices, and demands in the DN, the scenario approach is used. The proposed optimization problem is solved by the dragonfly algorithm (DA) and the best compromise solution is chosen using a fuzzy satisfying criterion. The results are also compared with the particle swarm optimization (PSO) algorithm. To confirm the effectiveness of the proposed MO model, it is implemented on the IEEE 33-bus DN and simulated in various case studies. The model is also applied to a real DN. The results confirm that the proposed model gives a more desired schedule than previous approaches, as all players in the DN including the PV owners, DisCo, and customers are satisfied at the same time.

1. Introduction

Recently, researchers have shown an increased interest in using distributed energy resources (DERs) such as wind and photovoltaic (PV) systems in distribution networks (DNs) [1, 2]. In addition, power quality and reliability improvements can be achieved for the customers by proper integration of DERs [3]. However, DNs can face serious security challenges, if DERs cannot appropriately and optimally integrate into the network. Accordingly, optimal sitting/sizing of DERs in the DN plays an important role in increasing the security, power quality, and reliability of the power system and reducing the costs of distribution companies (DisCos) [4]. Moreover, solving this optimization problem can lead to reducing customer interruption costs and increasing DER owners’ profit in a deregulated power system. To date, various methods have been developed and introduced for optimal sitting/sizing of DER based on single-objective (SO)/multi-objective (MO) functions [5, 6, 7, 8, 9]. Moreover, optimal sitting/sizing of DER along with optimal network reconfiguration has received critical attention due to high performance and efficiency [10].

Recent advances in the electricity industry have brought many benefits to grid operators and other players of DNs. Distribution network reconfiguration is one of the best tools to address the problem of DNs [11]. It is a problem in which the open/close conditions of switchable ties are determined to attain optimal configuration. The most important benefits of reconfiguration are the reduction of losses and improvement of voltage profile as well as reliability. Therefore, optimal distribution network reconfiguration can be introduced individually as a critical optimization problem to improve the power quality and reliability of DNs. Nevertheless, simultaneous optimal sitting/sizing of DER and network reconfiguration can provide more advantages for DER owners by changing the switch conditions in such a way that more power can be supplied to the consumers [10].

1.1. Literature Review

The optimal sitting/sizing of DER with optimal network reconfiguration as a separate optimization problem in DN is the best solution for coping with the challenges stemming from the high penetration of such sources. In [12], a MO reconfiguration for enhancing the voltage profile, reducing real power losses, and improving the voltage unbalance index for a DN is suggested based on the fast nondominated sorting genetic algorithm. Niknam [13] proposed a MO reconfiguration based on honey bee mating optimization to reduce the number of switching operations, and the real power loss and to improve the voltage profile. To minimize the loss of large-scale distribution systems, a system reconfiguration is also presented in [14]. Mazza et al. [15] offered an optimal MO reconfiguration for a distribution network to reduce energy not supplied (ENS) and power loss. The major drawback of this study is that the objective function is optimized only from DisCo’s viewpoint. In [16], an optimal reconfiguration for a real feeder is investigated. In a similar study, Ahuja et al. [17] suggested a MO reconfiguration. A MO reconfiguration using the discrete particle swarm optimization is proposed in [18]. Reduction of power loss, the number of switching operations, and enhancement of voltage profile are the main objectives of this paper. In [19], a reconfiguration method to reduce active power losses and improve the reliability index using the Ԑ-constraint is presented. A runner-root algorithm is used to cope with system reconfiguration in [20].

Several papers have been published on the joint optimal placement of DERs and system reconfiguration. In [10], the authors use system reconfiguration in the presence of DERs for power loss reduction and load restoration improvement. In [21], a method is suggested for optimal network reconfiguration in radial distribution networks with DERs to increase the load balance factor index and reduce power loss. A MO reconfiguration using an enhanced gravitational search algorithm for radial systems considering DERs is presented in [22]. In [23], using mixed-integer linear programing (MILP), the reconfiguration issue in the distribution network in the presence of DERs is investigated. The loss reduction from the DisCo view is the only objective of this paper. In another major study, Nikkhah and Rabiee [24] suggested a long-term planning model for a hybrid system in which the grid voltage stability is considerably improved.

In [25], in addition to considering reliability and power quality issues from the DisCo view, the cost of DERs from the distributed generation (DG) owners’ point of view is optimized using the PSO. The PSO is also used for dynamic and static reconfiguration with the optimized allocation of PV-DG and storage systems in [26]. Adaptive GA is employed to optimize the allocation of DERs in the DN considering uncertainties for loads and generations in [27]. In [28], the optimal network reconfiguration considering DERs is presented to reduce power and operation costs as well as to improve the voltage profile. In the same vein, Nasiraghdam and Jadid [29] presented the optimal network reconfiguration considering DERs using the artificial bee colony algorithm. Reconfiguration of DNs in the presence of DERs is done using the PSO algorithm in [30], to achieve an improved voltage profile and minimize switching operation costs. A joint feeder reconfiguration and optimal sizing method for DERs using the teaching–learning algorithm is proposed in [31]. In this study, ENS, power loss, and voltage profile are optimized only from the DisCo view. An optimal network reconfiguration with the presence of DERs to improve the distribution grid hosting capacity using a linearized power flow model is proposed in [32]. In [33], the optimal DG allocation and network reconfiguration are optimized considering probabilistic loads and DGs to enhance the voltage stability and loss profile. In [34], an optimization method is suggested for the dynamic feeder reconfiguration problem in the distribution system over multiple time intervals considering DERs. In another major study, Lotfi et al. [35] suggested a MO framework for feeder reconfiguration along with capacitor allocation problems over multiple time intervals considering DERs. A network reconfiguration and allocation of capacitor units in a radial distribution system using an enhanced artificial bee colony optimization is also proposed in [36]. In [36], the MO problem is considered as a combination of ENS and emission produced by DG units and grid; moreover, network loss is defined as the other objective function.

For better comparison, a summary of the abovementioned papers is given in Table 1. As can be seen, remarkable papers either separately or jointly have been published on DG sitting/sizing and network reconfiguration. However, the optimal sitting/sizing of DGs with network reconfiguration at the same time is not considerably taken into account due to the complexity of the problem. As stated before, it is required to take into account the influence of intermittency of DERs such as PV systems, the fluctuations in load demand, and electricity price in system reconfiguration. As can be observed in Table 1, very few studies have investigated the impact of uncertainties of electricity price, load as well as DERs at the same time. Furthermore, most of the MO optimization models presented in the above literature have been investigated only from DisCo’s point of view. It is apparent from the table that very few papers are focused on optimization models from DG owners’ or customers’ perspectives. However, there appears to be an absence of an MO optimization model for optimal sitting/sizing of DGs and network reconfiguration from DisCo’s, generating companies (GenCos), and customers’ points of view, simultaneously.

Table 1. Comparison between the existing papers and the proposed approach.

References	Objective		Reconfiguration	DG			Uncertainty			Objectives
References	O1	O2	R1	DG1	DG2	DG3	U1	U2	U3	A1	A2	A3	A4	A5
[12]	●	—	●	—	—	—	—	—	—	●	—	●	—	—
[13]	●	—	●	—	—	—	—	—	—	●	—	●	—	—
[14]	—	●	●	—	—	—	—	—	—	●	—	—	—	—
[15]	●	—	●	—	—	—	—	—	—	●	●	—	—	—
[16]	●	—	●	—	—	—	—	—	—	●	●	—	—	—
[17]	●	—	●	—	—	—	—	—	—	●	—	●	—	—
[18]	●	—	●	—	—	—	—	—	—	●	—	●	—	—
[19]	●	—	●	—	—	—	—	—	—	●	●	—	—	—
[20]	●	—	●	—	—	—	—	—	—	●	—	●	—	—
[21]	—	●	●	●	—	—	—	—	—	●	—	—	—	—
[22]	●	—	●	●	—	—	—	—	—	●	●	—	—	—
[23]	—	●	●	●	—	—	—	—	—	●	—	—	—	—
[24]	—	●	●	●	●	●	—	—	—	—	—	—	—	●
[25]	●	—	●	●	●	●	—	—	—	—	●	—	●	●
[26]	●	—	●	●	●	—	●	●	—	●	—	●	—	—
[27]	—	●	●	●	●	●	●	●	—	●	—	●	—	—
[28]	—	●	●	●	—	—	—	—	—	—	—	—	—	—
[29]	●	—	●	●	●	—	—	—	—	●	—	●	—	—
[30]	●	—	●	●	—	—	—	—	—	—	—	●	●	—
[31]	●	—	●	●	●	—	—	—	—	●	●	—	—	—
[32]	—	●	●	●	—	—	—	—	—	—	●	—	—	—
[33]	●	—	●	●	—	●	●	—	—	●	—	●	—	—
[37]	—	—	—	—	—	—	—	—	—	—	—	—	—	—
[35]	—	—	—	—	—	—	—	—	—	—	—	—	—	—
[36]	—	—	—	—	—	—	—	—	—	—	—	—	—	—
Proposed method	●	●	●	●	●	●	●	●	●	●	●	●	●	●

O1, multi-objective; O2, single-objective; R1, considering reconfiguration; DG1, the attendance of DGs; DG2, optimal DG sizing; DG3, optimal DG siting; U1, demand uncertainty; U2, DERs uncertainty; U3, price uncertainty; A1, loss minimization; A2, reliability enhancement; A3, voltage profile enhancement; A4, DisCo’s cost minimization; and A5, DG owner’s profit maximization.

1.2. Contributions and Paper Organization

This study suggests an optimal probabilistic MO network reconfiguration along with the sitting/sizing of PV systems in a DN. The impact of uncertainties in electricity price, loads, and PV systems is considered using a scenario-based approach. The suggested method jointly minimizes the cost of the DisCo, and expected interruption cost (ECOST) and maximizes the profit attained by the PV owners as GenCos. The optimization problem is solved using the dragonfly algorithm (DA) and compared with the PSO algorithm. The major contributions of the present paper are as follows:

(i)
The optimal reconfiguration model for a restructured distribution network is suggested with the economic aims from PV owners’, DisCo’s, and customers’ perspectives.
(ii)
The scenario method is used to deal with the uncertainties of loads, PV output, and electricity price.
(iii)
The sitting/sizing of PV systems in the DN is optimized using the proposed stochastic MO model.
(iv)
The proposed optimization problem is solved by the DA and the best compromise solution is chosen using fuzzy satisfying criterion.
(v)
The model is implemented on a standard test system and a real DN in various case studies.

The study is organized as follows. Section 2 describes the uncertainty modeling. Section 3 presents the problem formulation. The DA is described in Section 4. Simulation results are provided in Section 5. Finally, the conclusion is given in Section 6.

2. Uncertainty Modeling

PV systems have received great attention in Iran in recent years due to numerous advantages such as high availability of sunlight and cleanliness. However, the output power of PV systems considerably depends on solar radiation, thereby requiring the modeling of the solar system probabilistically. In other words, the output power of PV systems is intermittent owing to solar radiation variation. Owing to several reasons such as environmental conditions, time of day, month, season, and the orientation of the PV arrays to the sun radiation, there is a high degree of uncertainty in solar radiation. The solar radiation can be modeled with the beta distribution as follows [38]:

(1)

where α and β are, respectively, the beta distribution shape and scale factors (W/m²) and R is solar radiation (W/m²).

In this paper, the solar variation is separated into several scenarios to provide multistate variable modeling. The following equations have described the probability of each scenario [38]:

(2)

(3)

where π_PV and R_PV are the probability and mean value of solar radiation at the Rth scenario. In addition, R_f,PV and R_i,PV denote the ending and starting point.

The power generation of a PV system can be also written as follows:

(4)

where P_PV, P_PV,r, R_STD, and R_c are output power of the PV power generation (MW), rated power of the PV power generation (MW), solar radiation in the standard radiation, which normally is set to 1,000 W/m², and a certain radiation point typically is set to 150 W/m², respectively.

The typical radiation power curve for a PV system in Iran and the solar radiation probability density function (PDF) of the typical day are extracted from Aien et al. [39]. In addition, for power system planning studies, it is required to model the load demand probabilistically. Normal PDF is one of the most common ways to model the uncertainty of the load demand. Using the historical data achieved from the load consumption, the PDF of the load can be approximated similarly to the solar radiation. In the scenario-based method, the probability and demand for various scenarios can be written as follows:

(5)

(6)

where μ and σ are mean and variance of load. Also, π_l and

are the probability and demand of the lth load scenario in the interval from

Similar to solar radiation and load, market price uncertainty plays an important role in optimal PV allocation and reconfiguration. In this regard, the uncertainty of the electricity price is modeled based on three scenarios as presented in [40]. To obtain the mixed probability scenarios of the PV, load, and price, several scenarios can be joined by multiplying the probabilities as follows:

(7)

where π_PV, π_l, and π_p are the probability scenarios PV, l, and p of the PV, load, and price, respectively.

3. Problem Formulation

The competition among different entities in a deregulated environment such as DisCos, PV owners GenCos, and consumers can give many advantages to the power system. In a deregulated power system, DisCos are the owner and operator of the distribution system, which are responsible for buying wholesale electricity either from the upstream market or through direct contracts with GenCos and supplying electricity to the customers. The main objectives of the DisCos are reducing the distribution cost and enhancing the distribution network performance. In addition, a customer is an entity that buys the required electricity demand from DisCos. Therefore, the DN has the responsibility to provide uninterruptible power for the consumer to improve the reliability of the whole power system. On the other hand, a GenCo is an owner–operator of one or more power plants and DGs that sell electricity to the network. The profit of the owners of PVs can be maximized by selling more electricity to the DN. As mentioned above, each of the entities including DisCos, GenCos, and consumers has a unique benefit, but they may have conflicted relationships. Hence, the main aim of this paper is to suggest an optimal network reconfiguration and DGs sitting/sizing at the same time using economic MO functions to reach a trade-off among the three mentioned entities.

3.1. Objective Functions

In this part, three objective functions are presented to model DisCo’s cost, ECOST, and PV owners’ profit as follows.

3.1.1. PV Owners’ Profit Maximization

As PV owners are not in charge of the security constraints of the DN, only two costs containing the expected maintenance cost as well as the expected income are considered in the modeling. For the sake of simplicity, the expected maintenance cost, including monitoring and washing costs of PV power generation is neglected here. In Iran’s power market, PVs sell energy to DisCos through direct contracts; therefore, the uncertainty in the electricity price of PV owners is not considered. Consequently, the expected income of the PV owner can be expressed as follows:

(8)

where

is the active power of PV connected to bus i in scenario s and

is the contract price of PV systems placed at bus i ($/MWhr). Moreover, κ_s and κ_PV are set of all possible scenarios and PVs installed in buses.

Therefore, the objective function to optimally allocate PVs in the DN from the owner’s point of view can be achieved as follows:

(9)

where

is the expected profit of PV owners.

3.1.2. DisCo’s Cost Minimization

DisCo is responsible for operating the DN properly by considering all security and operational constraints as well as providing the required power for the customers. Generally, the costs of DisCos include the expected cost of buying energy from the upscale grid and the expected cost of electricity provided through direct contracts with DG owners. As there exists a limitation in generating power with DGs such as PV systems, the DisCo must procure the needed electricity from the upstream market. However, the price of electricity procured through the upscale market is different from the electricity price of PV systems and contains uncertainties. The expected cost of DisCo can be modeled stochastically as follows:

(10)

where

is the active power inserted from the substation to bus i in scenario s and

is the electricity price at scenarios.

It should be noted here that the cost of power bought from the PV owners is already given in Equation (8). In addition, the price of electricity bought through PV owners has been modeled deterministically. Consequently, the objective function to optimally allocate PVs in the DN from the DisCo’s point of view can be formulated as follows:

(11)

where

is the expected cost of DisCo.

3.1.3. ECOST Minimization

To improve the reliability of the DN, the minimization of the ECOST is also considered as the objective function. Assessing ECOST gives the ability to planners and engineers to achieve a satisfactory level of reliability for end-users and improve suitable operation strategies. The following equation can be used for the calculation of the ECOST at bus i [37]:

(12)

where L_ij is the power of interruption by losing line ij (kW), C is the cost of interruption ($/MW), which has a constant value equal to 50 $/MW, λ_ij is the expected failure rate of the DN equipment, and κ_l is the set of lines (branches). It should be noted that the section with the highest impedance has the biggest failure rate of 0.5 f/year and the section with the smallest impedance has the least failure rate of 0.1 f/year.

Before PV installation, each feeder between i and j contains an uncompensated failure rate of

. If the feeder branch is completely compensated, the corresponding failure rate decreases to

. If components of the current are not fully compensated, a failure rate is presented with a linear link to the percentage of compensation. Therefore, the compensation coefficient of the ith branch can be given as follows:

(13)

where

and

are the reactive/active components of the ith branch current after/before compensation, correspondingly. The new failure rate of the ith branch is calculated as follows:

(14)

where in the above equation

(15)

where

is the expected interruption cost.

3.2. Constraints

To achieve optimal values for the objective functions, the optimization problems in the power system have specific constraints. In this study, the following constraints are defined for the proposed model.

3.2.1. Radial Constraints

The radial structure offers many advantages for DNs such as the simple protection scheme and low short circuit current. Therefore, it is necessary to maintain the network structure radially after any change in the DN. Based on the graph theory, the structure of a DN remains radial, if the number of closed switches is equal to the number of nodes minus one. This network’s radially constraints can be defined as (γ_ij = γ_ji, ∀i, j ∈ κ_l):

(16)

where γ_ij is the decision variable that can be 1 (closed) or 0 (open). N_l is the total number of system branches.

3.2.2. Branch Capacity Limit

One of the most important limitations of distribution lines is the current that is delivered through lines and can be defined as follows:

(17)

The above constraints indicate that for the line ij including a closed switch, the current of the line is lower than its maximum limit.

3.2.3. Voltage Profile

The safe operation limits for the voltage of buses also can be given as follows:

(18)

3.2.4. PV Power Generation Limit

The generation of PV units is limited as follows:

(19)

3.2.5. Limitation on the Maximum Number of PVs

In order to solve problems such as stability difficulties with high DG penetration, the number of these resources must be limited based on their size and number:

(20)

where N_PV is the maximum number of permissible PVs for installation in the DN.

is the binary variable for modeling the location of the PV system at bus i.

Using this constraint and the PV power generation constraint, the optimal sitting/sizing of PV systems can be attained with optimal reconfiguration.

4. Dragonfly Algorithm (DA)

Here, the DA is used for solving the MO optimization problem. The main reason behind choosing this algorithm is that it can improve the initial random population for a given problem, converge toward the global optimum, and provide very competitive results compared to conventional algorithms. In addition, it can find very precise approximations of Pareto optimal solutions with high uniform distribution for MO problems.

The DA is a swarm intelligence optimization method initiated by the static and dynamic swarming behaviors of dragonflies, which was first reported by Mirjalili [41]. Swarm intelligence and the particular behavior of dragonflies are the main factors in developing this type of metaheuristic algorithm. Two crucial stages of optimization, including exploration and exploitation, are planned by modeling the social interaction of dragonflies in navigating, finding foods, and escaping enemies when swarming dynamically or statistically. A group of dragonflies with small directions and velocity hunting the prey in a small area are static swarm dragonflies. On the other hand, a variety of dragonflies with the ability to travel long distances in constant directions are called the dynamic swarm. Normally, two vectors including step (DX) and position (X) are applied to update the position of dragonflies in a search space and simulate their movements. The modeling of the DA can be presented in five steps as follows:

Separation: This refers to the avoidance of any static collision between dragonflies.

Alignment: It indicates that the velocity of individual dragonflies matches the velocity of other dragonflies in the neighborhood.

Cohesion: It refers to the tendency of individuals to the center of the mass of the neighborhood.

Attraction: it refers to being attracted to the food source.

Distraction: It refers to an escape from the enemy.

The combination of all five mentioned motions reflects the behaviors of dragonflies. More details about this algorithm can be found in [41].

The mentioned steps can be modeled mathematically as shown below.

The separation can be modeled as:

(21)

Alignment can be written as follows:

(22)

The cohesion can be modeled as follows:

(23)

Attraction toward a food source can be presented as follows:

(24)

Distraction outwards an enemy can be given as follows:

(25)

where X indicates the position of the current individual, X_j shows the position jth neighboring individual, and N is the number of neighboring individuals, X⁺and X⁻ indicate the position of the food source and enemy, respectively.

The flowchart of the proposed method is depicted in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The flowchart of the proposed method.

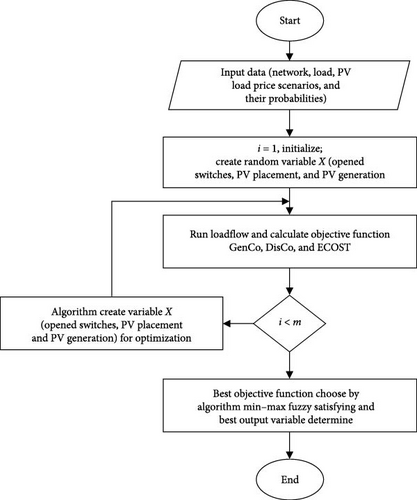
5. Simulation Results

To confirm the effectiveness of the proposed model, two different systems including the IEEE 33-bus system and a real DN in Iran are considered and simulated in various cases. In both systems, the stochastic MO model is solved using the DA. In the following subsections, numerical results are provided for both test systems.

5.1. Numerical Results for IEEE 33-Bus DN

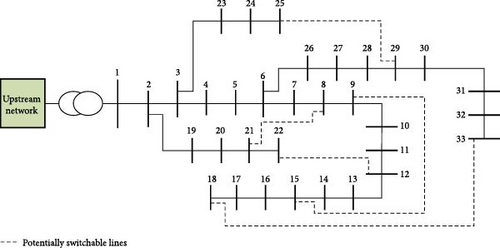
The single-line diagram of the IEEE 33-bus DN contains 37 branches, 32 sectionalizing switches, and five tie switches, as depicted in Figure 2 [42]. The suggested model is simulated in the MATLAB software package, which can solve the optimization problem. The model is optimized by the DA and compared with the PSO. Table 2 depicts the PV-demand-price scenarios of uncertain parameters. For straightforwardness, a single point is considered an operation horizon. It can be extended to a multipoint horizon. Three PV systems are assumed to be dispatched in the test network with a capacity of 1.2 MW for each PV system. As seen, three scenarios for the price of electricity are considered to be paid to the utility grid as $42, $46, and $50. It should be noted that the contract price of PV systems is taken into account as $50 as the transmission cost within the network is ignored. This type of contract with a high price can attract more private investors to install more renewable sources. This paper does not address the uncertainties in the price of electricity for PV systems. In other words, the price of purchasing power from PVs is considered to be fixed as there exists no cost of transmission for the PV units. In the electricity market of Iran, the network policy-makers buy the generated power of PVs at a fixed and attractive price to provide significant profits and support private investors for them. Moreover, to model the load uncertainties, three various scenarios are considered. The solar radiation scenarios of PV systems are also shown in Table 2.

Table 2. PV–load–price scenarios and their probabilities.

			Scenario number	($/MWhr)	P_Dl (%)	R_PV(%)	π_s
			s1	50	0.95	0	0.015126
			s2	50	0.95	0.25	0.00348
			s3	50	0.95	0.5	0.002556
			s4	50	0.95	0.75	0.004071
			s5	50	0.95	1	0.004764
	Price scenario:		s6	50	1	0	0.070588
	($/MWhr)	π_p	s7	50	1	0.25	0.01624
P1	50	0.2	s8	50	1	0.5	0.011928
P2	46	0.6	s9	50	1	0.75	0.018998
P3	42	0.2	s10	50	1	1	0.022232
			s11	50	1.05	0	0.015126
			s12	50	1.05	0.25	0.00348
			s13	50	1.05	0.5	0.002556
			s14	50	1.05	0.75	0.004071
			s15	50	1.05	1	0.004764

			s16	46	0.95	0	0.045378
			s17	46	0.95	0.25	0.01044
			s18	46	0.95	0.5	0.007668
			s19	46	0.95	0.75	0.012213
	Solar radiation scenario:		s20	46	0.95	1	0.014292
	R_PV (%)	π_PV	s21	46	1	0	0.211764
R1	0	0.4726	s22	46	1	0.25	0.04872
R2	0.25	0.1087	s23	46	1	0.5	0.035784
R3	0.5	0.0798	s24	46	1	0.75	0.056994
R4	0.75	0.1272	s25	46	1	1	0.066696
R5	1	0.1488	s26	46	1.05	0	0.045378
			s27	46	1.05	0.25	0.01044
			s28	46	1.05	0.5	0.007668
			s29	46	1.05	0.75	0.012213
			s30	46	1.05	1	0.014292

			s31	42	0.95	0	0.015126
			s32	42	0.95	0.25	0.00348
			s33	42	0.95	0.5	0.002556
			s34	42	0.95	0.75	0.004071
			s35	42	0.95	1	0.004764
	Load scenario:		s36	42	1	0	0.070588
	P_Dl (%)	π_p	s37	42	1	0.25	0.01624
P1	0.95	0.16	s38	42	1	0.5	0.011928
P2	1	0.68	s39	42	1	0.75	0.018998
P3	1.05	0.16	s40	42	1	1	0.022232
			s41	42	1.05	0	0.015126
			s42	42	1.05	0.25	0.00348
			s43	42	1.05	0.5	0.002556
			s44	42	1.05	0.75	0.004071
			s45	42	1.05	1	0.004764

5.1.1. Case 1: SO Reconfiguration Aiming to Maximize PV Owner’s Profit

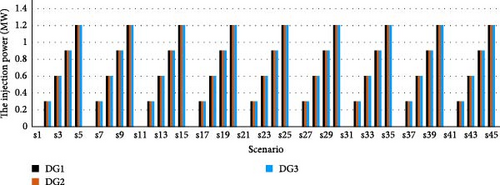
In this case study, the main objective is to maximize the profit of PV owners. The results including the profit of PV owners, PV placement, and the reconfiguration are shown in Table 3. As seen, the profit of PV owners using the DA is $59.9. The cost of the DisCo in this case is $191.563. As can be observed, PV systems are installed at buses 30, 31, and 32, and switches L₆₋₇, L₉₋₁₀, L₁₂₋₁₃, L₁₅₋₁₆, and L₂₈₋₂₉ are opened in the test system. The installed PVs are not close to the substation and only supply the nearby buses. Moreover, the injection power of PV systems optimized by the proposed DA in all scenarios is depicted in Figure 3. As can be observed, the power generation of PVs is zero in some scenarios, and it is nonzero in most scenarios with the available capacity.

Table 3. Profit of PV owners, optimal placement of PV units, and reconfiguration in Case 1.

Optimization method	Profit of DG owners ($)	PV placement	Opened switches
PSO	59.9	B₃₀, B₃₁, B₃₂	L₆₋₇, L₉₋₁₀, L₁₂₋₁₃, L₁₅₋₁₆, L₂₈₋₂₉
DA	59.9	B₃₀, B₃₁, B₃₂	L₆₋₇, L₉₋₁₀, L₁₂₋₁₃, L₁₅₋₁₆, L₂₈₋₂₉

5.1.2. Case 2: SO Reconfiguration Aiming to Minimize DisCo’s Cost

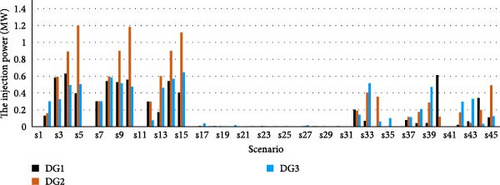
Here, it is aimed to minimize the cost of energy bought from both PVs and the upscale grid. Using this objective, the DisCo pays the lowest money to the PV owners and the upscale grid. The cost of DisCo, optimal PV placement, and network reconfiguration optimized with the DA and PSO, in this case, are presented in Table 4. As seen, the cost of DisCo is considerably reduced in comparison with Case 1. The profit of PV owners is also $11.3748, which its value is notably reduced in comparison with Case 1, due to the changing of the objective function. The ECOST is also equal to $213.49, which is very high. As seen in Table 4, PV systems are installed at buses 6, 12, and 16 in both algorithms. A comparison of Cases 1 and 2 shows that by changing objective functions the location of PVs and network reconfiguration can be changed. Furthermore, the injection power of PV units optimized by the DA is illustrated in Figure 4. As observed, the provided energy by PVs is considerably reduced in this case as the purchased energy from PVs is based on an expensive fixed price that is higher than the utility grid price. The results confirm that the appropriate PV placement and optimal reconfiguration can reduce the costs of DisCos. It is clear that in this case, the power losses of the network are inherently reduced.

Table 4. Disco’s cost, optimal location of PV units, and reconfiguration of the IEEE 33-bus in Case 2.

Optimization method	Disco’s cost ($)	PV placement	Opened switches
PSO	177.37	B₆, B₁₂, B₁₆	L₇₋₈, L₉₋₁₀, L₁₄₋₁₅, L₃₂₋₃₃, L₂₅₋₂₉
DA	177.37	B₆, B₁₂, B₁₆	L₇₋₈, L₉₋₁₀, L₁₄₋₁₅, L₃₂₋₃₃, L₂₅₋₂₉

5.1.3. Case 3: SO Reconfiguration Aiming to Minimize the ECOST

In this part, the main objective is to minimize the ECOST. Minimizing ECOST empowers the planners to select the adequate class of reliability for end-users and develop proper operation policies with low cost. The jointly optimal PV placement and network reconfiguration are optimized with the DA and compared with the PSO to minimize the ECOST. Table 5 gives the ECOST, optimal PV placement, and reconfiguration with both algorithms. The profit of PV owners and the cost of the DisCo, in this case, are $55.9 and $186.38, which varies with Cases 1 and 2. Here, the locations of PVs and configuration are changed such that the interruption cost of customers is minimized to $154.2. In addition, the injection power of PV systems optimized by used algorithm is explained in Figure 5. As seen, the purchased energy through PVs is significantly increased in this case to minimize the ECOST. As observed from the results, the ECOST can be minimized by optimal reconfiguration and PV placement at the same time.

Table 5. ECOST, the optimal location of PV units, and reconfiguration of IEEE 33-bus in Case 3.

Optimization method	ECOST ($)	PV placement	Opened switches
PSO	155.1	B₃₀, B₃₁, B₃₂	L₆₋₇, L₉₋₁₀, L₁₂₋₁₃, L₁₅₋₁₆, L₂₈₋₂₉
DA	154.2	B₁₆, B₁₇, B₁₈	L₇₋₈, L₁₀₋₁₁, L₁₄₋₁₅, L₁₇₋₁₈, L₂₈₋₂₉

5.1.4. Case 4: MO Reconfiguration Aiming to Maximize PV Owner’s Profit and Minimize ECOST

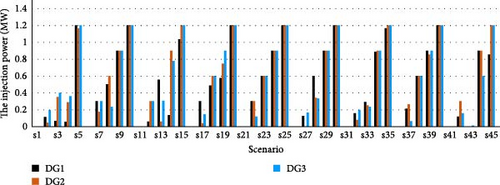
In this part, the Pareto front is attained for the suggested model to optimize the PV owner’s profit and minimize the ECOST. Figure 6 shows the Pareto optimal front achieved for this case study. Table 6 also presents the Pareto results based on the best compromise solution, which is achieved using the min–max fuzzy satisfying method introduced in [43]. As seen, the best trade-off result with the DA is related to solution#3, which is equal to 1.06. For the best result in solution#3, the PV systems are installed at buses 28, 32, and 33, and switches L₇₋₈, L₉₋₁₀, L₁₄₋₁₅, L₁₆₋₁₇, and L₂₈₋₂₉ are opened, as depicted in Table 7. The maximum PV owner’s profit and the minimum ECOST optimized with the DA and PSO are also given in Table 7. The cost of DisCo in this case is equal to $180.87. The injected power of PV systems optimized by the DA is given in Figure 7.

Table 6. Pareto optimal results in Case 4.

Solution#	Ψ₁ ($)	Ψ₂ ($)			Sum (, )
PSO
1	36.52	188.02	1.00	0.00	1.00
2	36.26	187.02	0.89	0.13	1.02
3^∗	35.42	183.59	0.53	0.58	1.11
4	34.18	180.36	0.00	1.00	1.00
5	36.52	188.02	1.00	0.00	1.00
DA
1	59.28	182.68	1.00	0.00	1.00
2	56.68	181.55	0.81	0.09	0.91
3^∗	51.99	181.46	0.80	0.26	1.06
4	49.93	177.83	0.21	0.33	0.54
5	40.14	177.79	0.20	0.68	0.88
6	31.24	176.56	0.00	1.00	1.00
7	59.28	182.68	1.00	0.00	1.00

^∗The best trade-off result.

Table 7. PV owner’s profit, ECOST, optimal placement of PV units, and reconfiguration Case 4.

Case 4	PV owner’s profit ($)	ECOST ($)	PV placement	Opened switches
PSO	35.42	183.59	B₁₃, B₁₈, B₂₆	L₇₋₉, L₉₋₁₀, L₁₄₋₁₅, L₁₈₋₃₃, L₂₈₋₂₉
DA	51.99	181.46	B₂₈, B₃₂, B₃₃	L₇₋₈, L₉₋₁₀, L₁₄₋₁₅, L₁₆₋₁₇, L₂₈₋₂₉

5.1.5. Case 5: MO Reconfiguration Aiming to Maximize PV Owner’s Profit and Minimize DisCo’s Cost

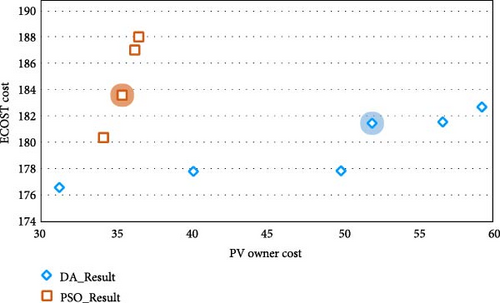
In this case study, the Pareto front is achieved for the recommended MO problem to maximize the PV owner’s profit and minimize DisCo’s cost at the same time. Table 8 also summarizes the Pareto results. As observed, the best trade-off result with the DA is related to solution#3, which is equal to 1.32. Moreover, the best trade-off outcome with the PSO is related to solution#7, which is equal to 1.28. For the best result in solution#3 with the DA, the PV systems can be installed at buses 21, 30, and 32, as depicted in Table 9. As seen, the reconfiguration can have a considerable effect on optimal PV placement. The PV owner’s profit, the DisCo’s cost, and the optimal reconfiguration optimized with the DA and PSO in this case study are also presented in Table 9. The injected power of PV systems optimized by the DA is given in Figure 8. As mentioned earlier, the proposed MO optimization approach can provide many economic and operational advantages for the players in the DN. It should be noted here that by achieving a trade-off between the PV owner’s profit and DisCo’s cost, the losses in the DN are also noticeably minimized inherently through DisCo’s cost, which is highly advantageous from DisCo’s perspective.

Table 8. Pareto optimal results in Case 5.

Solution#	Ψ₁($)	Ψ₂($)			Sum (, )
DA result
1	181.27	52.79	0.00	1.00	1.00
2	180.80	51.75	0.38	0.82	1.20
3^∗	180.55	51.34	0.57	0.75	1.32
4	180.55	51.28	0.58	0.74	1.32
5	180.55	51.28	0.58	0.74	1.32
6	180.51	50.95	0.61	0.68	1.29
7	180.42	50.22	0.68	0.55	1.24
8	180.40	50.15	0.69	0.54	1.23
9	180.36	49.70	0.73	0.46	1.19
10	180.36	49.70	0.73	0.46	1.19
11	180.34	49.42	0.74	0.41	1.16
12	180.28	49.21	0.79	0.38	1.17
13	180.13	47.25	0.91	0.04	0.95
14	180.13	47.24	0.91	0.04	0.95
15	180.02	47.03	1.00	0.00	1.00

^∗The best trade-off result.

Table 9. PV owner’s profit, DisCo’s cost, optimal location of PVs, and reconfiguration of IEEE 33-bus in Case 5.

Case 5	PV owner’s profit ($)	Disco’s cost ($)	PV placement	Open switch
PSO	34.56	178.99	B₁₂, B₁₈, B₂₄	L₇₋₈, L₁₀₋₁₁, L₁₄₋₁₅, L₁₇₋₁₈, L₂₈₋₂₉
DA	51.34	180.55	B₂₁, B₃₀, B₃₂	L₁₀₋₁₁, L₁₄₋₁₅, L₁₆₋₁₇, L₂₈₋₂₉, L₈₋₂₁

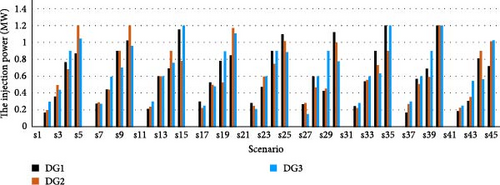
5.1.6. Case 6: MO Reconfiguration Aiming to Minimize DisCo’s Cost and ECOST

Here, the minimization of the cost of the DisCo and ECOST are considered and the Pareto front is attained for the proposed MO problem. Pareto optimal solution of the proposed model in Case 6 is summarized in Table 10, in which the best trade-off result is achieved in comparison with each SO problem. The min–max fuzzy satisfying technique is employed to attain the best trade-off result related to solution#9 with the DA, which is equal to 1.65. It is related to solution#6 with the PSO, which is equal to 1.49. For the best result in solution#9 with the DA, the PV systems are installed at buses 17, 18, and 31, as shown in Table 11. The ECOST, Disco’s cost, and the optimal configuration optimized with the DA and PSO are also presented in Table 11. The profit of PV owners is also equal to $28.6.

Table 10. Pareto optimal solutions of the suggested model in Case 6.

Solution#	Ψ₁ ($)	Ψ₂ ($)			Sum (, )
DA result
1	209.61	178.13	0.00	1.00	1.00
2	191.08	178.27	0.52	0.96	1.47
3	189.73	178.31	0.56	0.94	1.50
4	188.90	178.63	0.58	0.84	1.42
5	188.89	178.63	0.58	0.84	1.42
6	188.89	178.63	0.58	0.84	1.42
7	183.74	178.71	0.73	0.81	1.54
8	181.66	178.79	0.78	0.79	1.57
9^∗	178.43	178.83	0.87	0.78	1.65
10	176.81	179.29	0.92	0.63	1.55
11	176.38	179.29	0.93	0.63	1.56
12	175.22	179.70	0.96	0.50	1.46
13	175.19	179.71	0.96	0.50	1.46
14	174.91	181.08	0.97	0.06	1.03
15	173.93	181.27	1.00	0.00	1.00

^∗The best trade-off result.

Table 11. DisCo’s cost, ECOST, optimal placement of PVs, and reconfiguration in Case 6.

Case 6	DisCo’s cost ($)	ECOST ($)	PV placement	Opened switches
PSO	178.81	180.16	B₁₁, B₂₅, B₃₂	L₇₋₈, L₉₋₁₀, L₁₄₋₁₅, L₂₈₋₂₉, L₃₂₋₃₃
DA	178.43	178.83	B₁₇, B₁₈, B₃₁	L₇₋₈, L₁₀₋₁₁, L₁₃₋₁₄, L₂₇₋₂₈, L₃₂₋₃₃

5.1.7. Case 7: MO Reconfiguration Aiming to Maximize PV Owner’s Profit, Minimize DisCo’s Cost, and ECOST

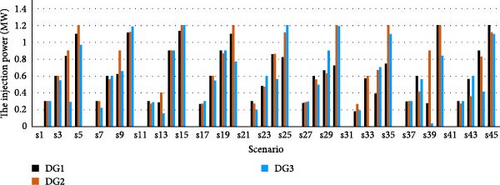
In this part, the Pareto front is attained for the offered MO problem to maximize the PV owner’s profit as well as to minimize DisCo’s cost and ECOST at the same time. Figure 9 displays the results of this case study. The Pareto solutions with DA are presented in Table 12. To select the greatest trade-off result, the min–max fuzzy satisfying method is used. As seen, the best trade-off result is achieved in solution#25, which is equal to 2.23. Table 13 depicts ECOST, DisCo’s cost, and the PV owner’s profit optimized using the DA and PSO. According to the table, the PV systems are installed at buses 26, 32, and 33, and L₇₋₈, L₁₀₋₁₁, L₁₄₋₁₅, L₂₈₋₂₉, and L₁₈₋₃₃ are opened. The injected power of the PVs for Case 7 using the DA and PSO are presented in Figures 10 and 11, respectively. According to the results of the IEEE 33-bus DN, dealing with the problem of optimal reconfiguration and PV placement provides a more efficient schedule, as all players in the DN including DisCos, GenCos, and customers are fulfilled jointly. In addition, another important issue affecting PV owners and DisCo plans is the contract price of PV energy. The power loss reduction resulting from the optimal network configuration and PV capacities is calculated in this case to assess the degree of efficient operation of the network.

Table 12. Pareto optimal solutions of the model in Case 7.

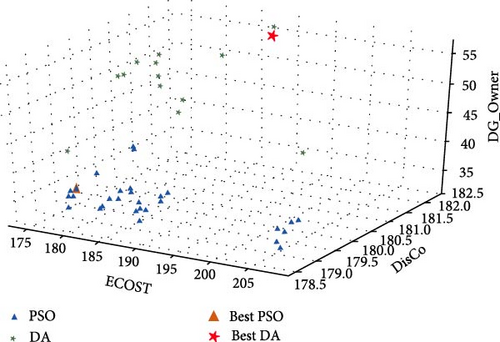
Solution#	Ψ₁ ($)	Ψ₂ ($)	Ψ₃ ($)				Sum (, , )
1	204.10	179.90	45.45	0.00	0.82	0.28	1.11
2	204.10	179.90	45.45	0.00	0.82	0.28	1.11
3	204.10	179.90	45.45	0.00	0.82	0.28	1.11
4	204.10	179.90	45.45	0.00	0.82	0.28	1.11
5	204.10	179.90	45.45	0.00	0.82	0.28	1.11
6	204.10	179.90	45.45	0.00	0.82	0.28	1.11
7	204.10	179.90	45.45	0.00	0.82	0.28	1.11
8	204.10	179.90	45.45	0.00	0.82	0.28	1.11
9	188.93	182.14	55.44	0.52	0.07	0.96	1.56
10	187.87	180.96	55.15	0.56	0.46	0.94	1.97
11	187.87	180.96	55.15	0.56	0.46	0.94	1.97
12	187.79	182.35	55.99	0.56	0.00	1.00	1.56
13	186.77	180.05	48.08	0.60	0.77	0.46	1.83
14	185.92	180.31	49.39	0.63	0.68	0.55	1.86
15	185.92	180.31	49.39	0.63	0.68	0.55	1.86
16	185.92	180.31	49.39	0.63	0.68	0.55	1.86
17	182.26	180.43	50.68	0.75	0.64	0.64	2.04
18	182.26	180.43	50.68	0.75	0.64	0.64	2.04
19	182.26	180.43	50.68	0.75	0.64	0.64	2.04
20	181.29	180.58	51.63	0.79	0.59	0.70	2.08
21	181.29	180.58	51.63	0.79	0.59	0.70	2.08
22	179.74	180.81	53.01	0.84	0.52	0.80	2.15
23	179.68	180.89	54.14	0.84	0.49	0.87	2.21
24	179.68	180.89	54.14	0.84	0.49	0.87	2.21
25^∗	176.82	180.51	51.19	0.94	0.61	0.67	2.23
26	176.20	180.96	51.99	0.96	0.46	0.73	2.15
27	175.96	180.53	50.77	0.97	0.61	0.65	2.23
28	175.96	180.53	50.77	0.97	0.61	0.65	2.23
29	175.96	180.53	50.77	0.97	0.61	0.65	2.23
30	175.10	179.37	41.26	1.00	1.00	0.00	2.00

^∗The best trade-off result.

Table 13. ECOST, DisCo’s cost, PV owner’s profit, the optimallocation of PVs, and reconfiguration of IEEE 33-bus in Case 7.

Case 7	ECOST ($)	DisCo’s cost ($)	PV owner’s profit ($)	DG placement	Opened switches
PSO	177.86	179.05	36.58	B₁₅, B₂₀, B₃₀	L_7–8, L_9–10, L_14–15, L_28–29, L_18–33
DA	188.93	182.14	55.44	B₂₆, B₃₂, B₃₃	L_7–8, L_10–11, L_14–15, L_28–29, L_18–33

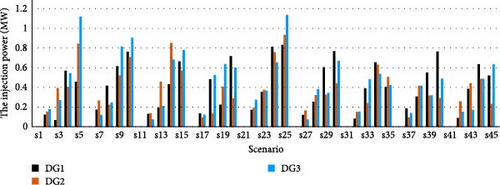
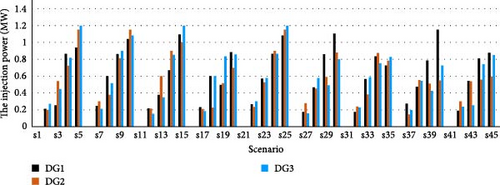
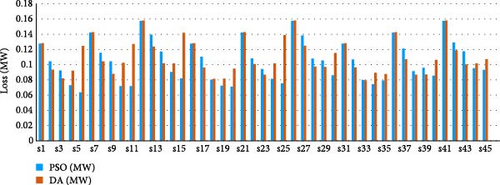
The variation of active power loss of the test system in all scenarios for this case is depicted in Figure 12. As can be seen in this case, when a trade-off is achieved among the PV owner’s profit, DisCo’s cost, and ECOST, power losses of the network is minimized significantly. For better assessments, all considered indexes for optimization and the standard deviation (std) of the voltages in all cases using the DA are provided in Table 14. It is obvious from the results that this problem can be addressed as a multi-objective problem that considers the benefits of all players in the DN. Moreover, using the proposed optimization approach, the standard deviation of the voltage is reached to one per unit compared with without using the proposed approach.

Table 14. Comparison indexes in all scenarios.

Scenario	S1	S2	S3	S4	S5	S6	S7
ECost ($)	178.574	213.495	154.216	181.464	195.991	178.434	181.516
Disco ($)	181.711	177.369	186.551	180.877	180.551	178.831	180.474
DG owner ($)	59.750	11.375	55.901	51.992	51.344	28.610	50.841
Power loss (MW)	0.132	0.132	0.243	0.127	0.124	0.125	0.124
Voltage std	0.017	0.016	0.027	0.017	0.016	0.017	0.017

5.2. Real DN

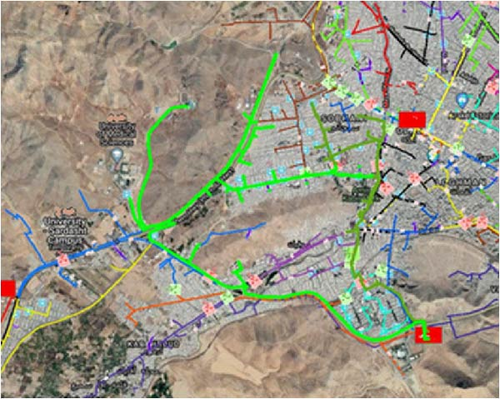
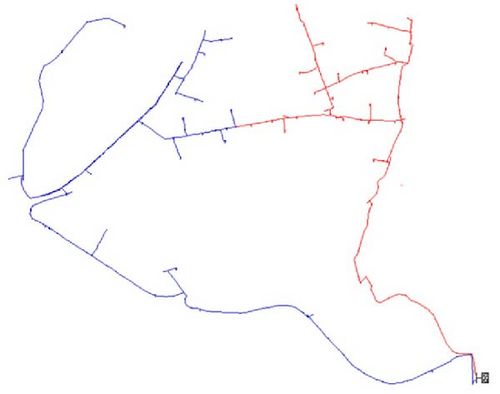
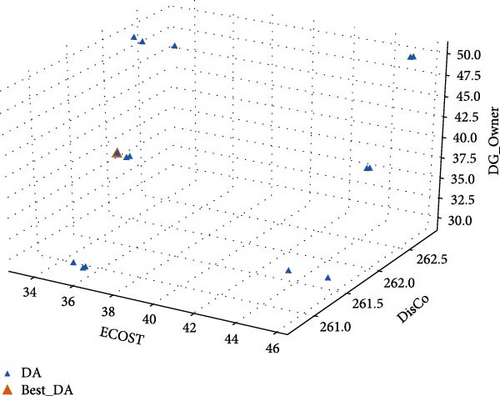
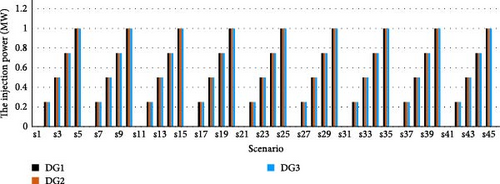
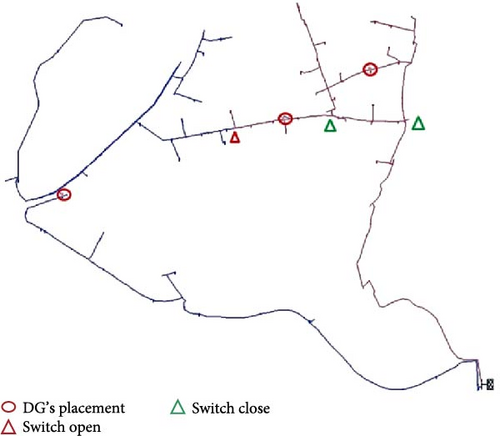
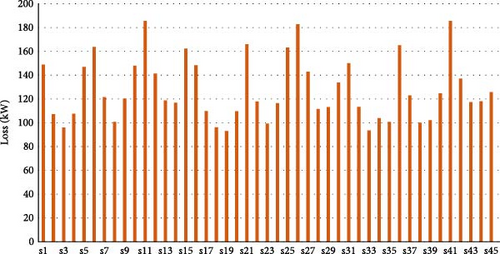
In this part, the suggested model is applied to a real DN in Iran. The real distribution network is shown in Figure 13. The name of the right-side feeder with red color is #518 and the left side with blue color is #512. For this case study, three PV systems are permitted to be installed in the DN, each with a rated capacity of 1 MW. The Pareto front is achieved for the suggested model to optimize the PV owner’s profit, minimizing DisCo’s cost, and ECOST. Figure 14 shows the Pareto optimal front achieved for this case study. Table 15 illustrates the Pareto results. As seen, the best trade-off results are attained using the DA in solution#9, which is equal to 2.3. Table 16 presents the values of the ECOST, Disco’s cost, and PV owner’s profit before PV installation and reconfiguration as well as after optimal reconfiguration and PV allocation using the DA. The power generation of PV systems in the real DN is shown in Figure 15. The optimal placement of PVs and optimal reconfiguration of DN in real system are also depicted in Figure 16. The variation of active power loss of the real DN in all scenarios is shown in Figure 17. As seen, when a compromise is attained among all players in the DN, power losses of the system is reduced considerably. Table 17 also compares the amount of load, losses, maximum loading, and minimum voltage before and after optimization in two considered feeders.

Table 15. Pareto optimal solutions of the proposed model for real DN.

Solution#	Ψ₁ ($)	Ψ₂ ($)	Ψ₃ ($)				Sum (, , )
DA result
1	35.99	260.79	29.90	0.80	0.99	0.00	1.79
2	35.87	261.48	39.86	0.81	0.66	0.50	1.97
3	35.76	262.18	49.83	0.82	0.31	1.00	2.14
4	43.71	261.48	29.90	0.16	0.66	0.00	0.81
5	45.37	262.13	39.86	0.02	0.34	0.50	0.86
6	45.21	262.81	49.83	0.03	0.01	1.00	1.04
7	35.27	260.82	29.90	0.86	0.97	0.00	1.84
8	35.15	261.50	39.86	0.87	0.64	0.50	2.02
9^∗	33.63	262.20	49.83	1.00	0.30	1.00	2.30
10	45.43	262.15	39.86	0.01	0.33	0.50	0.84
11	45.59	261.49	29.90	0.00	0.65	0.00	0.65
12	35.95	260.76	29.90	0.81	1.00	0.00	1.81
13	35.82	261.45	39.86	0.82	0.67	0.50	1.99
14	34.26	262.15	49.83	0.95	0.33	1.00	2.28
15	45.28	262.83	49.83	0.03	0.00	1.00	1.03

^∗The best trade-off result.

Table 16. ECOST, Disco’s cost, and PV owner’s profit for real DN.

Real DN case	ECOST	DisCo’s cost	PV owner’s profit
Before optimization	46.217	259.643	0
DA	33.632	262.202	49.826

Table 17. Comparison of the indexes in two considered feeders before and after optimization.

Feeder name	Load (MW)	Losses (kW)	Max line loading (%)	Min voltage (p.u.)
Before optimization
#518	2.30	67	86	0.957
# 512	3.16	126	92	0.943
After optimization
#518	3.419	65	82	0.964
#512	2.043	52	87	0.957

6. Conclusion

A MO stochastic model for PV placement and reconfiguration of DNs at the same time is proposed in this paper. The model is investigated on a standard test system and a areal DN in the Iran power market from GenCo’s point of view in which the profit of PV owners are maximized. It is also evaluated from DisCo’s point of view in which the total cost of power procurementis minimized and also assessed from the customer’s perspective in which the ECOST is minimized. The mentioned objectives are satisfied by considering the operational and physical limitations of the DN. To achieve more practical results, the uncertainties of PV systems, electricity prices, and demands are modeled using the scenario approach. To solve the suggested model, the DA is employed. The performance of the DA in all case studies is compared with the PSO. The fuzzy satisfying criterion is also used to find the best compromise solution. The DA is very simple and easy to implement and shows reasonable performance to optimize various problems in different areas. Furthermore, having few parameters for tuning is another advantage of DA. Moreover, the convergence time of the algorithm is reasonable. This study is expected to be a beneficial reference for researchers and engineers involved in deregulated power distribution systems.

Abbreviations

ENS:: Energy not supplied
DA:: Dragonfly algorithm
PV:: Photovoltaic
PSO:: Particle swarm optimization
DN:: Distribution network
ECOST:: Expected interruption cost
GenCos:: Generating companies
DER:: Distributed energy resource
DisCos:: Distribution companies
MILP:: Mixed-integer linear programing
SO:: Single-objective
DG:: Distributed generation
MO:: Multi-objective
PDF:: Probability density function.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Authors’ Contributions

Mohammad Najafi and Mohammad Reza Miveh contributed equally to this manuscript.

Open Research

Data Availability

All data used to support the findings of this study are available from the corresponding author upon request.

References

1 Miveh M. R., Rahmat M. F., Ghadimi A. A., and Mustafa M. W., Control techniques for three-phase four-leg voltage source inverters in autonomous microgrids: a review, Renewable and Sustainable Energy Reviews. (2016) 54, 1592–1610, https://doi.org/10.1016/j.rser.2015.10.079, 2-s2.0-84947218318.
10.1016/j.rser.2015.10.079
Web of Science® Google Scholar
2 Khosravi N., Abdolmohammadi H., Bagheri S., and Miveh M., Improvement the harmonic conditions of the AC/DC microgrids with the presence of filter compensation modules, Renewable and Sustainable Energy Reviews. (2021) 143, https://doi.org/10.1016/j.rser.2021.110898, 110898.
10.1016/j.rser.2021.110898
Web of Science® Google Scholar
3 Biswas P. P., Suganthan P. N., and Amaratunga G. A., Minimizing harmonic distortion in power system with optimal design of hybrid active power filter using differential evolution, Applied Soft Computing. (2017) 61, 486–496, https://doi.org/10.1016/j.asoc.2017.08.031, 2-s2.0-85028394209.
10.1016/j.asoc.2017.08.031
Web of Science® Google Scholar
4 Sultana S. and Roy P. K., Krill herd algorithm for optimal location of distributed generator in radial distribution system, Applied Soft Computing. (2016) 40, 391–404, https://doi.org/10.1016/j.asoc.2015.11.036, 2-s2.0-84951191963.
10.1016/j.asoc.2015.11.036
Web of Science® Google Scholar
5 Moravej Z., Ardejani P. E., and Imani A., Optimum placement and sizing of DG units based on improving voltage stability using multi-objective evolutionary algorithm, Journal of Renewable and Sustainable Energy. (2018) 10, no. 5, https://doi.org/10.1063/1.5018885, 2-s2.0-85056127619, 055304.
10.1063/1.5018885
Web of Science® Google Scholar
6 Nadeem M. F., Malik T., Imtiaz A. R., and Ali G., Simultaneous placement and sizing of multi-DG units in distribution system using IGSA, 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), 2018, IEEE, 1–6:.
Google Scholar
7 Kumar S., Mandal K. K., and Chakraborty N., Optimal DG placement by multi-objective opposition based chaotic differential evolution for techno-economic analysis, Applied Soft Computing. (2019) 78, 70–83, https://doi.org/10.1016/j.asoc.2019.02.013, 2-s2.0-85061797373.
10.1016/j.asoc.2019.02.013
Web of Science® Google Scholar
8 Reddy P. D. P., Reddy V. C. V., and Manohar T. G., Optimal renewable resources placement in distribution networks by combined power loss index and whale optimization algorithms, Journal of Electrical Systems and Information Technology. (2018) 5, no. 2, 175–191, https://doi.org/10.1016/j.jesit.2017.05.006.
10.1016/j.jesit.2017.05.006
Google Scholar
9 Pinto R. S., Unsihuay-Vila C., and Fernandes T. S., Multi-objective and multi-period distribution expansion planning considering reliability, distributed generation and self-healing, IET Generation, Transmission & Distribution. (2018) 13, no. 2, 219–228, https://doi.org/10.1049/iet-gtd.2018.5037, 2-s2.0-85060090780.
10.1049/iet-gtd.2018.5037
Web of Science® Google Scholar
10 Haifeng H., Zhesheng H., Ruipeng G., Jun M., and Jiong T., Directed graph-based distribution network reconfiguration for operation mode adjustment and service restoration considering distributed generation, Journal of Modern Power Systems and Clean Energy. (2017) 5, no. 1, 142–149, https://doi.org/10.1007/s40565-016-0198-3, 2-s2.0-85009072551.
10.1007/s40565-016-0198-3
Web of Science® Google Scholar
11 Shaheen A., Elsayed A., El-Sehiemy R. A., and Abdelaziz A. Y., Equilibrium optimization algorithm for network reconfiguration and distributed generation allocation in power systems, Applied Soft Computing. (2021) 98, https://doi.org/10.1016/j.asoc.2020.106867, 106867.
10.1016/j.asoc.2020.106867
Web of Science® Google Scholar
12 Eldurssi A. M. and O’Connell R. M., A fast nondominated sorting guided genetic algorithm for multi-objective power distribution system reconfiguration problem, IEEE Transactions on Power Systems. (2015) 30, no. 2, 593–601, https://doi.org/10.1109/TPWRS.2014.2332953, 2-s2.0-85027950470.
10.1109/TPWRS.2014.2332953
Web of Science® Google Scholar
13 Niknam T., An efficient multi-objective HBMO algorithm for distribution feeder reconfiguration, Expert Systems with Applications. (2011) 38, no. 3, 2878–2887, https://doi.org/10.1016/j.eswa.2010.08.081, 2-s2.0-78049529460.
10.1016/j.eswa.2010.08.081
Web of Science® Google Scholar
14 Jeon Y.-J., Kim J.-C., Kim J.-O., Shin J.-R., and Lee K. Y., An efficient simulated annealing algorithm for network reconfiguration in large-scale distribution systems, IEEE Transactions on Power Delivery. (2002) 17, no. 4, 1070–1078, https://doi.org/10.1109/TPWRD.2002.803823, 2-s2.0-0036814898.
10.1109/TPWRD.2002.803823
Web of Science® Google Scholar
15 Mazza A., Chicco G., and Russo A., Optimal multi-objective distribution system reconfiguration with multi criteria decision making-based solution ranking and enhanced genetic operators, International Journal of Electrical Power & Energy Systems. (2014) 54, 255–267, https://doi.org/10.1016/j.ijepes.2013.07.006, 2-s2.0-84881331112.
10.1016/j.ijepes.2013.07.006
Web of Science® Google Scholar
16 Alonso F., Oliveira D., and de Souza A. Z., Artificial immune systems optimization approach for multiobjective distribution system reconfiguration, IEEE Transactions on Power Systems. (2015) 30, no. 2, 840–847, https://doi.org/10.1109/TPWRS.2014.2330628, 2-s2.0-85027952077.
10.1109/TPWRS.2014.2330628
Web of Science® Google Scholar
17 Ahuja A., Das S., and Pahwa A., An AIS-ACO hybrid approach for multi-objective distribution system reconfiguration, IEEE Transactions on Power Systems. (2007) 22, no. 3, 1101–1111, https://doi.org/10.1109/TPWRS.2007.901286, 2-s2.0-34548073590.
10.1109/TPWRS.2007.901286
Web of Science® Google Scholar
18 Andervazh M.-R., Olamaei J., and Haghifam M.-R., Adaptive multi-objective distribution network reconfiguration using multi-objective discrete particles swarm optimisation algorithm and graph theory, IET Generation, Transmission & Distribution. (2013) 7, no. 12, 1367–1382, https://doi.org/10.1049/iet-gtd.2012.0712, 2-s2.0-84888865803.
10.1049/iet-gtd.2012.0712
Web of Science® Google Scholar
19 Paterakis N. G., Mazza A., Santos S. F., Erdinç O., Chicco G., Bakirtzis A. G., and Catalão J. P., Multi-objective reconfiguration of radial distribution systems using reliability indices, IEEE Transactions on Power Systems. (2016) 31, no. 2, 1048–1062, https://doi.org/10.1109/TPWRS.2015.2425801, 2-s2.0-84929017921.
10.1109/TPWRS.2015.2425801
Web of Science® Google Scholar
20 Nguyen T. T., Nguyen T. T., Truong A. V., Nguyen Q. T., and Phung T. A., Multi-objective electric distribution network reconfiguration solution using runner-root algorithm, Applied Soft Computing. (2017) 52, 93–108, https://doi.org/10.1016/j.asoc.2016.12.018, 2-s2.0-85007420643.
10.1016/j.asoc.2016.12.018
Web of Science® Google Scholar
21 Wu Y.-K., Lee C.-Y., Liu L.-C., and Tsai S.-H., Study of reconfiguration for the distribution system with distributed generators, IEEE Transactions on Power Delivery. (2010) 25, no. 3, 1678–1685, https://doi.org/10.1109/TPWRD.2010.2046339, 2-s2.0-77954035331.
10.1109/TPWRD.2010.2046339
Web of Science® Google Scholar
22 Narimani M. R., Vahed A. A., Azizipanah-Abarghooee R., and Javidsharifi M., Enhanced gravitational search algorithm for multi-objective distribution feeder reconfiguration considering reliability, loss and operational cost, IET Generation, Transmission & Distribution. (2014) 8, no. 1, 55–69, https://doi.org/10.1049/iet-gtd.2013.0117, 2-s2.0-84892992107.
10.1049/iet-gtd.2013.0117
Web of Science® Google Scholar
23 Franco J. F., Rider M. J., Lavorato M., and Romero R., A mixed-integer LP model for the reconfiguration of radial electric distribution systems considering distributed generation, Electric Power Systems Research. (2013) 97, 51–60, https://doi.org/10.1016/j.epsr.2012.12.005, 2-s2.0-84872305854.
10.1016/j.epsr.2012.12.005
Web of Science® Google Scholar
24 Nikkhah S. and Rabiee A., A joint energy storage systems and wind farms long-term planning model considering voltage stability, Operation, Planning, and Analysis of Energy Storage Systems in Smart Energy, 2018, Springer, Hubs, 337–363.
10.1007/978-3-319-75097-2_14
Google Scholar
25 Ameli A., Bahrami S., Khazaeli F., and Haghifam M.-R., A multiobjective particle swarm optimization for sizing and placement of DGs from DG owner’s and distribution company’s viewpoints, IEEE Transactions on Power Delivery. (2014) 29, no. 4, 1831–1840, https://doi.org/10.1109/TPWRD.2014.2300845, 2-s2.0-84905113854.
10.1109/TPWRD.2014.2300845
Web of Science® Google Scholar
26 Mukhopadhyay B. and Das D., Multi-objective dynamic and static reconfiguration with optimized allocation of PV-DG and battery energy storage system, Renewable and Sustainable Energy Reviews. (2020) 124, https://doi.org/10.1016/j.rser.2020.109777, 109777.
10.1016/j.rser.2020.109777
Web of Science® Google Scholar
27 Ganguly S. and Samajpati D., Distributed generation allocation on radial distribution networks under uncertainties of load and generation using genetic algorithm, IEEE Transactions on Sustainable Energy. (2015) 6, no. 3, 688–697, https://doi.org/10.1109/TSTE.2015.2406915, 2-s2.0-85027953144.
10.1109/TSTE.2015.2406915
Web of Science® Google Scholar
28 Zidan A. and El-Saadany E. F., Distribution system reconfiguration for energy loss reduction considering the variability of load and local renewable generation, Energy. (2013) 59, 698–707, https://doi.org/10.1016/j.energy.2013.06.061, 2-s2.0-84883263506.
10.1016/j.energy.2013.06.061
Web of Science® Google Scholar
29 Nasiraghdam H. and Jadid S., Optimal hybrid PV/WT/FC sizing and distribution system reconfiguration using multi-objective artificial bee colony (MOABC) algorithm, Solar Energy. (2012) 86, no. 10, 3057–3071, https://doi.org/10.1016/j.solener.2012.07.014, 2-s2.0-84865716365.
10.1016/j.solener.2012.07.014
Web of Science® Google Scholar
30 Olamaei J., Niknam T., and Gharehpetian G., Application of particle swarm optimization for distribution feeder reconfiguration considering distributed generators, Applied Mathematics and Computation. (2008) 201, no. 1-2, 575–586, https://doi.org/10.1016/j.amc.2007.12.053, 2-s2.0-44649131436.
10.1016/j.amc.2007.12.053
Web of Science® Google Scholar
31 Naghizadeh R., Afrakhte H., and Ziapour M., Smart distribution network reconfiguration based on optimal planning of distributed generation resources using teaching learning based algorithm to reduce generation costs, losses and improve reliability, Electrical Engineering (ICEE), Iranian Conference on, 2018, Mashhad, Iran, IEEE, 1125–1131:, https://doi.org/10.1109/ICEE.2018.8472451, 2-s2.0-85055657944.
10.1109/ICEE.2018.8472451
Google Scholar
32 Alturki M. and Khodaei A., Increasing distribution grid hosting capacity through optimal network reconfiguration, 2018 North American Power Symposium (NAPS), 2018, IEEE, 1–6:.
Google Scholar
33 Uniyal A. and Sarangi S., Optimal network reconfiguration and DG allocation using adaptive modified whale optimization algorithm considering probabilistic load flow, Electric Power Systems Research. (2021) 192, https://doi.org/10.1016/j.epsr.2020.106909, 106909.
10.1016/j.epsr.2020.106909
Web of Science® Google Scholar
34 Lotfi H. and Ghazi R., Optimal participation of demand response aggregators in reconfigurable distribution system considering photovoltaic and storage units, Journal of Ambient Intelligence and Humanized Computing. (2021) 12, no. 2, 2233–2255, https://doi.org/10.1007/s12652-020-02322-2.
10.1007/s12652-020-02322-2
Web of Science® Google Scholar
35 Lotfi H., Ghazi R., and Naghibi-Sistani M., Multi-objective dynamic distribution feeder reconfiguration along with capacitor allocation using a new hybrid evolutionary algorithm, Energy Systems. (2020) 11, no. 3, 779–809, https://doi.org/10.1007/s12667-019-00333-3, 2-s2.0-85064354433.
10.1007/s12667-019-00333-3
Google Scholar
36 Lotfi H., Multi-objective network reconfiguration and allocation of capacitor units in radial distribution system using an enhanced artificial bee colony optimization, Electric Power Components and Systems. (2022) 49, no. 13-14, 1130–1142, https://doi.org/10.1080/15325008.2022.2049661.
10.1080/15325008.2022.2049661
Web of Science® Google Scholar
37 Biju E. and Anitha M., Placement of DG and capacitor for loss reduction and reliability improvement in radial distribution systems using BFA, ARPN Journal of Engineering and Applied Sciences. (2015) 12, no. 10, 9604–9613.
Google Scholar
38 Aien M., Khajeh M. G., Rashidinejad M., and Fotuhi-Firuzabad M., Probabilistic power flow of correlated hybrid wind-photovoltaic power systems, IET Renewable Power Generation. (2014) 8, no. 6, 649–658, https://doi.org/10.1049/iet-rpg.2013.0120, 2-s2.0-84904972340.
10.1049/iet-rpg.2013.0120
Web of Science® Google Scholar
39 Aien M., Biglari A., and Rashidinejad M., Probabilistic reliability evaluation of hybrid wind-photovoltaic power systems, 2013 21st Iranian Conference on Electrical Engineering (ICEE), 2013, IEEE, 1–6:.
Google Scholar
40 Conejo A. J., Carrión M., and Morales J. M., Decision Making Under Uncertainty in Electricity Markets, 2010, Springer.
10.1007/978-1-4419-7421-1
Google Scholar
41 Mirjalili S., Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems, Neural Computing and Applications. (2016) 27, no. 4, 1053–1073, https://doi.org/10.1007/s00521-015-1920-1, 2-s2.0-84930165782.
10.1007/s00521-015-1920-1
Web of Science® Google Scholar
42 Baran M. E. and Wu F. F., Network reconfiguration in distribution systems for loss reduction and load balancing, IEEE Transactions on Power Delivery. (1989) 4, no. 2, 1401–1407, https://doi.org/10.1109/61.25627, 2-s2.0-84863333614.
10.1109/61.25627
Web of Science® Google Scholar
43 Wang X., Gong Y., and Jiang C., Regional carbon emission management based on probabilistic power flow with correlated stochastic variables, IEEE Transactions on Power Systems. (2014) 30, no. 2, 1094–1103, https://doi.org/10.1109/TPWRS.2014.2344861, 2-s2.0-85028146653.
10.1109/TPWRS.2014.2344861
Web of Science® Google Scholar

Citing Literature

All articles

Stochastic Optimal Reconfiguration and Placement of Photovoltaic Systems in Distribution Networks: A Real Case Study

Abstract

1. Introduction

1.1. Literature Review

1.2. Contributions and Paper Organization

2. Uncertainty Modeling

3. Problem Formulation

3.1. Objective Functions

3.1.1. PV Owners’ Profit Maximization

3.1.2. DisCo’s Cost Minimization

3.1.3. ECOST Minimization

3.2. Constraints

3.2.1. Radial Constraints

3.2.2. Branch Capacity Limit

3.2.3. Voltage Profile

3.2.4. PV Power Generation Limit

3.2.5. Limitation on the Maximum Number of PVs

4. Dragonfly Algorithm (DA)

5. Simulation Results

5.1. Numerical Results for IEEE 33-Bus DN

5.1.1. Case 1: SO Reconfiguration Aiming to Maximize PV Owner’s Profit

5.1.2. Case 2: SO Reconfiguration Aiming to Minimize DisCo’s Cost

5.1.3. Case 3: SO Reconfiguration Aiming to Minimize the ECOST

5.1.4. Case 4: MO Reconfiguration Aiming to Maximize PV Owner’s Profit and Minimize ECOST

5.1.5. Case 5: MO Reconfiguration Aiming to Maximize PV Owner’s Profit and Minimize DisCo’s Cost

5.1.6. Case 6: MO Reconfiguration Aiming to Minimize DisCo’s Cost and ECOST

5.1.7. Case 7: MO Reconfiguration Aiming to Maximize PV Owner’s Profit, Minimize DisCo’s Cost, and ECOST

5.2. Real DN

6. Conclusion

Abbreviations

Conflicts of Interest

Authors’ Contributions

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information