Buffer-aided cooperative nonorthogonal multiple access (NOMA) improves the effectiveness of the spectral by allowing more than one user to share the same resources to realize massive connectivity. This is notably attractive in the fifth generation (5G) and beyond systems, where a massive number of connections are essential such as the Internet of Things (IoT). Wireless-powered communication through energy harvesting is another 5G promising solution for the future massively dense networks. To sufficiently utilize energy harvesting in a buffer-aided cooperative NOMA network, the relay selection rule must consider the energy level of the selected relay in addition to its data content to avoid an outage. This paper proposes a relay selection rule for energy-harvesting buffer-aided cooperative NOMA networks. The proposed relay selection scheme considers the state of both the data buffer and the energy buffer. The simulations show that the proposed selection rule has improved the network outage probability and throughput as well. This enhancement is kept with changing the number of relays. The results also show that the impact of changing the energy buffer size is crucial, and the larger, the better. Furthermore, making the source transmitting power larger than the relay transmitting power is beneficial, especially with large enough energy buffer sizes.

1. Introduction

Currently, wireless connection is the most important form of communication; therefore, the unprecedented increase in the number of online devices makes wireless communications in upcoming applications more challenging. For example, the Internet of Things (IoT) (a fifth generation (5G) and beyond technology) requires massive wireless connectivity while maintaining a low outage probability, and these requirements cannot be met with the current infrastructure [1].

In traditional wireless communication, the main transmission form is the orthogonal transmission that ensures an exclusive frequency band, time slot, or code for each link between transmitters and receivers, to make sure that communications among different links do not interfere with each other. This transmission technique degrades the spectral efficiency and makes it insufficient for the forthcoming era of communications [2], resulting in the establishment of nonorthogonal multiple access (NOMA) for simultaneous use of the same resources. NOMA is conceptually different from orthogonal schemes; in NOMA, multiple users are allowed to transmit at the same code, time, and frequency, but with different levels of power. Particularly, NOMA gives lower power to the users with better channel states, because they can decode their own messages with less power and we call them the strong users. Due to the progression in the domain of signal processing, NOMA becomes realizable with advanced receivers, with which strong users can eliminate mutual interference caused by sharing the same resources by utilizing successive interference cancellation (SIC) [3]. Since higher power is sent to the weak user, the weak user (with the poor channel) can cancel the strong user signal (treating it as interference) and decode its signal successfully. Therefore, NOMA connects more users in the same resource such as frequency band or time slot, but with different levels of power which improves spectral efficiency [4]. Hence, NOMA is an attractive solution to achieve the massive connectivity required for 5G applications such as the IoT [5, 6]. Currently, NOMA is under consideration for 3GPP Release 16 standards of 5G systems [7].

Another essential network performance enhancement technique is relay [8]. Relays help the source to transmit packets to the users by providing an alternative connection between source and destination [9]. Based on that, LTE Release 10 has recognized the cooperation with relay nodes as an effective part of realizing modern wireless communications [10]. Relaying can be performed in two methods: amplify and forward (AF) and decode and forward (DF) [11, 12]. Relay selection is a key solution to avoid performance loss of cooperative relaying [13]. Early work selects relays aiming to maximize signal-to-noise ratio SNR [14]. Relay selection is extensively studied in the literature. We focus on those related to this study, particularly, buffer-aided relays. The idea behind buffer-aided relays is driven by the fact that the relay with the best channel for reception does not have to be the transmitting relay if it does not have the best transmission channel [15]. In [16], max–max relay selection (MMRS) selects the relay with the best-receiving channel in one slot and the relay with the best channel for transmission in the subsequent slot. The short back of MMRS is forcing transmission after reception. Max-link relay selection releases this constraint by selecting the best channel always [17]. Another improvement is the state-based scheme [18], where the data buffer state is considered in selection to avoid empty and full buffers. With an empty buffer, no transmission is possible and no reception with a full buffer.

Energy harvesting is appealing to avoid frequent battery change which increases the flexibility of relay deployment. By harvesting energy through solar or RF, a relay can charge itself. There are two methods to make efficient energy harvesting. In the first method, part of the received energy is for signal processing and the left is for transmission [19]. This is the popular simultaneous wireless information and power transfer (SWIPT). Another method is to store the harvested energy from the source signal in an energy buffer for future use.

After introducing these 5G technologies, it is noticeable that combining various technologies to overcome their shortcomings is popular in the literature. For example, NOMA has been successfully applied in buffer-aided cooperative relay networks. Several studies have applied the mentioned relay selection schemes with NOMA transmission and gained a better performance [20–22]. Another example of combining technologies is energy-harvesting buffer-aided relay networks. In [23], a relay is selected randomly from a set of relays with their energy buffers that are nonempty. The work in [24] considers both data buffer and energy buffer in relay selection; the authors assumed that relays harvest energy with energy arrivals according to a deterministic process. This is not practical; therefore, [25] considered a nondeterministic energy arrival and proposed a relay selection scheme based on the instantaneous state of both data buffers and energy buffers. As stated in [26], finding an optimal protocol that can achieve the minimum outage probability at a given delay constraint is still an open problem even in the most elementary buffer-aided relay network. As a result, the optimal selection scheme is still an open problem for relays with finite (practical) buffer size. Table 1 summarizes the related literature.

Table 1. Related literature.

Rule	Data buffer	Energy buffer	Data buffer state	Energy buffer state	Energy source	Multiple access
[16]	Infinite	X	X	X	Permanent	Orthogonal
[17]	Infinite	X	X	X	Permanent	Orthogonal
[18]	Finite	X	Available	X	Permanent	Orthogonal
[22]	Finite	X	Available	X	Permanent	Nonorthogonal
[23]	X	Finite	X	Available	RF	Orthogonal
[24]	Finite	Finite	Available	Available	RF	Orthogonal
[25]	Finite	Finite	Available	Available	RF	Orthogonal
This work	Finite	Finite	Available	Available	RF	Nonorthogonal

However, to the best of the author’s knowledge, none of the available studies has suggested a relay selection scheme which is adequate for NOMA with energy harvesting in a random energy-arriving environment. Accordingly, motivated by filling this gap, the key novelty of this article is to propose a suitable relay selection scheme that minimizes the outage probability in a random energy-harvesting cooperative NOMA network by taking the state of data and energy buffers into consideration in the selection scheme. The contributions of this article are summarized as follows: (1) proposing a novel relay selection scheme for energy-harvesting buffer-aided cooperative NOMA networks, (2) studying the impact of varying the energy buffer size on the network outage probability, and (3) Studying the outage probability of the network under increasing the source transmitted power to give the relays the chance to gather more charges.

The rest of the article is organized as follows: the system model for the suggested energy-harvesting buffer-aided cooperative NOMA network is in Section 2. The proposed relay selection scheme and its performance analysis are presented in Section 3. Simulation trials of the proposed system along with comparison with other available solutions are discussed in detail in Section 4. Finally, the conclusion is presented in Section 5.

2. System Model

The system model of the proposed energy-harvesting buffer-aided cooperative NOMA network is shown in Figure 1. Figure 1 illustrates a source node S, k half-duplex DF buffer-aided relays, and k = 1, 2, 3.⋯, K, with R₁ transmitting via NOMA to two users U₁ and U₂ simultaneously. The system model can be extended to any number of users as in [27]. The interconnection between relays in Figure 1 assures the balancing of data packets to avoid full and empty buffers.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Energy-harvesting buffer-aided cooperative NOMA network.

Each relay R_k has a L-size data buffer to store the packets and an E-size energy buffer to store charges. The S − R_k, S − U, and R_k − U links have the channel coefficients h_srk, h_su, and h_rku, respectively. The channels are assumed to have flat Rayleigh fading coefficients which hold its value during the time slot, and its value changes randomly in different time slots. P_t is the notation for source transmit power, P_r is the transmit power of relays, and σ² is the noise variances for all receiving points. The target rate for data transmission is assumed to be constant at ε. If the capacity of a link is higher than or equal to ε, then that link is up; hence, it can handle the transmission. Otherwise, the link is down and no transmission can take place, and the link is said to be in an outage. Due to shadowing, the direct link between S and users S − U is assumed to be blocked. All nodes are assumed to have the information about the states of all links. At time slot t, channel capacities are calculated as follows:

(1)

where

and

. The channel gains of

and

are distributed according to the exponential distribution with the average

and

, where E[.] stands for the expectation.

and

are also following the exponential distribution with average

and

. Thus,

, γ_su(t), and

are the instantaneous SNR, while

and

are the average SNR for channels

and

, respectively. As mentioned above, if the capacity of the link is lower than the target data rate outage that occurs, the outage is calculated based on the fact that

and

are following the exponential distribution; their CDFs are:

(2)

After the analysis of data packets, we analyze the energy harvesting. Each relay node can harvest energy from the source signal. As in [28], the noise energy is ignored as the noise power is often lower than the sensitivity of the circuit that harvests energy. The amount of harvested energy by relay R_k in one-time slot with duration t is equal to [29]

(3)

where 0 < η < 1 denotes the energy conversion efficiency. The energy consumed for reception is ignored in the current study and can be included with minor changes.

There is an outage analysis of the cooperative NOMA network. In orthogonal transmission networks, an outage occurs if the link capacity is less than the target data rate. Since NOMA is applied from R_k to users, the relay R_k needs to have the packets of the two users prior to applying NOMA. As in [26], we assume that NOMA is not applicable unless the link between S and R_k supports the transmission of the two packets simultaneously. For the S⟶R_k link, if it satisfies

(4)

This makes the outage of the S − R_k link

. On the other hand, for the R_k⟶U_m (m = 1 or 2) link, NOMA can be applied to transmit packets to U₁ and U₂ simultaneously. The superimposed NOMA symbol at R_k is given by

(5)

where

and

are data for users U₁ and U₂, respectively, and 0 ≤ α ≤ 1 is the power allocation factor. Then, the received signal at U_m is given by

(6)

where n_m(t) is the noise at user U_m. When NOMA is applied, when

, the SNR to decode

at U₂ is given by

(7)

Because

can also be decoded at U₁ if it can be decoded at U₂. Removing

from the received signal at U₁ by SIC, the required SNR to decode

at U₁ is given by

(8)

Following similar procedures as those in [17], the condition that there exists an α to support NOMA transmission to both U₁ and U₂ (i.e.,

and

is given by

(9)

(10)

from (9) and (10)

(11)

(12)

Similarly, if

, NOMA condition becomes

(13)

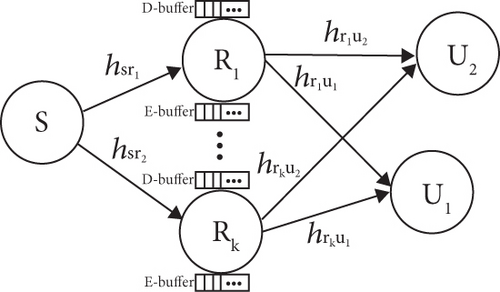
If the SNR for the R_k⟶U_m (m = 1 or 2) links is not large enough to satisfy (12) or (13), NOMA transmission is not possible or not efficient. In this case, if , OMA can be used to transmit one packet to U_m.

Following the similar procedures as those in [30, 31], the NOMA transmission is not supported with the probability

(14)

and we have

(15)

where (m, n) ∈ {(1, 2), (2, 1)}.

3. Proposed Relay Selection Scheme

In this section, a new relay selection scheme is suggested for energy-harvesting relays in buffer-aided cooperative NOMA. At first, we define two sets of relays according to their instantaneous SNR of the channels. One is the receiving set

. And the transmitting set is

. After selecting the relays that have channels that satisfy the SNR threshold to support reception and transmission, the data buffer content has to be considered in the selection because the data buffer content is crucial in allowing communication or forbidding it. Specifically, a full buffer stops the reception and an empty buffer stops the transmission. Therefore, the relays with full buffers have to be excluded from RS to get the modified set

(16)

l_k is the length of R_k data buffer. Regarding the transmission set TS, the emptiness of the data buffer is not the only reason to break the transmission. The other aspect that needs to be considered is the state of the energy buffer to avoid selecting a transmitting relay with insufficient energy which causes an outage. In this study, we assume that each slot in the energy buffer contains sufficient energy for transmission. Knowing that the modified receiving set becomes

(17)

e_k is the length of R_k energy buffer. After that, the available relays for selection are known. Now, we need to select the best relay among the available relays. To this end, the best-receiving relay is the one closer to the empty data buffer, and the best-transmitting relay is the one closer to the full buffer. Hence, the best-receiving relay is

(18)

and the best-transmitting relay is

(19)

With this scheme, the capability of the buffer-aided relay is fully exploited by releasing the necessity to make the receiving and the transmitting subsequent. In summary, from a practical production perspective, in the beginning, each relay sends its data and energy buffer length along with the channel state information (CSI) to the source node to decide on the relay selection. Then, the selected receiving relay stores the received packet in its data buffer from the source. The other relays harvest the energy from the source signal. Similarly, the selected transmitting relay sends a packet to the users by the energy in its energy buffer. To analyze the performance of the energy-harvesting relays in buffer-aided cooperative NOMA, we study the probability of selecting a transmitting relay; then, that relay can not send a data packet because of its empty energy buffer. That is, P({R_k|(R_k ∈ TS)∩(l_k > 0)∩(e_k = 0)}) ≥ 0 which increases the outage. This is likely to be the case because the most receiving relay or the relay with closer to a full buffer is likely to be the least energy-harvesting relay. Hence, the proposed selection scheme outperforms the available state-based scheme.

4. Simulation Results

This section presents the outcomes of the experimental simulations to confirm the proposed relay selection scheme. We test the validity of considering the energy buffer state in relay selection in the energy-harvesting cooperative NOMA network. In the simulations, we assume that the variance of the noise σ² is normalized to unity and we follow [30] in assuming that data rate ε = 2 bps/Hz. The data and energy buffer size are set to L = 5, E = 5, unless stated otherwise. All simulation results are gathered with 10⁶ Monte Carlo trials.

Firstly, we show the effect of considering the energy buffer state in relay selection on the NOMA network outage probability. The positive impact of this consideration on the outage probability is obvious in Figure 2. Figure 2 shows the comparison between selecting relays based on the state of the data buffer (the traditional state-based) and considering both data and energy buffer states in selection for the two relay NOMA networks. The proposed selection scheme enhances the network performance. This is the case because considering the energy buffer state in the selection scheme saves the network from being in outage by avoiding the selection of a transmitting relay with an empty energy buffer. For instance, to get a 0.3 outage probability in the two relay cases, the required SNR is about 11 dB and above 15 dB for the proposed and state-based selection scheme, respectively. So the reduction in the required SNR is more than 4 dB.

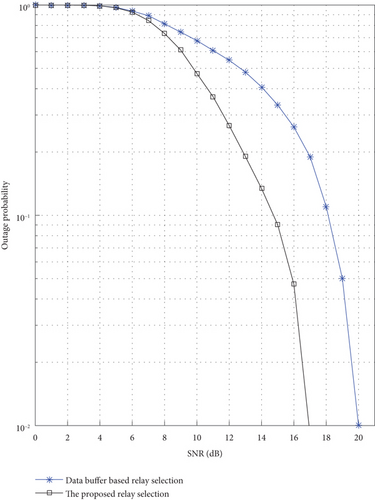
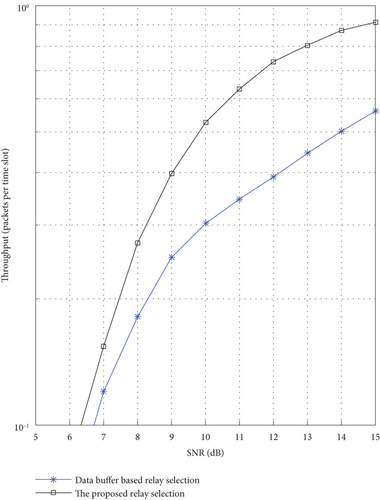
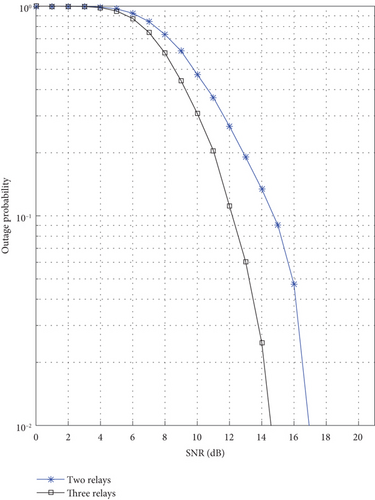
Figure 3 stresses the importance of the proposed selection scheme as it shows its impact on the throughput of the NOMA network. For the 2 relay case, the throughput improvement can be higher than 0.3 packets per time slot at 13 dB SNR. Based on the proportionality between outage probability and throughput, we can infer that the improvement in the outage performance by considering the energy buffer state will always raise the throughput of the network. This is the case with adding more relays; in Figure 4, the proposed scheme is applied in three relay networks, and it has enhanced the outage performance better than applying the proposed scheme in the two relay networks. It is worth mentioning that thanks to NOMA, reaching 1 packet per slot is possible with half-duplex transmission.

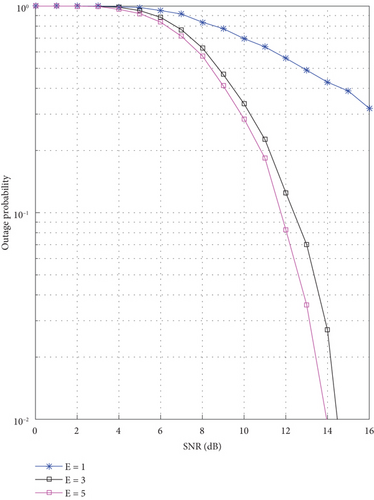
Another important aspect is the size of the energy buffer. The larger the size, the better in terms of outage probability; however, this is limited by the compactness of IoT devices. The impact of the energy sizes is shown in Figure 5. It is clear that with E = 1 (the smallest size), the performance of the three relay NOMA networks is the worst. This is due to the weak capabilities of the energy buffer in keeping charges. The performance is better with a larger energy buffer size; this is the case with E = 3 and E = 5. It is noticeable that the impact of increasing the size of the energy is weakened with larger sizes, so the difference in performance between E = 1 and E = 3 is much larger than the difference in performance between E = 3 and E = 5.

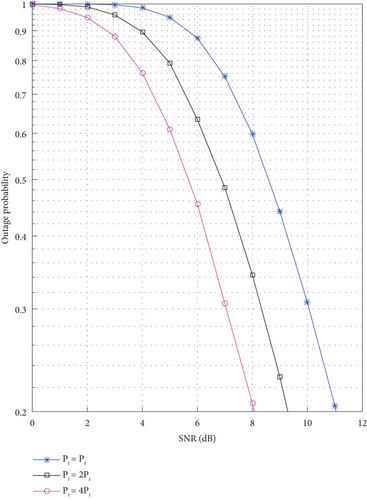
After studying the benefits of considering the energy buffer states in relay selection in NOMA networks, the impact of changing the transmitted power on the proposed scheme performance is shown in Figure 6. Three cases are considered: (1) the transmitted power from the source to the relays P_t is similar to the power of transmission from the relays to the users P_r. (2) P_t = 2P_r. (3) P_t = 4P_r. For example, the enhancement can reach 3 dB to achieve 0.3 outage probability with P_t = 4P_r when compared with P_t = P_r. The reason for this improvement is that with P_t = 4P_r if the relay received this power, its energy buffer will be charged in four slots. This means with one charging instance, the relay can transmit four times, which means more availability for the relay to users’ links. Before ending this section, it is noteworthy that the importance of large energy buffer size is increased. Specifically, it is known that the channel state changes from one-time slot to another, so it is important to keep the whole charge, especially with good channels. For instance, charging the relay with 4 slots in P_t = 4P_r is not possible if the energy buffer size is less than 4 E ≤ 4, with noting that charging the relay with 4 slots happens only with good channels which makes losing these charges pricey.

5. Conclusions

This study proposes considering the state of the energy buffer in relay selection in energy-harvesting buffer-aided cooperative NOMA networks. This is motivated due to the lack of performance caused by selecting a transmitting relay which is a lack of sufficient energy for transmission, which causes an outage. The proposed scheme improves the network performance by avoiding noncapable transmitting relays as this problem appears only with transmitting relays and not in the receiving ones. The improvements of the proposed scheme on the outage probability are valid even with adding more relays. The improvement in outage probability led to achieving higher throughput with the proposed scheme. Furthermore, the size of the energy buffer dictates the performance of the NOMA network; in general, the larger the value of E, the better. However, this value of E is limited to keep the compactness of devices. It is noticed that the impact of increasing the value of E is decreased with larger sizes. Finally, increasing the ratio of the source transmitting power and the relay transmitting power is beneficial in reducing the outage probability since it gives the relay the chance to harvest more energy, which increases the need for a large size energy buffer.

Conflicts of Interest

The author declares that there are no conflicts of interest.

Open Research

Data Availability

All required data are presented in the paper.

References

1 Nguyen D., Ding M., Pathirana N., Seneviratne A., Li J., Niyato D., Dobre O., and Poor H. V., 6G Internet of Things: a comprehensive survey, IEEE Internet of Things Journal. (2022) 9, no. 1, 359–383, https://doi.org/10.1109/JIOT.2021.3103320.
10.1109/JIOT.2021.3103320
Web of Science® Google Scholar
2 Alkhawatrah M., Cooperative NOMA based on OAM transmission for beyond 5G applications, Computer Systems Science and Engineering. (2023) 45, no. 2, 1187–1197, https://doi.org/10.32604/csse.2023.030699.
10.32604/csse.2023.030699
Google Scholar
3 Ding Z., Peng M., and Poor H. V., Cooperative non-orthogonal multiple access in 5G systems, IEEE Communications Letters. (2015) 19, no. 8, 1462–1465, https://doi.org/10.1109/LCOMM.2015.2441064, 2-s2.0-84939484100.
10.1109/LCOMM.2015.2441064
Web of Science® Google Scholar
4 Lv L., Chen J., and Ni Q., Cooperative non-orthogonal multiple access in cognitive radio, IEEE Communications Letters. (2016) 20, no. 10, 2059–2062, https://doi.org/10.1109/LCOMM.2016.2596763, 2-s2.0-84992197988.
10.1109/LCOMM.2016.2596763
Web of Science® Google Scholar
5 Alkhawatrah M., Buffer-aided cooperative millimeter waves for IOT networks, Journal of Electrical and Computer Engineering. (2022) 2022, 8, https://doi.org/10.1155/2022/7474679, 7474679.
10.1155/2022/7474679
Web of Science® Google Scholar
6 Alkhawatrah M., The performance of supervised machine learning based relay selection in cooperative NOMA, IEEE Access. (2023) 11, 1570–1577, https://doi.org/10.1109/ACCESS.2022.3233443.
10.1109/ACCESS.2022.3233443
Web of Science® Google Scholar
7 Ghazi H. S. and Wesołowski K. W., Improved detection in successive interference cancellation NOMA OFDM receiver, IEEE Access. (2019) 7, 103325–103335, https://doi.org/10.1109/ACCESS.2019.2931809.
10.1109/ACCESS.2019.2931809
Web of Science® Google Scholar
8 Andrews J. G., Buzzi S., Choi W., Hanly S. V., Lozano A., Soong A. C., and Zhang J. C., What will 5G be?, IEEE Journal on Selected Areas in Communications. (2014) 32, no. 6, 1065–1082, https://doi.org/10.1109/JSAC.2014.2328098, 2-s2.0-84904979683.
10.1109/JSAC.2014.2328098
Web of Science® Google Scholar
9 Alkhawatrah M., Alamayreh A., and Qasem N., Cooperative relay networks based on the OAM technique for 5G applications, Computer Systems Science and Engineering. (2022) 44, no. 3, 1911–1919.
10.32604/csse.2023.028614
Web of Science® Google Scholar
10 Laneman J. N., Wornell G. W., and Tse D. N. C., An efficient protocol for realizing cooperative diversity in wireless networks, Proceedings. 2001 IEEE International Symposium on Information Theory (IEEE Cat. No.01CH37252), 2001, Washington, DC, USA, https://doi.org/10.1109/ISIT.2001.936157, 2-s2.0-0034869777.
10.1109/ISIT.2001.936157
Google Scholar
11 Nosratinia A., Hunter T., and Hedayat A., Cooperative communication in wireless networks, IEEE Communications Magazine. (2004) 42, no. 10, 74–80, https://doi.org/10.1109/MCOM.2004.1341264, 2-s2.0-7244244208.
10.1109/MCOM.2004.1341264
Web of Science® Google Scholar
12 Laneman J. N., Tse D. N., and Wornell G. W., Cooperative diversity in wireless networks: efficient protocols and outage behavior, IEEE Transactions on Information Theory. (2004) 50, no. 12, 3062–3080, https://doi.org/10.1109/TIT.2004.838089, 2-s2.0-5044252003.
10.1109/TIT.2004.838089
Web of Science® Google Scholar
13 Bletsas A., Shin H., and Win M., Cooperative communications with outage-optimal opportunistic relaying, IEEE Transactions on Wireless Communications. (2007) 6, no. 9, 3450–3460, https://doi.org/10.1109/TWC.2007.06020050, 2-s2.0-35448931484.
10.1109/TWC.2007.06020050
Web of Science® Google Scholar
14 Ikki S. and Ahmed M. H., On the performance of cooperative diversity networks with the nth best-relay selection scheme, IEEE Transactions on Communications. (2010) 58, no. 11, 3062–3069, https://doi.org/10.1109/TCOMM.2010.092810.090322, 2-s2.0-78349310972.
10.1109/TCOMM.2010.092810.090322
Web of Science® Google Scholar
15 Nomikos N., Charalambous T., Krikidis I., Skoutas D. N., Vouyioukas D., Johansson M., and Skianis C., A survey on buffer-aided relay selection, IEEE Communications Surveys & Tutorials. (2016) 18, no. 2, 1073–1097, https://doi.org/10.1109/COMST.2015.2512441, 2-s2.0-84971554724.
10.1109/COMST.2015.2512441
Web of Science® Google Scholar
16 Ikhlef A., Michalopoulos D., and Schober R., Max-max relay selection for relays with buffers, IEEE Transactions on Wireless Communications. (2012) 11, no. 3, 1124–1135, https://doi.org/10.1109/TWC.2012.011012.110682, 2-s2.0-84858342202.
10.1109/TWC.2012.011012.110682
Web of Science® Google Scholar
17 Krikidis I., Charalambous T., and Thompson J. S., Buffer-aided relay selection for cooperative diversity systems without delay constraints, IEEE Transactions on Wireless Communications. (2012) 11, no. 5, 1957–1967, https://doi.org/10.1109/TWC.2012.032712.111970, 2-s2.0-84861461183.
10.1109/TWC.2012.032712.111970
Web of Science® Google Scholar
18 Luo S. and Teh K. C., Buffer state based relay selection for buffer-aided cooperative relaying systems, IEEE Transactions on Wireless Communications. (2015) 14, no. 10, 5430–5439, https://doi.org/10.1109/TWC.2015.2438296, 2-s2.0-84959534330.
10.1109/TWC.2015.2438296
Web of Science® Google Scholar
19 Nasir A. A., Zhou X., Durrani S., and Kennedy R. A., Relaying protocols for wireless energy harvesting and information processing, IEEE Transactions on Wireless Communications. (2013) 12, no. 7, 3622–3636, https://doi.org/10.1109/TWC.2013.062413.122042, 2-s2.0-84881478956.
10.1109/TWC.2013.062413.122042
Web of Science® Google Scholar
20 Ding Z., Dai H., and Poor H. V., Relay selection for cooperative NOMA, IEEE Wireless Communications Letters. (2016) 5, no. 4, 416–419, https://doi.org/10.1109/LWC.2016.2574709, 2-s2.0-84984846909.
10.1109/LWC.2016.2574709
Web of Science® Google Scholar
21 Luo S. and Teh K. C., Adaptive transmission for cooperative NOMA system with buffer-aided relaying, IEEE Communications Letters. (2017) 21, no. 4, 937–940, https://doi.org/10.1109/LCOMM.2016.2647250, 2-s2.0-85018188112.
10.1109/LCOMM.2016.2647250
Web of Science® Google Scholar
22 Alkhawatrah M., Gong Y., Chen G., Lambotharan S., and Chambers J. A., Buffer-aided relay selection for cooperative NOMA in the Internet of Things, IEEE Internet of Things Journal. (2019) 6, no. 3, 5722–5731, https://doi.org/10.1109/JIOT.2019.2905169, 2-s2.0-85067859596.
10.1109/JIOT.2019.2905169
Web of Science® Google Scholar
23 Krikidis I., Relay selection in wireless powered cooperative networks with energy storage, IEEE Journal on Selected Areas in Communications. (2015) 33, no. 12, 2596–2610, https://doi.org/10.1109/JSAC.2015.2479015, 2-s2.0-84959240680.
10.1109/JSAC.2015.2479015
Web of Science® Google Scholar
24 Wu Y., Qian L. P., Huang L., and Shen X., Optimal relay selection and power control for energy-harvesting wireless relay networks, IEEE Transactions on Green Communications and Networking. (2018) 2, no. 2, 471–481, https://doi.org/10.1109/TGCN.2017.2786704, 2-s2.0-85060563016.
10.1109/TGCN.2017.2786704
Google Scholar
25 Lin C. H. and Liu K. H., Relay selection for energy-harvesting relays with finite data buffer and energy storage, IEEE Internet of Things Journal. (2021) 8, no. 14, 11249–11259, https://doi.org/10.1109/JIOT.2021.3053290.
10.1109/JIOT.2021.3053290
Web of Science® Google Scholar
26 Jamali V., Zlatanov N., and Schober R., Bidirectional buffer-aided relay networks with fixed rate transmission–part II: delay-constrained case, IEEE Transactions on Wireless Communications. (2015) 14, no. 3, 1339–1355, https://doi.org/10.1109/TWC.2014.2365806, 2-s2.0-84924872189.
10.1109/TWC.2014.2365806
Web of Science® Google Scholar
27 Wei Z., Guo J., Ng D. W. K., and Yuan J., Fairness comparison of uplink NOMA and OMA, 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), 2017, Sydney, NSW, Australia, 1–6, https://doi.org/10.1109/VTCSpring.2017.8108680, 2-s2.0-85040535784.
10.1109/VTCSpring.2017.8108680
Google Scholar
28 Gu Y., Chen H., Li Y., Liang Y.-C., and Vucetic B., Distributed multi-relay selection in accumulate-then-forward energy harvesting relay networks, IEEE Transactions on Green Communications and Networking. (2018) 2, no. 1, 74–86, https://doi.org/10.1109/TGCN.2017.2761872, 2-s2.0-85067529497.
10.1109/TGCN.2017.2761872
Google Scholar
29 Yan P., Zou Y., Ding X., and Zhu J., Energy-aware relay selection improves security-reliability tradeoff in energy harvesting cooperative cognitive radio systems, IEEE Transactions on Vehicular Technology. (2020) 69, no. 5, 5115–5128, https://doi.org/10.1109/TVT.2020.2979267.
10.1109/TVT.2020.2979267
Web of Science® Google Scholar
30 Zhang Q., Liang Z., Li Q., and Qin J., Buffer-aided non-orthogonal multiple access relaying systems in Rayleigh fading channels, IEEE Transactions on Communications. (2016) 65, no. 1, 1–106, https://doi.org/10.1109/TCOMM.2016.2630050, 2-s2.0-85009837017.
10.1109/TCOMM.2016.2630050
Web of Science® Google Scholar
31 Mondal S., Dhar Roy S., and Kundu S., Outage analysis for NOMA–based energy harvesting relay network with imperfect CSI and transmit antenna selection, IET Communications. (2020) 14, no. 14, 2240–2249, https://doi.org/10.1049/iet-com.2019.0841.
10.1049/iet-com.2019.0841
Web of Science® Google Scholar

All articles

Energy-Harvesting Cooperative NOMA in IOT Networks

Abstract

1. Introduction

2. System Model

3. Proposed Relay Selection Scheme

4. Simulation Results

5. Conclusions

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley