In this paper, a forced vibration caused by drag and lift forces with time-varying mass is studied. The construction of the model is conducted by adding impact force to the previous model. The periodicity of the solution is yet known. Hence, the model is seen as a perturbation problem. Since the unperturbed problem has a periodic solution, we applied the averaging method to determine the sufficient condition such that the limit cycle exists.

1. Introduction

Vibration is a dynamic phenomenon that is quite complicated. In particular, the stability of a system that experiences vibrations is usually challenging to determine; however, it is essential to know. In engineering, numerical approaches and experiments are used to determine the system’s state experiencing vibrations. Nevertheless, theoretical studies of this phenomenon are also widely carried out by scientists since they are expected to provide a better approximation.

One of the essential problems to be studied is the vibrations in bridge cables due to rainwater and wind. Raindrops that fall on the bridge cable will remain on the line until a certain mass and then fall, dripping. This fact repeatedly happened until the rain stopped. The fluid forces are divided into two components as follows: drag force in line with the flow direction and lift force perpendicular to the flow direction [1]. If the mass of raindrops and rainfall is assumed to be equal, then there is no change in the total mass, so the mass is constant. Under this assumption, the mathematical model that describes a vibration of cables in a vertical direction was studied by Haaker and van der Burgh in [2]. Moreover, the authors assumed that the vibration force is affected by the angle between the symmetric axis and the horizontal wind velocity or used to call a static angle of attack. Under this assumption, the authors could present conditions for the existence and uniqueness of a stable limit cycle. If Den Hartog’s criterion applies, the linearized equation in [2] has an unbounded solution.

The phenomena of rain-wind induced vibration because of occurrence of the rivulet of water in the inclined cable. An inclined cable is aerodynamically stable without rain but unstable with rain. The experimental data showed that the rivulet of water and the angle of the wind to the cable could make vibration phenomena [3].

A different assumption was studied in [4] associated with the variation of the position of the water ridge. The authors assume that it depends on time, i.e., a periodic function with a nonzero initial value using the cosines function. In contrast with the result in [2], the linearized equation in [4] leads to periodic solutions. A more detailed explanation was presented in [5]. Another assumption was also presented by Waluya in [6]. He studied the dynamic of the cable-stayed bridge as in [4] using the assumption that the variation of the position is a periodic function with zero initial value using the sinus function. Using the perturbation technique, he presents the approximation of the solution for different cases of angular frequency. All these references assume that the mass is constant, whereas in this case, it makes more sense if the masses are unbalanced.

Studying the dynamics of oscillator systems whose mass varies with time is essential for many mechanical and astronomical systems problems. Irchik and Holl in [7] provided a complete bibliography with references to the application problem in various areas such as biomechanics, robotics, conveyor systems, and many others. Wisdom et al. mentioned in [8] that in celestial mechanics, the issue of mass varies very closely concerning the planar oscillations of a satellite. Moreover, in solid and fluid mechanics, the main principle of mass conservation may be incompatible with many mechanical systems that release or capture material with a particular mechanism. Numerous studies about the vibration related to external force and time-varying mass with numerical and analytic approaches have been carried out (see, for instance, [9–13]).

General formulation of the variable-mass system was presented in [7] by considering the velocity of the impacting mass while deriving the time-varying mass model. Numerous studies were then carried out using the results of this study. van Horssen et al. in [14] provided a mathematical analysis of the stability region for a free vibration force and zero velocity, with the ratio of the time-varying mass of the raindrops and the mass of the oscillator as a periodic step function. Waluya in [15] assumed that the ratio is a periodic sinusoidal function. A year later, further analysis was conducted in [16, 17] by adding vibration force as a harmonic force.

A new model of the vibrations in bridge cables due to rainwater and wind was redeveloped in [18], taking into account that the system’s mass is no longer constant. The total mass (cable and water) changes periodically. The mass increases when water attaches to the cable and decreases when water drips from it. Thus, in this system, the mass varies with time. However, this model still does not involve the velocity of the impacting mass. Therefore, this research will improve the model in [18] by involving the velocity of the impacting mass. Later, the dynamic of the forced vibrations oscillator is studied. One of the important discussions in system dynamics is related to the existence of a limit cycle.

The aim and novelty of this research is to study the oscillation behaviour of the cable, seen from the existence of a limit cycle. The existence of the stable limit cycle can be interpreted that the vibration of the structure is periodically. This paper is organized as follows. Section 1 discusses the urgency of this research. Section 2 contains the method of research. Section 3 constructs a model involving mass variation and velocity of impacting mass. Section 4 analyzes the existence of limit cycles. Last, Section 5 concludes and formulates future research.

2. Method of Research

This research starts with making a mathematical model of rain-wind-induced vibration of one degree of freedom of the dynamic of a cable-stayed bridge. By assuming that mass increases when the water attaches to the cable and decreases when the water leaves the cable, we can assume that the mass varies over time. Furthermore, by assuming that the mass of water compared to the mass of cable is small, the model can be categorized into perturbation problems. The next step is transforming the equation of the model into the Lagrange form by using the method of variation parameter. Applying the averaging method to the Lagrange standard form equation yields the averaged equation. The method of averaging is appropriate to systems of

()

where

is C^r, r ≥ 1, bounded on bounded sets, and T-periodic in t; U is bounded and open. The associated autonomous averaged system is presented by

()

The averaged system (2) should be simpler to analyze, and its properties should reflect the dynamics of system (1); see [19]. The final step is to analyze the averaged equation to get the limit cycle and bifurcation.

3. Forced Vibrations Oscillator with a Time-Varying Mass Model

A mathematical model that describes the rain-wind-induced vibrations of a straightforward one-degree-of-freedom system associated with the dynamics of cable-stayed bridges will be developed in this section. The model is an oscillator with a single degree of freedom that consists of a solid-state ridge travelling in a horizontal stiff wire (cylinder) supported by springs [6, 19]. A portion of the raindrops that hit the cylinder will stay on its surface for a while before being blown or shaken off later. This phenomenon could cause aerodynamic instability in vibrations. Hence, in this system, we consider a force vibration influenced by an external force, later called an aerodynamic force.

First, we derived the aerodynamic force, i.e., drag and lift forces, model in the vertical direction as given in [1, 2, 20]. This phenomenon may occur when the frequency is very small while the amplitude is large. This model is illustrated in Figure 1. Let us denote that the drag and lift force are D and L, respectively. Suppose that the positive angle measured in the clockwise direction between the resultant of wind velocity, U_r, and the horizontal uniform velocity of the wind containing raindrops, U, is denoted by ϕ. Hence, the aerodynamic force in the vertical direction, F_y, can be written as the following equation.

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Model of the oscillator in cross-section with drag and lift force.

The value of D shift and L lift force are given by equations (2) and (3).

()

with ρ as the air density, d as the cable diameter, l as the cable length, and C_D and C_L are the drag and lift coefficient curve that the curve obtained based on the wind tunnel experiment. In addition, it is obtained also that

()

Hence, we can rewrite the aerodynamic force as

()

Next, we derived the equation of the oscillator’s motion according to Newton’s Second Law. The forces acting on the cable movement which are considered in this paper are damping force, linear spring force with spring constant k_y, and aerodynamic force, F_y. Let M = M(t) be cable mass, w = w(t) be the mean velocity of falling water, and k_y be the spring linear constant. The equation of cable movement is given in the following equation [7].

()

Following [14, 16], let us denote M(t) = M₀ − m(t), with m(t) as the time-varying mass of the raindrops on the cylinder and M₀ a positive constant, then equation (7) becomes

()

Assume that B(t) = m(t)/M₀, and according to Waluyo [15], by transformation and descaling, it is obtained that

()

The mass of water flowing in the cable is considerably less than the mass of the cable, hence B(t) ≠ 1 for all t ≥ 0. Moreover, it also significantly lower compared to the water that is released from the cable due to the wind or sticks to the cable again. As a result, periodic changes in the mass of water in the cable occur. We assumed it is a sine function with a small amplitude. Let us define a periodic function B(t). According to [21],

()

After dividing equation (9) by 1 − B(t), one yields

()

Let us note that using Taylor expansion near zero, we can approximate

()

Suppose C_D(α) is a constant function and C_L(α) is a third order function as given in equations (13) and (14) [5],

()

where

and

. Moreover, assume that

, then

()

This paper considers a case where α_s = α₀. According to the derivation above, we conclude the final model that we consider is

()

with

()

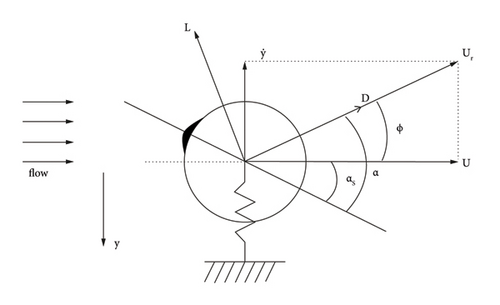
In the next session, we formulate the sufficient condition for the existence of the limit cycle of equation (16). The limit cycle for a mass constant has been discussed in [2]. The corresponding model can be transformed into a Liénard system. Hence, the existence of a stable limit cycle is guaranteed using the existence theorem by Dragilev as cited by Ye et al. in [22]. Nevertheless, problem (16) is a perturbation problem that cannot be transformed into a Liénard system. For , the unperturbed problem has a periodic solution. Therefore, we use a perturbation method called the averaging method.

4. Existence of the Limit Cycle

Verhulst in [19] identified the existence of a periodic solution of a weakly nonlinear nonautonomous equation for a harmonic oscillator using the Poincare theorem. Since the periodicity of the solution is yet unknown, the existence of a limit cycle in this system will be evaluated from its averaged equation.

First, we transformed equation (16) into the Lagrange standard form. Expanding the right-hand side with respect to

near

, note that

()

Thus, the aerodynamic force is approximated as follows:

()

As mentioned before, suppose that

()

By neglecting O(ε²) and higher terms, equation (16) can be written as the following equation.

()

where

()

The solution of the unperturbed equation is y(t) = Z₁ cos(t) + Z₂ sin(t), where Z₁ and Z₂ are arbitrary constants. Next, we will apply a variation of parameter method to analyze this perturbation problem. Let us denote

()

Substituting these equations into equation (21), we can obtain two differential equations as given in the following equations:

()

For ω = 1, the right-hand side of equations (24) and (25) are periodic functions with period 2π. Therefore, the method of averaging is applicable, i.e., integrating the right-hand sides over t from 0 to 2π and then dividing the result by 2π. In performing the integration, Z₁ and Z₂ have been kept constant. The corresponding averaged system is given in the following equation.

()

where

()

where N₁ and N₂ are nonlinear parts of both functions.

It is easy to show that (0, 0) is the equilibrium point of system (26). Now, we would like to analyze the existence of the limit cycle using the determinant of its Jacobian matrix evaluated at this equilibrium point. If the determinant is nonzero, then there exists a limit cycle around the equilibrium point. The Jacobian matrix of the system evaluated at equilibrium point (0, 0) is given by the following equation.

()

with

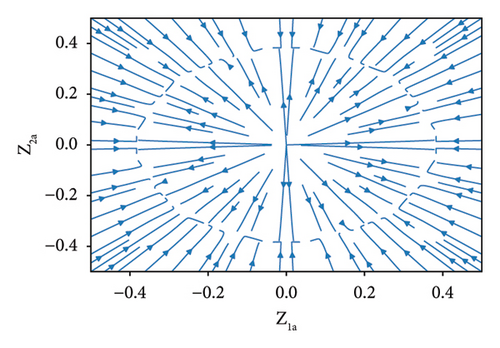
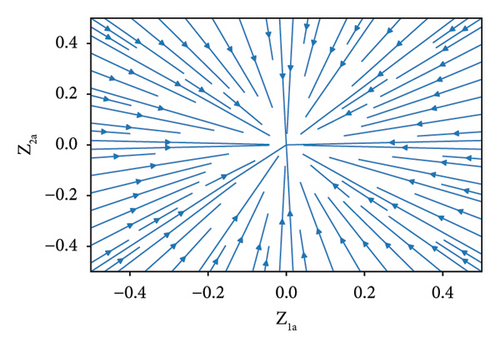
The determinant is not equal to zero for all values of parameters except . Thus, it is reasonable to conclude that there exists a limit cycle around the equilibrium point (0, 0), and the stability of the limit cycle follows the stability of equilibrium points (0, 0). Thus, for condition , the limit cycle is unstable and for condition , the limit cycle asymptotic stable as well as the equilibrium points. Moreover, if the equilibrium point is unstable, then a limit cycle occurs. The illustration can be seen in the figure phase portrait of the averaged system (26) for rU/k_y = 1 and (see Figure 2).

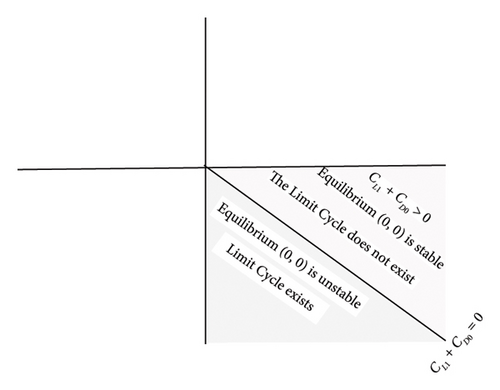
In addition, Figure 3 shows the bifurcation diagram of and parameters. The bifurcation domain occurs only in region when and . The limit cycle appears when , and the equilibrium point is unstable. In contrast, the equilibrium point is stable when .

5. Concluding Remarks

In this paper, we approximate the nonlinear part of aerodynamic force using Taylor expansion, particularly for case α_s = α₀. The system was transformed according to the variation parameter method. The result showed that by implementing the averaging method for a new system, the determinant of the Jacobian matrix near equilibrium (0, 0) is nonzero. Therefore, the limit cycle exists. The stability of equilibrium points depends on the sign of . For future research, it is interesting to study for ω = 1 + εβ. In addition, the research will be more attractive when the model is a two-dimensional case with nonlinear terms (not weakly nonlinear).

Conflicts of Interest

The authors declare there are no conflicts of interest.

Acknowledgments

This research was funded by DIPA Universitas Negeri Yogyakarta in the context of implementing the Research Group Program 2019, no. B/3/UN34.13/HK.06.00/2019.

Open Research

Data Availability

No data were used to support the findings of this study.

References

1 van der Beek C. G. A., Asymptotic analysis of wind-induced vibrations, 1989, Department of Technical Mathematics and Computer Science, Delft University of Technology, Delft, Netherlands, Ph.D. thesis.
Google Scholar
2 Haaker T. I. and van der Burgh A. H. P., On the dynamics of aeroelastic oscillators with one degree of freedom, SIAM Journal on Applied Mathematics. (1994) 54, no. 4, 1033–1047, https://doi.org/10.1137/s0036139993244806, 2-s2.0-0028483734.
10.1137/S0036139993244806
Google Scholar
3 Matsumoto M., Shiraishi N., Kitazawa M., Knisely C., Shirato H., Kim Y., and Tsuji M., Aerodynamic behavior of inclined circular cylindres-cable aerodynamics, Journal of Wind Engineering. (1988) 37.
Google Scholar
4 van der Burgh A. and P van der Burgh A. H., A linear differential equation with a time-periodic damping coefficient: stability diagram and an application, Journal of Engineering Mathematics. (2004) 49, no. 2, 99–112, https://doi.org/10.1023/b:engi.0000017475.20596.cb, 2-s2.0-1942475431.
10.1023/B:ENGI.0000017475.20596.cb
Google Scholar
5 van der Burgh A. H. P. and Hartono, Rain-wind-induced vibrations of a simple oscillator, International Journal of Non-Linear Mechanics. (2004) 39, no. 1, 93–100, https://doi.org/10.1016/s0020-7462(02)00140-3, 2-s2.0-0037475218.
10.1016/S0020-7462(02)00140-3
Google Scholar
6 Waluyo S. B., The dynamic of cable stayed bridges with a time periodic damping coefficient, International Journal of Mathematical Sciences and Engineering Applications (IJMSEA). (2010) 4, no. II, 385–394.
Google Scholar
7 Irschik and H. and Holl H. J., Mechanics of variable-mass systems—Part 1: Balance of mass and linear momentum, Applied Mechanics Reviews. (2004) 57, no. 2, 145–160, https://doi.org/10.1115/1.1687409, 2-s2.0-19944368788.
10.1115/1.1687409
Google Scholar
8 Wisdom J., Peale S. J., and Mignard F., The chaotic rotation of Hyperion, Icarus. (1984) 58, no. 2, 137–152, https://doi.org/10.1016/0019-1035(84)90032-0, 2-s2.0-0001334822.
10.1016/0019-1035(84)90032-0
Web of Science® Google Scholar
9 Abramyan A. K. and Vakulenko S. A., Oscillations of a beam with a time-varying mass, Nonlinear Dynamics. (2010) 63, no. 1-2, 135–147, https://doi.org/10.1007/s11071-010-9791-6, 2-s2.0-78650779721.
10.1007/s11071-010-9791-6
Google Scholar
10 Cveticanin L., Self-excited vibrations of the variable mass rotor fluid system, Journal of Sound and Vibration. (1998) 212, no. 4, 685–702, https://doi.org/10.1006/jsvi.1997.1455, 2-s2.0-0001169053.
10.1006/jsvi.1997.1455
Google Scholar
11 Geurts C., Vrouwenvelder T., van Staalduinen P., and Reusink J., Numerical modelling of rain wind-induced vibration: Erasmus bridge, Rotterdam, Structural Engineering International. (1998) 8, no. 2, 129–135, https://doi.org/10.2749/101686698780489351, 2-s2.0-1542571064.
10.2749/101686698780489351
Google Scholar
12 Nunez D. and Torrex P. J., On the motion of an oscillator with a periodically time-varying mass, Nonlinear Analysis RWA. (2009) 10, no. 15, 1976–1983.
10.1016/j.nonrwa.2008.03.003
Google Scholar
13 Pernot S. and Lamarque C. H., Wavelet-Galerkin procedure to investigate time-periodic systems: transient, vibration and stability analysis, Journal of Sound and Vibration. (2001) 245, no. 5, 845–875, https://doi.org/10.1006/jsvi.2001.3610, 2-s2.0-0035974953.
10.1006/jsvi.2001.3610
Web of Science® Google Scholar
14 van Horssen W. T., Abramian A. K., and Hartono, On the free vibrations of an oscillator with a periodically time-varying mass, Journal of Sound and Vibration. (2006) 298, no. 4-5, 1166–1172, https://doi.org/10.1016/j.jsv.2006.06.008, 2-s2.0-33748762236.
10.1016/j.jsv.2006.06.008
Google Scholar
15 Waluyo S. B., On the analysis of an oscillator with periodically time-varying mass and forced vibration, International Journal of Mathematical Sciences and Engineering Applications (IJMSEA). (2012) 6, no. 1, 249–261.
Google Scholar
16 van Horssen W. T., Pischanskyy O. V., and Dubbeldam J. L. A., On the forced vibrations of an oscillator with a periodically time-varying mass, Journal of Sound and Vibration. (2010) 329, no. 6, 721–732, https://doi.org/10.1016/j.jsv.2009.10.001, 2-s2.0-70649093852.
10.1016/j.jsv.2009.10.001
Web of Science® Google Scholar
17 van Horssen W. T. and Pischanskyy O. V., On the stability properties of a damped oscillator with a periodically time-varying mass, Journal of Sound and Vibration. (2011) 330, no. 13, 3257–3269, https://doi.org/10.1016/j.jsv.2011.01.027, 2-s2.0-79953719362.
10.1016/j.jsv.2011.01.027
Web of Science® Google Scholar
18 van der Burgh A. H. P., Hartono, and Abramian A. K., A new model for the study of rain-wind-induced vibrations of a simple oscillator, International Journal of Non-Linear Mechanics. (2006) 41, no. 3, 345–358, https://doi.org/10.1016/j.ijnonlinmec.2005.04.005, 2-s2.0-32044466948.
10.1016/j.ijnonlinmec.2005.04.005
Google Scholar
19 Verhulst F., Nonlinear Differential Equations and Dynamical Systems, 1990, Springer-Verlag, New York, NY, USA.
10.1007/978-3-642-97149-5
Google Scholar
20 van der Burgh A. H. P., D. Habault, Nonlinear dynamics of structures excited by flows, Fluid-Structure Interactions in Acoustics, 1999, 396, Springer, Vienna, Austria, 221–259, https://doi.org/10.1007/978-3-7091-2482-6_6.
10.1007/978-3-7091-2482-6_6
Google Scholar
21 Waluya S. B., Rosyida I., and Kharis M., On perturbation method of an oscillator single degree of freedom with mass that changes periodically and forced vibrations, Journal of Physics: Conference Series. (2019) 1321, no. 2, 022066, https://doi.org/10.1088/1742-6596/1321/2/022066.
10.1088/1742-6596/1321/2/022066
Google Scholar
22 Ye Y. Q., Cai S. L., Chen L. S., Huang K. C., Luo D. J., Ma Z. E., Wang E. N., Wang M. S., and Yang X. A., Theory of limit cycles, Translations of Mathematical Monographs, 1986, 66, American Mathematical Society, Washington, DC, USA.
Google Scholar

All articles

Limit Cycle on the Forced Vibrations Oscillator with a Time-Varying Mass

Abstract

1. Introduction

2. Method of Research

3. Forced Vibrations Oscillator with a Time-Varying Mass Model

4. Existence of the Limit Cycle

5. Concluding Remarks

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Limit Cycle on the Forced Vibrations Oscillator with a Time-Varying Mass

Abstract

1. Introduction

2. Method of Research

3. Forced Vibrations Oscillator with a Time-Varying Mass Model

4. Existence of the Limit Cycle

5. Concluding Remarks

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information