Multiple hypersonic gliding vehicles’ (HGVs’) formation control problems with obstacle and collision avoidance are investigated in this paper, which is addressed in the stage of entry gliding. The originality of this paper stems from the formation control algorithm where constraints of dynamic pressure, heating rate, total aerodynamic load, control inputs, collision avoidance, obstacle avoidance, and the terminal states are considered simultaneously. The algorithm implements a control framework designed to be of two terms: distributed virtual controller and actual control input solver. The distributed virtual controller is based on distributed model predictive control with synchronous update strategy, where the virtual control signals are derived by the optimization simultaneously at each time step for each HGV under directed communication topology. Subsequently, according to the virtual control signals obtained, a coupled nonlinear equation set is solved to get actual control signals: each HGV’s bank angle together with the angle of attack. The actual control input solver adopts a feasible solution process to calculate the actual control signals while dealing with constraints. Finally, extensive numerical simulations are implemented to unveil the proposed algorithm’s performance and superiority.

1. Introduction

Hypersonic glide vehicles (HGVs), which exhibit high speeds, strong maneuverability, and controllable trajectories, have acquired significant attention in recent years [1, 2]. The flight process of HGVs consists of four stages: the adjustment stage, the powered stage, the entry gliding stage, and the terminal guidance stage [3]. The longest working range and duration make the entry gliding phase of HGVs a significant focus of attention in its flight process. In [4], to safely direct the vehicle to the intended terminal point under specified conditions, an entry guidance system is set. For HGV which has high ratios of lift-to-drag, a viable entry flight trajectory with three-degree-of-freedom is created via combining real-time updated commands from the adaptive guidance approach proposed in [5]. The guidance system employs analytical schemes for a 3-D hypersonic gliding trajectory, allowing for rapid onboard planning of reference trajectories. As a result, it exhibits exceptional computational efficiency, as studied in [6–8]. Some novel hybrid algorithms are evolved for real-time trajectory planning of a single HGV during the reentry phase, which offers improved reliability for online applications [9, 10]. Extensive research on the entry gliding phase has demonstrated the significant controllability of the entry trajectory. Furthermore, many entry trajectory planning algorithms have emerged to address diverse mission requirements under increasingly complex environments. Consequently, exploring new operational paradigms for HGVs during the entry gliding phase holds immense significance.

Compared to a single HGV, employing a cooperative strategy for HGVs can bring significant improvements in efficiency, information sharing, and robustness. Coordinating HGVs to arrive at the same target simultaneously with varied trajectories are a commonly encountered challenge during the cooperative flight of multi-HGVs. Significant progress has been made through the application of modern approaches including the impact time control approach [11], consensus-based guidance [12], and trajectory planning approach [13], which have yielded interesting results. In [14, 15], the focus is on achieving precise control over both the timing and angle of impact for multiple HGVs. Through merging the decentralized and centralized communication topologies, an integrated framework for the cooperative guidance presented in [16] addressed the challenge of cooperative attack with multimissiles on a single stationary target. In [17], the design and analysis of a distributed cooperative guidance strategy of encirclement hunting for multivehicles in a leader-follower coordination structure are investigated, which effectively engages and tracks a maneuvering target using a cooperative approach. Due to the challenges associated with handling complex dynamics and underactuated problems brought by HGVs, there is limited research dedicated to the HGVs’ formation control. In [18], with normal positions as the coordination variables, the second-order consensus protocol is implemented to the formation controller. Following multiple HGVs’ formation flight framework, with the hierarchical control theory, the fixed-time stability is used for a globally fixed-time formation control scheme [19]. Considering the lack of thrust to counteract the complicated impact for lateral maneuvers of longitudinal motion, a feasible flight mode called rendezvous and formation flight mode is raised [20], where the corresponding guidance strategy is set as a combination of online guidance and offline planning. According to the methods presented in [18–20], various flight modes are utilized to address the challenge of formation control for multiple HGVs. These methods aim to generate and maintain desired formation configurations by an online algorithm and only depend on the neighbor-to-neighbor communication. It means that it is being called upon to require an online algorithm with faster computing power and a smaller communication load for multiple HGVs’ formation control. Furthermore, due to the complexity of the dynamics involved, the formation controllers designed by the above methods may have limited consideration for certain constraints. Therefore, studying formation control with multiple constraints for HGVs is indeed important and intriguing.

Considering the practical applications of HGVs, it is crucial to account for multiple constraints that must be satisfied during the entry gliding phase. Trajectory constraints for HGVs arise from various hardware limitations and factors related to the vehicle’s dynamics, aerodynamics, and thermal characteristics, such as state and control constraints, overload constraints, dynamic pressure constraints, and aerodynamic thermal constraints. One way to handle the complicated multiple flight constraints is the introduction of the quasi equilibrium gliding condition [21]. In [22], under complicated multiconstraint, the trajectory optimization problems were transformed to the problems of nonlinear optimal control, which were handled with Gauss pseudospectral method. In [23], researchers focused on studying the analytical solution for the HGVs’ gliding problem, which aimed to develop a solution that allows for real-time boundary corridors along with control variables that can be online corrected. Furthermore, the stochastic gradient PSO method [24, 25] together with the pigeon-inspired optimization method [26] has been proven to be useful in acquiring optimal trajectories that satisfy multiple constraints. In [24], for hypersonic glide vehicles under significant constraints, the stochastic gradient particle swarm optimization (SGPSO) method is employed as a global optimization method to quickly produce smooth and feasible trajectories. Firstly, a velocity-dependent profile for bank angle is devised to narrow down the search space for parameters using the constrained particle swarm optimization method. Then, the reentry constraints are carried out by assigning an infinite fitness function value when particles exceed the maximum allowable values [25]. By incorporating control profiles, the entry trajectory optimization question is effectively addressed using the pigeon-inspired optimization (PIO) algorithm [26]. This approach allows for the determination of control profiles that satisfy equilibrium glide conditions, terminal conditions, and a range of load factor constraints while also minimizing the peak heat rate. Meanwhile, mission constraints such as specifying a particular destination or satisfying a particular flight trajectory are requirements that depend on different missions [27]. The collision and obstacle avoidance problem is a fundamental research area in the domain of multiagent systems and has recently acquired significant attention in the robotics and control system communities. In [28], with the employment of uncertainty and disturbance estimator (UDE), the paper investigated a distributed formation control strategy for unmanned marine surface vehicle (MSV) system. The algorithm achieves the formation control objective, which includes satisfaction of prescribed performance constraints, asymptotic convergence for formation errors, connectivity preservation constraints, and compliance with collision avoidance constraints. Through introducing the improved repulsive and attractive potential fields, the algorithm transforms the avoidance for no-fly zone and the problems for waypoint passage into a problem of determination for reference heading angle [29]. Under the obstacle environment, for avoiding obstacle and collision and retaining the formation configuration, the creation of the null-space-based behavioral control structure is realized via defining the fundamental missions’ priorities and computing the vectors for corresponding velocity, which addresses the problem for the coordinated control of spacecraft formation flying which has a leader [30]. To summarize, obstacle and collision avoidance play an indispensable role in the formation flight of HGVs. Additionally, combined with the second paragraph, the interaction between trajectory constraints and mission constraints presents considerable challenges when aiming to achieve successful formation control for HGVs.

The issue of multiple constraints in formation control has been tackled by various strategies, among which model predictive control (MPC) has emerged as a practical approach due to the ability to handle constraints and deliver satisfactory control performance [31–33]. However, the computational complexity associated with MPC is significant since it requires solving optimization problems numerically in a repetitive manner. Consequently, this high computational burden poses a challenge, particularly when applying MPC to multiagent systems, which demand substantial computing power. Distributed model predictive control (DMPC) is highlighted by its reduced computation cost, structural flexibility, and lower communication burden [34, 35]. In [36], it is proposed that only one agent sequentially solves its optimization problem within each sampling period, which allows each agent to independently optimize its control actions while considering the constraints and objectives of the overall system. In [37], a novel cooperative distributed method for trajectory optimization is introduced for systems that include independent dynamics but hard constraints and coupled targets. In this approach, vehicles or agents solve their respective subproblems iteratively. Both [36, 37] highlight the benefits of distributing the optimization among the agents, resulting in reduced computation cost and improved scalability in multiagent systems. However, in both the iterative and sequential solutions, for a cycle of all agents, it takes more time to obtain their optimal control inputs compared to a synchronous solution. In the DMPC method, every agent is able to synchronously solve its local optimization problem via communicating its assumed information with its neighbors, where the assumed information is updated simultaneously. Many studies have adopted the synchronous DMPC approach due to its advantages in terms of computational efficiency and coordination. In [38], with collision avoidance, aiming at the tracking and forming for homogeneous multiagent systems, a synthesis method of synchronous DMPC is introduced. Introducing hypothetical input and state trajectories yields a computationally tractable distributed optimization problem, which also solves the obstacle avoidance problem [39]. [40] proposed solution through incorporating a control Lyapunov function (CLF) into DMPC, and this scheme inherits CLF’s sturdy stability and optimizes the formation performance. Based on the results in the field of DMPC, the advantages of its ability to handle constraints and the synchronous update strategy have inspired the application of DMPC to address multiple HGVs’ formation control problem. However, adopting DMPC in the context of multiple HGVs, where the system dynamics are nonlinear, underactuated, and highly coupled, poses its challenges and requires further investigation.

Driven by the aforementioned current state of research and impending future challenges discussed above, in this study, under directed communication topology, multiple HGVs’ distributed formation control algorithm is proposed. Meanwhile, obstacle and collision avoidance with multiple constraints such as trajectory constraints, control constraints, and terminal state constraints which can be referred to as the achievement of the desired formation configuration are satisfied simultaneously in the entry gliding phase. Firstly, equations of motion of multiple HGVs and formation coordinate systems are created for the formation control problem. Subsequently, the combination of distributed virtual controller and actual control inputs solver forms a control framework designed for multiple HGVs’ formation control. In the distributed virtual controller, with directed communication topology, the virtual control inputs are brought by setting the distributed model predictive control laws where multiple HGVs implement optimization simultaneously at each time step for every HGV. In the actual control input solver, the actual control inputs can be acquired through introducing a novel process to calculate synchronously while satisfying the multiple constraints for each HGV. Finally, the distributed formation control issues for the HGVs with obstacle and collision avoidance are resolved under the multiple constraints. In line with this, this paper makes four aspects of contribution when compared to prior studies in the field:

(1)
Under the directed communication topology, the distributed formation control algorithm is investigated, enabling the attainment of the desired formation configuration and ensuring collision and obstacle avoidance
(2)
Consider the premise of satisfaction for mission constraints consists of obstacle avoidance constraints, collision avoidance constraints, control constraints, and terminal state constraints. The set of trajectory constraints encompasses dynamic pressure constraints, heating rate constraints, and total aerodynamic load constraints, all of which are effectively satisfied simultaneously during the phase of formation control
(3)
For a cycle of all HGVs acquiring their actual input bank and attack angle, based on a framework composed of distributed virtual controller and actual input solver separately, a novel solution process to calculate the actual inputs is investigated with synchronous solutions. This proposed approach results in reduced computing burden and further handling of multiple constraints
(4)
For multiple HGVs’ formation control problems, without regard to the constraints first involved in this paper, which include collision avoidance, trajectory constraints, and obstacle avoidance, the proposed formation control algorithm offers a faster convergence rate and improved formation accuracy compared to existing methods

In this paper, the remaining sections’ architecture is as follows: Section 2 introduces preliminaries pertinent to this study. Section 3 presents an in-depth exploration of the proposed algorithm. Section 4 demonstrates extensive simulation outcomes and conducts comparative analyses. Finally, Section 5 supplies a summary of this work.

2. Problem Statement and Preliminaries

2.1. Basic Theory

Define ℕ_a≜{1, 2, ⋯, N_a} as the index set of HGVs with N_a homogeneous hypersonic gliding vehicles. Let be a weighted directed network with order N_a and the set of nodes , the set of directed edges , and a weighted adjacency matrix . A directed edge in is indicated by the ordered pair of nodes (v_i, v_j) with terminal node v_i and initial node v_j, suggesting that node v_i is able to obtain information from node v_j. Define a_ij = 1 if a directed edge (v_i, v_j) is found in and a_ii = 0. Degree diagonal matrix , . Laplacian matrix is counted by L = D − A.

Definition 1. A directed path from node v_j to v_i is a sequence of edges (v_i, v_i,1), (v_i,1, v_i,2), ⋯, (v_i,l, v_j) in the with distinct nodes v_i,k, k = 1, 2, ⋯, l. If between any pair of distinct nodes v_i and v_j in , is tightly connected, and there shows a directed path from v_i to v_j, i, j ∈ ℕ_a.

Definition 2. I_n denotes the identity matrices of n order. diag{⋯} stands for the diagonal block matrix. Define 0 as the zero vector or zero matrix which has appropriate dimensions. For column vector x, ‖x‖ (i.e., ) represents the two-norm, and ‖x‖_P (i.e., ) signifies the P-weight two-norm of x.

Assumption 3. Treat any HGV in the multiple HGVs as a node with number i. The communication topology be a weighted directed network is established for multi-HGVs. The directed communication topology is tightly connected. Meanwhile, the communication delay is not considered in the multiple HGVs.

2.2. Equations of Motion

During the entry gliding phase, the formation flight mission assumes that the form generation process occurs within a range of several hundred kilometers, encompassing the transition from the initial states to the desired formation configuration. Hence, for the multiple HGVs, the earth’s curvature and rotation are not taken into consideration.

At the earth, designating a point on the surface as the origin, a plane rectangular coordinate system can be constructed. Define xOy as a horizontal plane, while Ox axis points from the origin to the target location. Oy axis is established by the right-hand relationship, where Oz axis is perpendicular to the local horizontal plane and then extends vertically upward, and then next, the relative motion and the reference frame between the HGV and the target location can be defined. Consider M_i(i ∈ ℕ_a) to signify the mass point of i-th HGV included in multi-HGVs. The equations of motion of HGVs and formation coordinate system are displayed in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Model diagram of HGV in the formation coordinate system.

The i-th HGV is termed as [18, 19]

(1)

where V_i represents the velocity, ψ_i is defined as the heading angle, θ_i stands for the flight path angle, g = 9.8 m/s² indicates the gravity acceleration, σ_i represents the angle of bank, and D_i and L_i are the accelerations for drag and lift and calculated by

(2)

(3)

where S_i and m_i, respectively, stand for the reference area and mass of the i-th HGV; α_i is the angle of attack; C_L and C_D, respectively, denote the coefficients for lift and drag which depend on α_i and V_i; and ρ_i indicates the air density, which can be counted by

(4)

where h₀ = 7110 m and ρ₀ = 1.225 kg/m³ indicates the air density around sea level.

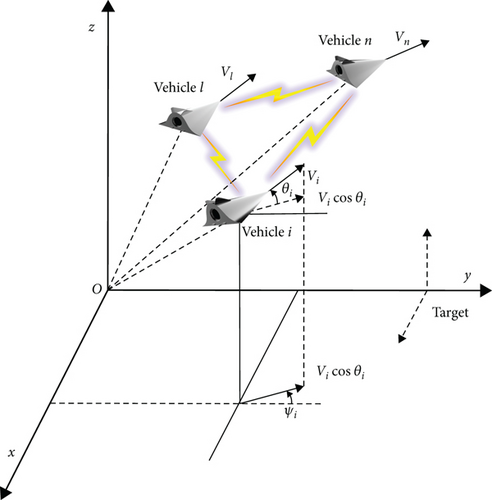
2.3. Multiple Constraints of Hypersonic Gliding Vehicles

This section provides a detailed explanation of both mission constraints and trajectory constraints, where the mission constraints encompass terminal constraints, control constraints, obstacle avoidance constraints, and collision avoidance constraints.

2.3.1. Terminal Constraints

is the position variable. Define

as the desired formation configuration parameters for the multiple HGVs, where

, and

are the desired positions of the i-th HGV influenced by the desired formation configuration. The control problem for forming is converted to the terminal constraints

(5)

2.3.2. Trajectory Constraints

Trajectory constraints of multiple HGVs are described as follows:

(6)

(7)

(8)

where k_Q = 7.97 × 10⁻⁸ indicates the heat transfer coefficient and

, and

denote the maximum limits of the total aerodynamic load n_i, dynamic pressure q_i, and stagnation point heating rate

, respectively. These are rigid constraints and must be satisfied.

2.3.3. Control Constraints

In the rest of this paper, the control variables which are called the actual control inputs are the bank angle σ_i and the angle of attack α_i and for i-th HGV. Define

as the maximum and minimum constrained values for α_i and

and

as the maximum and minimum constrained values for σ_i. The constraints for σ_i and α_i are as follows:

(9)

2.3.4. Collision Avoidance Constraints

Firstly, the expected relative positions between HGVs are in consensus with the collision avoidance constraints:

(10)

Define

as the set of neighbors of i-th HGV. Secondly, define R as the safety radius for each HGV; the following constraints should be satisfied to avoid collisions with another HGV:

(11)

2.3.5. Obstacle Avoidance Constraints

Obstacle avoidance can be defined as no-fly zones of geographic constraints that should be satisfied before the desired formation configuration is achieved. Define ℕ_o≜{1, 2, ⋯, N_o} as the index set of all the obstacles and

as the position of obstacle m. The obstacle constraints are as follows:

(12)

2.4. Control Objective

For unpowered HGV, however, the velocity is so unmanageable that it is challenging for x_i, y_i, and z_i to reach the expected value determined according expected formation configuration. Owing to the characteristics of initial states of the entry gliding stage, to decrease the conundrum of design for formation control, control of y_i is ignored. Define

as the expected relative distance along Ox axis between HGV i and HGV j, where

. Similarly,

can be defined. Define

and

. The objective is to design α_i and σ_i for every HGV i, such that the formation of multiple HGVs is stabilized to its desired position:

(13)

and tracking errors of the HGVs reach consensus:

(14)

3. Formation Control Algorithm

Based on a control framework that is organized into two separate terms. Firstly, the distributed virtual controller is designed. Then, an actual control input solver is introduced to obtain the actual control inputs. Finally, a formation control algorithm is devised to consolidate all of the aforementioned aspects.

3.1. Distributed Virtual Controller

Consider a second-order multiagent system consisting of N_a agents defined by

(15)

where for agent i, p_i and q_i ∈ ℝ² stand for the position and the velocity states. Control input is represented as u_i ∈ ℝ². The discrete-time system (15) can be rewritten into

(16)

where k denotes the time instant and N ∈ ℝ is the length of predictive horizon and

∈ℝ⁴ and u_i(k) = [u_i,1(k), u_i,2(k)] ∈ ℝ² are the states and inputs. Define

. v_x,i(k) ∈ ℝ and x_i(k) ∈ ℝ denote the velocity and position along Ox axis. v_z,i(k) and z_i(k) are defined equally. Denote ξ_i(k + l|k) and u_i(k + l|k) as the predicted states and inputs at time step k + l from time step k, where ξ_i(k|k) = ξ_i(k). T is a constant sampling period; there have

(17)

Multiple HGV systems are mapped to a discrete-time system (16) with the knowledge of

at current time t = T₀ s. Based on the mapped system (16), the DMPC is implemented to obtain the virtual signals

and

. It should be noted that, at every time step, all agents should be optimized simultaneously with the synchronous update scheme. To facilitate this process, assumed states are introduced as the information transmitted among neighbors instead of the real states. The assumed control inputs for HGV i are as follows:

(18)

where κ_i(⋅) is the terminal controller which is set in the form of

(19)

where

is compatible with d_ij and can be defined as

. Substituting Eq. (19) into (16), define

, l = 0, 1, ⋯, N − 1, as error variable; then, the error system is given by

, where A^′ = A + BK_i,1 and B^′ = I₄ − A − BK_i,1 − BK_i,2. It is easy to find K_i,1 to stabilize Δξ_i(k + 1|k) = A^′Δξ_i(k|k). Selecting K_i,1 and K_i,2 for

, there have K_i,2 = −K_i,1. Next, the assumed states of HGV i are defined as

(20)

where

3.1.1. Construction of Objective Function

Every individual objective function is composed of a tracking index , a consensus index , an input index , and a terminal index for each HGV i ∈ ℕ_a.

To minimize the errors between current states and desired states for HGV i, the tracking index is expressed as

(21)

where P_i ∈ ℝ^4×4 is a symmetrical positive definite weight matrix for HGV i.

Define

, and Q_i = δ_iI₄ indicates positive definite weight matrix. The consensus index is given by

(22)

The index on control inputs for HGV i can be designed by

(23)

where R_i = τ_iI₄ is the positive definite diagonal weight matrices.

Finally, the index of the terminal cost is designed by

(24)

where for the designated matrix H_i which is negative definite, ϕ_i = A^′ and S_i indicates a matrix which is positive definite and meets this Lyapunov equation:

(25)

The objective function to be optimized at every time instant can be constructed as

(26)

3.1.2. Construction of Constraints

is defined as the assumed state vector for neighbors of i-th HGV. The inputs of the mapped discrete-time system (16) are derived from the states of multiple HGVs system at the current time t = T₀s. Then, the initial state constraints are defined as

(27)

For HGV i, defining

for

, l = 0, 1, ⋯, N − 1, and

, there have μ_ij(k + l|k) = μ_ji(k + l|k) ≥ 0. Limiting the deviation of the actual predictive positions and the corresponding assumed positions, the constraints for achieving collision avoidance are presented by

(28)

The constraints to ensure the closed-loop system’s stability are as follows:

(29)

where for 0 < υ_i < 1,

. Define

, and

, where

. There has

The uncontrollable velocity of a single HGV brings difficulty for obstacle avoidance. Hence, the constraints of collision avoidance can be simplified as

(30)

However, in a real case, collision avoidance constraints cannot be satisfied by replacing

with

in Eq. (30). Constraints (30) are redesigned as

(31)

In a real case, the constraints of collision avoidance are as below:

(32)

The handling method for collision avoidance is the same as Eq. (30). Define

; the constraints for obstacle avoidance can be simplified as

(33)

where the simplified constraints still guarantee the obstacle avoidance constraints. Then, define

, where

(34)

where

is a positive constant. The introduction of

gives a faster convergence rate for the formation control by selecting a reasonable

. Finally, the obstacle avoidance constraints are as follows:

(35)

To guarantee the closed-loop stability and the recursive feasibility for system (16).

represents the corresponding terminal set

(36)

where D_i = min{D_i,1, D_i,2},

, and

To meet the constraints of dynamic pressure and stagnation point heating rate, a relatively conservative strategy is to replace V_i with V_0,i in Eqs. (6) and (7). The replaced constraints will be added in the DMPC at time k as follows. Define ρ_i(k + l|k) = ρ₀exp(−ξ_i,2(k + l|k)/h₀), l = 0, 1, ⋯, N − 1, where ξ_i,2 represent the second component of ξ_i. Accordingly, if

and

, l = 0, 1, ⋯, N − 1, are satisfied, constraints (6) and (7) are satisfied successfully because V_i is a monotonous decrease function of time t. Define the state constraint set for HGV i as

(37)

Accordingly, the constraints for stagnation point heating rate

and dynamic pressure

can be given by

(38)

Finally, in the multiple HGV systems, it is imperative to apply specific constraints on the magnitude of virtual signals within the system (16). Define

and

; the input constraint set contains the origin which is expressed as

(39)

where u_i,1 and u_i,2 represent the first and second component of u_i, respectively. The input constraints are detailed as

(40)

Remark 4. The problem of obstacle avoidance in this paper considers obstacle avoidance before the achievement of the desired formation configuration. Hence, the terminal constraints of HGVs are consistent with the obstacle avoidance constraints for the mission constraints, i.e.,

(41)

Assumption 5. The terminal set (36) is defined in a manner that ensures , i ∈ ℕ_a, and the terminal controller (19) is specifically devised to fulfill , , and i ∈ ℕ_a under all circumstances.

Problem 6. At time step k (i.e., t = T₀ s), given ξ_i(k + l|k), , , i ∈ ℕ_a, and l = 0, 1, ⋯, N − 1, DMPC optimization problem is as below:

(42)

(43)

Algorithm 1: Distributed model predictive control algorithm.

Offline stage: for i ∈ ℕ_a, provided P_i, Q_i, R_i, υ_i, , d_ij, , and H_i, determine K_i,1, K_i,2, S_i, and D_i. is delivered into mapped system (16).
Online stage: at the initial time step k = 0 when the current time is t = T₀ s, wait for the initial optimal control inputs , l = 0, 1, ⋯, N − 1, and the initial optimal states , l = 0, 1, ⋯, N, for HGV i ∈ ℕ_a. There are four steps at online stage as follows:
Step 1. At time step k, k ≥ 0 for HGV i ∈ ℕ_a. Apply to compute the assumed control inputs together with the assumed states , l = 0, 1, ⋯, N, by Eqs. (18) and (20). Then, transmit , l = 0, 1, ⋯, N, to HGV and receive , l = 0, 1, ⋯, N, from HGV .
Step 2. At the next time step k + 1, k ≥ 0, for HGV i ∈ ℕ_a, the current states ξ_i(k + 1|k + 1) are sampled to compute μ_ij(k + 1 + l|k + 1), μ_i(k + 1 + l|k + 1), l = 0, 1, ⋯, N − 1, , and ν_i(k + 1). Then, Problem 6 is solved to get the optimal control inputs , l = 0, 1, ⋯, N − 1, and the optimal states , l = 0, 1, ⋯, N.
Step 3. Apply and for the passing of virtual signals between the distributed virtual controller and the actual input solver.
Step 4. Return to Step 1.

Theorem 7. At every time step k, each HGV possesses the ability to optimize with a distributed manner using Algorithm 1 with a synchronous update strategy. Assuming Assumption 5 holds, if there is at least a feasible solution available for every HGV at the initial time step k (i.e., t = T₀ s), all of the subsequent optimization problems will remain practicable. Moreover, every HGV converges to the expected formation configuration asymptotically while satisfying collision and obstacle avoidance constraints, stagnation point heating rate constraints, terminal constraints, and dynamic pressure constraints.

Proof. With the DMPC implemented by Algorithm 1. The optimization Problem 6’s recursive feasibility and the closed-loop system’s stability where system (16) adopted Algorithm 1 are analyzed, respectively.

(1)
Feasibility: firstly, it is presumed that the optimization of Problem 6 for i-HGV is practicable at time step k. Accordingly, , l = 0, 1, ⋯, N − 1, is the optimal control inputs, and , l = 0, 1, ⋯, N, is the corresponding optimal states. Then, the assumed control inputs and the assumed states , l = 0, 1, ⋯, N − 1, can be calculated according to Eqs. (18) and (20). Taking the information discussed above into account, the feasible control input , l = 0, 1, ⋯, N − 1, and feasible state , l = 0, 1, ⋯, N, are introduced. Define and . Next, at time step k + 1, consider input sequence for HGV i. Applying to HGV i, the satisfaction of constraints (43) except follows directly from the assumed control inputs’ definition and Assumption 5. The positive invariance of the terminal set further results in the satisfaction of constraint . Therefore, the input sequence is a feasible solution to HGV i at time step k + 1, which means the feasibility of Problem 6 at time step k implies the feasibility at time step k + 1. Problem 6 is practicable at all future time instants by recursion
(2)
Stability: the optimal cost summation for all the HGVs is defined as a Lyapunov function of the whole system, which is indicated by

(44)

Then, the summation of the costs is considered at time step k + 1 related to the feasible solutions for all the HGVs, represented by

(45)

For the ease of subsequent proof, the objective function to be optimized at every time instant for each HGV is built up of two components: stage objective function and terminal objective function .

The difference between the optimal objective function and the feasible objective function at two successive time steps is

(46)

Then, there have the following formulas:

(47)

(48)

(49)

(50)

Owing to the satisfaction of , there have

(51)

where and . From the definition of K_i,2 and K_i,1, there have . And . From Eq. (25),

(52)

Also, there have

(53)

Furthermore, define variables as follows:

(54)

Then, it follows that

(55)

where by the definition of ν_i(k), there have

(56)

Substitute Eqs. (52), (53), and (56) into (47). Given the solution’s optimality, the following result is derived accordingly:

(57)

Define 0 < υ_i < 1 as the convergence speed for closed-loop system. Then, the mapped multiple HGV systems converge to expected states influenced by the desired configuration asymptotically. Moreover, the terminal constraints, stagnation point heating rate constraints, dynamic pressure constraints, and collision and obstacle avoidance constraints will be obtained according to Theorem 7.

3.2. Actual Input Solver

In the horizontal plane, define

as the virtual control input. Meanwhile, in the longitudinal plane,

represents the virtual control input. The virtual control signals

and

should be designed according to the neighbor information gathered through i-th hypersonic gliding vehicle from its neighboring vehicles. The dynamics of the coordinated variables of x_i and z_i, as well as their first and second derivatives versus time, can be counted by

(58)

After the optimization of the distributed virtual controller at current time t = T₀ s, applying the virtual control signals

and

into Eq. (58), there have

(59)

(60)

By solving Eqs. (59) and (60), the actual control inputs

and

to be solved are further obtained. However, it is too complicated and time-consuming to solve Eqs. (59) and (60) adopting numerical methods. Hence, to decrease the complexity and coupling of calculation for

and

, a feasible process is proposed. Consider σ_i and α_i are inherent with regard to L_isinσ_i and L_icosσ_i, which satisfy

(61)

According to Eq. (61), the bank angle σ_i can be ignored temporarily to decrease the complexity of calculation. Then, consider α_i is implicit in terms of D_i. Obviously, L_i and D_i are the function of α_i. Although V_i also affects L_i and D_i, V_i of L_i and D_i are the same, which means that the actual input can be calculated inversely according to Eq. (61) by calculating and satisfying Eqs. (59) and (60).

Define

as the states of multiple HGVs at current time t = T₀ s. According to Eq. (60),

(62)

Meanwhile, according to Eq. (59),

(63)

However, there exists a coupling among Eqs. (62) and (63). To get the angle of attack

, the designed procedures are given as follows. Initially, to gather the actual inputs at the current moment t = T₀ s, treat the drag accelerations D_i as a parameter rather with the value of current time than the variable to be solved, i.e.,

. Then,

are obtained by Eq. (62). Then, according to Eq. (63),

is obtained easily. There have

(64)

Therefore,

and

are calculated by using the current states of multi-HGVs. In line with Eq. (2), the angle of attack

can be counted inversely.

(65)

Additionally, to satisfy the control constraints for HGV i, limit the minimum and maximum constrained values of

based on the calculation result of Eq. (65) by

(66)

Then, the bank angle

can be counted with

(67)

Additionally, to satisfy the control constraints for HGV i, limit the minimum and maximum constrained values of

based on the calculation result of Eq. (67) by

(68)

In summary, the implementation procedure of the calculation for the actual inputs and is given as follows.

Procedure 1: Procedure of the calculation for the actual inputs.

Initialization: for HGV i ∈ ℕ_a, Step 3 of Algorithm 1 is completed. Then, the virtual control signals and are obtained accordingly. Denote as the states of multiple HGVs at current time t = T₀ s. and are the actual inputs to be solved at current time t = T₀ s.
Step 1. Substitute into Eq. (62) to get .
Step 2. is obtained by applying D_i and into Eq. (63). Then, can be calculated by Eq. (64) with the knowledge of and .
Step 3. According to Eqs. (65)–(68), and can be calculated.

It is noted that the constraint of aerodynamic load cannot be considered in the design of virtual controller because of coupling. To constrain the violation of the aerodynamic load, the following process are proposed.

At the time step k in the distributed virtual controller, the virtual signals

and

are obtained, the temporary variables

and

are calculated by Procedure 1. Then, apply the temporary variables

and

into the system dynamic (1) at the current time t = T₀ s. The state variables

and

at time t = T₀ + T s are obtained directly with the fourth-order Runge-Kutta method with initial conditions

. Define

as feasible actual input. Then,

, and

are considered in

(69)

Accordingly, the maximum value of

, which is

, is calculated successfully by Eq. (69). The actual signal of

is described as

(70)

and the actual signal of

is described as

(71)

In summary, suppose that Assumption 3 and Assumption 5 are both met in the distributed virtual controller, multiple HGVs’ formation control is achieved by the formation control algorithm exhibited in Figure 2.

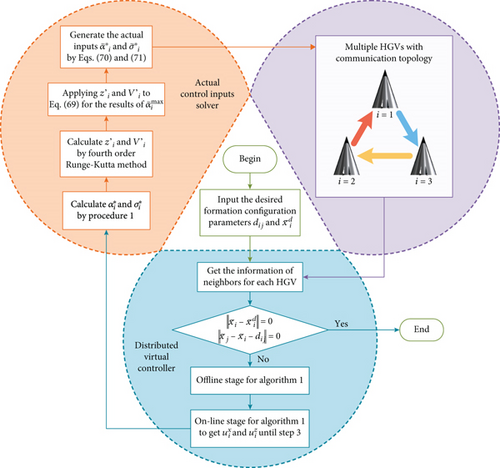
4. Simulation Examples

Three simulation examples are provided in this section: (1) simulation of formation accomplished with different control parameters, (2) simulation of formation control satisfying multiple constraints, and (3) simulation comparison with existing methods. Example 1 unveils the characteristic of the proposed algorithm by setting different control parameters and conservative constraint parameters. The desired formation achieved in example 1 serves as reasonable initial states for example 2 that will be studied in the middle of entry gliding phase. Then, the successful achievements of obstacle and collision avoidance for formation control while dealing with multiple constraints simultaneously are demonstrated in example 2. Examples 3 and 1 share the same initial states for multiple HGVs. After successfully demonstrating the characteristics of the proposed formation control algorithm in example 1 by setting various parameters, example 3 utilizes the same parameters from example 1 to compare with other algorithms, which exhibits superior performance compared to other existing formation control strategies for the multiple HGVs. Consider N_a = 3. The simulations in this study utilize the CAV-H model [1]. Multiple HGVs’ communication topology is shown in Figure 2. Then, each HGV’s maximum maneuvering ability is limited by the limitation of the actual inputs, where , , , and . Define the formation error variables for x_i and for z_i.

4.1. Simulation of Formation Accomplished with Different Control Parameters

The initial states for the multi-HGVs are exhibited in Table 1. t ∈ [0, 60 s) is the initial phase where each HGV flies in maximum lift-drag ratio with α_i = 10^∘ and σ_i = 0^∘. Then, the proposed algorithm is to be studied when t ≥ 60 s. The desired formation configuration is depicted in case 1 of Table 2. To unveil the characteristic of the proposed algorithm, various parameters which are vital are shown in Table 3. It is noted that to better illustrate the characteristics of the control performance, the investigations of collision avoidance, obstacle avoidance, and trajectory constraints are all ignored in this simulation by setting conservative constraint parameters. The rationale for conducting the simulation prior to the simulation in Section 4.2 is to establish reasonable initial states for the simulation that will be studied in the middle of entry gliding phase. The other parameters are selected as T = 1, δ_i = 0.1, τ_i = 0.1, υ_i = 0.9, , and .

Table 1. Initial states of multiple HGVs.

HGV i	x_i (km)	z_i (km)	V_i (m/s)	ψ_i (°)
i = 1	−10	77.28	3717	90
i = 2	0	79.19	3688	90
i = 3	10	78.42	3701	90

Table 2. Desired formation configurations.

Term	Case 1	Case 2
HGV 1
HGV 2
HGV 3

Table 3. Different control parameters.

Term	Control parameters
Parameter 1	P = diag{1, 1, 100, 100}, N = 5
Parameter 2	P = diag{1, 1, 100, 100}, N = 15
Parameter 3	P = diag{1, 1, 10, 10}, N = 15

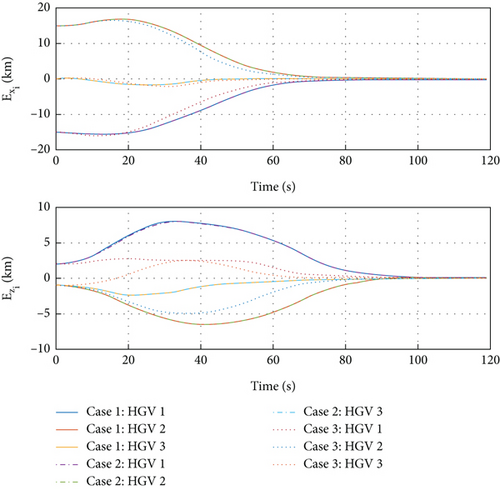
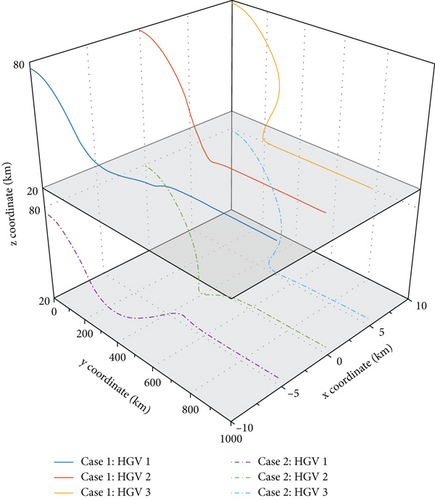
Define case 1 as the desired formation configuration with control parameter 1, and case 2 and case 3 are defined similarly. Figure 3 shows the different formation flight trajectories from the proposed algorithm with different control parameters. The desired formation configuration can be successfully acquired with the proposed algorithm. Figure 4 demonstrates the histories of value and convergence rate for formation error variables, where and converge to a small constant with different convergence rate. Comparing case 2 with case 1, a bigger prediction horizon N brings a faster convergence rate. Comparing case 2 with case 3, a bigger weight matrix P_i also brings a faster convergence rate. Case 2 brings a faster convergence rate together with a higher control accuracy than case 1 and case 3.

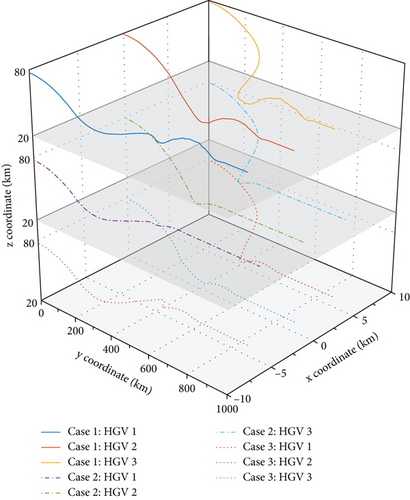
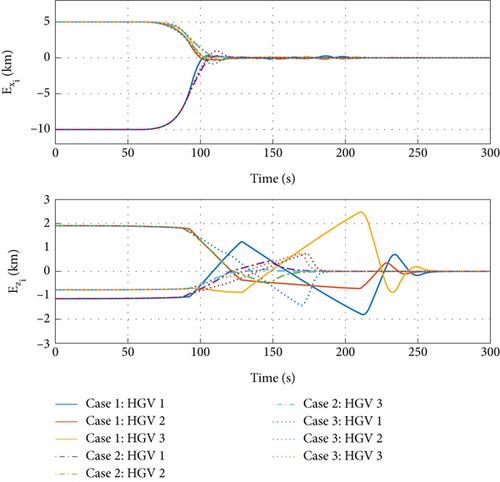
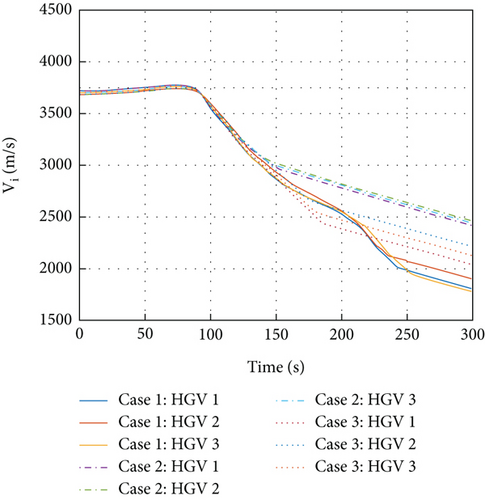
Figure 5 shows that the constrains of α_i and σ_i are all satisfied in three cases. In Figure 6, time histories of V_i are given. From Figures 4–6, it can be seen that the increase of N and P_i not only increases the convergence rate but also decreases the energy consumed. However, a bigger N will bring higher computational load, and a bigger P_i may bring chattering problem for the actual control inputs. Thus, the selection of optimal parameters for N and P_i should be made by considering the actual circumstances.

4.2. Simulation of Formation Control Satisfying Multiple Constraints

Then, the cardinal contributions of our work are the achievement for obstacle and collision avoidance for formation control while dealing with multiple constraints simultaneously. Therefore, this simulation uses three comparative experiments to reveal the function of the proposed algorithm. The initial states in this section are given in Table 4 according to Figure 6 in Section 4.1. Then, the desired formation configuration in this section is depicted in case 2 of Table 2. And the positions of obstacles are set in Table 5.

Table 4. Initial states of multiple HGVs.

HGV i	x_i (km)	z_i (km)	V_i (m/s)	ψ_i (°)
i = 1	−5	33	2944	90
i = 2	0	32	2958	90
i = 3	5	31	2983	90

Table 5. States of obstacles.

Term	(m)	(m)	(m)
Obstacle 1	-2100	32500	35000
Obstacle 2	2800	31000	80000

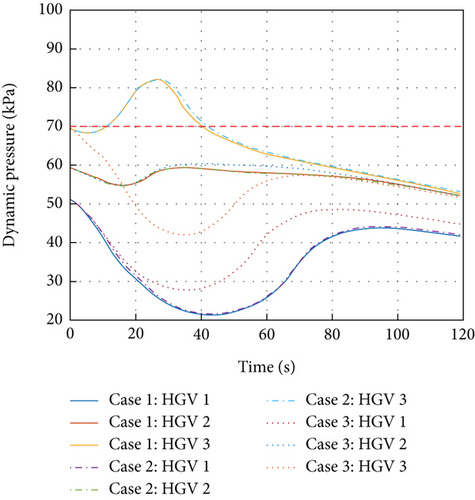
The constraints of avoidance for both obstacle and collision are all included in three cases. In the presence of two obstacles, case 1 tends to achieve the desired formation configurations without considering the trajectory constraints for dynamic pressure, stagnation point heating rate, and total aerodynamic load. With the same goal as case 1, the total aerodynamic load is considered additionally in case 2. Finally, in case 3, which corresponds to case 2, both dynamic pressure constraints and stagnation point heating rate constraints are encompassed additionally. The constraints in Eqs. (6)–(8) are given as , q_max = 40 kPa, and n_max = 3. The other parameters are selected as T = 1, δ_i = 0.1, τ_i = 0.1, υ_i = 0.9, , , P = diag{1, 1, 100, 100}, N = 40, , and R = 1 km.

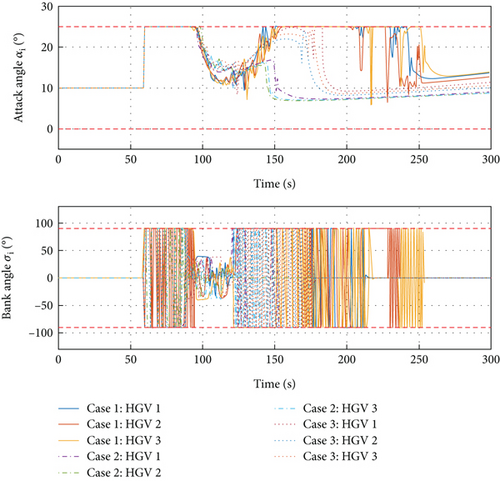
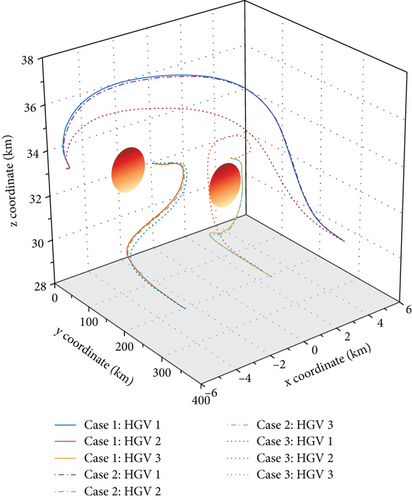
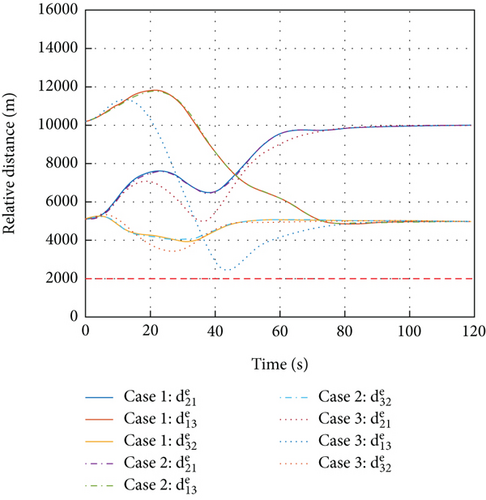
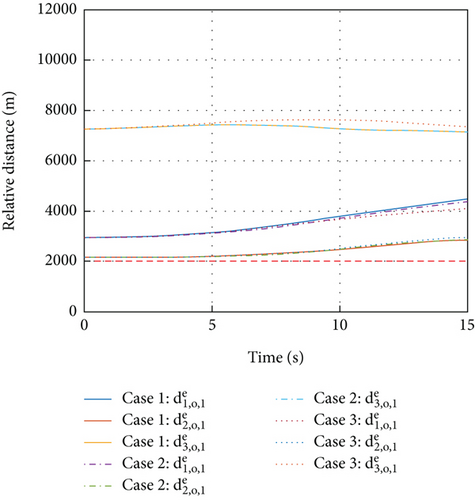
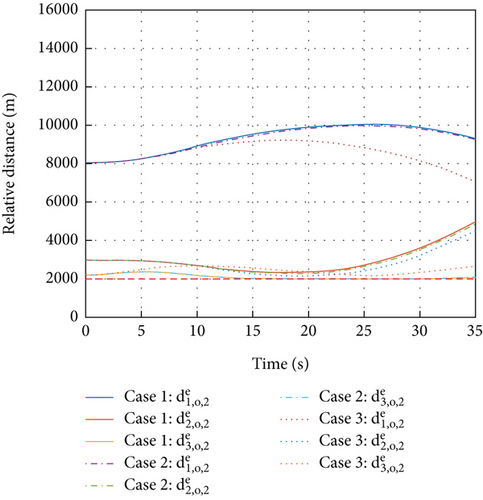
To begin with, Figure 7 shows the different flight trajectories of multiple HGVs of three cases. Figure 8 shows that and converge to zero, which means the goal of the desired formation configurations is achieved in spite of different constraints. Figures 8–15 analyze the three cases in detail. From Figure 10, collision avoidance is ensured; the relative distances between every HGV are greater than the safety distance 2R. In Figure 11, when t ≤ 15 s and y_i ≤ 36000 m for each HGV, the relative distances between each HGV and obstacle 1 have a safety distance. In Figure 12, similarly, when t ≤ 35 s and y_i ≤ 81000 m for each HGV, the relative distances between each HGV and obstacle 2 have a safety distance as well. Meanwhile, Figure 9 shows the histories of α_i and σ_i, where the constraints of the maximum value are satisfied. The mission constraints are satisfied successfully by the proposed algorithm in case 1, case 2, and case 3.

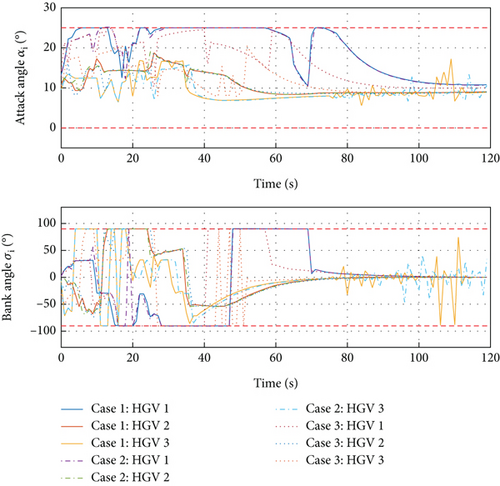
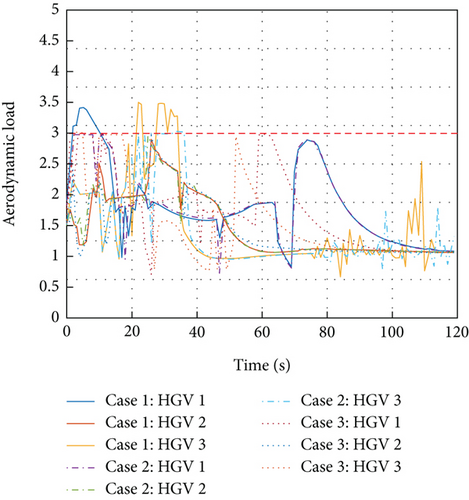
Moreover, the trajectory constraints’ satisfaction is analyzed with the mission constraints’ satisfaction. For case 1, Figure 13 shows that the aerodynamic load constraints are violated. In case 2, the aerodynamic load has a maximum value of 3, which means the aerodynamic load constraints are satisfied by the proposed algorithm. Although the trajectories of case 1 and case 2 are almost identical as exhibited in Figure 7, the aerodynamic load constraints should be considered seriously. Case 3 and case 2 both satisfy the aerodynamic load constraints as shown in Figure 13.

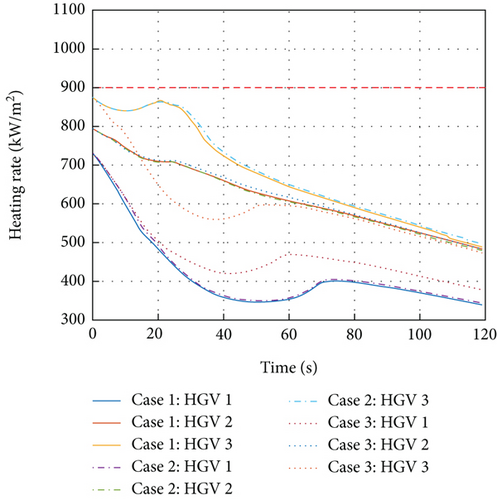
In Figure 14, both in case 1 and case 2, the dynamic pressure constraints are violated. Comparing case 3 with case 2, Figure 7 suggests that the significant change of the trajectory for multiple HGVs is the trajectory of HGV 2. To avoid the obstacle 2, HGV 2 flies beneath the obstacle in case 2 but flies above the obstacle in case 3 to achieve the obstacle avoidance. From Figure 14, the proposed algorithm enables HGVs flying with different trajectories with obstacle avoidance, which makes the violation of dynamic pressure constraints disappear in case 3. Hence, the multiple constraints are satisfied simultaneously in case 3. One thing worth noting is that the stagnation point heating rate is all satisfied in three cases. Although the simulation does not give a contrast example to show the suppression of stagnation point heating rate constraints violation as displayed in Figures 13 and 14, the state constraint set designed in Eq. (37) and the satisfaction of Assumption 5 make the suppression of dynamic press constraints equally persuasive towards the stagnation point heating rate constraints as exhibited in Figure 15. In summary, the aforementioned results convincingly unveil the proposed formation control algorithm’s strong performance in handling multiple constraints.

4.3. Simulation Comparison with Existing Approaches

Finally, to verify the proposed control algorithm’s superiority despite its ability to deal with multiple constraints. The comparison simulation is performed in this section. An insightful study for multiple HGVs is shown in [19], where a globally fixed-time formation control algorithm with the hierarchical control theory is introduced named fixed-time formation control, which ensures the fixed-time stability. Meanwhile, the proposed algorithm is named DMPC formation control to make comparison.

The initial states as demonstrated in Table 1 and the initial phase are the same as in Section 4.1. The desired formation configuration is given in case 1 of Table 2. The parameters for the two methods are shown in Table 6. In this section, to make better comparisons by control variates, the proposed control algorithm does not consider the constraints discussed in Section 4.2. Thus, the obstacle avoidance constraints, the total aerodynamic load constraints, the collision avoidance constraints, the stagnation point heating rate constraints, and the dynamic pressure constraints are all ignored by setting conservative constraint values for the proposed algorithm. The other parameters are selected as T = 1, δ_i = 0.1, τ_i = 0.1, υ_i = 0.9, , and .

Table 6. Control parameters for the comparison of different methods.

Term	Parameters
Fixed-time formation control	k₁ = k₂ = k₃ = k₄ = 0.01, p = 11, q = 13
DMPC formation control	P = diag{1, 1, 100, 100}, N = 30

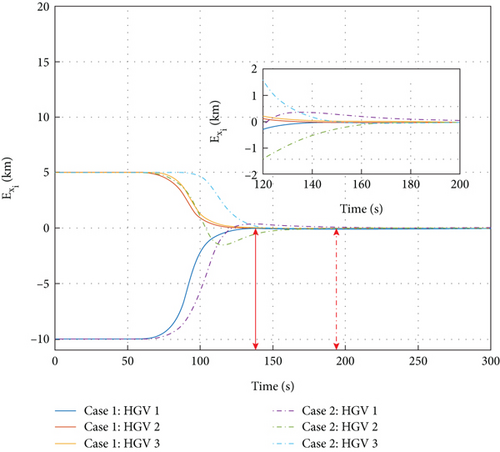
Figure 16 shows the comparison of the formation flight trajectories, which demonstrates the achievement of the desired formation configuration using the fixed-time formation control and the DMPC formation control. In Figure 17, time histories of the formation error variables are displayed; it can be seen that converge to the vicinity near zero within 140 s under the DMPC formation control. And converge to the vicinity near zero after 200 s with the fixed-time formation control.

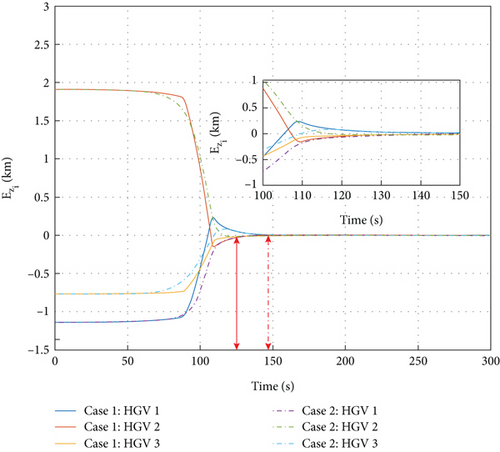
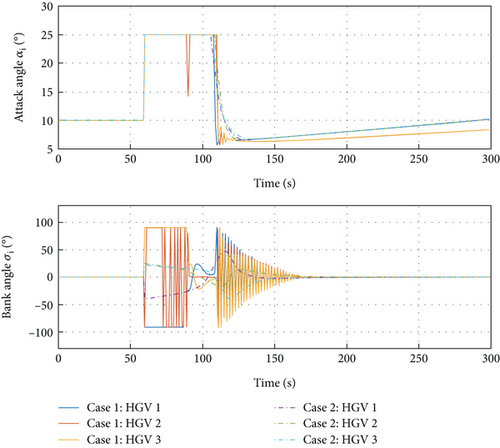
It can be seen in Figure 18 that converge to the vicinity near zero within 130 s under the DMPC formation control and converge to the vicinity near zero within 150 s under the condition of the fixed-time formation control. From Figures 16–18, DMPC formation control gives a faster convergence rate and smaller steady-state value for formation error variables than the fixed-time formation control. Regarding the fixed-time formation control, the formation error variables have a faster convergence speed which is illustrated in [19] by comparing with classical and finite-time formation control. Therefore, the DMPC formation control has a relatively fast convergence speed rather than the fixed-time formation control and a rapidly faster convergence speed and improved convergence precision rather than other methods. In Figure 19, the maximum maneuvering ability is the same for the two methods, where the limitations of the α_i and σ_i are the same and are satisfied during the formation control. Accordingly, the simulation illustrates that in spite of the ability to cope with multiple constraints during the formation flight, the proposed formation algorithm has a superiority in convergence speed and convergence precision. The proposed formation algorithm exhibits superior performance compared to other existing formation control strategies for the multiple HGVs.

5. Conclusion

In our work, a distributed formation control algorithm is investigated for multi-HGVs under multiple constraints consisting of mission constraints and trajectory constraints. The first difference between previous algorithms and the proposed algorithm is the fulfilment of the obstacle avoidance constraints, the collision avoidance constraints, and the terminal state constraints for the mission constraints for multiple HGV formation flights. The second difference is that, with the satisfaction of the necessary mission constraints, the trajectory constraints were considered additionally the first time for the formation flight of multi-HGVs. A distributed virtual controller and an actual control input solver were designed for the control framework, where the virtual controller introduced an optimization problem with a synchronous update strategy for the formation control in a distributed way and the actual control input solver adopted a novel solution process to calculate the actual control inputs while dealing with multiple constraints. Extensive simulation results disclose that the proposed algorithm has the ability to guarantee multiple constraints for formation flight with obstacle and collision avoidance simultaneously. And the superiority in the control performance is demonstrated.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This work was funded by the National Natural Science Foundation of China (grant number 61473229).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Lu P., Entry guidance: a unified method, Journal of Guidance, Control, and Dynamics. (2014) 37, no. 3, 713–728, https://doi.org/10.2514/1.62605, 2-s2.0-84901444016.
10.2514/1.62605
Web of Science® Google Scholar
2 Bao C., Wang P., and Tang G., Data-driven based model-free adaptive optimal control method for hypersonic morphing vehicle, IEEE Transactions on Aerospace and Electronic Systems. (2022) 59, no. 4, 3713–3725, https://doi.org/10.1109/TAES.2022.3230633.
10.1109/TAES.2022.3230633
Web of Science® Google Scholar
3 Acton J. M., Hypersonic boost-glide weapons, Science and Global Security. (2015) 23, no. 3, 191–219, https://doi.org/10.1080/08929882.2015.1087242, 2-s2.0-84945131386.
10.1080/08929882.2015.1087242
Web of Science® Google Scholar
4 Wang X., Guo J., Tang S., Qi S., and Wang Z., Entry trajectory planning with terminal full states constraints and multiple geographic constraints, Aerospace Science and Technology. (2019) 84, 620–631, https://doi.org/10.1016/j.ast.2018.10.035, 2-s2.0-85056700120.
10.1016/j.ast.2018.10.035
Web of Science® Google Scholar
5 Yan X., Wang P., Xu S., Wang S., and Jiang H., Adaptive entry guidance for hypersonic gliding vehicles using analytic feedback control, International Journal of Aerospace Engineering. (2020) 2020, 18, https://doi.org/10.1155/2020/8874251, 8874251.
10.1155/2020/8874251
Web of Science® Google Scholar
6 Cheng L., Jiang F., Wang Z., and Li J., Multiconstrained real-time entry guidance using deep neural networks, IEEE Transactions on Aerospace and Electronic Systems. (2021) 57, no. 1, 325–340, https://doi.org/10.1109/TAES.2020.3015321.
10.1109/TAES.2020.3015321
Web of Science® Google Scholar
7 Chen H., Zhao K., Guirao J. L. G., and Cao D., Analytical predictor–corrector entry guidance for hypersonic gliding vehicles, International Journal of Nonlinear Sciences and Numerical Simulation. (2021) 22, no. 7-8, 955–971, https://doi.org/10.1515/ijnsns-2019-0290.
10.1515/ijnsns-2019-0290
Web of Science® Google Scholar
8 Yu W., Yang J., and Chen W., Entry guidance based on analytical trajectory solutions, IEEE Transactions on Aerospace and Electronic Systems. (2021) 58, no. 3, 2438–2466, https://doi.org/10.1109/TAES.2021.3133387.
10.1109/TAES.2021.3133387
Web of Science® Google Scholar
9 Sana K. S. and Weiduo H. U., Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm, Chinese Journal of Aeronautics. (2021) 34, no. 1, 50–67, https://doi.org/10.1016/j.cja.2020.09.039.
10.1016/j.cja.2020.09.039
Web of Science® Google Scholar
10 Chai R., Tsourdos A., Savvaris A., Xia Y., and Chai S., Real-time reentry trajectory planning of hypersonic vehicles: a two-step strategy incorporating fuzzy multiobjective transcription and deep neural network, IEEE Transactions on Industrial Electronics. (2019) 67, no. 8, 6904–6915, https://doi.org/10.1109/TIE.2019.2939934.
10.1109/TIE.2019.2939934
Web of Science® Google Scholar
11 Cho D., Kim H. J., and Tahk M. J., Nonsingular sliding mode guidance for impact time control, Journal of Guidance, Control, and Dynamics. (2016) 39, no. 1, 61–68, https://doi.org/10.2514/1.G001167, 2-s2.0-84957652533.
10.2514/1.G001167
Web of Science® Google Scholar
12 Song J., Song S., and Xu S., Three-dimensional cooperative guidance law for multiple missiles with finite-time convergence, Aerospace Science and Technology. (2017) 67, 193–205, https://doi.org/10.1016/j.ast.2017.04.007, 2-s2.0-85018495353.
10.1016/j.ast.2017.04.007
Web of Science® Google Scholar
13 Zeng J., Dou L., and Xin B., A joint mid-course and terminal course cooperative guidance law for multi-missile salvo attack, Chinese Journal of Aeronautics. (2018) 31, no. 6, 1311–1326, https://doi.org/10.1016/j.cja.2018.03.016, 2-s2.0-85046170097.
10.1016/j.cja.2018.03.016
Web of Science® Google Scholar
14 Yu J., Dong X., Li Q., Ren Z., and Lv J., Cooperative guidance strategy for multiple hypersonic gliding vehicles system, Chinese Journal of Aeronautics. (2020) 33, no. 3, 990–1005, https://doi.org/10.1016/j.cja.2019.12.003.
10.1016/j.cja.2019.12.003
Web of Science® Google Scholar
15 Zhao J. and Zhou R., Distributed three-dimensional cooperative guidance via receding horizon control, Chinese Journal of Aeronautics. (2016) 29, no. 4, 972–983, https://doi.org/10.1016/j.cja.2016.06.011, 2-s2.0-84979257054.
10.1016/j.cja.2016.06.011
Web of Science® Google Scholar
16 Zhao J. and Yang S., Integrated cooperative guidance framework and cooperative guidance law for multi-missile, Chinese Journal of Aeronautics. (2018) 31, no. 3, 546–555, https://doi.org/10.1016/j.cja.2017.12.013, 2-s2.0-85042014838.
10.1016/j.cja.2017.12.013
Web of Science® Google Scholar
17 Yu J., Dong X., Li Q., and Ren Z., Distributed cooperative encirclement hunting guidance for multiple flight vehicles system, Aerospace Science and Technology. (2019) 95, article 105475, https://doi.org/10.1016/j.ast.2019.105475, 2-s2.0-85073612135.
10.1016/j.ast.2019.105475
Web of Science® Google Scholar
18 Jia S., Wang X., Li F., and Wang Y., Distributed analytical formation control and cooperative guidance for gliding vehicles, International Journal of Aerospace Engineering. (2020) 2020, 14, https://doi.org/10.1155/2020/8826968, 8826968.
10.1155/2020/8826968
Web of Science® Google Scholar
19 Zhang Y., Wang X., and Tang S., A globally fixed-time solution of distributed formation control for multiple hypersonic gliding vehicles, Aerospace Science and Technology. (2020) 98, article 105643, https://doi.org/10.1016/j.ast.2019.105643.
10.1016/j.ast.2019.105643
Web of Science® Google Scholar
20 Yu W., Yao Y., and Chen W., Analytical cooperative entry guidance for rendezvous and formation flight, Acta Astronautica. (2020) 171, 118–138, https://doi.org/10.1016/j.actaastro.2020.02.044.
10.1016/j.actaastro.2020.02.044
Web of Science® Google Scholar
21 Xue S. and Lu P., Constrained predictor-corrector entry guidance, Journal of Guidance, Control, and Dynamics. (2010) 33, no. 4, 1273–1281, https://doi.org/10.2514/1.49557, 2-s2.0-77956377901.
10.2514/1.49557
Web of Science® Google Scholar
22 Zhao J. and Zhou R., Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints, Chinese Journal of Aeronautics. (2013) 26, no. 6, 1544–1553, https://doi.org/10.1016/j.cja.2013.10.009, 2-s2.0-84891605622.
10.1016/j.cja.2013.10.009
Web of Science® Google Scholar
23 Yu W. and Chen W., Entry guidance with real-time planning of reference based on analytical solutions, Advances in Space Research. (2015) 55, no. 9, 2325–2345, https://doi.org/10.1016/j.asr.2015.02.002, 2-s2.0-84925382402.
10.1016/j.asr.2015.02.002
Web of Science® Google Scholar
24 Li Z., Hu C., Ding C., Liu G., and He B., Stochastic gradient particle swarm optimization based entry trajectory rapid planning for hypersonic glide vehicles, Aerospace Science and Technology. (2018) 76, 176–186, https://doi.org/10.1016/j.ast.2018.01.033, 2-s2.0-85042186598.
10.1016/j.ast.2018.01.033
Web of Science® Google Scholar
25 Zhao J. and Zhou R., Particle swarm optimization applied to hypersonic reentry trajectories, Chinese Journal of Aeronautics. (2015) 28, no. 3, 822–831, https://doi.org/10.1016/j.cja.2015.04.007, 2-s2.0-84931577408.
10.1016/j.cja.2015.04.007
Web of Science® Google Scholar
26 Sushnigdha G. and Joshi A., Re-entry trajectory optimization using pigeon inspired optimization based control profiles, Advances in Space Research. (2018) 62, no. 11, 3170–3186, https://doi.org/10.1016/j.asr.2018.08.009, 2-s2.0-85052094105.
10.1016/j.asr.2018.08.009
Web of Science® Google Scholar
27 Zhang Y., Zhang R., and Li H., Online path decision of no-fly zones avoidance for hypersonic vehicles based on a graph attention network, IEEE Transactions on Aerospace and Electronic Systems. (2023) 59, no. 5, 5554–5567, https://doi.org/10.1109/TAES.2023.3260071.
10.1109/TAES.2023.3260071
Web of Science® Google Scholar
28 He S., Dai S. L., Zhao Z., Zou T., and Ma Y., UDE-based distributed formation control for MSVs with collision avoidance and connectivity preservation, IEEE Transactions on Industrial Informatics. (2023) 1–12, https://doi.org/10.1109/TII.2023.3274234.
10.1109/TII.2023.3274234
Web of Science® Google Scholar
29 Li Z., Yang X., Sun X., Liu G., and Hu C., Improved artificial potential field based lateral entry guidance for waypoints passage and no-fly zones avoidance, Aerospace Science and Technology. (2019) 86, 119–131, https://doi.org/10.1016/j.ast.2019.01.015, 2-s2.0-85060089952.
10.1016/j.ast.2019.01.015
Web of Science® Google Scholar
30 Wang W., Li C., and Guo Y., Relative position coordinated control for spacecraft formation flying with obstacle/collision avoidance, Nonlinear Dynamics. (2021) 104, 1329–1342, https://doi.org/10.1007/s11071-021-06348-9.
10.1007/s11071-021-06348-9
Web of Science® Google Scholar
31 Mayne D. Q., Rawlings J. B., Rao C. V., and Scokaert P. O. M., Constrained model predictive control: stability and optimality, Automatica. (2000) 36, no. 6, 789–814, https://doi.org/10.1016/S0005-1098(99)00214-9, 2-s2.0-0033876326.
10.1016/S0005-1098(99)00214-9
Web of Science® Google Scholar
32 Rodriguez J., Cortes P., Kennel R., and Kazmierkowski M. P., Model predictive control - a simple and powerful method to control power converters, IEEE Transactions on Industrial Electronics. (2009) 56, no. 6, 41–49, https://doi.org/10.1109/TIE.2008.2008349, 2-s2.0-67649353151.
10.1109/TIE.2008.2008349
Web of Science® Google Scholar
33 Mayne D. Q., Model predictive control: recent developments and future promise, Automatica. (2014) 50, no. 12, 2967–2986, https://doi.org/10.1016/j.automatica.2014.10.128, 2-s2.0-84919460942.
10.1016/j.automatica.2014.10.128
Web of Science® Google Scholar
34 Negenborn R. R. and Maestre J. M., Distributed model predictive control: an overview and roadmap of future research opportunities, IEEE Control Systems Magazine. (2014) 34, no. 4, 87–97, https://doi.org/10.1109/MCS.2014.2320397, 2-s2.0-84904624715.
10.1109/MCS.2014.2320397
Web of Science® Google Scholar
35 Maestre J. M. and Negenborn R. R., Distributed Model Predictive Control Made Easyed, 2014, Springer, London, https://doi.org/10.1007/978-94-007-7006-5, 2-s2.0-84896509219.
10.1007/978-94-007-7006-5
Google Scholar
36 Trodden P. and Richards A., Distributed model predictive control of linear systems with persistent disturbances, International Journal of Control. (2010) 83, no. 8, 1653–1663, https://doi.org/10.1080/00207179.2010.485280, 2-s2.0-77954911804.
10.1080/00207179.2010.485280
Web of Science® Google Scholar
37 Kuwata Y. and How J. P., Cooperative distributed robust trajectory optimization using receding horizon MILP, IEEE Transactions on Control Systems Technology. (2011) 19, no. 2, 423–431, https://doi.org/10.1109/TCST.2010.2045501, 2-s2.0-79951954833.
10.1109/TCST.2010.2045501
Web of Science® Google Scholar
38 Wang P. and Ding B., A synthesis approach of distributed model predictive control for homogeneous multi-agent system with collision avoidance, International Journal of Control. (2013) 11, 1–12, https://doi.org/10.1080/00207179.2013.822100, 2-s2.0-84890860201.
10.1080/00207179.2013.868607
CAS Google Scholar
39 Dai L., Cao Q., Xia Y., and Gao Y., Distributed MPC for formation of multi-agent systems with collision avoidance and obstacle avoidance, Journal of the Franklin Institute. (2017) 354, no. 4, 2068–2085, https://doi.org/10.1016/j.jfranklin.2016.12.021, 2-s2.0-85009352894.
10.1016/j.jfranklin.2016.12.021
Web of Science® Google Scholar
40 Guo Y., Zhou J., and Liu Y., Distributed Lyapunov-based model predictive control for collision avoidance of multi-agent formation, IET Control Theory & Applications. (2018) 12, no. 18, 2569–2577, https://doi.org/10.1049/iet-cta.2018.5317, 2-s2.0-85057612836.
10.1049/iet-cta.2018.5317
Web of Science® Google Scholar

All articles

Distributed Formation Control with Obstacle and Collision Avoidance for Hypersonic Gliding Vehicles Subject to Multiple Constraints

Abstract

1. Introduction

2. Problem Statement and Preliminaries

2.1. Basic Theory

2.2. Equations of Motion

2.3. Multiple Constraints of Hypersonic Gliding Vehicles

2.3.1. Terminal Constraints

2.3.2. Trajectory Constraints

2.3.3. Control Constraints

2.3.4. Collision Avoidance Constraints

2.3.5. Obstacle Avoidance Constraints

2.4. Control Objective

3. Formation Control Algorithm

3.1. Distributed Virtual Controller

3.1.1. Construction of Objective Function

3.1.2. Construction of Constraints

3.2. Actual Input Solver

4. Simulation Examples

4.1. Simulation of Formation Accomplished with Different Control Parameters

4.2. Simulation of Formation Control Satisfying Multiple Constraints

4.3. Simulation Comparison with Existing Approaches

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Distributed Formation Control with Obstacle and Collision Avoidance for Hypersonic Gliding Vehicles Subject to Multiple Constraints

Abstract

1. Introduction

2. Problem Statement and Preliminaries

2.1. Basic Theory

2.2. Equations of Motion

2.3. Multiple Constraints of Hypersonic Gliding Vehicles

2.3.1. Terminal Constraints

2.3.2. Trajectory Constraints

2.3.3. Control Constraints

2.3.4. Collision Avoidance Constraints

2.3.5. Obstacle Avoidance Constraints

2.4. Control Objective

3. Formation Control Algorithm

3.1. Distributed Virtual Controller

3.1.1. Construction of Objective Function

3.1.2. Construction of Constraints

3.2. Actual Input Solver

4. Simulation Examples

4.1. Simulation of Formation Accomplished with Different Control Parameters

4.2. Simulation of Formation Control Satisfying Multiple Constraints

4.3. Simulation Comparison with Existing Approaches

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information