1. Introduction

When μ = 1 and μ = λ = 1, (1) and (2) reduce to the classical tangent polynomials, respectively (see [1]).

It is worth mentioning that results obtained in [2, 3] may have potential applications in mathematics and physics. More precisely, the numerical values of the zeros of the tangent polynomials may represent important values in engineering and physics while the twisted q-analogue of tangent polynomials may be used in quantum physics, particularly in the study of quantum groups and their representation theory.

Ryoo [4] introduced a variation of tangent numbers and polynomials, known as twisted tangent numbers and polynomials, associated with the p-adic integral on ℤ_p. Through his work, Ryoo presented intriguing findings and established connections related to these concepts. In addition, Ryoo [5] explored differential equations arising from the generating functions of generalized tangent polynomials and derived explicit identities for them. Furthermore, Ryoo [6] investigated the symmetry property of the deformed fermionic integral on ℤ_p, which is a mathematical structure defined over a prime field. Specifically, he focused on establishing recurrence identities for tangent polynomials and alternating sums of powers of consecutive even integers within this context. These discoveries expand our knowledge and understanding of this specialized area of mathematics, providing insights into its unique properties and potential applications across different domains. Moreover, a study by Corcino et al. [7] obtained the Fourier expansion of tangent polynomials of integer order.

In this paper, the same method described by Lόpez and Temme ([8], p. 4) has been followed in deriving the asymptotic expansion which only gives a first-order approximation. C. Corcino and R. Corcino ([9], p. 2) describe a similar method and provide a first-order and second-order approximations.

2. Asymptotic Expansions

In this section, the asymptotic expansions for large values of n of tangent $$ and Apostol-tangent $$ polynomials of complex order are derived.

2.1. Tangent Polynomials of Complex Order μ

Applying Cauchy’s integral formula for derivatives to (1), we have

$$ (3)

where C is a circle about 0 with radius <π/2.

We observe in (3) that the singularities at ±πi/2 are the sources for the main asymptotic contributions. We integrate around a circle C₁ about 0 with radius π avoiding the branch cuts running from ±πi/2 to +∞ (see Figure 1). Denote the loops by $$ and $$ and the remaining part of the circle C₁ by C^∗. Then, we have

$$ (4)

where f(w) is the integrand on the right-hand side of (3). By the principle of deformation of paths,

$$ (5)

Then, (4) and (5) yield

$$ (6)

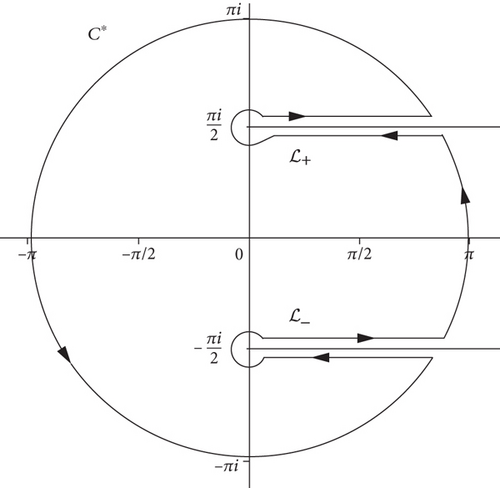
The following lemma gives the contribution from the circular arc C^∗.

Lemma 1. The integral along C^∗ is O((π)⁻ⁿ). That is,

$$ (7)

Proof. Taking the modulus of the integral, we have

$$ (8)

for all w ∈ C^∗. Since C^∗ does not pass any singularity, e^2w + 1 is not zero. Thus,

$$ (9)

for some positive number A. So that,

$$ (10)

This proves the lemma.

Remark 2. Lemma 1 shows that, for large values of n (as n⟶∞), the contribution from the circular arc C^∗ is exponentially small with respect to the main contributions.

For the contributions from the loops, let I₊ and I₋ be the integrals along $$ and $$, respectively. We first compute the integral I₊:

$$ (11)

Let w = πi/2e^s. Then, dw = πi/2e^sds and

$$ (12)

where C₊ is the image of $$ under the transformation w = πi/2e^s. C₊ is the contour that encircles the origin in the clockwise direction. Multiplying the last array by e^−πiz/2e^πiz/2(πi)^μ(πi)^−μ and since e^πi = −1,

$$ (13)

where η = πi(e^s − 1)/2. Multiplying the last array by s^−μs^μ,

$$ (14)

where

$$ (15)

To obtain an asymptotic expansion, we apply Watson’s lemma for loop integrals (see [10], p. 120). We expand

$$ (16)

Substituting (16)–(14), I₊ becomes

$$ (17)

where

$$ (18)

with C₊ extended to +∞. That is, the path of integration starts at +∞ with arg s = 2π, encircles the origin in the clockwise direction, and returns to +∞, now with arg s = 0.

Now, we evaluate F_k. First, we turn the path by writing s = e^πit:

$$ (19)

where D₊ is the image of C₊ under the transformation s = e^πit. D₊ is the contour that starts at −∞ with arg t = +π, encircles the origin in clockwise direction, and returns to −∞ with arg t = −π.

We recall Hankel’s loop integral representation for the reciprocal gamma function (see [11, 12], p. 48 and p. 153, respectively):

$$ (20)

where H is the Hankel contour (see Figure 2) that runs from −∞ with arg w = −π, encircles the origin in positive direction (that is, counterclockwise), and terminates at −∞, now with arg w = +π.

Observe that, by deformation of paths, the contour D₊ is the Hankel contour H traversed in the opposite direction. So that,

$$ (21)

Let u = nt; du = n dt. Then,

$$ (22)

Moreover,

$$ (23)

where 〈x〉_k = x(x + 1) ⋯ (x + k − 1), the rising factorial of x of degree k. Hence,

$$ (24)

Applying (24)–(17) and noting that i⁻¹ = e^−iπ/2, we get

$$ (25)

where β = α − (nπ/2) and α = (z − μ)π/2.

Now, the integral I₋ along the loop $$,

$$ (26)

can be obtained similarly. After the substitution w = (−πi/2)e^s, we obtain

$$ (27)

where

$$ (28)

We expand $$ and interchange the summation and integration in (27) and get

$$ (29)

where $$ are the integrals in (18). Applying (24) and noting that −i⁻¹ = e^πi/2, we obtain

$$ (30)

where β = α − (nπ/2) and α = (z − μ)π/2.

We observe that $$ is just the complex conjugate of g(s) (not considering z and μ as complex numbers). So that, if we write $$ (with $$ real when z and μ are real), then $$. Hence, by Remark 2 and applying (25) and (30), we obtain

$$ (31)

Consequently, we have the following theorem.

Theorem 3. As n⟶∞, μ and z are fixed complex numbers.

$$ (32)

where β = α − (nπ/2) and α = (z − μ)π/2.

Compute the first few values of $$ and $$ using Mathematica:

$$ (33)

A first-order approximation is obtained by taking $$ and $$ for $$ and $$, respectively, and taking the first term of the sum. This is given in the following theorem.

Theorem 4. As n⟶∞, μ and z are fixed complex numbers.

$$ (34)

where β = α − (nπ/2) and α = (z − μ)π/2.

A second-order approximation is given as follows.

Theorem 5. As n⟶∞, μ and z are fixed complex numbers.

$$ (35)

where β = α − (nπ/2) and α = (z − μ)π/2.

2.2. Apostol-Tangent Polynomials of Complex Order μ

We apply the same method as in the previous subsection.

For convenience, we take λ = e^2ξπi, where ξ ∈ ℝ and |ξ| < 1/2. Then, (2) reduces to

$$ (36)

Applying Cauchy’s integral formula for derivative to (36), we have

$$ (37)

where C is a circle about 0 with radius <(π/2) − |ξ|π.

We consider (37) and observe that the singularities at w₀ = (πi/2) − ξπi and w₋₁ = (−πi/2) − ξπi are the source for the main asymptotic contribution. We integrate around a circle C₂ about 0 with radius π avoiding the branch cuts running from (πi/2) − ξπi to +∞ and (−πi/2) − ξπi to +∞ (see Figure 3). Denote the loops by $$ and $$ and the remaining part of the circle C₂ by C^∗∗. Then, we have

$$ (38)

where f(w) is the integrand on the right-hand side of (37). By the principle of deformation of paths,

$$ (39)

Then, (38) and (39) yield

$$ (40)

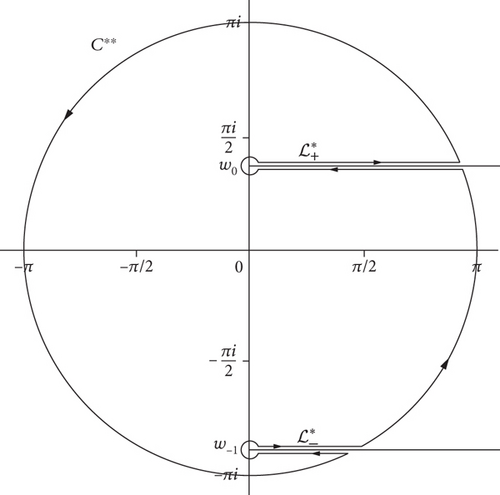
Remark 6. It follows from Lemma 1 that the contribution from the circular arc C^∗∗ is also O((π)⁻ⁿ), so that, for large values of n (as n⟶∞), it is exponentially small with respect to the main contributions.

We proceed to compute the contributions from the loops $$ and $$. Let $$ be the integral along the loop $$. Then,

$$ (41)

Let w = ((πi/2) − ξπi)e^s = 2⁻¹(πi − 2ξπi)e^s. Then, dw = 2⁻¹(πi − 2ξπi)e^sds and

$$ (42)

where $$ is the image of $$ under the transformation w = ((πi/2) − ξπi)e^s. $$ is the contour that encircles the origin in the clockwise direction. Multiplying the last array by e^{(πi/2)(1 − 2ξ)z}e^{(−πi/2)(1 − 2ξ)z}(πi − 2ξπi)^μ(πi − 2ξπi)^−μ and since e^−πi = −1,

$$ (43)

where η = (πi/2)(1 − 2ξ)(e^s − 1). Multiplying the last array by s^μs^−μ,

$$ (44)

where

$$ (45)

We expand $$; (49) becomes

$$ (46)

where $$ are the integrals in (18).

Applying (24)–(51) and noting that i⁻¹ = e^−iπ/2, we get

$$ (47)

where β = α − (nπ/2) and α = (z − μ)π/2.

Next, let $$ be the integral along loop $$. Then,

$$ (48)

After the substitution w = ((−πi/2) − ξπi)e^s = 2⁻¹(−πi − 2ξπi)e^s, we obtain

$$ (49)

where

$$ (50)

We expand $$ and interchange the summation and integration in (49) and get

$$ (51)

where $$ are the integrals in (18). Applying (24) to (51) and noting that −i⁻¹ = e^iπ/2, we get

$$ (52)

where β = α − (nπ/2) and α = (z − μ)π/2.

Then, by Remark 6 and applying (47) and (52), we obtain

$$ (53)

Hence, we have the following theorem.

Theorem 7. As n⟶∞, μ and z are fixed complex numbers.

$$ (54)

where β = α − (nπ/2) and α = (z − μ)π/2.

Remark 8. When ξ = 0, Theorem 7 reduces to Theorem 3.

Compute for the first few values of h_k and f_k using Mathematica:

$$ (55)

$$ (56)

A first-order approximation is obtained by taking h₀ and f₀ for h_k and f_k, respectively, and taking the first term of the sum. This is given in the following theorem.

Theorem 9. As n⟶∞, μ and z are fixed complex numbers.

$$ (57)

where β = α − (nπ/2) and α = (z − μ)π/2.

Remark 10. When ξ = 0, Theorem 9 reduces to Theorem 4.

3. Summary

These findings contribute to our comprehension of the behaviors exhibited by these polynomials and can prove beneficial in various applications that necessitate approximations for significant values of n.

Conflicts of Interest

The authors declare that they have no conflicts of interest.