Despite the recent progress of global control efforts, tuberculosis (TB) remains a significant public health threat worldwide, especially in developing countries, including Ethiopia. Furthermore, the emergence of multidrug-resistant tuberculosis (MDR-TB) has further complicated the situation. This study aims at identifying the most effective strategies for combating MDR-TB in Ethiopia. We first present a compartmental model of MDR-TB transmission dynamics in Ethiopia. The model is shown to have positive solutions, and the stability of the equilibrium points is analyzed. Then, we extend the model by incorporating time-dependent control variables. These control variables are vaccination, distancing, and treatment for DS-TB and MDR-TB. Finally, the optimality system is numerically simulated by considering different combinations of the strategies, and their cost effectiveness is analysed. Our finding shows that, among single control strategies, the successful treatment of drug-susceptible tuberculosis (DS-TB) is the most effective control factor for eliminating MDR-TB transmission in Ethiopia. Furthermore, within the six dual control strategies, the combination of distancing and successful treatment of DS-TB is less costly and more effective than other strategies. Finally, out of the triple control strategies, the combination of distancing, successful treatment for DS-TB, and treatment for MDR-TB is the most efficient strategy for curbing the MDR-TB disease in Ethiopia. Thus, to reduce MDR-TB efficiently, it is recommended that authorities focus on treating MDR-TB, effective treatment of DS-TB, and promoting social distancing through public health education and awareness programs.

1. Introduction

Tuberculosis (TB) is a bacterial infection that primarily affects the lungs. The transmission of TB occurs through the air when an infected individual coughs, sneezes, or spits [1].

Tuberculosis infection has two stages. The first period of TB infection is called the latent phase. An individual in the latent phase does not show symptoms and is noncontagious to others. Tuberculin skin tests or blood tests are used to diagnose latent TB. Most latent TB patients will stay long without progressing to the next stage. However, persons infected with HIV and other diseases and children are at high risk for progressing from latent TB to the second stage. The second stage of infection is called active TB infection. At this stage, individuals can infect susceptible people and show TB symptoms. Chest X-ray screening can identify active tuberculosis. Taking antibiotics for six months can effectively treat active TB [2].

We can categorize TB disease into two classes based on its response to drugs: drug-susceptible TB (DS-TB) and multidrug-resistant TB (MDR-TB). Drug-susceptible TB is a type of tuberculosis that can be treated with the usual medicines. On the other hand, multidrug-resistant TB is resistant to at least two medications, isoniazid (INH) and rifampin (RIF) [3]. The improper treatment of patients and poor management of the supply and quality of drugs result in the bacterium acquiring multidrug-resistant tuberculosis [4, 5].

The treatment of MDR-TB has always been more complicated than the treatment of DS-TB. It requires the use of second-line drugs or reserved drugs for up to two years. These drugs are more costly and cause more side effects. Also, because it takes a longer time to recover from MDR-TB, this may result in more people being infected [6]. The best way to stop the spread of drug-resistant TB is to take all DS-TB drugs as directed by your physician. There should be no early treatment termination or missed doses [3].

According to the 2022 WHO report, there has been a rise in the global number of tuberculosis cases and deaths from 2019 to 2021. In 2021, it is estimated that around 10.6 million individuals contracted tuberculosis, compared to 10.1 million in 2020. Additionally, the number of tuberculosis-related deaths reached 1.6 million in 2021 (including 187,000 individuals living with HIV), while in 2020, there were 1.5 million deaths recorded (including 214,000 individuals with HIV). Furthermore, the incidence rate of tuberculosis increased by approximately 3.6% in 2021 compared to 2020 [7].

Tuberculosis continues to be a significant public health problem in Ethiopia. Ethiopia ranked twelfth among the top 30 countries with high TB burden. Ethiopia ranked twenty-fourth among the countries with high multidrug-resistant TB (MDR-TB) burden [8]. Although progress has been achieved in reducing the incidence of tuberculosis, with a decrease from 421 cases per 100,000 (in 2000) to 132 cases per 100,000 (in 2020), the occurrence of drug-susceptible TB (DS-TB) and the associated mortality rate remain high [9].

Mathematical modelling is essential in understanding the epidemic’s trajectory and designing effective control measures under assumptions [10, 11]. In this study, a mathematical model is formulated for the transmission dynamics of MDR-TB in Ethiopia with optimal control and cost-effectiveness analysis.

2. Model Formulation and Analysis

2.1. MDR-TB Model

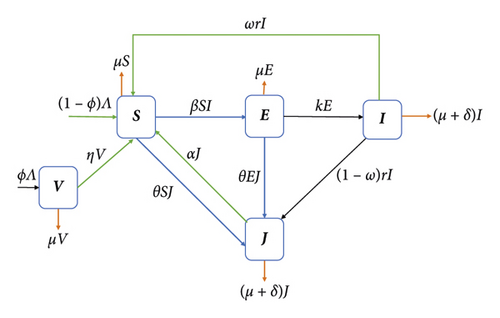
This section presents the mathematical model for multidrug-resistant tuberculosis (MDR-TB). This model is comprised of a set of ordinary differential equations. By considering a homogeneous mixing within the population, the total population N(t) is subdivided into five epidemiological groups: susceptible individuals S(t), vaccinated individuals V(t), individuals exposed to drug-susceptible TB E(t), infectious individuals with drug-susceptible TB I(t), and infectious individuals with MDR-TB J(t).

Within the model, the parameter Λ represents the rate at which individuals are recruited into the susceptible class. On the other hand, the parameter μ represents the natural death rate for each class within the system. The vaccination rate for healthy individuals is denoted as ϕ. We assume the vaccine is imperfect. Therefore, some of those who have received vaccinations are expected to be exposed to bacteria at a rate of η.

Susceptible individuals will be exposed to drug-susceptible TB if they come into effective contact, at a rate β, with individuals from the I-class. Moreover, it is assumed that the susceptible individuals became MDR-TB infected at a rate θ. Some individuals in class E may progress to class I at rate k. If treatment is administered for the I-class with a rate r, then some will complete their treatment correctly at a rate ωr for (0 ≤ ω ≤ 1). However, some individuals in the I class may fail to take their treatment correctly and may develop MDR-TB at a rate (1 − ω)r. The recovery rate of individuals from infected MDR-TB after treatment is α. It is assumed that the recovered individuals from both classes will move to the S-class. Furthermore, infectious individuals in I and J classes will die due to the disease at a rate δ. Figure 1 shows the model flow diagram.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flow diagram of the model.

The following system of differential equations gives the dynamics of DS-TB and MDR-TB.

()

2.2. Model Analysis

2.2.1. Positivity of the Solution Set

The variables S(t), V(t), E(t), I(t), and J(t) denote the number of people and are assumed to take positive values. From biological and mathematical considerations, it is necessary to prove that starting from positive initial conditions implies that the solution always remains positive.

Theorem 1. If the initial data S(0), V(0), E(0), I(0), and J(0) ≥ 0 are nonnegative, then the solution S(t), V(t), E(t), I(t), and J(t) of system (1) is positive for all t > 0.

Proof. From the first equation of the model, we have (1)

()

By letting

()

We have

()

Then, equation (4) can be described as

()

So,

()

Integrating both sides of (6) gives

()

Similarly, using the second equation of model (1), we obtain that

()

Equation (8) can be rewritten as

()

Integrating both sides of (9) gives

()

Note that from equation (10), we can show that

()

Similarly, we can show that E(t), I(t), and J(t) are nonnegative. So, the solutions S(t), V(t), E(t), I(t), J(t) of system (1) are positive for all t > 0.

2.2.2. Invariant Region

The invariant region of the model describes the region in which the solution of the model (1) is biologically meaningful.

Theorem 2. The invariant region Ω defined by

()

with nonnegative initial conditions is positively invariant for system (1).

Proof. Adding the equations of system (1), we have

()

It follows that

()

where N(0) represents the initial values of the total population.

Therefore, lim_t⟶∞ Sup N(t) ≤ Λ. It implies that the region

()

is a positive invariant set for system (1).

2.2.3. The Basic Reproduction Number

Model (1) has a disease-free equilibrium point (DFE), obtained by setting the right-hand sides of the equations in model (1) as well as the disease classes (E, I, J) to zero, given by

()

where

()

The basic reproduction number denoted by R₀ is the average number of secondary infectious individuals caused by an average primary infectious individual in its entire period in a completely susceptible population. Using the next-generation approach [12], the right-hand side of system (1) is written as

, where

()

The corresponding Jacobian matrices evaluated at the disease-free equilibrium are given by

()

Therefore,

()

The basic reproduction number is the magnitude of the dominant eigenvalue of FG⁻¹. For multigroup disease models or models dealing with more than one strain, the basic reproduction number is the maximum of a few numbers; see, for instance, [13, 14]. Since our model has two types of disease, DS-TB and MDR-TB, we have two reproduction numbers. The reproduction number for DS-TB is given by

()

and the reproduction number for MDR-TB is

()

Generally, the reproduction number for the coexistence of both diseases in the population is R₀ = Max {R₁, R₂}.

2.2.4. Stability Analysis of the Disease-Free Equilibrium Point

Theorem 3. The DFE, P₀, is locally asymptotically stable (LAS) when the basic reproduction number R₀ < 1 and is unstable for R₀ > 1.

Proof. We determine the local stability of P₀ using the eigenvalues of the Jacobian matrix at P₀, which is given by

()

If R₂ < 1, then the eigenvalues λ₁ = −μ₁, λ₂ = −(η + μ) and λ₃ = (α + δ + μ)(R₂ − 1) contain negative real parts. The remaining eigenvalues of G(P₀) can be determined from the following submatrix:

()

The characteristic polynomial of Q is given by

()

where

()

Applying the Routh–Hurwitz stability criterion [15], it can be shown that the eigenvalues of the submatrix Q have negative real parts for R₁ < 1. Hence, the disease-free equilibrium point of system (1) is locally asymptotically stable if R₀ < 1 and unstable if R₀ > 1.

Hence, both DS-TB and MDR-TB will die out from the population if R₀ < 1, while both diseases will invade and persist in the population if R₀ > 1.

2.2.5. Existence of the Endemic Equilibrium Point (EEP)

The endemic equilibrium point of model (1) is the steady state at which disease persists in the population when at least one of the model’s infectious compartments is nonzero. It is obtained as follows:

()

where

()

with

()

Clearly, it is evident from the above that model (1) has positive EEP if and only if one of the following conditions holds:

(1)
1 < R₁ < 1 + (μ/k) and 0 < R₁ − R₂ < (1/x₂ + x₃)[θμ²(r + δ + μ)² + x₂θ(δ + μ) + x₃rβ(1 − ω)]
(2)
R₁ > 1 + (μ/k) and 0 < R₁ − R₂ > (1/x₂ + x₃)[θμ²(r + δ + μ)² + x₂θ(δ + μ) + x₃rβ(1 − ω)]

2.2.6. Analysis of the MDR-TB-Only Model

The submodel with MDR-TB-only (obtained by setting E = 0, I = 0 in the model (1)) is given by

()

For this model, it can be shown that the region,

()

is a positively invariant region for system (30).

Theorem 4. Model (30) at DFE, M₀ = (Λ(η + μ(1 − ϕ)/μ(η + μ)), (Λϕ/η + μ), 0), is globally asymptotically stable (GAS) for R₂ < 1 and unstable for R₂ > 1.

Proof. We follow a methodology similar to the stability analysis of [16–20]. We observe that

()

In view of (11), we have

()

Let us define a function

()

We prove now that is negative-definite.

()

This proves that , whenever R₂ < 1. Hence, F(t) is a Lyapunov function on Ω₁. Therefore, by LaSalle’s invariance principle [21], every solution of model (30), with any initial conditions in Ω₁, approaches M₀ as t⟶∞, whenever R₂ < 1. Thus, M₀ is GAS in the region Ω₁.

Theorem 5. If R₂ > 1, then model (30) has a unique positive endemic equilibrium M₁ = (S^∗, V^∗, J^∗), where

()

Proof. It follows logically from the above that whenever R₂ > 1, a unique positive MDR-TB-only endemic equilibrium point exists.

3. Extension of the Model to Optimal Control

In this section, we expand model (1) by incorporating four control interventions. The objective is to determine the most effective strategies for eliminating MDR-TB within a specified time frame. The interventions are defined as follows:

(i)
Vaccination control (u₁): It represents using the Bacillus of Calmette and Guerin (BCG) vaccine.
(ii)
Distancing control (u₂): It represents an effort to protect susceptible individuals from exposure to tuberculosis by effectively reducing contact between vulnerable and infectious individuals. These include isolation of infected persons, social distancing, wearing face masks, diagnostic campaigns, and public health awareness programs.
(iii)
Treatment for DS-TB (u₃): It represents the effort to reduce treatment failure in DS-TB infectious individuals, such as taking care of patients until they complete the treatment.
(iv)
Treatment for MDR-TB (u₄): It represents the effort of treating and curing MDR-TB-infected individuals.

After incorporating the control variables u₁, u₂, u₃, and u₄ into model (1), it takes the following form:

()

In this optimal control problem, our main objective is to reduce the number of MDR-TB-infected individuals in the population while reducing the overall cost of controlling the disease dynamics.

Let us consider the following objective functional:

()

Subject to the terms of model system (37), the constant B_i measures the relative cost interventions associated with the control u_i for i = 1, 2, 3, 4. The functions are the cost functions that correspond to the controls u_i, which is nonlinear (as in [22, 23]). In equation (38), the values of t₀ and t_f are taken as 0 and 20, respectively, to determine Ethiopia’s 20-year (2019–2038) effective MDR-TB control strategy.

The main goal is to find the optimal controls

and

such that

()

where U = {(u₁, u₂, u₃, u₄)|u₁, u₂, u₃ and u₄ are Lebesgue integrable functions on the interval [0,∞), with 0 ≤ u_i ≤ 1, i = 1,2,3,4}.

3.1. Existence of an Optimal Control

We show the existence of optimal control by using an approach as in [24]. The boundedness of the model’s solution has already been established. The boundedness of the solution is used to demonstrate that an optimal control exists. For detailed proof, see [25]. By using the maximum principle of Pontryagin [26], the Hamiltonian (H), which combines the state equations (1) and the integrand of the objective functional (38), is given by

()

Here, are the adjoint functions. The following result can be obtained by applying Pontryagin’s maximum principle to the existence of the optimal control problem.

Theorem 6. Let , and be the control functions for the control problem given in (37) and , and be the solutions of state variables. Then, there are adjoint variables λ₁, λ₂, λ₃, and λ₄ that satisfy the following equations:

()

with transversality conditions

()

Proof. The form of the adjoint system and the transversality conditions associated with this optimal control problem are obtained by applying Pontryagin’s maximum principle [26]. For this purpose, we differentiate the formulated Hamiltonian function with respect to S, V, E, I, and J as follows:

()

with

()

Finally, by applying the optimality condition

()

and using the bounds for the controls u₁, u₂, u₃, and u₄, we can derive the optimal control

as in equation (43).

4. Numerical Simulations

The forward-backward sweeping method is used to solve the optimal control problem. The solution’s algorithm is based on the approach suggested in [28]. System (37) is simulated forward to achieve convergence, while the Hamiltonian function is simulated backward in time.

The unit of time used for the parameter values is one year. We calculate the initial number of vaccinated children as the product of the average number of newborns and the vaccination coverage, which is V₀ = 1.001 × 10⁶. In 2019, the incidence rate of MDR-TB in Ethiopia was 0.71% [27]. Hence, we take J₀ = 0.0071 × I₀ = 1115. In the same year, 75% of MDR-TB patients in Ethiopia were treated successfully [8]. So, we take the value of α as 0.75.

A recent estimation indicated that 3.3% of MDR-TB cases worldwide occurred among new TB cases in 2019 [29]. We take 3.3% of β to get the value of θ. Hence, θ = 5.43 × 10⁻⁵. The values of the remaining parameters and the initial values of the variables used in our simulations are presented in Tables 1 and 2.

Table 1. Initial values of the variables.

Symbols	Description	Units	Value	Reference
N₀	Total population	Humans	1.12 × 10⁸	[25]
S₀	Susceptible	Humans	3.404 × 10⁷	Estimated
V₀	Vaccinated	Humans	1.001 × 10⁶	[18]
E₀	DS-TB latent	Humans	1.83 × 10⁷	[25]
I₀	DS-TB infected	Humans	1.57 × 10⁵	[9]
J₀	MDR-TB infected	Humans	1.115 × 10³	[27]

Table 2. Parameter values.

Symbols	Description	Units	Value	Source
Λ	Recruitment rate	Humans/year	1.4 × 10⁶	[25]
β	Transmission rate for DS-TB	1/ year	1.646 × 10⁻⁷	[25]
θ	Transmission rate for MDR-TB	1/year	5.43 × 10⁻⁵	Estimated
ϕ	Vaccination rate of newborns	1/ year	0.715	[18]
η	Loss of protection for vaccination	1/ year	0.5	[18]
μ	Natural mortality rate	1/ year	0.016	[30]
k	The transfer rate from E to I	1/ year	0.023	[25]
r	Treatment rate of I	1/ year	0.546	[18]
ω	The recovery rate from DS-TB	Dimensionless	0.832	[29]
α	The recovery rate from MDR-TB	1/ year	0.75	[8]
δ	Death rate due to TB	1/ year	0.17	[8]

4.1. Use of Single Control

For this control strategy, we have four alternatives:

Strategy A: u₁, vaccination control
Strategy B: u₂, distancing control
Strategy C: u₃, treatment for DS-TB
Strategy D: u₄, treatment for MDR-TB

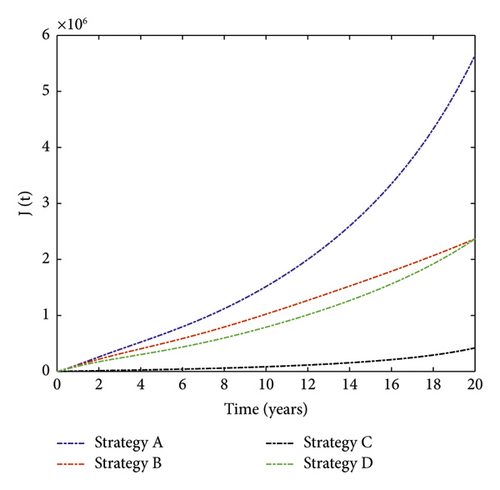
The simulation result of MDR-TB-infected individuals with different single control interventions is plotted in Figure 2. It can be observed that the number of MDR-TB-infected individuals can be significantly decreased when Strategy C (successful treatment for DS-TB) is applied. In contrast, Strategy A (only vaccination control) has the least impact on reducing the number of patients. This shows that it is beneficial to use treatment for DS-TB to prevent the disease.

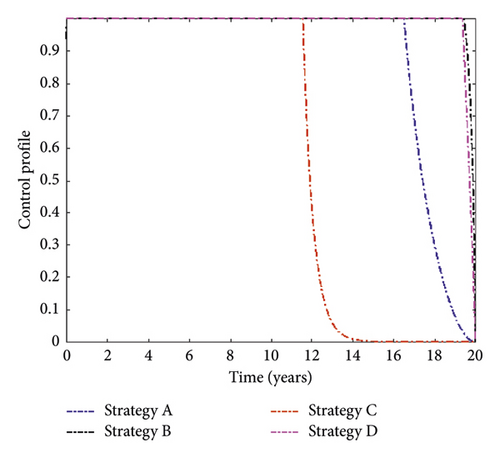
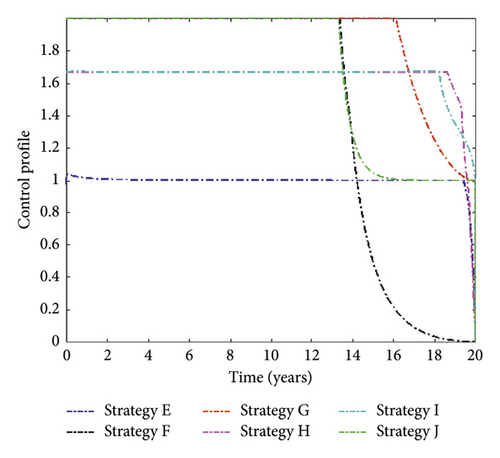
The control profiles in Figure 3 indicate that distancing and treatment for MDR-TB controls should be implemented at the maximum level until the end of the implementation. In contrast, the treatment for DS-TB and vaccination controls retained their highest bound for 13 and 18 years, respectively, and then declined until they reached their minimum value.

4.2. Use of Dual Controls

In this scenario, we consider a combination of two control functions, and we have six alternative strategies:

Strategy E: vaccination (u₁) and distancing (u₂)
Strategy F: vaccination (u₁) and treatment for DS-TB (u₃)
Strategy G: vaccination (u₁) and treatment for MDR-TB (u₄)
Strategy H: distancing (u₂) and treatment for DS-TB (u₃)
Strategy I: distancing (u₂) and treatment for MDR-TB (u₄)
Strategy J: treatment for DS-TB (u₃) and treatment for MDR-TB (u₄)

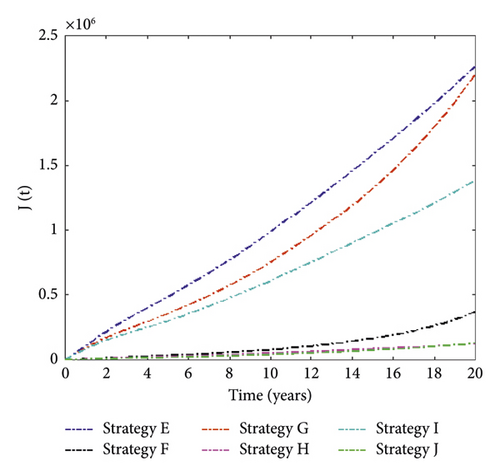
We noticed in Figure 4 that Strategy J has the highest number of MDR-TB infections averted, followed by Strategies H, F, I, G, and E. The control solution profile is shown in Figure 5.

4.3. Use of Triple Controls

In this section, we conduct numerical simulations by considering the application of triple control functions. For the combination of three different control practices, we have the following four alternative strategies:

Strategy K: vaccination, distancing, and treatment for MDR-TB
Strategy L: vaccination, distancing, and treatment for DS-TB
Strategy M: vaccination, treatment for DS-TB, and treatment for MDR-TB
Strategy N: distancing, treatment for DS-TB, and treatment for MDR-TB

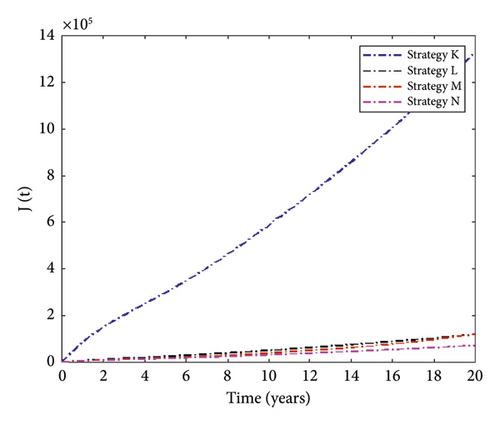
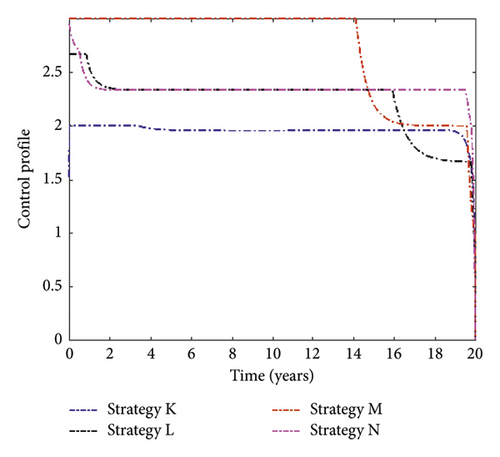
Figure 6 presents simulation results for MDR-TB-infected individuals with different triple control interventions. We can see that Strategy N (the combination of distancing, treatment for DS-TB, and treatment for MDR-TB) can significantly reduce the number of people infected with MDR-TB. In contrast, Strategy K (the combination of vaccination, distancing, and treatment for MDR-TB) has the least effect on reducing case numbers. The control function of this strategy is displayed in Figure 7.

5. Cost-Effectiveness Analysis

We used cost-effectiveness analysis to determine the most effective strategy to control MDR-TB in Ethiopia. This is performed by the incremental cost-effectiveness ratio (ICER) mentioned in [9, 31]. This ratio compares the differences between the total costs and the total decrement of MDR-TB patients for two alternative control strategies. The following formula obtains the ICER:

()

5.1. ICER for Single Control Strategy

Based on the total number of people averted from MDR-TB infection, Strategies B, D, A, and C are ranked in increasing order, as shown in Table 3. We first compare the ICER of Strategy B and Strategy D based on this rank.

()

Table 3. The number of MDR-TB infections averted and the total cost of each single control strategy.

Strategy	Total infection averted	Total cost ($)
B(u₂)	3.85 × 10⁶	3.86 × 10⁶
D(u₄)	3.85 × 10⁶	4.03 × 10⁶
A(u₁)	5.7 × 10⁵	6.85 × 10⁵
C(u₃)	5.8 × 10⁶	5.8 × 10⁶

ICER (Strategy D with respect to Strategy B) = (4.03 × 10⁶ − 3.86 × 10⁶/3.8497 × 10⁶ − 3.8487 × 10⁶) = 174.28.

This shows that Strategy B is less costly compared to Strategy D. Strategy D is then ignored, and the analysis continues by comparing Strategy B with A:

()

ICER (Strategy A with respect to Strategy B) = (6.85 × 10⁵ − 3.86 × 10⁶/5.723 × 10⁵ − 3.8487 × 10⁶) = 0.97.

It follows that Strategy A is cheaper compared to Strategy B, and hence, Strategy B is ignored, and the analysis continues by comparing Strategy A and Strategy C as follows:

()

ICER (Strategy C with respect to Strategy A) = (5.8 × 10⁶ − 6.85 × 10⁵/5.79 × 10⁶ − 5.723 × 10⁵) = 0.98.

Eventually, Strategy C is more cost-effective than Strategy A. Therefore, the control program that considers the application of Strategy C (successful treatment of DS-TB) will achieve a more efficient result.

5.2. ICER for the Dual Control Strategy

First, we must rank the strategies in order of increasing based on averted infection, as shown in Table 4. The incremental cost-effectiveness ratio for the dual control strategies is calculated in Table 5. From the table, we conclude that Strategy H (i.e., the combination of distancing and the successful treatment of DS-TB) is the most cost-effective of all dual control strategies.

Table 4. The number of MDR-TB infections averted and the total cost of each dual control strategy.

Strategy	Total infection averted	Total cost ($)
E(u₁ and u₂)	3.95 × 10⁶	4.07 × 10⁶
G(u₁ and u₄)	4.01 × 10⁶	4.12 × 10⁶
I(u₂ and u₄)	4.83 × 10⁶	5.02 × 10⁶
F(u₁ and u₃)	5.84 × 10⁶	5.96 × 10⁶
H(u₂ and u₃)	6.003 × 10⁶	6.02 × 10⁶
J(u₃ and u₄)	6.086 × 10⁶	6.27 × 10⁶

Table 5. The incremental cost-effectiveness ratio of the dual control strategies.

ICER	Decision
ICER⁡(E) = (4.07 × 10⁶/3.95 × 10⁶) = 1,03	—
ICER(G, E) = 4.12 × 10⁶ − 4.07 × 10⁶/4.01 × 10⁶ − 3.95 × 10⁶ = 0.84	Strategy G is less costly than strategy E. Strategy E is then ignored, and the analysis continues by comparing strategy I with G
ICER⁡(G) = 4.12 × 10⁶/4.01 × 10⁶ = 1.03	—
ICER⁡(I, G) = (5.02 × 10⁶ − 4.12 × 10⁶/4.83 × 10⁶ − 4.01 × 10⁶) = 1.097	Strategy I is cheaper and more effective than strategy G and hence, the analysis continues by comparing strategy I and strategy F
ICER⁡(I) = (5.02 × 10⁶/4.83 × 10⁶) = 1,04	—
ICER⁡(F, I) = (5.96 × 10⁶ − 5.02 × 10⁶/5.84 × 10⁶ − 4.83 × 10⁶) = 0.93	This comparison indicates that strategy F is cheaper than strategy I, and the analysis continues by comparing strategy F and strategy H
ICER⁡(F) = (5.96 × 10⁶/4.83 × 10⁶) = 1.02	—
ICER⁡(H, F) = (6.02 × 10⁶ − 5.96 × 10⁶/6.003 × 10⁶ − 4.83 × 10⁶) = 0.35	Strategy H is less costly and more effective than strategy F. As a result, strategy F is eliminated from subsequent ICER computations
ICER⁡(H) = (6.02 × 10⁶/6.003 × 10⁶) = 1,002	—
ICE⁡R(J, H) = (6.27 × 10⁶ − 6.02 × 10⁶/6.086 × 10⁶ − 4.83 × 10⁶) = 3.07	Strategy H is less costly and more effective than strategy J

5.3. ICER for the Triple Control Strategy

Using these simulation results, we rank the control strategies in increasing order of effectiveness based on infection averted. This ranking procedure shows that Strategy K averted the least number of infections, followed by Strategies M, L, and N (see Table 6). Based on this rank, we first compare the ICER of Strategy K and Strategy M as follows:

()

Table 6. The number of MDR-TB infections averted and the total cost of each triple control strategy.

Strategy	Total infection averted	Total cost ($)
K(u₁, u₂, u₄)	4.89 × 10⁷	5.19 × 10⁶
M(u₁, u₃, u₄)	6.09 × 10⁷	6.37 × 10⁶
L(u₁, u₂, u₃)	6.098 × 10⁷	6.22 × 10⁶
N(u₂, u₃, u₄)	6.14 × 10⁶	6.34 × 10⁶

This implies that Strategy K is more costly and less effective than Strategy M. Thus, we exclude Strategy K from further consideration and continue to compare strategies M and L.

()

This comparison indicates that Strategy L is cheaper than Strategy M. Therefore, Strategy M is rejected and the analysis continues by comparing Strategy L with Strategy N.

()

This indicates that Strategy L is cheaper and more effective than Strategy N.

Finally, the comparison result reveals that Strategy L is cheaper and more effective than Strategy N. Therefore, Strategy L (combination of vaccination, distancing, and successful treatment of DS-TB) is the best of all triple control strategies.

6. Conclusions

In this study, we presented a compartmental model to understand the transmission dynamics of MDR-TB in Ethiopia. We first established that model (1) is well posed epidemiologically and mathematically. Then, we have described the conditions for the stability of the equilibrium points.

We applied preventive controls in the form of vaccination, distancing, and two treatment controls for DS-TB and MDR-TB. Theoretically, we proved the existence of optimal control and studied the characterization of optimal control by Pontryagin’s maximum principle. In addition, the incremental cost-effectiveness ratio of single, coupled, and triple combinations of control strategies was investigated to determine the most effective method to control the spread of MDR-TB in Ethiopia.

Among the four single controls, it is found that the successful treatment of DS-TB is the most effective strategy in curtailing the spread of MDR-TB. Therefore, the Ethiopian government should improve DS-TB therapy by reducing treatment failures in DS-TB patients if only one control strategy is used.

Within the six dual control strategies, a combination of distancing and successful treatment of DS-TB is the most cost-effective strategy compared to others. Therefore, if dual control strategies are considered, we recommend the Ethiopian government focus on isolation policy, educational campaigns, and monitoring DS-TB patients to complete their treatment correctly. Considering the combination of the triple control strategy, the combination of successful treatment of DS-TB with distancing and vaccination control is the most cost-effective strategy.

This study is unique from other studies because the model was fitted to Ethiopian data and suggested effective methods to eradicate MDR-TB from the country. On the other hand, the study will yield better results if we include more control strategies. For example, directly observed therapy (DOT) is a strategy that helps DS-TB patients complete their treatment effectively. Therefore, our future research will focus on incorporating this strategy.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

The data used to support the study′s findings are included in the article.

References

All articles

Cost-Effectiveness Analysis of the Optimal Control Strategies for Multidrug-Resistant Tuberculosis Transmission in Ethiopia

Abstract

1. Introduction

2. Model Formulation and Analysis

2.1. MDR-TB Model

2.2. Model Analysis

2.2.1. Positivity of the Solution Set

2.2.2. Invariant Region

2.2.3. The Basic Reproduction Number

2.2.4. Stability Analysis of the Disease-Free Equilibrium Point

2.2.5. Existence of the Endemic Equilibrium Point (EEP)

2.2.6. Analysis of the MDR-TB-Only Model

3. Extension of the Model to Optimal Control

3.1. Existence of an Optimal Control

4. Numerical Simulations

4.1. Use of Single Control

4.2. Use of Dual Controls

4.3. Use of Triple Controls

5. Cost-Effectiveness Analysis

5.1. ICER for Single Control Strategy

5.2. ICER for the Dual Control Strategy

5.3. ICER for the Triple Control Strategy

6. Conclusions

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Cost-Effectiveness Analysis of the Optimal Control Strategies for Multidrug-Resistant Tuberculosis Transmission in Ethiopia

Abstract

1. Introduction

2. Model Formulation and Analysis

2.1. MDR-TB Model

2.2. Model Analysis

2.2.1. Positivity of the Solution Set

2.2.2. Invariant Region

2.2.3. The Basic Reproduction Number

2.2.4. Stability Analysis of the Disease-Free Equilibrium Point

2.2.5. Existence of the Endemic Equilibrium Point (EEP)

2.2.6. Analysis of the MDR-TB-Only Model

3. Extension of the Model to Optimal Control

3.1. Existence of an Optimal Control

4. Numerical Simulations

4.1. Use of Single Control

4.2. Use of Dual Controls

4.3. Use of Triple Controls

5. Cost-Effectiveness Analysis

5.1. ICER for Single Control Strategy

5.2. ICER for the Dual Control Strategy

5.3. ICER for the Triple Control Strategy

6. Conclusions

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Related

Information