This paper presents a method to identify the damages in frame structures with slender beams. This method adjusts the parameters of the structure to match the analytical and the measured displacements. The effect of transverse shear deformation on the nodal analytical displacement is analyzed, and the parameter identification of frame structures with slender beams is performed. The results demonstrate that parameter-identification accuracy can be considerably improved by considering the transverse shear deformation in the frame structure with slender beams. The proposed method can accurately identify the damages in frame structures with slender beams using displacement measurements.

1. Introduction

Frame structures are widely used in civil engineering applications, such as constructions and industrial buildings. However, they are susceptible to damage due to aging, load, and environmental influences, such as corrosion [1–3]. One or more components of the frame structure may be damaged, resulting in changes in the physical properties of the structure, mainly at the damaged location. The “as-is” conditions of these structures are different from the original design. To assess the “as-is” condition of the structure and conduct the safety evaluation, it is necessary to identify parameters of the structure model [4–6]. Although many identification methods are effective in analog measurement, some of them are prone to error, such as modeling error, when used in real situations. Even the slightest error affects the parameter identification of the structure model.

Parameter identification is achieved by adjusting the parameters of the structure to match the analytical and the measured data [7]. The methods of parameter identification can be categorized as static and dynamic parameter-identification methods [8–14]. Sanayei and Onipede [15] proposed a method to identify the structural parameters of the truss and frame structural elements using applied static forces and measured displacements. Banan et al. [16] studied the method of identifying the structural parameters using static displacements. Ghrib et al. [17] presented a method for damage identification of Euler–Bernoulli beams using static-deflection measurements. Bonessio et al. [18] presented a multimode approach for multidirectional damage identification in frame structures; the method reduces damage identification errors by analyzing the multidirectional effects of damages. Vaez and Fallah [19] identified the site and extent of multiple damage cases of frame structure using a two-stage damage-identification approach. Zhang and Johnsonb [20] proposed a novel substructure-identification method to identify the damage of multistory multibay plane frame structures and revealed how structural responses affect the identification accuracy using identification-error analysis. In these studies, various aspects of parameter identification of frame structures, including the optimal placement of sensors, improvements in measurement technique, and error analysis, have been studied.

The classical Euler–Bernoulli beam theory is usually used to analyze the behavior of structural elements because it can properly simulate the behavior of slender beams [21–24]. For slender beams, various studies have suggested that using Timoshenko beam theory can improve the accuracy of structural analysis. Dixit [25] used the natural frequency and mode shape generated by the analysis frame to compare the effects of Euler–Bernoulli beam theory and the beam theory considering shear deformation on structural parameters. Even though the Euler–Bernoulli beam theory is basically accurate in estimating the frequency of slender beam, the results obtained by Timoshenko beam theory have almost no errors. Silva et al. [26] considered the shear deformation and performed an inelastic second-order analysis on steel Vogel portal frames with slender beams. According to the results of this study, compared with the analysis of the Euler–Bernoulli beam theory, the numerical results of the frame considering the shear deformation have larger displacements and provide better structural response. Su and Ma [27] used ray and normal mode methods to study the dynamic transient responses of a simply supported Timoshenko beam subjected to an impact force. Although the error in the resonant frequency obtained by the Euler–Bernoulli beam theory has been reduced, all the resonant frequencies obtained from the Timoshenko beam theory are very consistent with those of the ABAQUS 3-D model. The study suggests that Timoshenko beam theory is suitable for evaluating the resonant frequency of a slender simply supported beam. Assuming that the measured data is accurate, the difference between measured and analytical data can be used to effectively identify the damage of the structure. Therefore, errors in analytical model may affect the accuracy of damage identification [28, 29]. However, a limited number of studies discuss the influence of transverse shear deformation on the parameter identification of frame structures with slender beams.

In this study, steel-frame structures with slender beams were identified based on the static parameter-identification method, and to include the shear effect, Timoshenko beam theory is considered and compared with the Euler–Bernoulli beam theory. The effect of shear deformation on the nodal analytical displacement of wide flange cross-section and rectangular cross-section frames is analyzed. Damage considered in the present study is mainly due to corrosion and would result in reduced cross-sectional areas. The damage identification is performed by minimizing the measured and analytical displacements, and the optimization method used is the interior-point method. Furthermore, the influence of transverse shear deformation on the parameter-identification accuracy of the frames with different cross-sectional slender beams is discussed.

2. Formulation for Parameter Identification

In this parameter-identification method, the objective function is defined in terms of the difference between the analytical and measured displacements. The analytical displacements can be obtained using the stiffness method [30, 31]. The damage conditions of the members of the structure can be determined on the basis of the applied static forces and the measurements of the nodal displacements of the structure.

The stiffness method is based on the force–displacement relationship of the structure, as expressed in equation (1).

()

where Q represents the global forces, D represents the global displacements, and K is the entire-structure stiffness matrix that can be obtained by assembling the member global stiffness matrices k.

()

where k^′ is the member stiffness matrix of the structure and T is referred to as the displacement transformation matrix. Equation (1) can be separated according to known and unknown displacements.

()

where Q_k represents the known external loads, D_k is the known displacements, Q_a represents the analytical loads, and D_a represents the analytical displacements. By solving equation (3), we obtain

()

The sum of the squares of the differences between the analytical displacement

and the measured displacement

at the i^th measurement point is defined as the objective function, f, and is given as

()

where n is the total number of measured displacements. In this study, finite element models were built to simulate the measured displacements,

based on the “as-is” condition. For a damaged structure, a certain parameter p is different from that in “as-built” condition. This unknown parameter p can be set as a variable and can be obtained by minimizing the objective function f, assuming that the optimal value of p is p^∗, which can be calculated by equation (6).

()

3. Member Stiffness Matrix of Frame Structure

For the member stiffness matrix k^′ in equation (2), it is necessary to consider if shear deformation is included. The transverse shear deformation of the frame structure affects its nodal displacements [32]. Both the Euler–Bernoulli and Timoshenko beam theories are methods of structural analysis; however, they differ in their assumptions [33]. The Euler–Bernoulli theory assumes that the cross-section is perpendicular to the bending line. The Timoshenko beam theory allows rotation between the cross-section and the bending line. This rotation is caused by a transverse shear deformation, which is not considered in the Bernoulli beam theory. The plane frame’s member stiffness with the consideration of the transverse shear deformation [33] is shown in equation (7).

()

where E is the modulus of elasticity and L is the length of the member. The cross-sectional area A and its moment of inertia I can be determined on the basis of the geometric shape. The parameters m_x are defined, using the nondimensional shear correction term α, as follows:

()

The nondimensional shear correction term [33] α that can be defined using the shear correction factor of the cross-sectional shapes is shown in equation (9).

()

where G is shear modulus. The shear area A_s is defined using Specification for Structural Steel Buildings [33, 34]. On setting α equal to zero in equation (9), equation (7) becomes the member stiffness matrix based on the Euler–Bernoulli beam theory.

Changes in the atmospheric environment lead to structural corrosion, causing a reduction in the thickness of components [35]. The subject of this study is the wide flange cross-section and rectangular cross-section. In this study, the frame structure’s “as-is” condition is different from its “as-built” condition owing to the corrosion. Assuming that the depth of corrosion is d, which is unknown and needs to be determined, it represents parameter p in equation (6).

The cross-sectional size of the wide flange is defined by the upper and lower flange width b, the height of section h, upper and lower flange thickness t₁, and web thickness t₂. Therefore, for the “as-is” condition, the shear area is expressed as follows:

()

The rectangular cross-section size is defined by the height of section h and width of section b; the shear area is expressed as follows:

()

4. Effect of Shear Deformation on Nodal Displacement

Considering the shear deformation can improve the accuracy of the analytical displacement D_a of equation (4). A large error in the analytical displacement causes the objective function of equation (5) to fail to converge during the optimization. To study the effect of shear deformation on the nodal displacements of steel-frame structures, frame structures with different cross-sectional dimensions were studied by considering shear deformation. The results were compared with the nodal displacements of the structure neglecting the shear deformation.

A one-story, one-bay steel-frame structure (Figure 1) with slender beams (depth-to-span ratio < 1/15) was analyzed. The frame members are wide flange cross-sections, and all members have the same cross-section. Three different dimensions are studied, and the dimensions are presented in Table 1. The modulus of elasticity is 206 GPa, and the shear modulus of the material is 79.23077 GPa. Forces of 10 kN and -10 kN were applied along degrees of freedom 4 and 5, respectively, to excite the frame structure, and displacements were determined along degrees of freedom 1–9.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Three-member frame sample.

Table 1. The wide flange cross-sectional dimensions.

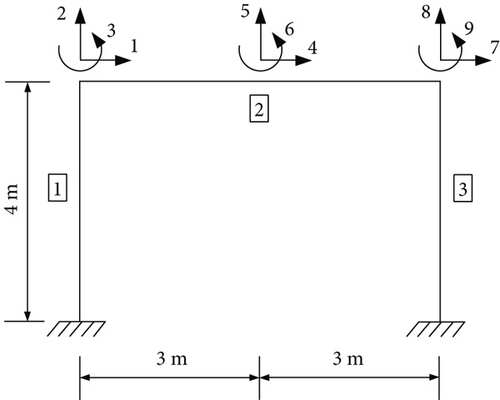
Shape	h (mm)	b (mm)	t₁ (mm)	t₂ (mm)
A	150	100	5	4
B	200	100	5	4
C	250	100	5	4

Therefore, the sensitivity of the wide flange cross-section to the shear deformation can be analyzed by comparing the nodal displacement errors caused by shear deformation.

First, nodal displacements based on the Euler–Bernoulli beam theory were obtained. The member stiffness matrixk^′based on the Euler–Bernoulli beam theory was obtained from equation (7) on settingαin equation (9) as 0. The nodal displacement can also be obtained by equation (4). Subsequently, nodal displacements were recalculated based on the Timoshenko beam theory. The member stiffness matrix k^′ of the frame member is obtained from equation (7); the nodal displacement can also be obtained by equation (4). Finally, nodal displacements were obtained from the finite element model. The absolute value of the relative error in the nodal displacements can be calculated based on the nodal displacements calculated using the Timoshenko beam theory, the Euler–Bernoulli beam theory, and the finite element method.

Figure 2 shows the nodal displacement errors from the Euler–Bernoulli beam theory and the Timoshenko beam theory, the grey bar represents the absolute value of the relative error between the Euler–Bernoulli beam theory and finite element model’s calculation, and the blue bar represents the error between the Timoshenko beam theory and finite element model’s calculation. Figures 2(a)–2(c) correspond to the errors for shapes A, B, and C, respectively.

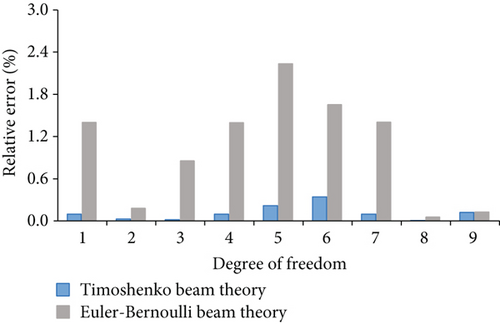
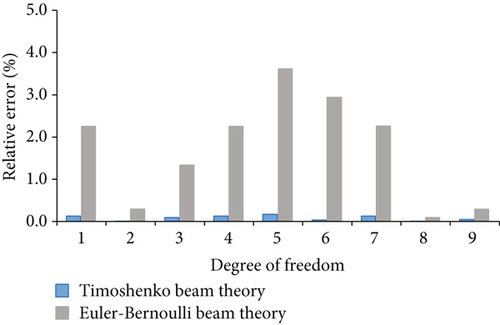
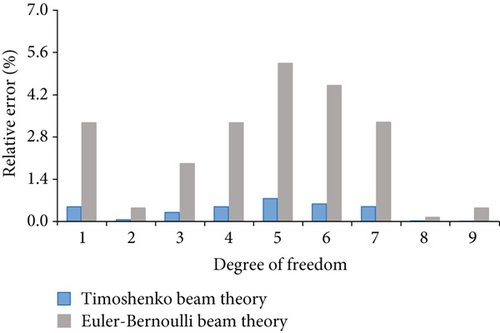
In Figure 2, the horizontal axis represents the degree of freedom, and the vertical axis represents the error. It can be seen from Figure 2 that the error of the nodal displacement for all the wide flange frames considering the shear deformation is less than 1%. The maximum errors between the nodal displacements calculated using the Euler–Bernoulli beam theory and finite element method are 2.23%, 3.62%, and 5.24% for shapes A, B, and C, respectively. According to Figure 2, the calculations of both the Euler–Bernoulli beam theory and the Timoshenko beam theory are close to the finite element model’s calculation. However, the results from the Timoshenko beam theory can provide more accurate results by considering the shear deformation.

5. Parameter Identification by considering Shear Deformation

To demonstrate the effect of the transverse shear deformation on the parameter-identification method of the frame using static displacements, the one-story frame structure with wide flange cross-section described in Figure 1 is analyzed. For the “as-built” condition, the cross-sections of all the members are assumed to be shape C (Table 1). Assuming that corrosions exist in members 1–3, the depths of corrosion for members 1–3 are 0.25, 0.5, and 0.75 mm, respectively. The “as-is” depths of corrosion of the members 1–3 need to be determined. To excite the structure, forces of 10 kN and -10 kN were applied along the degrees of freedom 4 and 5, respectively. The measured displacements are along the degrees of freedom 1, 4, 5, and 7.

First, the structural parameters were identified based on the Euler–Bernoulli beam theory. On setting α in equation (9) equal to 0, the member stiffness matrix k^′ based on the Euler–Bernoulli beam theory was obtained from equation (7); equation (5) expresses the objective function to identify the corrosion condition. In this analysis, the start point of depth of corrosion d was equal to 1 at the midpoint of the boundary condition. The constraints on d were set between 0 and 2 according to the “as-built” condition. The interior-point method [36] can converge quickly and solve complex problems with several variables. The relative error for the identified results can be calculated based on the difference between the optimal values and “as-is” values for each damaged member, and the mean relative error (MRE) can then be calculated based on the relative error for all the damaged members from the following equation:

()

where N is the number of damaged members,

is the “as-is” i^th depth of corrosion, and

is the i^th optimal value of the depth of corrosion. Figure 3 depicts the results for parameter identification based on the Euler–Bernoulli beam theory.

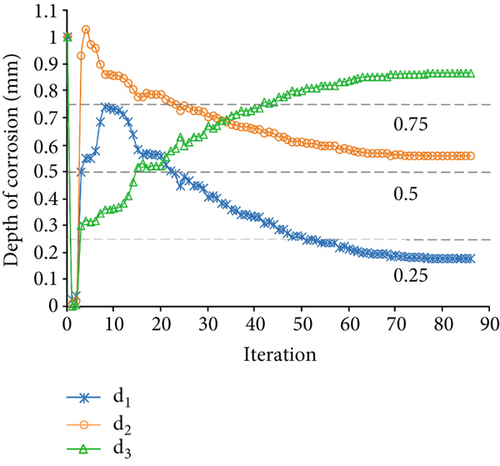
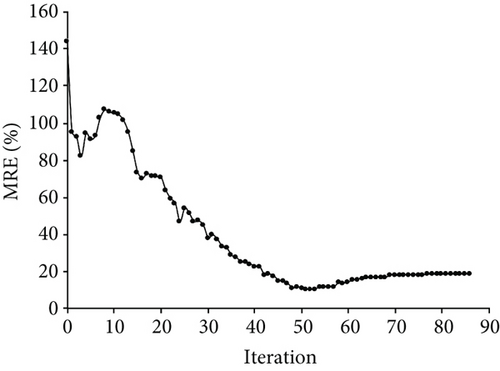
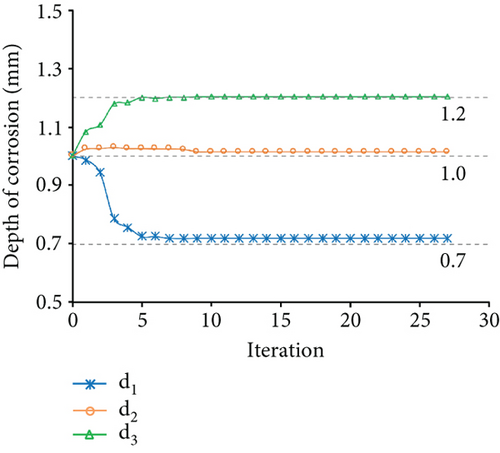
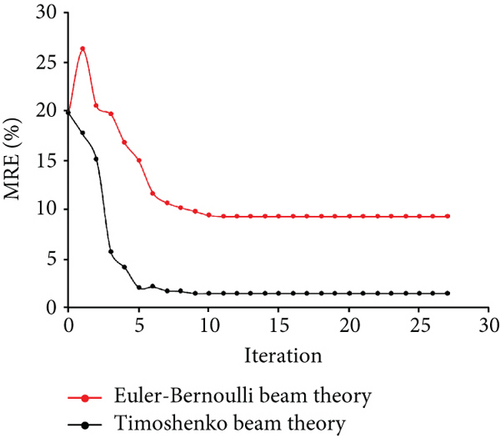
Figure 3(a) displays the changes in d₁, d₂, and d₃ during the optimization process. The dashed lines in the figure represent the “as-is” depth of correction of members 1, 2, and 3. According to Figure 3(a), the final optimal values of d₁, d₂, and d₃ were identified, and the results were found to be inconsistent with the “as-is” condition. The variation of MRE during the optimization process is shown in Figure 3(b). The error in the final optimal values based on the Euler–Bernoulli beam theory is 18.36%.

Next, the structural parameters were identified based on the Timoshenko beam theory. The member stiffness matrix k^′ of the frame member was obtained from equation (7); equation (5) expresses the objective function to identify the corrosion condition. The start point of depth of corrosion d was equal to 1. The constraints on d were set between 0 and 2 according to the “as-built” condition. The interior-point method was also used to solve the optimization problem. Figure 4(a) displays the changes in d₁, d₂, and d₃ during the optimization process. After 97 iterations, the final optimal values of d₁, d₂, and d₃ were identified, and the results were found to be consistent with the “as-is” condition. The variation of MRE during the optimization process is shown in Figure 4(b), and the final MRE value is 1.67%.

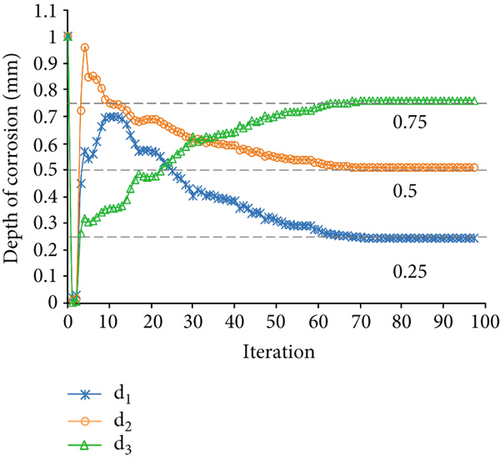
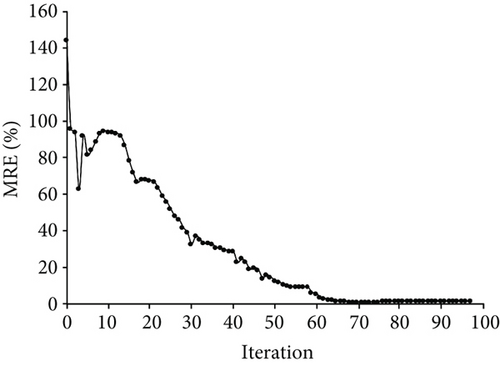
Compared to the Euler–Bernoulli beam theory-based method, the final optimal values determined by using the Timoshenko beam theory-based parameter-identification method can improve the accuracy of MRE by 16.69%.

6. Parameter Identification for Frame Structures with Different Wide Flange Cross-Section

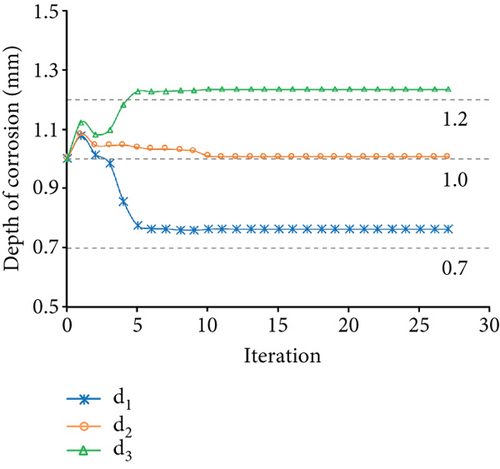
The effect of shear deformation on the accuracy of parameter identification has been presented in Section 5. A two-story, one-bay steel-frame structure with slender beams is shown in Figure 5. This structure is used to demonstrate the effect of the transverse shear deformation on the frame-structure parameter identification with different wide flange cross-sections. All the members have the same cross-section. The frame “as-built” condition has three different cases. In cases 1, 2, and 3, the cross-sections of the members are shapes A, B, and C, respectively. The cross-sectional dimensions of shapes A, B, and C are listed in Table 1. Assuming that corrosions exist in members 1, 2, and 4, the depths of corrosion for members 1, 2, and 4 are 0.7, 1, and 1.2 mm, respectively. The “as-is” depths of corrosion for members 1, 2, and 4 are unknown and need to be determined. In this study, forces of 2 kN and -2 kN were applied along degrees of freedom 4 and 11, respectively, to excite the structure.

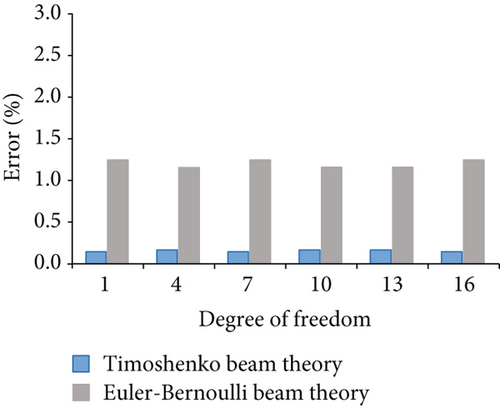
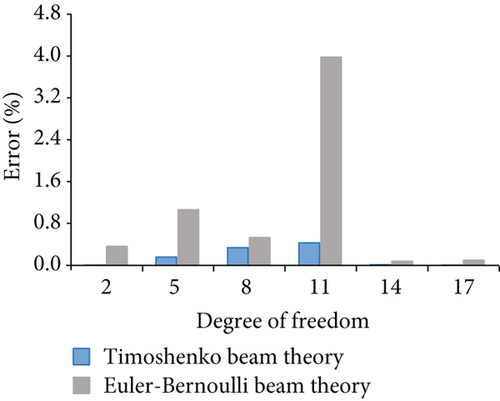
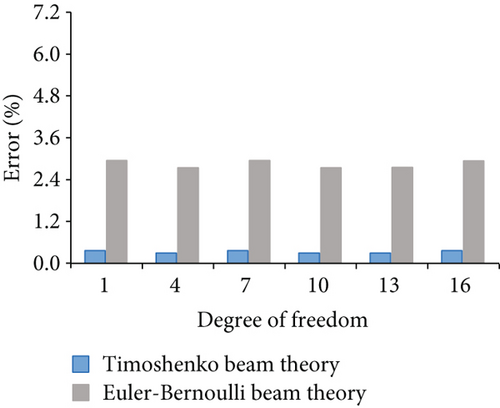
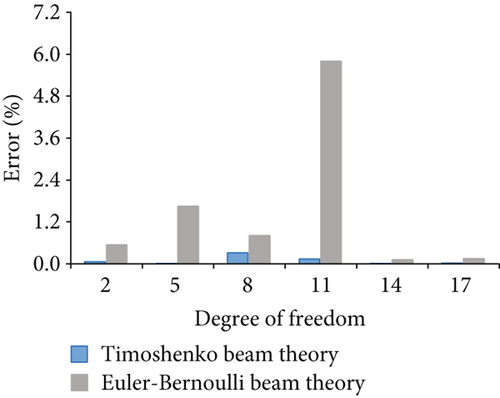
Figure 6 shows the nodal displacement errors for case 1 from the Euler–Bernoulli beam theory and the Timoshenko beam theory. Figure 6(a) shows the errors corresponding to horizontal degrees of freedom 1, 4, 7, 10, 13, and 16. Figure 6(b) shows the errors corresponding to vertical degrees of freedom 2, 5, 8, 11, 14, and 17. The maximum error from the Timoshenko beam theory is 0.77% and from the Euler–Bernoulli beam theory is 2.41%. Figure 7 shows the errors for case 2, and the maximum error from Timoshenko beam theory is 0.43% and from the Euler–Bernoulli beam theory is 3.98%. Figure 8 shows the errors for case 3, and the maximum errors from the Timoshenko beam theory and the Euler–Bernoulli beam theory are 0.36% and 5.80% for the horizontal and vertical degree of freedom, respectively. According to Figures 6–8, the nodal displacements calculated using the Timoshenko beam theory are closer to the finite element model’s calculation, and all the errors are less than 1%.

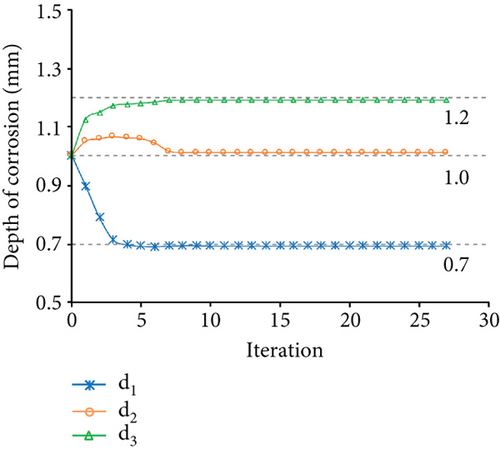
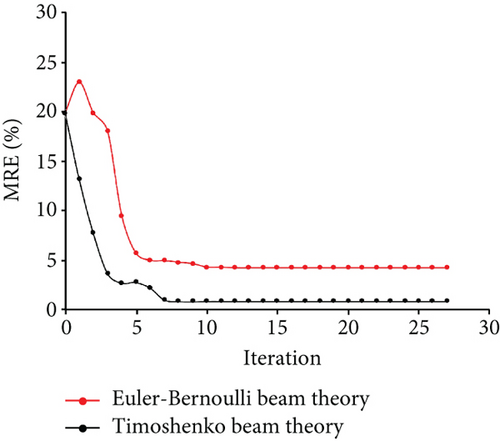
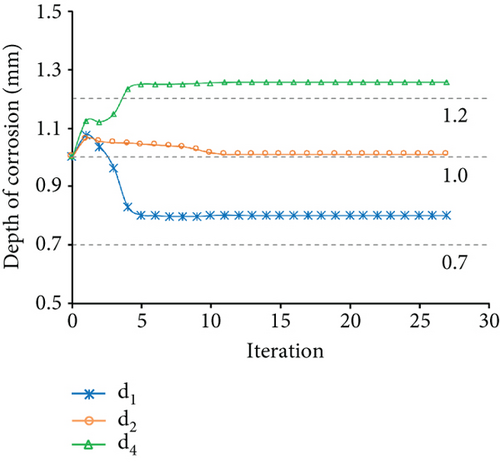
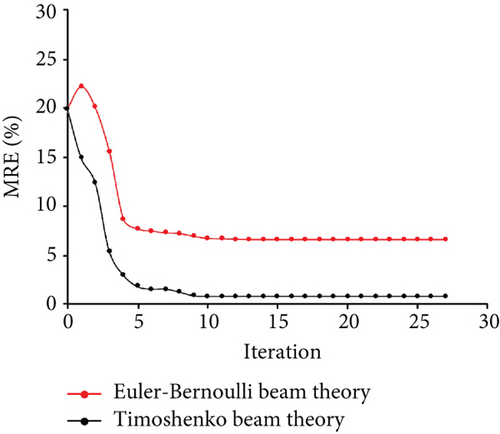
The measured displacements are along degrees of freedom 1, 4, 7, 10, 11, 13, and 16. Figure 9 shows the identification results of case 1. Figures 9(a) and 9(b) show the optimization results of the parameter identification for the frame structure, based on the Euler–Bernoulli beam theory and the Timoshenko beam theory, respectively. Figure 9(a) reflects the variations of d₁, d₂, and d₄ with the number of iterations, based on the interior-point method, and the final optimal value of d was found to be inconsistent with the “as-is” values. Figure 9(b) shows that the final optimal value of d was consistent with the “as-is” values. The variation of MRE during the optimization process is shown in Figure 9(c) based on the Euler–Bernoulli beam theory and the Timoshenko beam theory. Figures 10 and 11 show the identification results of case 2 and case 3, respectively. Based on Figures 9–11, the final MRE values for shapes A, B, and C corresponding to different beam theories are listed in Table 2.

Table 2. The final MRE values.

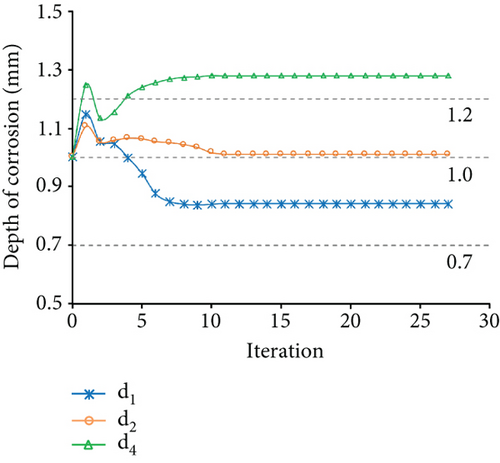
Method	Shape A	Shape B	Shape C
Euler–Bernoulli	4.21%	6.54%	9.30%
Timoshenko	0.88%	0.81%	1.51%

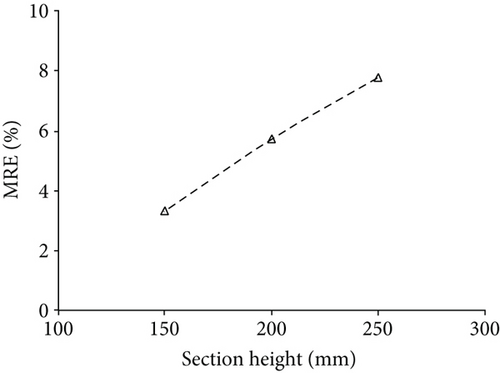
Figure 12 shows the accuracy improvement in the final optimal values with different shapes; the vertical axis represents the improvement in MRE by using the Timoshenko beam theory, and the horizontal axis represents the variation in the height of section. Compared to the parameter-identification method based on the Euler–Bernoulli beam theory, the parameter-identification method using the Timoshenko beam theory can improve the accuracy of MRE by 3.33%, 5.73%, and 7.79% for cases 1, 2, and 3, respectively. Thus, it can be observed from the identification results that the parameter-identification method based on Timoshenko beam theory can improve the identification accuracy significantly.

7. Parameter Identification for Frame Structures with Different Rectangular Cross-Section

Figure 13 shows a three-story, two-bay frame structure with slender beams. This structure was used to analyze the effect of transverse shear deformation on the frame-structure parameter identification with different rectangular cross-section. Table 3 shows the rectangular cross-sectional dimensions. There are three different cases corresponding to the frame “as-built” condition. In cases 4, 5, and 6, all the members’ cross-sections are shapes D, E, and F, respectively. Assuming the corrosion exists in members 1 and 9 of the frame. The depths of corrosion for members 1 and 9 are 0.8 and 1.5 mm, respectively. The “as-is” depths of corrosion for members 1 and 9 are unknown and need to be identified. In this analysis, force of 2.5 kN is applied along degrees of freedom 1, 4, and 7, respectively, to excite the structure.

Table 3. The rectangular cross-sectional dimensions.

Shape	h (mm)	b (mm)
D	30	15
E	35	15
F	40	15

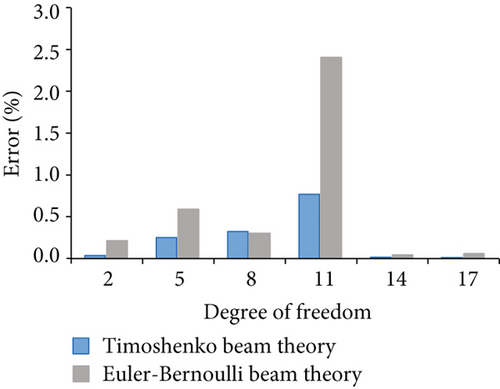
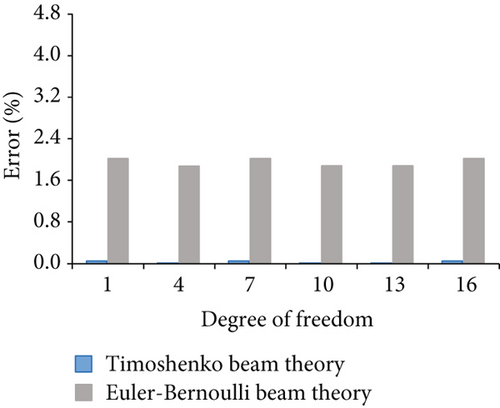
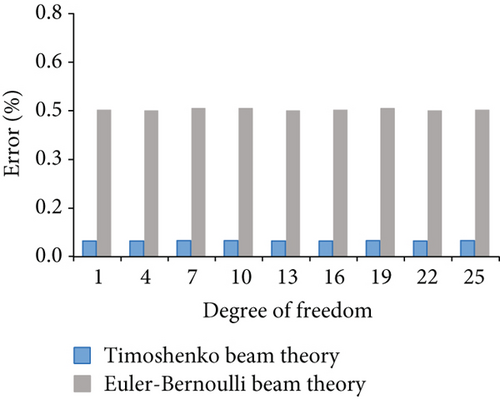
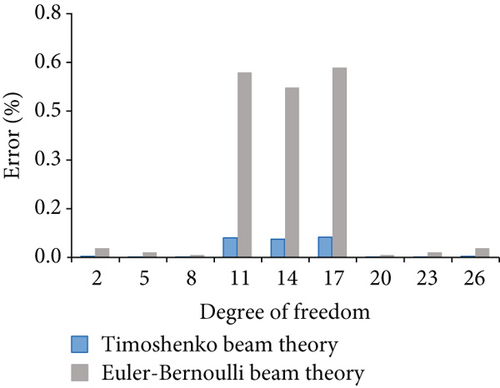
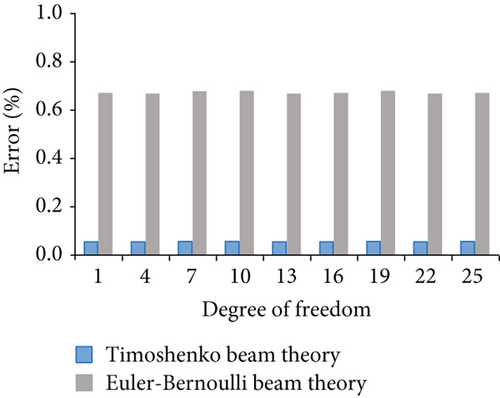
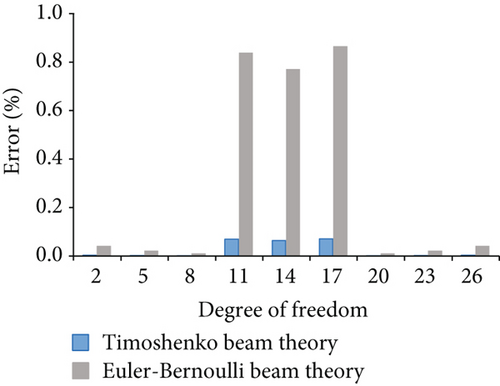
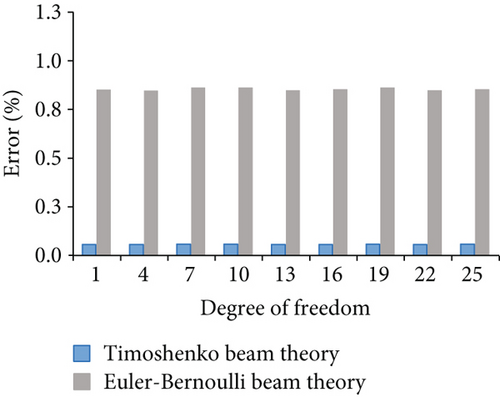
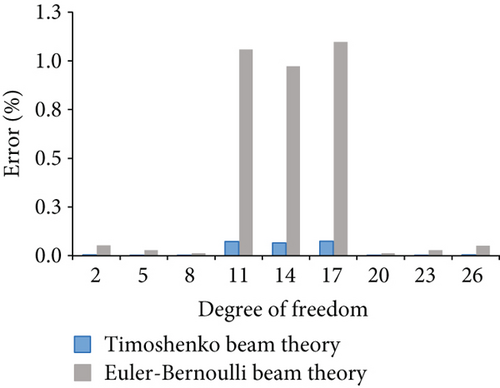
Figure 14 displays the nodal displacement errors for case 4. Figure 14(a) shows the errors corresponding to horizontal degrees of freedom 1, 4, 7, 10, 13, 16, 19, 22, and 25. Figure 14(b) shows the errors corresponding to vertical degree of freedom 2, 5, 8, 11, 14, 17, 20, 23, and 26. Although the calculations of the Euler–Bernoulli beam and Timoshenko beam theory are close to those of the finite element model, the nodal displacement of the frame considered shear deformation is less error. Figures 15 and 16 show the errors for case 5 and case 6, respectively.

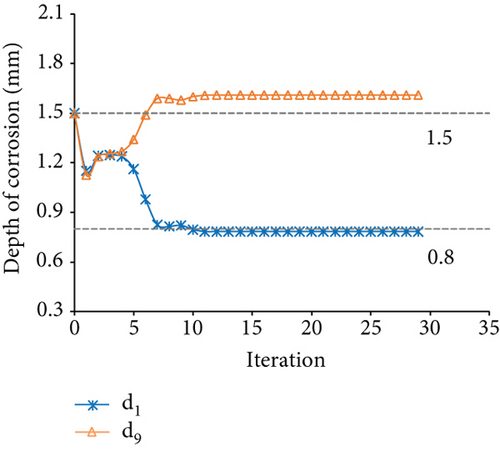
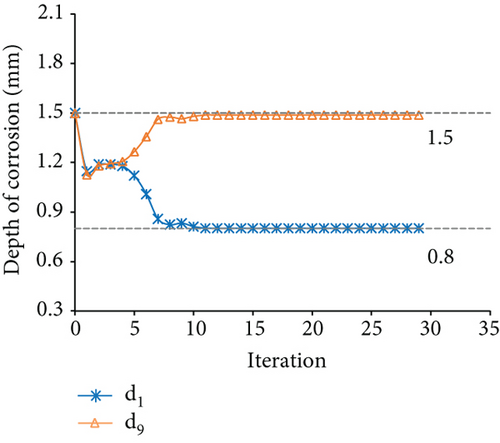
The measured displacements are along degrees of freedom 1, 4, 7, 10, 13, 16, 19, 22, and 25. Figure 17 displays the results of the identification for case 4. Figures 17(a) and 17(b) show the optimization results of the parameter identification for the frame structure, based on the Euler–Bernoulli beam theory and the Timoshenko beam theory, respectively. Figure 17(a) reflects the variations of d₁ and d₉ with the number of iterations, based on the interior-point method. The final optimal value of d was identified and was inconsistent with the “as-is” values. Figure 17(b) demonstrates that the final optimal value of d was identified, which was consistent with the “as-is” values. The variation of MRE during the optimization process is shown in Figure 17(c), based on the Euler–Bernoulli beam theory and the Timoshenko beam theory. Figures 18 and 19 show the identification results for case 5 and case 6, respectively. Table 4 shows the final MRE values for shapes D, E, and F using different beam theories.

Table 4. The final MRE values.

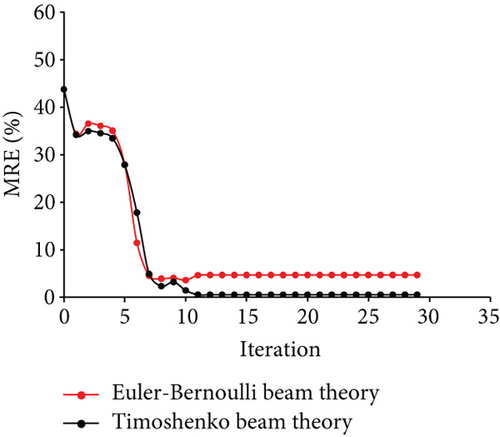
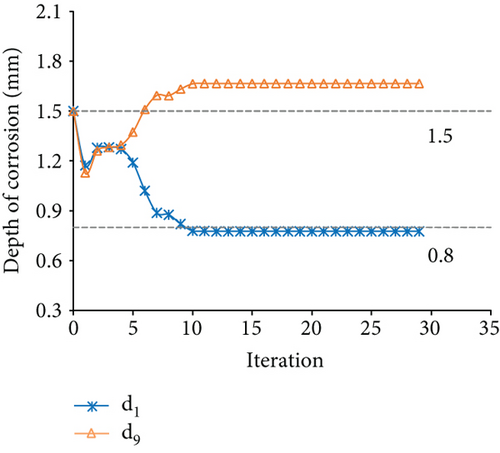
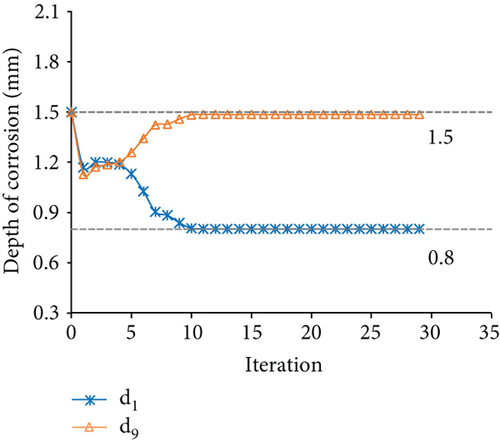
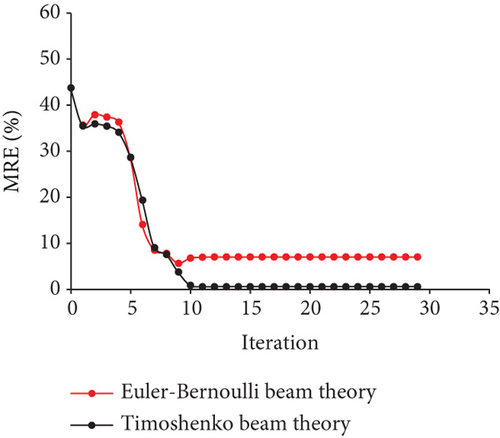
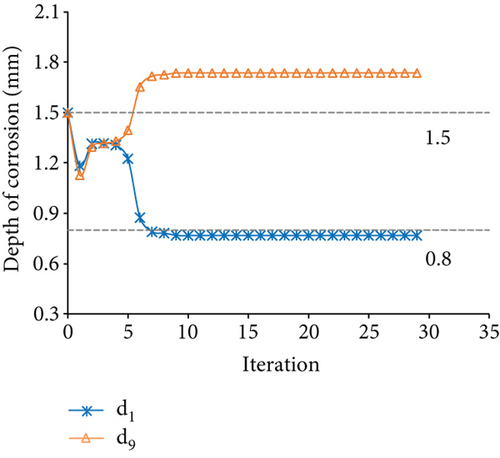
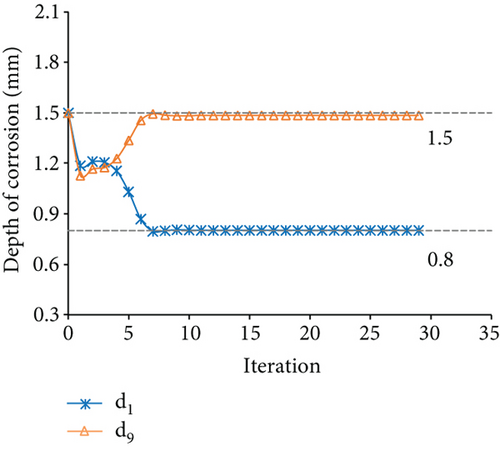
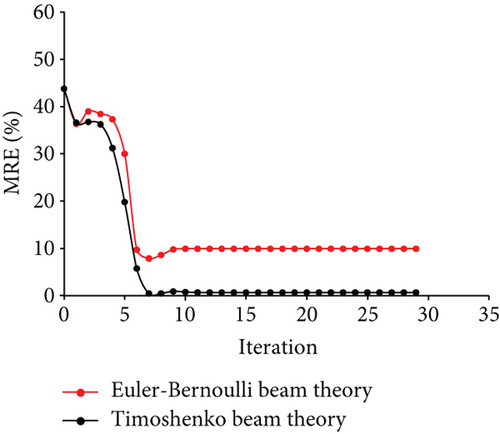
Method	Shape D	Shape E	Shape F
Euler–Bernoulli	4.66%	7.04%	9.92%
Timoshenko	0.50%	0.58%	0.68%

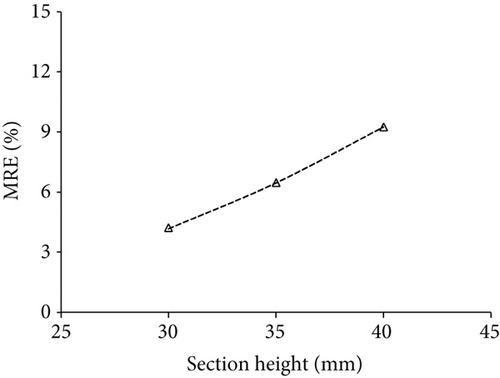
Figure 20 displays the accuracy improvement in the final optimal values for different rectangular cross-sections. Compared to the parameter-identification method based on the Euler–Bernoulli beam theory, the parameter-identification method using the Timoshenko beam theory can improve the accuracy of MRE by 4.16%, 6.46%, and 9.24% for cases 4, 5, and 6, respectively. It can be inferred from the results that using the Timoshenko beam theory to identify damage can substantially enhance the performance of damage identification methods for frames with rectangular cross-section.

8. Conclusions

In this study, the effect of shear deformation on the nodal displacement and parameter identification of steel-frame structures with slender beams was analyzed. This study presents a novel method to identify damaged frames with slender beams by considering shear deformation. To reduce the frame-structure analytical errors in the optimization processes, the parameter-identification method was modified to include the transverse shear deformation. It was shown that for different cross-sectional steel frames with slender beams, the errors of the nodal displacements obtained by the two beam theories and finite element method are relatively small. In this case, the theories are generally accepted as equivalent. However, this paper demonstrated that although errors from these theories are not obvious when calculating nodal displacements, the errors in parameter identification are very significant. Considering the transverse shear deformation can effectively improve the accuracy of parameter identification, and the results are consistent with the structure “as-is” condition.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This research was funded by the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20200492).

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Zapico-Valle J. L., García-Diéguez M., and Alonso-Camblor R., Nonlinear modal identification of a steel frame, Engineering Structures. (2013) 56, 246–259, https://doi.org/10.1016/j.engstruct.2013.04.026, 2-s2.0-84878921035.
10.1016/j.engstruct.2013.04.026
Web of Science® Google Scholar
2 Nick H., Aziminejad A., Hosseini M. H., and Laknejadi K., Damage identification in steel girder bridges using modal strain energy-based damage index method and artificial neural network, Engineering Failure Analysis. (2021) 119, article 105010, https://doi.org/10.1016/j.engfailanal.2020.105010.
10.1016/j.engfailanal.2020.105010
Web of Science® Google Scholar
3 Wu J. R. and Li Q. S., Structural parameter identification and damage detection for a steel structure using a two-stage finite element model updating method, Journal of Constructional Steel Research. (2006) 62, no. 3, 231–239, https://doi.org/10.1016/j.jcsr.2005.07.003, 2-s2.0-29144521558.
10.1016/j.jcsr.2005.07.003
Web of Science® Google Scholar
4 Barontini A., Masciotta M. G., Amado-Mendes P., Ramos L., and Lourenco P., Negative selection algorithm based methodology for online structural health monitoring, Engineering Structures. (2021) 229, article 111662, https://doi.org/10.1016/j.engstruct.2020.111662.
10.1016/j.engstruct.2020.111662
Web of Science® Google Scholar
5 Baisthakur S. and Chakraborty A., Modified Hamiltonian Monte Carlo-based Bayesian finite element model updating of steel truss bridge, Structural Control and Health Monitoring. (2020) 27, no. 8, https://doi.org/10.1002/stc.2556.
10.1002/stc.2556
Web of Science® Google Scholar
6 Janeliukstis R., Rucevskis S., and Chate A., Condition monitoring with defect localisation in a two-dimensional structure based on linear discriminant and nearest neighbour classification of strain features, Nondestructive Testing and Evaluation. (2020) 35, no. 1, 48–72, https://doi.org/10.1080/10589759.2019.1635594, 2-s2.0-85068719713.
10.1080/10589759.2019.1635594
Web of Science® Google Scholar
7 Schommera S., Nguyena V. H., Maasa S., and Zürbes A., Model updating for structural health monitoring using static and dynamic measurements, Procedia Engineering. (2017) 199, 2146–2153, https://doi.org/10.1016/j.proeng.2017.09.156, 2-s2.0-85029907515.
10.1016/j.proeng.2017.09.156
Google Scholar
8 Sanayei M. and Saletnik M. J., Parameter estimation of structures from static strain measurements I: formulation, Journal of Structural Engineering. (1996) 122, no. 5, 555–562, https://doi.org/10.1061/(ASCE)0733-9445(1996)122:5(555), 2-s2.0-0030151308.
10.1061/(ASCE)0733-9445(1996)122:5(555)
Web of Science® Google Scholar
9 Xiao F., Hulsey J. L., Chen G. S., and Xiang Y., Optimal static strain sensor placement for truss bridges, International Journal of Distributed Sensor Networks. (2017) 13, no. 5, https://doi.org/10.1177/1550147717707929, 2-s2.0-85019966198.
10.1177/1550147717707929
PubMed Web of Science® Google Scholar
10 Xiao F., Fan J., Chen G. S., and Hulsey J. L., Bridge health monitoring and damage identification of truss bridge using strain measurements, Advances in Mechanical Engineering. (2019) 11, no. 3, https://doi.org/10.1177/1687814019832216, 2-s2.0-85062970085.
10.1177/1687814019832216
Web of Science® Google Scholar
11 Xiao F., Chen G. S., Hulsey J. L., Dolan J. D., and Dong Y., Ambient loading and modal parameters for the Chulitna River Bridge, Advances in Structural Engineering. (2016) 19, no. 4, 660–670, https://doi.org/10.1177/1369433216630045, 2-s2.0-84963838273.
10.1177/1369433216630045
Web of Science® Google Scholar
12 Casas J. R. and Aparicio A. C., Structural damage identification from dynamic-test data, Journal of Structural Engineering. (1994) 120, no. 8, 2437–2450, https://doi.org/10.1061/(ASCE)0733-9445(1994)120:8(2437), 2-s2.0-0028480643.
10.1061/(ASCE)0733-9445(1994)120:8(2437)
Web of Science® Google Scholar
13 Bu H., Wang D., Zhou P., and Zhu H., An improved wavelet-Galerkin method for dynamic response reconstruction and parameter identification of shear-type frames, Journal of Sound and Vibration. (2018) 419, 140–157, https://doi.org/10.1016/j.jsv.2017.12.013, 2-s2.0-85041547817.
10.1016/j.jsv.2017.12.013
Web of Science® Google Scholar
14 Zembaty Z., Kowalski M., and Pospisil S., Dynamic identification of a reinforced concrete frame in progressive states of damage, Engineering Structures. (2006) 28, no. 5, 668–681, https://doi.org/10.1016/j.engstruct.2005.09.025, 2-s2.0-30844441374.
10.1016/j.engstruct.2005.09.025
Web of Science® Google Scholar
15 Sanayei M. and Onipede O., Damage assessment of structures using static test data, AIAA Journal. (1991) 29, no. 7, 1174–1179, https://doi.org/10.2514/3.10720, 2-s2.0-0026189874.
10.2514/3.10720
Web of Science® Google Scholar
16 Banan M. R., Banan M. R., and Hjelmstad K. D., Parameter estimation of structures from static response. II: numerical simulation studies, Journal of Structural Engineering. (1994) 120, no. 11, 3259–3283, https://doi.org/10.1061/(ASCE)0733-9445(1994)120:11(3259), 2-s2.0-0028547577.
10.1061/(ASCE)0733-9445(1994)120:11(3259)
Web of Science® Google Scholar
17 Ghrib F., Eng P., Li L., and Wilbur P., Damage identification of Euler–Bernoulli beams using static responses, Journal of Engineering Mechanics. (2012) 138, no. 5, 405–415, https://doi.org/10.1061/(ASCE)EM.1943-7889.0000345, 2-s2.0-84860877542.
10.1061/(ASCE)EM.1943-7889.0000345
Web of Science® Google Scholar
18 Bonessio N., Benzoni G., and Lomiento G., A multi-mode approach for multi-directional damage detection in frame structures, Engineering Structures. (2017) 147, 505–516, https://doi.org/10.1016/j.engstruct.2017.05.060, 2-s2.0-85020804638.
10.1016/j.engstruct.2017.05.060
Web of Science® Google Scholar
19 Vaez S. R. H. and Fallah N., Damage identification of a 2D frame structure using two-stage approach, Journal of Mechanical Science and Technology. (2018) 32, no. 3, 1125–1133, https://doi.org/10.1007/s12206-018-0215-8, 2-s2.0-85045616006.
10.1007/s12206-018-0215-8
Web of Science® Google Scholar
20 Zhang D. and Johnsonb E. A., Substructure identification for plane frame building structures, Engineering Structures. (2014) 60, 276–286, https://doi.org/10.1016/j.engstruct.2013.12.008, 2-s2.0-84893380602.
10.1016/j.engstruct.2013.12.008
Web of Science® Google Scholar
21 Ma Z., Chung J., Liu P., and Sohn H., Bridge displacement estimation by fusing accelerometer and strain gauge measurements, Structural Control and Health Monitoring. (2021) 28, no. 6, 1–19, https://doi.org/10.1002/stc.2733.
10.1002/stc.2733
Web of Science® Google Scholar
22 Greco A. and Pau A., Damage identification in Euler frames, Computers and Structures. (2012) 92-93, 328–336, https://doi.org/10.1016/j.compstruc.2011.10.007, 2-s2.0-84655167768.
10.1016/j.compstruc.2011.10.007
Web of Science® Google Scholar
23 Zeinali Y. and Story B. A., Framework for flexural rigidity estimation in Euler-Bernoulli beams using deformation influence lines, Infrastructures. (2017) 2, no. 4, 23–42, https://doi.org/10.3390/infrastructures2040023.
10.3390/infrastructures2040023
Google Scholar
24 Ghannadiasl A. and Mortazavi S., Assessment of bending solution of beam with arbitrary boundary conditions: an accurate comparison of various approaches, Numerical Methods in Civil Engineering. (2017) 2, no. 2, 63–76, https://doi.org/10.29252/nmce.2.2.63.
10.29252/nmce.2.2.63
Google Scholar
25 Dixit A., Single-beam analysis of damaged beams: comparison using Euler-Bernoulli and Timoshenko beam theory, Journal of Sound and Vibration. (2014) 333, no. 18, 4341–4353, https://doi.org/10.1016/j.jsv.2014.04.034, 2-s2.0-84946159735.
10.1016/j.jsv.2014.04.034
Web of Science® Google Scholar
26 Silva R. G. L. D., Lavall A. C. C., Costa R. S., and Viana H. F., Formulation for second-order inelastic analysis of steel frames including shear deformation effect, Journal of Constructional Steel Research. (2018) 151, 216–227, https://doi.org/10.1016/j.jcsr.2018.09.011, 2-s2.0-85054412779.
10.1016/j.jcsr.2018.09.011
Web of Science® Google Scholar
27 Su Y. and Ma C., Theoretical analysis of transient waves in a simply-supported Timoshenko beam by ray and normal mode methods, International Journal of Solids and Structures. (2011) 48, no. 3-4, 535–552, https://doi.org/10.1016/j.ijsolstr.2010.10.021, 2-s2.0-78650174479.
10.1016/j.ijsolstr.2010.10.021
Web of Science® Google Scholar
28 Wu Z., Huang B., Tee K. F., and Zhang W., A novel stochastic approach for static damage identification of beam structures using homotopy analysis algorithm, Sensors. (2021) 21, no. 7, 2366–2391, https://doi.org/10.3390/s21072366, 33805366.
10.3390/s21072366
PubMed Web of Science® Google Scholar
29 Han Z., Zhang S., Li B., Ma C., Liu J., Ma X., and Ju X., Study on the influence of the identification model on the accuracy of the thermal response test, Geothermics. (2018) 72, 316–322, https://doi.org/10.1016/j.geothermics.2017.11.018, 2-s2.0-85038971807.
10.1016/j.geothermics.2017.11.018
Web of Science® Google Scholar
30 McGuire W., Gallagher R. H., and Ziemian R. D., Matrix Structural Analysis, 2014, Second edition.
Google Scholar
31 Hibbeler R. C., Structural Analysis, 2009, Pearson Prentice Hall, Upper Saddle River, NJ.
Google Scholar
32 Davari S. M., Malekinejad M., and Rahgozar R., Static analysis of tall buildings based on Timoshenko beam theory, International Journal of Advanced Structural Engineering. (2019) 11, no. 4, 455–461, https://doi.org/10.1007/s40091-019-00245-7.
10.1007/s40091-019-00245-7
CAS Google Scholar
33 Logan D. L., A First Course in the Finite Element Method, 2012, Cengage Learning, First Stamford Place, California.
Google Scholar
34 American Institute of Steel Construction, Specification for Structural Steel Buildings, 2016.
Google Scholar
35 Secer M. and TurkerUzun E., Corrosion damage analysis of steel frames considering lateral torsional buckling, Procedia Engineering. (2017) 171, 1234–1241, https://doi.org/10.1016/j.proeng.2017.01.415, 2-s2.0-85014530092.
10.1016/j.proeng.2017.01.415
Google Scholar
36 Forsgren A., Gill P. E., and Wright M. H., Interior methods for nonlinear optimization, Society for Industrial and Applied Mathematics. (2002) 44, no. 4, 525–597, https://doi.org/10.1137/S0036144502414942, 2-s2.0-0036959271.
10.1137/S0036144502414942
Web of Science® Google Scholar

Citing Literature

All articles

Parameter Identification of Frame Structures by considering Shear Deformation

Abstract

1. Introduction

2. Formulation for Parameter Identification

3. Member Stiffness Matrix of Frame Structure

4. Effect of Shear Deformation on Nodal Displacement

5. Parameter Identification by considering Shear Deformation

6. Parameter Identification for Frame Structures with Different Wide Flange Cross-Section

7. Parameter Identification for Frame Structures with Different Rectangular Cross-Section

8. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Parameter Identification of Frame Structures by considering Shear Deformation

Abstract

1. Introduction

2. Formulation for Parameter Identification

3. Member Stiffness Matrix of Frame Structure

4. Effect of Shear Deformation on Nodal Displacement

5. Parameter Identification by considering Shear Deformation

6. Parameter Identification for Frame Structures with Different Wide Flange Cross-Section

7. Parameter Identification for Frame Structures with Different Rectangular Cross-Section

8. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information