In this study, Caputo fractional derivative model of HIV and COVID-19 infections is analyzed. Moreover, the well-posedness of a model is verified to depict that the developed model is mathematically meaningful and biologically acceptable. Particularly, Mittag Leffler function is incorporated to show that total population size is bounded whereas fixed point theory is applied to show the existence and uniqueness of solution of the constructed Caputo fractional derivative model of HIV and COVID-19 infections. The study depicts that as the order of fractional derivative increase the size of the infected variable decrease as time increase. Additionally, memory effects correspond to order of derivative in the reduction of a number of populations infected both with HIV and COVID-19 infections. Numerical simulations are performed using MATLAB platform.

1. Introduction

COVID-19 wreaked havoc on both human life and the immense economic development. A severe economic crisis and the struggle for survival gripped the entire planet. Even the most economically developed nation lost faith and was unable to supply the urgently required resources asked by doctors at medical facilities [1]. The dynamic transmission of COVID-19 crises and attack on the upper respiratory organs cause the breathing system to quickly narrow, which has a significant negative impact [2]. Additionally, the prevalence of the virus has decreased overall as a result of the use of masks and the COVID-19 vaccine that reinforced through activation of memory effects by public health interventions [3]. Recently, in the worldwide it is registered that 692,576,573 cases, 6,903,976 deaths, and 664,687,106 recovered of COVID-19 [4]. On the other hand, the transmission of human immunodeficiency virus transmission through act of sexual practices, blood transfusion, and possible exposure to the virus is a burden in the worldwide [5]. Hence, different mathematical models have been developed to address the impact of diseases in the whole world [6–8]. For instance in engineering problems, the application of a regularized ψ–Hilfer fractional derivative is described by Jajarmi et al. [9] whereas Caputo fractional derivative is applied in the analysis of accelerated mass-spring system by Defterli et al. [10]. Recently, fractional derivative get a great attention due to indication of order of fractional derivative impact on memory effects to control the transmission and prevalence of infection in the population [11]. Caputo fractional derivative is applied in controlling the transmission dynamics of Nipah virus [12]. Also, some studies supported with mathematical modeling show that the occurrence of COVID-19 has significant impact on the HIV carriers [13, 14]. Moreover, the availability of the infections within the community inspires further investigation to consider the impact of memory effects through public health education intervention [15–18]. Also, the Caputo fractional derivative is incorporated to investigate banking data competition [19]. Recently, fractional derivative models are fitted to real data to describe the behavior of the real-world phenomena [20–26]. Therefore, in this study the memory effect is incorporated and a model with Caputo fractional derivative is developed and analyzed. The remaining portion of the paper is divided into the following sections: Section 2, which introduces preliminary ideas and the formulation of a mathematical model; Section 3, which analyzes the fractional model mathematically; Section 4, which uses numerical simulation; Section 5, which discusses the results; and Section 6, which contains the paper’s conclusion.

2. Mathematical Preliminary and Model Formulation

2.1. Mathematical Preliminary

In this section, revise basic definitions and theorems in fractional calculus that supports the main results of the current study.

Definition 2.1. [27] The order α fractional integral of Riemann–Liouville of a function f with is given by

(1)

Definition 2.2. [28] Let f be an element of the space of absolutely continuous function on [a, b], α > 0 and n − 1 < α ≤ n. The left and right Caputo fractional derivative of a function f(t) with order α is given by

(2)

(3)

Definition 2.3. [29] The Laplace transform of the left Caputo fractional derivative is defined as follows:

(4)

Definition 2.4. [29] The Laplace transform of the function t^β−1E_α,β(±μt^α) is given by

(5)

where E_α,β(t) is the two-parameter Mittage–Leffler function with parameters α, β > 0.

Definition 2.5. [29] Let E_α,β(Z) be Mittage–Leffler function. Then

(6)

Lemma 1. (Generalized Mean Value Theorem) Suppose that f(t) ∈ C[a, b] and for 0 < α ≤ 1, then we have

(7)

with a ≤ ξ ≤ t, for all t ∈ (a, b].

Moreover, if , then there is a neighborhood N of t₀ such that f(t) > f(a), ∀t ∈ N. Also, if , then there is a neighborhood N of t₀ such that f(t) < f(a), ∀t ∈ N.

2.2. Model Formulation

To construct our current model, we have modified the coinfection model of HIV and cholera virus developed in [30]. We formulate S, C, R, H, H_c, H_r model of HIV and COVID-19 coinfection by dividing the total population under consideration as classes consists of (i) susceptible individuals (S). They are infection free individuals with possibility of acquiring HIV from HIV infected individuals through sexual contact and acquiring COVID-19 from COVID-19 infected individuals only through effective direct contacts; (ii) COVID-19 infected individuals (C). They are individuals infected with COVID-19 and capable of transmitting infection to susceptible population through direct contact; (iii) COVID-19 recovered individuals (R). They are individuals recovered from COVID-19 infection with temporary immunity; (iv) HIV/AIDS infected individuals (H). They are individual infected with only HIV/AIDS and capable of transmitting HIV to susceptible population through sexual contacts; (v) coinfected individuals (H_c). They are individuals infected with HIV and COVID-19. They can transmit disease with effective contacts with susceptible population; (vi) COVID-19 recovered and HIV/AIDS individuals (H_r). They are HIV/AIDS individuals recovered from COVID-19 with temporary immunity. The following assumptions are also stated:

(i)
For this study a total population size is not constant;
(ii)
Susceptible persons recruited at the rate τ;
(iii)
A naturally death rate is μ;
(iv)
Only COVID-19 infected individuals die as a result of infection at the rate φ;
(v)
Only HIV/AIDS infected individuals die at the rate δ = ζ;
(vi)
Death rate of coinfected individuals die due to infection at the rate ψ;
(vii)
COVID-19 transmission rate due to direct contact is β_c;
(viii)
Transmission rate of HIV/AIDS due to unsafe exposure to virus is β_h;
(ix)
Recovery rate of only COVID-19 infected with temporary immunity is ω;
(x)
Recovery rate of coinfected with temporary immunity is κ.
(xi)
γ is immunity loss rate of COVID-19 recovered individuals R;
(xii)
ξ is COVID-19 infection vaccination rate for only HIV infected individuals;
(xiii)
ρ is COVID-19 infection vaccination rate for only susceptible individuals;
(xiv)
η is immunity loss rate of COVID-19 infection recovered individuals H_r.

The total size of population under study is denoted by P(t) and defined as P(t) = S(t) + C(t) + R(t) + H(t) + H_c(t) + H_r(t) where S(t) is the size of susceptible population at time t, C(t) size of COVID-19 population at time t, R(t) size of only COVID-19 recovered population at time t, H(t) size of HIV/AIDS population at time t, H_c(t) size of coinfected population at time t, and H_r(t) size of COVID-19 recovered HIV population at time.

The aforementioned assumptions and supporting flow diagram described in Figure 1 lead to a model with Caputo fractional derivative as given by subsequent equations.

(8)

with initial value conditions for the problem S(0) > 0, C(0) ≥ 0, R(0) ≥ 0, H(0) ≥ 0, H_c(0) ≥ 0, H_r(0) ≥ 0.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Simulation of COVID-19 and HIV dynamics through direct transmission.

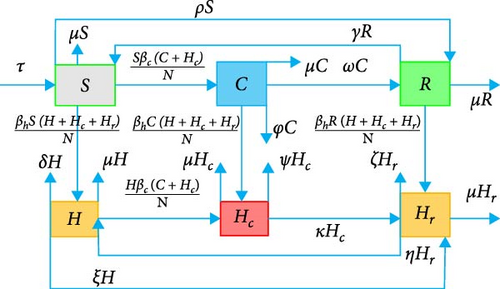
3. Fractional Model Analysis

3.1. Invariant Region

Theorem 1. The solutions of the model (1) are invariant in the region Ω proper subset of six-dimensional space over nonnegative real numbers such that

(9)

Proof. To show the boundedness of solution we employ the method employed by Qian et al. [31]. So, adding corresponding terms on left and right of qualities in model (1) we obtain

(10)

Implies,

(11)

Moreover, for computation purpose, we set the preceding expression to the form

(12)

Also, from the preceding expression, we obtain

(13)

Moreover, applying the Laplace transform on both sides of the preceding equation yields

(14)

According to Podlubny [29], applying Laplace transform definition in Caputo fractional derivative sense such that , the preceding equation reduces to the form

(15)

Also, for n = 1, 0 < α < 1, he preceding equation reduces to

(16)

Also, by summation property the preceding equation reduces to

(17)

Moreover, arranging the terms, the preceding equation can be written as follows:

(18)

Further, solving for , the foregoing equation reduces to

(19)

Also, applying inverse Laplace transform on both sides of the preceding equation, we obtain

(20)

Again applying property of inverse Laplace transform, the preceding equation gives

(21)

Also, using the relationship between inverse Laplace transform and Mittag Leffler function given by Qian et al. [31], , the preceding equation reduces to

(22)

Implies,

(23)

Also, the definition of Mittag Leffler function, , the preceding equation reduces to

(24)

Implies,

(25)

Hence, taking into consideration the Equation (3), we obtain:

(26)

Hence, as time t gets larger and larger the total population size is bounded between 0 and τ^α/μ^α.

3.2. Positivity Property

Theorem 2. The solution of the developed fractional model (1) is positive for all time t in the invariant region .

Proof. To show positivity of solutions, we employ the techniques applied by Baleanu et al. [12]. In similar fashion, the trajectory of solution of solution of model (1) along only one state-axis, where other state variables vanishes, gives

(27)

Similar to the procedures done for the boundedness computed in Section 3.1, the solution of the foregoing equation is solved, respectively, as follows:

(28)

Therefore, the preceding computed results show that the solution is positively invariant along the axis of state variables. Moreover, since the solution of the fractional model (1) is positive in the plane C − R − H − H_c − H_r plane, let t^∗ > 0 such that S(t^∗) = 0, C(t^∗) > 0, R(t^∗) > 0, H(t^∗) > 0, H_c(t^∗) > 0, H_r(t^∗) > 0 and S(t) < S(t^∗). On this plane,

(29)

Moreover, by Caputo fractional derivative mean value theorem sated and applied by Musa et al. [32], we have

(30)

Therefore, we get S(t) > S(t^∗) which contradicts our earlier assumption for t^∗. Hence, the state variable S(t) is nonnegative for all time t. Similarly, other state variables are nonnegative for all time t. Therefore, any solution of fractional derivative is nonnegative for all time t.

3.3. Existence and Uniqueness of Solution

In this section, as presented by Ahmad et al. [28], we show uniqueness and existence of the solution. However, before we prove the existence and uniqueness of solution define the kernel functions from fractional derivative model (1) as follows:

(31)

Moreover, let .

Then model (1) can be written as follows:

(32)

In the preceding expression, the condition X₀ ≥ 0 is to be taken component wise. Problem (32) which is equivalent to model (1), can be described by the integral of

(33)

Next we shall analyze model (1) through the integral representation given above. For that case, let

denotes Banach space of all continuous functions that maps from (0, τ) to

endowed with the norm

(34)

where |X(t)| = |S(t)| + |C(t)| + |R(t)| + |H(t)| + |H_c(t)| + |H_r(t)|. Note that, S, C, R, H, H_c, H_r all belong to

. Moreover, we define the operator T : ζ⟶ζ by

(35)

Hence, the operator T is well-defined due to obvious continuity of H.

Theorem 4. Let , the function defined above satisfies

(36)

for some L_k > 0.

Proof. The first component of ϕ gives,

(37)

Let , then the preceding equation can be reduced to

(38)

where,

(39)

Therefore,

(40)

In similar fashion the remaining can be shown. Consequently, we can conclude that

(41)

where L_k = L₁ + L₂ + L₃ + L₄ + L₅ + L₆.

Theorem 5. Let the result of preceding theorem holds Ω = τ^α/Γ(α + 1). If ΩL_k < 1, then there exists a unique solution of model (1) on (0, τ^α) which is uniformly Lyapunov stable.

Proof. The function is obviously continuous on its stated domain. Thus, the existence of the solution follows from the works done by Ahmad et al. [28].

For uniqueness, we apply Banach contraction mapping on operator T defined above. Next, we show T is both a self-map and a contraction. By definition, . Let us now define κ > ∥X₀∥+Ωτ^α/1 − ΩL_k and a closed convex set B_k = {X ∈ ζ : ∥X∥_ζ ≤ k}. Thus, for self-map property it is enough to show that TB_k ⊂ B_k. So let X ∈ B_k, then

(42)

It follows that the operator TX⊆B_k and T is indeed a self-map. Next, we prove that T is a contraction. Let X and satisfy the abbreviated dynamical system. The using the result of theorem above, we have

(43)

Hence, if ΩL_k < 1 then T is contraction mapping and by Banach contraction mapping principle, T has a unique fixed point on [0, τ^α] which is a solution of model (1). Moreover, the uniformly Lyapunov stability of solutions follows as stated by Ahmad et al. [28].

3.4. Disease-Free Equilibrium

The disease-free equilibrium,

of fractional model (1) is a steady state point where the disease extinct. Setting the state variables for disease equal to zero, at steady state model (1) gives a disease-free equilibrium as follows:

(44)

That is, we set model (1) equal to zero and solve as given below

(45)

Moreover, at vanishing point of C, H, H_c, and H_r, we obtain

(46)

Therefore, the disease-free equilibrium of fractional model is computed by applying simple mathematical calculation as follows:

(47)

3.5. Endemic Equilibrium

The endemic equilibrium,

, of fractional derivative model (1) is a point where the diseases persist in the population. Hence, we can write the endemic equilibrium as follows:

(48)

where

, and

are obtained by solving the subsequent equation

(49)

Moreover, due to trick of the problem, we obtain the endemic equilibrium from numerical simulation.

3.6. Basic Reproduction Number

The basic reproduction number

is the indicator of disease status at any time of investigation and defined as the average number of infected persons flow into a fully susceptible population due to generation of infected individuals by typical infectious individual. In mathematical biology of epidemiology, the next-generation matrix method is widely applied to systematically obtain basic reproduction number from a model with more compartments. Let consider model (1) and construct the subsequent Jacobian matrices at disease-free equilibrium as follows:

(50)

Moreover, the next-generation matrix constructed from the preceding matrices F and V is given by

(51)

where a = φ^α + ω^α + μ^α, b = ξ^α + μ^α + δ^α, c = ψ^α + κ^α + μ^α, d = ζ^α + η^α + μ^α.

The eigenvalues of the preceding matrices are computed as follows:

(52)

We know that the basic reproduction number is the spectral radius of next-generation matrix. Thus, the basic reproduction is computed as given below

(53)

4. Numerical Simulations

4.1. Numerical Schemes for Caputo Fractional Derivative

The numerical solution of Caputo fractional derivative is performed using FDE12 [33]. Moreover, the initial population sizes are S(0) = 300, 000, C(0) = 300, R(0) = 0, H(0) = 5, 000, H_c = 0, H_r = 0. Moreover, parameter value is given in Table 1.

Table 1. Parameter and source description.

Parameter	Value	Source
μ	0.0000548/day	[30]
β_c	0.02/day	Assumed
λ	200	Assumed
ξ	0.5/day	Assumed
ρ	0.5/day	Assumed
β_h	0.034/day	[30]
γ	0.2/day	Assumed
φ	0.1/day	[5]
δ	0.09/day	Assumed
ζ	0.09/day	Assumed
ω	1/15/day	[5]
ψ	0.15/day	Assumed
η	0.1/day	Assumed
κ	0.02/day	Assumed

5. Results and Discussion

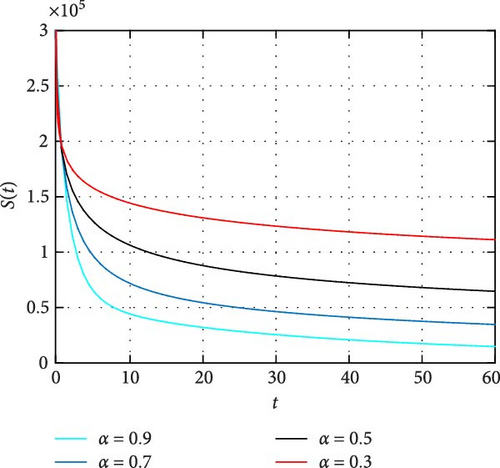
In Figure 2 the size of susceptible population decrease as time increase which shows the higher activation of human memory toward vaccination the less the population are susceptible. Moreover, the higher the order of fractional derivative the higher the mobilization of population toward vaccination. Figure 3 describes the dynamics of population size subject to the transmission dynamics of novel COVID-19 and memory effects through public health education. It is noticed that the intervention to activate memory of population significantly contributes to control the pandemic COVID-19. Moreover, the simulation shows that less memory effect contributes less in controlling of the infection whereas high involvement in the activation of human memory results in better way to control the infection.

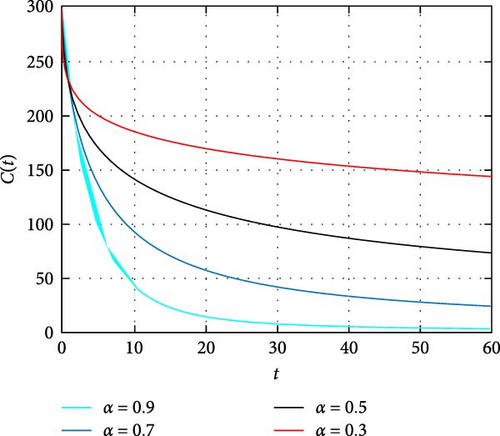
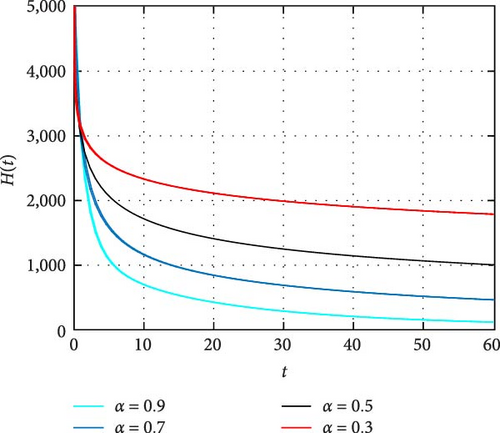
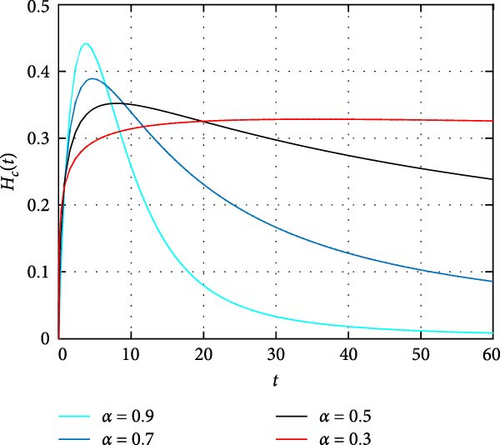
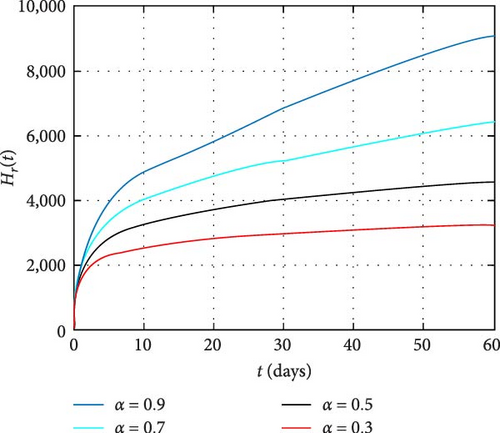
In Figure 4, dynamics of only HIV-infected population size is simulated. It is observed that the memory effect works well to control the transmission dynamics of HIV infection. Moreover, the simulation depicts there is comprise of population in the long run. Thus, effectively apply the memory effects before HIV infects many people. In Figure 5, the simulation of coinfected population size is depicted. It is shown that the number of individuals infected with both infections is high at the beginning and the memory effect is less effective. On the other hand, the memory effects work well for reducing coinfected individuals as time increase. In Figure 6, the dynamics of only HIV infected population with COVID-19 recovered status is simulated. It is observed that memory effect activation works continually for controlling COVID-19 for HIV infected population. Hence, a continuum memory effect helps HIV-infected population for recovery from pandemic COVID-19.

In Figure 7, the dynamics of population size is simulated. It is shown that the impact of COVID-19 can be controlled with effective memory effect whereas the HIV infection persists with population. In Figure 8, we observe that the more individuals are susceptible the more they get infected with COVID-19 infection whereas less the number of susceptible individuals the less the number of individuals infected with COVID-19 infection. In Figure 9, we observe that the more individuals are susceptible to HIV the more they get attacked with HIV infection whereas the less the number of susceptible individuals toward HIV the less the number of individuals exposed to the HIV infection. Figure 10 depicts the transferring of individuals to R(t) with immunity reduces the number of susceptible individuals.

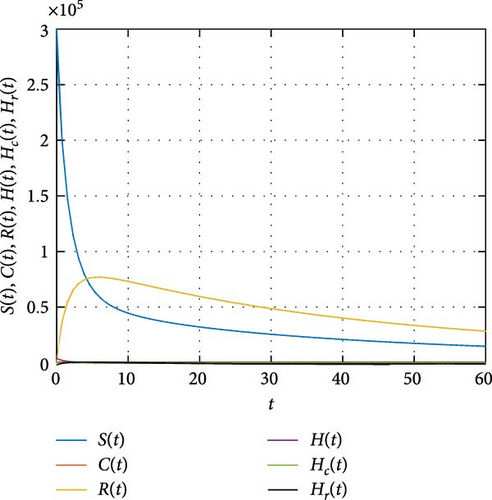
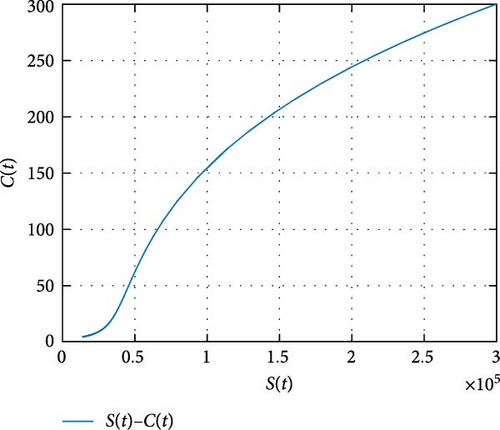
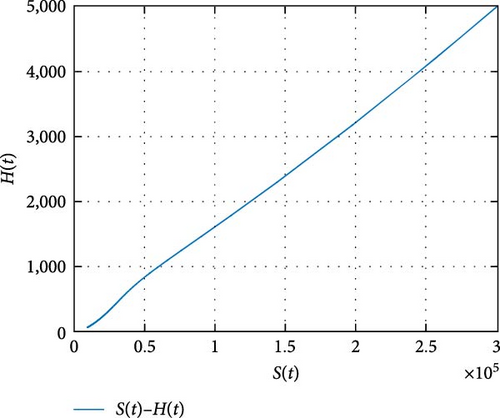
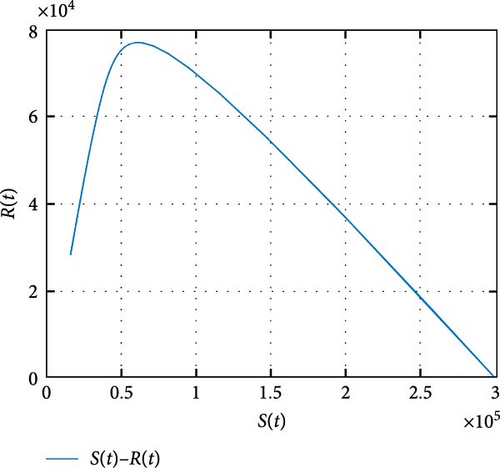
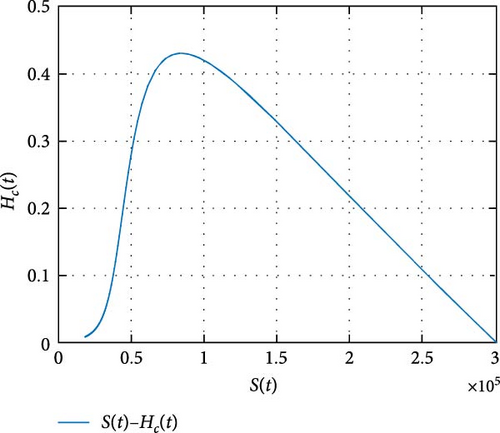
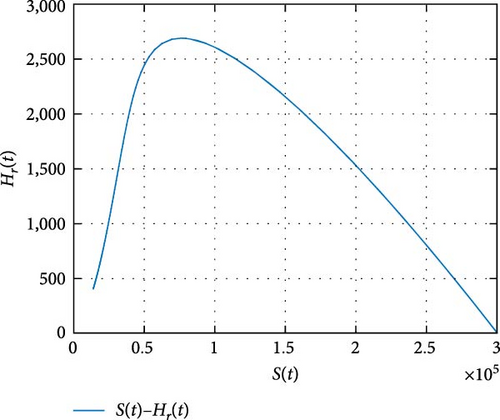
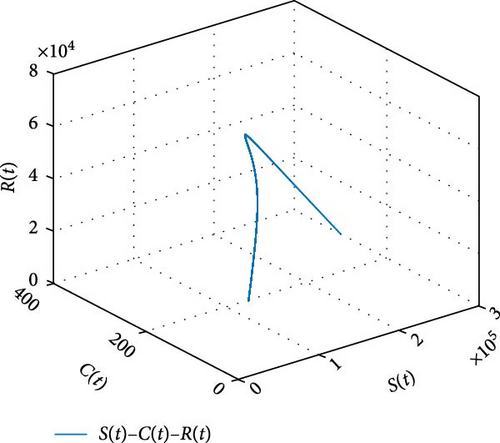
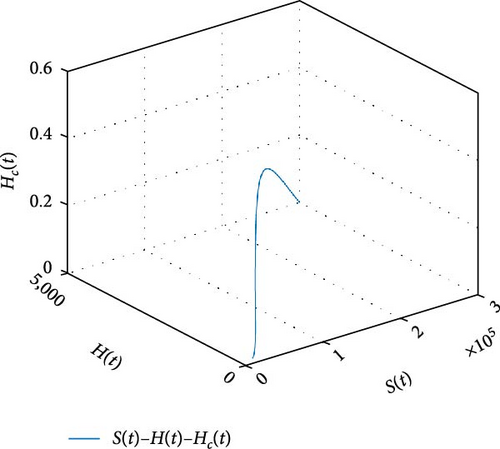
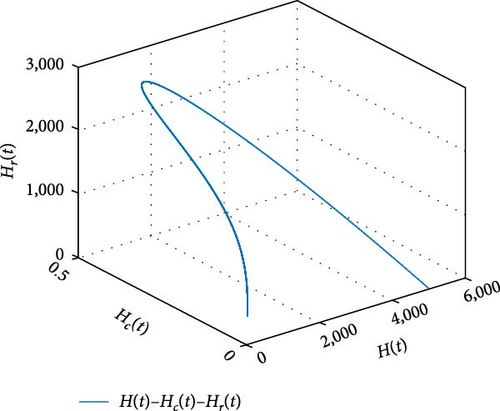
Figure 11 shows that the number of coinfected individuals decreases or increases along susceptible population size. Figure 12 describes that the number of HIV infection recovered individuals increases as susceptible decrease, but lately decrease as the number of susceptible individuals decreases. Figure 13 describes the dynamics of S(t), C(t), and R(t). The behavior of S(t) and C(t) alike as they decreases from the beginning whereas R(t) increase initially and decrease lately. Figure 14 describes the dynamics of S(t), H(t), and H_c(t). The behaviors of S(t) and H(t) are similarly get decrease from the beginning whereas H_c(t) increase initially and decrease lately. Figure 15 describes the dynamics of H(t), H_c(t), and H_r(t). The behaviors of H_c(t) and H_c(t) are similarly get increases from the beginning and decreases lately whereas S(t)decreases from the beginning.

6. Conclusion

In this study, fractional derivative is incorporated and the model of HIV and COVID-19 dynamics is developed and analyzed. Based on the simulations of HIV and COVID-19 dynamics, infections can be controlled for basic reproduction number is less than unity. The study depicts that HIV/AIDS and COVID-19 coinfection may increase, through direct interaction of coinfected individuals. Also, fractional derivative analysis shows increasing memory of population toward COVID-19 and HIV infections will increase the ability of population to control the infections. In the future study, one can extend our model to a new generalized fractional derivative and use real data to describe the biological phenomena. Numerical simulations are performed using MATLAB platform.

Conflicts of Interest

The author declares that there is no conflict of interest.

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Hattaf K., Mohsen A. A., Harraq J., and Achtaich N., Modeling the dynamics of COVID-19 with carrier effect and environmental contamination, International Journal of Modeling, Simulation, and Scientific. (2021) 12, no. 3, https://doi.org/10.1142/S1793962321500483, 2150048.
10.1142/S1793962321500483
Google Scholar
2 Hattaf K., El Karimi M. I., Mohsen A. A., Hajhouji Z., El Younoussi M., and Yousfi N., Mathematical modeling and analysis of the dynamics of RNA viruses in presence of immunity and treatment: a case study of SARS-CoV-2, Vaccines. (2023) 11, no. 2, 201.
10.3390/vaccines11020201
CAS Web of Science® Google Scholar
3 Hattaf K. and Yousfi N., Dynamics of SARS-CoV-2 infection model with two modes of transmission and immune response, Mathematical Biosciences. (2020) 17, no. 5, 5326–5340.
10.3934/mbe.2020288
Web of Science® Google Scholar
4 02: 21 GMT, August 2023, https://www.worldometers.info, / corona virusvirus/.
Google Scholar
5 Mohsen A. A. and Hattaf K., Dynamics of a generalized fractional epidemic model of COVID-19 with carrier effect, Advances in Systems Science and Applications. (2022) 22, no. 3, 36–48.
Google Scholar
6 Hattaf K. and Dutta H., Mathematical Modeling and Analysis of Infectious Diseases, 2020, 302, Springer, Berlin.
10.1007/978-3-030-49896-2
Google Scholar
7 Hattaf K. and Dutta H., Modeling the dynamics of viral infections in presence of latently infected cells, Chaos, Solitons & Fractals. (2020) 136, https://doi.org/10.1016/j.chaos.2020.109916, 109916.
10.1016/j.chaos.2020.109916
PubMed Web of Science® Google Scholar
8 Baleanu D., Jajarmi A., Mohammadi H., and Rezapour S., A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative, Chaos, Solitons & Fractals. (2020) 134, 109705.
10.1016/j.chaos.2020.109705
Web of Science® Google Scholar
9 Jajarmi A., Baleanu D., Sajjadi S. S., and Nieto J. J., Analysis and some applications of a regularized ψ–Hilfer fractional derivative, Journal of Computational and Applied. (2022) 415, 114476.
10.1016/j.cam.2022.114476
Google Scholar
10 Defterli O., Baleanu D., Jajarmi A., Sajjadi S. S., Alshaikh N., and Asad J., Fractional treatment: an accelerated mass-spring system, Romanian Reports in Physics. (2022) 74, no. 4, 122.
Web of Science® Google Scholar
11 Hattaf K., A new generalized definition of fractional derivative with non-singular kernel, Computation. (2020) 8, no. 2, 49.
10.3390/computation8020049
Web of Science® Google Scholar
12 Baleanu D., Shekari P., Torkzadeh L., Ranjbar H., and Jajarmi A., Stability analysis and system properties of Nipah virus transmission: a fractional calculus case study, Chaos, Solitons & Fractals. (2023) 166, 112990.
10.1016/j.chaos.2022.112990
Web of Science® Google Scholar
13 Jewell B. L., Medium E., Stover J., Ten Brink D., Phillips A. N., Smith J. A., and Kelly S. L., Potential effects of disruption to HIV programmes in sub-Saharan Africa caused by COVID-19: results from multiple mathematical models., The Lancet HIV. (2020) 7, no. 9, e629–e640.
10.1016/S2352-3018(20)30211-3
PubMed Web of Science® Google Scholar
14 Goufo E. F. D., Khan Y., and Chaudhry Q. A., HIV and shifting epicenters for COVID-19, an alert for some countries, Chaos, Solitons & Fractals. (2020) 139, 110030.
10.1016/j.chaos.2020.110030
PubMed Web of Science® Google Scholar
15 Ahmad S., Owyed S., Abdel-Aty A. H., Mahmoud E. E., Shah K., and Alrabaiah H., Mathematical analysis of COVID-19 via new mathematical model, Chaos, Solitons & Fractals. (2021) 143, 110585.
10.1016/j.chaos.2020.110585
PubMed Web of Science® Google Scholar
16 James L. P., Salomon J. A., Buckee C. O., and Menzies N. A., The use and misuse of mathematical modeling for infectious disease policymaking: lessons for the COVID-19 pandemic, Medical Decision Making. (2021) 41, no. 4, 379–385, https://doi.org/10.1177/0272989X21990391.
10.1177/0272989X21990391
PubMed Web of Science® Google Scholar
17 Fatmawati, Yuliani E., Alfiniyah C., Juga M. L., and Chukwu C. W., On the modeling of COVID-19 transmission dynamics with two strains: insight through caputo fractional derivative, Fractal and Fractional. (2022) 6, no. 7, https://doi.org/10.3390/fractalfract6070346, 346.
10.3390/fractalfract6070346
Web of Science® Google Scholar
18 Cheneke K. R., Rao K. P., and Edessa G. K., Application of a new generalized fractional derivative and rank of control measures on cholera transmission dynamics, International Journal of Mathematics and Mathematical Sciences. (2021) 2021, 9, https://doi.org/10.1155/2021/2104051, 2104051.
10.1155/2021/2104051
Google Scholar
19 DarAssi M. H., Khan M. A., Fatmawati, and Alqarni M. S., Analysis of the competition system using parameterized fractional differential equations: application to real data, Symmetry. (2023) 15, no. 2, 542.
10.3390/sym15020542
Web of Science® Google Scholar
20 Naik P. A., Yavuz M., Qureshi S., Zu J., and Townley S., Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan, The European Physical Journal Plus. (2020) 135, 1–42.
10.1140/epjp/s13360-020-00819-5
Web of Science® Google Scholar
21 Qureshi S. and Atangana A., Fractal–fractional differentiation for the modeling and mathematical analysis of nonlinear diarrhea transmission dynamics under the use of real data, Chaos, Solitons & Fractals. (2020) 136, 109812.
10.1016/j.chaos.2020.109812
Web of Science® Google Scholar
22 Qureshi Sania and Yusuf Abdullahi, Fractional derivatives applied to MSEIR problems: comparative study with real world data, The European Physical Journal. (2019) 134, no. 4, https://doi.org/10.1140/epjp/i2019-12661-7, 2-s2.0-85064914685, 171.
10.1140/epjp/i2019-12661-7
Web of Science® Google Scholar
23 Atangana A. and Khan M. A., Modeling and analysis of competition model of bank data with fractal–fractional Caputo–Fabrizio operator, Alexandria Engineering Journal. (2020) 59, no. 4, 1985–1998.
10.1016/j.aej.2019.12.032
Web of Science® Google Scholar
24 Area I., Batarfi H., Losada J., Nieto J. J., Shammakh W., and Torres Á., On a fractional order Ebola epidemic model, Advances in Difference. (2015) 2015, no. 1, 1–12.
10.1186/s13662-015-0613-5
Web of Science® Google Scholar
25 Baleanu D., Ghassabzade F. A., Nieto J. J., and Jajarmi A., On a new and generalized fractional model for a real cholera outbreak, Alexandria Engineering Journal. (2022) 61, no. 11, 9175–9186.
10.1016/j.aej.2022.02.054
Web of Science® Google Scholar
26 Silva C. J., Cruz C., Torres D. F., Munuzuri A. P., Carballosa A., Area I., and Mira J., Optimal control of the COVID-19 pandemic: controlled sanitary deconfinement in Portugal, Scientific Reports. (2021) 11, no. 1, https://doi.org/10.1038/s41598-021-83075-6, 3451.
10.1038/s41598-021-83075-6
CAS PubMed Web of Science® Google Scholar
27 Logeswari K., Ravichandran C., and Nisar K. S., Mathematical model for spreading of COVID-19 virus with the Mittag–Leffler kernel, Numerical Methods for Partial Differential Equations. (2020) 26, https://doi.org/10.1002/num.22652, 33362342.
10.1002/num.22652
Google Scholar
28 Ahmad S., Ullah A., Al-Mdallal Q. M., Khan H., Shah K., and Khan A., Fractional order mathematical modeling of COVID-19 transmission, Chaos, Solitons & Fractals. (2020) 139, 110256.
10.1016/j.chaos.2020.110256
PubMed Web of Science® Google Scholar
29 Podlubny I., Fractional Differential Equations, 2009, Academic Press, New York.
Google Scholar
30 Cheneke K. R., Rao K. P., and Edessa G. K., Modeling and analysis of HIV and cholera direct transmission with optimal control, Discrete Dynamics in Nature and Society. (2022) 2022, 16, https://doi.org/10.1155/2022/5460337.
10.1155/2022/5460337
Web of Science® Google Scholar
31 Qian D., Li C., Agarwal R. P., and Wong P. J., Stability analysis of fractional differential system with Riemann–Liouville derivative, Mathematical and Computer Modelling. (2010) 52, no. 5-6, 862–874.
10.1016/j.mcm.2010.05.016
Web of Science® Google Scholar
32 Musa S. S., Qureshi S., Zhao S., Yusuf A., Mustapha U. T., and He D., Mathematical modeling of COVID-19 epidemic with effect of awareness programs, Infectious Disease Modeling. (2021) 6, 448–460.
10.1016/j.idm.2021.01.012
PubMed Google Scholar
33 Rosa S. and Torres D. F., Numerical fractional optimal control of respiratory syncytial virus infection in Octave/MATLAB, Mathematics. (2023) 11, no. 6, 1511.
10.3390/math11061511
Web of Science® Google Scholar

Citing Literature

All articles

Caputo Fractional Derivative for Analysis of COVID-19 and HIV/AIDS Transmission

Abstract

1. Introduction