This paper uses Müntz orthogonal functions to numerically solve the fractional Bagley–Torvik equation with initial and boundary conditions. Müntz orthogonal functions are defined on the interval [0, 1] and have simple and distinct real roots on this interval. For the function f ∈ L²(0, 1), we obtain the best unique approximation using Müntz orthogonal functions. We obtain the Riemann–Liouville fractional integral operator for Müntz orthogonal functions so that we can reduce the complexity of calculations and increase the speed of solving the problem, which can be seen in the process of running the Maple program. To solve the fractional Bagley–Torvik equation with initial and boundary conditions, we use Müntz orthogonal functions and consider simple and distinct real roots of Müntz orthogonal functions as collocation points. By using the Riemann–Liouville fractional integral operator that we define for the Müntz orthogonal functions, the process of numerically solving the fractional Bagley–Torvik equation that is solved using Müntz orthogonal functions is reduced, and finally, we reach a system of algebraic equations. By solving algebraic equations and obtaining the vector of unknowns, the fractional Bagley–Torvik equation is solved using Müntz orthogonal functions, and the error value of the method can be calculated. The low error value of this numerical solution method shows the high accuracy of this method. With the help of the Müntz functions, we obtain the error bound for the approximation of the function. We have obtained the error bounds for the numerical method using which we solved the fractional Bagley–Torvik equation with initial and boundary conditions. Finally, we have given a numerical example to show the accuracy of the solution of the method presented in this paper. The results of solving this example using Müntz orthogonal functions and comparing the results with other methods that have been used the solve this example show the higher accuracy of the method proposed in this paper.

1. Introduction

To approximate the fractional Bagley–Torvik equation via Müntz orthogonal functions, we have the following [1]:

(1)

with the initial condition

(2)

or the boundary condition

(3)

To solve the fractional Bagley–Torvik equation, several numerical solutions and analytical solutions have been used. Hybrid functions approximation [1] fractional-order Legendre collocation method [2], Haar wavelet [3], Laplacetransform [4], Laguerre polynomials [5], shifted Chebyshev operational matrix [6], Legendre artificial neural network method [7], Chebyshev collocation method [8], the fractional Taylor method [9], exponential integrators [10], Gegenbauer wavelet method [11], Müntz–Legendre polynomials [12], discrete spline methods [13], Hermit solution [14], local discontinuous Galerkin approximations [15], numerical inverse Laplace transform [16], generalized Fibonacci operational tau algorithm [17], Jacobi collocation methods [18], polynomial least squares method [19], and fast multiscale Galerkin algorithm [20] are methods by which Bagley–Torvik equation solved numerically. In the study of Alshammari et al. [21], residual power series are used to obtain the numerical solution of a class of Bagley–Torvik problems in Newtonian fluid, and in the study of Karaaslan et al. [22], using the discontinuous Galerkin method that can be combined in the equation of motion of a plate immersed in a Newtonian fluid, the numerical solution of Bagley–Torvik equation has been discussed. Analytical solutions of the generalized Bagley–Torvik equation [23], Sumudu transformation method [24], generalized differential transform [25], Sine–Gordon expansion method, and Bernoulli equation method [26] are analytical solutions for solving the Bagley–Torvik equation in this work.

Several numerical techniques have been proposed for solving fractional integrodifferential equations, such as Legendre wavelet [27], Euler function [28], Chebyshev series [29], and also methods such as stable least residue [30], discrete Galerkin [31], homotopy perturbation [32], variational interaction [33], Runge–Kutta convolution quadrature [34], and Hermite spectral collocation [35].

Fractional derivatives can be used to solve classical problems in viscous fluid motion [36]. A fluid half-space is considered, and the plate at the boundary is allowed to initiate a general transverse motion. It will be shown that the shear pressure at any point of the fluid can be expressed in terms of the time derivative of the fractional order for the fluid velocity characteristic. The equation of motion [36]

(4)

is a diffusion equation where ρ is the fluid concentration, μ is the viscosity, ν is the transverse velocity of the fluid, t is the time and z is the distance from the wet plate. By taking the Laplace transform, the following ordinary differential equation is obtained

(5)

where in

(6)

and ν(0, z) is the characteristic of the initial velocity of the fluid. If the initial velocity in the fluid is assumed to be zero and the boundary conditions are applied, then the fluid velocity at the wetted surface must match the plane velocity, and the fluid velocity in the half-space must be bounded.

is the speed conversion of the plate, and

(7)

After obtaining the transformation of the fluid velocity characteristic,

, by writing the transformation of the shear pressure relation of for a Newtonian fluid

(8)

and

(9)

the result for the pressure conversion in the speed conversion condition of Equation (7) as

(10)

it is expressed. This relation can be written again as a time relation. So

(11)

and

(12)

Therefore, the pressure is equal to the convolution of two functions of time, that is

(13)

Since ν(0, z) reached zero, it can be shown that Equation (13) is equivalent to [36]

(14)

Equation (14) can be written as follows:

(15)

The index (t) indicates the fractional derivative with respect to time. Equation (15) seems to be an unusual relationship between pressure and velocity, but using this method provides significant satisfaction in pressure–velocity relationships for Newtonian fluid. Equation (8) is a combination equation for a Newtonian fluid. Equation (15) describes the relationship between pressure and velocity in the fluid for any semi-infinite fluid domain and any allowed velocity at the boundary. The priority of this problem is to show the behavior of a real physical system using fractional derivatives [36].

This article is organized into six sections. In Section 1, the introduction is presented. Section 2 is devoted to the preliminary and practical definitions. In Section 3, Müntz orthogonal functions and the best unique approximation for the arbitrary function are introduced also the Riemann–Liouville fractional integral operator for the Müntz orthogonal functions is defined to shorten the process of solving the fractional Bagley–Torvik. Section 4 is dedicated to the method of numerical solution of the fractional Bagley–Torvik equation with initial-boundary conditions using orthogonal functions as well as the error bound of the presented method. In Section 5, a numerical example is given to demonstrate the efficiency and capability of the proposed method. Finally, Section 6 is allocated to the general conclusion.

2. Preliminaries and Notations

2.1. Fractional Integral and Derivative

Definition 1. The Riemann–Liouville fractional integral operator of the order α with the assumption and I^α in [a, b] is defined as follows [37]:

(16)

where t^α−1 × f(t) is the convolution product of f(t) and t^α−1.

Definition 2. The Caputo fractional derivative operator of order α with the assumption and ^CD^α is defined as follows [37]:

(17)

As it is obvious for and , the Caputo derivative and Riemann–Liouville integral satisfy the following properties [37]:

(18)

(19)

where λ₁, λ₂, and c are real constants.

Definition 3. The two-scale fractal derivatives with dimensions α and β with respect to t and x, respectively, are defined as follows [38]:

(20)

(21)

Definition 4. The He’s fractional derivative defined as (0 < α ≤ 1) [39]

(22)

Definition 5. Suppose that f ∈ H^r(0, 1) with integers r ≥ 0 where [40]

(23)

is the Sobolev space. Let a function f ∈ H¹(a, b) and v ∈ (0, 1). The Atangana–Baleanu–Caputo fractional derivative of order v of u with a based point a is defined as follows [41, 42]:

(24)

where B(v) is defined as

(25)

one parameter and two-parameter Mittag–Leffler functions are defined as follows, respectively.

(26)

(27)

3. Müntz Orthogonal Functions and Their Properties

3.1. Müntz Orthogonal Functions

Definition 6. The family is Müntz orthogonal functions and is defined as follows [43]:

(28)

R_n(t) and S_n(t) are algebraic polynomials of degree [n/2] and [(n − 1)/2], respectively, which are as follows:

(29)

If n = 2m is an even number, then for each 0 ≤ v ≤ m − 1, we have the following:

(30)

and

(31)

For v = m,

(32)

If n = 2m + 1 is an odd number, then for each 0 ≤ v ≤ m, we have the following:

(33)

and

(34)

Some Müntz orthogonal functions are shown as follows:

(35)

Table 1 shows the roots of P_n(t) for n = 1, 2, 3, 4, 5.

Table 1. Roots of P_n(t).

n	t₁	t₂	t₃	t₄	t₅
1	0.3678794412	−	−	−	−
2	0.06442096633	0.6374173264	−	−	−
3	0.01871588194	0.2651887508	0.7969679223	−	−
4	0.007047297639	0.1154772486	0.4569410332	0.8683835323	−
5	0.003221796109	0.05672067679	0.2565492462	0.5974812127	0.9100748739

Theorem 1. The Müntz orthogonal function P_n(t) for n = 0, 1, 2, …, has exactly n simple and distinct real root in [0, 1] [43].

3.2. Function Approximation Using Orthogonal Müntz Basis

Let {P₀(t), P₁(t), …, P_N(t)} be a set of orthogonal Müntz functions and

(36)

If f is an arbitrary element of L²(0, 1) then f is the best approximation out of Y such that I_Nf ∈ Y, that is

(37)

where I_Nf ∈ Y, there exist unique coefficients c₀, c₁, …, c_N such that

(38)

where

(39)

and

(40)

3.3. Fractional Riemann–Liouville Integral Operator for Müntz Functions

The Riemann–Liouville fractional integral I^α is defined in Equation (16) for orthogonal Müntz functions as follows:

(41)

where

(42)

To obtain I^αP_n(t) by taking the Laplace transform from Equation (28), we have the following:

(43)

By using Equation (16), we get the following:

(44)

Taking the inverse Laplace transform of Equation (44) yields I^αP_n(t)

(45)

4. Numerical Method and Its Error Estimation

4.1. Müntz Collocation Method

In this section, it is explained how the fractional Bagley–Torvik equation with initial conditions and boundary conditions is solved using Müntz orthogonal functions.

A)
To solve Equation (1) with conditions given Equation (2), the Riemann–Liouville integral is taken from Equation (1)
(46)
Using Equations (18) and (19), we have the following:
(47)
According to Equation (38), the approximation solution for f(t) is as follows:
(48)

According to Equation (41), we have the following:

(49)

By substituting Equations (48) and (49) in Equation (47), the following equation is obtained

(50)

Interpolating Equation (50) in points t_i, i = 0, 1, …, N which are the roots of Müntz orthogonal functions P_N+1(t), we have the following:

(51)

These equations lead to getting N + 1 algebraic equations, which can be solved for the unknown vector C^T. The results show that the value of f(t) in Equation (48) can be approximated by using Müntz orthogonal functions.

B)
To solve Equation (1) with conditions given Equation (3), we suppose
(52)

Using Equations (18) and (41), we have the following:

(53)

Due to Equations (19) and (41), we also have the following:

(54)

By substituting Equations (52)–(54) in Equation (1), the following equation is obtained

(55)

Let t = 1 in Equation (53) and with conditions given Equation (3), we have the following:

(56)

Now by interpolating Equation (55) in points t_i, i = 0, 1, …, N which are the roots of Müntz orthogonal functions P_N+1(t) and considering Equation (56) that leads to generating N + 2 equations and N + 2 unknown coefficients which can be used to get the unknown vector C^T and

Remark 1. One of the problems of this method is to find the roots of Müntz orthogonal functions for large n. With the help of maple software, We calculated the for n ≤ 60 up to 50 meaningful digits and there was numerical stability.

4.2. Error Estimation

First consider the following lemma that will be used in deriving our main convergence results.

Lemma 1. Let be the best approximation of f in Y. Then, if r ≤ N + 1 we have the following:

(57)

and for 1 ≤ μ ≤ r we have the following:

(58)

where c is a constant depending only on r.

Proof. Suppose that L_Nf be the truncated Legendre series of the function f, then according to Equation (5.4.11) in the study of Canuto et al. [44] for r ≤ N + 1 we have the following:

(59)

AS I_Nf is the best approximation of f in L²−norm, we can write

(60)

and Equation (57) is proved. Equation (58) is proved using Equation (5.5.11) in the study of Canuto et al. [44] in a similar manner.

Theorem 2. If f ∈ H^r(0, 1) and r ≥ 0 then the error bound E_N for Equation (1) with the conditions given in Equation (2) is as following:

(61)

Proof. According to Equation (47), we have the following:

(62)

From Equation (16) and Equation (57), we have the following:

(63)

Similarly

(64)

Then Equation (61) is obtained based on Equations (57) and (62)–(64).

Theorem 3. If f ∈ H^r(0, 1) and r ≥ 0, the error bound for Equation (1) with the conditions in Equation (3) is as follows:

(65)

Proof. According to Equation (1), we have the following:

(66)

Using Equations (16), (19), and (58), we have the following:

(67)

Also

(68)

Then Equation (65) is obtained based on Equations (57) and (66)–(68).

5. Numerical Example

In this section, a numerical example for solving the fractional Bagley–Torvik equation with initial-boundary conditions is given to show the efficiency and applicability of the numerical method in this paper.

Example 1. Consider following properties [1, 6]:

(69)

(70)

(71)

where

(72)

In the two-parameter Mittag-Leffler function with λ, μ > 0 indices, is equal to

(73)

(74)

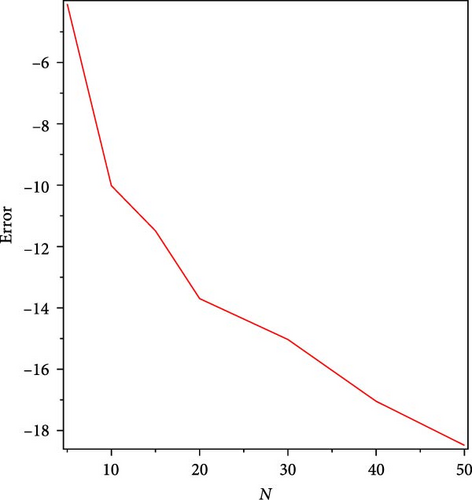
By solving this example with the initial conditions and coefficients A = 1, B = 1/2, and C = 1/2 are considered, then the approximate values of the function f(t) are obtained. These approximate values in Table 2 are compared with the approximate values in the study of Mashayekhi and Razzaghi [1], which was obtained by using combined functions, and in the study of Ji et al. [6], which was obtained by using the shifted Chebyshev operational matrix. In Figure 1, the logarithmic values of the absolute errors for different values of N are depicted, which shows the exponential convergence.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Logarithmic values of absolute errors for A = 1, B = 1/2 and C = 1/2.

Table 2. Approximate values of f(t) for A = 1, B = 1/2 and C = 1/2 and N = 16.

t	Method [1]	Method [6]	Present method	Exact
t	(M = 3, N = 8)	(N = 16)	(N = 16)	Exact
0.1	0.0364875	0.036487532	0.03648747992	0.03648747990
0.2	0.1406398	0.140639669	0.14063962121	0.14063962117
0.3	0.3074848	0.3074844733	0.30748462710	0.30748462713
0.4	0.5332842	0.533283636	0.53328410990	0.53328410988
0.5	0.8147568	0.814758247	0.81475694936	0.81475694938
0.6	1.1488372	1.148848315	1.14883742229	1.14883742227
0.7	1.5325655	1.532537770	1.53256542649	1.53256542650
0.8	1.9630293	1.963013767	1.96302925484	1.96302925484
0.9	2.4373338	2.437896842	2.43733397083	2.43733397084
1.0	2.9525839	−	2.95258387995	2.95258388004

Table 3 shows the results of the comparison of the method presented in this paper with the method in the study of Uddin and Ahmad [4], which is used to solve the fractional Bagley–Torvik equation using the Laplace transform. C₁, C₂, and C₃ are three different paths for optimal parameters [4].

Table 3. Absolute errors of f(t) for A = 1, B = 1/2, and C = 1/2.

N	Method [4]	Method [4]	Method [4]	Present method
N	(C₁)	(C₂)	(C₃)	Present method
10	7.7161e − 3	4.9000e − 8	1.0000e − 9	9.6216e − 11
20	1.0552e − 5	1.0000e − 9	1.0000e − 9	2.0024e − 14
23	9.8800e − 7	1.0000e − 9	1.0000e − 9	3.1158e − 14
50	1.0000e − 9	1.0000e − 9	1.0000e − 9	3.2920e − 19
60	1.0000e − 9	1.0000e − 9	2.9000e − 8	2.9127e − 19
90	1.0000e − 9	2.0000e − 9	1.1000e − 1	2.2831e − 24
100	1.0000e − 9	1.3700e − 7	9.5387e − 0	1.3631e − 24

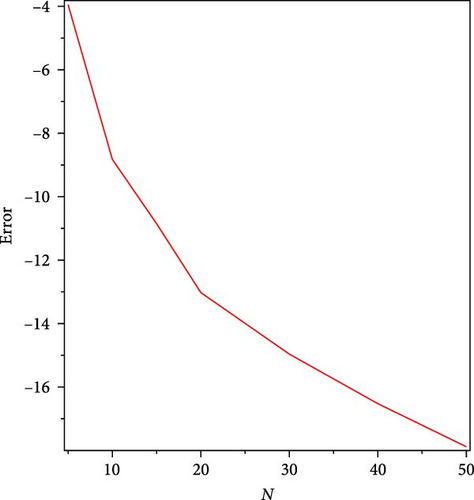
If the coefficients A = B = C = 1 are considered, the values of logarithmic values of absolute errors are shown in Figure 2. In Table 4, the absolute errors of the function f(t) for A = B = C = 1 using the method presented in this paper are compared with the method in the study of Mashayekhi and Razzaghi [1].

Table 4. Absolute errors of f(t) for A = B = C = 1.

t	Method [1]	Present method
t	(M = 4, N = 8)	(N = 14)
0.5	2.4e − 9	1.2e − 10
1	8.4e − 9	1.0e − 9
2	6.3e − 8	2.3e − 9
5	2.8e − 4	1.2e − 6

Table 5 shows the results of the comparison of the method presented in this paper with the method in the study of Zolfaghari et al. [45], which is used to solve the fractional Bagley–Torvik equation using the homotopy perturbation method.

Table 5. Approximate values of f(t) for A = B = C = 1 and N = 10.

t	Method [45]	Present method	Exact
t	Method [45]	N = 10	Exact
0	0.0000	0.000000000	0.000000000
0.1	0.0335	0.033507355	0.033507310
0.2	0.1252	0.125221248	0.125221280
0.3	0.2677	0.267609447	0.267609420
0.4	0.4555	0.455435396	0.455435398
0.5	0.6843	0.684334730	0.684334753
0.6	0.9501	0.950392575	0.950392563
0.7	1.2494	1.249959149	1.249959133
0.8	1.5788	1.579557186	1.579557209
0.9	1.9351	1.935832303	1.965832293
1	2.3149	2.315525744	2.315525823

Moreover, by solving this example with the boundary conditions and coefficients A = 1, B = 1/2, and C = 1/2 are considered, then the approximate values of the function f(t) are obtained. In Table 6, approximate values are compared with exact values.

Table 6. Approximate values of f(t) for A = 1, B = 1/2 and C = 1/2 and different values of N.

t	N = 10	N = 30	N = 60	Exact
0.1	0.036487404375	0.036487479864	0.0364874799011	0.0364874799009
0.2	0.140639724816	0.140639621157	0.1406396211738	0.1406396211740
0.3	0.307484496274	0.307484627118	0.3074846271334	0.3074846271337
0.4	0.533284101747	0.533284109806	0.5332841098751	0.5332841098756
0.5	0.814757087316	0.814756949317	0.8147569493835	0.8147569493833
0.6	1.148837366742	1.148837422295	1.1488374222698	1.1488374222703
0.7	1.532565319887	1.532565426547	1.5325654264985	1.5325654264982
0.8	1.963029329581	1.963029254846	1.9630292548366	1.9630292548369
0.9	2.437333969513	2.437333970854	2.4373339708438	2.4373339708440
1.0	2.952583880039	2.952583880039	2.9525838800390	2.9525838800390

If the coefficients A = B = C = 1 are considered, in Table 7, the approximate values of function f(t) for N = 10, N = 30, and N = 60, are compared with its exact values. As we can see, increasing the value N leads to a low absolute error and high accuracy of the method, which proves the stability of the proposed method.

Table 7. Approximate values of f(t) for A = B = C = 1 and different values of N.

t	N = 10	N = 30	N = 60	Exact
0.1	0.033507162346	0.0335073099353	0.0335073100169	0.0335073100166
0.2	0.125221479995	0.1252212803110	0.1252212803466	0.1252212803471
0.3	0.267609140575	0.2676094195004	0.2676094195331	0.2676094195339
0.4	0.455435400934	0.4554353974487	0.4554353975927	0.4554353975939
0.5	0.684335033706	0.6843347530036	0.6843347531505	0.6843347531500
0.6	0.950392421075	0.9503925632445	0.9503925632016	0.9503925632028
0.7	1.249958912764	1.2499591326644	1.2499591325649	1.2499591325644
0.8	1.579557379566	1.5795572087353	1.5795572087127	1.5795572087133
0.9	1.935832277274	1.9358322930399	1.9358322930172	1.9358322930176
1.0	2.315525822793	2.3155258227926	2.3155258227926	2.3155258227926

6. Conclusions

In this paper, we utilize Müntz orthogonal functions to provide the approximate solution of the fractional Bagley–Torvik equation subjected to initial-boundary conditions. First, the functional equations are introduced, which help to solve the problem effectively. Then the fractional integral operator is defined as Müntz orthogonal functions that shorten the solution of the Bagley–Torvik fractional equation in a system of algebraic equations. The roots of Müntz orthogonal functions on the interval [0, 1] are simple and distinct considered collocation points. Furthermore, solving these algebraic equations help us to approximate the desired function using Müntz orthogonal functions. In the end, several numerical examples with initial-boundary conditions are solved with this method. The results obtained by the present method are computationally more accurate compared with the existing methods for solving the fractional Bagley–Torvik equation.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

No data were used for the research described in the article.

References

1 Mashayekhi S. and Razzaghi M., Numerical solution of the fractional Bagley–Torvik equation by using hybrid functions approximation, Mathematical Methods in the Applied Sciences. (2016) 39, no. 3, 353–365, https://doi.org/10.1002/mma.3486, 2-s2.0-84956876682.
10.1002/mma.3486
Web of Science® Google Scholar
2 Mohammadi F. and Mohyud-Din S. T., A fractional-order Legendre collocation method for solving the Bagley–Torvik equations, Advances in Difference Equations. (2016) 2016, https://doi.org/10.1186/s13662-016-0989-x, 2-s2.0-84992426116, 269.
10.1186/s13662-016-0989-x
Google Scholar
3 Deshi A. B. and Gudodagi G. A., Numerical solution of Bagley–Torvik, nonlinear and higher order fractional differential equations using Haar wavelet, SeMA Journal. (2022) 79, 663–675, https://doi.org/10.1007/s40324-021-00264-z.
10.1007/s40324-021-00264-z
Google Scholar
4 Uddin M. and Ahmad S., On the numerical solution of Bagley–Torvik equation via the Laplace transform, Tbilisi Mathematical Journal. (2017) 10, no. 1, 279–284.
10.1515/tmj-2017-0017
Google Scholar
5 Ji T. and Hou J., Numerical solution of the Bagley–Torvik equation using Laguerre polynomials, SeMA Journal. (2020) 77, 97–106, https://doi.org/10.1007/s40324-019-00204-y.
10.1007/s40324-019-00204-y
Google Scholar
6 Ji T., Hou J., and Yang C., Numerical solution of the Bagley–Torvik equation using shifted Chebyshev operational matrix, Advances in Difference Equations. (2020) 2020, https://doi.org/10.1186/s13662-020-03110-0, 648.
10.1186/s13662-020-03110-0
Web of Science® Google Scholar
7 Verma A. and Kumar M., Numerical solution of Bagley–Torvik equations using Legendre artificial neural network method, Evolutionary Intelligence. (2021) 14, 2027–2037, https://doi.org/10.1007/s12065-020-00481-x.
10.1007/s12065-020-00481-x
Web of Science® Google Scholar
8 Saw V. and Kumar S., Numerical solution of fraction Bagley–Torvik boundary value problem based on chebyshev collocation method, International Journal of Applied and Computational Mathematics. (2019) 5, https://doi.org/10.1007/s40819-019-0653-8, 68.
10.1007/s40819-019-0653-8
Google Scholar
9 Krishnasamy V. S. and Razzaghi M., The numerical solution of the Bagley–Torvik equation with fractional Taylor method, Journal of Computational and Nonlinear Dynamics. (2016) 11, no. 5, https://doi.org/10.1115/1.4032390, 2-s2.0-84957593451, 051010.
10.1115/1.4032390
Web of Science® Google Scholar
10 Esmaeili S., The numerical solution of the Bagley–Torvik equation by exponential integrators, Scientia Iranica. (2017) 24, no. 6, 2941–2951, https://doi.org/10.24200/sci.2017.4503, 2-s2.0-85039705156.
10.24200/sci.2017.4503
Web of Science® Google Scholar
11 Srivastava H. M., Shah F. A., and Abass R., An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley–Torvik equation, Russian Journal of Mathematical Physics. (2019) 26, 77–93, https://doi.org/10.1134/S1061920819010096, 2-s2.0-85063618387.
10.1134/S1061920819010096
Web of Science® Google Scholar
12 Rahimkhani P. and Ordokhani Y., Application of Müntz–Legendre polynomials for solving the Bagley–Torvik equation in a large interval, SeMA Journal. (2018) 75, 517–533, https://doi.org/10.1007/s40324-018-0148-2.
10.1007/s40324-018-0148-2
Google Scholar
13 Zahra W. K. and Van Daele M., Discrete spline methods for solving two point fractional Bagley–Torvik equation, Applied Mathematics and Computation. (2017) 296, 42–56, https://doi.org/10.1016/j.amc.2016.09.016, 2-s2.0-84993995820.
10.1016/j.amc.2016.09.016
Web of Science® Google Scholar
14 Zubair T., Sajjad M., Madni R., and Shabir A., Hermite solution of Bagley–Torvik equation of fractional order, International Journal of Modern Nonlinear Theory and Application. (2017) 6, no. 3, 104–118, https://doi.org/10.4236/ijmnta.2017.63010.
10.4236/ijmnta.2017.63010
Google Scholar
15 Izadi M. and Negar M. R., Local discontinuous Galerkin approximations to fractional Bagley–Torvik equation, Mathematical Methods in the Applied Sciences. (2020) 43, no. 7, 4798–4813, https://doi.org/10.1002/mma.6233.
10.1002/mma.6233
Web of Science® Google Scholar
16 Nouri K., Elahi-Mehr S., and Torkzadeh L., Investigation of the behavior of the fractional Bagley–Torvik and Basset equations via numerical inverse Laplace transform, Romanian Reports in Physics. (2016) 68, no. 2, 503–514.
Web of Science® Google Scholar
17 Atta A. G., Moatimid G. M., and Youssri Y. H., Generalized Fibonacci operational tau algorithm for fractional Bagley–Torvik equation, Progress in Fractional Differentiation and Applications. (2020) 6, no. 3, 215–224.
10.18576/pfda/060305
Google Scholar
18 Hou J., Yang C., and Lv X., Jacobi collocation methods for solving the fractional Bagley–Torvik equation, IAENG International Journal of Applied Mathematics. (2020) 50, no. 1, 114–120.
Google Scholar
19 Pasca M. S., Razzaghi M., and Lapadat M., Approximate solutions for the Bagley–Torvik fractional equation with boundary conditions using the polynomial least Squares method, 29, ITM Web of Conferences, 2019, EDP Sciences, https://doi.org/10.1051/itmconf/20192901011, 01011.
10.1051/itmconf/20192901011
Google Scholar
20 Chen J., A fast multiscale Galerkin algorithm for solving boundary value problem of the fractional Bagley–Torvik equation, Boundary Value Problems. (2020) 2020, https://doi.org/10.1186/s13661-020-01391-8, 91.
10.1186/s13661-020-01391-8
Web of Science® Google Scholar
21 Alshammari S., Al-Smadi M., Hashim I., and Alias M. A., Residual power series technique for simulating fractional Bagley–Torvik problems emerging in applied physics, Applied Sciences. (2019) 9, no. 23, https://doi.org/10.3390/app9235029, 5029.
10.3390/app9235029
Google Scholar
22 Karaaslan M. F., Celiker F., and Kurulay M., Approximate solution of the Bagley–Torvik equation by hybridizable discontinuous Galerkin methods, Applied Mathematics and Computation. (2016) 285, 51–58, https://doi.org/10.1016/j.amc.2016.03.024, 2-s2.0-84962911421.
10.1016/j.amc.2016.03.024
Web of Science® Google Scholar
23 Pang D., Jiang W., Du J., and Niazi A. U. K., Analytical solution of the generalized Bagley–Torvik equation, Advances in Difference Equations. (2019) 2019, https://doi.org/10.1186/s13662-019-2082-8, 2-s2.0-85066472364, 207.
10.1186/s13662-019-2082-8
Google Scholar
24 Jena R. M. and Chakraverty S., Analytical solution of Bagley–Torvik equations using Sumudu transformation method, SN Applied Sciences. (2019) 1, https://doi.org/10.1007/s42452-019-0259-0, 246.
10.1007/s42452-019-0259-0
Web of Science® Google Scholar
25 Bansal M. K. and Jain R., Analytical solution of Bagley Torvik equation by generalize differential transform, International Journal of Pure and Apllied Mathematics. (2016) 110, no. 2, 265–273, https://doi.org/10.12732/ijpam.v110i2.3, 2-s2.0-84995551126.
10.12732/ijpam.v110i2.3
Google Scholar
26 Pinar Z., On the explicit solutions of fractional Bagley–Torvik equation arises in engineering, An International Journal of Optimization and Control: Theories & Applications (IJOCTA). (2019) 9, no. 3, 52–58, https://doi.org/10.11121/ijocta.01.2019.00638, 2-s2.0-85068829690.
10.11121/ijocta.01.2019.00638
Google Scholar
27 Yi M., Wang L., and Huang J., Legendre wavelets method for the numerical solution of fractional integro-differential equations with weakly singular kernel, Applied Mathematical Modelling. (2016) 40, no. 4, 3422–3437, https://doi.org/10.1016/j.apm.2015.10.009, 2-s2.0-84959297843.
10.1016/j.apm.2015.10.009
Web of Science® Google Scholar
28 Wang Y., Zhu L., and Wang Z., Fractional-order Euler functions for solving fractional integro-differential equations with weakly singular kernel, Advances in Difference Equations. (2018) 2018, https://doi.org/10.1186/s13662-018-1699-3, 2-s2.0-85050408914, 254.
10.1186/s13662-018-1699-3
Google Scholar
29 Ali K. K., Abd El Salam M. A., Mohamed E. M. H., Samet B., Kumar S., and Osman M. S., Numerical solution for generalized nonlinear fractional integro-differential equations with linear functional arguments using Chebyshev series, Advances in Difference Equations. (2020) 2020, https://doi.org/10.1186/s13662-020-02951-z, 494.
10.1186/s13662-020-02951-z
Web of Science® Google Scholar
30 Du H., Chen Z., and Yang T., A stable least residue method in reproducing kernel space for solving a nonlinear fractional integro-differential equation with a weakly singular kernel, Applied Numerical Mathematics. (2020) 157, 210–222, https://doi.org/10.1016/j.apnum.2020.06.004.
10.1016/j.apnum.2020.06.004
Web of Science® Google Scholar
31 Mokhtary P., Discrete galerkin method for fractional integro-differential equations, Acta Mathematica Scientia. (2016) 36, no. 2, 560–578, https://doi.org/10.1016/S0252-9602(16)30021-2, 2-s2.0-84958225668.
10.1016/S0252-9602(16)30021-2
Web of Science® Google Scholar
32 Abbasbandy S., Hashemi M. S., and Hashim I., On convergence of homotopy analysis method and its application to fractional integro-differential equations, Quaestiones Mathematicae. (2013) 36, no. 1, 93–105, https://doi.org/10.2989/16073606.2013.780336, 2-s2.0-84876037987.
10.2989/16073606.2013.780336
Web of Science® Google Scholar
33 Kurulay M. and Secer A., Variational iteration method for solving nonlinear fractional integro-differential equations, International Journal of Computer Science and Emerging Technologies. (2011) 2, 18–20.
Google Scholar
34 Zhang G. and Zhu R., Runge–Kutta convolution quadrature methods with convergence and stability analysis for nonlinear singular fractional integro-differential equations, Communications in Nonlinear Science and Numerical Simulation. (2020) 84, https://doi.org/10.1016/j.cnsns.2019.105132, 105132.
10.1016/j.cnsns.2019.105132
Web of Science® Google Scholar
35 Amer Y. A., Mahdy A. M. S., and Youssef E. S. M., Solving fractional integro-differential equations by using sumudu transform method and Hermite spectral collocation method, Computers, Materials & Continua. (2018) 54, no. 2, 161–180, https://doi.org/10.3970/cmc.2018.054.161, 2-s2.0-85042878237.
10.3970/cmc.2018.054.161
Web of Science® Google Scholar
36 Torvik P. J. and Bagley R. L., On the appearance of the fractional derivative in the behavior of real materials, Journal of Applied Mechanics. (1984) 51, no. 2, 294–298, https://doi.org/10.1115/1.3167615, 2-s2.0-0021439912.
10.1115/1.3167615
Web of Science® Google Scholar
37 Saadatmandi A. and Akhlaghi S., Using hybrid of Block-Pulse functions and Bernoulli polynomials to solve fractional Fredholm-Volterra integro-differential equations, Sains Malaysiana. (2020) 49, no. 4, 953–962, https://doi.org/10.17576/jsm-2020-4904-24.
10.17576/jsm-2020-4904-24
Web of Science® Google Scholar
38 He J.-H. and El-Dib Y. O., A tutorial introduction to the two-scale fractal calculus and its application to the fractal zhiber–shabat oscillator, Fractals. (2021) 29, no. 8, https://doi.org/10.1142/S0218348X21502686, 2150268.
10.1142/S0218348X21502686
Web of Science® Google Scholar
39 Wang K.-L. and Yao S.-W., Numerical method for fractional Zakharov–Kuznetsov equations with he’s fractional derivative, Thermal Science. (2019) 23, no. 4, 2163–2170, https://doi.org/10.2298/TSCI1904163W, 2-s2.0-85073695339.
10.2298/TSCI1904163W
Web of Science® Google Scholar
40 Bahmanpour M., Kajani M. T., and Maleki M., Solving Fredholm integral equations of the first kind using Müntz wavelets, Applied Numerical Mathematics. (2019) 143, 159–171, https://doi.org/10.1016/j.apnum.2019.04.007, 2-s2.0-85064319099.
10.1016/j.apnum.2019.04.007
Web of Science® Google Scholar
41 Dokuyucu M. A., Caputo and Atangana–Baleanu–Caputo fractional derivative applied to garden equation, Turkish Journal of Science. (2020) 5, no. 1, 1–7.
Google Scholar
42 Kilbas A. A., Koroleva A. A., and Rogosin S. V., Multi-parametric mittag-leffler functions and their extension, Fractional Calculus and Applied Analysis. (2013) 16, 378–404, https://doi.org/10.2478/s13540-013-0024-9, 2-s2.0-84879636146.
10.2478/s13540-013-0024-9
Web of Science® Google Scholar
43 Milovanović G. V., Müntz orthogonal polynomials and their numerical evaluation, Applications and Computation of Orthogonal Polynomials, 1999, Birkhäuser, Basel, 179–194, https://doi.org/10.1007/978-3-0348-8685-7_13.
10.1007/978-3-0348-8685-7_13
Google Scholar
44 Canuto C., Hussaini M. Y., Quarteroni A., and Zang T. A., Spectral methods: fundamentals in single domains, 2007, Springer Science & Business Media.
10.1007/978-3-540-30728-0
Google Scholar
45 Zolfaghari M., Ghaderi R., SheikholEslami A., Ranjbar A., Hosseinnia S. H., Momani S., and Sadati J., Application of the enhanced homotopy perturbation method to solve the fractional-order Bagley–Torvik differential equation, Physica Scripta. (2009) 2009, no. T136, https://doi.org/10.1088/0031-8949/2009/T136/014032, 2-s2.0-77952807944, 014032.
10.1088/0031-8949/2009/T136/014032
Google Scholar

All articles

Application of Müntz Orthogonal Functions on the Solution of the Fractional Bagley–Torvik Equation Using Collocation Method with Error Stimate

Abstract

1. Introduction