Volume 2023, Issue 1 4348758

Research Article

Open Access

Abundant Soliton Structures to the (2 + 1)-Dimensional Heisenberg Ferromagnetic Spin Chain Dynamical Model

Corresponding Author

Kang-Jia Wang

[email protected]

orcid.org/0000-0002-3905-0844

School of Physics and Electronic Information Engineering, Henan Polytechnic University, Jiaozuo 454003, China hpu.edu.cn

Search for more papers by this author

Feng Shi,

Feng Shi

School of Physics and Electronic Information Engineering, Henan Polytechnic University, Jiaozuo 454003, China hpu.edu.cn

Search for more papers by this author

Guo-Dong Wang,

Guo-Dong Wang

School of Physics and Electronic Information Engineering, Henan Polytechnic University, Jiaozuo 454003, China hpu.edu.cn

Search for more papers by this author

Kang-Jia Wang,

Corresponding Author

Kang-Jia Wang

[email protected]

orcid.org/0000-0002-3905-0844

School of Physics and Electronic Information Engineering, Henan Polytechnic University, Jiaozuo 454003, China hpu.edu.cn

Search for more papers by this author

Feng Shi,

Feng Shi

School of Physics and Electronic Information Engineering, Henan Polytechnic University, Jiaozuo 454003, China hpu.edu.cn

Search for more papers by this author

Guo-Dong Wang,

Guo-Dong Wang

School of Physics and Electronic Information Engineering, Henan Polytechnic University, Jiaozuo 454003, China hpu.edu.cn

Search for more papers by this author

First published: 25 January 2023

https://doi.org/10.1155/2023/4348758

Citations: 12

Academic Editor: Ghulam Rasool

Share a link

Email
Wechat
Bluesky

Abstract

In this paper, we aim to investigate the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation that is used to describe the nonlinear dynamics of magnets. Two recent effective technologies, namely, the variational method and subequation method, are employed to construct the abundant soliton solutions. By these two methods, diverse solutions such as the bright soliton, dark soliton, bright-dark soliton, perfect periodic soliton, and singular periodic soliton are successfully extracted. The numerical results are illustrated in the form of 3-D plots and 2-D curves by choosing proper parametric values to interpret the dynamics of wave profiles. Finally, the physical interpretation of the acquired results is elaborated in detail. The results obtained in this study are helpful to explain some physical meanings of some nonlinear physical models in electromagnetic waves.

1. Introduction

Many complex problems arising in nature can be described by nonlinear partial differential equations (NLPDEs). The exact solutions of the NLPDEs have been a hot topic for mathematicians and physicists. The soliton travels in a nonlinear media while maintaining a constant size, shape, and energy. The study of the soliton solutions can provide a theoretical reference for the research of nonlinear physical models, soliton control, optical switching equipment, and so on. Up to now, many effective and powerful methods have been obtained for constructing the soliton solutions of the NLPDEs: the extended trial equation method [1, 2], generalized exponential rational function method [3], sine-Gordon expansion method [4–6], generalized (G′/G) expansion method [7], extended rational sine-cosine and sinh-cosh method [8, 9], F-expansion method [10–12], Cole-Hopf transformation [13, 14], exp-function method [15–17], extended tanh-function method [18–20], Bäcklund transformation [21], Sardar subequation method [22, 23], and so on [24–31]. In this paper, we aim to study the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation (HFSCE) that is given by [32]:

(1)

where γ₁ = λ⁴(v + v₂), γ₂ = λ⁴(v₁ + v₂), γ₃ = 3λv₂, and γ₄ = 3λ⁴A. λ is the lattice parameter, v and v₁ are the coefficients of bilinear exchange interactions along the x- and y-directions, respectively. v₂ refers to the neighboring interaction along the diagonal, and A represents the uniaxial crystal field anisotropy parameter.

The (2 + 1)-dimensional HFSCE is used to describe the nonlinear dynamics of magnets. In [33], the two methods, improved auxiliary equation and generalized Riccati mapping methods, are used to seek for the diverse solitons. In [34], the Jacobi elliptic expansion method is adopted and bright and dark soliton solutions are obtained. In [35], the theory of dynamical systems is introduced for constructing the bounded traveling wave solutions. In [36], the modified Khater method is carried out to deal with Eq. (1). The generalized tanh methods is employed to solve Eq. (1) in [37], and dark, dark-bright, or combined optical and singular soliton solutions are attained. In [38], the authors use two approaches, namely, the modified F-expansion and projective Riccati equation methods to investigate (Eq. (1)). Inspired by these research results, here in this work, we mainly seek its abundant soliton solutions by using two effective methods, the variational method (VM) and subequation method (SEM). The VM which is based on the variational theory can provide the optimized solutions in only one step via the stationary condition. In addition, the SEM that is straightforward and effective can construct abundant solutions via the symbolic calculation. The structure of this paper is organized as follows. In Section 2, we introduce the algorithms of the two methods. In Section 3, the two methods are applied to find the soliton solutions. In Section 3, the behaviors of the solutions and their physical interpretations are presented. Finally, a conclusion is reached in Section 5.

2. The Two Methods

This section is to give a brief introduction to the VM and SEM. Considering a partial differential equation (PDE) with the form as

(2)

Applying the following transformation,

(3)

where k and r are arbitrary nonzero constants. Substituting Eq. (3) into Eq. (2), we can convert Eq. (3) into an ordinary differential equation (ODE):

(4)

2.1. The VM

Aided by the semi-inverse method [39–45], the variational principle of Eq. (4) can be developed as

(5)

Assuming that the solutions of Eq. (4) take the following different forms.

Hypothesis one: U(ξ) = H₁sech(ξ).

Hypothesis two: U(ξ) = H₂sech²(ξ).

Hypothesis three: U(ξ) = ((H₃sinh(ξ))/([cosh(ξ)]^(3/2))).

Hypothesis four: U(ξ) = H₄cos(ϖξ).

Then, taking the above-assumed expressions into Eq. (5) and applying the stationary conditions as

Result one: (dJ/dH₁) = 0.

Result two: (dJ/dH₂) = 0.

Result three: (dJ/dH₃) = 0.

Result four: (dJ/dH₄) = 0.

Solving the above different results, the expressions of H₁, H₂, H₃, and H₄ can be easily determined.

2.2. The SEM

By the SEM [46–49], the solution of Eq. (4) can be assumed as

(6)

where σ_i(i = 0, 1, 2.⋯, c) are the constants to be determined later. There is

(7)

Here, Ξ is a constant. Substituting Eq. (6) together with Eq. (7) into Eq. (4), we can determine the value of c by the balancing theory. With the determined c, we can get an overdetermined system of nonlinear algebraic equations by setting the coefficients of each power of φ(γ) to zero. Solving it, we can determine the expression of Eq. (6).

The solutions of Eq.(7) for the different conditions are

(8)

3. Applications

The following complex transformation is introduced:

(9)

Taking Eq. (9) into Eq. (1) produces the following the imaginary and real parts, respectively, as

(10)

(11)

where ψ^″ = (d²ψ/dξ²).

3.1. Application of the VM

With help of the semi-inverse method, we can get the Euler-Lagrange equation of Eq. (11) as

(12)

So, the variational formulation of Eq. (11) can be established as

(13)

For simplicity, we rewrite Eq. (13) as

(14)

where μ₁ = (1/2)[k − γ₁m² − n(γ₂n + γ₃m)], μ₂ = (3/4)γ₄, and μ₃ = (1/2)(γ₁a² + γ₂b² + γ₃ab).

3.1.1. Bright Soliton

We assume the solution of Eq. (11) has the following form:

(15)

Bringing the above equation into Eq. (14) yields

(16)

Taking the stationary value condition for Eq. (16) with respect to A, we attain

(17)

which leads to

(18)

With this, the solution of Eq. (11) can be obtained as

(19)

Thus, the bright soliton solution of Eq. (1) is attained as

(20)

3.1.2. Bright-Like Soliton

We can also suppose the solution of Eq. (11) as

(21)

In the same way, substituting Eq. (21) into Eq. (14) results in

(22)

Taking the stationary value condition of Eq. (22) yields

(23)

Solving Eq. (23), we have

(24)

Thus, we can get the solution of Eq. (4) as

(25)

Then, the bright-like soliton solution of Eq. (1) is found as

(26)

3.1.3. Bright-Dark Soliton

The solution of Eq. (11) can be assumed as

(27)

Taking the above equation into Eq. (14) yields

(28)

Computing the stationary condition of the above equation as

(29)

which leads to

(30)

So, we can determine the expression of A as

(31)

Then, Eq. (27) can be written as

(32)

Thus, we gain the bright-dark soliton solution of Eq. (1) as

(33)

3.1.4. Periodic Soliton

The periodic solution of Eq. (11) is assumed as

(34)

where ϖ is the frequency to be further determined. Injecting Eq. (34) into Eq. (7), there is

(35)

Taking its stationary value condition with respect to Θ yields

(36)

From which, we can determine the frequency as

(37)

Therefore, we attain the periodic solution of Eq. (4) as

(38)

So, the periodic soliton solution of Eq. (1) is obtained as

(39)

3.2. Application of the SEM

To use the SEM, we first rewrite Eq. (11) as

(40)

where δ₁ = ((k − γ₁m² − n(γ₂n + γ₃m))/(γ₁a² + γ₂b² + γ₃ab)) and δ₂ = (γ₄/(γ₁a² + γ₂b² + γ₃ab)).

Based on the SEM, the solution of Eq. (40) is considered as

(41)

Balancing ψ^″ and ψ³, it gives

(42)

so Eq. (41) becomes

(43)

And there is

(44)

Taking Eq. (43) along with Eq. (44) into Eq. (40) results into

φ⁰:

φ¹:

φ²:

φ³:

Solving the above equations, we have

(45)

Then, we get the solutions as follows:

Case 1. For ((k − γ₁m² − n(γ₂n + γ₃m))/(γ₁a² + γ₂b² + γ₃ab)) < 0, we have

(46)

(47)

Case 2. For ((k − γ₁m² − n(γ₂n + γ₃m))/(γ₁a² + γ₂b² + γ₃ab)) > 0, we have

(48)

Case 3. For ((k − γ₁m² − n(γ₂n + γ₃m))/(γ₁a² + γ₂b² + γ₃ab)) = 0, we have

(49)

For Eqs. (46)~(49), there is η = 2aγ₁m + 2bγ₂n + γ₃(bm + an).

4. Numerical Results and Physical Interpretation

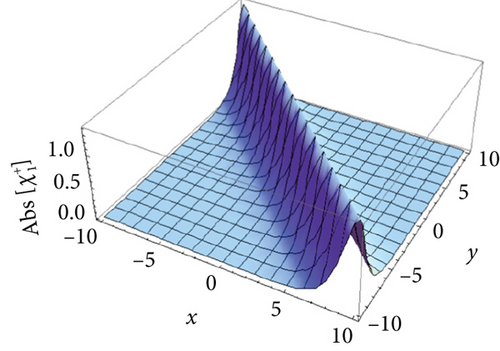
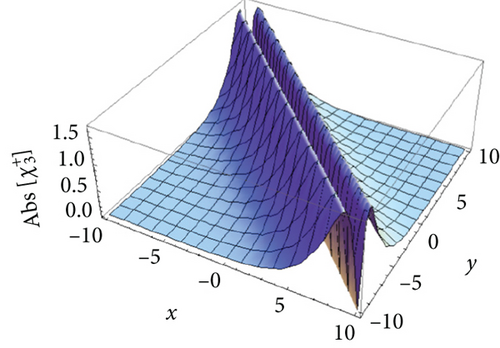
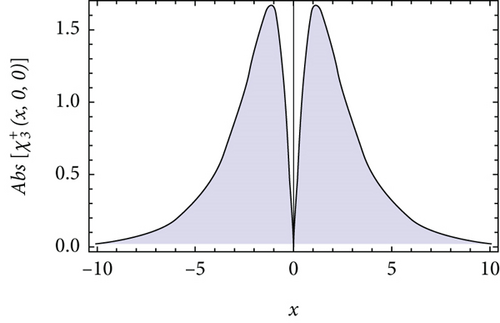
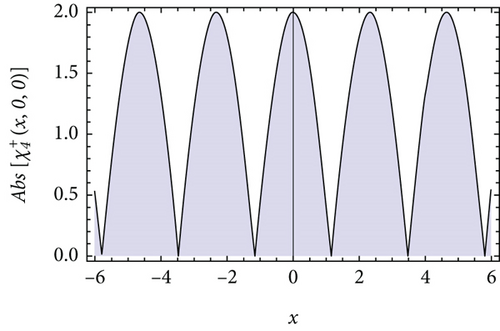
In this section, we mainly illustrate the results gained in Section 3 through the 3-D plot and 2-D curve to interpret the dynamics of wave profiles by selecting the proper parameters.

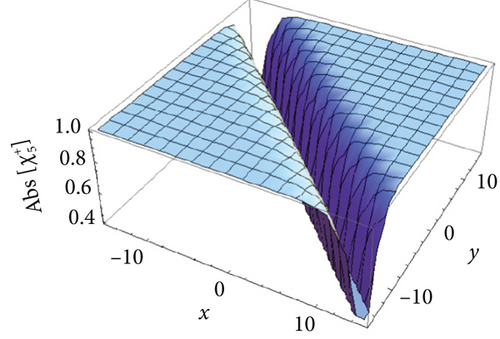
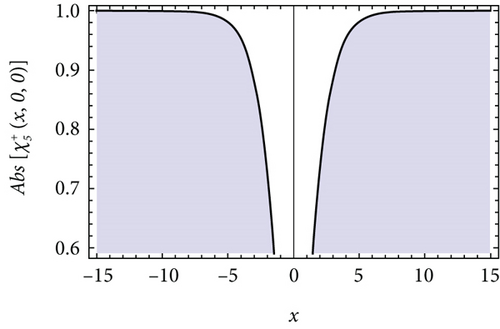
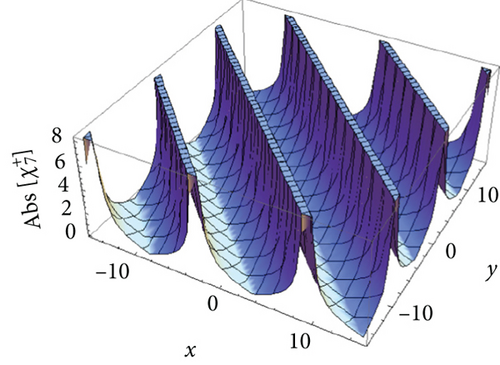
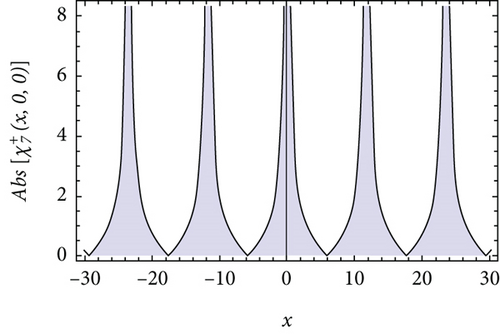
We plot the 3-D plots of absolute value of the solutions , , , , and in Figures 1(a), 2(a), 3(a), 4(a), and 5(a), respectively, for t = 0. Besides, we also draw the 2-D curves of the absolute value of the solutions , , , , and in Figures 1(b), 2(b), 3(b), 4(b), and 5(b), respectively, for y = 0 and t = 0. It can be observed that the absolute values of and are the bright soliton wave and dark soliton, the absolute values of is the bright-dark soliton, and the absolute values of and are perfect periodic soliton and singular periodic soliton.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The behavior of with the parameters λ = 1, v = 1, v₁ = 1, v₂ = −2, A = 1, a = 1, b = 1, m = 1, n = 1, k = 1, and ϕ₀ = 0. (a) The 3-D plot for t = 0. (b) The 2-D curve for y = 0 and t = 0.

5. Conclusion and Future Recommendation

In this work, abundant soliton solutions of the (2 + 1)-dimensional HFSCE such as the bright soliton, dark soliton, bright-dark soliton, perfect periodic soliton, and singular periodic soliton are successfully constructed by means of the VM and SEM. The absolute parts of the solutions are presented through the 3-D plot and 2-D curve by assigning the proper parameters. In addition, we give the physical explanation of the solutions in detail. Through the calculation process, it can be found that the VM can reduce the order of the differential equation to simplify the equation via the variational theory. In addition, the SEM is effective and direct and can construct the different types of solitons. The methods adopted in this study can be used to investigate the other PDEs arising in the physics.

In recent years, the fractal and fractional derivatives [50–61] have attracted extensive attention in different fields. How to apply the proposed methods to study the fractal and fractional PDEs will be the focus of our future research.

Conflicts of Interest

This work does not have any conflicts of interest.

Acknowledgments

This work is supported by the Key Programs of Universities in Henan Province of China (22A140006), the Fundamental Research Funds for the Universities of Henan Province (NSFRF210324), Program of Henan Polytechnic University (B2018-40), and the Opening Project of Henan Engineering Laboratory of Photoelectric Sensor and Intelligent Measurement and Control, Henan Polytechnic University (HELPSIMC-2020-004). This work is also supported by the Innovative Scientists and Technicians Team of Henan Provincial High Education (21IRTSTHN016), Key Project of the Scientific and Technology Research of Henan Province (212102210224), and the Doctoral Fund Project of Henan Polytechnic University (No. B2014-028).

Open Research

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Gurefe Y., Misirli E., Sonmezoglu A., and Ekici M., Extended trial equation method to generalized nonlinear partial differential equations, Applied Mathematics and Computation. (2013) 219, no. 10, 5253–5260, https://doi.org/10.1016/j.amc.2012.11.046, 2-s2.0-84872154677.
10.1016/j.amc.2012.11.046
Web of Science® Google Scholar
2 Hu J. Y., Feng X. B., and Yang Y. F., Optical envelope patterns perturbation with full nonlinearity for Gerdjikov-Ivanov equation by trial equation method, Optik. (2021) 240, article 166877, https://doi.org/10.1016/j.ijleo.2021.166877.
10.1016/j.ijleo.2021.166877
Web of Science® Google Scholar
3 Younas U., Younis M., Seadawy A. R., Rizvi S. T. R., Althobaiti S., and Sayed S., Diverse exact solutions for modified nonlinear Schrodinger equation with conformable fractional derivative, Results in Physics. (2021) 20, article 103766, https://doi.org/10.1016/j.rinp.2020.103766.
10.1016/j.rinp.2020.103766
Web of Science® Google Scholar
4 Baskonus H. M., Bulut H., and Sulaiman T. A., New complex hyperbolic structures to the Lonngren-wave equation by using sine-Gordon expansion method, Applied Mathematics and Nonlinear Sciences. (2019) 4, no. 1, 129–138, https://doi.org/10.2478/AMNS.2019.1.00013.
10.2478/AMNS.2019.1.00013
Google Scholar
5 Yel G., Baskonus H. M., and Bulut H., Novel archetypes of new coupled Konno-Oono equation by using sine-Gordon expansion method, Optical and Quantum Electronics. (2017) 49, no. 9, 1–10, https://doi.org/10.1007/s11082-017-1127-z, 2-s2.0-85026996830.
10.1007/s11082-017-1127-z
Web of Science® Google Scholar
6 Fahim M. R. A., Kundu P. R., Islam M. E., Akbar M. A., and Osman M. S., Wave profile analysis of a couple of (3+1)-dimensional nonlinear evolution equations by sine-Gordon expansion approach, Journal of Ocean Engineering and Science. (2022) 7, no. 3, 272–279, https://doi.org/10.1016/j.joes.2021.08.009.
10.1016/j.joes.2021.08.009
Web of Science® Google Scholar
7 Teymuri Sindi C. and Manafian J., Wave solutions for variants of the KdV–Burger and the K(n,n)–Burger equations by the generalized G′/G-expansion method, Mathematical Methods in the Applied Sciences. (2017) 40, no. 12, 4350–4363, https://doi.org/10.1002/mma.4309, 2-s2.0-85010908345.
10.1002/mma.4309
Web of Science® Google Scholar
8 Mahak N. and Akram G., Exact solitary wave solutions by extended rational sine-cosine and extended rational sinh-cosh techniques, Physica Scripta. (2019) 94, no. 11, article 115212, https://doi.org/10.1088/1402-4896/ab20f3.
10.1088/1402-4896/ab20f3
Web of Science® Google Scholar
9 Mahak N. and Akram G., Extension of rational sine-cosine and rational sinh-cosh techniques to extract solutions for the perturbed NLSE with Kerr law nonlinearity, The European Physical Journal Plus. (2019) 134, no. 4, 1–10, https://doi.org/10.1140/epjp/i2019-12545-x, 2-s2.0-85064566211.
10.1140/epjp/i2019-12545-x
Web of Science® Google Scholar
10 Islam M. S., Khan K., Akbar M. A., and Mastroberardino A., A note on improved F-expansion method combined with Riccati equation applied to nonlinear evolution equations, Royal Society Open Science. (2014) 1, no. 2, article 140038, https://doi.org/10.1098/rsos.140038, 2-s2.0-84930969714, 26064530.
10.1098/rsos.140038
PubMed Web of Science® Google Scholar
11 Islam M., Akbar M. A., and Khan K., Analytical solutions of nonlinear Klein–Gordon equation using the improved F-expansion method, Optical and Quantum Electronics. (2018) 50, no. 5, 1–11, https://doi.org/10.1007/s11082-018-1445-9, 2-s2.0-85046855198.
10.1007/s11082-018-1445-9
Web of Science® Google Scholar
12 Yıldırım Y., Optical solitons with Biswas-Arshed equation by F-expansion method, Optik. (2021) 227, article 165788, https://doi.org/10.1016/j.ijleo.2020.165788.
10.1016/j.ijleo.2020.165788
Web of Science® Google Scholar
13 Wang K. J., Diverse soliton solutions to the Fokas system via the Cole-Hopf transformation, Optik. (2023) 272, article 170250, https://doi.org/10.1016/j.ijleo.2022.170250.
10.1016/j.ijleo.2022.170250
Web of Science® Google Scholar
14 Wang K. J., Si J., and Liu J. H., Diverse optical soliton solutions to the Kundu-Mukherjee-Naskar equation via two novel techniques, Optik. (2023) 273, article 170403, https://doi.org/10.1016/j.ijleo.2022.170403.
10.1016/j.ijleo.2022.170403
Web of Science® Google Scholar
15 He J. H. and Wu X. H., Exp-function method for nonlinear wave equations, Chaos, Solitons & Fractals. (2006) 30, no. 3, 700–708, https://doi.org/10.1016/j.chaos.2006.03.020, 2-s2.0-33745177020.
10.1016/j.chaos.2006.03.020
Web of Science® Google Scholar
16 Zulfiqar A. and Ahmad J., Soliton solutions of fractional modified unstable Schrodinger equation using Exp-function method, Results in Physics. (2020) 19, article 103476, https://doi.org/10.1016/j.rinp.2020.103476.
10.1016/j.rinp.2020.103476
Web of Science® Google Scholar
17 Ahmed H. M., El-Sheikh M. M., Arnous A. H., and Rabie W. B., Solitons and other solutions to (n+1)-dimensional modified Zakharov–Kuznetsov equation by exp-function method, SeMA Journal. (2021) 78, no. 1, 1–13, https://doi.org/10.1007/s40324-020-00227-w.
10.1007/s40324-020-00227-w
Google Scholar
18 Elwakil S. A., El-Labany S. K., Zahran M. A., and Sabry R., Modified extended tanh-function method for solving nonlinear partial differential equations, Physics Letters A. (2002) 299, no. 2-3, 179–188, https://doi.org/10.1016/S0375-9601(02)00669-2, 2-s2.0-0036645735.
10.1016/S0375-9601(02)00669-2
CAS Web of Science® Google Scholar
19 Elsherbeny A. M., El–Barkouky R., Ahmed H. M., El-Hassani R. M., and Arnous A. H., Optical solitons and another solutions for Radhakrishnan-Kundu-Laksmannan equation by using improved modified extended tanh-function method, Optical and Quantum Electronics. (2021) 53, no. 12, 1–15, https://doi.org/10.1007/s11082-021-03382-0.
10.1007/s11082-021-03382-0
Web of Science® Google Scholar
20 Alam L. M. B., Jiang X., and Mamun A. A., Exact and explicit traveling wave solution to the time-fractional phi-four and (2+1) dimensional CBS equations using the modified extended tanh-function method in mathematical physics, Partial Differential Equations in Applied Mathematics. (2021) 4, article 100039, https://doi.org/10.1016/j.padiff.2021.100039.
10.1016/j.padiff.2021.100039
Google Scholar
21 Wang K. J., Bäcklund transformation and diverse exact explicit solutions of the fractal combined KdV-mKdV equation, Fractals. (2022) 30, no. 9, https://doi.org/10.1142/S0218348X22501894.
10.1142/S0218348X22501894
Web of Science® Google Scholar
22 Rezazadeh H., Inc M., and Baleanu D., New solitary wave solutions for variants of (3+1)-dimensional Wazwaz-Benjamin-Bona-Mahony equations, Frontiers in Physics. (2020) 8, https://doi.org/10.3389/fphy.2020.00332.
10.3389/fphy.2020.00332
Web of Science® Google Scholar
23 Wang K. J. and Si J., Optical solitons to the Radhakrishnan-Kundu-Lakshmanan equation by two effective approaches, The European Physical Journal Plus. (2022) 137, no. 9, https://doi.org/10.1140/epjp/s13360-022-03239-9.
10.1140/epjp/s13360-022-03239-9
Web of Science® Google Scholar
24 Mohammed W., Iqbal N., Ali A., and el-Morshedy M., Exact solutions of the stochastic new coupled Konno-Oono equation, Results in Physics. (2021) 21, article 103830, https://doi.org/10.1016/j.rinp.2021.103830.
10.1016/j.rinp.2021.103830
Web of Science® Google Scholar
25 Hubert M. B., Betchewe G., Justin M., Doka S. Y., Crepin K. T., Biswas A., Zhou Q., Alshomrani A. S., Ekici M., Moshokoa S. P., and Belic M., Optical solitons with Lakshmanan-Porsezian-Daniel model by modified extended direct algebraic method, Optik. (2018) 162, 228–236, https://doi.org/10.1016/j.ijleo.2018.02.091, 2-s2.0-85042784204.
10.1016/j.ijleo.2018.02.091
Web of Science® Google Scholar
26 Wang K. J., A fast insight into the optical solitons of the generalized third-order nonlinear Schrodinger′s equation, Results in physics. (2022) 40, article 105872, https://doi.org/10.1016/j.rinp.2022.105872.
10.1016/j.rinp.2022.105872
Web of Science® Google Scholar
27 Jian-Gen L., Feng Y. Y., and Zhang H. Y., Exploration of the algebraic traveling wave solutions of a higher order model, Engineering Computations. (2021) 38, no. 2, 618–631, https://doi.org/10.1108/EC-07-2019-0303.
10.1108/EC-07-2019-0303
Web of Science® Google Scholar
28 Younas U., Rezazadeh H., Ren J., and Bilal M., Propagation of diverse exact solitary wave solutions in separation phase of iron (Fe-Cr− X (X= Mo, cu)) for the ternary alloys, International Journal of Modern Physics B. (2022) 36, no. 4, https://doi.org/10.1142/S0217979222500394.
10.1142/S0217979222500394
Web of Science® Google Scholar
29 Akinyemi L., Veeresha P., Şenol M., and Rezazadeh H., An efficient technique for generalized conformable Pochhammer–Chree models of longitudinal wave propagation of elastic rod, Indian Journal of Physics. (2022) 96, no. 14, 4209–4218, https://doi.org/10.1007/s12648-022-02324-0.
10.1007/s12648-022-02324-0
CAS Web of Science® Google Scholar
30 Lü X. and Chen S.-J., Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: One-lump-multi-stripe and one-lump-multi-soliton types, Nonlinear Dynamics. (2021) 103, no. 1, 947–977, https://doi.org/10.1007/s11071-020-06068-6.
10.1007/s11071-020-06068-6
Web of Science® Google Scholar
31 Wang K.-J., Liu J.-H., Si J., and Wang G.-D., Nonlinear dynamic behaviors of the (3+1)-dimensional B-type Kadomtsev–Petviashvili equation in fluid mechanics, Axioms. (2023) 12, no. 1, https://doi.org/10.3390/axioms12010095.
10.3390/axioms12010095
PubMed Web of Science® Google Scholar
32 Sulaiman T. A., Aktürk T., Bulut H., and Baskonus H. M., Investigation of various soliton solutions to the Heisenberg ferromagnetic spin chain equation, Journal of Electromagnetic Waves & Applications. (2018) 32, no. 9, 1093–1105, https://doi.org/10.1080/09205071.2017.1417919, 2-s2.0-85039148331.
10.1080/09205071.2017.1417919
Web of Science® Google Scholar
33 Seadawy A. R., Nasreen N., Lu D., and Arshad M., Arising wave propagation in nonlinear media for the (2+1)-dimensional Heisenberg ferromagnetic spin chain dynamical model, Physica A: Statistical Mechanics and its Applications. (2020) 538, article 122846, https://doi.org/10.1016/j.physa.2019.122846.
10.1016/j.physa.2019.122846
Web of Science® Google Scholar
34 Hosseini K., Salahshour S., Mirzazadeh M., Ahmadian A., Baleanu D., and Khoshrang A., The (2+1)-dimensional Heisenberg ferromagnetic spin chain equation: its solitons and Jacobi elliptic function solutions, The European Physical Journal Plus. (2021) 136, no. 2, 1–9, https://doi.org/10.1140/epjp/s13360-021-01160-1.
10.1140/epjp/s13360-021-01160-1
Web of Science® Google Scholar
35 Yang D., Traveling waves and bifurcations for the (2+1)-dimensional Heisenberg ferromagnetic spin chain equation, Optik. (2021) 248, article 168058, https://doi.org/10.1016/j.ijleo.2021.168058.
10.1016/j.ijleo.2021.168058
Web of Science® Google Scholar
36 Sahoo S. and Tripathy A., New exact solitary solutions of the (2+1)-dimensional Heisenberg ferromagnetic spin chain equation, The European Physical Journal Plus. (2022) 137, no. 3, 1–11, https://doi.org/10.1140/epjp/s13360-022-02609-7.
10.1140/epjp/s13360-022-02609-7
PubMed Web of Science® Google Scholar
37 Inc M., Aliyu A. I., Yusuf A., and Baleanu D., Optical solitons and modulation instability analysis of an integrable model of (2+1)-dimensional Heisenberg ferromagnetic spin chain equation, Superlattices and Microstructures. (2017) 112, 628–638, https://doi.org/10.1016/j.spmi.2017.10.018, 2-s2.0-85033362124.
10.1016/j.spmi.2017.10.018
CAS Web of Science® Google Scholar
38 Aliyu A. I., Li Y., İnç M., Baleanu D., and Alshomrani A. S., Solitons and complexitons to the (2+1)-dimensional Heisenberg ferromagnetic spin chain model, International Journal of Modern Physics B. (2019) 33, no. 30, article 195036, https://doi.org/10.1142/S0217979219503685.
10.1142/S0217979219503685
Web of Science® Google Scholar
39 He J.-H., Semi-inverse method of establishing generalized variational principles for fluid mechanics with emphasis on turbomachinery aerodynamics, International Journal of Turbo & Jet Engines. (1997) 14, no. 1, 23–28, https://doi.org/10.1515/TJJ.1997.14.1.23, 2-s2.0-0031441505.
10.1515/TJJ.1997.14.1.23
Web of Science® Google Scholar
40 Wang K. J., Variational principle and diverse wave structures of the modified Benjamin-Bona-Mahony equation arising in the optical illusions field, Axioms. (2022) 11, no. 9, https://doi.org/10.3390/axioms11090445.
10.3390/axioms11090445
Web of Science® Google Scholar
41 He J. H., Qie N., He C., and Saeed T., On a strong minimum condition of a fractal variational principle, Applied Mathematics Letters. (2021) 119, article 107199, https://doi.org/10.1016/j.aml.2021.107199.
10.1016/j.aml.2021.107199
Web of Science® Google Scholar
42 Wang K. J., Shi F., and Wang G. D., Periodic wave structure of the fractal generalized fourth-order Boussinesq equation traveling along the non-smooth boundary, Fractals. (2022) 30, no. 9, https://doi.org/10.1142/S0218348X22501687.
10.1142/S0218348X22501687
Web of Science® Google Scholar
43 He J. H., Variational principle for the generalized KdV-burgers equation with fractal derivatives for shallow water waves, Journal of Applied and Computational Mechanics. (2020) 6, no. 4, 735–740.
Web of Science® Google Scholar
44 Cao X. Q., Guo Y. N., Hou S. C., Zhang C. Z., and Peng K. C., Variational principles for two kinds of coupled nonlinear equations in shallow water, Symmetry. (2020) 12, no. 5, https://doi.org/10.3390/sym12050850.
10.3390/sym12050850
Web of Science® Google Scholar
45 Wang K. J., Variational approach for the fractional exothermic reactions model with constant heat source in porous medium, Thermal Science. (2022) https://doi.org/10.2298/TSCI220922211W.
10.2298/TSCI220922211W
Web of Science® Google Scholar
46 Liu M. Z., Cao X. Q., Zhu X. Q., Liu B. N., and Peng K. C., Variational principles and solitary wave solutions of generalized nonlinear Schrödinger equation in the ocean, Journal of Applied and Computational Mechanics. (2021) 7, no. 3, 1639–1648.
Web of Science® Google Scholar
47 Yépez-Martínez H., Pashrashid A., Gómez-Aguilar J. F., Akinyemi L., and Rezazadeh H., The novel soliton solutions for the conformable perturbed nonlinear Schrödinger equation, Modern Physics Letters B. (2022) 36, no. 8, https://doi.org/10.1142/S0217984921505977.
10.1142/S0217984921505977
Web of Science® Google Scholar
48 Durur H., Kurt A., and Tasbozan O., New travelling wave solutions for KdV6 equation using sub equation method, Applied Mathematics and Nonlinear Sciences. (2020) 5, no. 1, 455–460, https://doi.org/10.2478/amns.2020.1.00043.
10.2478/amns.2020.1.00043
Google Scholar
49 Akinyemi L., Şenol M., and Iyiola O. S., Exact solutions of the generalized multidimensional mathematical physics models via sub-equation method, Mathematics and Computers in Simulation. (2021) 182, 211–233, https://doi.org/10.1016/j.matcom.2020.10.017.
10.1016/j.matcom.2020.10.017
Web of Science® Google Scholar
50 Wang K. J., A fractal modification of the unsteady Korteweg-de Vries model and its generalized fractal variational principle and diverse exact solutions, Fractals. (2022) 30, no. 9, article 2250192, https://doi.org/10.1142/S0218348X22501924.
10.1142/S0218348X22501924
Web of Science® Google Scholar
51 Singh J., Analysis of fractional blood alcohol model with composite fractional derivative, Chaos, Solitons & Fractals. (2020) 140, article 110127, https://doi.org/10.1016/j.chaos.2020.110127.
10.1016/j.chaos.2020.110127
Web of Science® Google Scholar
52 He J. H., Kou S. J., He C. H., Zhang Z. W., and Gepreel K. A., Fractal oscillation and its frequency-amplitude property, Fractals. (2021) 29, no. 4, https://doi.org/10.1142/S0218348X2150105X.
10.1142/S0218348X2150105X
Web of Science® Google Scholar
53 Wang K. J. and Shi F., A new perspective on the exact solutions of the local fractional modified Benjamin-Bona-Mahony equation on cantor sets, Fractal and Fractional. (2023) 7, no. 1, https://doi.org/10.3390/fractalfract7010072.
10.3390/fractalfract7010072
Google Scholar
54 Singh J., Ganbari B., Kumar D., and Baleanu D., Analysis of fractional model of guava for biological pest control with memory effect, Journal of Advanced Research. (2021) 32, 99–108, https://doi.org/10.1016/j.jare.2020.12.004, 34484829.
10.1016/j.jare.2020.12.004
PubMed Web of Science® Google Scholar
55 Wang K. J. and Si J., On the non-differentiable exact solutions of the (2 + 1)-dimensional local fractional breaking soliton equation on Cantor sets, Mathematical Methods in the Applied Sciences. (2023) 46, no. 2, 1456–1465, https://doi.org/10.1002/mma.8588.
10.1002/mma.8588
Web of Science® Google Scholar
56 Shaikh A. S., Shaikh I. N., and Nisar K. S., A mathematical model of COVID-19 using fractional derivative: outbreak in India with dynamics of transmission and control, Advances in Difference Equations. (2020) 2020, no. 1, https://doi.org/10.1186/s13662-020-02834-3, 32834815.
10.1186/s13662-020-02834-3
PubMed Web of Science® Google Scholar
57 Wang K. J., The fractal active low-pass filter within the local fractional derivative on the cantor set, COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering. (2023) https://doi.org/10.1108/COMPEL-09-2022-0326.
10.1108/COMPEL-09-2022-0326
Web of Science® Google Scholar
58 Sweilam N. H., Al-Mekhlafi S. M., Assiri T., and Atangana A., Optimal control for cancer treatment mathematical model using Atangana–Baleanu–Caputo fractional derivative, Advances in Difference Equations. (2020) 2020, no. 1, https://doi.org/10.1186/s13662-020-02793-9.
10.1186/s13662-020-02793-9
PubMed Web of Science® Google Scholar
59 Wang K. L., New perspective to the fractal Konopelchenko-Dubrovsky equations with M-truncated fractional derivative, International Journal of Geometric Methods in Modern Physics. (2023) 2023, article 2350072.
Google Scholar
60 Wang K. L., Exact travelling wave solution for the local fractional Camassa-holm-Kadomtsev-Petviashvili equation, Alexandria Engineering Journal. (2023) 2022, no. 63, 371–376.
10.1016/j.aej.2022.08.011
Google Scholar
61 Sun H. G., Zhang Y., Baleanu D., Chen W., and Chen Y. Q., A new collection of real world applications of fractional calculus in science and engineering, Communications in Nonlinear Science and Numerical Simulation. (2018) 64, 213–231, https://doi.org/10.1016/j.cnsns.2018.04.019, 2-s2.0-85046409994.
10.1016/j.cnsns.2018.04.019
Web of Science® Google Scholar

Citing Literature

All articles

Abundant Soliton Structures to the (2 + 1)-Dimensional Heisenberg Ferromagnetic Spin Chain Dynamical Model

Abstract

1. Introduction