Advances in Mathematical Physics
Volume 2023, Issue 1 1091355
Research Article
Open Access

The Modified Exponential Function Method for Beta Time Fractional Biswas-Arshed Equation

Yusuf Pandir, 

Yusuf Pandir

Department of Mathematics, Faculty of Science and Arts, Yozgat Bozok University, Yozgat, Turkey

Search for more papers by this author
Tolga Akturk, 

Tolga Akturk

Department of Mathematics and Science Education, Faculty of Education, Ordu University, Ordu, Turkey odu.edu.tr

Search for more papers by this author
Yusuf Gurefe, 

Corresponding Author

Yusuf Gurefe

Department of Mathematics, Faculty of Science, Mersin University, Mersin, Turkey mersin.edu.tr

Search for more papers by this author
Hussain Juya, 

Corresponding Author

Hussain Juya

Department of Mathematics, Faculty of Science, Mersin University, Mersin, Turkey mersin.edu.tr

Faculty of Information Technology and Communication, Department of Science, Kabul University, Kabul, Afghanistan ku.edu.af

Search for more papers by this author
First published: 27 April 2023
https://doi.org/10.1155/2023/1091355
Citations: 3
Academic Editor: Muhammad Nadeem

Abstract

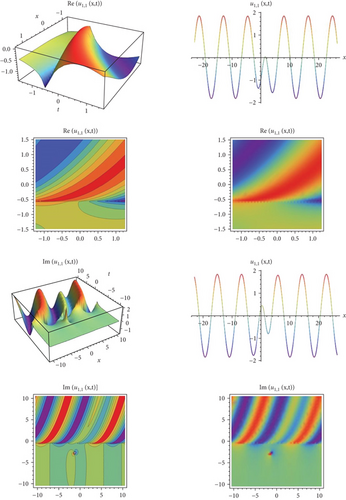
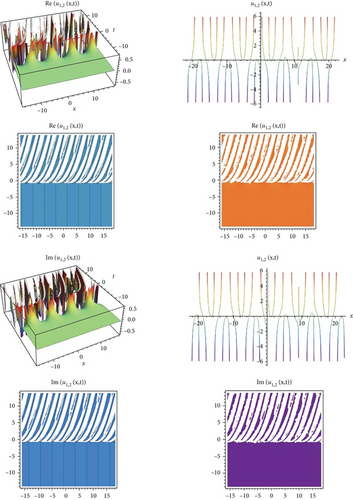
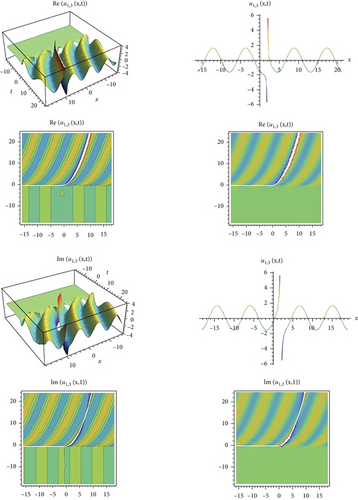
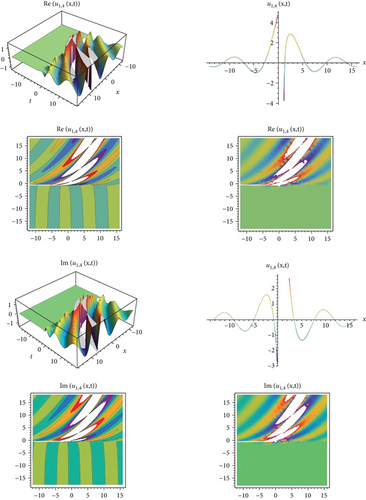
In this study, the exact solutions of the Biswas-Arshed equation with the beta time derivative, which has an important role and physically means that it represents the pulse propagation in an optical fiber, nuclear, and particle physics, are obtained using the modified exponential function method. Exact solutions consisting of hyperbolic, trigonometric, rational trigonometric, and rational function solutions demonstrate the competence and relevance of the proposed method. In addition, the physical properties of the obtained exact solutions are shown by making graphical representations according to different parameter values. It is seen that the method used is an effective technique, since these solution functions obtained with all these cases have periodic function properties.

1. Introduction

Differential equations with fractional derivatives have been used very popularly in many fields of science recently, just like integer order derivative equations. It is used effectively in many branches of science such as health, biology, engineering, and stochastic models. Because such equations contain terms that represent many of the behaviors studied in these cases, each equation is defined as a mathematical model. To obtain the solutions of these mathematical models, there are various methods in the literature such as the improved Bernoulli subequation method [1], the trial equation method [2], the extended trial equation method [3], the G′/G method [4, 5], the extended tanh method [6], the Kudryashov method [7, 8], the generalized Kudryashov method [9], the new function method [10], the first integral method [11, 12], the differential transform method [13], the variational iteration method [14], the exp-function method [15, 16], the Adomian decomposition method [17], some numerical methods [18–22], the Chebyshev collocation method [23], the integral transform operator [24], the Chebyshev-Tau method [25], the Taylor expansion method [26], the modified exponential function method [27, 28], and the new type F-expansion method [29].

In this study, the modified exponential function method was applied to obtain the exact solutions of the Biswas-Arshed equation with the beta time derivative.

The outline of this study can be expressed as follows: In the 2nd chapter, some information about the definitions and properties of the Atangana’s beta derivative is given. In the third chapter, the modified exponential function method is introduced in detail with its features. In the fourth chapter, the analysis of the nonlinear fractional mathematical model with Atangana’s derivative is given. In the last section, there is a conclusion that includes all the outputs presented in this article.

2. The Properties and Definition of Beta Derivative

Definition 1. Khalil et al. added a new fractional derivative term to the fractional derivative topic and brought it to the literature [30]. Let us analyzed the conformable derivative function g : [0, ∞) of the α order from type t > 0, α ∈ (0, 1) as follows:

(1)

When g is α-differentiable in the interval of (0, a), a > 0 and consists, then it can be defined as .

Definition 2. The beta derivative term is described by Atangana et al. as follows [31]:

(2)

The mathematical model used in the study that consists of the Atangana’s fractional derivative is preferred because it provides some features of the basic derivative rules. According to all these cases, the various properties of the conformable derivative are as follows:
  • (i)

    Let h ≠ 0 and g be functions that are differentiable with respect to beta in the range β ∈ (0, 1]. Accordingly, the equation that can satisfy all the real numbers q and r is as follows:

(3)
  • (ii)

    p is defined as any constant that satisfies the following equation:

(4)
(5)
(6)
If λ = (x + (1/(Γ(α))))α−1v is written instead of λ in Equation (2) and v⟶0, when λ⟶0, is taken as follows
(7)
with
(8)
where δ is the constant, and therefore, the following equation is written:
(9)

3. Properties of the Modified Exponential Function Method

In this section, the modified exponential function method, which is an efficient method used to obtain the wave solutions of the nonlinear mathematical model defined by Atangana derivatives, will be explained in detail.

The general form of the nonlinear fractional partial differential equation containing the solution function u with two variables and its beta derivatives is as follows:
(10)
where x and t represent space and time to which the function u given in the general form is dependent.
Let us take the traveling wave transform generated according to the independent variables in the general form of the nonlinear partial differential as follows:
(11)
where γ is any constant. When the derivative terms in Equation (10) are written instead of those obtained from the wave transformation (11), the general form of the following nonlinear ordinary differential equation is found:
(12)
The solution function of the nonlinear fractional differential equation considered in this study is as follows:
(13)
where Ai, Bj, (0 ≤ i ≤ q, 0 ≤ j ≤ r) are constants and ϑ = ϑ(η). The terms of derivative in Equation (12) are obtained from Equation (13). However, in this process, while the derivatives of the function u with respect to η are taken, the function ϑ and its derivative with respect to η are required. For this case, the following equation is used as
(14)
If Equation (14) is arranged, the following equation is obtained:
(15)

While integrating Equation (15) according to the functions η and ϑ, the following family cases are obtained according to the states of the coefficients in the same equation [27, 28]:

Family 1. If μ ≠ 0 and λ2 − 4μ > 0,

(16)

Family 2. If μ ≠ 0 and λ2 − 4μ < 0,

(17)

Family 3. If μ = 0, λ ≠ 0, and λ2 − 4μ > 0,

(18)

Family 4. If μ ≠ 0, λ ≠ 0, and λ2 − 4μ = 0,

(19)

Family 5. If μ = 0, λ = 0, and λ2 − 4μ = 0,

(20)
where E, λ, μ are coefficients.

After determining the function ϑ in Equation (13) according to the conditions stated above, another step that needs to be done is to determine the upper bounds in Equation (13). For this, the balance procedure must be used. In other words, there is a relationship between q and r, which is analyzed as the upper boundary, with the balancing of the highest order derivative term in the nonlinear ordinary differential equation and the highest order nonlinear term. Then, appropriate values are determined to provide this correlation. In this way, the boundaries of Equation (13) are stated. Then, the terms of derivative required in Equation (12) are obtained from Equation (13) and written in their place. The system of algebraic equations consisting of the coefficients of the function ϑ in this equation is obtained. The coefficients in the form of A0, A1, A2, ⋯, Aq and B0, B1, B2, ⋯, Br are found together with the solution of this system of equations. Then, the obtained coefficients are written in Equation (13). The functions ϑ determined according to the family conditions are also put in their place. It is checked that these functions, which are obtained together with the necessary mathematical operations, provide the nonlinear mathematical model with beta derivatives. Finally, the graphs simulating the physical behavior of wave solutions satisfying the equation are obtained according to the appropriate parameters.

4. Analysis of the Nonlinear Mathematical Model with the Beta Time Derivative

In this section, the traveling wave solutions satisfying the Biswas-Arshed equation with the beta time derivative will be analyzed by using the modified exponential function method. The Biswas-Arshed equation physically means that it represents the pulse propagation in an optical fiber. The Biswas-Arshed equation with the beta time derivative is as follows [32, 33]:
(21)
where a1, a2, b1, b2, σ, τ, and ζ are arbitrary constants. Here, the functions uxx, uxxx, , and are, respectively, given as the group velocity, the third order, spatiotemporal dispersions, and spatiotemporal third-order dispersions whereas u = u(x, t) is defined as a complex-valued function. Also, is the self-steepening term and and |u|2ux are the terms of nonlinear dispersions. To solve the nonlinear fractional differential equation, firstly using the wave transform given below, this equation is reduced to a system of nonlinear ordinary differential equations. For this, let us consider the traveling wave transform in the form
(22)
where ρ, κ, w, and ℘ are constants. When the terms containing derivatives required in Equation (21) are obtained from the wave transform (22) and written in their place, we get the following system of nonlinear ordinary differential equations:
(23a)
(23b)
By equating the coefficients of Equation (23b) to zero, the following results are obtained:
(24)
A nonlinear ordinary differential equation is obtained by substituting the values in Equation (24) into Equation (23a) as follows:
(25)
When the balance procedure is applied to Equation (25), the following balance relation is obtained between the term ϕ″ with the highest order derivative and the term ϕ3 with the highest order nonlinear term:
(26)
For m = 1, we obtain n = 2. In this case, it is assumed that the solution function determined according to Equation (13) is as follows:
(27)
The derivative terms required for Equation (25) are obtained from Equation (27) as follows:
(28)
(29)

The system of algebraic equations, observed by substituting the terms obtained in Equations ((27)–(29)) into Equation (25), is solved by using the Mathematica program, and thus, the following coefficients are obtained by this way. In addition, two different cases of solutions such as Case 1 and Case 2, where each case consists of five different solution families, are given below. Now, let us consider these solution cases.

Case 1.

(30)

When the coefficients obtained above are, respectively, substituted in Equations (27) and (22), the following wave solutions are found according to the family states.

Family 1. When μ ≠ 0 and λ2 − 4μ > 0,

(31)
where .

Family 2. When μ ≠ 0 and λ2 − 4μ < 0,

(32)
where .

Family 3. When μ = 0, λ ≠ 0, and λ2 − 4μ > 0,

(33)
where .

Family 4. When μ ≠ 0, λ ≠ 0, and λ2 − 4μ = 0,

(34)
where .

Family 5. When μ = 0, λ = 0, and λ2 − 4μ = 0,

(35)
where .

Case 2.

(36)

Let us investigate the wave solutions of the following family of solutions according to another set of coefficients obtained by solving the system of algebraic equations.

Family 1. If μ ≠ 0 and λ2 − 4μ > 0, then

(37)

where η = x − (b1/βb2)(t + (1/(Γ(β))))β, , and .

Family 2. If μ ≠ 0 and λ2 − 4μ < 0, then

(38)
where and .

Family 3. If μ = 0, λ ≠ 0, and λ2 − 4μ > 0, then

(39)

Family 4. If μ ≠ 0, λ ≠ 0, and λ2 − 4μ = 0, then

(40)

Family 5. If μ = 0, λ = 0, and λ2 − 4μ = 0, then

(41)
where and .

5. Conclusions

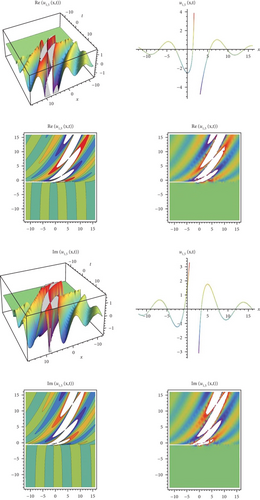
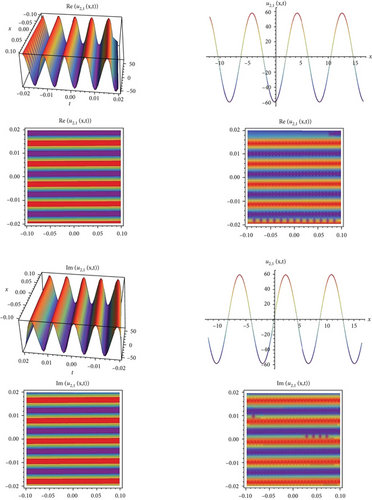
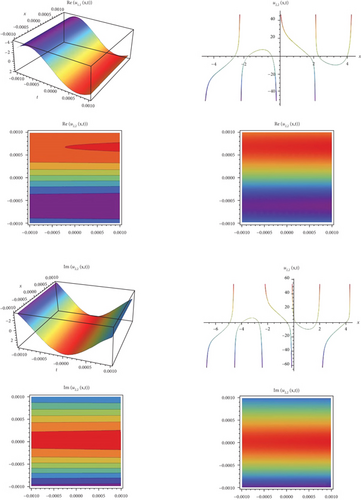
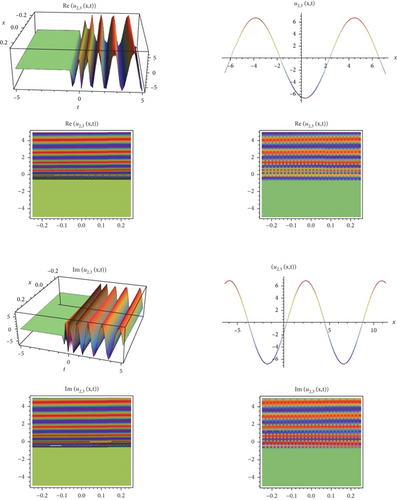
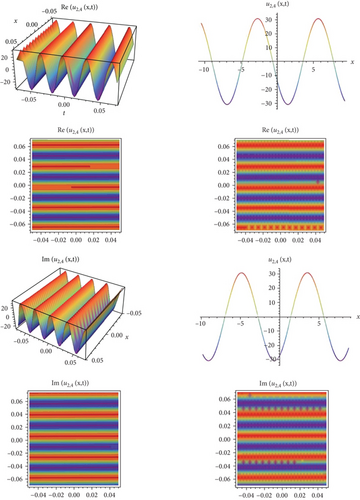
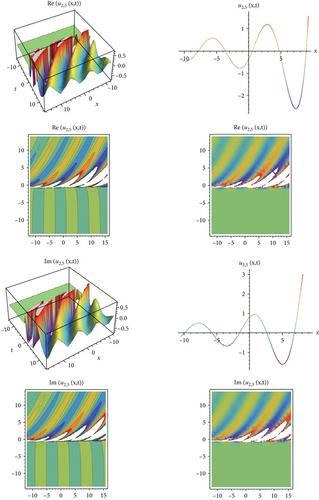
In this study, an effective technique, the modified exponential function method for the Biswas-Arshed equation with the beta time derivative, was applied. It can be said that this method is an advantageous technique for obtaining wave solutions of nonlinear partial differential equations. This advantage can be explained as follows. The traveling wave solutions of the mathematical model contain periodic functions. By obtaining these functions, the behavior model obtained in a range can be generalized to an infinite range. In this study, a package program was used for all mathematical operations and graphics that simulate the behavior of the mathematical model and for all the operations related to showing that solution functions provide the mathematical model. Using the method, two case situations consisting of coefficients were analyzed. According to these situations, hyperbolic, trigonometric, and rational solution functions belonging to the mathematical model were obtained. In addition, in the second case, the solution functions belonging to the mathematical model were obtained in a complex form. For this reason, while determining the graphs simulating the behaviors, they were examined separately as real and imaginary parts in Figures 1-9–10. When all these results are analyzed, it is concluded that obtaining periodic solution functions is of great importance, because such functions will allow to make comments about a desired range.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (31) for the values of δ = 0.96, λ = 3, b1 = 2.5, B0 = 0.2,  κ = 0.75, ζ = 0.21, τ = 0.45, μ = 2, a2 = 3.6, b2 = 2.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = −1.10702, A1 = −5.44284, A2 = −3.13655, a1 = 2.81046, ω = 0.730188, ρ = 1.04167, and t = 1.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (32) for the values of δ = 0.96,  λ = 2, b1 = 2.5, B0 = 0.2, κ = 0.75, ζ = 0.45, τ = 0.21, μ = 3, a2 = 3.6, b2 = 2.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = −0.215706, A1 = −1.13245, A2 = −0.916749, a1 = 4.58403, ω = 1.09968, ρ = 1.04167, and t = 1.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (33) for the values of δ = 0.96 , λ = 2, b1 = 2.5, B0 = 0.2, κ = 0.75, ζ = 0.21, τ = 0.45, μ = 0, a2 = 3.6, b2 = 2.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = −0.322547, A1 = −1.69337, A2 = −1.37083, a1 = 4.13233, ω = 1.00558, ρ = 1.04167, and t = 1.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (34) for the values of δ = 0.96, λ = 2, b1 = 2.5, B0 = 0.2, κ = 0.75, ζ = 0.45, τ = 0.21, μ = 1, a2 = 3.6, b2 = 2.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = −1.15011, A1 = −6.03807, A2 = −4.88796, a1 = 8.4127, ω = 1.89732, ρ = 1.04167, and t = 1.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (35) for the values of δ = 0.96, λ = 0, b1 = 2.5, B0 = 0.2, κ = 0.75, ζ = 0.45,  τ = 0.21, μ = 0, a2 = 3.6, b2 = 2.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = 0 , A1 = −1.15011, A2 = −4.88796, a1 = 8.4127, ω = 1.89732, ρ = 1.04167, and t = 1.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (37) for the values of δ = 0.96, λ = 3, b1 = 2.5, B0 = 0.2,  κ = 0.75,  ζ = 0.21, τ = 0.45, μ = 2, a2 = 0.6, b2 = 0.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = −11.8153, A1 = −50.215, A2 = 0, a1 = 429.477, ω = 542.055, ρ = 6.25, and t = 1.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (38) for the values of δ = 0.96, λ = 2, b1 = 2.5, B0 = 0.2, κ = 0.75, ζ = 0.21,  τ = 0.45, μ = 3, a2 = 0.6, b2 = 0.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = −21.5605, A1 = −91.6323, A2 = 0, a1 = −1442.39, ω = −1797.78, ρ = 6.25, and t = 1.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (39) for the values of δ = 0.96, λ = 2, b1 = 2.5, B0 = 0.2, κ = 0.75, ζ = 0.21, τ = 0.45, μ = 0, a2 = 0.6, b2 = 0.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = 1.32803, A1 = 5.64414, A2 = 0, a1 = 2.62566, ω = 8.49041, ρ = 6.25, and t = 1.
Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (40) for the values of δ = 0.96, λ = 2, b1 = 2.5, B0 = 0.2, κ = 0.75, ζ = 0.21, τ = 0.45, μ = 1, a2 = 0.6, b2 = 0.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = −6.15292, A1 = −26.1499, A2 = 0, a1 = 114.403, ω = 148.212, ρ = 6.25, and  t = 1.
Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
The graphs simulating the behavior of the model (41) for the values of δ = 0.96, λ = 2, b1 = 2.5, B0 = 0.2, κ = 0.75, ζ = 0.21, τ = 0.45, μ = 1, a2 = 0.6, b2 = 0.4, B1 = 0.85, E = 0.65, β = 0.5, A0 = 0, A1 = 1.89321, A2 = 0, a1 = −2.83602, ω = 1.66331, ρ = 6.25, and t = 1.

Conflicts of Interest

The authors declare that they have no competing interests.

Authors’ Contributions

All authors read and approved the final manuscript.

Data Availability

No data were used to support this study.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.