In this article, the applications of the Power Index Method (PIM) are presented to ascertain function solutions of the AKNS equation. We find out adequate explicit general solutions for the AKNS in the form of exponential, trigonometric, and logarithmic functions which have their importance in the physical sciences. We have used function transformations in which indexes of independent variables are nonrestricted parameters. During our investigation, we have seen that the nonlinear AKNS can be reduced to linear ODE by using PIM. All the solutions contain independent variables with parameters, and they are graphically represented by choosing suitable values of parameters.

1. Introduction

The exact solutions of the partial differential equation have their own consequence in the numerous branches of physical sciences, applied sciences, and other areas of engineering to comprehend their physical interpretation. Therefore, the search for an exact solution of nonlinear systems has been an interesting and valuable topic for mathematicians and physicists in applied science. A transformation of variables can sometimes be found that transforms a nonlinear PDE into a nonlinear ODE such as Lie Symmetry Transformations [1, 2], the traveling wave transformation, and the Cole–Hopf transformation method [3]. In the current year, many effective methods including the simple and modified equation methods [4, 5] and the sine-cosine method [6] have been employed to attain exact solutions of the equation.

In models of partial differential equations (PDEs), the AKNS equations play a central role and have many applications in applied physics. Various methods have been established for obtaining analytic solutions of the AKNS equations, for instance, the Exp-function method [7], multilinear variable separation approach method, variable coefficient method, and extended auxiliary equation method [8, 9]. The truncated Painlevé analysis of the AKNS equation with their symmetries [10] and the complex combined dark-bright solutions of the AKNS equation using SGEM [11] are obtained. Some transformations like the inverse-scattering [12–15] Backlund transformations [16] and the Darboux transformation [17] have been applied to find solutions of the AKNS equation.

The paper preparation is as follows: in Section 2, we describe briefly the Power Index Method. In Section 3, we apply this method to the nonlinear AKNS equation by using function transformation. In this method, by using transformations like (8) and (12), we have obtained linear ODEs. Our exact solutions are an explicit general form and contain independent variables with nonrestricted parameters. Our findings are a more general form; see for details (60) and (61).

2. Power Index Method

Step 1. Consider the partial differential equation [18]

(1)

where α is a perturbation parameter with α > 0. We have employed the Power Index Method on (1) to obtain its exact solutions.

We introduce the new variable

(2)

and the travelling transformation

(3)

Some forms of the new variable are

(4)

Figure 1 shows the procedure of transformation of PDE to ODE.

Step 2. Express the nonlinear PDE into a mixed algebraic form

(5)

where

(6)

Step 3. We choose the highest power index term of one variable in the algebraic equation equal with the other highest power index term of the same variable p_t(n₁, n₂, n₃) = q_t(n₁, n₂, n₃). Similarly, we get other relations of power indexes so that we can choose particular values of power indexes. We continue the same process for other variables. Now, we have selected a new variable and transformation with adjustable indexes. Next, each term is replaced by a new variable and transformation, and we have reduced PDE into ODE.

Step 4. Solve the obtained ODE by using computerized symbolic packages. The exact solution of PDE can be obtained from the analytic solution of ODE and the new variable transformation.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flow chart of solution of the PDE (1).

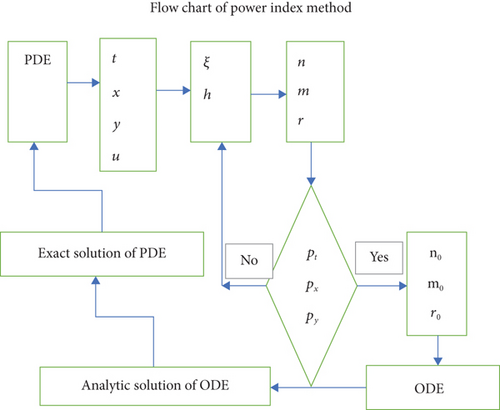
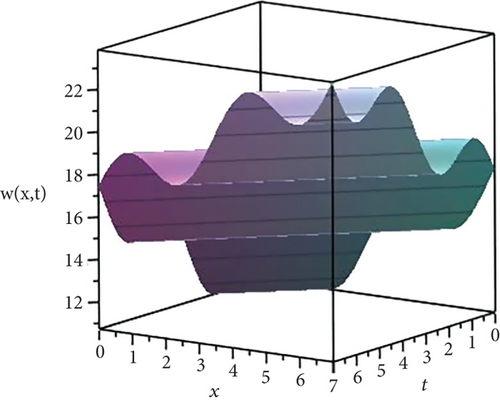
Figure 2 demonstrates the exact solution of (10).

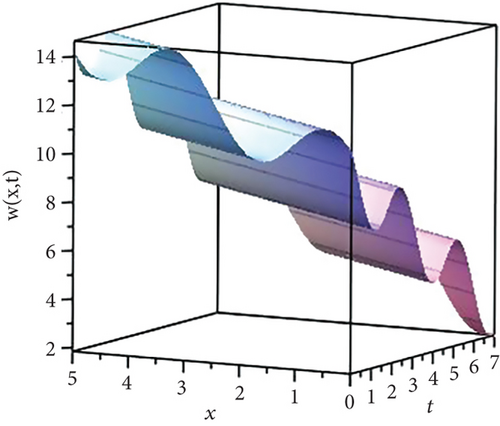
3. Exact Solutions of AKND by Using Function Transformations

Case 1. Let us start with an elementary exponential function and introduce a new variable as

(7)

Using (7), equation (1) can be expressed into ODE of the form

(8)

Equation (8) shows that for each real value of m₁ and n₁, the PDE (1) can be reduced to ODE (8). If we choose m₁ = 1 and n₁ = 1, then we have the following analytic solution of (8).

(9)

From (7) and (9), the analytic solution of the PDE is as follows:

(10)

If we choose m₁ = 1 and n₁ = −1, then we have the following exact solution of the PDE (1).

(11)

Figure 3 displays the graphical illustration of the analytical solution of (11).

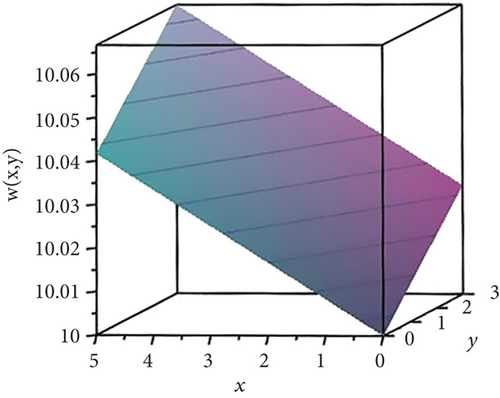
We have observed that for the valuesm₁andn₁with the same sign or opposite signs, the ODE (8) has the same analytic solution.

Case 2. Now, we consider another exponential function of the form

(12)

The transformation (12) reduces (1) to ODE in the form

(13)

With the help of Symbolic Packages, the analytic solution of (13) is given as follows:

(14)

(15)

By (12), (14), and (15), we get the exact solution of the PDE (1) as follows:

(16)

(17)

We note that the solutions u₂₁ and u₂₂ contain parameters n₂ and m₂. For different values of n₂ and m₂, we can find more solutions of (1).

Figure 4 contrasts with (1) which is given in (16).

For n₂ = 0 in (13), we get the following ODE.

(18)

The analytic solution of the ODE (18) is

(19)

We obtain the exact solution of (1) in the term of x:

(20)

We note that the exponential function in terms of y and t has no ODE reduction form.

Case 3. Next, we consider a monomial of the form

(21)

Using (21), the PDE (1) is reduced in the form

(22)

The analytic solution of the ODE (22) is

(23)

The exact solution of the PDE (1) is obtained from (23) and transformation (21)

(24)

Figure 5 presents the solution of (1) which is given in (20).

Case 4. In this case, we have considered the polynomial of the form

(25)

Using (25), the PDE (1) is reduced in the form

(26)

The analytic solution of the ODE (26) are

(27)

(28)

(29)

(30)

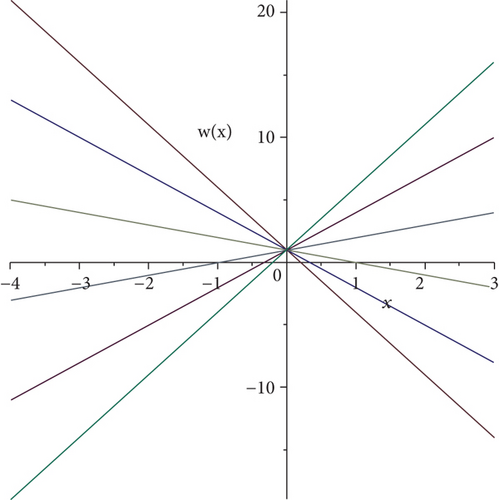
Figures 6 and 7 show the performance of the solution of (1) which is given in (24).

If we replace y by t in (25), the new transformation becomes

(31)

Using (31), the PDE (1) is reduced in the form

(32)

The analytic solutions of the ODE (32) are

(33)

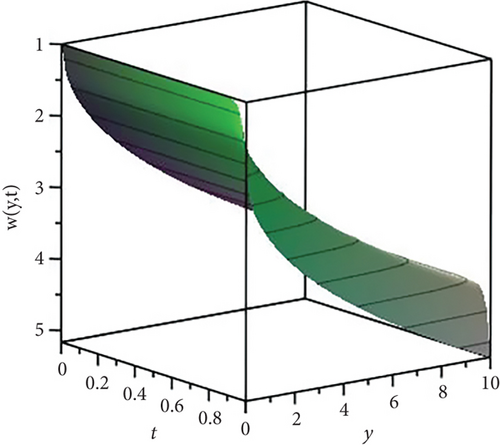
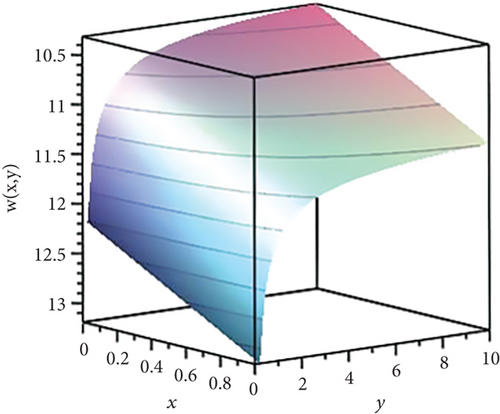
Figure 8 acts as the solution of (1) which is given in (30).

Case 5. We define a new variable as

(34)

(35)

In (35), two terms contain only the y variable, so if we want to make this variable vanish in these terms, we have to take 2s₅ + r₅ − 1 = s₅ + r₅. This implies s₅ = 1. Further, the term that contain must have the r₅ power of y. From this, we get 2s₅ + 2r₅ − 1 = r₅ or s₅ + 2r₅ = r₅; these imply r₅ = −1. First, we take m₅ = 1, r₅ = −1, and s₅ = 1 in ((34)) and get the following ODE:

(36)

The analytic solution of (36) is given as follows:

(37)

(38)

(39)

(40)

Now, we take r₅ = 1, m₅ = 1, and s₅ = 1 in (35) and get the following ODE.

(41)

The analytic solution of (41) is given as follows:

(42)

(43)

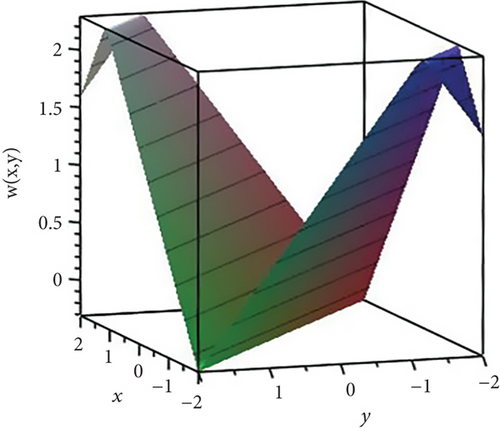
Case 6. In this case, we have considered a polynomial with a logarithmic function of the form

(44)

The algebraic form of the PDE (1) has the following y-index terms:

(45)

Figure 9 acts as the solution of (1) which is given in (39). Figure 10 entertains the solution of (1) which is given in (43).

To find the suitable value of m₆ and n₆, we can take different combinations of the y-index terms, and finally, we get m₆ = 0 and n₆ = 1. We have the following final form of the transformation (44).

(46)

and the corresponding ODE is given as follows:

(47)

The analytic solution of (47) is given as follows:

(48)

The exact solution of (1) is given as follows:

(49)

(50)

(51)

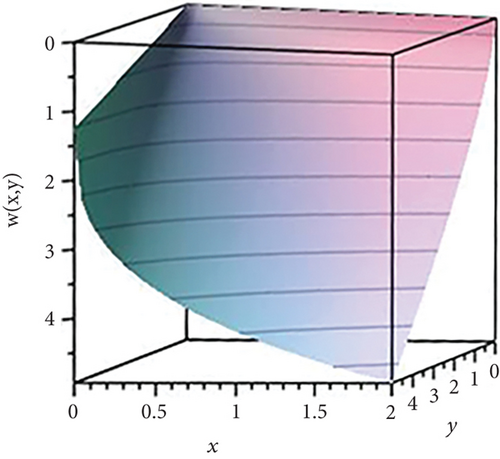
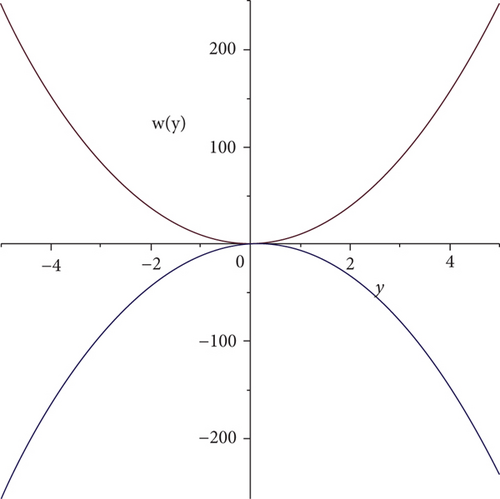
Case 7. In this case, we have considered the logarithmic function of the form

(52)

The algebraic form of the PDE (1) has the following y-index terms:

(53)

To choose the suitable index value of y, we take 2n₇ − 1 = n₇, and we get n₇ = 1. Finally, we have the following transformation:

(54)

and the corresponding ODE is obtained when the PDE (1) is transformed.

(55)

Figures 11, 12, and 13 present the graphical diagrams of the analytical solutions of (49), (50), and (51), respectively.

The analytic solution of (55) is given by

(56)

(57)

(58)

(59)

(60)

The exact solution of (1) has the form

(61)

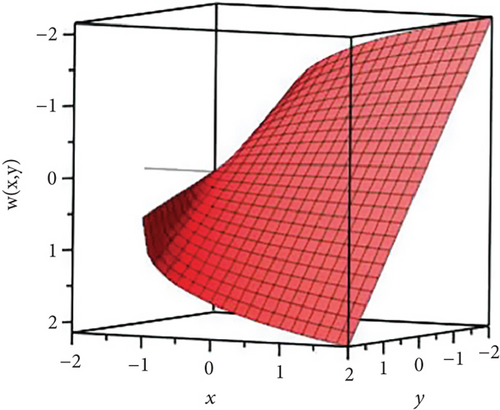
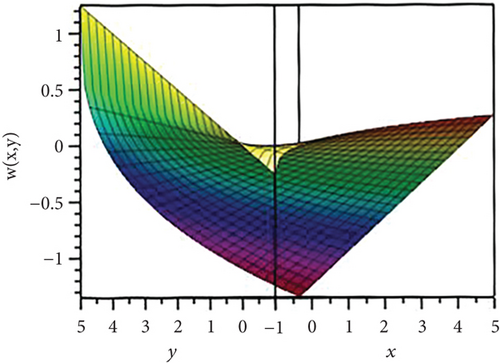
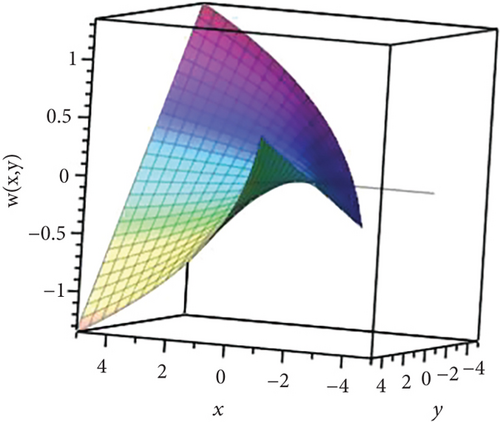
Case 8. In this case, we have considered a trigonometric function of the form

(62)

This transformation transformed the nonlinear PDE (1) to a product of two linear ODEs.

(63)

(64)

(65)

(66)

Using (62), (65), and (66), the exact solutions of (1) are

(67)

(68)

Figures 14, 15, and 16 present the graphical diagrams of the analytical solutions of (59), (60), and (61), respectively.

If we choose following transformations,

(69)

(70)

then we get the first two ODEs by using (69) and the next two ODEs by using (70).

(71)

Solving these ODEs by using Maple, we get the same solutions of (1) which are given in (67) and (68).

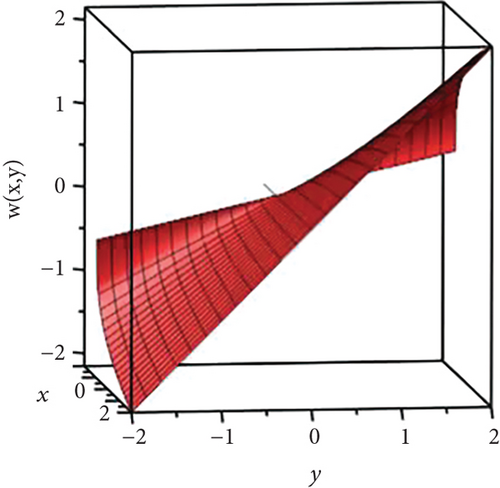
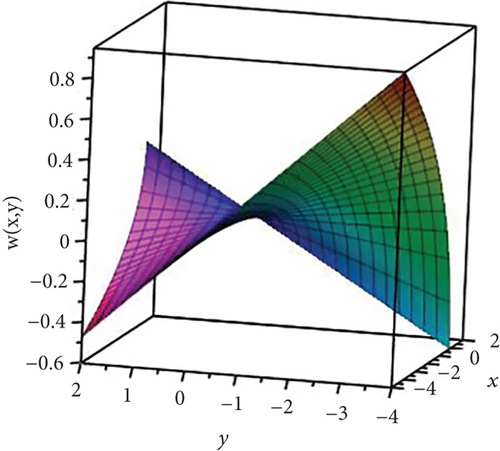
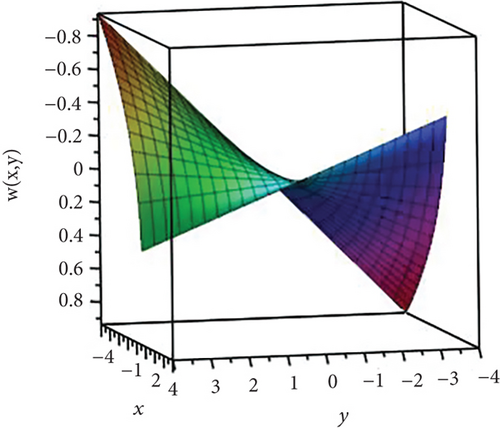
Figure 17 displays the graphical illustration of the analytical solution of (61).

Case 9. In this case, we have considered the trigonometric function of the form

(72)

This transformation reduces the nonlinear PDE (1) to linear ODE.

(73)

The analytic solution of (73) has the form

(74)

The closed form function solution of (1) is given by

(75)

4. Conclusion

The intention of this research paper is to find function solutions using exponential, logarithmic, trigonometric, and rational functions which are attained from the AKNS equation via PIM. Our attained solutions are an explicit form, and they contain independent variables with parameter indexes. We have seen that for some of our transformations which are applied to nonlinear AKNS, we get linear ODEs. All the found solutions of the equation are new, and some solutions are more general (see (59), (60), and (61)). The exact solutions of AKNS which we have obtained in this article are useful to understand the physical phenomenon in many aspects. They are explicitly characterized by choosing appropriate values of parameters. This method has been efficaciously employed to get exact solutions of the equation.

Conflicts of Interest

The authors have no competing interests.

Authors’ Contributions

All authors contributed equally to finishing the manuscript.

Acknowledgments

The first author is thankful to AM. Javed Ahmed, HI(M)(Retd), Vice-Chancellor, Air University, Islamabad, Pakistan, for assuming the outstanding research amenities.

Open Research

Data Availability

Please contact the authors for data requests.

References

1 Bibi K. and Ahmad K., Exact solutions of Newell-Whitehead-Segel equations using symmetry transformations, Journal of Function Spaces. (2021) 2021, 8, https://doi.org/10.1155/2021/6658081.
10.1155/2021/6658081
Web of Science® Google Scholar
2 Bibi K. and Ahmad K., Exact solutions of the two-dimensional Cattaneo model using Lie symmetry transformations, Discrete Dynamics in Nature and Society. (2021) 2021, 8, https://doi.org/10.1155/2021/6629074, 6629074.
10.1155/2021/6629074
Web of Science® Google Scholar
3 Wazwaz A. M., A sine–cosine method for handling nonlinear wave equations, Mathematical and Computer Modelling. (2004) 40, no. 5-6, 499–508, https://doi.org/10.1016/j.mcm.2003.12.010, 2-s2.0-12944300203.
10.1016/j.mcm.2003.12.010
Web of Science® Google Scholar
4 Taghizadeh N., Mirzazadeh M., Paghaleh A. S., and Vahidi J., Exact solutions of nonlinear evolution equations by using the modified simple equation method, Ain Shams Engineering Journal. (2012) 3, no. 3, 321–325, https://doi.org/10.1016/j.asej.2012.03.010, 2-s2.0-84867404678.
10.1016/j.asej.2012.03.010
Google Scholar
5 Mirzazadeh M., Modified simple equation method and its applications to nonlinear partial differential equations, Information Sciences Letters. (2014) 3, no. 1, 1–9, https://doi.org/10.12785/isl/030101.
10.12785/isl/030101
Google Scholar
6 Yusufoglu E., Bekir A., and Alp M., Periodic and solitary wave solutions of Kawahara and modified Kawahara equations by using sine–cosine method, Chaos, Solitons and Fractals. (2008) 37, no. 4, 1193–1197, https://doi.org/10.1016/j.chaos.2006.10.012, 2-s2.0-40749094121.
10.1016/j.chaos.2006.10.012
Web of Science® Google Scholar
7 Ebadi G. and Biswas A., The method and topological soliton solution of the K(m, n) equation, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 6, 2377–2382, https://doi.org/10.1016/j.cnsns.2010.09.009, 2-s2.0-78651456274.
10.1016/j.cnsns.2010.09.009
Web of Science® Google Scholar
8 Matveev V. B. and Smirnov A. O., Solutions of the Ablowitz–Kaup–Newell–Segur hierarchy equations of the “rogue wave” type: a unified approach, Theoretical and Mathematical Physics. (2016) 186, no. 2, 156–182, https://doi.org/10.1134/S0040577916020033, 2-s2.0-84962361555.
10.1134/S0040577916020033
Web of Science® Google Scholar
9 Esin I. E., Akta M. B., and Baskonus H. M., New complex and hyperbolic forms for Ablowitz–Kaup–Newell–Segur wave equation with fourth order, Applied Mathematics and Nonlinear Sciences. (2019) 4, no. 1, 93–100, https://doi.org/10.2478/AMNS.2019.1.00010.
10.2478/AMNS.2019.1.00010
Google Scholar
10 Ping L., Bao-Qing Z., Jian-Rong Y., and Bo R., Chinese Physics B, 2015, 24.
Google Scholar
11 Gao W., Yel G., Baskonus H. M., and Cattani C., Book of Abstracts, 2019.
Google Scholar
12 Zakharov V. E. and Shabat A. B., An exact theory of two-dimensional self-focussing and of one-dimensional self-modulation of waves in nonlinear media, Sov. Phy. Jet.(1972) 34, 62–69.
Web of Science® Google Scholar
13 Ablowitz M. J., Kaup D. J., Newell A. C., and Segur H., Nonlinear evolution equations of physical significance, Physical Review Letters. (1973) 31, no. 2, 125–127, https://doi.org/10.1103/PhysRevLett.31.125, 2-s2.0-14944339642.
10.1103/PhysRevLett.31.125
Web of Science® Google Scholar
14 Ablowitz M. J., Kaup D. J., Newell A. C., and Segur H., The inverse scattering transform-Fourier analysis for nonlinear problems, Studies in Applied Mathematics. (1974) 53, no. 4, 249–315, https://doi.org/10.1002/sapm1974534249, 2-s2.0-0016369301.
10.1002/sapm1974534249
Web of Science® Google Scholar
15 Zakharov V. E. and Shabat A. B., A scheme for integrating the nonlinear equations of mathematical physics by the method of inverse scattering transform, Funktsional'nyi Analiz i ego Prilozheniya. (1974) 8, 43–53.
Google Scholar
16 Rogers C. and Schief W. K., Bäcklund and Darboux Transformations, Geometry and Modern Applications in Soliton Theory, 2010, Cam. Uni. Press, Cambridge.
Google Scholar
17 Matveev V. B. and Salle A. M., Darboux Transformation and Solitons, 1991, Springer, Berlin, https://doi.org/10.1007/978-3-662-00922-2.
10.1007/978-3-662-00922-2
Google Scholar
18 Helal M. A., Seadawy A. R., and Zekry M. H., Stability analysis solutions for the fourth-order nonlinear Ablowitz-Kaup-Newell-Segur water wave equation, Applied Mathematical Sciences. (2013) 7, 3355–3365, https://doi.org/10.12988/ams.2013.34239.
10.12988/ams.2013.34239
Google Scholar
19 Seadawy A. R., Travelling wave solutions of a weakly nonlinear two-dimensional higher order Kadomtsev-Petviashvili dynamical equation for dispersive shallow water waves, The European Physical Journal Plus. (2017) 132, no. 29, 1–13.
10.1140/epjp/i2017-11313-4
CAS Web of Science® Google Scholar

Citing Literature

All articles

New Function Solutions of Ablowitz-Kaup-Newell-Segur Water Wave Equation via Power Index Method

Abstract

1. Introduction

2. Power Index Method

3. Exact Solutions of AKND by Using Function Transformations

4. Conclusion

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

New Function Solutions of Ablowitz-Kaup-Newell-Segur Water Wave Equation via Power Index Method

Abstract

1. Introduction

2. Power Index Method

3. Exact Solutions of AKND by Using Function Transformations

4. Conclusion

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information