Journal of Advanced Transportation
Volume 2022, Issue 1 9241112
Research Article
Open Access

Advanced Phasmatodea Population Evolution Algorithm for Capacitated Vehicle Routing Problem

Jiawen Zhuang, 

Jiawen Zhuang

School of Computer Science and Mathematics, Fujian University of Technology, Fuzhou 350118, China fjut.edu.cn

Search for more papers by this author
Shu-Chuan Chu, 

Shu-Chuan Chu

College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China sdust.edu.cn

Search for more papers by this author
Chia-Cheng Hu, 

Chia-Cheng Hu

College of Artificial Intelligence, Yango University, Fuzhou 350015, China ygu.edu.cn

Search for more papers by this author
Lyuchao Liao, 

Lyuchao Liao

School of Computer Science and Mathematics, Fujian University of Technology, Fuzhou 350118, China fjut.edu.cn

Search for more papers by this author
Jeng-Shyang Pan, 

Corresponding Author

Jeng-Shyang Pan

School of Computer Science and Mathematics, Fujian University of Technology, Fuzhou 350118, China fjut.edu.cn

College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China sdust.edu.cn

Department of Information Management, Chaoyang University of Technology, Taichung 413310, Taiwan cyut.edu.tw

Search for more papers by this author
First published: 20 March 2022
https://doi.org/10.1155/2022/9241112
Citations: 3
Academic Editor: Chi-Hua Chen

Abstract

Capacitated Vehicle Routing Problem (CVRP) is difficult to solve by the traditional precise methods in the transportation area. The metaheuristic algorithm is often used to solve CVRP and can obtain approximate optimal solutions. Phasmatodea population evolution algorithm (PPE) is a recently proposed metaheuristic algorithm. Given the shortcomings of PPE, such as its low convergence precision, its nature to fall into local optima easily, and it being time-consuming, we propose an advanced Phasmatodea population evolution algorithm (APPE). In APPE, we delete competition, delete conditional acceptance and correspondingevolutionary trend update, and add jump mechanism, history-based searching, and population closing moving. Deleting competition and conditional acceptance and correspondingevolutionary trend update can shorten PPE running time. Adding a jump mechanism makes PPE more likely to jump out of the local optimum. Adding history-based searching and population closing moving improves PPE’s convergence accuracy. Then, we test APPE by CEC2013. We compare the proposed APPE with differential evolution (DE), sparrow search algorithm (SSA), Harris Hawk optimization (HHO), and PPE. Experiment results show that APPE has higher convergence accuracy and shorter running time. Finally, APPE also is applied to solve CVRP. From the test results of the instances, APPE is more suitable to solve CVRP.

1. Introduction

The population-based algorithm is a kind of metaheuristic algorithm, and it is widely used in transportation [1, 2]. Particle swarm optimization (PSO) [3, 4], equilibrium optimizer [5, 6], flower pollination algorithm (FPA) [7–9], fish migration optimization (FMO) [10], and quasiaffine transformation evolutionary (QUATRE) [11, 12] are some popular population-based algorithms. PPE, as a novel swarm intelligence algorithm, is proposed by Song [13], and the enlightenment of PPE is from the stick insect population’s evolution process.

As a novel population-based algorithm, PPE was introduced in 2020. It has some merits, e.g., the principle of the algorithm is simple and easy to implement. However, there are also some disadvantages, e.g., it is time-consuming, it has low precision, and it falls into the local solution easily. Therefore, the improvement of PPE is a challenging and meaningful study.

VRP was proposed by Dantzig and Ramser in 1959 and has been developed for many years [14], and as a branch of VRP, the related research of CVRP was very popular in transportation. CVRP refers to some customers with known demands served by some vehicles with certain capacity limits.

CVRP is an important issue. On the one hand, it is a practical problem because many real-world problems can be abstracted into CVRP. For example, in a restaurant, a waiter needs to serve multiple tables to meet customers' order needs. When only one waiter is considered, the problem is abstracted into CVRP. Another example is that the heart of the human body supplies blood to other organs, and the blood vessels are regarded as pathways. After simplification and hypothesis, this process can be modeled as a CVRP. On the other hand, CVRP is also a challenging scientific issue. VRP is an NP-hard problem [15, 16] that is difficult to a use precise algorithm to get the optimal solution in finite time.

Many scholars have studied CVRP. In 2006, Wu et al. used a new real number encoding method of PSO for solving VRP [17]. Chen et al. proposed a novel hybrid algorithm for CVRP, and in the hybrid algorithm, discrete PSO searches for optimal results and simulated annealing are used to jump out of the local optimum [18]. In 2009, Ai and Kachitvichyanukul proposed two solution representation methods, namely SR-1 and SR-2, for CVRP [19]. In 2015, Zhang and Lee proposed a routing-directed artificial bee colony algorithm to solve CVRP [20]. In 2019, Altabeeb et al. put forward an improved hybrid firefly algorithm for CVRP, and it was tested by 82 instances [21]. In 2020, Khairy et al. put forward the enhanced group teaching optimization algorithm to solve CVRP, and it was tested by 14 instances with promising time results [22]. In 2021, Fu et al. proposed the parallel equilibrium optimizer algorithm to solve CVRP [23].

In this paper, the proposed APPE deletes competition, deletes conditional acceptance and corresponding evolutionary trend update, combines a novel jump mechanism, and adds a history-based searching for population’s position update and the population closing moving method for early phase searching. Then, the algorithms are tested by CEC2013 [24]. We also apply APPE to solve CVRP.

The following is the remaining of this paper. The CVRP model is described in section 2. Section 3 introduces PPE. APPE is described in section 4. In section 5, the experiments of CEC2013 functions and CVRP are described. In section 6, a conclusion is given.

2. CVRP

The objective of CVRP is to minimize the sum of distance. The path taken by each vehicle satisfies the capacity constraint. There is only one warehouse or depot. The model of CVRP is as follows:
(1)
s. t.
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
where Nc is the customer number, Kvehicle is the vehicle number, is the distance from the ith customer to the jth customer by the kth vehicle, and di is the ith customer’s demand. The kth vehicle’s capacity is Qk.

Formula (1) is the objective function. Formulae (2) and (3) describe the decision variables. Formula (4) shows the vehicle’s capacity constraint. Equation (5) guarantees that every customer is served only once. Equations (6) and (7) ensure that one vehicle serves one custom. Equation (8) ensures the continuity of the route so that every vehicle coming in from the customer point would go out from that point, as well as back to the depot. Formula (9) is to eliminate the subloop.

3. PPE

PPE is inspired by the evolution process of the stick insect population. PPE initializes Np solutions randomly like other population-based algorithms. Every solution x has two properties, the first property is population number p, and the second property is population growth rate a. ev reflects the current evolution trend.

Then, calculate the fitness value, and find the global optimum, which is denoted as g best. The first k best solutions are stored in Ho, and k is equal to log(Np) + 1.

Next, in iteration, the new position is the sum of old position and evolution trend, which is as follows:
(10)
where t is the current generation, and xt means the current solution’s position. Then, calculate new solutions’ fitness and update the global optimum gbest and Ho.
When the new solution’s fitness is better, the current solution is absolutely replaced with it. Growth rate a, population quantity p, and population evolution trend ev are updated as follows:
(11)
(12)
(13)

In equation (13), the population evolution trend ev consists of three parts. In the first part, s(Ho, xt) means the nearest solution to xt in Ho. This part reflects similar evolution. The second part preserves the inertia of evolutionary trends. The final part is the mutation.

When the new solution’s fitness is worse, the current solution is conditionally updated by the new solution. If a generated random number in [0, 1] is less than the population number p, namely acceptance probability, the worse solution is accepted, and growth rate a and population quantity p are conditionally updated as equations (11) and (12). The evolution trend ev will change, irrespective of whether conditional acceptance probabilities are met, as follows:
(14)
(15)
(16)
where stt+1 controls the exploration range. c initializes to 2, and cis updated by using (16), when the new solution of the algorithm is a worse solution.
Competition also affects population evolution trend. When two solutions’ distance is less than G, competition will occur. Population quantity p and population evolution trend ev are updated in competition as follows:
(17)
(18)
where xj is a random selected solution from Np − 1 solution. The distance from xi is less than that from G. PPE’s pseudocode is shown in Figure 1.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
PPE’s pseudocode.

4. Advanced PPE

PPE also has shortcomings, such as low convergence precision, high consumption of time, and it falls into local optimum easily. Given the shortcomings of PPE, we propose APPE, which deletes competition, deletes conditional acceptance and correspondingevolutionary trend update, and adds jump mechanism, history-based searching, and population closing moving.

4.1. Without Competition

The competition mechanism exists in many algorithms. The imperialist competitive algorithm is based on imperial competition, in which weaker empires collapse and stronger empires take over colonies [25]. In the PPE, the competition mechanism is also considered. When the distance between the two solutions is too close, the population quantity p and population evolution trend ev will be updated. However, when the algorithm converges to the global or local optimal solution, this competition mechanism will affect its convergence tendency. At the same time, the calculation of particle distance takes time. Therefore, we remove the competition mechanism, thus effectively reducing the algorithm’s running time. It is equivalent to deleting the di  st(xj , xi)  <  G part of the PPE pseudo-code.

4.2. Without Conditional Acceptance and CorrespondingEvolutionary Trend Update

Some algorithms adopt the method of conditionally accepting a worse solution to improve the algorithm diversity, such as simulated annealing [26, 27]. Similarly, PPE will adopt a worse solution with probability, increasing the algorithm diversity and also increasing the algorithm running time. Therefore, we delete the conditional acceptance and corresponding evolutionary trend update of the PPE to save time consumption and maintain a certain convergence trend. It is equivalent to deleting the f(newx) > f(x) part of the PPE pseudo-code.

4.3. Jump Mechanism

We introduce a kind of jump mechanism, increasing the algorithm’s probability of jumping out of local optimum. When the algorithm enters the late iteration, the optimal solution will either keep the INV generation unchanged or the standard deviation of the optimal solution in the INV generation will be less than the threshold value INVGate, and we let the solution jump by the following formula:
(19)
where is a t + 1 generation solution modified by the jump mechanism to replace the nth solution. is a selected solution from population. g best is current generation’s optimal solution. r0 is the random number, and it obeys uniform distribution from 0 to 1. In this paper, we use the jump mechanism to modify Jump Num = 5 solutions, i.e., the worst solutions from the second to the sixth. When the probability is greater than rJump and the current population is not less than 8, we delete the worst solution. Moreover, when the number of Ho is more than the current population number, the number of Ho is reset again by k = log(Np) + 1, and the redundant poor solutions are deleted as well.

4.4. History-Based Searching

Most swarm intelligence algorithms use the current information to interact with the information of the last generation, and the information before the last generation is lost, however, this information will also affect the convergence performance of the algorithm. Therefore, we design a history-based container HA, whose capacity is HAnum.

If the container is not full, the optimal new solution generated in each round adds to the container, which is the best particle of xt+1 generated by equation (10). Otherwise, the global optimal solution g best of the previous generation is used to replace any solution in the container. Meanwhile, in the second half of the iteration, if the random number generated is less than 0.5, the worst new solution generated in each round is used to replace any solution in the container, which is the worst particle of xt+1 generated by equation (10).

Based on the above container, we design a history-based searching method, which is used to update the population. The history-based searching formula is as follows:
(20)
where is a new solution generated by history-based searching method, xHA best is a solution randomly selected from the top 5 better solutions of HA. xH Arandom is randomly selected from HA. means the ith solution of the current iteration, and and are the randomly selected solutions from the population that are different from . r1 is an indirect random number, and r1 = 0.1  tan(π(r3 − 0.5)). r2 and r3 are the direct random numbers, and they obey uniform distribution from 0 to 1.
In this paper, the population position update of APPE combines PPE’s update with history-based searching, and the detailed equation is as follows:
(21)
where t is the current generation. When a random number rand is less than 0.5 or the current generation is no more than HAnum, the population position is updated by equation (10) or equation (20).

4.5. Population Closing Moving

Swarm intelligence algorithm in the early stage is mainly exploration. Here, we use HA, and in the first half of the iteration cycle of the algorithm, when the random number is greater than 50%, the whole PPE population is moving toward the HA solution to produce new solutions. The moving formula is as follows:
(22)
(23)
where xt and are the whole population, r  dn  1 and r  dn  2 are random number matrices that follow standard normal distribution, and ran  d is the random number matrix that follows uniform distribution from 0 to 1. The number of rows in xt, , r  dn  1, r  dn  2, and rand matrix is the population size, and the number of columns is the dimension. The ∗ symbol is the multiplication of the corresponding positional elements of the matrix and is neither matrix multiplication nor convolution. Notice that 2∗r  dn  1 means that every element of the matrix r  dn  1 is multiplied with 2. Then, we compare the new solution by equation (21)with thenew solutiongenerated by moving method (18) and retain the excellent solution as the new solution.

4.6. APPE

In this paper, we combine the above methods to form APPE. The following are the detailed steps of APPE.
  • (1)

    Initialization: Np stick insect populations xt are initialized, and p, a, and ev of each stick insect are initialized to 1/Np, 1.1, and 0, respectively. Initialize the parameter k of Ho, and k = log(Np) + 1. Initialize parameter INV = 4 of jump mechanism and threshold value INV Gate = 10−6. Initialize parameter HAnum of history-based archive HA and HAnum = Np. Initialize current iteration t = 1 and the maximum iteration MAXGENS. Calculate fitness f(xt). Update the global best solution gbest and global best value gbestval. If t = 1, initialize Ho with the current best k solutions. The global best solution gbest is put into HA.

  • (2)

    Jump mechanism: If the global best solution gbest has kept the INV generation unchanged and the algorithm enters the late iteration or the standard deviation of the optimal solution in the INV generation is less than the threshold value INVGate, then the jump mechanism is applied. Using (19) to modify worse solutions from the second to the sixth. If a uniform random number is larger than probability rJump and the current population number is not less than 8, then delete the worst solution of PPE population and HA solutions. Moreover, when the number of Ho is more than the current population number, the number of Ho is reset again by k = log(Np) + 1, and the redundant poor solutions are deleted.

  • (3)

    Population position updating: In our algorithm, equation (21) is used for position updating. New solution is . Calculate fitness f(new xt+1).

  • (4)

    Population closing moving: In the first half of the iteration cycle of the algorithm, when the random number is greater than 0.5, the whole PPE population is moving toward the HA solution, and new solutions are generated by equation (22). Calculate fitness . Then, compare the new solution generated by equation (22) with the new solution generated by equation (21), the good one is reserved as current iteration’s new solution.

  • (5)

    HA and Ho update: If HA is not full, HA is filled one-by-one with optimal new solution of each round. If t > HAnum, the g best of each round replaces the random one solution of HA. When the number of iterations is more than half, the algorithm has a 50% chance of randomly replacing one of the HA solutions with the worst new solution per round. Update the global best solution g best and the global best value g bestval. If t > 1, the current best k solutions are comparing with the corresponding solution of Ho, the good ones replaces the solution in Ho.

  • (6)

    Absolutely accept: When the new solution’s fitness is better than that of the old one, accept it, and update p, a, and ev of each stick insect by equations (11)–(13).

  • (7)

    Parameter border check: If pi ≤ 0, ai ≤ 0, or ai > 4, reinitialize the corresponding stick insect.

  • (8)

    Termination: Steps 2 to 7 are repeated until reaching the maximum generation. Finally, record the best fitness gbestval and the best solution g best.

4.7. Setting for CVRP

We adopt the SR-1 method for solution representation, which means that the dimension of the PPE’s particle is n + 2 m [19]. The first n dimensions of the solution are related to the customer, and each dimension represents the corresponding customer. The smaller the value of this dimension, the higher the priority of the customer. Thus, the priority list of the customer can be obtained. The last dimension of 2 m represents the coordinates of m vehicles. According to the distance of coordinates, the priority matrix of vehicles for each customer can be obtained. Arrange customer points to vehicle route one byone according to customer priority order. For a customer point, which vehiclepath it is arranged into is determined by the vehicle priority matrix.According to the priority order of vehicles, arrange a customer point into thevehicle path with higher priority. If the current vehicle path meets thecapacity constraint, arrange the customer in this vehicle path. If the currentvehicle path exceeds the capacity constraint, place the customer in the lowerpriority vehicle path. Then, the corresponding path is formed. The example of SR-1 is as shown in Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
SR-1 method example.

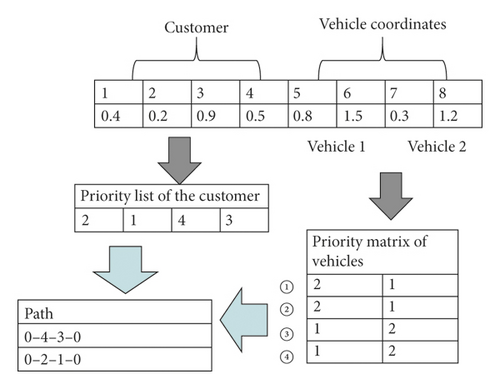
We use some local searching methods to optimize the routes. These methods are divided into inter-route optimization and intra-route optimization. Inter-route optimization mainly consists of three-point communication and deleting-adding communication, and the search time is the sum of the instance’s points and vehicles. Three-point communication refers to the random selection of three paths in the solution. A point of each path is randomly selected, and the points of the path are exchanged in the order of 3, 1, and 2. If the newly generated three paths are better than the original three paths, then the original path will be replaced [28]. Deleting-adding communication refers to the random selection of two paths in the solution, with a point randomly selected in each path. One of the paths deletes the selected points and adds the selected points to the other path. If the new two paths are better than the original two paths, then the original path is replaced [29]. Intra-route optimization consists of path scrambling, path inversion, and path 2-point swapping. The number of executions of these methods is the square of the number of points in each path of the solution. Path scrambling refers to the random rearrangement of paths, except the starting and ending points, which are rearranged using the randperm function of Matlab. If the generated new path is better than the best solution, then it replaces the original best solution, and the next searching will still change the original path, however, the comparison object is the best solution. Path inversion means that two points of the path are selected each time, and then the paths between the two points are rearranged in the reverse order. If the new solution produced is good, then retain it as the best solution for the next search [28]. Path 2-point swapping means that two points of the path are selected each time, and then the two points are exchanged. If the new solution produced is good, then retain it as the best solution for the next search [28].

5. Experiment and Application

In this section, we utilized CEC2013 to test our proposed algorithm, as shown in Table 1. APPE experiment results are shown in Tables 2–13. Then, the CVRP results are as shown in Tables 14–15. These are the results APPE compares with DE, SSA, PSO, and PPE. We also compare APPE with some existing work in Tables 6–19.

Table 1. Benchmark functions of CEC2013 (Test APPE’s performance).
No. Type Optimum No. Type Optimum
F1 Unimodal −1400 F15 BasicMultimodal 100
F2 −1300 F16 200
F3 −1200 F17 300
F4 −1100 F18 400
F5 −1000 F19 500
F6 BasicMultimodal −900 F20 600
F7 −800 F21 Composition 700
F8 −700 F22 800
F9 −600 F23 900
F10 −500 F24 1000
F11 −400 F25 1100
F12 −300 F26 1200
F13 −200 F27 1300
F14 −100 F28 1400
Table 2. Comparison of the best result of 51 runs on 10D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 739.79074 0 1.548022 1.5277E-06 0
F2 3699523.589 16892.6651 675269.84 16924.6562 68.614074
F3 588747385.1 13.3876934 689596211 74894.9703 0.000959781
F4 7128.473 988.32578 7833.35511 121.0451 68.06974
F5 50.3104 0 39.12572 8.5511E-05 1.05729E-11
F6 68.95087 0.0109923 4.216561 8.1355E-06 1.07889E-09
F7 55.7164 15.0799 47.66596 7.27598 0.44489
F8 20.1983 20.1385 20.1618 20.1326 20.2161
F9 7.2138 2.78402 5.1737 1.90882 0.822382
F10 78.52804 0.243969 13.60727 0.135769 0.0270174
F11 46.2114 3.97984 29.0232 5.1115E-06 2.69438E-11
F12 55.7539 15.9193 24.9419 14.9245 4.9748
F13 61.5672 23.5856 37.8746 16.0905 8.16871
F14 761.00596 35.1763 369.54088 137.2404 12.39519
F15 1162.7414 515.11843 208.5453 225.1287 458.76209
F16 0.780144 0.190384 0.260976 0.10284 0.679173
F17 89.55631 19.0217 41.6638 10.4437 5.15832
F18 91.67574 31.03869 34.0257 12.8986 19.6821
F19 11.1484 0.351582 3.319064 0.0606383 0.348941
F20 3.60832 3.11728 3.22622 1.83506 1.2217
F21 454.7408 200 306.5969 100.0283 400.1939
F22 1287.114 178.2702 291.18665 15.40419 14.11783
F23 1497.5974 765.85882 986.55529 73.788553 271.18111
F24 184.698 132.6267 124.3565 138.2729 105.7783
F25 173.5373 208.2578 219.6212 132.3753 109.5371
F26 168.4389 119.8991 132.0062 119.9186 105.9698
F27 560.8726 312.6709 415.0833 307.2788 301.8725
F28 476.735 100 734.1271 100.0221 100
W/D/L 0/0/28 3/0/25 1/0/27 6/0/22 20/0/8
Table 3. Comparison of the mean result of 51 runs on 10D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 1416.5787 1.605E-13 811.9416 9.9958E-06 2.675E-14
F2 10084933.05 197537.945 6878233.51 78209.7076 6115.1032
F3 3118637483 152909331 7255467596 116898667 944921.1013
F4 12971.2353 7083.6651 15628.6068 641.8292 702.1065
F5 83.7238 1.226E-13 398.3362 0.00037539 4.16834E-10
F6 116.0168 12.8841 107.4564 18.6264 7.63911
F7 78.7358 84.1336 105.41 37.9462 16.6702
F8 20.3327 20.3472 20.3168 20.3303 20.4067
F9 8.94373 7.22868 8.71324 4.84641 3.76595
F10 181.5071 2.21159 178.7806 0.627955 0.206199
F11 69.3683 16.8379 73.7286 0.254539 3.49337
F12 79.6579 59.2814 80.4332 38.9032 17.5971
F13 80.0367 62.5323 97.0562 36.2642 29.1881
F14 1314.4366 371.4428 1017.8572 354.5957 286.6114
F15 1529.7766 1120.4131 872.7005 715.3729 1080.2465
F16 1.13441 0.661732 0.747968 0.357594 1.15523
F17 125.3906 84.2239 96.2605 11.3378 19.3253
F18 129.3592 139.6976 95.3178 31.9006 40.797
F19 35.1423 1.96173 150.0135 0.806923 0.900422
F20 3.97465 3.73039 3.97293 3.01931 2.82778
F21 507.7433 396.2685 413.4744 388.4232 400.1939
F22 1603.7803 544.8418 1458.3753 362.7106 296.2929
F23 1842.0891 1518.7686 1649.8481 1124.1341 1095.8663
F24 223.9939 221.1283 226.6401 216.8546 198.7732
F25 216.4075 222.4582 228.3634 212.0031 192.7499
F26 196.4968 197.3708 232.3701 161.1619 154.8035
F27 629.3467 562.4606 638.4348 393.6886 387.5239
F28 746.0777 699.0044 912.4083 578.1929 344.4934
W/D/L 0/0/28 1/0/27 1/0/27 8/0/20 18/0/10
Table 4. Comparison of the standard deviation result of 51 runs on 10D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 336.29231 1.1409E-13 840.7906 6.8679E-06 7.3986E-14
F2 3591008.967 126630.817 4663751.77 43253.9733 6050.4934
F3 1017194416 357131948 4644005056 183252405 3551542.55
F4 3315.33688 3588.503 2250.98706 404.5624 745.7658
F5 17.8996 5.4962E-14 321.9183 0.00018596 4.76424E-10
F6 22.96358 18.2449 56.81199 27.8417 8.28299
F7 12.4518 39.8206 38.77687 19.4452 13.3872
F8 0.0648398 0.0660583 0.0803062 0.084776 0.0790714
F9 0.489928 1.4337 1.17197 1.4601 1.48489
F10 49.44543 1.39021 120.7778 0.364935 0.115752
F11 8.12773 9.77683 28.7959 0.684481 2.17383
F12 9.1472 27.3009 31.8621 15.4218 7.28016
F13 8.76245 22.1908 28.2487 11.3712 10.3039
F14 162.82672 204.7426 238.51942 141.844 190.2989
F15 136.11119 289.33376 279.989 294.5977 301.37034
F16 0.178596 0.307342 0.226042 0.185098 0.212344
F17 13.70235 45.1711 26.9561 0.595998 7.21938
F18 15.4126 28.03248 24.9926 8.60915 7.23762
F19 19.6514 1.16874 239.7625 0.328438 0.509409
F20 0.156375 0.26237 0.341358 0.415301 0.609363
F21 25.66769 28.03275 24.7686 58.84134 3.21555E-14
F22 139.6671 261.2185 414.21438 178.3056 182.963
F23 142.08612 346.663 349.63326 388.70003 494.49528
F24 9.186187 13.39515 17.40012 16.21229 32.52391
F25 14.01808 4.603786 3.639165 15.41364 32.96771
F26 7.597635 56.24498 64.94274 34.55174 41.58459
F27 22.37158 85.9428 89.94543 33.9609 41.40027
F28 130.9133 265.6456 89.81761 225.5822 191.5919
W/D/L 12/0/16 1/0/27 2/0/26 5/0/23 8/0/20
Table 5. Comparison of the average running time result of 51 runs on 10D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 0.727436531 0.8287859 1.15685042 7.18115574 0.671487292
F2 0.791050904 0.924853635 1.3439542 7.20013287 0.70339359
F3 0.774887343 0.907082424 1.29866165 7.21305981 0.790544096
F4 0.763615047 0.903257461 1.30124119 7.14854095 0.386089429
F5 0.764020171 0.887531624 1.26940391 7.26179316 0.686430051
F6 0.726979804 0.844920447 1.16895654 7.2806207 0.670751492
F7 0.894148461 1.040195514 1.60901454 7.41189731 0.803711176
F8 0.855579947 1.018726375 1.54419505 7.22193355 0.322570457
F9 2.219833976 2.641704835 4.92032594 8.67749507 2.310656547
F10 0.773372886 0.891785363 1.28616139 7.27650189 0.668267453
F11 0.816651865 0.962051961 1.4769969 7.27590196 0.746390108
F12 0.843791384 0.99691912 1.51443125 7.49711857 0.609939676
F13 0.83997619 0.98404201 1.48591037 7.3828366 0.510813414
F14 0.822789535 0.943898739 1.47654896 7.28391574 0.582743498
F15 0.829717169 0.957212175 1.48187512 7.38718168 0.461557804
F16 1.83420029 2.180153114 4.0038432 8.25544575 1.247958082
F17 0.781633394 0.907479276 1.36932876 7.24234632 0.577252965
F18 0.79514379 0.932933855 1.42243596 7.20300338 0.388129488
F19 0.743986608 0.862446631 1.27623414 7.29507605 0.715902753
F20 0.801560351 0.916730906 1.4320129 7.30689116 0.494742363
F21 1.065321725 1.263061847 1.98997494 7.57730783 0.883767925
F22 1.159216551 1.320134182 2.28246203 7.58581411 0.931372729
F23 1.168561278 1.348461751 2.30642576 7.61082738 0.817745671
F24 2.571608424 3.024779602 5.6708838 8.99084936 2.541635441
F25 2.591145233 3.013362006 5.71097513 8.91483909 2.597728576
F26 2.784730184 3.323031224 6.20988149 9.09719149 2.571828318
F27 2.745837339 3.261529955 6.11941155 9.10913397 2.372727906
F28 1.288557314 1.523347316 2.596839 7.62935641 1.087740337
W/D/L 3/0/25 0/0/28 0/0/28 0/0/28 25/0/3
Table 6. Comparison of the best result of 51 runs on 30D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 20965.5117 2.2737E-13 3115.0987 3.4641E-05 2.2737E-13
F2 184302669.7 556561.902 42409000.72 1551822.08 36796.10533
F3 99304872220 10402522.9 24129867958 14277792 11979.52113
F4 47671.1384 17895.2805 41958.6448 436.4169 277.24218
F5 2736.1858 4.5475E-13 845.64218 0.00122154 2.01521E-09
F6 2192.6367 2.59305 371.83971 0.304544 1.69745E-05
F7 326.5177 107.2508 227.7295456 44.6206 39.1504
F8 20.8505 20.7428 20.7042 20.8119 20.7702
F9 36.6723 27.5559 34.1636 23.3817 15.4945
F10 2740.0071 0.0640834 544.29708 0.0702674 6.77581E-08
F11 475.3545 93.52546 342.582 15.122 17.9093
F12 536.0034 303.4593 288.8458 251.7349 72.63182
F13 477.1505 333.4405 499.8886 261.1692 190.6686
F14 6284.6022 1787.2956 2549.475 766.94606 431.50235
F15 6306.8434 2999.2399 3353.0779 2500.5042 5525.0534
F16 1.64039 0.267507 0.822458 0.193588 1.58162
F17 1008.295 287.815 323.721 43.6346 65.20754
F18 1102.4916 350.691 487.3008 174.6342 156.3594
F19 43694.72938 9.84876 342.97435 2.91789 2.43391
F20 14.521 12.6801 14.5097 13.8654 9.58436
F21 2801.7822 100 929.77219 100.2957 100
F22 6985.8846 1760.6213 4701.2418 592.84675 362.0814
F23 7504.1003 3830.2633 3760.2452 3520.5278 3135.9944
F24 325.3054 282.8699 307.7325 251.8537 234.3891
F25 336.8065 291.219 310.1113 308.9248 270.7536
F26 216.1884 200.0521 204.6498 200.0465 200.0016
F27 1365.8604 936.36559 1246.5007 945.20441 746.8349
F28 3662.6068 300 3717.7686 100.27997 100
W/D/L 0/0/28 2/0/26 1/0/27 4/0/24 22/0/6
Table 7. Comparison of the mean result of 51 runs on 30D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 32193.5619 6.5537E-13 9711.9121 8.1178E-05 4.6812E-13
F2 368242452.8 2081301.22 179774792.8 3096187.31 126305.9182
F3 7.10045E + 11 698447995 9.77373E + 13 434470674 31758287.64
F4 75322.0536 28653.0937 52077.4646 930.919 1330.2804
F5 4522.474 1.0867E-11 2695.5244 0.00195401 5.23523E-08
F6 3552.4961 30.175 1758.4039 59.1902 6.12643
F7 747.6163 211.4113 108509.3088 94.8052 84.0757
F8 20.9546 20.922 20.9005 20.9443 20.9755
F9 39.276 33.915 39.5487 30.821 24.7972
F10 4134.0267 0.211734 1991.4149 0.44158 0.0650486
F11 579.6098 240.4308 584.3916 28.1263 33.9158
F12 628.6948 511.8694 606.0292 353.5071 183.0126
F13 624.5928 440.3657 701.2616 379.6572 266.1043
F14 7069.1658 2731.909 4328.8102 1243.0858 1814.8754
F15 7431.2237 4754.6443 4829.5591 3951.5532 6617.3184
F16 2.49294 1.25122 1.56921 0.745032 2.49028
F17 1262.8753 652.2582 666.9315 62.4704 108.3917
F18 1269.4583 702.0829 684.1028 287.4171 300.5752
F19 167474.7719 19.342 4354.8665 6.46873 5.63526
F20 14.9018 14.7589 14.8377 14.6797 12.2536
F21 3210.8721 364.2293 1623.5516 315.6636 320.9034
F22 7723.8174 3374.4772 6251.9555 1336.6024 940.461
F23 8097.5094 5851.2557 6602.7644 5180.4845 6658.3955
F24 334.942 303.6476 339.2056 286.0378 263.803
F25 353.4227 314.6729 343.4621 348.9108 297.3444
F26 241.288 363.4894 384.4514 315.0175 200.0092
F27 1428.7773 1254.8879 1429.8648 1145.826 927.6687
F28 4413.077 3213.3913 4978.1659 3248.566 690.8847
W/D/L 0/0/28 1/0/27 1/0/27 9/0/19 17/0/11
Table 8. Comparison of the standard deviation results of 51 runs on 30D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 3909.09245 2.4761E-13 3561.6764 2.2148E-05 1.5362E-13
F2 74221490.37 941488.26 89397375.81 816426.966 83074.86122
F3 7.20796E + 11 1065594457 3.23802E + 14 358944299 85733576.72
F4 8466.66261 4475.09793 3760.44355 309.9896 1143.5652
F5 755.38339 1.8485E-11 1543.1381 0.00050402 5.65084E-08
F6 640.64055 24.7472 1147.0894 25.2244 6.49659
F7 393.6556 106.0421 271133.1512 19.8107 26.8212
F8 0.0491254 0.0573101 0.0718902 0.0532219 0.0504813
F9 1.1558 3.41188 2.12293 2.9527 3.79688
F10 540.80016 0.114618 984.78042 0.220342 0.0490094
F11 44.57488 75.69394 105.7453 7.26775 9.97949
F12 40.49799 134.3097 119.1011 53.33428 50.99063
F13 46.1267 76.22904 86.99332 48.55205 40.97781
F14 262.46923 535.39708 819.82348 236.31161 1441.8054
F15 271.96764 730.40653 835.72922 627.96769 417.02913
F16 0.320608 0.547221 0.43001 0.300076 0.346913
F17 107.2886 136.14 97.29982 7.74407 21.66193
F18 78.052688 126.3105 83.33826 53.92487 41.8762
F19 67584.43532 5.63479 3353.4627 2.11375 1.76896
F20 0.114222 0.529039 0.231521 0.282559 0.684561
F21 172.3487 96.53369 301.79304 72.4779 85.50782
F22 269.7388 869.43735 845.09278 295.70899 339.5195
F23 243.52231 856.05385 1075.8917 756.67546 1221.6536
F24 4.086933 9.678988 18.7233 16.02537 14.32264
F25 4.969392 11.83765 16.5024 21.20163 13.09351
F26 8.458015 66.57767 64.77045 82.44704 0.005305383
F27 27.630268 109.75615 75.82382 82.797679 89.73993
F28 269.10614 1467.6047 630.94737 773.56802 916.4915
W/D/L 11/0/17 1/0/27 0/0/28 7/0/21 9/0/19
Table 9. Comparison of the average running time result of 51 runs on 30D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 2.733809878 2.65437004 4.1709789 21.8721739 2.407070994
F2 3.238093776 3.28368366 5.52267889 22.1806176 3.242242859
F3 3.387544408 3.44985781 5.79780013 22.1986548 2.802126447
F4 3.033938118 2.98933781 5.04895915 21.8332192 1.460134582
F5 3.060770578 3.05556757 4.96295184 22.2294468 2.630876359
F6 2.912188557 2.89667259 4.5023418 22.1873498 3.894232227
F7 4.585807916 4.73127061 9.05654281 23.5809211 4.413959241
F8 3.954471206 4.07066223 7.33255408 22.9174646 1.585859245
F9 17.05689298 18.9060265 40.0398491 35.2771729 12.41038709
F10 3.334638673 3.29820511 5.4339282 22.2756434 2.716332702
F11 3.444212914 3.48815126 5.99635844 22.3046879 3.0724273
F12 3.981317933 4.03849017 7.26727993 22.886067 2.921447771
F13 3.976971841 4.00729305 7.10558566 22.9836765 1.930308529
F14 3.685780082 3.67497535 6.60276835 22.7189149 2.713648625
F15 3.830101522 3.86078174 6.65525209 22.8490806 1.75100859
F16 13.45326515 14.7837753 29.2868758 31.7040965 8.918082525
F17 3.147515716 3.21549638 5.08030391 22.1923851 2.652192106
F18 3.500081333 3.59570355 5.83726951 22.3467761 1.447078869
F19 3.011889486 3.04511699 4.66262677 21.9862949 3.609727229
F20 3.670195529 3.77716328 6.92572923 22.390139 1.774093445
F21 5.8482322 6.27261929 10.5518727 24.3638556 4.451286106
F22 6.232905657 6.51323347 12.1217653 24.7453143 5.447029629
F23 6.791029171 7.08679317 13.3236218 25.1882066 4.829456082
F24 20.09962069 22.2324157 43.2164071 37.7097732 14.63043557
F25 20.0838764 22.4150292 42.3260732 37.7248481 14.5165233
F26 21.67665217 24.595264 46.7010523 39.2097254 24.28157111
F27 21.23823786 24.2659194 46.0547195 38.9343311 15.58041748
F28 8.259479129 8.96047216 16.5444839 26.6793565 6.434003169
W/D/L 3/0/25 1/0/27 0/0/28 0/0/28 24/0/4
Table 10. Comparison of the best result of 51 runs on 50D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 68441.6877 6.8212E-13 4421.5318 9.1774E-05 1.13687E-12
F2 796828451.2 897706.17 27754539.4 2311976.79 114810.9289
F3 4.11102E + 11 36730944.5 45009339893 64993978.4 3218012.379
F4 103396.927 33164.3416 56242.6043 233.6512 428.55484
F5 9117.13317 2.2907E-09 991.73975 0.00229062 2.2956E-07
F6 6066.8624 29.1158 444.7514 39.7167 0.128249
F7 321.54597 96.81021 282.559833 70.85565 56.4843
F8 21.0487 21.051 20.9601 21.0257 21.0471
F9 70.0516 49.8706 65.8906 48.0806 39.9872
F10 8540.84996 0.0394587 760.25367 0.857053 3.88815E-05
F11 1120.4763 382.0615 591.099 69.93432 62.6823
F12 1157.4674 587.01751 695.9241 461.6641 204.9601
F13 1132.7369 640.2518 953.41855 566.5412 421.8479
F14 12375.2343 3470.8789 5201.6947 1011.1859 1039.3238
F15 13171.1787 6238.7238 7676.88995 5808.5115 11569.9181
F16 2.68248 0.689805 1.27295 0.546151 2.42801
F17 2686.1285 502.0316 782.54144 112.7755 155.0626
F18 2698.9651 987.4102 870.71601 451.2733 360.0513
F19 466278.7647 24.3778 912.66167 7.4999 7.79172
F20 24.4448 21.9486 23.6975 21.8148 18.6627
F21 5875.3627 836.4425 1831.4087 836.4425 100
F22 13466.9914 5826.1274 7811.75043 1936.8612 1064.7735
F23 14407.6167 8117.39148 9107.61415 7311.61553 8301.79767
F24 432.5152 371.4055 415.414 327.2399 310.6605
F25 488.8236 387.3883 412.8656 434.7963 380.0998
F26 296.6734 440.0132 469.8953 200.2743 200.0272
F27 2321.1044 1775.5901 2151.7305 1692.6655 1292.2378
F28 7644.2744 400 6451.9363 474.57092 400
W/D/L 0/0/28 3/0/25 1/0/27 7/0/21 18/0/10
Table 11. Comparison of the mean result of 51 runs on 50D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 80496.6275 1.2528E-12 9600.2818 0.00017649 3.49487E-11
F2 1170022441 2226137.48 192268997.5 4042717.04 400359.6315
F3 4.40463E + 12 1369573907 2.04922E + 11 392037714 69788181.12
F4 136314.9379 53168.688 69134.0056 674.8522 1286.1218
F5 15201.5539 1.821E-08 1625.4642 0.00374727 1.4891E-06
F6 7949.0109 72.5883 902.9159 86.2859 35.1058
F7 1086.8641 192.4685 11581.7115 116.5335 83.5833
F8 21.1353 21.1317 21.1175 21.1177 21.1504
F9 72.941 65.2474 73.2972 57.8761 52.102
F10 10371.6231 0.202345 1961.669 1.52074 0.0368955
F11 1327.7597 547.3071 745.3906 110.0593 93.4338
F12 1336.6887 1014.754 916.3933 570.8822 412.2794
F13 1324.4015 956.3305 1168.9616 725.9276 536.2261
F14 13453.7746 5825.0496 7675.3836 1963.8542 2825.8275
F15 14290.1024 8553.19 10356.5828 7728.0556 12892.3516
F16 3.28518 1.83319 2.27207 1.2382 3.31238
F17 3020.4296 981.1095 1024.8344 146.7249 226.2728
F18 3053.1201 1155.8584 1096.2182 593.7946 627.5738
F19 1429662.26 49.627 2624.7591 13.2586 12.7787
F20 24.8789 24.3835 24.485 24.0914 21.9659
F21 7181.9716 998.9602 3051.678 948.5251 870.4084
F22 14742.4834 7413.6214 10468.5507 3276.6393 2423.8416
F23 15334.0567 10546.0751 12655.7041 10424.3902 13606.4302
F24 464.8197 391.9212 470.8258 373.7801 342.4159
F25 502.6936 415.216 459.7346 504.9336 408.2602
F26 368.9144 470.2997 495.343 411.5417 283.8361
F27 2446.8166 2076.0709 2433.0726 2107.7286 1650.236
F28 8778.8527 5148.5057 9186.8097 5936.9657 1470.4027
W/D/L 0/0/28 2/0/26 1/0/27 7/0/21 18/0/10
Table 12. Comparison of the standard deviation result of 51 runs on 50D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 5405.61377 3.9217E-13 2679.9505 4.1786E-05 7.0273E-11
F2 170612616.4 824253.494 89445562.68 1007133.92 179412.3457
F3 3.2854E + 12 1557568439 4.01457E + 11 379016850 94471867.3
F4 11084.63859 11809.0884 5827.04834 184.5265 668.48665
F5 2116.93995 1.7468E-08 324.03013 0.00084021 1.5852E-06
F6 955.60891 31.5493 456.9381 32.6704 18.3843
F7 525.90396 79.70547 13589.3232 21.04326 14.1085
F8 0.0363517 0.0364229 0.0481815 0.0365593 0.042277
F9 1.36303 4.67854 3.15456 3.72436 5.71436
F10 882.747601 0.115331 607.18573 0.256366 0.024425
F11 81.157358 92.02943 70.68308 20.84648 15.7099
F12 64.758226 116.40179 97.13284 56.83782 96.05942
F13 77.218129 183.0932 94.733558 69.5969 66.06756
F14 326.008925 1029.6185 1404.319 399.01654 2150.2895
F15 393.289928 960.32527 1506.75168 942.05543 609.042346
F16 0.239473 0.61187 0.531921 0.350457 0.371027
F17 146.22569 147.6494 75.297952 14.74808 36.31978
F18 125.67353 46.142709 79.748497 71.51158 94.5146
F19 322868.2211 16.5907 1522.0331 2.10674 4.34599
F20 0.1289 0.482846 0.129266 0.631614 1.0936
F21 362.66356 142.9595 313.42278 140.9302 306.9437
F22 365.40434 1019.4687 1239.58645 838.11989 1044.5246
F23 367.202851 1354.96456 1416.92288 1245.35206 1138.12779
F24 11.07239 13.63289 38.71835 25.27126 18.62976
F25 7.704087 17.48497 35.64058 36.57497 19.04745
F26 26.48411 14.2354 11.83787 105.9412 110.0795
F27 44.650405 136.27279 144.65187 159.38326 122.3399
F28 416.1356 3120.0947 991.68671 988.11438 1868.8146
W/D/L 12/0/16 3/0/25 1/0/27 5/0/23 7/0/21
Table 13. Comparison of the average running time result of 51 runs on 50D in 28 benchmark functions.
Fun DE SSA HHO PPE APPE
F1 5.371938416 4.57383823 7.23377461 38.1038224 4.446575594
F2 7.157403912 6.62089211 11.3540526 39.1676853 7.158186551
F3 7.839430525 7.3246534 12.5236647 39.9919087 6.214457253
F4 6.484470433 5.91526308 10.1147916 38.58679 3.307264696
F5 6.159703835 5.54299413 9.14633452 37.6149204 4.968641435
F6 6.300308008 5.60679982 9.2921294 37.6352779 6.911794831
F7 11.10656359 10.7296947 20.4603011 41.5075489 10.88083133
F8 9.318202392 8.70874237 16.4839356 39.6187509 3.878486443
F9 46.05065865 48.7456533 101.389658 75.4380672 32.79673965
F10 7.527485204 6.72485453 11.9008743 40.0126535 6.521356616
F11 7.303516457 6.65447378 11.9370057 40.183341 6.179351049
F12 9.596861269 9.09086465 17.1752837 42.2132078 6.93119691
F13 9.743597688 9.1466903 17.1017582 42.4066013 4.65911769
F14 7.889016759 7.25925715 13.828576 40.8411437 6.670441894
F15 8.824859059 8.19700595 15.6963778 41.2855432 4.436260716
F16 35.43426225 38.0182758 78.9101852 66.163459 23.73375013
F17 6.545739804 5.81661149 10.4148023 38.0207576 5.578457125
F18 8.349048814 7.82492584 14.3796084 39.1149567 3.9553397
F19 6.863519427 5.93801426 10.3868958 37.8526068 7.639078567
F20 8.741159843 7.85354537 15.0667554 38.94757 3.508262818
F21 15.61953418 16.2938313 29.2424287 45.2747967 11.12546115
F22 15.09370126 15.3303718 29.6861623 45.1094114 13.92498259
F23 17.74963977 18.3327347 35.4951246 47.3597377 11.49145802
F24 55.77218786 61.9013014 118.547038 81.9097344 39.63127379
F25 52.60461786 63.011092 116.425617 82.0330892 39.2314303
F26 57.51527773 70.9420056 132.969794 86.6588994 58.37427563
F27 56.10193225 69.4253279 129.134722 85.362875 42.25193263
F28 21.45543076 24.3204501 46.9656329 51.9634444 18.04838259
W/D/L 1/0/27 4/0/24 0/0/28 0/0/28 23/0/5
Table 14. Comparison of the best result of 10 runs in CVRP instances.
Instances BKV DE SSA PSO PPE APPE
A-n32-k5 784 794.4865 787.0819 787.2024 787.0819 787.0819
A-n33-k5 661 678.0007 662.2642 673.1471 662.2642 662.1101
A-n33-k6 742 746.125 742.6933 742.6933 742.6933 742.6933
A-n34-k5 778 787.6693 786.437 786.437 786.7965 786.437
A-n36-k5 799 808.5726 802.1318 802.1318 802.1318 802.1318
A-n37-k5 669 688.7647 672.7407 672.7407 672.5174 672.5174
A-n37-k6 949 960.1145 956.8075 966.0936 957.0298 957.0298
A-n38-k5 730 747.4928 738.0118 734.4416 734.4416 733.9458
A-n39-k5 822 836.0773 829.4541 829.5219 829.5219 829.5219
A-n39-k6 831 841.5609 833.2046 835.2518 835.2518 835.2518
A-n44-k7 937 955.3702 943.4791 948.8242 952.5564 943.6351
A-n45-k6 944 984.3388 959.2347 994.68528 970.79579 945.3614
A-n45-k7 1146 1186.559 1159.7315 1165.812 1170.0275 1153.0785
A-n46-k7 914 942.1947 921.7679 921.8017 918.1274 918.1274
A-n48-k7 1073 1134.015 1095.2564 1106.6835 1100.3926 1094.9122
A-n53-k7 1010 1098.815 1042.8605 1054.9787 1030.8244 1045.9452
A-n54-k7 1167 1226.547 1184.6926 1188.767 1196.2087 1182.8441
A-n55-k9 1073 1135.431 1082.8527 1082.9222 1088.2412 1078.39
A-n60-k9 1408 1434.627 1364.6654 1386.0294 1369.973 1379.077
A-n61-k9 1035 1182.316 1071.5384 1147.6217 1080.8725 1104.0151
A-n62-k8 1290 1372.683 1348.8174 1339.6425 1338.6479 1331.7414
A-n63-k10 1315 1384.93 1352.951 1363.3655 1345.4533 1323.9144
A-n63-k9 1634 1725.011 1661.5273 1701.0925 1692.2855 1639.9246
A-n64-k9 1402 1501.943 1425.8711 1446.1263 1424.9294 1433.2557
A-n65-k9 1177 1267.51 1201.895 1260.8151 1186.6736 1208.8699
A-n69-k9 1168 1243.583 1183.333 1198.7175 1190.5865 1183.0729
A-n80-k10 1764 1911.073 1828.1481 1828.8761 1831.7224 1823.0898
W/D/L   0/0/27 10/0/17 3/0/24 8/0/19 18/0/9
Table 15. Comparison of the mean result of 10 runs in CVRP instances.
Instances BKV DE SSA PSO PPE APPE
A-n32-k5 784 802.3796 791.6953 789.5103 794.8186 788.8223
A-n33-k5 661 684.0878 675.9522 678.5661 671.0078 665.5313
A-n33-k6 742 754.7865 747.2399 745.6267 744.6511 743.8523
A-n34-k5 778 792.6542 792.4126 792.1176 792.9502 788.4026
A-n36-k5 799 816.6452 808.0167 810.3682 811.9299 807.2603
A-n37-k5 669 700.4381 689.2895 687.5505 683.889 678.6079
A-n37-k6 949 981.1734 970.0739 974.8255 970.9061 967.2458
A-n38-k5 730 758.8868 749.0006 751.4792 741.9858 740.0858
A-n39-k5 822 847.8701 837.9498 844.841 833.7223 833.781
A-n39-k6 831 852.229 838.8618 838.0234 836.9315 836.5501
A-n44-k7 937 978.7361 962.6828 969.9482 967.2578 951.4784
A-n45-k6 944 1021.858 997.9943 1038.8207 1034.7167 999.428
A-n45-k7 1146 1200.789 1182.0618 1184.3241 1185.3844 1164.4213
A-n46-k7 914 964.4004 940.755 950.2408 941.6035 933.0219
A-n48-k7 1073 1144.862 1109.3274 1112.9579 1116.9883 1103.2999
A-n53-k7 1010 1106.072 1064.1732 1073.4099 1063.4356 1057.0531
A-n54-k7 1167 1245.638 1204.771 1228.5166 1231.2475 1202.2122
A-n55-k9 1073 1150.691 1106.4484 1113.959 1117.2283 1095.4729
A-n60-k9 1408 1443.306 1396.0582 1406.6868 1408.4423 1395.4768
A-n61-k9 1035 1206.694 1160.0295 1190.2004 1139.945 1146.3305
A-n62-k8 1290 1388.059 1360.9244 1356.5061 1363.7038 1345.357
A-n63-k10 1315 1412.946 1385.1111 1393.813 1372.8607 1348.2184
A-n63-k9 1634 1743.69 1690.8434 1735.573 1727.2144 1695.1167
A-n64-k9 1402 1518.639 1463.5227 1463.5476 1448.9618 1450.4584
A-n65-k9 1177 1306.929 1244.3624 1283.902 1257.6103 1239.5486
A-n69-k9 1168 1269.933 1208.9972 1228.6695 1216.934 1203.1344
A-n80-k10 1764 1929.862 1864.3596 1874.9804 1868.4458 1852.7933
W/D/L   0/0/27 2/0/25 0/0/27 3/0/24 22/0/5
Table 16. Comparison of the best result of 10 runs of APPE with the algorithms proposed by Korayem et al.
Instance Optimum KmeansFnO KmeansFnP KmeansFnR APPE
A-n33-k6 742 828 754 754 742.6933
A-n34-k5 778 792 822 839 786.437
A-n36-k5 799 814 846 846 802.1318
A-n39-k6 831 868 856 837 835.2518
A-n60-k9 1354 1395 1421 1423 1373.4651
A-n62-k8 1288 1366 1329 1329 1346.9532
B-n31-k5 672 684 672 672 676.0884
B-n34-k5 788 793 817 817 790.9678
B-n39-k5 549 571 564 566 553.1565
B-n41-k6 829 845 920 877 836.7407
B-n44-k7 909 940 954 944 932.0102
B-n50-k7 741 765 783 774 745.16
B-n50-k8 1312 1348 1359 1361 1341.876
W/D/L   0/0/13 2/0/11 2/0/11 11/0/2
Table 17. Comparison of the best result of 20 runs of APPE with the algorithms in Yan et al.
Instance CO-HS PSO GA APPE
A-n32-k5 807 829 818 797.7186
A-n33-k5 669 705 674 680.4111
A-n34-k5 790 832 821 786.437
A-n39-k6 852 872 866 842.8981
W/D/L 1/0/3 0/0/4 0/0/4 3/0/1
Table 18. Comparison of the best and mean results of 10 runs of APPE with the algorithms in Zhao et al.
Instance QDE/Best QDE/Mean QEA/Best QEA/Mean DE/Best DE/Mean APPE/Best APPE/Mean
P-n76-k4 718 728 718 728 746 765 615.72618 622.3824
P-n76-k5 740 751 740 751 803 813 643.98732 664.62492
A-n32-k5 784 810 835 861 910 924 787.08189 788.26212
A-n33-k5 707 716 707 716 724 735 662.2642 664.95601
A-n33-k6 785 787 785 787 857 872 742.69326 743.77421
W/D/L 1/0/4 0/0/5 0/0/5 0/0/5 0/0/5 0/0/5 4/0/1 5/0/0
Table 19. Comparison of the mean result of 10 runs of APPE with the algorithms in Khairy et al.
Instance GA ACO GTO APPE
A-n32-k5 812.9 982.5 901.7 790.3117
A-n33-k5 674.9 787.7 746.7 667.0751
A-n34-k5 803.4 911.8 862.8 790.7029
A-n36-k5 839.3 1008 903.3 809.091
A-n39-k6 894.9 1085 975.9 835.5559
A-n46-k7 987.8 1206 1138 932.0442
A-n80-k10 1987 2369 2470 1840.5895
X-n106-k14 28897 30450 31928 27751.5143
X-n129-k18 33893 38098 41710 30742.9103
X-n143-k7 21664 22674 39979 17318.072
X-n167-k10 28347 28859 48205 22904.9479
X-n209-k16 42587 42286 70080 33887.9638
W/D/L 0/0/12 0/0/12 0/0/12 12/0/0

Three types of functions are included in CEC2013, as shown in Table 1. The first type is the unimodal function, which tests the exploitation ability. The second is the basic multimodal function, which tests the exploration ability. The third type is the composition function, which is composed by the above-mentioned function, representing the challenging problems. The search range is [−100, 100] for each dimension.

5.1. Experiment Setting

In this experiment, we compare APPE with DE, SSA, HHO, and PPE. Each algorithm has 100 solutions, i.e., ps = 100, with Di  m = 10,  30,  50. Each algorithm has 51 independent runs in each benchmark, and Maxgen equal to 10000 × Dim/ps. The parameter setting is as follows: for DE, F = 2, CR = 0.9, and it uses DE/rand/1/bin. For HHO, β = 1.5. For SSA, the number of producers accounts for 20%, S  D = 20, and ST = 0.8. For PPE, k = log(Np) + 1, p, a, and ev of each stick insect are initialized to 1/Np, 1.1, and 0, and G = (ub − lb)((Maxgen + 1 − t)/Maxgen)/10. For APPE, INV = 4, INVGate = 10−6, JumpNum = 5, rJump = 0.05, HAnum = Np = ps, and other parameters are the same as the PPE.

The qualitative metric uses the convergence curve, and the quantitative measure comprises the best, mean, standard deviation, and average running time of the specific benchmark functions.

5.2. Experiment Test

Table 2 is the best experimental result of APPE with Di  m = 10, which is the best of 51 runs. Table 3 is the mean experimental result of APPE with Di  m = 10, which is the mean of 51 runs. Table 4 is the standard deviation experimental result of APPE with Di  m = 10, which is the standard deviation of 51 runs. Table 5 is the time experimental result of APPE with Di  m = 10, which is the average running time of each algorithm in 51 runs. Similarly, Tables 6–9 are the result of Di  m = 30, and Tables 10–13 are the result of Di  m = 50. We use fitness error f − foptimum for simplicity. We also use W/D/L to record each algorithm’s win/draw/loss number in 28 benchmark functions from Tables 2–13. Under a benchmark function test, if the algorithm has the best performance (minimum fitness value), then W adds one. If the algorithm is equal to other algorithms (with the same fitness value), then D adds one. Otherwise (the algorithm's fitness value is not minimum), L adds one. Figure 3 shows the convergence curves of APPE, and the dimension is 10. APPE compares with DE, SSA, HHO, and PPE.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
APPE’s convergence curve with the dimension of 10.

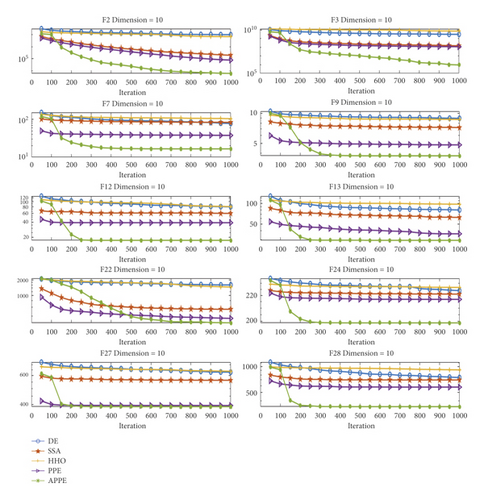
As shown in Tables 2, 6, 10, APPE’s W/D/L of the best experimental result are 20/0/8, 22/0/6, 18/0/10, respectively. It indicates that APPE can search better solutions and is more likely to jump out of local solutions. From Tables 3, 7, 11, APPE’s W/D/L of mean experimental result are 18/0/10, 17/0/11, 18/0/10, respectively. It means that APPE has a higher convergence accuracy. As shown in Tables 4, 8, 12, APPE’s W/D/L of standard deviation experimental result are 8/0/20, 9/0/19, 7/0/21, respectively. Compared with other algorithms in these tables, it can be seen that APPE has moderate convergence stability. From Tables 5, 9, 13, APPE’s W/D/L of time experimental result are 25/0/3, 24/0/4, 23/0/5, respectively. It shows that the running time of APPE is relatively short compared with other algorithms. Therefore, the convergence precision and running time of APPE are quite well.

As shown in Figure 3, the convergence accuracy of APPE at the beginning of iteration is at a general level. In the middle of iteration, many algorithms are in a stable convergence state, which is similar to falling into the local optimum, while APPE still continues to search at this time, which has a certain exploration ability and can jump out of the local optimum. In the latter part of iteration, it enters the stable convergence stage like many algorithms. In Figure 3, APPE’s convergence curve is basically at the bottom, i.e., the convergence precision is the best. In addition, APPE convergence curve obviously has a steep slope of decline, i.e., APPE can get a better solution faster.

5.3. Applying for CVRP

In this section, we apply APPE for solving CVRP. We use instances from [30, 31] to test APPE’s performance. We compare APPE with DE, SSA, PSO, and PPE. For more effectively, we run 10 times for getting more reliable data. The BKV item means the best-known value of instance. The particles are 50. The iteration is 1000. The setting of DE, PPE, and APPE are the same as aforementioned. For SSA, the number of the producers accounts for 20%, S  D = 20, and ST = 0.8. For PSO, ω = 0.8, and c1 = c2 = 2. We also use W/D/L to record each algorithm’s win/draw/loss number in instances from Tables 14–19, and the compared fitness value is the sum of distances here. The CVRP experiment is shown in Tables 14 and 15.

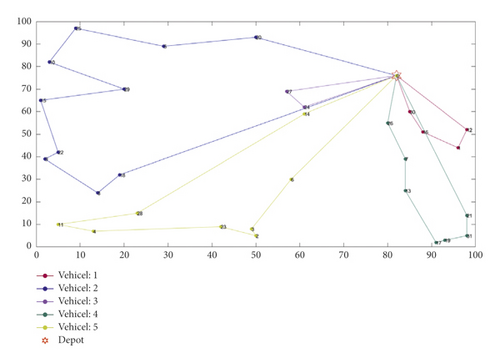
In Table 14, obviously, the performance of APPE searching for the global optimum is better than that of the comparison algorithms. Most of the instances obtain solutions close to BKV. Similarly, in Table 15, APPE has a better convergence accuracy for CVRP than the contrast algorithms. Figure 4 is the best route result of A-n32-k5 solved by APPE. It has 5 routes, and its fitness is 787.0819 that is close to BKV. It is proved that APPE can effectively solve CVRP.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The best route result of the A-n32-k5 by APPE.

We also compare APPE with some existing results. Table 16 is the comparison results of APPE with the results of Korayem et al. [32]. The setting is consistent with [32] that the population is 20, the maximum generations are 500, and each instance runs 10 times. In Table 16, the convergence precision of APPE is better than KmeansFnO, KmeansFnP, and KmeansFnR that are all cluster-first route-second methods, and they combine k-means with gray wolf optimizer [32]. Table 17 shows the comparison results of APPE with the results of Yan et al. [33]. The setting is consistent with [33], and each instance runs 20 times. In Table 17, the convergence precision of APPE is better than the constraint optimization harmony search (CO-HS) of [33], PSO, and GA, and three comparison algorithm's data comes from [33]. Table 18 shows the comparison results of APPE with the results of Zhao et al. [34]. The setting is consistent with [34] that the population is 200, the maximum generations are 500, and each instance is run 10 times. It can be seen from Table 18 that APPE is superior to quantum DE (QDE), quantum evolution algorithm (QEA), and DE in both best and mean performance, with data from [34]. Table 19 shows the results of APPE and the work of Khairy et al. [22]. The setting is consistent with [22] that the population is 40, the maximum generations are 1000, and each instance is run 10 times. In Table 19, the convergence accuracy of APPE is significantly better than GA, ant colony optimization (ACO), and group teaching optimization (GTO), with data from [22].

6. Conclusions

We propose APPE that deletes competition and conditional acceptance and corresponding evolutionary trend update for shortening the algorithm’s running time. It also adds a jump mechanism, history-based searching, and population closing moving for making PPE more likely to jump out of the local optimum and improving PPE’s convergence accuracy. Then, we test APPE by CEC2013, which compares with DE, SSA, HHO, and PPE. Experiment results show that APPE has higher convergence accuracy and shorter running time. Finally, APPE is applied to solve CVRP. From the test results of instances, APPE is more powerful to solve CVRP than DE, SSA, PSO, and PPE. We also compare our algorithm with some existing work. The results show that APPE is able to solve CVRP.

In the future, APPE can be improved by hybrid other algorithm, such as Flower Pollination Algorithm,Harmony Search [35] and adding cubic chaotic mapping [36], a version of multi-objective APPE can be proposed by referring to inverse model [37]. APPE can also be applied to other fields, such as power system problems [38, 39], wireless sensor network problems [39, 40], dispatching system of public transit vehicles [41, 42], traffic forecasting [43], sensor ontology matching [44, 45], feature selection [46], surrogate approach [47, 48], and deep learning [49, 50].

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (61872085) and the Natural Science Foundation of Fujian Province (2018J01638).

    Appendix

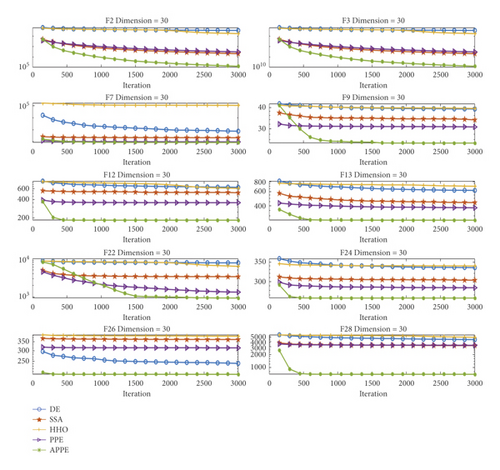
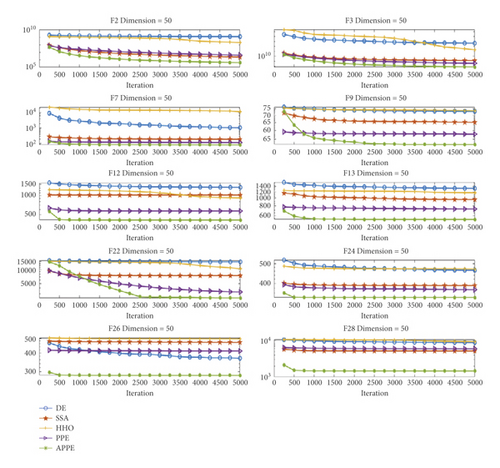
    In the CEC2013 experiment, for the convergence curves of the three dimensions are approximate, we only put the convergence curves of Di  m = 10 in the text and put Di  m = 30 and Di  m = 50 in the appendix. Figures 5 and 6 are the convergence curves of Di  m = 30 and Di  m = 50. It is similar to Figure 3, however, the convergence curve of APPE in Figures 5 and 6 has a relatively good convergence precision in the early stage of iteration. For Figures 5 and 6, in the middle of the iteration, APPE still continues to search at this time. In the latter part of the iteration, it enters the stable convergence stage like many algorithms. APPE’s convergence curve is also basically at the bottom, i.e., the convergence precision is the best. To sum up, APPE has better convergence performance.

    Details are in the caption following the image
    Figure 5
    Open in figure viewerPowerPoint
    APPE’s convergence curve with the dimension of 30.
    Details are in the caption following the image
    Figure 6
    Open in figure viewerPowerPoint
    APPE’s convergence curve with the dimension of 50.

    Data Availability

    The data used to support the findings of this study are included in the article.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.