Chemical graph theory is a field of mathematical chemistry that links mathematics, chemistry, and graph theory to solve chemistry-related issues quantitatively. Mathematical chemistry is an area of mathematics that employs mathematical methods to tackle chemical-related problems. A graphical representation of chemical molecules, known as the molecular graph of the chemical substance, is one of these tools. A topological index (TI) is a mathematical function that assigns a numerical value to a (molecular) graph and predicts many physical, chemical, biological, thermodynamical, and structural features of that network. In this work, we calculate a new topological index namely, the Sombor index, the Super Sombor index, and its reduced version for chemical networks. We also plot our computed results to examine how they were affected by the parameters involved. This document lists the distinct degrees and degree sums of enhanced mesh network, triangular mesh network, star of silicate network, and rhenium trioxide lattice. The edge partitions of these families of networks are tabled which depend on the sum of degrees of end vertices and the sum of the degree-based edges. These edge partitions are used to find closed formulae for numerous degree-based topological indices of the networks.

1. Introduction

In mathematics, the graph is an abstract structure formed by set of end points called nodes or vertices V (G) which are joined by a set of lines called edges E(G). The order and size of a graph is the total number of vertices and total number of edges of the graph G, respectively. In the theory of graphs, we usually analyze the chemical structures that appeared in different branches of chemistry.

Mathematical chemistry is the branch of mathematics in which mathematical tools are used to solve the problems arising in chemistry. One of these tools is a graphical representation of chemical compounds and this representation is known as the molecular graph of the concerned chemical compound [1, 2]. A topological index (TI) is a mathematical function that assigns a numerical value to a (molecular) graph and predicts many physical, chemical, biological, thermodynamical, and structural features of that network. A topological index is a molecular graph invariant that links the physicochemical features of a molecular graph with a number in the fields of chemical graph theory, molecular topology and mathematical chemistry [3]. Chemical graphs are graphs in which the vertices and edges represent the atoms and bonds of a chemical molecule. The vertices and edges are identified according to the atoms and types of bonds they represent [4, 5]. Topological invariants of a molecular graph can be used to learn about a chemical structure and its hidden properties without having to conduct experiments [6, 7]. Distance, degree, and eccentricity are the three major topological indices. Among them, degree-based indices have much importance and can be used as a tool for chemists [8]. Distance-based topological indices are concerned with graph distances, degree-based topological indices are concerned with the concept of degree, and counting-based topological indices are concerned with the counting of edges [9]. Topological indices have a wide range of applications in material science, math, informatics, biology, and other fields [10, 11]. The structure of the chemical graph is connected to topological indices [12, 13]. Physical and chemical features of the underlying molecule that can be determined from the TIs include heat of evaporation, heat of creation, boiling point, chromatographic retention, surface tension, and vapor pressure [14, 15].

The first topological index, known as the Wiener index, was developed by Wiener while examining the boiling point of alkanes [16]. The Randic index is a simple topological index which was introduced by Milan Randic [17]. Zagreb indices are the oldest topological indices written by Gutman and Trinajstic [18, 19]. In QSPRs, topological indices are utilized to guess the properties of the concerned compound [20]. There are no such type of topological index which give us an idea of all the properties of the concerned compound. As a result, there is constantly a need for new topological indices to be defined. The Sambor indices and reduced Sambor indices have lately been characterized by Gutman [21] as follows:

(1)

Only the Super Sambor and Super-reduced Sambor indices can be calculated if we can find the edge partition of these interconnection chemical networks based on the sum of the degrees of the end vertices of each edge in these graphs [9]as follows:

(2)

We compute SO(G), SO_red, SSO(G) and SSO_red(G) indices for certain chemical networks, as well as their graphical representations, in this study.

2. Enhanced Mesh

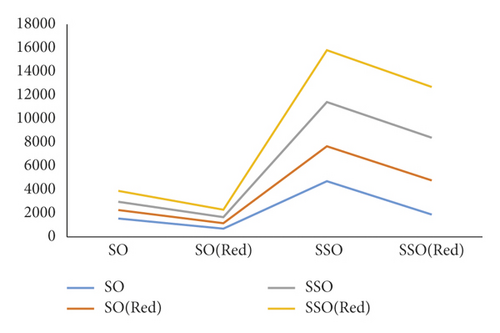
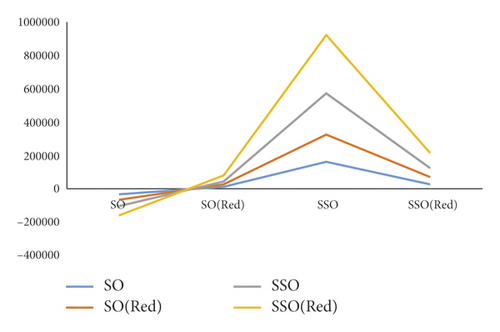
The degree-based topological descriptors of enhanced mesh networks are examined in this section. Also, the graphical comparison of SO, SO_red, SSO, and SSO_red indices is depicted in Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) 2D and (b) 3D graphical comparison of SO, SO_red, SSO, and SSO_red indices.

2.1. Construction

The end points of a common type of lattice graph relate to points in the grid with integer parameters, x-coordinates in the region 1, 2, …, s, and two vertices are associated by an edge whenever the corresponding points are at a distance of 1. In other words, for the point set mentioned, it is a unit distance graph. In literature, the name t-mesh has also been applied to a variety of different sorts of graphs with a specific structure, such as the Cartesian product of a number of path graphs. When we apply the Cartesian product of edges of order x₁, x₂, …, x_t, we get such a t-mesh M(x₁, x₂, …, x_t), which is written as follows:

(3)

If we take t-mesh, M(x₁, x₂, …, x_t) then it has order as follows:

(4)

and its size is

(5)

Now, we discuss enhance 2-mesh network M(x₁ × x₂), its vertex set is as follows:

(6)

and the set is

(7)

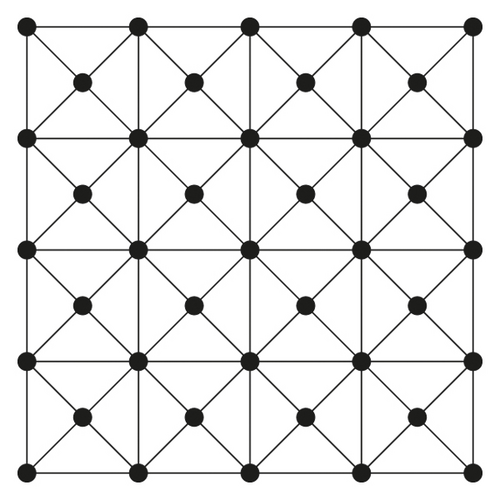
is the edge set. Now, enhanced mesh is the result by replacing each 4-cycle of by a wheel W₄ which has 4 vertices. As a result, a wheel W₄ is a graph obtained by connecting the central vertex of cycle C₄ to each vertex of cycle C₄. A new vertex is the hub (central vertex) of W₄. Let the collection of all hub (central) vertices be h_ij, 1 ≤ i ≤ s − 1,1 ≤ j ≤ t − 1. The graph of enhanced mesh is shown in Figure 2.

Theorem 1. SO and SO_red indices for the enhanced mesh network are as follows:

(i)
SO(G) = 82.7475 + 73.6081s − 69.4994t + 58.4045st
(ii)
SO_red(G) = 78.4639 − 62.9848(s + t) + 50.2618st

Proof. From the edge partitioning of enhanced mesh network given in Table 1, we have the following computations for SO and SO_red indices:

(8)

Table 1. Edge partitioning centered on the degree of each edge’s ending vertices of EM (s, t).

ϕ		Frequency
ϕ₁	ϕ_(3,4)	4
ϕ₂	ϕ_(3,5)	8
ϕ₃	ϕ_(4,5)	4(s + t − 4)
ϕ₄	ϕ_(4,8)	4(st − 2s − 2t + 4)
ϕ₄	ϕ_(5,5)	2(s + t − 6)
ϕ₄	ϕ_(5,8)	2(s + t − 4)
ϕ₅	ϕ_(8,8)	(2st − 5s − 5t + 12)

Theorem 2. SSO and SSO_red indices for the enhanced mesh network are as follows:

(i)
SSO(G) = 726.3922 − 521.7772(s + t) + 366.5203st
(ii)
SSO_red(G) = −1855.5167 − 522.7773(s + t) + 358.147st

Proof. From the edge partitioning of enhanced mesh network given in Table 2, we have the following computations for SSO and SSO_red indices:

(9)

Table 2. Edge partitioning on the basis of the sum of vertices which is a distance unit from the end vertices of each edge of EM (s, t).

ϕ		Frequency
ϕ₁	ϕ_(14,21)	4
ϕ₂	ϕ_(14,24)	8
ϕ₃	ϕ_(21,24)	8
ϕ₄	ϕ_(21,42)	4
ϕ₅	ϕ_(24,26)	16
ϕ₆	ϕ_(24,42)	8
ϕ₇	ϕ_(26,26)	2(3s + 3t − 26)
ϕ₈	ϕ_(26,42)	8
ϕ₉	ϕ_(26,45)	6(s + t − 8)
ϕ₁₀	ϕ_(32,42)	4
ϕ₁₁	ϕ_(32,45)	4(s + t − 8)
ϕ₁₂	ϕ_(32,48)	4(st − 4s − 4t + 16)
ϕ₁₃	ϕ_(42,45)	8
ϕ₁₄	ϕ_(45,45)	2(s + t − 10)
ϕ₁₅	ϕ_(45,48)	2(s + t − 8)
ϕ₁₆	ϕ_(48,48)	(2st − 9s − 9t + 40)

3. Triangular Mesh

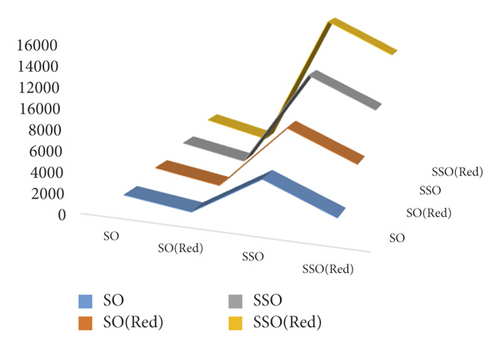
In the present section, we examined degree-based topological descriptors of the triangular mesh network. Also, the graphical comparison of SO, SO_red, SSO, and SSO_red indices is depicted in Figure 3.

3.1. Construction

Let T_t represent the radix—t triangular mesh network, which has the following node set:

(10)

and there always exist a mesh arc between the nodes (u₁, v₁) and (u₂, v₂) if |u₁ − u₂| + |v₁ − v₂| ≤ t − 1 and u₁ + v₁ ≤ u₂ + v₂. In a T_t, then the number of vertices (nodes) is equals to t(t + 1)/2. In the aforementioned network, the degree of node can be 2, 4, or 6. Three vertices of degree two are referred to as “corner vertices.” In the present section, G is symbolised by the graph of a triangular mesh network. The graph of a triangular mesh is shown in Figure 4.

Theorem 3. SO and SO_red indices for the triangular mesh network are as follows:

(i)
SO(G) = 155.4646 + 41.1213t + 2.7279t²
(ii)
SO_red(G) = 153.7212 − 110.7795t + 21.213t²

Proof. From the edge partitioning of triangular the mesh network given in Table 3, we have the following computations for SO and SO_red indices:

(11)

Table 3. Edge partitioning depends on the degree of the end vertices of T_t.

ϕ		Frequency
ϕ₁	ϕ_(2,4)	6
ϕ₂	ϕ_(4,4)	3(t − 2)
ϕ₃	ϕ_(4,6)	6(t − 3)
ϕ₄	ϕ_(6,6)	(3(t² − 7t + 12)/2)

Theorem 4. SSO and SSO_red indices for the triangular mesh network are as follows:

(i)
SSO(G) = 122.2908 − 256.8792t + 76.3675t²
(ii)
SSO_red(G) = 222 − 254.3856t + 74.2462t²

Proof. From the edge partitioning of triangular mesh network given in Table 4, we have the following computations for SSO and SSO_red indices:

(12)

Table 4. Edge partitioning for SSO of T_t.

ϕ		Frequency
ϕ₁	ϕ_(8,16)	6
ϕ₂	ϕ_(16,16)	3
ϕ₃	ϕ_(16,20)	6
ϕ₄	ϕ_(16,28)	6
ϕ₅	ϕ_(20,20)	3(t − 5)
ϕ₆	ϕ_(20,28)	6
ϕ₇	ϕ_(20,32)	6(t − 5)
ϕ₈	ϕ_(28,32)	6
ϕ₉	ϕ_(32,32)	3(t − 5)
ϕ₁₀	ϕ_(32,36)	6(t − 6)
ϕ₁₁	ϕ_(36,36)	(3(t² − 13t + 42)/2)

4. Star of the Silicate Network

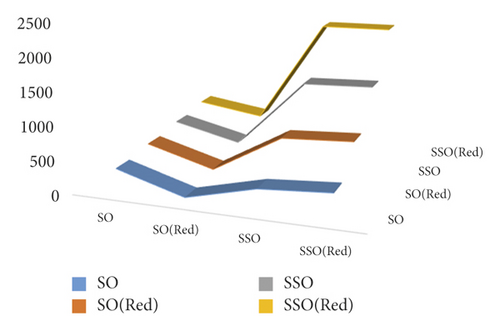
This section contains the analysis of degree-based topological descriptors for the star of the silicate network. Also, the graphical comparison of SO, SO_red, SSO, and SSO_red indices is depicted in Figure 5.

4.1. Construction

The star of the David network in Figure 6 indicates the expansion of a new star in a silicate network.

Step 1: Create an H-dimensional star of the David graph (Figure 6).
Step 2: To divide H into 2t 1 edges, apply 2t − 2 vertices to each edge.
Step 3:Excluding the pairings at a distance of 1, 3, 5, 7, …, (6t − 1) from one corner vertex, join any two vertices u and v by an edge in such a way that the first is the complete reflection of the second one, the distance between them is odd from one corner vertices (2t − 1).
Step 4: Except for the pairings at a distance, join every two vertices u and v with the help of an edge if one is the mirror image of the other and they are at an odd distance 1, 3, 5, 7, …, (6t − 1) from one corner vertices (2t − 1).
Step 5: A tetrahedron is used to replace each K3 subgraph. SSL denotes the t-dimensional star silicate star, also known as the star of silicate network star (t). Figure 7 depicts the graph for the SSL(2) silicate network star.

Here, G denotes the star silicate network SSL(t). Each tetrahedron has 6 corner vertices and a central vertex of degree 3 in G. The vertices that were added in the second step have degree four. The remaining vertices are all of degree 6. Thus, for u ∈ V(SSL(t)), the degrees d_u are 3, 4, and 6. The edge partitioning of G is shown in the table below.

Theorem 5. SO and SO_red indices for the star of a silicate network are as follows:

(i)
SO(G) = 291.4702 − 930.7296t + 546.9624t²
(ii)
SO_red(G) = 279.5208 − 583.2501t + 448.4238t²

Proof. From the edge partitioning of the star silicate network given in Table 5, we have the following computations for SO and SO_red indices:

(13)

Table 5. Edge partitioning centered on the degree of the end vertices of SSL (t).

ϕ		Frequency
ϕ₁	ϕ_(3,3)	6
ϕ₂	ϕ_(3,4)	12(2t − 1)
ϕ₃	ϕ_(3,6)	(36t² − 60t + 36)
ϕ₄	ϕ_(4,4)	(24t − 30)
ϕ₅	ϕ_(4,6)	24(t − 1)
ϕ₆	ϕ_(6,6)	(36t2 − 72t + 48)

Theorem 6. SSO and SSO_red indices for the star of a silicate network are as follows:

(i)
SSO(G) = 115.4495 − 3998.9124t + 2679.807t²
(ii)
SSO_red(G) = 1299.4434 − 2964n + 2579.3676t²

Proof. From the edge partitioning of the star silicate network given in Table 6, we have the following computations for SSO and SSO_red indices:

(14)

Table 6. Edge partitioning for SSO of SSL (t).

ϕ		Frequency
ϕ₁	ϕ_(11,11)	6
ϕ₂	ϕ_(11,14)	24
ϕ₃	ϕ_(14,14)	6
ϕ₄	ϕ_(14,17)	(24t − 36)
ϕ₅	ϕ_(14,26)	(12t − 24)
ϕ₆	ϕ_(16,19)	12
ϕ₇	ϕ_(16,26)	12
ϕ₈	ϕ_(16,28)	12
ϕ₉	ϕ_(17,17)	(24n − 60)
ϕ₁₀	ϕ_(17,19)	12
ϕ₁₁	ϕ_(17,26)	(24t − 48)
ϕ₁₂	ϕ_(18,26)	(12t² − 48n + 48)
ϕ₁₃	ϕ_(18,28)	(24t − 36)
ϕ₁₄	ϕ_(18,30)	(24n² − 48n + 24)
ϕ₁₅	ϕ_(19,26)	12
ϕ₁₆	ϕ_(19,28)	12
ϕ₁₇	ϕ_(26,26)	(6t² − 24t + 24)
ϕ₁₈	ϕ_(26,28)	12
ϕ₁₉	ϕ_(26,30)	(12t² − 48t + 48)
ϕ₂₀	ϕ_(28,28)	(12t − 18)
ϕ₂₁	ϕ_(28,30)	(24t − 36)
ϕ₂₂	ϕ_(30,30)	(18t² − 36t + 18)

5. Rhenium Trioxide Lattice

The topological indices of the RO(s, t, r) rhenium trioxide lattice on the basis of degree are studied in this part. It is a nonmetallic compound made up of rhenium and oxygen atoms. Rhenium trioxide, often known as ReO₃, is a red solid that forms a crystal. The corners of a hollow circle denote rhenium atoms, whereas the corners of solid circles denote oxygen atoms. 12 oxygen atoms and 8 rhenium atoms make up the unit cell of ReO₃ (Figure 8). Also, the graphical comparison of SO, SO_red, SSO, and SSO_red indices is depicted in Figure 9.

5.1. Construction

The s × t × rReO₃ lattice is represented by ReO₃. There are s unit cell rows along the X-axis, t unit cell columns along the Y-axis, and r unit cell pages along the Z-axis. The RO(s, t, r) graph is the rhenium trioxide graph RO(s, t, r), which is formed as follows:

Step 1: Here, we create a 3D grid M(s, q, r), that is defined by a Cartesian product of the paths P_s□P_t□P_r. The atoms of rhenium are displayed by such vertices.
Step 2: In this phase, partition each of the M(s, t, r) edges. The new vertices correspond to oxygen atoms. The vertices of RO will now be marked (s, t, r). The identical 3D-grid mark will be applied to the corners and rhenium atoms. Between two rhenium atoms (x^′, y^′, z^′) and (x^′′, y^′′, z^′′), the oxygen atom will receive the label (x, y, z), where x = (x^′ + x^′′/2), y = (y^′ + y^′′/2) and z = (z^′ + z^′′/2). Two vertices (l^′, m^′, n^′) and (l^′′, m^′′, n^′′) are adjacent if |(l^′ − l^′′) + (m^′ − m^′′) + (n^′ − n^′′)| = 1/2. The number of vertices and edges in RO(s, t, r) are 4str—st—tr—sr and 6str-2st—2tr—2sr, respectively. The graph of rhenium trioxide RO is denoted by the letter G throughout this section (s, t, r). The degree for every corner can correspond to the set {2,3,4,5,6} as a result of the formation of RO(s, t, r).

Theorem 7. SO and SO_red indices for the rhenium trioxide lattice are as follows:

(i)
SO(G) = −0.1506 + 7.9369(s + t + r) − 22.043(st + tr + sr) − 37.9473str
(ii)
SO_red(G) = 0.1064 + 8.0488(s + t) + 8.6788r − 19.9572(st + tr + sr) + 30.5941str

Proof. From the edge partitioning of the rhenium trioxide lattice given in Table 7, we have the following computations for SO and SO_red indices:

(15)

Table 7. Edge partitioning centered on degree of final (end) vertices of RO (s, t, r).

ϕ		Frequency
ϕ₁	ϕ_(2,3)	24
ϕ₂	ϕ_(2,4)	16(s + t + r − 6)
ϕ₃	ϕ_(2,5)	10(st + tr + sr − 4s − 4t − 4r + 12)
ϕ₄	ϕ_(2,6)	6(str − 2st − 2tr − 2sr + 4s + 4t + 4r − 8)

Theorem 8. SSO and SSO_red indices for the rhenium trioxide lattice are as follows:

(i)
SSO(G) = 255.2827 + 152.9129s + 45.286(t + r) − 94.7185(st + tr + sr) + 305.4699str
(ii)
SSO_red(G) = −356.6413 + 141.6272(s + t + r) − 89.0583(st + tr + sr) + 93.3381str

Proof. From the edge partitioning of the rhenium trioxide lattice given in Table 8, we have the following computations for SSO and SSO_red indices:

(16)

Table 8. Edge partitioning for SSO of RO (s, t, r).

ϕ		Frequency
ϕ₁	ϕ_(6,7)	24
ϕ₂	ϕ_(7,8)	24
ϕ₃	ϕ_(8,8)	8(s + t + r − 9)
ϕ₄	ϕ_(8,9)	8(s + t + r − 6)
ϕ₅	ϕ_(9,10)	8(s + t + r − 6)
ϕ₆	ϕ_(10,10)	8(st + tr + sr − 5p − 5t − 5r + 18)
ϕ₇	ϕ_(10,11)	2(st + tr + sr − 4s − 4t − 4r + 12)
ϕ₈	ϕ_(12,12)	2(3str − 7st − 7tr − 7sr + 16s + 16t + 16r − 36)

6. Conclusion

Various tools of mathematics are used to predict different properties of chemical compounds such as the topological index. We can associate a single number with a molecular graph of a chemical complex using the topological index. For the characterization of the unambiguous graph theoretical system of biological concern, we have appropriated various degree-based indices. We employed the Sombor index (SO), which has chemical relevance in determining numerous physicochemical properties of octane isomers since it has a coefficient of correlation near to one in the field of mathematical chemistry. Drugs and other chemical substances are frequently shown as polygonal shapes, trees, graphs, and other geometrical shapes. In this paper, we discuss the newly introduced Sombor index, Super Sombor index, and its reduced version for specific networks. These networks include triangular mesh, enhanced mesh, rhenium trioxide lattice, and star of silicate network. We also give a graphical comparison of computed results for the abovementioned chemical network. For these groups of chemical networks, the analytical closed formulae are derived.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

All authors contributed equally to this paper.

Open Research

Data Availability

All data required for this paper are included within this paper.

References

1 Bozkurt A. D. M. and Zhou B., Note on the distance energy of graphs, MATCH Communications in Mathematical and in Computer Chemistry. (2010) 64, 129–134.
Web of Science® Google Scholar
2 Milovanovi I. C., Glogit’E C., and Mateji M., On Kirchho? index, laplacian energy and their relations, MATCH Communications in Mathematical and in Computer Chemistry. (2019) 81, 405–418.
Web of Science® Google Scholar
3 Estrada E., Torres L., Rodriguez L., and Gutman I., An atombond connectivity index: modelling the enthalpy of formation of. alkanes, Indian Journal of Chemistry. (2018) 37, no. 10, 849–859.
Google Scholar
4 Aslam A., Ahmad S., Binyamin M. A., and Wei Gao W., Calculating topological indices of certain OTIS interconnection networks, Open Chemistry. (2019) https://doi.org/10.1515/chem-2019-0029, 2-s2.0-85064967435.
10.1515/chem-2019-0029
Web of Science® Google Scholar
5 Hu M., Ali H., Binyamin M. A., Ali B., Liu J. B., and Chengmei Fan C., On distance-based topological descriptors of chemical interconnection networks, Journal of Mathematics. (2021) 2021, 10, 5520619, https://doi.org/10.1155/2021/5520619.
10.1155/2021/5520619
Web of Science® Google Scholar
6 Gonzalez-Diaz H., Vilar S., Santana L., and Uriarte E., Medicinal chemistry and bioinformatics - current trends in drugs discovery with networks topological indices, Current Topics in Medicinal Chemistry. (2007) 7, no. 10, 1015–1029, https://doi.org/10.2174/156802607780906771, 2-s2.0-34447254270.
10.2174/156802607780906771
CAS PubMed Web of Science® Google Scholar
7 Hosoya H., Hosoi K., and Gutman I., A topological index for the total p-electron energy, Theoretica Chimica Acta. (1975) 38, no. 1, https://doi.org/10.1007/bf01046555, 2-s2.0-0002789437.
10.1007/BF01046555
Google Scholar
8 Alikhani1 S., Hasni R., and Arif N. E., On the atom-bond connectivity index of some families of dendrimers, Journal of Computational and Ceoretical Nanoscience. (2014) 11, no. 1-4, https://doi.org/10.1166/jctn.2014.3570, 2-s2.0-84899796028.
10.1166/jctn.2014.3570
Google Scholar
9 Huo Y., Ali H., Binyamin M. A., Asghar S. S., Babar U., and Liu J. B., On topological indices of mth chain hex-derived network of third type, Frontiers in Physics. (2020) 2020, https://doi.org/10.3389/fphy.2020.593275.
10.3389/fphy.2020.593275
Google Scholar
10 Baa̧ca M., Horvt’athovt’a J., Mokria̧sovt’a M., and Suht’anyiovća A., On topological indices of fullerenes, Applied Mathematics and Computation. (2015) 251, 154–161.
10.1016/j.amc.2014.11.069
Web of Science® Google Scholar
11 Brückler F. M., DoŽlic T., Graovac A., and Gutman I., On a class of distance-based molecular structure descriptors, Chemical Physics Letters. (2011) 503, no. 4-6, 336–338, https://doi.org/10.1016/j.cplett.2011.01.033, 2-s2.0-79952899557.
10.1016/j.cplett.2011.01.033
CAS Web of Science® Google Scholar
12 Randic M., Characterization of molecular branching, Journal of the American Chemical Society. (1975) 97, no. 23, 6609–6615, https://doi.org/10.1021/ja00856a001, 2-s2.0-8644280181.
10.1021/ja00856a001
CAS Web of Science® Google Scholar
13 Vukicevic D. and Furtula B., A forgotten topological index, Journal of Mathematical Chemistry. (2009) 46, no. 4, 1369–1379.
10.1007/s10910-009-9520-x
CAS Web of Science® Google Scholar
14 Ding L., Bokhary S. A., Rehman M. U., Ali U., Mubeen H., Iqbal Q., and Liu J. B., Degree-based indices of some complex networks, Journal of Mathematics. (2020) 2021, 16, 5531357, https://doi.org/10.1155/2021/5531357.
10.1155/2021/5531357
Web of Science® Google Scholar
15 Song P., Ali H., Binyamin M. A., Ali B., and Liu J. B., On computation of entropy of hex-derived network, Journal de Physique. (2021) 2021, 9993504, https://doi.org/10.1155/2021/9993504.
10.1155/2021/9993504
Google Scholar
16 Munir M., Nazeer W., Shahzadi Z., and Kang S., Some invariants of circulant graphs, Symmetry. (2016) 8, no. 11, https://doi.org/10.3390/sym8110134.
10.3390/sym8110134
Web of Science® Google Scholar
17 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
18 Kwun Y., Virk A., Nazeer W., Rehman M., and Kang S., On the multiplicative degree-based topological indices of silicon-carbon Si2C3-I[p,q] and Si2C3-II[p,q], Symmetry. (2018) 10, no. 8, https://doi.org/10.3390/sym10080320, 2-s2.0-85052501559.
10.3390/sym10080320
PubMed Web of Science® Google Scholar
19 Virk A. u. R., Jhangeer M. N., Jhangeer M. N., and Rehman M. A., Reverse Zagreb and reverse hyper-Zagreb indices for silicon carbide Si2C3I [r, s] and Si2C3II [r, s], Engineering and Applied Science Letters. (2018) 1, no. 2, 37–50, https://doi.org/10.30538/psrp-easl2018.0010.
10.30538/psrp-easl2018.0010
Google Scholar
20 Amin S., Virk A. R., Rehman M. A., and Shah N. A., Analysis of dendrimer generation by sombor indices, Journal of Chemistry. (2021) 2021, 11, 9930645, https://doi.org/10.1155/2021/9930645.
10.1155/2021/9930645
Web of Science® Google Scholar
21 Gutman I., Some basic properties of Sombor indices, Open Journal of Discrete Applied Mathematics. (2021) 4, no. 1, 1–3, https://doi.org/10.30538/psrp-odam2021.0047.
10.30538/psrp-odam2021.0047
Google Scholar

Citing Literature

All articles

Analysis of Complex Networks via Some Novel Topological Indices

Abstract

1. Introduction