Volume 2022, Issue 1 8966350

Research Article

Open Access

Nonlinear Optimization-Based Robust Control Approach for a Two-Stage Anaerobic Digestion Process

Corresponding Author

Atthasit Tawai

[email protected]

orcid.org/0000-0001-7363-781X

The Sirindhorn International Thai-German Graduate School of Engineering, King Mongkut’s University of Technology North Bangkok, Bangkok 10800, Thailand kmutnb.ac.th

Search for more papers by this author

Malinee Sriariyanun,

Malinee Sriariyanun

orcid.org/0000-0002-3088-9256

Biorefinery and Process Automation Engineering Center (BPAEC), King Mongkut’s University of Technology North Bangkok, Bangkok, Thailand kmutnb.ac.th

Search for more papers by this author

Atthasit Tawai,

Corresponding Author

Atthasit Tawai

[email protected]

orcid.org/0000-0001-7363-781X

The Sirindhorn International Thai-German Graduate School of Engineering, King Mongkut’s University of Technology North Bangkok, Bangkok 10800, Thailand kmutnb.ac.th

Search for more papers by this author

Malinee Sriariyanun,

Malinee Sriariyanun

orcid.org/0000-0002-3088-9256

Biorefinery and Process Automation Engineering Center (BPAEC), King Mongkut’s University of Technology North Bangkok, Bangkok, Thailand kmutnb.ac.th

Search for more papers by this author

First published: 08 July 2022

https://doi.org/10.1155/2022/8966350

Citations: 3

Academic Editor: Pier Luigi Gentili

Share a link

Email
Wechat
Bluesky

Abstract

A two-stage anaerobic digestion (AD) process has been applied to improve the efficiency of methane production from various organic materials. However, the performance of traditional process controllers may be limited by differences in the rate of biochemical reactions, process uncertainties, and the consequences of interconnection between the two bioreactors. In this work, a nonlinear optimization-based control strategy that applies an analytical model predictive control (AMPC) scheme with an adaptive optimal set-point is proposed for the control of the two-stage AD system. The objectives of the proposed control system are to stabilize the system under uncertain operating conditions and maximize biomethane production. The optimal set-points for the controller are adapted in real-time operation, and then the control system is performed to manipulate the controlled output to the optimal trajectories. Compensators and nonlinear state observers are applied to handle the process/model mismatch and estimate unmeasured variables. The proposed control system is applied to the process with disturbances, fluctuations of inlet stream concentrations, and changes in the bacterial growth rate, and the control performance is investigated. Simulation results show that the developed control scheme automatically adjusts the optimal set-points and provides adequate control actions to maintain the maximum rate of methane production. The results of this investigation demonstrate that the control strategy promotes different biochemical reactions, avoids the inhibition effect, and handles the mutual effects between acidogenic and methanogenic bioreactors for methane production effectively.

1. Introduction

Anaerobic digestion (AD) is a biochemical process to convert various organic materials to biogas that provides incentives for wastewater treatment. Since the AD process involves different microbial communities, the growth of microorganisms and the consumption of substrates in wastewater are important factors for methane production. Several advantages of the AD process include high efficiency of organic removal, smaller space requirements, and low sludge production [1]. However, the optimal condition for the whole microbial community is crucial because each microbial community requires different conditions for its growth [2]. Furthermore, some microorganisms are highly sensitive to environmental factors, thereby making it difficult to control and stabilize the AD processes. Control strategies for the AD processes have been proposed to improve efficiency, maintain stability, and meet environmental regulations.

During the past decades, several works have been proposed to develop control systems for bioprocesses, different types of control techniques and structures were developed to achieve their control objectives and desired targets [3, 4]. Liu et al. proposed a cascade model predictive control (MPC) and proportional integral derivative (PID) control strategy for the Benchmark Simulation Model 1 (BSM1) [5]. The analysis of control performance was conducted by a simulation using the identified prediction error method (PEM) to control the effluent NO₃ concentration. Since the methanogenic bacteria consume volatile fatty acids (VFAs) to produce methane, control strategies have been developed to regulate the VFAs’ concentration in bioreactor systems. García-Sandoval et al. proposed a cascade hybrid (continuous-discrete) controller for single-stage AD systems [6]. A continuous inner loop of the control system is used to control the VFA concentration and updates its reference according to the discrete outer loop information of the COD concentration. Rincón et al. developed an adaptive controller for a single-stage anaerobic digester with input constraints [7]. The control system was formulated by an application of Lyapunov-like function method; a state observer was combined to handle the saturation of the control input and estimate the unknown parameters. Robles et al. developed a fuzzy-logic controller to maximize biomethane production by controlling the VFA content in the effluent of a fixed-bed anaerobic reactor [8]. The controller was applied to a pilot-scale reactor to improve the process performance of a winery wastewater treatment. Recently, Kil et al. developed a control system based on nonlinear model predictive control (NMPC) algorithms for an AD system; the control approach was applied to the reduced model of a single-stage AD process [9]. In the studies, biogas flow rate was controlled to follow a defined set-point, and then the simulation results were compared with a traditional PID controller. Lara-Cisneros et al. proposed an extremum-seeking control strategy with a sliding mode to achieve the dynamic optimization of methane production for a single-stage AD process [10]. An open-loop analysis for a two-population model in the work showed that the accumulation of VFAs in the bioreactor can lead to system instability. The controller was designed to regulate the VFA concentration close to the optimal set-point while improving methane production.

However, the performance of widespread application AD processes may be limited by the highly nonlinear behaviors, such as differences in the rate of biochemical reactions, constraints on state and manipulated variables, and uncertainties of the system. To improve the stability and efficiency of the process, a novel bioreactor configuration design based on biological pathways has been proposed [11]. Pohland and Ghosh proposed to increase the production rate and improve the process stability of an AD process using two different reactors [12]. The first reactor is used to promote hydrolysis and acidogenesis, while the second reactor is applied to support acetogenesis and methanogenesis. Experimental studies have been conducted to support the significant motivation of this concept, develop process models, and improve the process operation [11, 13, 14]. Advanced control systems have been proposed to handle the process disturbances of the two-stage AD system and avoid the process instability. Furthermore, computer technologies have been applied to AD systems for process monitoring and control [15]. Méndez-Acosta et al. have proposed an extended study of the hybrid cascade controller to regulate both VFA and COD concentrations in two-stage AD processes [6, 15]. The change in concentration of the inlet stream is an important problem that commonly occurs in AD processes. The inlet stream with a low substrate concentration can reduce the methane production rate, but the inlet stream with a very high concentration leads to the inhibition of bacterial growth [16, 17]. A consequence of the interconnection between the two bioreactors is changes in the inlet VFA concentration of the second-stage reactor, which can reduce the methane production rate or inhibit the growth rate of methanogens. Because the two bioreactors of two-stage AD processes are connected in series, conventional controllers are usually applied to each reactor separately without consideration of variables that mutually affect the operation of the other one.

In this work, a nonlinear optimization-based control strategy that applies an analytical model predictive control (AMPC) technique with adaptive optimal set-points is proposed for the control of a two-stage AD system. The concept of AMPC is based on the input/output (I/O) linearization, which is considered a specific case of the model predictive control framework. The control action can be derived by minimizing a function norm of the deviations of the controlled outputs from its requesting linear reference trajectories. The main objectives of the proposed control system are to stabilize the system under uncertain operating conditions and maximize biomethane production. The AMPC controllers apply the adaptive optimal set-points, integral actions, and nonlinear state observer to enhance control robustness. The first control subsystem employs the inlet stream variables to compute the updated set-points that enhance the VFA formulation. The second control subsystem aims to enhance methane production at each time point by handling the bacterial growth rate and avoiding inhibition effects from a high concentration of accumulated VFAs. The state estimation can be used as an alternative task to estimate unmeasured states for the monitoring system, especially in the case of signal lacking from the online measurement. To promote the consumption of organic substrate and production of biomethane, the state and control variables of the two reactors must be incorporated by the control system to provide optimal control actions. Control performance of the control strategy is investigated by computer simulation and then compared with the results of a traditional PID controller. The advantages of the proposed control system, compared to classical controllers, are the ability to maximize the methane production rate during the operation; the availability of adaptive optimal set-points; and the application with few required tuning parameters to achieve the updated targets.

2. Preliminaries

2.1. Problem Formulation

Consider a mathematical model of the system in equation (1), for which the state variables are modeled by differential equations to describe the two-stage AD process. Since the two bioreactors are connected in series, dynamics of the second subsystem are directly affected by the outlet stream of the first bioreactor.

(1)

with the following initial conditions:

(2)

where

and

denote the vector of state variables of the first- and second-stage reactors, respectively. F₁ = D₁ξ_in And F₂ = D₂ξ₁ denote the feed of the reactors.

is the variables of the inlet stream, D₁, D₂, Q₁, and Q₂ are the dilution rate and the gas flow rate of the first and second reactors. K is a vector of the yield for substrate consumption or product formation. r₁(ξ₁) And r₂(ξ₂) are the reaction rates of the reactors. t ∈ [0, ∞] is the time,

and

denote the vectors of controlled outputs, and h₁ and h₂ are nonlinear functions.

2.2. Control Strategy for the Two-Stage Anaerobic Digestion Process

The proposed control system aims to stabilize the process operation against unpredictable changes in the influent composition and maximize the methane production rate. The first reactor of the two-stage AD process is used to enhance the VFA formulation by consuming the organic substrate and regulating the COD concentration to achieve effluent quality. To achieve this, the first control subsystem requires adaptive set-points to formulate a set-point tracking controller of the state ξ₁, and the steady-state pair of the first-stage model corresponding to the desired outputs is applied for the requirement. The steady-state pair of the first-stage model can be obtained by solving the following set of equations.

(3)

The corresponding nominal steady-state pair obtained by solving equation (3) can be written in a compact form as:

(4)

where ξ_1,ss denotes the steady-state pair of the states ξ₁, u_j,opt is the initial optimal manipulated inputs corresponding to the steady-state pair of the states ξ₁, and y_1,sp is the output set-point of the first stage.

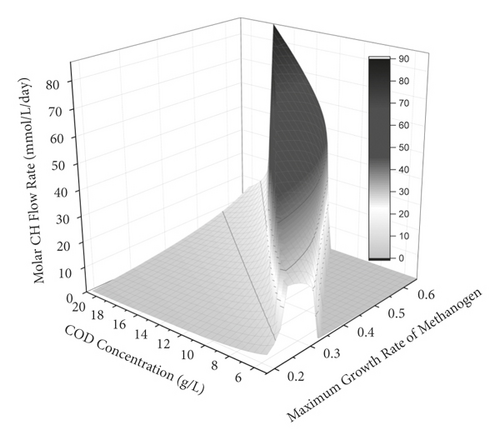
The second control subsystem attempts to maximize methane production by regulating the input stream that supports the growth of methanogens in the second bioreactor. It should be noted that the adjustment of the first control subsystem can cause a fluctuation of the substrate concentration for the second stage. Furthermore, the maximum growth rate of two-stage methanogens could change due to the diversity of the microbial group, thereby making it difficult to compute the control actions that can attain the maximum rate of methane production. A winery wastewater treatment is used to demonstrate the coupled effects of the first-stage substrate concentration and the second-stage maximum growth rate of methanogens on the methane production rate. An open-loop profile of methane flow rate is simulated by varying the inlet substrate concentration of the first-stage reactor and the second-stage maximum growth rate of methanogens. The evolution of the open-loop profile with an optimal set of dilution rate [18] is illustrated in Figure 1. More details of the mathematical model are given in the next section.

Details are in the caption following the image — Open in figure viewer PowerPoint

In the two-stage AD system, the condition of the first-stage reactor is prepared to support the growth of acidogens; an increase in inlet COD concentration can enhance the accumulated VFA concentration for the second reactor. In the second-stage reactor, the inlet VFAs can promote the growth of methanogens and enhance the methane production rate. However, the methanogenic growth could be inhibited by excess VFA concentration, depending on the maximum growth rate during the operation. Thus, the process operation with a predefined set-point under uncertainties may limit the methane production rate. To handle the effects of the interconnection between the first and second bioreactors, a real-time set-point calculator is integrated with the second control subsystem. The mathematical equation of the problem is formulated in the following form:

(5)

where Φ is a scalar function to be maximized and y_2,sp is the vector of the output set-point of the second stage, which is the decision variable. P denotes the vector of model parameters, F_m is a set of nonlinear equations arising from the second-stage model, and G is a function corresponding to the process constraints.

In this study, the concept of AMPC based on the I/O linearization is applied to formulate the nonlinear optimization problems for the control system [19]. Consider a compact form of the system in equation (1):

(6)

where u₁ is the vector of the manipulated inputs for the first stage, u₂ is the vector of the manipulated inputs for the second stage, and f₁ and f₂ are the vectors of nonlinear functions. For the nonlinear system presented in equation (6), the relationship between the controlled output y₁, y₂ and the manipulated input u₁, u₂ of the dynamic behaviors of the states ξ₁ and ξ₂ is investigated. The relative order of the controlled outputs y₁ and y₂ with respect to the inputs is denoted by r₁ and r₂. r_i are finite and are the smallest integers such that

. The following notation is used:

(7)

The system in equation (6) is used to formulate the nonlinear optimization that achieves the requested closed-loop responses. The concept of the I/O linearization technique is proposed. A linear response is requested of the following form [20]:

(8)

where D is the differential operator (i.e., D = (d/dt)) and ε is a vector of tuning parameters. The problem formulation depends on the defined relative order (r), as explained in equation (7). Then, the differential operator is applied to the controlled output y, and the derivation of a dynamic state feedback can be achieved. To derive the nonlinear state feedback by minimizing the function norm of the deviations of the process outputs, equation (8) is applied to formulate a constrained optimization problem [20–22]. The following equation expresses the constrained optimization problem to be solved at each time instant (t ∈ [t₀, t_f]).

(9)

subject to

(10)

where ε_i,j are tuning parameters that are positive, constant, and adjustable. ξ_i,max is the maximum allowable level of emissions, u_i,lb and u_i,ub denote the lower bound and upper bound of the manipulated input u_i, respectively, and v_i,k is the reference output set-point obtained from the real-time calculation at each time instant.

3. Mathematical Model of a Two-Stage Anaerobic Digestion Process

The wine industry produces a large amount of wastewater with variability throughout the year [23]. A two-stage AD process for winery wastewater treatment is considered as a case study in this work. As shown in Figure 2, the process composes of two continuous stirred-tank reactors (CSTR) connected in series. The bacterial populations are assumed to be divided into two groups with homogeneous characteristics. Anaerobic digestion can be described by two-step biological reactions for each reactor, acidogenesis and methanogenesis [1]. In acidogenesis, the organic substrate (characterized by chemical oxygen demand, COD) is converted to volatile fatty acids (VFAs) and carbon dioxide (CO₂) by acidogenic bacteria. Then, the methanogenic bacteria use the accumulated VFAs from the first stage for their growth and produce methane and CO₂. The operating conditions for two-stage bioreactors are generally designed to promote different biochemical reactions. The first reactor is used to promote hydrolysis/acidification, while the second one is used to support acetogenesis/methanogenesis.

The outlet stream of the first reactor is fed to the second one, and the biogas produced from both stages is removed from the top of each reactor. As is shown, the inlet stream is mainly composed of the organic soluble substrate (S_1,in), VFAs (S_2,in), and the biomass of acidogens (X_1,in) and methanogens (X_2,in). In the first-stage reactor, the organic substrate (S₁) is converted to VFAs (S₂) depending on the growth of acidogenic bacteria; the acids are then used to formulate biogas by methanogenic bacteria. The remaining organic substrate (S₃) is consumed by acidogens (X₃) in the second stage, while the accumulated VFAs (S₄) are employed by methanogens (X₄) to formulate biogas. Since the feed of the second stage is the liquid outflow of the first one, the methane production performance in the second reactor can be influenced by the substrate concentration, alkalinity (Z₁), and total inorganic carbon (C₁) of the interconnecting stream. A nonlinear model for the two-stage anaerobic digestion process is developed, with additional simplified assumptions:

(A1) The bacterial populations in the CSTR system are divided into two main groups, acidogens and methanogens. The anaerobic digestion of each reactor can be described by acidogenesis and methanogenesis.
(A2) The pH of each reactor is effectively regulated in a range; the impact of pH on bacterial growth can be ignored.
(A3) COD and VFA concentrations are available online in normal operations.

The advanced monitoring system of wine distillery effluents was developed in some previous works [24–26]. The samples from the bioreactor can be prepared using an ultrafiltration membrane and then apply the online automatic titrimetric sensor to measure the states. The process variables (VFAs, COD, and alkalinity) can be used to support the calculation of controllers. An investigation of optimal steady-state conditions for the two-stage operation was conducted in previous work and found that the system is vulnerable to large disturbances leading to process instability [18]. In the study, a mathematical model of the two-stage AD process was reduced and simulated with a set of parameters obtained from previous works [1, 27]. The steady-state optimization validates the benefits of the two-stage AD process compared to the traditional single-stage process. Although the kinetic model reduction is useful for some applications, the reduced kinetic parameters are very sensitive to unknown perturbations and uncertainties [28]. The purpose of this work is to regulate the process under the condition with unpredictable changes in process parameters. The dynamic model and the identified parameters validated using experimental data in [1] can be applied. The governing equations of the two-stage AD process are composed of dynamic models of the soluble organic substrate concentration, the VFA concentration, the biomass concentration of acidogenic and methanogenic bacteria, alkalinity, and total inorganic carbon, which are described as follows:

(11)

with the initial conditions

(12)

where

(13)

with

(14)

The molar flow rates of CH₄ for the first- and second-stage reactors are given by.

(15)

where Y₁ and Y₂ are the biomass yields for acidogens and methanogens, K_S1 and K_S2 are half-saturation constants, K_I2 is an inhibition constant, and μ₁, μ₂ and μ_1max, μ_2max are the specific growth rate and maximum growth rate of acidogenic and methanogenic bacteria, respectively. q_c1 and q_c2 are the molar CO₂ flow rates and P_c is CO₂ partial pressure. To present the model in a more general matrix form, the vector of model variables for the first-stage reactor can be denoted by

and for the second-stage reactor by

. The model parameters with their values, obtained from [1, 27], are listed in Table 1.

1. Parameter values for the two-stage anaerobic digestion process.

Parameter	Meaning	Value
X_1,in	Inlet concentration of acidogen	0.1 g/L
X_2,in	Inlet concentration of methanogen	0.1 g/L
S_1,in	Inlet concentration of organic substrate	10 g/L
S_2,in	Inlet concentration of VFAs	40 mmol/L
Z_in	Inlet concentration of alkalinity concentration	62 mmol/L
C_in	Inlet concentration of inorganic carbon concentration	65 mmol/L
μ_1max	Maximum growth rate of acidogenic biomass	4.2 d⁻¹
μ_2max	Maximum growth rate of methanogenic biomass	0.36 d⁻¹
K_S1	Half-saturation constant for S1	0.023 g/L
K_S2	Half-saturation constant for S2	2.3 mmol/L
K_I2	Inhibition constant for S2	66.67 mmol/L
Y₁	Biomass yield for acidogens	0.11 g/g
Y₂	Biomass yield for methanogens	0.00236 g/mmol
Y₃	Yield for CO2 production	50.6 mmol/g
Y₄	Yield for CO2 production	343.6 mmol/g
Y_m	Yield for CH4 production	1.07 mmol/g
c	Stoichiometric coefficient of the conversion of S1 to S2	16.95 mmol/g
P_T	Total pressure	1 atm
K_H	Henry’s constant	0.0246 kg·mol/m³bar
K_La	Liquid/gas transfer rate	19.8 d⁻¹

4. Formulation of the Control System

4.1. Nonlinear Optimization Problem for the Two-Stage Anaerobic Digestion Process

Since the operating conditions in each reactor are provided to promote the formation of different products, the optimization-based controllers with the adapted set-points for each stage are developed for different control objectives. The main purposes of the first-stage reactor are to enhance the VFA production while consuming the organic substrate (COD) and handle the changes in the composition of the inlet stream. Additionally, wastewater treatment processes are generally requested to meet environmental regulations; thus, the control system must have the ability to maintain the COD concentration below the maximum allowable level of emissions. A real-time set-point calculator is formulated to update the optimal set-points for the first-stage control subsystem. The compact equations of the process model in equation (11) that is considered at the steady-state are provided as follows:

(16)

The solution of the equation system is obtained using a numerical method, and it is updated online for each time instant. By substitution of equation (11) into the proposed AMPC approach of equation (9), the constrained optimization problem with a relative order (r = 1) can be formulated as follows:

(17)

subject to

(18)

For the first-stage bioreactor, the squared error between the VFA concentration response and the adaptive set-point is minimized as follows:

(19)

subject to

(20)

where y_1,sp,k is the VFA concentration set-point at each time instant and ε₁ is a tuning parameter. The dilution rate D₁ is applied as the manipulated input u₁ for the first-stage bioreactor.

The control objective of the second-stage bioreactor is to maximize the methane production rate by regulating the growth rate of methanogens. However, a high concentration of the accumulated VFAs obtained from the first-stage output stream could be able to inhibit the methanogenic growth rate. To enhance methane production and avoid the effects of substrate inhibition in the second-stage bioreactor, a set-point calculator with the biochemical reaction model is combined, and then the decision variable is applied as the optimal set-point to formulate the optimization problem for the second control subsystem. The application of the reaction model for the optimal set-point calculation is proposed as the following equation:

(21)

The molar methane flow rate of the second-stage reactor is applied as the nonlinear function to be maximized and the second-stage VFA concentration is used as the controlled output. The constrained optimization problem of the second-stage reactor is formulated by applying the proposed technique to minimize the function norm of the deviations of the controlled output from the desired target as the following equation:

(22)

subject to

(23)

where y_2,sp,k is the second-stage adaptive set-point at each time instant, ε₂ is a tuning parameter, and the dilution rate D₂ is used as the manipulated input u₂ for this stage. Note that the manipulated inputs of the two reactors must be limited through the process constraints to balance the working volume of the reactors and avoid washout.

4.2. Nonlinear State Observer and Integral Action

To provide the state feedback variables for the condition with unmeasured variable problems, a state estimation is proposed as a state observer. The following nonlinear state observer is added to the control system as an alternative task to estimate the unmeasured states,

, of the system.

(24)

where the vectors of the state observers are

, and the controlled output observers are

and

. Note that the estimated states are allowed to depend on signals; some measured variables may comprise reference signals that are available online [29]. The state estimation is used as an alternative task to estimate unmeasured states in the case of signal lacking from the online measurement. The nonlinear state observer of equation (24) applies the manipulated inputs u₁, u₂ from the controller to calculate the estimated states

and

directly. The time lag in measurement, noise detection, and reduction are not considered in this work. As discussed in a previous study, the optimization problem based on the I/O linearization technique does not have an analytical solution with active constraints [19]. A linear closed-loop response implies a closed-loop stability if the state feedback makes the performance index zero. Since the closed-loop stability depends on the AMPC stability, the proposed state observer could be applied for open-loop stable processes [21]. Additionally, first-order integral actions are combined to compensate the mismatch between the process and mathematical model as presented in the following equations:

(25)

where η₁ and η₂ are the integrals of error of the controlled outputs y₁ and y₂, respectively. λ₁, λ₂ are positive constants, ν₁ is the compensated set-point of the first-stage reactor, and ν₂ is the compensated set-point of the second-stage reactor.

4.3. The Control System

(26)

where

is a vector of the first-stage unmeasured disturbances and

is a vector of the second-stage unmeasured disturbances. Then, the closed-loop responses of the output to the introduced reference set-point can be written as:

(27)

Consider a compact form of the process with unmeasured disturbances as follows:

The constrained optimization problem based on the AMPC approach is then formulated as:

(28)

subject to

(29)

subject to.

(30)

where v_1,k and v_2,k denote the reference output set-points obtained from the online calculation at each time instant (t ∈ [t₀, t_f]). ς_lb(u₂) and ς_ub(u₂) are the functions that limit the maximum difference of manipulated inputs between the two reactors.

, and

denote the vectors of lower and upper limits of the estimated disturbances of the first and second reactors, respectively. The application of the real-time set-point calculators, nonlinear state observer, integral action, and the developed analytical model predictive controllers for the two-stage AD process is shown in Figure 3.

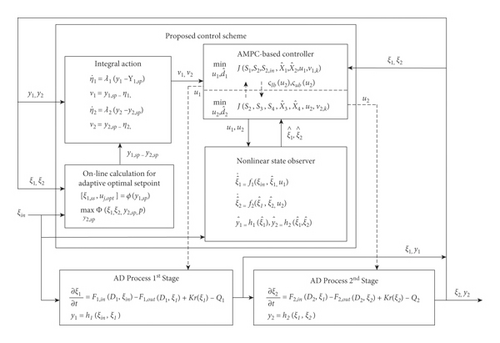
The flowchart in Figure 4 demonstrates the procedure of the developed control system applied to the two-stage AD process. The developed control system is performed to provide the control actions u₁ and u₁ for the two-stage process: the input constraints are applied to limit the adjustment of the manipulated inputs, the dilution rate for each reactor, and to avoid the washout of biomass. Then, the state variables, including the outputs, are fed back to the controller and are applied to calculate the integral actions for the next time step. A computer-implemented simulation in MATLAB is conducted to investigate the closed-loop responses of the proposed control system.

5. Results and Discussion

5.1. Closed-Loop Responses

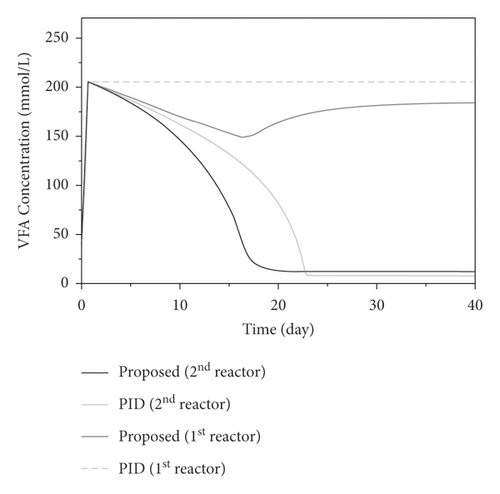
The process model presented in equation (11) is simulated to express the dynamic behaviors of the two-stage anaerobic digestion process. Simulations are performed for the closed-loop system; and the control performances are investigated through various problems. The initial conditions are applied: X₁(0) = 0.1 g/L, X₃(0) = 0.1 g/L, X₄(0) = 0.1 g/L, S₂(0) = 40 mmol/L, Z(0) = 62 mmol/L, and C(0) = 65 mmol/L [18]. The closed-loop simulation results of the proposed control system are compared with a traditional PID controller, with the tuning parameters, K_p,1 = 10, K_I,1 = 0.001, K_d,1 = 0.00001, K_p,2 = 0.08, K_I,2 = 0.0000001, and K_d,2 = 0.0000001. In all simulations, the two-stage process is operated with the same initial conditions used in the closed-loop system. The developed controller employs the adaptive set-points with the tuning parameters, ε₁ = 0.5s, ε₂ = 1s, λ₁ = 0.1s⁻¹, and λ₂ = 0.1s⁻¹. The maximum difference in the dilution rates between the reactors is 30%, with lower bounds and upper bounds, u_1,lb = 0.1d⁻¹u_2,lb = 0.1d⁻¹, u_1,ub = 0.7d⁻¹, and u_2,ub = 0.7d⁻¹. Closed-loop responses of the VFA concentration, methanogenic biomass concentration, the dilution rates, and methane flow rates are shownin Figures 5–7, respectively. As explained above, the operating condition of the first-stage reactor is adjusted to promote the VFA formulation, and then the accumulated VFAs are fed to support the methanogenesis in the second one. Thus, a high VFA concentration is presented in the process response of the first bioreactor, while the responses of the second bioreactor showed a high methane flow rate corresponding to the growth of the second-stage methanogens. The simulation results show that the controllers successfully force the controlled outputs to follow the adaptive optimal set-points asymptotically. From the results, it is clear that the developed control system can be used to support different control objectives for the two-stage bioreactor. The results demonstrate that the developed control system could achieve better control performance with faster responses compared with the PID controller.

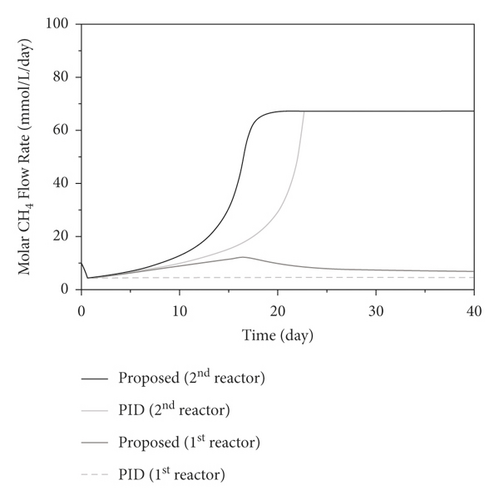
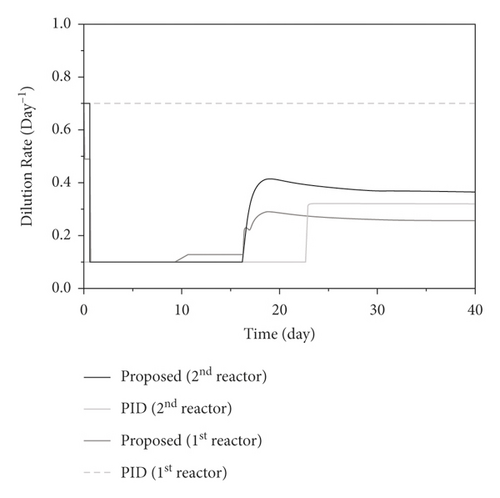
5.2. Control Performance

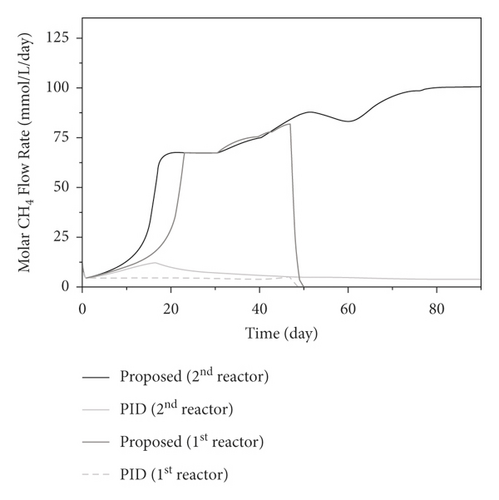
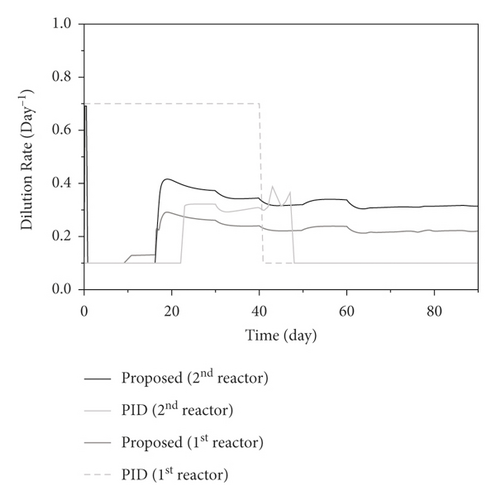
The robustness of the developed control system is investigated by changing the inlet COD concentration in the feed for the first bioreactor [30, 31]. The process is operated with the same parameters applied in the closed-loop system before unmeasured disturbances, being a 20% increase in the inlet COD concentration (S_1,in) after 25 days and a 50% increase in S₁,_in after 40 days, are introduced. Then, the inlet COD concentration changes to 13 g/L after 5 days and 17 g/L after 60 days. The responses of the proposed control scheme to the regulatory tests, compared to the PID control responses, are illustrated in Figures 8 and 9. To handle the problem, the first-stage optimal set-points corresponding to the fluctuating substrate concentration were adjusted and the first-stage control subsystem is performed to manipulate the controlled output at the optimal trajectories. Due to the changes in the first-stage VFA outlet concentration, affected by the proposed disturbances, the second-stage control subsystem needs to handle the fluctuations of the interconnecting stream and stabilize the process to maintain the maximum methane flow rate. It can be seen that the developed control system successfully forces the outputs to follow the optimal conditions updated at each time instant under the process constraints. Notice that the developed control scheme is capable of handling the introduced problems; the manipulated inputs of the second bioreactor were adjusted properly under the condition with fluctuating concentrations of inlet VFAs to enhance the methane production and avoid the effects of the inhibition. Meanwhile, the process responses under the PID controller showed the ability to manipulate a range of changes and are nearly uncontrollable after 45 days.

Since AD processes involve different microbial communities, regulatory tests related to the maximum growth rate are introduced during the process operation to investigate the robustness of the proposed control system. The process is operated with the same parameters applied in the normal closed-loop system before unmeasured disturbances, being a 20% increase in μ_2max after 25 days and a 30% increase in μ_1max after 35 days, are introduced. Following this, unmeasured step disturbances are added: 30% decrease in μ_1max and 10% decrease in μ_2max after 40 days, 20% increase in μ_2max after 45 days, 30% increases in μ_1max and μ_2max after 50 days, and 50% increase in μ_1max and μ_2max after 55 days. To handle this problem, the control system is required to maintain the maximum rate of methane production under the condition with changes in the bacterial growth rate. The responses to the proposed control scheme on the tests are depicted in Figures 10 and 11. The optimal set-point was automatically adjusted to create trajectories that can maximize methane production, and the second-stage control subsystem can stabilize the system with high methane production rates under the process constraints. Due to the limitation of the PID controller under the highly nonlinear processes, the responses showed that it can only stabilize the process with small changes in the maximum growth rate.

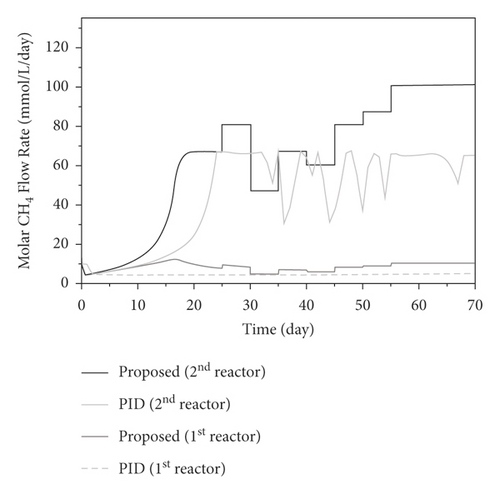
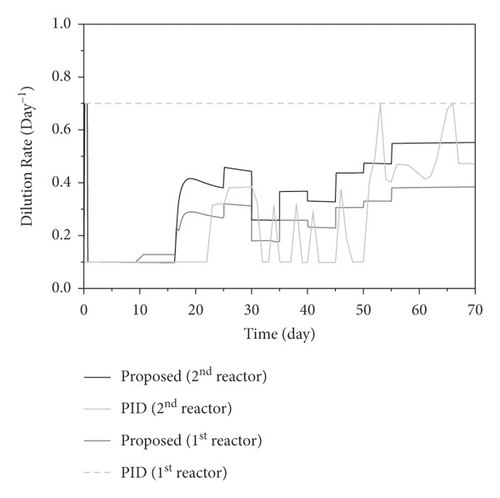
The developed control system is further investigated by introducing coupled disturbances, and changes in both the maximum growth rate and inlet COD concentration. The process is operated with the same parameters applied in the closed system before unmeasured disturbances, being a 30% increase in μ_1max and μ_2max after 30 days, are introduced. For this test, the following coupled step disturbances are added: 30% increase in S₁, in after 40 days, 30% decrease in μ_1max and 10% decrease of μ_2max after 50 days, and 30% increase in S₁,in, 50% increase in μ_1max and μ_2max after 60 days. The responses of the proposed control scheme on the regulatory tests are depicted in Figures 12 and 13. It is clear from the results that the proposed control strategy successfully improved the robustness and performance of the two-stage AD process.

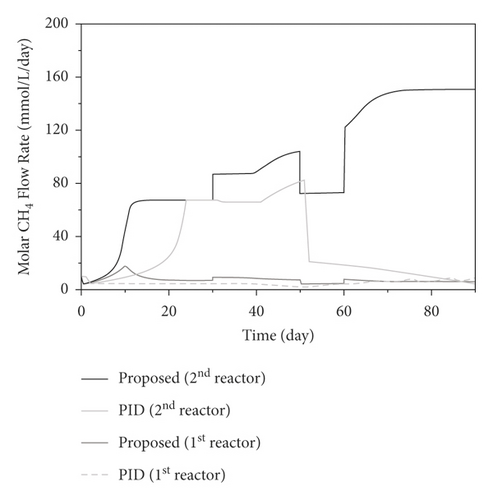
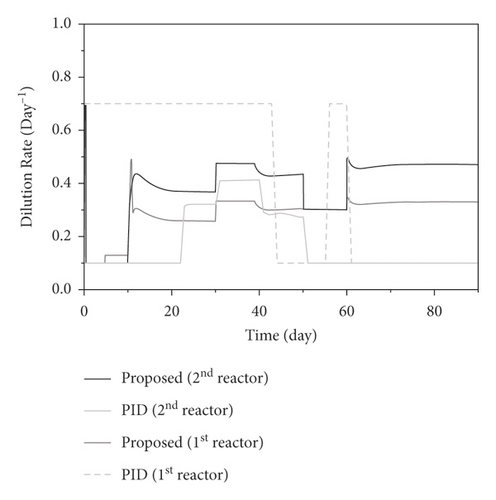
6. Conclusion

This research has proposed a nonlinear optimization-based control system for the two-stage anaerobic digestion process. The control strategy was developed to handle the problems that mutually affect the two reactors and reject the unmeasured disturbances while maintaining methane production at a maximum rate. In simulation experiments, fluctuations in inlet stream concentration and changes in the bacterial growth rate were introduced to investigate the control performance and robustness. The control system presented excellent performance under conditions of coupled disturbances by automatically adjusting the optimal set-points and providing adequate control actions to achieve the updated targets. The advantages of the resulting control scheme are that the controller requires only a few tuning parameters and it can maximize methane production under conditions of severe disturbances and process constraints.

Abbrevation

c:: Stoichiometric coefficient of the conversion of S1 to S2 (mmol/g)
C:: Inorganic carbon concentration (mmol/L)
D:: Dilution rate
f, h, M, N:: Nonlinear functions
K_I2:: Inhibition constant for S2 (mmol/L)
K_H:: Henry’s constant (kg mol/m3bar)
K_La:: Liquid/gas transfer rate (d-1)
K_S1:: Half-saturation constant for S1 (g/L)
K_S2:: Half-saturation constant for S2 (mmol/L)
P_T:: Total pressure (atm)
Q:: Gas flow rate
r:: Relative order
S₁:: Concentration of organic substrate (g/L)
S₂:: Concentration of VFAs (mmol/L)
t:: Time
u:: Vector of manipulated input
X:: Biomass concentration (g/L)
Y₁:: Biomass yield for acidogens (g/g)
Y₂:: Biomass yield for methanogens (g/mmol)
Y₃:: Yield for CO₂ production (mmol/g)
Y₄:: Yield for CO₂ production (mmol/g)
Y_m:: Yield for CH₄ production (mmol/g)
y:: Vector of controlled output
Z:: Alkalinity concentration (mmol/L)
ε:: Tuning parameter
η:: The integral of error
μ_1max:: Maximum growth rate of acidogenic biomass (d⁻¹)
μ_2max:: Maximum growth rate of methanogenic biomass (d⁻¹)
ξ:: Vector of state variables
ν:: Compensated set-point
in:: Inlet concentration
sp:: Set-point.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This work was supported by King Mongkut’s University of Technology North Bangkok (Contract no. KMUTNB-62-KNOW-10). Support from this source is gratefully acknowledged.

Open Research

Data Availability

All data generated or analyzed during this study are included in this published article.

References

1 Bernard O., Hadj-Sadok Z., Dochain D., Genovesi A., and Steyer J. P., Steyer, Dynamical model development and parameter identification for an anaerobic wastewater treatment process, Biotechnology and Bioengineering. (2001) 75, 424–438, https://doi.org/10.1002/bit.10036, 2-s2.0-0035923336.
10.1002/bit.10036
CAS PubMed Web of Science® Google Scholar
2 Nguyen D., Gadhamshetty V., Nitayavardhana S., and Khanal S. K., Automatic process control in anaerobic digestion technology: a critical review, Bioresource Technology. (2015) 193, 513–522, https://doi.org/10.1016/j.biortech.2015.06.080, 2-s2.0-84945442157.
10.1016/j.biortech.2015.06.080
CAS PubMed Web of Science® Google Scholar
3 Iratni A. and Chang N. B., Advances in control technologies for wastewater treatment processes: status, challenges, and perspectives, IEEE/CAA Journal of Automatica Sinica. (2019) 6, no. 2, 337–363, https://doi.org/10.1109/jas.2019.1911372, 2-s2.0-85062836161.
10.1109/JAS.2019.1911372
Google Scholar
4 Rahmat M. F., Samsudin S. I., Wahab N. A., Salim S. N. S., and Gaya M. S., Control strategies of wastewater treatment plants, Australian Journal of Basic and Applied Sciences. (2011) 5, no. 8, 446–455.
Google Scholar
5 Liu H., Kim M., Lim J., and Yoo C., Performance assessment of cascade control strategy in wastewater treatment process, Proceedings of the International Conference on Control, Automation and Systems (ICCAS), October 2010, Gyeonggi-do, Republic of Korea, https://doi.org/10.1109/iccas.2010.5670273.
10.1109/iccas.2010.5670273
Google Scholar
6 García-Sandoval J. P., Cascade hybrid control for anaerobic digestion systems, IFAC Proceedings. (2009) 42, 183–188.
10.3182/20090712-4-TR-2008.00027
Google Scholar
7 Rincón A., Erazo C., and Angulo F., A robust adaptive controller for an anaerobic digester with saturated input: guarantees for the boundedness and convergence properties, Journal of Process Control. (2012) 22, 1785–1792.
10.1016/j.jprocont.2012.07.014
CAS Web of Science® Google Scholar
8 Robles A., Capson-Tojo G., Ruano M. V., Latrille E., and Steyer J. P., Development and pilot-scale validation of a fuzzy-logic control system for optimization of methane production in fixed-bed reactors, Journal of Process Control. (2018) 68, 96–104, https://doi.org/10.1016/j.jprocont.2018.05.007, 2-s2.0-85047416534.
10.1016/j.jprocont.2018.05.007
CAS Web of Science® Google Scholar
9 Kil H., Li D., Xi Y., and Li J., Model predictive control with on-line model identification for anaerobic digestion processes, Biochemical Engineering Journal. (2017) 128, 63–75, https://doi.org/10.1016/j.bej.2017.08.004, 2-s2.0-85029678175.
10.1016/j.bej.2017.08.004
CAS Web of Science® Google Scholar
10 Lara-Cisneros G., Aguilar-López R., and Femat R., On the dynamic optimization of methane production in anaerobic digestion via extremum-seeking control approach, Computers and Chemical Engineering. (2015) 75, 49–59, https://doi.org/10.1016/j.compchemeng.2015.01.018, 2-s2.0-84922364206.
10.1016/j.compchemeng.2015.01.018
CAS Web of Science® Google Scholar
11 Salomoni C., Caputo A., Bonoli M., Francioso O., Rodriguez-Estrada M. T., and Palenzona D., Enhanced methane production in a two-phase anaerobic digestion plant, after CO₂ capture and addition to organic wastes, Bioresource Technology. (2011) 102, 6443–6448, https://doi.org/10.1016/j.biortech.2011.03.079, 2-s2.0-79955476711.
10.1016/j.biortech.2011.03.079
CAS PubMed Google Scholar
12 Pohland F. G. and Ghosh S., Developments in anaerobic stabilization of organic wastes-the two-phase concept, Environmental Letters. (1971) 1, 255–266, https://doi.org/10.1080/00139307109434990, 2-s2.0-0015162258.
10.1080/00139307109434990
CAS PubMed Google Scholar
13 Zhu H., Stadnyk A., Béland M., and Seto P., Co-production of hydrogen and methane from potato waste using a two-stage anaerobic digestion process, Bioresource Technology. (2008) 99, 5078–5084, https://doi.org/10.1016/j.biortech.2007.08.083, 2-s2.0-41849133599.
10.1016/j.biortech.2007.08.083
CAS PubMed Web of Science® Google Scholar
14 Francioso O., Rodriguez-Estrada M. T., Montecchio D., Salomoni C., Caputo A., and Palenzona D., Chemical characterization of municipal wastewater sludges produced by two-phase anaerobic digestion for biogas production, Journal of Hazardous Materials. (2010) 175, 740–746, https://doi.org/10.1016/j.jhazmat.2009.10.071, 2-s2.0-72049109926.
10.1016/j.jhazmat.2009.10.071
CAS PubMed Web of Science® Google Scholar
15 Méndez-Acosta H. O., Campos-Rodríguez A., González-Álvarez V., García-Sandoval J. P., Snell-Castro R., and Latrille E., A hybrid cascade control scheme for the VFA and COD regulation in two-stage anaerobic digestion processes, Bioresource Technology. (2016) 18, 1195–1202.
10.1016/j.biortech.2016.07.076
Google Scholar
16 Amha Y. M., Anwar M. Z., Brower A., Jacobsen C. S., Stadler L. B., Webster T. M., and Smith A. L., Inhibition of anaerobic digestion processes: applications of molecular tools, Bioresource Technology. (2018) 247, 999–1014, https://doi.org/10.1016/j.biortech.2017.08.210, 2-s2.0-85029230628.
10.1016/j.biortech.2017.08.210
CAS PubMed Web of Science® Google Scholar
17 Tian Z., Zhang Y., Li Y., Chi Y., and Yang M., Rapid establishment of thermophilic anaerobic microbial community during the one-step startup of thermophilic anaerobic digestion from a mesophilic digester, Water Research. (2015) 69, 9–19, https://doi.org/10.1016/j.watres.2014.11.001, 2-s2.0-84911407780.
10.1016/j.watres.2014.11.001
CAS PubMed Web of Science® Google Scholar
18 Duan Z., Bournazou M. N. C., and Kravaris C., Dynamic model reduction for two-stage anaerobic digestion processes, Chemical Engineering Journal. (2017) 327, 1102–1116, https://doi.org/10.1016/j.cej.2017.06.110, 2-s2.0-85022198797.
10.1016/j.cej.2017.06.110
CAS Web of Science® Google Scholar
19 Tawai A., Panjapornpon C., and Dittanet P., Control of ethylene dichloride cracking furnace using an analytical model predictive control strategy for a coupled partial differential equation/ordinary differential equation system, Industrial & Engineering Chemistry Research. (2016) 55, 10121–10131, https://doi.org/10.1021/acs.iecr.6b00916, 2-s2.0-84989236143.
10.1021/acs.iecr.6b00916
CAS Web of Science® Google Scholar
20 Soroush M. and Muske K. R., Analytical model predictive control Nonlinear Model Predictive Control 163-179, 2000, Birkhäuser, Basel, Switzerland, https://doi.org/10.1007/978-3-0348-8407-5_9.
10.1007/978-3-0348-8407-5_9
Google Scholar
21 Soroush M. and Kravaris C., MPC formulation of GLC, AIChE Journal. (1996) 42, 2377–2381, https://doi.org/10.1002/aic.690420828, 2-s2.0-0030216179.
10.1002/aic.690420828
CAS Web of Science® Google Scholar
22 Soroush M. and Kravaris C., A continuous-time formulation of nonlinear model predictive control, International Journal of Control. (1996) 63, 121–146, https://doi.org/10.1080/00207179608921835, 2-s2.0-0029772694.
10.1080/00207179608921835
Web of Science® Google Scholar
23 Bolzonella D., Papa M., Da Ros C., Anga Muthukumar L., and Rosso D., Winery wastewater treatment: a critical overview of advanced biological processes, Critical Reviews in Biotechnology. (2019) 39, no. 4, 489–507, https://doi.org/10.1080/07388551.2019.1573799, 2-s2.0-85063725961.
10.1080/07388551.2019.1573799
CAS PubMed Web of Science® Google Scholar
24 Steyer J. P., Bouvier J. C., Conte T., Gras P., Harmand J., and Delgenes J. P., On-line measurements of COD, TOC, VFA, total and partial alkalinity in anaerobic digestion processes using infra-red spectrometry, Water Science and Technology. (2002) 45, 133–138, https://doi.org/10.2166/wst.2002.0310.
10.2166/wst.2002.0310
CAS PubMed Web of Science® Google Scholar
25 Steyer J. P., Genovesi A., and Harmand J., Advanced monitoring and control of anaerobic wastewater treatment plants: fault detection and isolation, Water Science and Technology. (2001) 43, no. 7, 183–190, https://doi.org/10.2166/wst.2001.0420.
10.2166/wst.2001.0420
CAS PubMed Web of Science® Google Scholar
26 Steyer J. P., Bouvier J. C., Conte T., Gras P., and Sousbie P., Evaluation of a four year experience with a fully instrumented anaerobic digestion process, Water Science and Technology. (2002) 45, 495–502, https://doi.org/10.2166/wst.2002.0654.
10.2166/wst.2002.0654
CAS PubMed Web of Science® Google Scholar
27 Kalyuzhnyi S. V., Batch anaerobic digestion of glucose and its mathematical modeling. II. Description, verification and application of model, Bioresource Technology. (1997) 59, 249–258, https://doi.org/10.1016/s0960-8524(96)00125-3, 2-s2.0-0031080212.
10.1016/S0960-8524(96)00125-3
CAS Web of Science® Google Scholar
28 Wu W., Lai S. Y., Jang M. F., and Chou Y. S., Optimal adaptive control schemes for PHB production in fed-batch fermentation of Ralstonia eutropha, Journal of Process Control. (2013) 23, no. 8, 1159–1168, https://doi.org/10.1016/j.jprocont.2013.07.006, 2-s2.0-84881469757.
10.1016/j.jprocont.2013.07.006
CAS Web of Science® Google Scholar
29 Atassi A. N. and Khalil H. K., A separation principle for the control of a class of nonlinear systems, IEEE Transactions on Automatic Control. (2001) 46, no. 5, 742–746, https://doi.org/10.1109/9.920793, 2-s2.0-0035332585.
10.1109/9.920793
Web of Science® Google Scholar
30 Benitez F. J., Beltran-Heredia J., Real F. J., and Gonzalez T., Aerobic and anaerobic purification of wine distillery wastewater in batch reactors, Chemical Engineering and Technology: Industrial Chemistry-Plant Equipment-Process Engineering-Biotechnology. (1999) 22, no. 2, 165–172, https://doi.org/10.1002/(sici)1521-4125(199902)22:2<165::aid-ceat165>3.0.co;2-t.
10.1002/(SICI)1521-4125(199902)22:2<165::AID-CEAT165>3.0.CO;2-T
CAS Web of Science® Google Scholar
31 Borja R., Martin A., Luque M., and Duran M. M., Kinetic study of anaerobic digestion of wine distillery wastewater, Process Biochemistry (Oxford, United Kingdom). (1993) 28, no. 2, 83–90, https://doi.org/10.1016/0032-9592(93)80011-5, 2-s2.0-0002532951.
10.1016/0032-9592(93)80011-5
CAS Web of Science® Google Scholar

Citing Literature

All articles

Nonlinear Optimization-Based Robust Control Approach for a Two-Stage Anaerobic Digestion Process

Abstract

1. Introduction