Application of Cellular Automata with Improved Dynamic Analysis in Evacuation Management of Sports Events
Abstract
In this paper, the cellular automaton simulation technology is applied to the evacuation management of sports events, combined with the dynamic analysis method to analyze the collision of people in the evacuation process. At the same time, the cellular automaton model is used to refine the evacuation space to simplify environmental modeling, and the network model is used to determine the individual evacuation path from a macroperspective, simplify modeling, and improve simulation efficiency. In addition, this article simulates the evacuation process of the cellular automaton according to the actual evacuation situation of sports events and constructs the evacuation management system of sports events. Finally, this article evaluates the effect of the model in conjunction with experiments. The experimental results show that the role of the evacuation management system for sports events based on cellular automata proposed in this paper is obvious.
1. Introduction
The number of stadiums and sports venues with complex structures and diverse functions is rapidly increasing, and sports events of various levels are being held all over the world. In addition, due to the periodicity and intermittent nature of sports events, as well as the increasing use of postmatch use methods such as cultural performances, exhibitions, and food and entertainment [1], stadiums have become venues for large-scale cultural and entertainment activities. Therefore, stadiums have become one of the main gathering places for a large number of people in daily life. The magnificent buildings, complex structures, dense crowds, and numerous equipment have become the characteristics of stadiums. There is a major problem hidden behind these features, that is, security risks. The huge building and complex structure can easily cause the collapse of the stadium and make the safety exit not clear for evacuation [2]. Moreover, crowded people can easily lead to crowds, which can lead to stampede incidents. In addition, when there is many equipment, a little careless management can cause fire and explosion. At the same time, dense crowds and large-scale venues often become targets of international terrorist attacks. Once these emergencies happen, it will inevitably cause casualties and property losses [3].
Today’s stadium is a multipurpose venue mainly for holding sports events and carrying out a variety of activities. At the same time, stadiums have become densely populated places, full of major safety hazards. Therefore, relevant departments and related personnel are urgently required to take effective and feasible measures to minimize the occurrence of incidents and personal and property losses. At the same time, this also requires researchers and scholars to pay great attention to the evacuation of stadiums and gymnasiums. Due to the causes of casualties, there are not only the building structure of the venue itself but also the crowd and external human factors in the venue.
Cellular automata were originally used to simulate the self-replication function of living systems. Its core idea is to discretize the research object into cells with a finite number of states in space and then follow a certain random motion rule in the discretized time. This idea and method were adopted by evacuation researchers and established a cellular automaton model in the field of evacuation research. The core of the cellular automaton model is the discretization of space and time. It divides the evacuation simulation environment into grids of equal size, and each grid is a cell. Usually, a cell can have three states, namely, occupied by evacuated individuals, occupied by obstacles, and idle; the state of each cell at a time can only be one of the three states, other cells adjacent to a certain cell. It is called the neighbor of this cell; the entire evacuation time is divided into small time slices; these time slices are called time steps; in each time step, the evacuated individual moves from the cell where it is currently located to according to the set movement rule. The neighbors may stay where they are. Therefore, the content of the model mainly includes spatial division method, neighbor type, and time-step update method.
This paper applies dynamic analysis to the evacuation management process of sports events and simulates the evacuation process of sports events through cellular automata to improve the evacuation management effect of sports events.
2. Related Work
Literature [4] studied the time required for evacuation and obtained the corresponding mathematical formula. Researchers on evacuation began to rise. Literature [5] investigates the behaviors of survivors in fires and uses them for statistical analysis. Literature [6] gives the relationship curve between crowd density and average crowd speed and applies computational simulation research methods to the evacuation of fire personnel. During this period, the evacuation of people was studied mainly through observation, investigation, statistics, and mathematical simulation.
There are many simulation models for evacuation, but researchers usually divide them into micromodels, macromodels, and mesoscopic models. The micromodel treats each person in the evacuation crowd as an independent individual for evacuation research. This type of model can show the individual’s evacuation behavior more finely, but the amount of calculation is often large; the macromodel studies the evacuated crowd as a whole, and the evacuation crowd is regarded as a flowing fluid. An evacuated person is a particle in the fluid. This model mainly studies the characteristics of the evacuated crowd as a whole and cannot well represent the characteristics of the evacuated individuals; the mesoscopic model combines the microscopic model and the macroscopic model for evacuation of researchers. This model can not only study the individual behavior of evacuees but also study the overall characteristics of evacuees [6].
Models based on physical forces are also often regarded as continuous microscopic models. The model is continuous in time and space and simulates individual evacuation by calculating the force generated by itself and the environment on the individual. Its representative models are the magnetic field force model and the social force model. The magnetic field force model is a gravitational model of pedestrian motion established by the literature [7] based on the principle of magnetic force. In the model, the target is regarded as the negative pole of the magnetic field, and the obstacle and the person are regarded as the positive pole. In this way, a gravitational force is formed between the person and the target and between the obstacle and the obstacle. Repulsion is formed, and people are evacuated under the action of gravity and repulsion. The social force model is proposed in the literature [8]. This model describes the interaction between people and the environment and goals as repulsive force, gravitational force, and self-driving force and establishes a dynamic differential equation system to describe the movement of people according to Newton’s second law. The relationship between speed and position over time. Based on the agent theory in artificial intelligence based on the agent model, the literature [9] defines the evacuated individuals in the model as agent individuals with different characteristics to represent the differences between people in reality. This type of model is divided into single-agent model and multiagent model. The modeling ideas of the two are the same, but the multiagent model emphasizes the interaction between agents. The cellular automaton model is based on the cellular automaton idea proposed by Von Neumann. This model divides the evacuation space into discrete cell spaces with a finite number of states [10], so that the evacuees move in the cell space according to a certain rule to achieve the effect of evacuation simulation. Based on this model are the queuing model, route selection model, and random model. The difference between them is only the rules of individual movement on the cell. The queuing model emphasizes that people move in a certain queue order, the path selection model emphasizes to move according to the path search, and the random model emphasizes to move in the order of random selection. Based on agent and cellular automaton model [11], combine the agent model and cellular automaton model in evacuation modeling, use agent to describe individuals, and use cellular automata to divide the evacuation environment space, so that all the established model can better reflect the scalability of the environment and the intelligence of personnel.
For the study of crowd evacuation time, the literature [12] uses the Legion simulation system to simulate and calculate the three algorithms for evacuation time commonly used in domestic and foreign projects and analyzes and compares the results obtained. It is recommended to use the itinerary method as engineering calculation method for evacuation time of stadiums. For the research on how the structural characteristics of stadiums and stadiums affect the characteristics of evacuated individuals, the literature [13] studied the influence of the width of the safety exits of stadiums on crowding during evacuation and the influence of crowd panic on evacuation.
Literature [14] developed a simulation system for fire evacuation demonstration based on the Superscape system, which can be used for simulation training of evacuation in fire. Literature [15] developed a virtual exercise system named interFIRE VR, which is mainly used to train personnel how to evacuate in a fire situation. Literature [16] developed a virtual exercise program to train relevant personnel on how to find a safe evacuation exit in a fire building and successfully evacuate. Literature [17] developed a building fire simulation prototype system FVR based on virtual reality and data simulation, which can be used for evacuation drills and fire rescue training in fire situations. Literature [18] proposed a simulation technology DIS and developed a fire remediation simulation drill DIS system. Its application can replace the existing actual field simulation training. Literature [19] uses game engine technology to develop a three-dimensional virtual exercise system to simulate the process of evacuation of personnel to a safe area in an organized and orderly manner according to the unified dispatch and command on the spot after an incident occurs. It can be seen from the above that the virtual exercise technology has been successfully applied by researchers in the simulation research of personnel evacuation, which makes the visual effect of simulation stronger, and the interaction between people and the system makes the individual evacuation in the system more reflected. The characteristics of people in reality can greatly promote the research of personnel evacuation simulation.
3. Application of Cellular Automata Based on Dynamic Model in Evacuation Management of Sports Events
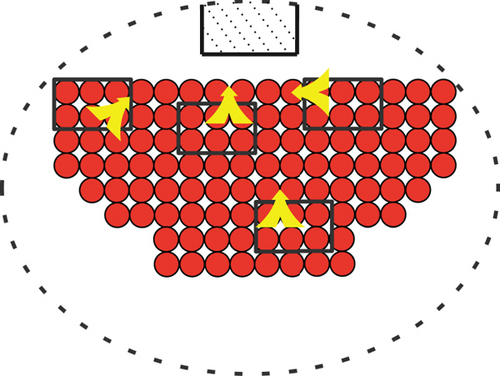
Among them, Sij is the shortest distance between a cell (xi, yi) around the pedestrian and a cell (xj, yj) belonging to the safety exit. When (xi, yi) is a wall, the pedestrian will not choose this position, and M is a large constant, which means that the pedestrian’s initial self-driving force F0 will not point to the wall.
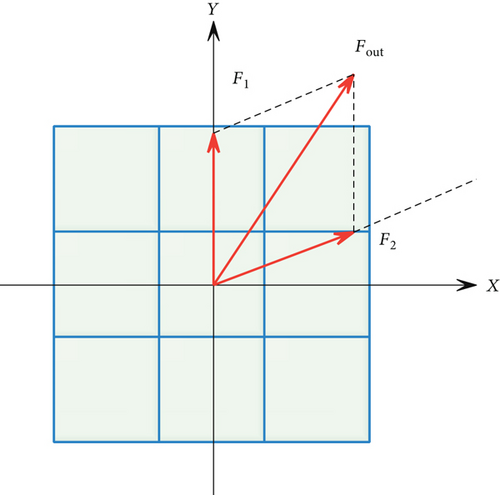
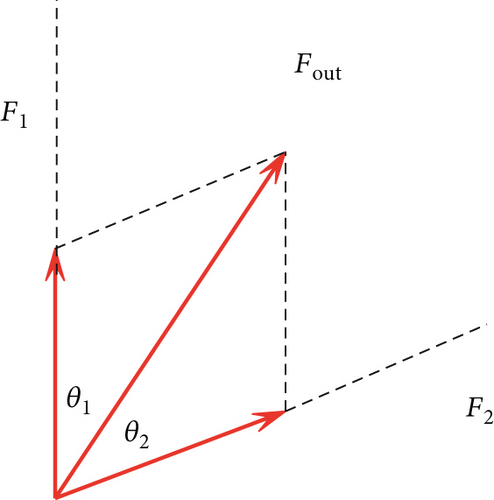
Among them, |Fm| is the force component of F0 in the θm direction, and θm is the angle between F0 and the pedestrian to the adjacent cell.
In addition, when there is a space in the two cell directions of the crowding force F0 decomposition, that is, when there is no pedestrian at that position, the component force in this direction remains on the pedestrian itself. Among them, pedestrians have a crowding force F0i for pedestrians. However, the cell without pedestrians does not produce the crowding force but keeps this F0j in the pedestrian itself, acts on the pedestrian itself, and exists as the pedestrian’s self-driving force, as shown in Figure 3. That is, at this time, pedestrians are driven by their own driving force F0j, which points to the space cell. Similarly, when the two directions are spaces, pedestrians are, respectively, driven by the driving forces F0i and F0j pointing to the two space cells, which may drive the pedestrian to move to these two positions.
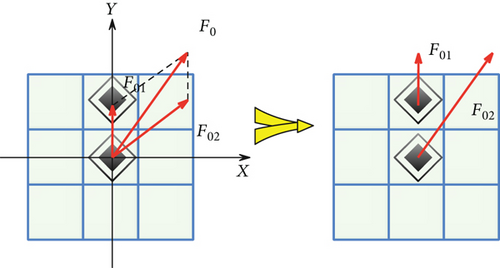
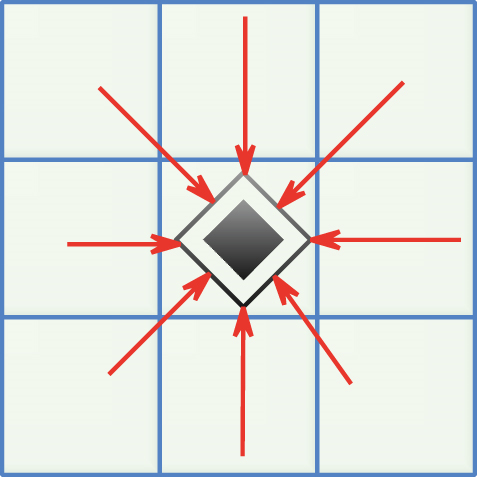
Among them, Fi⟶1 is the component of the crowding force of the ith pedestrian around the pedestrian to the pedestrian.
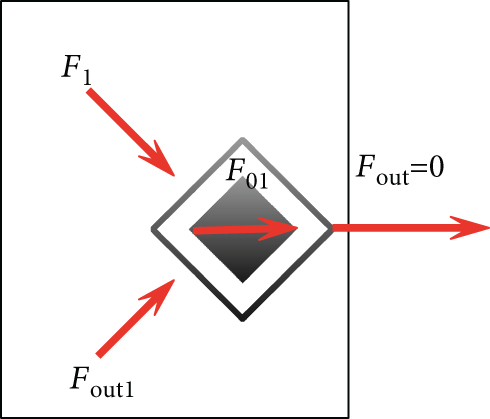
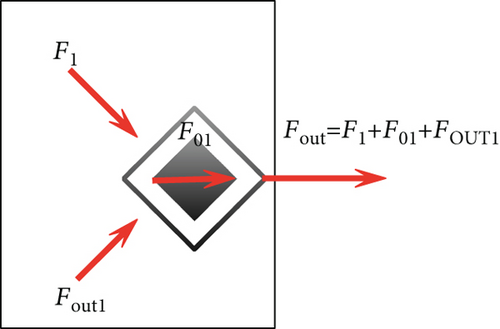
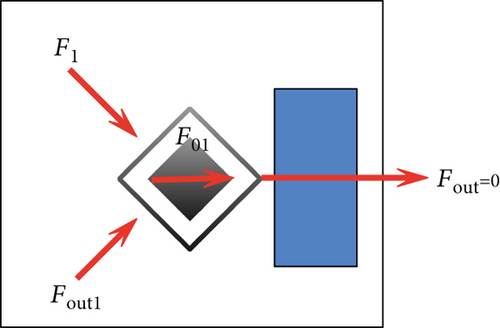
Among them, F1 is the combined force of the crowding force received by the pedestrian, F01 is the driving force transmitted by the pedestrian itself, Fout is the component of the crowding force that other pedestrians around cannot absorb the crowding force transmitted to the pedestrian, α is the absorption coefficient, and Fout is the crowding force transmitted by pedestrians. The process of its decomposition and transmission refers to the above-mentioned decomposition and transmission process.
- (1)
The self-driving force of pedestrians interacts with other pedestrians. With reference to Newton’s third law, the action of force is mutual, and pedestrians will receive a reaction force of the same magnitude and opposite direction as this driving force. Therefore, the pedestrian will receive the reaction force of the self-driving force, and the magnitude of this force is denoted as f0
- (2)
When the pedestrian’s self-driving force acts on the surrounding pedestrians, each pedestrian may be subjected to the crowding force of eight other pedestrians around him, and the scalar and accumulation of each crowding force need to be recorded as f1
- (3)
When pedestrians judge the absorption and retransmission of the congestion force, there are situations in which the congestion force cannot be absorbed and transferred. Pedestrians will be affected by the crowding force transmitted to the pedestrian that the surrounding pedestrians cannot absorb the crowding force and the reaction force generated by the pedestrians themselves being unable to absorb the crowding force and crowding other pedestrians. The scalar and accumulation of this part of the crowding force are denoted as f2
Through the analysis of simulation data and reference to related documents, the panic coefficient of pedestrians is calibrated. The relationship between the panic coefficient P and the crowding force effect is shown in Table 1.
| f | p |
|---|---|
| ≤100 | 0.00 |
| ≤200 | 0.10 |
| ≤300 | 0.20 |
| ≤400 | 0.30 |
| ≤500 | 0.40 |
| ≤600 | 0.50 |
| ≤700 | 0.60 |
| ≤800 | 0.70 |
| ≤900 | 0.80 |
| ≤1000 | 0.90 |
| ≥1000 | 1.00 |
The higher the pedestrian panic, the more the pedestrian expects to leave the evacuation space. Therefore, when the panic coefficient P is greater, the pedestrian’s self-driving force is also greater, and its direction is closer to the safety exit. The self-driving force of pedestrians consists of two parts: the self-driving force new F0 that is expected to leave the safety exit generated by the panic coefficient P and the congestion force F2 that has not been transmitted at this time step.
Among them, |newF0| is the magnitude of the pedestrian’s self-driving force, p is the pedestrian’s panic coefficient, Fmax is the maximum self-driving force, and A × RAND is the random self-driving force generated by different pedestrians.
Secondly, the direction of the self-driving force newF0 is also determined by the panic coefficient p. When the pedestrian is in the most panic state, that is, when p = 1, the pedestrian expects to leave the evacuation space very much, so the direction of the self-driving force points to the nearest safety exit. When the pedestrian’s fear coefficient is small, the pedestrian’s psychological state is relatively stable. However, since the ultimate goal of the pedestrian is still to leave the evacuation space, the direction of its self-driving force should deviate at a certain angle along the exit direction. As p decreases, the deviation range increases. Therefore, taking the direction of pedestrians to the nearest safety exit as the normal direction, this paper believes that the direction of self-driving force is randomly distributed within the range of (1 − p)∗90° on both sides of the normal, as shown in Figure 6.
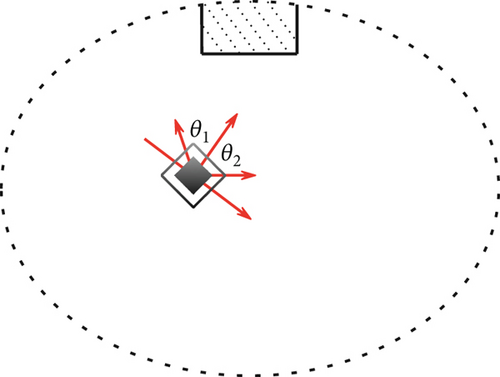
In addition, the crowding force of pedestrians cannot be passed on in a time step. Therefore, in the process of judging that the congestion force absorption will be transmitted again, some pedestrians still have untransmitted congestion force F2 themselves, rather than being in a balanced state. However, force cannot disappear out of thin air. Therefore, this part of the force F2 is combined with the self-driving force new F0 generated by pedestrians and updated as the self-driving force for the next time step.
Among them, F0 is the initial self-driving force of the pedestrian at the next time step, newF is the self-driving force generated by the pedestrian itself, and F2 is the congestion force that has not yet been transmitted.
In the dynamic parameter model, all the positions that can be moved within a time step of the pedestrian are defined as the pedestrian’s moving area. In the cellular automaton simulation, the pedestrian’s moving area is a 3 × 3 cellular area. Pedestrians occupy the center of the mobile field. Pedestrians can choose to wait or move to the other eight cells within a time step. Mobile revenue is the evaluation of pedestrians on all locations in the mobile field, as shown in Figure 7.
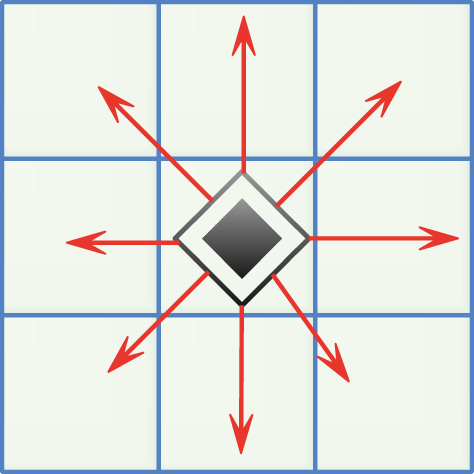

Because in the process of pedestrian evacuation, the main consideration is the pedestrian direction parameter and space parameter, therefore, these two parameters are used in the simulation of crowded evacuation to describe the movement benefits of pedestrians.
During the evacuation of pedestrians, the purpose of pedestrians is to leave the evacuation space. Therefore, pedestrians always move in the direction of the safety exit; that is, pedestrians will choose the position closest to the safety exit in the moving area as their target location. The direction parameter Dij refers to the reduced value of the distance for the pedestrian to reach the safety exit when the pedestrian moves from the initial position to the target position within a unit step.
Among them, (x, Y) is the coordinate of a cell in the system, Sxy is the static field parameter value of the cell (x, Y), are the mth cell in the nth gate, and M is a large positive number, which means that pedestrians cannot move to this location.
Among them, Soo is the static field parameter value of the center position of the pedestrian moving field, and Sxy is the static field parameter value of the moving position that the pedestrian can choose.
When Dij = 0, it means that when pedestrians choose this location, the distance to the safety exit will neither increase nor decrease. When Dij > 0, it means that pedestrians choosing this location will reduce the distance to the safety exit; that is, pedestrians are more inclined to choose this location. When Dij < 0, it means that pedestrians choosing this location will increase the distance to the safety exit. Therefore, pedestrians will reduce the possibility of choosing the location.
Among them, Pij is the pedestrian’s movement income, Dij is the pedestrian’s direction parameter, Eij is the pedestrian’s space parameter, and max(D) is the maximum value of the direction parameter’s profit in the pedestrian movement field.
Similar to the moving area of pedestrians, the moving area of the space cell refers to the space cell as the center, and pedestrians in the eight positions around it may move to the space position, as shown in Figure 8. When formulating an appropriate probability model, the movement probability of the surrounding pedestrians is determined by the crowding force received and the initial target position, and the movement probability determines the moving pedestrian.
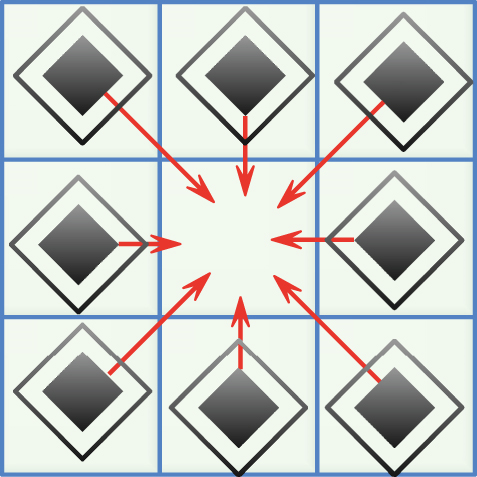
Among them, |Fij⟶oo| is the force component of the pedestrian (i, j) in the direction of the space cell in the moving field, and Fij⟶∞ is the force component of the pedestrian (i, j) in the direction of the space cell.
Among them, mij is the probability of pedestrians (i, j) in the mobile field choosing space cells due to crowding forces.
The greater the crowding force component of the pedestrian in the direction of the space cell, the greater the probability that the pedestrian will choose the location, which is consistent with the fact that pedestrians are crowded to other locations due to the crowding force in the actual movement.
Among them, mij is the probability of pedestrians (i, j) choosing the space cell due to crowding force, nij is the probability of pedestrians (i, j) choosing the space cell due to their own initial target position selection, and β is the adjustment parameter. When β is close to 1, the influence of pedestrian crowding force is relatively large. When β is close to 0, the influence of pedestrian’s initial target position selection is relatively large. In this paper, 0.5 is considered to be equivalent. When ∑mij = 0 and ∑nij = 0, it means that no pedestrian in the moving area has selected the space cell.
4. Model Effect Analysis
The third part builds an intelligent evacuation model and evaluates the evacuation management effect of sports events on this basis. Generally speaking, whether a person can reach a goal grid is affected by knowledge, reason, physical strength, and other comprehensive forces. The method of movement is as follows in Figure 9.
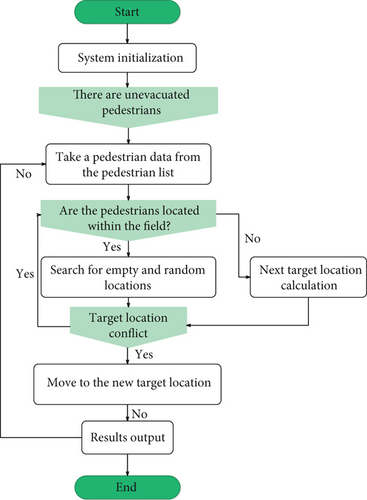
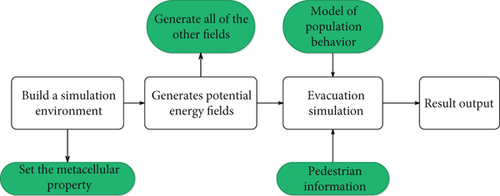
According to cellular automata, this system includes scene editing, potential energy field calculation, crowd behavior model, and evacuation simulation. The structure is as follows in Figure 10.
The dynamic analysis model of this paper is studied through experimental research, and the performance effect of the cellular automata in the dynamic analysis model is statistically evaluated by the expert evaluation method, and the results shown in Table 2 below are obtained.
| Number | Dynamic simulation |
|---|---|
| 1 | 87.9 |
| 2 | 88.9 |
| 3 | 94.6 |
| 4 | 92.9 |
| 5 | 87.0 |
| 6 | 92.2 |
| 7 | 94.0 |
| 8 | 86.8 |
| 9 | 89.6 |
| 10 | 89.2 |
| 11 | 86.4 |
| 12 | 91.2 |
| 13 | 87.0 |
| 14 | 93.2 |
| 15 | 92.6 |
| 16 | 86.4 |
| 17 | 94.0 |
| 18 | 89.7 |
| 19 | 93.3 |
| 20 | 90.1 |
| 21 | 89.7 |
| 22 | 86.1 |
| 23 | 92.3 |
| 24 | 90.1 |
| 25 | 95.0 |
| 26 | 90.8 |
| 27 | 94.9 |
| 28 | 91.4 |
| 29 | 93.1 |
| 30 | 89.5 |
| 31 | 94.6 |
| 32 | 92.6 |
| 33 | 93.7 |
| 34 | 90.0 |
| 35 | 91.1 |
| 36 | 92.0 |
| 37 | 90.2 |
| 38 | 93.4 |
| 39 | 90.3 |
| 40 | 91.7 |
| 41 | 90.7 |
| 42 | 88.1 |
| 43 | 87.9 |
| 44 | 88.7 |
| 45 | 92.6 |
| 46 | 93.8 |
| 47 | 87.5 |
| 48 | 86.3 |
| 49 | 91.4 |
| 50 | 94.2 |
| 51 | 93.0 |
| 52 | 94.6 |
| 53 | 88.1 |
| 54 | 89.4 |
| 55 | 89.9 |
| 56 | 91.7 |
| 57 | 94.7 |
| 58 | 93.6 |
| 59 | 91.7 |
| 60 | 93.0 |
It can be seen from Table 2 that the cellular automata perform very well in the dynamic analysis model. On the basis of the above research, the evacuation management system of sports events based on the cellular automata constructed in this paper is evaluated, and the evaluation results are shown in Table 3 below.
| Number | Evacuation effect |
|---|---|
| 1 | 72.3 |
| 2 | 72.1 |
| 3 | 80.3 |
| 4 | 70.4 |
| 5 | 81.7 |
| 6 | 71.3 |
| 7 | 83.3 |
| 8 | 82.4 |
| 9 | 79.3 |
| 10 | 80.8 |
| 11 | 72.2 |
| 12 | 71.0 |
| 13 | 72.5 |
| 14 | 86.2 |
| 15 | 84.6 |
| 16 | 74.1 |
| 17 | 79.5 |
| 18 | 77.2 |
| 19 | 81.4 |
| 20 | 81.7 |
| 21 | 77.4 |
| 22 | 85.2 |
| 23 | 75.5 |
| 24 | 69.1 |
| 25 | 69.3 |
| 26 | 82.2 |
| 27 | 81.0 |
| 28 | 78.6 |
| 29 | 86.7 |
| 30 | 86.5 |
| 31 | 72.4 |
| 32 | 69.9 |
| 33 | 70.5 |
| 34 | 77.9 |
| 35 | 69.2 |
| 36 | 82.5 |
| 37 | 70.0 |
| 38 | 75.9 |
| 39 | 78.5 |
| 40 | 83.2 |
| 41 | 80.1 |
| 42 | 69.5 |
| 43 | 83.7 |
| 44 | 80.6 |
| 45 | 83.8 |
| 46 | 81.4 |
| 47 | 80.8 |
| 48 | 75.7 |
| 49 | 84.2 |
| 50 | 74.3 |
| 51 | 70.3 |
| 52 | 76.2 |
| 53 | 77.1 |
| 54 | 84.0 |
| 55 | 85.3 |
| 56 | 76.8 |
| 57 | 85.1 |
| 58 | 86.1 |
| 59 | 74.1 |
| 60 | 72.7 |
From the experimental analysis, it can be seen that the evacuation management system for sports events based on the cellular automata proposed in this paper can play an important role in the evacuation of sports events.
5. Conclusion
In the study of evacuation of stadium personnel, it is necessary to study the evacuation characteristics of stadiums as well as the characteristics of individual personnel in evacuation situations. The research on the virtual exercise of stadium personnel evacuation includes the above two research aspects, which can provide an effective research approach for the evacuation of stadium personnel and even other venues. Therefore, the research on the virtual exercise system for evacuation of stadiums can not only provide a basis for determining the rationality of stadium construction but also provide a basis for the formulation of evacuation plans. This paper applies dynamic analysis to the evacuation management process of sports events and simulates the evacuation process of sports events through cellular automata to improve the evacuation management effect of sports events. The experimental research results show that the evacuation management system for sports events based on cellular automata proposed in this paper can play an important role in the evacuation of sports events.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by the project of Basic scientific research operation fees of central universities (2020SKTY01).
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.




