[Retracted] Computation of M-Polynomial and Topological Indices of Phenol Formaldehyde
Abstract
Phenol formaldehyde (phenolic resin) has a wide range of moldings. However, it has immense consumption in manufacturing electrical equipment due to its insulating property. Phenolic resin retains properties at the freezing point, and also its age cannot be determined. Due to its insulator property, it has wide use in electrical equipment. In this article, degree-based topological indices of phenol formaldehyde are determined with the help of M-polynomial. We calculate the Zagreb index, Randić index, K-Banhatti indices, modified K-Banhatti indices, atom-bond connectivity index, geometric arithmetic index, symmetric index, inverse sum index, and harmonic index.
1. Introduction
Phenol formaldehyde (PF) is a synthetic polymer that is formed by the reaction of phenol and formaldehyde. Due to its molding power, it is used for many purposes in different industries. An in-circuit board like PCB and many electronic equipment like buttons, knobs, cameras, and vacuum cleaner phenolic resins are used. It is also used in laminate, fabric, and paper. There are two methods of production in industrial practice. In the first method, excess formaldehyde reacts with phenol in an alkaline solution. In the second method, excess phenol reacts with formaldehyde in an acidic solution [1]. It was firstly used in the first decades of 20th century.
In chemical graphs, atoms are represented by vertices, and bonding is represented by edges in molecular structure. A topological index is a numerical parameter that predicts the characteristics of that chemical graph. Mathematical models, based on polynomial representations of chemical compounds, can be used to predict their properties. Mathematical chemistry is rich in tools such as polynomials and functions which can forecast the properties of compounds. Topological indices are numerical parameters of a graph that characterize its topology and are usually graph invariant. They describe the structure of molecules numerically and are used in the development of quantitative structure-activity relationships (QSARs). These numerical values correlate structural facts and chemical reactivity, biological activities, and physical properties [2–4].
| Topological index | Derivative from M(G; a, b) |
|---|---|
| First Zagreb index |
|
| Second Zagreb index |
|
| First K-Banhatti index |
|
| Modified first K-Banhatti index |
|
| Randić index |
|
| Symmetric index |
|
| Harmonic index |
|
| Inverse sum index |
|
| K harmonic Banhatti index |
|
| Atom-bond connectivity index |
|
| Geometric-arithmetic index |
|
2. Formation and Result for Phenol Formaldehyde Polymer Chain
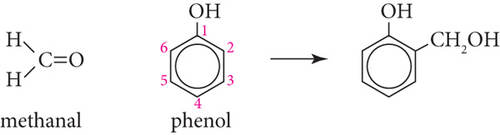
In alkaline or acidic solution, when phenol and methanal are heated phenol formaldehyde (PF), polymer chain is formed in condensation reaction. Ortho and para substitute phenol is produced in the first step, then ortho isomer reacts with other same molecule, and polymer chain is produced. A polymer chain is formed when in acidic condition, and methanal and phenol rings in 2 or 4 position react with 0.5 : 1 ratio.
In Table 2, p represents number of units.
Theorem 1. Consider the phenol formaldehyde polymer chain (PF); then, its M-polynomial is as follows.
Proof. From Figure 1, and using Table 2, we can compute the M-polynomial of chemical structure of phenol formaldehyde polymer chain (PF) as follows:
Proposition 2. Consider the phenol formaldehyde polymer (PF) chain structure.
- (i)
First Zagreb index:
- (ii)
Second Zagreb index:
- (iii)
First K-Banhatti index:
- (iv)
Modified first K-Banhatti index:
- (v)
Randić index:
- (vi)
Symmetric index:
- (vii)
Harmonic index:
- (viii)
Inverse sum index:
- (ix)
Atom-bond connectivity index:
- (x)
Geometric-arithmetic index:
- (xi)
K harmonic Banhatti index:
Proof. Let M(PF; a, b) = (p + 1)ab3 + (2p + 1)a2b2 + (4p − 2)a2b3 + (2p − 1)a3b3. Now, we apply the formulas from Table 1, and compute the following required results.
- (i)
First Zagreb index:
- (ii)
Second Zagreb index:
- (iii)
First K-Banhatti index:
- (iv)
Modified first K-Banhatti index:
- (v)
Randić index:
- (vi)
Symmetric index:
- (vii)
Harmonic index:
- (viii)
Inverse sum index:
- (ix)
Atom-bond connectivity index:
- (x)
Geometric-arithmetic index:
- (xi)
K harmonic Banhatti index:
| Types of edges | (1, 3) | (2, 2) | (2, 3) | (3, 3) |
| Frequency | p + 1 | 2p + 1 | 4p − 2 | 2p − 1 |

3. Numerical and Graphical Representation
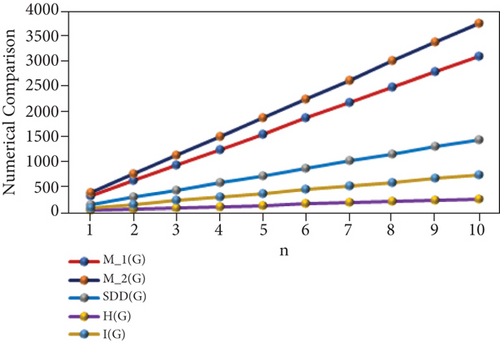
“The numerical representation of the above computed results is depicted in Tables 3 and 4, and the graphical representation is dedicated in Figures 2 and 3. We can easily see from Figures 2 and 3 that all indices are in increasing order as the value of n is increasing.”
| p | M1(PF) | M2(PF) | SDD(PF) | H(PF) | I(PF) | B1(PF) | mB1(PF) | Hb(PF) | ABC(PF) | GA(PF) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 36 | 39 | 19 | 3.64 | 7.4 | 76 | 3.56 | 7.11 | 5.83 | 7.69 |
| 2 | 80 | 92 | 39 | 7.41 | 17.95 | 172 | 7.13 | 14.25 | 12.23 | 16.47 |
| 3 | 124 | 145 | 59 | 11.18 | 28.5 | 268 | 10.7 | 21.39 | 18.63 | 25.25 |
| 4 | 168 | 198 | 79 | 14.95 | 39.05 | 364 | 14.27 | 28.53 | 25.03 | 34.03 |
| 5 | 212 | 251 | 99 | 18.72 | 49.6 | 460 | 17.84 | 35.67 | 31.43 | 42.81 |
| 6 | 256 | 304 | 119 | 22.49 | 60.15 | 556 | 21.41 | 42.81 | 37.83 | 51.59 |
| 7 | 300 | 357 | 139 | 26.26 | 70.7 | 652 | 24.98 | 49.95 | 44.23 | 60.37 |
| 8 | 344 | 410 | 159 | 30.03 | 81.25 | 748 | 28.55 | 57.09 | 50.63 | 69.15 |
| 9 | 388 | 463 | 179 | 33.8 | 91.8 | 844 | 32.12 | 64.23 | 57.03 | 77.93 |
| 10 | 432 | 516 | 199 | 37.57 | 102.35 | 940 | 35.69 | 71.37 | 63.43 | 86.71 |
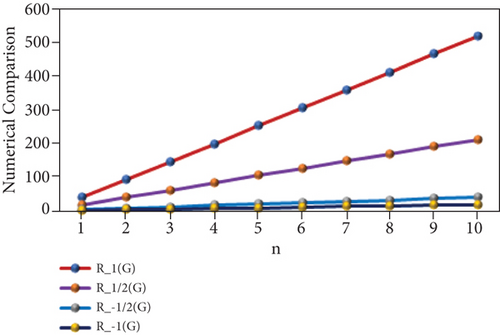
| p | R1(PF) | R1/2(PF) | R−1/2(PF) | R−1(PF) |
|---|---|---|---|---|
| 1 | 39 | 17.36 | 3.81 | 1.58 |
| 2 | 92 | 38.89 | 7.69 | 3.3 |
| 3 | 145 | 60.42 | 11.57 | 5.02 |
| 4 | 198 | 81.95 | 15.45 | 6.74 |
| 5 | 251 | 103.48 | 19.33 | 8.46 |
| 6 | 304 | 125.01 | 23.21 | 10.18 |
| 7 | 357 | 146.54 | 27.09 | 11.9 |
| 8 | 410 | 168.07 | 30.97 | 13.62 |
| 9 | 463 | 189.6 | 34.85 | 15.34 |
| 10 | 516 | 211.13 | 38.73 | 17.06 |
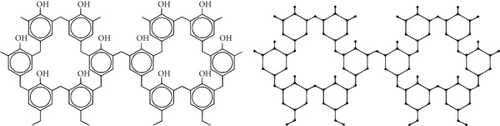
4. Formation and Result Cross-Linked Phenol Formaldehyde Structure
The polymer chain reacts with formaldehyde to produce branching. Branching is possible when methanal reacts with higher proportion, because it provides a CH2 and on heating resin is produced.
Theorem 3. Consider the cross-linked phenol formaldehyde (PF) structure; then, its M-polynomial is as follows.
Proof. From Figure 4, and using Table 5, we can compute the M-polynomial of chemical structure of phenol formaldehyde (PF) network as follows:
Proposition 4. Consider the cross-linked phenol formaldehyde (PF) structure.
- (i)
First Zagreb index:
- (ii)
Second Zagreb index:
- (iii)
First K-Banhatti index:
- (iv)
Modified first K-Banhatti index:
- (v)
Randić index:
- (vi)
Symmetric index:
- (vii)
Harmonic index:
- (viii)
Inverse sum index:
- (ix)
Atom-bond connectivity index:
- (x)
Geometric-arithmetic index:
- (xi)
K harmonic Banhatti index:
Proof. Let M(PF; a, b) = 2nab2 + 9nab3 + 39na2b3 + 12na3b3. Now, we apply the formulas from Table 1, and compute the following required results.
- (i)
First Zagreb index:
- (ii)
Second Zagreb index:
- (iii)
First K-Banhatti index:
- (iv)
Modified first K-Banhatti index:
- (v)
Randić index:
- (vi)
Symmetric index:
- (vii)
Harmonic index:
- (viii)
Inverse sum index:
- (ix)
Atom-bond connectivity index:
- (x)
Geometric-arithmetic index:
- (xi)
K harmonic Banhatti index:
| Types of edges | (1, 2) | (1, 3) | (2, 3) | (3, 3) |
| Frequency | 2n | 9n | 39n | 12n |
5. Numerical and Graphical Representation
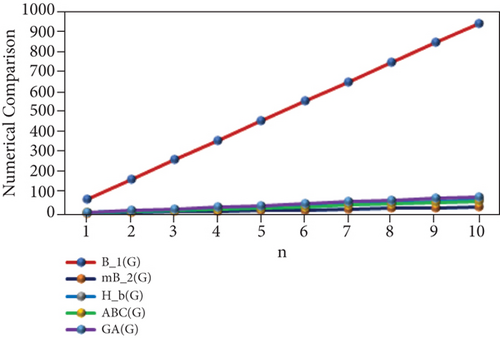
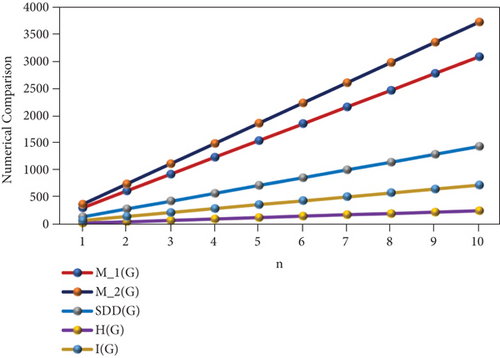
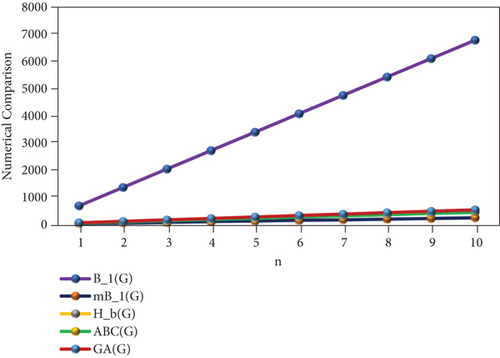
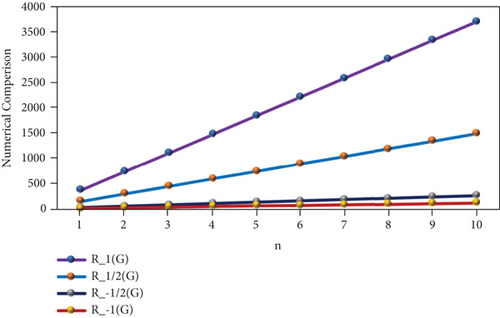
The numerical representation of the above computed results is depicted in Tables 6 and 7, and the graphical representation is dedicated in Figures 5 and 6. Tables 6 and 7 depict the mathematical equations as topological indices. Furthermore, these indices are being illustrated graphically in Figures 5 and 6. It has been observed clearly from the figures that all indices are in an ascending order as the value of n is increasing gradually. Thus, the increasing trend indicates that the values of topological indices are increasing accordingly in Tables 6 and 7.
| n | M1(PF) | M2(PF) | SDD(PF) | H(PF) | I(PF) | B1(PF) | mB1(PF) | Hb(PF) | ABC(PF) | GA(PF) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 309 | 373 | 143.5 | 25.43 | 72.88 | 679 | 24.19 | 48.39 | 44.34 | 53.52 |
| 2 | 618 | 746 | 287 | 50.86 | 145.76 | 1358 | 48.38 | 96.78 | 88.68 | 107.04 |
| 3 | 927 | 1119 | 430.5 | 76.29 | 218.64 | 2037 | 72.57 | 145.17 | 133.02 | 160.56 |
| 4 | 1236 | 1492 | 574 | 101.72 | 291.52 | 2716 | 96.76 | 193.56 | 177.36 | 214.08 |
| 5 | 1545 | 1865 | 717.5 | 127.15 | 364.4 | 3395 | 120.95 | 241.95 | 221.7 | 267.6 |
| 6 | 1854 | 2238 | 861 | 152.58 | 437.28 | 4074 | 145.14 | 290.34 | 266.04 | 321.12 |
| 7 | 2163 | 2611 | 1004.5 | 178.01 | 510.16 | 4753 | 169.33 | 338.73 | 310.38 | 374.64 |
| 8 | 2472 | 2984 | 1148 | 203.44 | 583.04 | 5432 | 193.52 | 387.12 | 354.72 | 428.16 |
| 9 | 2781 | 3357 | 1291.5 | 228.87 | 655.92 | 6111 | 217.71 | 435.51 | 399.06 | 481.68 |
| 10 | 3090 | 3730 | 1435 | 254.3 | 728.8 | 6790 | 241.9 | 483.9 | 443.4 | 535.2 |
| n | R1(PF) | R1/2(PF) | R−1/2(PF) | R−1(PF) |
|---|---|---|---|---|
| 1 | 373 | 149.95 | 26.53 | 11.83 |
| 2 | 746 | 299.9 | 53.06 | 23.66 |
| 3 | 1119 | 449.85 | 79.59 | 35.49 |
| 4 | 1492 | 599.8 | 106.12 | 47.32 |
| 5 | 1865 | 749.75 | 132.65 | 59.15 |
| 6 | 2238 | 899.7 | 159.18 | 70.98 |
| 7 | 2611 | 1049.65 | 185.71 | 82.81 |
| 8 | 2984 | 1199.6 | 212.24 | 94.64 |
| 9 | 3357 | 1349.55 | 238.77 | 106.47 |
| 10 | 3730 | 1499.5 | 265.3 | 118.3 |
6. Conclusion
In this article, the M-polynomial of phenol formaldehyde was found, and then, degree-dependent topological indices were calculated. These topological indices will be helpful for the preparation of electronic devices such as buttons, knobs, cameras, and vacuum cleaners. The numerical values that are found in this manuscript are valuable for betterment synthetic production and quality on a commercial base. For the assessment of the production, quality is easily measured by these numerical values.
Conflicts of Interest
The authors declare no conflicts of interest.
Acknowledgments
This paper is funded by Md. Ashraful Alam and M. K. Pandit of Jahangirnagar University, Savar, Dhaka, Bangladesh.
Open Research
Data Availability
No data availability for this research.