[Retracted] On Development of Neutrosophic Cubic Graphs with Applications in Decision Sciences
Abstract
In this study, the neutrosophic cubic graphs are further developed. We discussed and explored the open and the closed neighborhood for any vertex in neutrosophic cubic graphs, regular and totally regular neutrosophic cubic graphs, complete neutrosophic cubic graphs, balanced and strictly balanced neutrosophic cubic graphs, irregular and totally irregular neutrosophic cubic graphs, complement of a neutrosophic cubic graph, neighborly irregular and neighborly totally irregular neutrosophic cubic graphs, and highly irregular neutrosophic cubic graphs. It has been demonstrated that the proposed neutrosophic cubic graphs are associated with specific conditions. The comparison study of the proposed graphs with the existing cubic graphs has been carried out. Eventually, decision-making approaches for handling daily life problems such as effects of different factors on the neighboring countries of Pakistan and selection of a house based on the notions of proposed graphs are presented.
1. Introduction
A human being has a higher position among all the creatures due to his ability to analyze and make decisions. The decisions are made by carefully scrutinizing the problem based on the experience and the current situation. In the past, this used to be a mental activity with its successful execution. With the advancement of science and technology, it is now possible to use some modern techniques to address this problem better. These methodologies rely on traditional knowledge virtually. The ability of humans has been mimicked out effectively by making use of artificial intelligence. Some artificial intelligence techniques have been used successfully to chalk out good decisions. In this approach, various instruments related to decision-making are used. There is a well-known approach called graph theory. Graph theory is the systematic and logical way to analyze and model many applications related to science and other social issues. Graph theory is an essential tool and has played a significant role in developing graph algorithms in computer-related applications. These algorithms are quite helpful in solving theoretical aspects of the problems. These techniques help in solving geometry, algebra, number theory, topology, and many other fields. But many issues are not practically solvable due to the crisp nature of the classical sets. So in 1965, Zadeh [1] introduced the notion of the fuzzy subset of a set. Many other extensions of fuzzy sets have been developed so far like interval-valued fuzzy sets [2] by Zadeh, intuitionistic fuzzy sets [3, 4] by Atanassov, and cubic sets [5, 6] by Jun et al. In [7], Akram et al. developed cubic KU-subalgebras. Smarandache extended the concept of Atanassov and gave the idea of neutrosophic sets [8, 9], and interval neutrosophic sets were introduced by Wang et al. [10]. Jun et al. gave the idea of a neutrosophic cubic set [11]. Rosenfeld [12] developed the fuzzy graphs in 1975. Bhattacharya [13] had started contributing in fuzzy graphs in 1987. Arya and Hazarika [14] developed functions with closed fuzzy graphs. Bhattacharya and Suraweera [15] had developed an algorithm to compute the supremum of max-min powers and a property of fuzzy graphs. Bhutani [16] studied automorphisms of fuzzy graphs. Cerruti [17] used graphs and fuzzy graphs in fuzzy information and decision processes. Chen [18] discuss matrix representations of fuzzy graphs. Crain [19] studied characterization of fuzzy interval graphs. After that, many others contributed to fuzzy graph’s theory like Mordeson and Nair’s contribution [20], Gani and Radha [21], Rashmanlou and Pal [22], Nandhini and Nandhini [23], Elmoasry et al. [24], and Akram et al. [25–27]. Other contributions are from Gani and Latha [28], Poulik et al. [29–32], Borzooei and Rashmanlou [33], Buckley [34], Rashmanlou and Pal [35], Mishra et al. [36], Pal et al. [37], Pramanik et al. [38, 39], Shannon and Atanassov [40], Parvathi et al. [41, 42], and Sahoo and Pal [43]. Akram [44, 45] initiated the concept of bipolar fuzzy graphs. Many others contributed on bipolar fuzzy graphs, like Rashmanlou et al. [46], Akram and Karunabigai [47], and Samanta and Pal [48]. Graphs in terms of neutrosophic’s set have been studied by Huang et al. [49], Naz et al. [50], Dey et al. [51], Broumi et al. [52], and Karaaslan and Dawaz [53]. Zuo et al. [54] discussed picture fuzzy graphs. Kandasamy et al. and Smarandache [55, 56] developed neutrosophic graphs for the first time. Broumi et al. [57–61] discussed different versions of neutrosophic graphs. More development on the neutrosophic graphs can be seen in [50, 62–64]. After reading the extensive literature at neutrosophic graphs, recently, Gulistan et al. [65] discussed the cubic graphs with the application, neutrosophic graphs, and presented the idea of neutrosophic cubic graphs and their structures in their work [66, 67].
To further extend the work of Gulistan et al. [66, 67], in this paper we developed different types of neutrosophic cubic graphs including balanced, strictly balanced, complete, regular, totally regular, and irregular neutrosophic cubic graphs and complement of neutrosophic cubic graphs. Also, we established an open and close neighborhood of a vertex for neutrosophic cubic graphs and their application to the art of decision-making. The properties related to these newly suggested neutrosophic cubic graphs are also shown and how they are correlated. The arrangements of the paper are as follows: Section 2 is a review of basic concepts with their properties of neutrosophic cubic graphs. Section 3 describes different types of neutrosophic cubic graphs with examples. We also provide some results related to different types of neutrosophic cubic graphs. We present applications and a decision-making technique in Section 4. In Section 5, we provide a comparative analysis. Conclusions and suggested future work are presented in Section 6.
2. Preliminaries
This section consists of two parts: notations and predefined definitions.
2.1. Notations
Some notations with their descriptions are given in Table 1.
| S.no | Notation | Description |
|---|---|---|
| 1 | G | An arbitrary graph |
| 2 | A | Vertex set for G graph |
| 3 | B | Edge set for G graph |
| 4 | FG | Fuzzy graph |
| 5 | θ | Degree |
| 6 | ℘ | Density |
| 7 | α | Membership function for vertex set in FG |
| 8 | β | Membership function for edge set in FG |
| 9 | N | Neighborhood |
| 10 |
|
Represents an interval [al, ar] with 0 ≤ al ≤ ar ≤ 1 |
| 11 |
|
Neutrosophic cubic set |
| 12 |
|
Neutrosophic cubic graph |
| 13 | Φ | Membership function for vertex set in |
| 14 | Ψ | Membership function for edge set in . |
| 15 |
|
Fuzzy neighborhood of a vertex g in FG |
| 16 | ℕncg(g) | Open neighborhood for any vertex g in |
| 17 | ℕncg[g] | Closed neighborhood for any vertex g in |
2.2. Predefined Definitions
In this subsection, we added some important definitions which are directly used in our work.
Definition 1 (see [66].)A neutrosophic cubic graph for a crisp graph G = (A, B) is a pair with
3. Different Types of Neutrosophic Cubic Graphs
This section contains definitions for different neutrosophic cubic graphs with a good discussion on some of their related results.
3.1. The Open and the Closed Neighborhood for Any Vertex in
In this subsection, we present the idea of open neighborhood ℕncg(g), degree of open neighborhood θ(ℕncg(g)), and closed neighborhood degree of neutrosophic cubic graph .
Definition 2. An open neighborhood ℕncg(g) for any vertex g in is given by
where
It consists of membership functions for all vertices adjacent to g, excluding s.
Definition 3. The degree of open neighborhood θ(ℕncg(g)) for any vertex g in is defined by
Example 4. Let G = (A, B) with vertices A = {g1, g2, g3} and edges B = {g1g2, g2g3, g1g3}. Also, such that
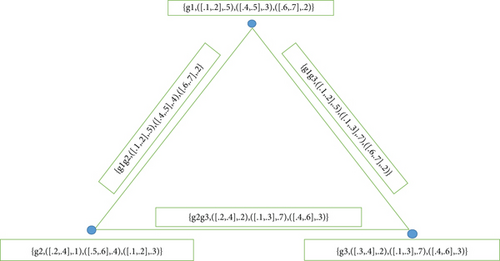
Definition 5. A closed neighborhood degree for a vertex g in is given by
It consists of the sum of membership functions of all vertices adjacent to x and membership function of x.
Example 6. Consider Example 4, closed neighborhood degree θ(ℕncg[g]) for each element g ∈ A in is given by
3.2. Regular and Totally Regular Neutrosophic Cubic Graphs
In this subsection, we present the idea of regular and totally regular neutrosophic cubic graphs based on the open neighborhood degree and closed neighborhood degree.
Definition 7. If every vertex in has the same open neighborhood degree n, i.e., if θ(ℕncg(g)) = n, for all g ∈ A, then is called an n regular neutrosophic cubic graph.
Definition 8. If closed neighborhood degree is the same for all vertices in , i.e., if θ(ℕncg[g]) = m, for all g ∈ A, then is called an m-totally regular neutrosophic cubic graph.
Example 9. Consider Example 4; here, is a totally regular but not a regular neutrosophic cubic graph.
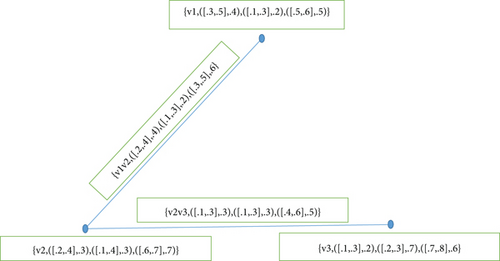
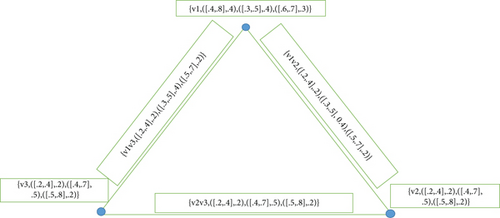
Example 10. Consider for any graph G = (A, B) with A = {v1, v2, v3}, B = {v1v2, v2v3, v1v3} and let
As θ(ℕncg(v1)) = θ(ℕncg(v2)) = θ(ℕncg(v3)) also θ(ℕncg[v1]) = θ(ℕncg[v2]) = θ(ℕncg[v3]). Hence, is regular, also totally regular neutrosophic cubic graph, as shown in Figure 2.
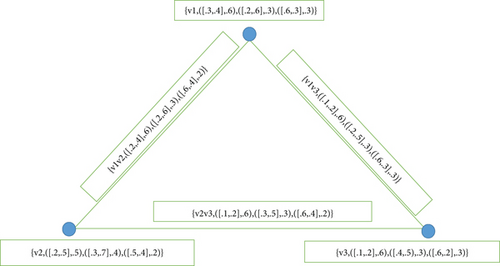
Example 11. Let be a neutrosophic cubic graph of G = (A, B) with A = {v1, v2, v3}, B = {v1v2, v2v3, v1v3} such that Γ and Λ are given by Tables 2 and 3.

| Γ = | A |
|
αT |
|
αI |
|
αF |
| v1 | [.3.5] | .4 | [.1.3] | .2 | [.5.6] | .5 | |
| v2 | [.2.4] | .3 | [:1.4] | .3 | [.6.7] | .7 | |
| v3 | [.1.3] | .2 | [:2.3] | .7 | [.7.8] | .6 |
| Λ = | B |
|
βT |
|
βI |
|
βF |
| v1v2 | [.2.4] | .4 | [.1.3] | .2 | [.3.5] | .6 | |
| v2v3 | [.1.3] | .3 | [.1.3] | .3 | [.4.6] | .5 |
Since θ(ℕncg(v1) ≠ θ(ℕncg(v2)) although θ(ℕncg(v1)) = θ(ℕncg(v3)), so is not regular as well as totally regular as shown in Figure 3.
Theorem 12. Let be a neutrosophic cubic graph of G, with Γ showing for vertex set A and Λ is for edge set B. Then,
- (I)
is regular
- (II)
is totally regular
Proof. Suppose
(I)⇒(II) Let be a regular, then θ(ℕncg(g)) = n for all g ∈ A. So,
Hence, for all g ∈ A, we have
Thus,
(II)⇒(I) Suppose that is totally regular. Then, for all g ∈ A,
Let
Then,
a constant no for every g ∈ A. Hence,
for all g ∈ A is a constant function.
Theorem 13. Consider as a neutrosophic cubic graph with crisp graph G of an odd cycle. Then, is regular if and only if Λ is a constant function.
Proof. Let
be a constant function for all xy ∈ B. Then,
Now,
Since G is an odd cycle, is regular. Conversely, suppose that is an n- regular, where
Let e1, e2, e3, ⋯, e2n+1 be edges of in that order. Let
This implies
So, if e1 and e2n+1 are incident at a vertex v1, then
Hence,
Thus, So, if e2 and e2n are incident at a vertex v2, then
Hence,
and so, k2 = n2t/2, which shows that is a constant function.
Similar results hold for membership functions . This shows that
is a constant function.
3.3. Complete Neutrosophic Cubic Graphs
In this subsection, we present complete neutrosophic cubic graph .
Definition 14. Consider be a neutrosophic cubic graph for any arbitrary graph G = (A, B). Then, is complete if
Example 15. Consider for a graph G = (A, B) with A = {v1, v2, v3}, B = {v1v2, v2v3, v1v3} and let
Also,
Definition 16. Let be a neutrosophic cubic graph for some graph G = (V, E). The density of is defined as
Example 17. Consider for a graph G = (A, B), with vertex set A = {v1, v2, v3} and edge set B = {v1v2, v2v3, v1v3}. Also, let Γ and Λ be neutrosophic membership functions for vertices and edges, respectively, shown in Tables 4 and 5.
| Γ = | A |
|
αT |
|
αI |
|
αF |
| v1 | [.1.5] | .6 | [.5.7] | 1 | [.6.7] | .9 | |
| v2 | [.2.6] | .5 | [.6.8] | .8 | [.7.8] | .8 | |
| v3 | [.3.7] | .8 | [.7.8] | .7 | [.5.6] | .7 |
| Λ = | B |
|
βT |
|
βI |
|
βF |
| v1v2 | [.1.2] | .5 | [.4.5] | .4 | [.5.6] | .2 | |
| v2v3 | [.2.4] | .2 | [.1.3] | .5 | [.4.5] | .3 | |
| v1v3 | [.1.2] | .5 | [.1.3] | .6 | [.4.6] | .2 |
3.4. Balanced and Strictly Balanced Neutrosophic Cubic Graphs
In this subsection, we use the density function ℘ to discuss the idea of balanced and strictly balanced neutrosophic cubic graph .
Definition 18. is balanced if for all subgraphs H of .
Definition 19. is strictly balanced if for all nonempty subgraphs H of .
Example 20. Consider as given in Example 17. Let H1 = {a, b}, H2 = {a, c}, H3 = {b, c}. Then,
Hence,
Remark 21. All regular neutrosophic cubic graphs are not necessarily balanced.
3.5. Irregular and Totally Irregular Neutrosophic Cubic Graphs
In this subsection, we use the neighborhood degrees to discuss the idea of irregular and totally irregular neutrosophic cubic graph .
Definition 22. If there is at least one vertex in adjacent to vertices having different open neighborhood degrees, then is called irregular, i.e., if θ(ℕncg(v)) ≠ n for all v ∈ A.
Example 23. Consider for some graph G = (A, B), with A = {v1, v2, v3, v4} and
Hence, is irregular as shown in Figure 5.
Definition 24. A connected is totally irregular, if at least one vertex is adjacent to the vertices having different closed neighborhood degrees.
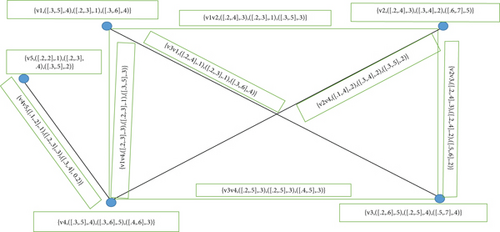
Example 25. Consider for G = (A, B), with
and let
Then,
Clearly, is totally irregular as in Figure 6.
3.6. Complement of a Neutrosophic Cubic Graph
Complement of a neutrosophic cubic graph is a very important concept we discuss here.
Definition 26. The complement of is a neutrosophic cubic graph where
similarly, for indeterminate membership functions, we have
Proposition 27. For self-complementary , we have
Proof. Given is self-complementary, so ; also, by definition of a self-complementary neutrosophic cubic graph, we have
Dividing both sides of equation (77) by min{Φ(x), Φ(y)},
Hence,
Proposition 28. Let be strictly balanced, let be its complement, then
Proof. Let be strictly balanced; let be its complement. Let H be a nonempty subgraph of Since is strictly balanced, for every subset and for any x, y ∈ A. In , we have , and so, for truth membership functions, we have
Dividing equation (82) by , we get
Hence,
Multiplying both sides by 2,we get
Hence, . Similarly for right end point of interval in truth valued membership functions, we have . Similar results hold for the rest of membership functions. Hence,
This completes the proof.
3.7. Neighborly Irregular and Neighborly Totally Irregular Neutrosophic Cubic Graphs
In this subsection, we use the neighborhood degrees to discuss the idea of neighborly irregular and neighborly totally irregular neutrosophic cubic graphs.
Definition 29. A connected is neighborly irregular if every two adjacent vertices in have different closed neighborhood degrees.
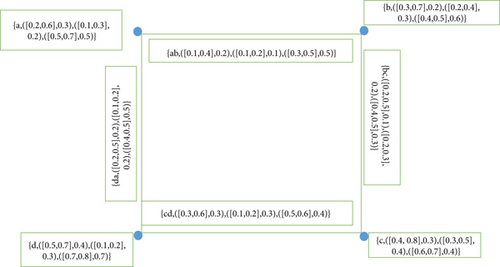
Example 30. Consider for any G = (A, B) with A = {a, b, c, d} and B = {ab, bc, cd, da} and let neutrosophic cubic membership functions for vertices and edges be represented in Tables 6 and 7, respectively.
| Γ = | A |
|
αT |
|
αI |
|
αF |
| a | [.2.6] | .3 | [.1.3] | .2 | [.5.7] | .5 | |
| b | [.3.7] | .2 | [.2.4] | .3 | [.4.5] | .6 | |
| c | [.4.8] | .3 | [.3.5] | .4 | [.6.7] | .4 | |
| d | [.5.7] | .4 | [.1.2] | .3 | [.7.8] | .7 |
| Λ = | B |
|
βT |
|
βI |
|
βF |
| ab | [.1.4] | .2 | [.1.2] | .1 | [.3.5] | .5 | |
| bc | [.2.5] | .1 | [.2.3] | .2 | [.4.5] | .3 | |
| cd | [.3.6] | .3 | [.1.2] | .3 | [.5.6] | .4 | |
| da | [.2.5] | .2 | [.1.2] | .2 | [.4.5] | .5 |
Then, clearly is neighborly irregular, as shown in Figure 7.
Definition 31. is said to be neighborly totally irregular if every two adjacent vertices of have different closed neighborhood degrees.
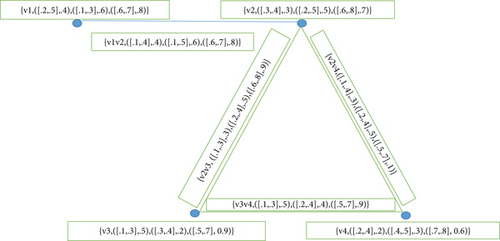
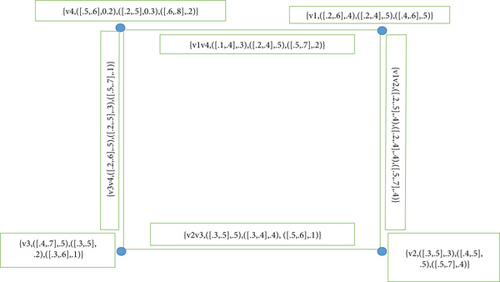
Example 32. Consider for any G = (A, B) with A = {v1, v2, v3, v4} and B = {v1v2, v2v3, v3v4, v1v4}. Also, let
Then, clearly is neighborly totally irregular, as shown in Figure 8.
3.8. Highly Irregular Neutrosophic Cubic Graphs
In this subsection, we use the neighborhood degrees to discuss the idea of highly irregular neutrosophic cubic graphs.
Definition 33. Consider a connected ; then, is highly irregular if every vertex in is adjacent to vertices with different neighborhood degrees.
Example 34. Consider for a graph G = (A, B) with A = {v1, v2, v3, v4, v5, v6} and B = {v1v2, v2v3, v2v6, v3v4, v3v5, v4v5, v1v5} and let
By routine computations, we have
Clearly, as shown in Figure 9 is highly irregular.
Theorem 35. is highly irregular and neighborly irregular if and only if open neighborhood degrees for all vertices of are different.
Proof. Suppose has n vertices v1, v2, ⋯, vn. Also, let be highly irregular and neighborly irregular.
Claim 1. The open neighborhood degrees for all vertices in are different. Let
for all i = 1, 2, 3, ⋯, n. Let the adjacent vertices of v1 be v2, v3, ⋯, vn with open neighborhood degrees:
Claim 2. is highly irregular and neighborly irregular. Let
Remark 36. A complete may not be neighborly irregular.
Example 37. Let for any G = (A, B), with A = {v1, v2, v3} and B = {v1v2, v2v3, v1v3} such that
By simple computation, we get
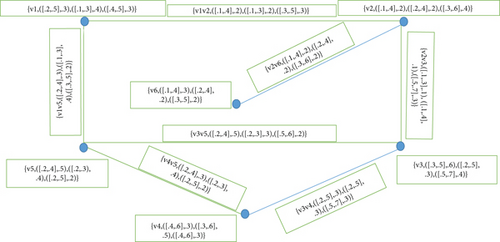
Here, θ(ℕncg(v2)) = θ(ℕncg(v3)), so the neighborhood degree is not different. Hence, is not neighborly irregular; also, we have similar holds for all vertices and edges. So, is complete. Hence, a complete may not be neighborly irregular as shown in Figure 10.
Theorem 38. If is neighborly irregular and
Proof. Assume that is a neighborly irregular. Then, open neighborhood degrees of every two adjacent vertices are different. Let vi, vj ∈ A be adjacent vertices with different open neighborhood degrees. Then, θ(ℕncg(vi)) ≠ θ(ℕncg(vj)) for all i ≠ j; let θ(ℕncg(vi)) = d1&θ(ℕncg(vj)) = d2 then d1 ≠ d2. Also, as
Hence,
Theorem 39. If is neighborly totally irregular and
Proof. Assume that is a neighborly totally irregular. Then, closed neighborhood degrees of every two adjacent vertices are distinct. Let vi, vj ∈ A be adjacent vertices with distinct closed neighborhood degrees. Then, for all i ≠ j,
Proposition 40. If is neighborly irregular as well as neighborly totally irregular, then
Remark 41. If is neighborly irregular, then a neutrosophic cubic subgraph H of may not be neighborly irregular.
Remark 42. If is neighborly totally irregular, then a neutrosophic cubic subgraph H of may not be neighborly totally irregular.
4. Applications
As neutrosophic cubic graph theory is a developing field of modern mathematics, it has many applications in different fields. In this section, we discuss applications of neutrosophic cubic graphs in finding the effects of different factors in the neighboring countries of Pakistan. Further, we used our proposed model in decision-making while selecting a house in a certain locality.
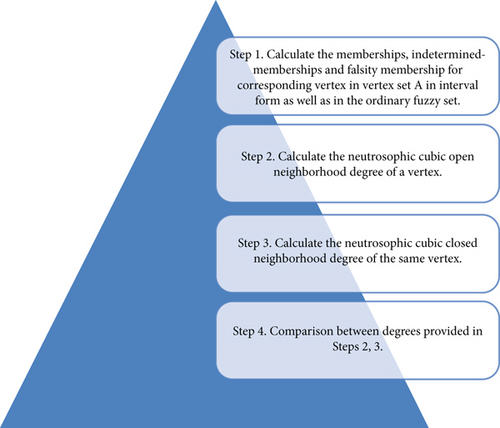
We will use the following proposed algorithm in the following real-life problems.
Step 1. Calculate the memberships, indetermined-memberships and falsity membership for corresponding vertex in vertex set A in interval form as well as in the ordinary fuzzy set.
Step 2. Calculate the neutrosophic cubic open neighborhood degree of a vertex.
Step 3. Calculate the neutrosophic cubic closed neighborhood degree of the same vertex.
The frame diagram to clarify the organization of the proposed method is given in Figure 11.
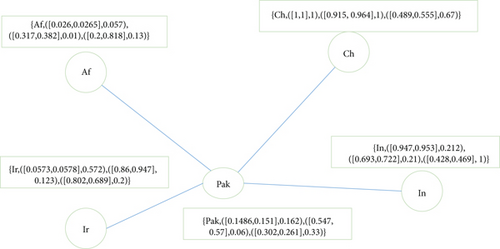
4.1. Effects of Different Factors on the Neighboring Countries of Pakistan
- (i)
Pop represents interval membership for the population of a country in the duration (1st July 2018, 1st July 2019)/max population of the corresponding country in the same duration. Here, interval represents past and future to represent truth membership and indetermined-membership for members of the vertex set A
- (ii)
PCI is for per capita income of a country which represents falsity membership for the corresponding vertex in vertex set A
- (iii)
LR represents interval membership for literacy rate of a country in the duration [2011, 2014]. Here again, we have interval to represent past and future for truth membership and indetermined-memberships for members of vertex set A
- (iv)
WTRU is the position of the corresponding country in the world’s top-ranking universities/max number of universities in these countries
- (v)
HE represents interval membership for %age of health expenditure of a country in the duration [2010, 2015] where interval shows past and future to represent truth membership and indetermined-membership for members of vertex set A
- (vi)
PSI is the number of popular sports interest/max number of sports played in the corresponding country as health depends on sports
By data collection for different time intervals, we have neutrosophic cubic membership for vertex set A represented in Table 8.
| A | Pop [past, future] | PCI (present) | LR [past, future] | WTRU (present) | HE [past, future] | PSI (present) |
|---|---|---|---|---|---|---|
| Af | [.026.026] | .06 | [.32.38] | .01 | [.92.82] | .13 |
| Ch | [1, 1] | 1 | [.92.96] | 1 | [.49.55] | .67 |
| In | [.94.95] | .212 | [.69.72] | .21 | [.43.47] | 1 |
| Ir | [.057.058] | .57 | [.86.95] | .123 | [.81.69] | .2 |
| Pak | [.148.151] | .162 | [.55.57] | .06 | [.31.26] | .33 |
The neutrosophic cubic open neighborhood degree of a vertex (say Pak) is less than the neutrosophic cubic closed neighborhood degree of a vertex (say, Pak). Thus, we may conclude that the vertex (say, Pak) has more closed neighborhoods than the open neighborhoods that can change their loyalties according to time as shown in Figure 12. Similarly, we may check other countries.
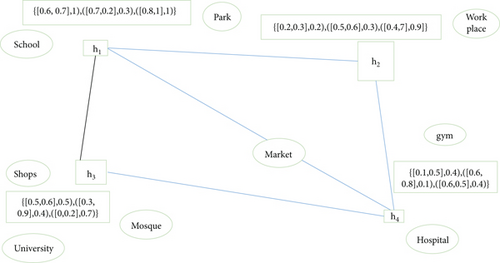
4.2. Decision-Making while Selecting a House
We compare neutrosophic cubic open neighborhood and observe that neutrosophic cubic open neighborhood of h2 and h3 is the same, but comparison of neutrosophic cubic open neighborhood of h1 and h4 shows that h1 and h4 are more effective than h2 and h3. Also, we observe that neutrosophic cubic open neighborhood of h4 is effective than h1. Moreover, one can observe that the neutrosophic cubic closed neighborhood degree of houses h1 and h4 is the same, but in view of neutrosophic cubic open neighborhood, h4 is the best choice in all respects as compared to other houses h2 and h3. So, choice of house h4 is the best choice for our selection of an ideal house. Position of four houses with different facilities is shown in Figure 13.
5. Comparison Analysis
In this paper, our focus is to introduce some different types of neutrosophic cubic graphs. These include balanced, strictly balanced, complete, regular, totally regular, and irregular neutrosophic cubic graphs. In this regard, we explained the open and closed neighborhood of a vertex of the neutrosophic cubic graph and its role in the art of decision-making. Many of these graphs have already been discussed from a different perspective by the other researchers, for example, Poulik et al. [29–32], Akram [44, 45], and Gulistan et al. [65]. We have tried to discuss them concerning the neutrosophic cubic graphs. The neutrosophic cubic graphs are the generalization of different versions of the fuzzy graph which is extended to the neutrosophic cubic graph. The idea is summarized in the form of a flow chart (Figure 14).
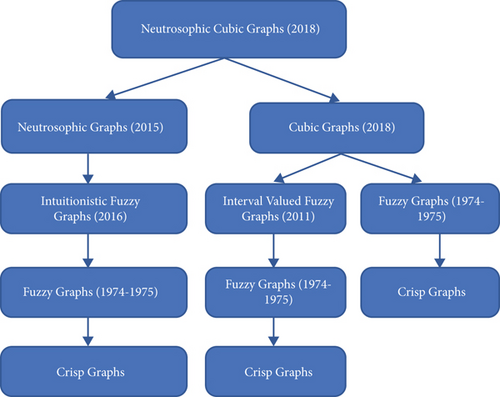
This flow chart shows under certain conditions neutrosophic cubic graphs reduced to crisp graphs. So, under certain conditions, all the different types described are reduced for neutrosophic graphs, cubic graphs, intuitionistic graphs, fuzzy graphs, and crisp graphs.
6. Conclusion and Future Work
In this article, we provided different types of neutrosophic cubic graphs with examples and give many results which correlate with these neutrosophic cubic graphs. We used the idea of the neutrosophic cubic open neighborhood degree and neutrosophic cubic closed neighborhood degree of the same vertex in two real-life problems. We concluded the following: (1) As the neutrosophic cubic open neighborhood degree of a vertex (say Pak) is less than the neutrosophic cubic closed neighborhood degree of a vertex (say, Pak), the vertex (say, Pak) has more closed neighborhoods than the open neighborhoods. (2) Also, we observe that house h4 is the best choice for our selection of an ideal house using the idea of neutrosophic cubic open neighborhood degree and neutrosophic cubic closed neighborhood degree of the same vertex. The limitation of the presented method is the data collection which is not an easy task. In the future, we aim to make more different types of graphs such as line, planer, and directed neutrosophic cubic graphs. We are also aiming to have more real-life applications of neutrosophic cubic graphs.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
The authors express their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Public Research Project under Grant Number (R.G.P.1/208/41).
Open Research
Data Availability
There is no data related to this article.




