The main objective of this research study is to amplify the schematic representation of human reasoning by launching the most generalized fantastic theories of bipolar type-2 fuzzy set (BT2FS) and bipolar type-2 fuzzy soft set (BT2FS _f S). These incredible models are exclusively developed for the simultaneous capturing of both polarity and abstruseness inherent in equivocal interpretations. The proposed BT2FS _f S theory renders an outstanding parameterized framework that skilfully wipes out the high-order uncertainty of imprecise knowledge-based systems. First, we keenly provide the formal structure of both proposed models along with the deep exploration of their elementary properties. Moreover, we explore rudimentary set-theoretical operations of developed frameworks inclusive of equality, subset, complement, union, and intersection with their noticeable results. We brilliantly formulate a highly proficient algorithm using proposed theory to disentangle the real-world multiattribute decision-making conundrums with two-sided ambiguous information. Finally, we holistically scrutinize an empirical analysis for the selection best way to cultivate the dessert city to demonstrate the remarkable accountability of the proposed methodology.

1. Introduction

A modern trend in contemporaneous information processing focuses on bipolar information. Bipolarity is important to identify between positive information which acts for what is guaranteed to be possible and negative information which acts for what is impossible or prohibited [1, 2]. This generic domain has recently contributed in several directions, including knowledge representation, preference modeling, multicriteria decision analysis, argumentation, and many others disciplines of science and technology [2–14]. Akram et al. [15] skillfully developed graphical representations for the comprehensive analysis of bipolar fuzzy information and presented novel decision-making techniques for the scrutinization of real-world complexities. Ali et al. [16] introduced competent attributes reduction algorithms for bipolar fuzzy relation decision systems to properly investigate sophisticated decision-making problems. Akram et al. [17] admirably designed multiskilled TOPSIS and ELECTRE-1 methods equipped with bipolar fuzzy information and patently demonstrated its empirical application in medical diagnosis.

The theory of bipolar fuzzy sets (BFSs) and its various generalizations were investigated by many researchers and practitioners as they render such brilliant mathematical tools that skillfully address the double-sided or bipolar human vague annotations [14, 18–21]. Akram et al. [22] launched a modified version of PROMETHEE method by employing bipolar fuzzy information for the determination of best green supplier in the supply chain management system. Al-Qudah and Hassan [23] introduced bipolar fuzzy soft expert sets by the amalgamation of BFSs and soft expert sets and defined algebraic operations of union, intersection, and complement for the proposed bipolar fuzzy soft expert sets. Akram et al. [24] presented an advanced trapezoidal bipolar fuzzy TOPSIS method and dexterously illustrated its application for the selection of the best construction project proposal.

All the contemporary approaches have a common limitation that arises because of their nonparameterized modeling capabilities. To overcome this problem, Molodtsov [25] developed an advanced novel theory of soft sets (S _f Ss) that integrates parametrization for the specification of the expertise of rational alternatives. One of the most important applications that are mentioned in this theory is the evaluation of many practical problems in engineering, economics, medical science, social science, and in various other modern directions. Later, Maji [26] has further studied the theory of S _f Ss for the proper examination of some complex realistic problems. Maji [27] explored some fundamental properties of S _f Ss and also defined its algebraic operations inclusive of restricted and extended union, intersection, and difference. Chan [28], Zou and Xiao [29], Ali [30], Kong [31], Cagman and Enginoglu [32, 33], and many other pedagogues contributed to the development and improvement of the S _f S theory. Moreover, Maji [34] combined the proficient theories of both S _f Ss and fuzzy sets and developed an innovative concept of fuzzy soft sets (FS _f Ss). Akram et al. [35] admirably proposed a hybrid theory of bipolar fuzzy N-soft sets and established the TOPSIS method under such a versatile environment for the robust inspection of its high potential applications.

Zadeh [36] proposed an entirely new theory of fuzzy sets for capturing the imprecision of obscure data with the assistance of a MF (MF) that can grab values from the closed unit interval. The traditional fuzzy sets are also called type-1 fuzzy sets [37]. The most important application in FS _f Ss is the investigation of actual decision-making perplexities [38–40]. Later, Zadeh [41–43] introduced the notion of a type-2 fuzzy set (T2FS) in which the membership degree of each element is given by another type-1 fuzzy set defined over the interval [0,1]. It can also be generalized from type-1 FS _f Ss to type-2 FS _f Ss. Matsumoto and Tanaka [44, 45] discussed some elementary algebraic properties of T2FSs. Dubois and Prade [46] remarkably presented several notions and applications of T2FSs. Later, many researchers conducted a lot of theoretical work on the properties of T2FS and manifested its many pragmatic applications [47–50]. Type-2 fuzzy sets were applied in several domains, especially in decision-making [51], connection admission control [52], mobile robotic control [53], equalization of nonlinear fading channels [54–57], extraction of knowledge from questionnaire surveys [52, 58], forecasting of time-series [57, 59, 60], function approximation [58], learning linguistic membership grades [61], preprocessing radiographic images [62], relational databases [63], solving fuzzy relation equations [64], and transport scheduling [65]. Zhang and Zhang [66] considered type-2 FS _f Ss with applications.

In several tricky practical applications, we often face an intricate situation during evaluation processes in which stipulated parameters are highly equivocal. It can be represented by fuzzy sets rather than exact numerical values, intervals, and interval-valued intuitionistic fuzzy numbers. Obviously, it is very difficult for the classical S _f S and its contemporary extensions to deal with such arduous problems. Therefore, it is necessary to extend the soft set theory for the accommodation of problematic scenarios in which the specified evaluation parameters are totally ambiguous in nature. The purpose of this paper is to further generalize the concept of type-2 fuzzy sets and type-2 FS _f Ss to BT2FSs and bipolar type-2 S _f Ss, respectively. Now, we present the highly competent novel theories of BT2FSs and BT2FS _f Ss and define some basic operations on them. Moreover, we also examine the applications of BT2FSs and BT2FS _f Ss and weighted type-2 FS _f Ss in decision-making problems.

The rest of this paper is organized as follows. Section 2 recollects some relevant studies of the literature. Section 3 explicates the novel theory of BT2FSs, its elementary properties, and some algebraic operations inclusive of union, intersection, and complement. Section 4 presents an advanced concept of BT2FS _f Ss and discusses its basic algebraic operations along with some fundamental characteristics. Section 5 illustrates the applications of BT2FSs, BT2FS _f Ss, and weighted BT2FS _f Ss in decision-making problems. Section 6 explores some concluding remarks and future research directions.

2. Preliminaries

In this section, we shall review the concepts of S _f S, fuzzy soft set, BFS and bipolar fuzzy soft set.

Definition 1 (see [25].)Let E be a set of parameters and let Let F be a mapping defined by

(1)

where P(ℚ) is a collocation of all subsets of the initial universal set ℚ. Then, the pair

is a S _f S.

Definition 2 (see [67], [68].)Let be a subset of parameters set. Let P_F(ℚ) be a collocation of all fuzzy subset of the initial universal set ℚ and let F be a mapping defined by

(2)

Then, we call the pair is a FS _f S over ℚ.

Definition 3. A BFS on U is an object having the form

(3)

where

represent positive information and

represents negative information.

Definition 4. Let pair be a bipolar FS _f S over initial universal set ℚ, where is a parameters set and F_b is a mapping such that

(4)

where BF(ℚ) illustrates all bipolar fuzzy subsets of ℚ.

Definition 5. is called a T2FS over initial universe ℚ if it is characterized by a secondary MF where is primary membership value of an element such that Thus we define the set by

(5)

or by

(6)

Take into account the symbol ∫∫ denotes union over all and and + also denotes union [69].

3. Bipolar Type-2 Fuzzy Set

In this section, we present a new concept of BT2FS, its operations, and some of its basic fundamental properties.

Definition 6. Let ℚ be the initial universal set. Then is called a BT2FS if it is characterized by a pair where and represents positive and negative secondary MF of respectively, and denotes the primary membership value of an element such that Then, the set is defined by

(7)

The set of all BT2FSs in ℚ is denoted by BF_T2.

Remark 7. The notion ∫ denotes union over all admissible and and + also denotes union [70].

To clarify the concept of BT2FS, let us consider the following example.

Example 1. Let be the initial universal set and let be a BT2FS defined as

(8)

Graphical representation is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Bipolar type-2 fuzzy sets.

Suppose

then

(9)

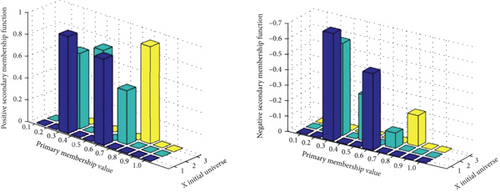
Definition 8. For two BT2FSs and of ℚ, we say that is a bipolar type-2 fuzzy (BT2F) subset of if and only if

(i)
(ii)
for a positive secondary MF
(iii)
for a negative secondary MF

where

is a primary membership value of

and v is a primary membership value of

Example 2. Consider two sets of BF_T2 “used in Example 1” and define

(10)

So, is a BT2F subset of

Remark 9. and two BF_T2 sets of ℚ are said to be equal, if is a BT2F subset of and is a BT2F subset of

3.1. Operations of BF_T2

In this section, we dialogue three essential arithmetic operations inclusive of complement, union, and intersection of BF_T2.

(1)
Complement: the complement of a BF_T2 is denoted and defined by
(11)
(2)
Union: let , so we defined the union of and by :
(12)
where ; ∨ is a maximum and ∧ is a minimum.
(3)
Intersection: let , so defined the intersection of and by :
(13)
where ; and where

Example 3. Let us consider two BF_T2 of the initial universe ℚ as

(14)

then

(15)

3.2. Properties

Consider three BF_T2 sets

, and

(16)

Example 4. Reconsider Example 3 and let defined by

(17)

Thus, we have

(18)

We also have

(19)

So, we obtain

(20)

Then, we deduce

(21)

Indeed

(22)

Theorem 10. If BT2F is a subset of and BT2F a subset of then BT2F is a subset of

Proof. Suppose that BT2F subset of thus for primary membership values and for, respectively, positive and negative secondary membership functions of and suppose that BT2F subset of thus v ≤ w for primary membership values and for, respectively, positive and negative secondary membership functions of

Therefore, , and

Hence, BT2F is a subset of

Theorem 11. If BT2FS is equal to and BT2FS is equal to then BT2FS is equal to

Proof. Same proof as Theorem 10.

4. Bipolar Type-2 Fuzzy Soft Set

Throughout this section, we call ℚ is an initial universe set, E is a set of all possible parameters under consideration with respect to ℚ, BF_T2(ℚ) is all BT2FSs of ℚ, v, and w be primary membership degrees, and are, respectively, the positive and negative secondary MF of ℚ.

Definition 12. Let be a set of parameters, and τ is a mapping given by

(23)

Then the pair is called a BT2FS _f S over ℚ, and BFS_T2(ℚ) refers to all BT2FS _f Ss over ℚ.

So far a BT2FS _f S is a parameterized family of BT2F subset of ℚ.

For any

τ(ξ) refers to the set of ξ-approximate element of the BT2FS _f S

it is actually a BT2FS on ℚ, and it can be written as

(24)

where

is the primary membership degree and

are, respectively, the positive and negative secondary membership degree that object

holds on parameter ξ.

Example 5. Consider a over ℚ, where ℚ is a set of four cars under the consideration of decision-maker to purchase and is a parameter set, where . The BT2FS _f S describes the “attractiveness of the cars” to this decision-maker.

Assume that

(25)

Definition 13. Let Let If and τ(ξ)⊆ψ(ξ) then is called a bipolar type-2 fuzzy soft (BT2FS _f) subset of

Remark 14. For are said to be equal, if and only if is BT2FS _f subset of and is BT2FS _f subset of

4.1. Operations on BFS_T2(ℚ)

In this section, we debate five operations, namely, complement, union, intersection, AND, and OR of a BFS_T2(ℚ). Let E = {ξ₁, ξ₂, ⋯, ξ_n} be a parameter set, and defined ¬E = {¬ξ₁, ¬ξ₂, ⋯, ¬ξ_n} where ¬ξ_i is not ξ_i and let

(1)
Complement
The complement of BT2FS _f S is defined by
(26)
where τ^c(ξ) = ¬(τ(¬ξ); for all
(2)
Union
Let the union of and is and defined it for all
(27)
(3)
Intersection
Let with the intersection of and is , defined by
(28)
(4)
AND
AND is defined by where for all
(5)
OR
OR is defined by which is φ(a, b) = τ(a)⊔ψ(b) for all

Example 6. Let E = {ξ₁, ξ₂, ξ₃} be a parameter set, and let and be subsets of E. Now consider two BT2FS _f Ss and over ℚ, where and define by

(29)

and

(30)

We will compute complement, union, intersection, AND, and OR of BFS_T2 sets.

(i)
The complement of BFS_T2 set is given
(31)
(ii)
The union of where is as follows since then
(32)
since then
(33)
since then
(34)
(iii)
The intersection of where is given
(35)
(iv)
A and = are as follows:
(36)
(v)
A or is as follows:
(37)

Proposition 15. Let and let Then, the following results hold:

(1)
and
(2)
and
(3)
(4)
(5)
(6)

Proof. Suppose that , where , so we deduce

(38)

This imply

(39)

And if we suppose

(40)

then we obtain

(41)

Hence

Suppose that , where

And also suppose

(42)

this imply

(43)

so, we deduce

(44)

Therefore

(45)

Hence,

Theorem 16. Let For If is BT2FS _f subset of and is BT2FS _f subset of thus is BT2FS _f subset of

Proof. Assume that is a BT2FS _f subset of over ℚ, then we have

(i)
(ii)

And also assume that is a BT2FS _f subset of over ℚ, then we get:

(i)
(ii)

Hence, is a BT2FS _f subset of over ℚ.

Theorem 17. Let For If and are equal and at the same time and are also equal, then and are equal.

Proof. Same proof as the previous theorem.

Definition 18. A null BT2FS _f S denoted is a BT2FS _f S over ℚ which is for all for all :

(46)

Definition 19. An absolute BT2FS _f S denoted is a BT2FS _f S over ℚ which is for all and for all :

(47)

Theorem 20. Let be a BFS_T2(ℚ). Let and be a null and absolute BT2FS _f S over ℚ, then

(i)
and
(ii)
(iii)

But and

Proof.

(i)
Suppose that is a null BT2FS _f S over ℚ, and define for all
(48)

So, we get defined by

(49)

Therefore

Same proof for

(ii)
Let be a BFS_T2(ℚ). Let be an absolute BT2FS _f S over ℚ. So, we have
(50)

Thus

(iii)
Let be a BFS_T2(ℚ). Let be a null BT2FS _f S over ℚ. So, we have
(51)

Thus,

Theorem 21. Let and be the two BFS_T2(ℚ), where Then the following equations hold:

(i)
(ii)

Proof.

(i)
Suppose that and are two BFS_T2(ℚ), we have
(52)

Then

On the other hand, we have

(53)

Therefore

(ii)
Suppose that and are two BFS_T2(ℚ), we have

(54)

Then

On the other hand, we obtain

(55)

Therefore,

Proposition 22. Let Let two BFS_T2(ℚ) sets and over ℚ. Then

(i)
(ii)

Proof.

(i)
Let two Then we get
(56)
since

Therefore, , where

On the other hand, we have

(57)

where

(ii)
In the same way.

As we noted earlier, the De Morgan’s laws does not hold. Thus, we can define two conditions under union and intersection operations.

Definition 23. For two BT2FS _f Ss and with over ℚ. Then the restricted union of and is the BT2FS _f S defined by

(58)

Definition 24. For two BT2FS _f Ss and over ℚ. Then the extended intersection of and is the BT2FS _f S , where defined by

(59)

Theorem 25. Let Let Then

(i)
(ii)

Proof.

(i)
For Then we have

(60)

Thus, we obtain

(61)

On the other hand, we obtain

(62)

we conclude that

(63)

(ii)
Can be done in the same way.

5. Application of BFS_T2 Set in Decision Making

Decision making is one of the most popular applications of S _f S theory which has a lot of applications in many practical problems. Maji et al. introduced the idea of S _f Ss for the evaluation of parameterized decision-making problems. Moreover, Roy and Maji presented an algorithm to solve the recognition problem by employing FS _f Ss. Subsequently, Kong et al. gave a counterexample to illustrate a fact that the optimal choice could not be obtained in general by using Roy and Maji’s algorithm and conferred a modified version. Feng et al. gave deeper insights into decision-making methods based on FS _f Ss. They conferred an adjustable approach for fuzzy-soft-set-based decision making by employing level S _f Ss. By generalizing the adjustable approach for fuzzy-soft-set-based decision making, Jiang et al. presented an adjustable approach for intuitionistic fuzzy-soft-set-based decision making and explore some illustrative examples.

In this section, we shall present an adjustable approach for BT2FS _f S-based decision-making problems. This technique is based on the concept of level S _f Ss.

Definition 26. Let Let be a BT2FS _f S over the initial universe ℚ. For γ ∈ [0, 1] and β ∈ [0, 1], the (γ, β)-level (the threshold) S _f S of is crisp soft set for all defined by

(64)

where

Definition 27. Let Let be a BFS_T2 set over ℚ. Let and be two fuzzy sets in which are two threshold fuzzy sets. Then, the level S _f S of with respect to γ and β is crisp soft set for all defined by

(65)

where

Definition 28. Let be a parameter set. Let be a BFS_T2 set over ℚ, and let be the weight function specifying the weight Λ_i = Λ(ξ_i) for all Then, the triple is a weighted BT2FS _f S.

5.1. Algorithm

Consider the following.

Step 1: Input a weighted BT2FS _f S

Step 2: Input two threshold fuzzy sets and for decision making.

Step 3: Compute the level S _f S of Γ w.r.t the two threshold fuzzy sets γ and β.

Step 4: Present the level S _f S in tabular form. For all compute the weighted choice value c of where

Step 5: The optimal decision is to select if

Step 6: If k has more than one value then any one of h_k may be chosen.

Example 7. Suppose that a company is planning to increase its green area in the center of a desert city, so by raising a large number of trees and plants, it will improve generally. There are two ways for the cultivation of area, one is the traditional way and the other one is by groasis technology Let there exist are four parameters E = {e₁, e₂, e₃, e₄} = {Temperature, Soilfertility, Humidity, Sunlight}. Assume that weight for the parameters in E: Λ₁ = Λ(ξ₁) = 0.2, Λ₂ = Λ(ξ₂) = 0.9, Λ₃ = Λ(ξ₃) = 0.7 and Λ₄ = Λ(ξ₄) = 0.4; and two threshold fuzzy sets γ : E⟶[0, 1] and β : E⟶[, 1] defined by

(66)

Consider bipolar type-2 FS _f S as follows:

(67)

The values are shown in Tables 1, 2

Table 1. Tabular representation of

ℚ	ξ₁, Λ₁ = 0.2	ξ₂, Λ₂ = 0.9	ξ₃, Λ₃ = 0.7	ξ₄, Λ₄ = 0.4

Table 2. Tabular representation of

with weighted choice value.

ℚ	ξ₁, Λ₁ = 0.2	ξ₂, Λ₂ = 0.9	ξ₃, Λ₃ = 0.7	ξ₄, Λ₄ = 0.4	Weighted choice value c_i
	0	0	1	1	c₁ = 1.1
	1	1	0	1	c₂ = 1.40

We deduced that weighted optimal choice value max_1≤i≤2{c_i} = c₂. Hence, be the required optimal choice.

6. Conclusion

In this research article, we have rapturously consummated our goal by establishing the ground-breaking incredible theories of BT2FS and BT2FS _f S. These flexible models are highly dexterous for addressing a comprehensive range of ambiguity embedded in bipolar human interpretations. The newly developed BT2FS _f S provides an outstanding mathematical framework that admirably integrates the specialities of novel BT2FS with the parametric nature of S _f S. The proposed theories have extrapolated the contemporary unipolar fuzzy structures because of their fantastic representational and reasoning potentialities. Firstly, we have explicated the systematic definitions of presented notions and discussed some of their fundamental properties. We have thrown light on some elementary set-theoretical operations for these emerging theories inclusive of equality, subset, complement, union and intersection. Another noteworthy contribution of this study is the development of a highly proficient MCDM algorithm for the specification of the best pragmatic alternative on the grounds of multiple rational parameters. Finally, we have skilfully implemented the proposed methodology on real-life heuristic application to demonstrate the versatility of our developed strategy. The presented frameworks have an edge over the already existing notions, as they remarkably decipher all the faults and shortcomings of recent approaches by capturing both polarity and abstruseness of paradoxical data set. Admittedly, our proposed models have some difficulties because of their limited one-dimensional modeling capabilities. Thus in the future, we are envisioning to amplify our research study for the two dimensional vague information by presenting the excellent frameworks of complex BT2FS and complex BT2FS _f S in order to design more advanced decision-making strategies. We intend to deliberate the scope of these decision-making approaches in the disciplines of artificial intelligence, medical sciences, logistics and aeronautical industries. Another goal is to unfold significant fusions of ELECTRE methods with the proposed theories to develop more practical decision-making approaches.

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

Researchers would like to thank the Deanship of Scientific Research, Qassim University, for funding publication of this project.

Open Research

Data Availability

No data were used to support this study.

References

1 Dubois D., Kaci S., and Prade H., Bipolarity in reasoning and decision - An introduction. The case of the possibility theory framework, 10th International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems (IPMU), July 2004, Perugia, Italy.
Google Scholar
2 Dubois D. and Prade H., An introduction to bipolar representations of information and preference, International Journal of Intelligent Systems. (2008) 23, no. 8, 866–877, https://doi.org/10.1002/int.20297, 2-s2.0-48849090539.
10.1002/int.20297
Web of Science® Google Scholar
3 Akram M., Zahid K., and Alcantud J. C. R., A new outranking method for multicriteria decision making with complex Pythagorean fuzzy information, Neural Computing and Applications. (2022) 34, https://doi.org/10.1007/s00521-021-06847-1.
10.1007/s00521-021-06847-1
Web of Science® Google Scholar
4 Benferhat S., Dubois D., Kaci S., and Prade H., Modeling positive and negative information in possibility theory, International Journal of Intelligent Systems. (2008) 23, no. 10, 1094–1118, https://doi.org/10.1002/int.20308, 2-s2.0-55349083673.
10.1002/int.20308
Web of Science® Google Scholar
5 Bonnefon J. F., Two routes for bipolar information processing, and a blind spot in between, International Journal of Intelligent Systems. (2008) 23, no. 9, 923–929, https://doi.org/10.1002/int.20300, 2-s2.0-51049117518.
10.1002/int.20300
Web of Science® Google Scholar
6 Caferra R. and Peltier N., Accepting/rejecting propositions from accepted/rejected propositions: a unifying overview, International Journal of Intelligent Systems. (2008) 23, no. 10, 999–1020, https://doi.org/10.1002/int.20304, 2-s2.0-55349087584.
10.1002/int.20304
Web of Science® Google Scholar
7 Grabisch M., Greco S., and Pirlot M., Bipolar and bivariate models in multicriteria decision analysis: descriptive and constructive approaches, International Journal of Intelligent Systems. (2008) 23, no. 9, 930–969, https://doi.org/10.1002/int.20301, 2-s2.0-51049091865.
10.1002/int.20301
Web of Science® Google Scholar
8 Kaci S., Logical formalisms for representing bipolar preferences, International Journal of Intelligent Systems. (2008) 23, no. 9, 985–997, https://doi.org/10.1002/int.20303, 2-s2.0-51049096547.
10.1002/int.20303
Web of Science® Google Scholar
9 Konieczny S., Marquis P., and Besnard P., Bipolarity in bilattice logics, International Journal of Intelligent Systems. (2008) 23, no. 10, 1046–1061, https://doi.org/10.1002/int.20306, 2-s2.0-55349083674.
10.1002/int.20306
Web of Science® Google Scholar
10 Neves R. D. S. and Livet P., Bipolarity in human reasoning and affective decision making, International Journal of Intelligent Systems. (2008) 23, no. 8, 898–922, https://doi.org/10.1002/int.20299, 2-s2.0-48849113307.
10.1002/int.20299
Web of Science® Google Scholar
11 Öztürk M. and Tsoukias A., Bipolar preference modeling and aggregation in decision support, International Journal of Intelligent Systems. (2008) 23, no. 9, 970–984, https://doi.org/10.1002/int.20302, 2-s2.0-51049083590.
10.1002/int.20302
Web of Science® Google Scholar
12 Raufaste E. and Vautier S., An evolutionist approach to information bipolarity: representations and affects in human cognition, International Journal of Intelligent Systems. (2008) 23, no. 8, 878–897, https://doi.org/10.1002/int.20298, 2-s2.0-48849112361.
10.1002/int.20298
Web of Science® Google Scholar
13 Zahid K., Akram M., and Kahraman C., A new ELECTRE-based method for group decision-making with complex spherical fuzzy information, Knowledge-Based Systems. (2022) 243, article 108525, https://doi.org/10.1016/j.knosys.2022.108525.
10.1016/j.knosys.2022.108525
Web of Science® Google Scholar
14 Zhou M. and Li S., Applications of bipolar fuzzy theory to hemirings, International Journal of Innovative Computing, Information and Control. (2014) 10, no. 2, 767–781.
Google Scholar
15 Akram M., Sarwar M., and Dudek W. A., Graphs for the analysis of bipolar fuzzy information, studies in fuzziness and soft computing, Springerplus. (2021) 401, https://doi.org/10.1007/978-981-15-8756-6.
10.1007/978-981-15-8756-6
Google Scholar
16 Ali G., Akram M., and Alcantud J. C. R., Attributes reductions of bipolar fuzzy relation decision systems, Neural Computing and Applications. (2020) 32, no. 14, 10051–10071, https://doi.org/10.1007/s00521-019-04536-8.
10.1007/s00521-019-04536-8
Web of Science® Google Scholar
17 Akram M. and Arshad M., Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis, Computational and Applied Mathematics. (2020) 39, no. 1, 1–21, https://doi.org/10.1007/s40314-019-0980-8.
10.1007/s40314-019-0980-8
Web of Science® Google Scholar
18 Akram M. and Dudek W. A., Regular bipolar fuzzy graphs, Neural Computing and Applications. (2012) 21, no. S1, 197–205, https://doi.org/10.1007/s00521-011-0772-6, 2-s2.0-84865790747.
10.1007/s00521-011-0772-6
Web of Science® Google Scholar
19 Kang M. K. and Kang J. G., Bipolar fuzzy set theory applied to sub-semigroups with operators in semigroups, The Pure and Applied Mathematics. (2012) 19, no. 1, 23–35, https://doi.org/10.7468/jksmeb.2012.19.1.23.
10.7468/jksmeb.2012.19.1.23
Google Scholar
20 Majumder S. K., Bipolar valued fuzzy sets in semigroups, Mathematica Aeterna. (2012) 2, no. 3, 203–213.
Google Scholar
21 Ulucay V., Deli I., and Sahin M., Similarity measures of bipolar neutrosophic sets and their application to multiple criteria decision making, Neural Computing and Applications. (2018) 29, no. 3, 739–748, https://doi.org/10.1007/s00521-016-2479-1, 2-s2.0-84979231011.
10.1007/s00521-016-2479-1
Web of Science® Google Scholar
22 Akram M., Shumaiza A. N., and Al-Kenani, Multi-criteria group decision-making for selection of green suppliers under bipolar fuzzy PROMETHEE process, Symmetry. (2020) 12, no. 1, https://doi.org/10.3390/sym12010077.
10.3390/sym12010077
Web of Science® Google Scholar
23 Al-Qudah Y. and Hassan N., Bipolar fuzzy soft expert set and its application in decision making, International Journal of Applied Decision Sciences. (2017) 10, no. 2, 175–191, https://doi.org/10.1504/IJADS.2017.084310, 2-s2.0-85020005866.
10.1504/IJADS.2017.084310
Google Scholar
24 Akram M. and Arshad M., A novel trapezoidal bipolar fuzzy TOPSIS method for group decision-making, Group Decision and Negotiation. (2019) 28, no. 3, 565–584, https://doi.org/10.1007/s10726-018-9606-6, 2-s2.0-85058115317.
10.1007/s10726-018-9606-6
Web of Science® Google Scholar
25 Molodtsov D., Soft set theory--First results, Computers and Mathematics with Applications. (1999) 37, no. 4-5, 19–31, https://doi.org/10.1016/S0898-1221(99)00056-5.
10.1016/S0898-1221(99)00056-5
Web of Science® Google Scholar
26 Maji P., Roy A. R., and Biswas R., An application of soft sets in a decision making problem, Computers and Mathematics with Applications. (2002) 44, no. 8-9, 1077–1083, https://doi.org/10.1016/S0898-1221(02)00216-X, 2-s2.0-0036772771.
10.1016/S0898-1221(02)00216-X
Web of Science® Google Scholar
27 Maji P. K., Biswas R., and Roy A. R., Soft set theory, Computers and Mathematics with Applications. (2003) 45, no. 4-5, 555–562, https://doi.org/10.1016/S0898-1221(03)00016-6, 2-s2.0-0037301143.
10.1016/S0898-1221(03)00016-6
Web of Science® Google Scholar
28 Chen D., Tsang E. C. C., Yeung D. S., and Wang X., The parameterization reduction of soft sets and its applications, Computers & Mathematics with Applications. (2005) 49, no. 5-6, 757–763, https://doi.org/10.1016/j.camwa.2004.10.036, 2-s2.0-18444402496.
10.1016/j.camwa.2004.10.036
Web of Science® Google Scholar
29 Zou Y. and Xiao Z., Data analysis approaches of soft sets under incomplete information, Knowledge-Based Systems. (2008) 21, no. 8, 941–945, https://doi.org/10.1016/j.knosys.2008.04.004, 2-s2.0-54949136913.
10.1016/j.knosys.2008.04.004
Web of Science® Google Scholar
30 Ali M. I., Feng F., Liu X., Min W. K., and Shabir M., On some new operations in soft set theory, Computers and Mathematics with Applications. (2009) 57, no. 9, 1547–1553, https://doi.org/10.1016/j.camwa.2008.11.009, 2-s2.0-63049126255.
10.1016/j.camwa.2008.11.009
Web of Science® Google Scholar
31 Kong Z., Gao L., Wang L., and Li S., The normal parameter reduction of soft sets and its algorithm, Computers and Mathematics with Applications. (2008) 56, no. 12, 3029–3037, https://doi.org/10.1016/j.camwa.2008.07.013, 2-s2.0-55649098572.
10.1016/j.camwa.2008.07.013
Web of Science® Google Scholar
32 Çağman N. and Enginoğlu S., Soft matrix theory and its decision making, Computers and Mathematics with Applications. (2010) 59, no. 10, 3308–3314, https://doi.org/10.1016/j.camwa.2010.03.015, 2-s2.0-77953139147.
10.1016/j.camwa.2010.03.015
Web of Science® Google Scholar
33 Çağman N. and Enginoğlu S., Soft set theory and uni-int decision making, European Journal of Operational Research. (2010) 207, no. 2, 848–855, https://doi.org/10.1016/j.ejor.2010.05.004, 2-s2.0-77955559824.
10.1016/j.ejor.2010.05.004
Web of Science® Google Scholar
34 Maji P. K., Biswas R., and Roy A. R., Fuzzy soft sets, The Journal of Fuzzy Mathematics. (2001) 9, no. 3, 589–602.
Google Scholar
35 Akram M., Amjad U., and Davvaz B., Decision-making analysis based on bipolar fuzzy N-soft information, Computational and Applied Mathematics. (2021) 40, no. 6, 1–39, https://doi.org/10.1007/s40314-021-01570-y.
10.1007/s40314-021-01570-y
Web of Science® Google Scholar
36 Zadeh L. A., Fuzzy sets, Information and Control. (1965) 8, no. 3, 338–353, https://doi.org/10.1016/S0019-9958(65)90241-X, 2-s2.0-34248666540.
10.1016/S0019-9958(65)90241-X
CAS Web of Science® Google Scholar
37 Chetia B. and Das P. K., An application of interval-valued fuzzy soft, International Journal of Contemporary Mathematical Sciences. (2010) 5, no. 38, 1887–1894.
Google Scholar
38 Agarwal M., Biswas K. K., and Hanmandlu M., Generalized intuitionistic fuzzy soft sets with applications in decision- making, Applied Soft Computing. (2013) 13, no. 8, 3552–3566, https://doi.org/10.1016/j.asoc.2013.03.015, 2-s2.0-84878421809.
10.1016/j.asoc.2013.03.015
Web of Science® Google Scholar
39 Alsager K., Waqar S., Furrukh H., and Alattas N., Donor-derived strongyloidiasis in a saudi pediatric kidney transplant recipient: a case report and mini-review, Pediatric Transplantation. (2019) 23, no. 2, article e13315, https://doi.org/10.1111/petr.13315, 2-s2.0-85058946682.
10.1111/petr.13315
PubMed Google Scholar
40 Alsager K. M., Alshehri N. O., and Akram M., A decision-making approach based on a multi q-hesitant fuzzy soft multi-granulation rough model, Symmetry. (2018) 10, no. 12, https://doi.org/10.3390/sym10120711, 2-s2.0-85058989898.
10.3390/sym10120711
PubMed Web of Science® Google Scholar
41 Zadeh L. A., The concept of a linguistic variable and its application to approximate reasoning-iii, Information Sciences. (1975) 9, no. 1, 43–80, https://doi.org/10.1016/0020-0255(75)90017-1, 2-s2.0-0016631726.
10.1016/0020-0255(75)90017-1
Web of Science® Google Scholar
42 Zadeh L. A., The concept of a linguistic variable and its application to approximate reasoning--II, Information Sciences. (1975) 8, no. 4, 301–357, https://doi.org/10.1016/0020-0255(75)90046-8, 2-s2.0-0016459349.
10.1016/0020-0255(75)90046-8
Web of Science® Google Scholar
43 Zadeh L. A., Fuzzy sets as a basis for a theory of possibility, Fuzzy Sets and Systems. (1978) 1, no. 1, 3–28, https://doi.org/10.1016/0165-0114(78)90029-5, 2-s2.0-49349133217.
10.1016/0165-0114(78)90029-5
Google Scholar
44 Mizumoto M. and Tanaka K., Some properties of fuzzy sets of type 2, Information and Control. (1976) 31, no. 4, 312–340, https://doi.org/10.1016/S0019-9958(76)80011-3, 2-s2.0-0001296806.
10.1016/S0019-9958(76)80011-3
Web of Science® Google Scholar
45 Mizumoto M. and Tanaka K., Fuzzy sets and type 2 under algebraic product and algebraic sum, Fuzzy Sets and Systems. (1981) 5, no. 3, 277–290, https://doi.org/10.1016/0165-0114(81)90056-7, 2-s2.0-0001562060.
10.1016/0165-0114(81)90056-7
Web of Science® Google Scholar
46 Dubois D. and Prade H., Fuzzy sets and systems: theory and applications, Mathematics in Science and Engineering. (1980) 144.
Google Scholar
47 Coupland S. and John R., A fast geometric method for defuzzification of type-2 fuzzy sets, IEEE Transactions on Fuzzy Systems. (2008) 16, no. 4, 929–941, https://doi.org/10.1109/TFUZZ.2008.924345, 2-s2.0-50549104523.
10.1109/TFUZZ.2008.924345
Web of Science® Google Scholar
48 Garca J. C. F., Solving fuzzy linear programming problems with interval type-2 rhs, IEEE International Conference on Systems, Man and Cybernetics, 2009, San Antonio, TX, USA, 262–267, https://doi.org/10.1109/ICSMC.2009.5345943, 2-s2.0-74849140673.
10.1109/ICSMC.2009.5345943
Google Scholar
49 Karnik N. N. and Mendel J. M., Centroid of a type-2 fuzzy set, Information Sciences. (2001) 132, no. 1-4, 195–220, https://doi.org/10.1016/S0020-0255(01)00069-X, 2-s2.0-0035247535.
10.1016/S0020-0255(01)00069-X
Web of Science® Google Scholar
50 Pal S. S. and Kar S., A hybridized forecasting method based on weight adjustment of neural network using generalized type-2 fuzzy set, International Journal of Fuzzy Systems. (2019) 21, no. 1, 308–320, https://doi.org/10.1007/s40815-018-0534-z, 2-s2.0-85061868052.
10.1007/s40815-018-0534-z
Web of Science® Google Scholar
51 Yager R. R., Fuzzy subsets of type ii in decisions, Cybernetics and Systems. (1980) 10, no. 1-3, 137–159, https://doi.org/10.1080/01969728008927629, 2-s2.0-84960623699.
10.1080/01969728008927629
Web of Science® Google Scholar
52 Liang Q., Karnik N. N., and Mendel J. M., Connection admission control in atm networks using survey-based type-2 fuzzy logic systems, In IEEE Transactions on Systems, Man, and Cybernetics. (2000) 30, no. 3, 329–339, https://doi.org/10.1109/5326.885114, 2-s2.0-0034240475.
10.1109/5326.885114
Web of Science® Google Scholar
53 Wu K. C., Fuzzy interval control of mobile robots, Computers and Electrical Engineering. (1996) 22, no. 3, 211–229, https://doi.org/10.1016/0045-7906(95)00038-0, 2-s2.0-0030149210.
10.1016/0045-7906(95)00038-0
Web of Science® Google Scholar
54 Karnik N. N., Mendel J. M., and Liang Q., Type-2 fuzzy logic systems, IEEE Transactions on Fuzzy Systems. (1999) 7, no. 6, 643–658, https://doi.org/10.1109/91.811231, 2-s2.0-0033281209.
10.1109/91.811231
Web of Science® Google Scholar
55 Liang Q. and Mendel J. M., Decision feedback equalizer for nonlinear time-varying channels using type-2 fuzzy adaptive filters, In Ninth IEEE International Conference on Fuzzy Systems. (2000) 2, 883–888.
Google Scholar
56 Liang Q. and Mendel J. M., Equalization of nonlinear time-varying channels using type-2 fuzzy adaptive filters, IEEE Transactions on Fuzzy Systems. (2000) 8, no. 5, 551–563, https://doi.org/10.1109/91.873578, 2-s2.0-0034297774.
10.1109/91.873578
Web of Science® Google Scholar
57 Mendel J. M., Uncertainty, fuzzy logic, and signal processing, Signal Processing. (2000) 80, no. 6, 913–933, https://doi.org/10.1016/S0165-1684(00)00011-6, 2-s2.0-0033733785.
10.1016/S0165-1684(00)00011-6
Web of Science® Google Scholar
58 Karnik N. N. and Mendel J. M., Introduction to type-2 fuzzy logic systems, IEEE International Conference on Fuzzy Systems Proceedings. (1998) 2, 915–920.
Google Scholar
59 Karnik N. N. and Mendel J. M., Applications of type-2 fuzzy logic systems to forecasting of time-series, Information Sciences. (1999) 120, no. 1-4, 89–111, https://doi.org/10.1016/S0020-0255(99)00067-5, 2-s2.0-0033323770.
10.1016/S0020-0255(99)00067-5
Web of Science® Google Scholar
60 Liang Q. and Mendel J. M., Interval type-2 fuzzy logic systems: theory and design, IEEE Transactions on Fuzzy Systems. (2000) 8, no. 5, 535–550, https://doi.org/10.1109/91.873577, 2-s2.0-0034295771.
10.1109/91.873577
Web of Science® Google Scholar
61 John R. and Czarnecki C., An adaptive type-2 fuzzy system for learning linguistic membership grades, In IEEE International Fuzzy Systems, Conference Proceedings. (1999) 3, 1552–1556.
Google Scholar
62 John R., Innocent P., and Barnes M., Type 2 fuzzy sets and neuro-fuzzy clustering of radiographic tibia images, IEEE International Conference on Fuzzy Systems Proceedings. (1997) 3, 1375–1380.
10.1109/FUZZY.1997.619744
Google Scholar
63 Chiang D. A., Chow L. R., and Hsien N. C., Fuzzy information in extended fuzzy relational databases, Fuzzy Sets and Systems. (1997) 92, no. 1, 1–20, https://doi.org/10.1016/S0165-0114(96)00168-6, 2-s2.0-0006242661.
10.1016/S0165-0114(96)00168-6
Web of Science® Google Scholar
64 Wagenknecht M. and Hartmann K., Application of fuzzy sets of type 2 to the solution of fuzzy equations systems, Fuzzy Sets and Systems. (1988) 25, no. 2, 183–190, https://doi.org/10.1016/0165-0114(88)90186-8, 2-s2.0-0001586159.
10.1016/0165-0114(88)90186-8
Web of Science® Google Scholar
65 John R., Type-2 inferencing and community transport scheduling, Proceeding 4th Euro. Congress Intelligent Techniques Soft Computing, 1996, 1369–1372.
Google Scholar
66 Zhang Z. and Zhang S., Type-2 fuzzy soft sets and their applications in decision making, Journal of Applied Mathematics. (2012) 2012, 35, 608681, https://doi.org/10.1155/2012/608681, 2-s2.0-84872158208.
10.1155/2012/608681
Google Scholar
67 Cagman N., Enginoglu S., and Citak F., Fuzzy soft set theory and its applications, Iranian Journal of Fuzzy Systems. (2011) 8, no. 3, 137–147.
Web of Science® Google Scholar
68 Ebrahimnejad A. and Verdegay J. L., Fuzzy sets-based methods and techniques for modern analytics, Springerplus. (2018) 364, https://doi.org/10.1007/978-3-319-73903-8.
10.1007/978-3-319-73903-8
Google Scholar
69 Alsager K. M. and Alshehri N. O., A decision-making approach based on multi q-dual hesitant fuzzy soft rough model, Journal of Intelligent Fuzzy Systems. (2020) 38, no. 2, 1623–1635, https://doi.org/10.3233/JIFS-182624.
10.3233/JIFS-182624
Web of Science® Google Scholar
70 Mendel J. M. and John R. B., Type-2 fuzzy sets made simple, IEEE Transactions on Fuzzy Systems. (2002) 10, no. 2, 117–127, https://doi.org/10.1109/91.995115, 2-s2.0-0036530350.
10.1109/91.995115
Web of Science® Google Scholar

Citing Literature

All articles

A New Optimization Approach Based on Bipolar Type-2 Fuzzy Soft Sets

Abstract

1. Introduction

2. Preliminaries

3. Bipolar Type-2 Fuzzy Set

3.1. Operations of BF_T2

3.2. Properties

4. Bipolar Type-2 Fuzzy Soft Set

4.1. Operations on BFS_T2(ℚ)

5. Application of BFS_T2 Set in Decision Making

5.1. Algorithm

6. Conclusion

Ethical Approval

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A New Optimization Approach Based on Bipolar Type-2 Fuzzy Soft Sets

Abstract

1. Introduction

2. Preliminaries

3. Bipolar Type-2 Fuzzy Set

3.1. Operations of BFT2

3.2. Properties

4. Bipolar Type-2 Fuzzy Soft Set

4.1. Operations on BFST2(ℚ)

5. Application of BFST2 Set in Decision Making

5.1. Algorithm

6. Conclusion

Ethical Approval

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

3.1. Operations of BF_T2

4.1. Operations on BFS_T2(ℚ)

5. Application of BFS_T2 Set in Decision Making