The current article discusses the fuzzy new iterative transform approach, which is a combination of a fuzzy hybrid methodology and an iterative transformation technique. We establish the consistence of our strategy by obtaining fractional fuzzy Helmholtz equations with the initial fuzzy condition using the Caputo derivative under generalized Hukuhara differentiability. The series obtained result was calculated and compared to the proposed equations of the actual result. Three challenges were provided to validate our method, and the outcomes were approximated in fuzzy form. In each of the three examples, the upper and bottom halves of the fuzzy solution were approximated utilizing two various fractional order between 0 and 1. Due to the fact that it globalizes the dynamical behavior of the specified equation, it produces all forms of fuzzy results at any fractional order between 0 and 1. Due to the fact that the fuzzy numbers presents the result in a lower and upper branches fuzzy type, the unknown quantity incorporates fuzziness as well. It is critical to emphasize that the purpose of the proposed fuzziness approach is to demonstrate the efficiency and superiority of numerical solutions to nonlinear fractional fuzzy partial differential equations that arise in complex and physical structures.

1. Introduction

Modeling uncertain issues with the theory of fuzzy sets are a great technique. As a result, fuzzy concepts have been used to model a broad variety of natural events. The fuzzy fractional differential equation, in particular, is frequent models in several scientific domains, such as assessing weapon systems, population models, electrohydraulics, and civil engineering models. As a solution, the fuzzy calculus idea of the fractional derivative is critical [1–4]. As a solution, fractional fuzzy in the domains of mathematics and engineering, differential equations have gotten a lot of attention. The very first is the study by Agarwal et al. [5] devoted to fuzzy fractional differential equations. They established the Riemann-Liouville differentiability concept under the Hukuhara differentiability to analysis fractional fuzzy differential equations [6–8].

Recently, fractional calculus has been offered as a valuable topic to produce precise outcomes of engineering and mathematics issues like signal processing, aerodynamics and control [9–12] systems, biomathematical difficulties, and others. Furthermore, several writers have researched fractional differential equations in fuzzy situations [5], solved using various approaches [13–16]. Hoa investigated fractional fuzzy differential equation under Caputo gH-differentiability in [17]. At the same time, Agarwal et al. conducted a study on the same subject in [18] to highlight its connection to optimal control issues. Long et al. [19] demonstrated the solvability of fractional fuzzy differential problems, while Salahshour et al. [20] solved the issue using Laplace fuzzy transformation.

The Helmholtz equation (HE) is an elliptic partial differential equation (PDE) developed from a wave model. It is also known as the reduced wave equation. The HE is a partial differential equation representing mechanical growth that is time-independent throughout the cosmos. The HE is fundamental in applied physics and mathematics [21–24]. The HE findings, which are commonly obtained by separating variables, deal with crucial scientific phenomena [25]. Equations include magnetic fields in plates, fluid, wall, vibrating lines, nuclear power reactors, electromagnetic field, geology’s Lamb equation, and acoustics. Consider a nonhomogeneous isotropic material in three dimensions with a velocity of c in Euclidean space [26, 27]. The resulting wave is μ(℘, ζ) in phase with the harmonic origin. The HE for the given field R is satisfied when ϕ(℘, ζ) vibrates at the recognized fixed frequency ω > 0:

(1)

where υ(℘, φ) is an appropriately differentiable function at the boundary of R, g(℘, φ) is a specified function, χ > 0 is a constant value, and

is a wave number with a wave length of

. If ϕ(℘, φ) = 0 is necessary, then equation (1) the HE is homogeneous. When the positive sign (in front of the χ term) is improved to a negative sign, most steady-state oscillations (thermoelectric, acoustic, hydraulic, electromagnetic) lead to a two-dimensional HE describing mass transport systems using chemical mixtures of first-order volume. In linear acoustics, for example, ϕ(℘, φ) might represent a disruption of the reference state pressure (Thompson and Pinsky, 1995). Conservation equations, also known as HEs, are used to solve a wide range of physical issues, including fluid restricted or shear viscosity streams inside thermophysical barriers [26–29], such as Laplace variational iteration method [30], homotopy perturbation method [31], q-homotopy analysis transform method [32], reduced differential transform method [33], He’s variational iteration method [34], and a spectral method [35] have all been used to solve fractional-order HEs in recent years [36, 37].

2. Basic Definition

Definition 1. Consider a continuous function fuzzy on [0, β] ∈ R, we express fractional fuzzy Riemann-Liouvilli integral in the presence of as

(2)

Moreover, if , where C^F[0, β] is the universe of fuzzy continuous function, and L^F[0, β] is the space of continuous fuzzy functions. If the functions are Lebesgue integrable, then the fuzzy fractional integral is given as

(3)

such that

(4)

Definition 2. For a function , such that and , then the fractional Caputo fuzzy derivative is given as

(5)

where

(6)

in such a way that the integrating on the right sides convergence and m = ⌈ϱ⌉. Since ϱ ∈ (0, 1]m = 1.

Definition 3. The Laplace fuzzy transformation for f(℘), where f(℘) is value fuzzy term, is define as

(7)

Definition 4. In terms of fuzzy convolution, a fuzzy Laplace transformation is described as

(8)

where f₁∗f₂ define the fuzzy convolution between f₁ and f₂, i.e.,

(9)

Definition 5. The “Mittag-Leffler function” Eρ(p) is expressed as

(10)

where ρ > 0.

Definition 6. Let be a number of fuzzy which have the specified properties

κ is an upper semicontinuous number
κ{μ(χ₁) + μ(χ₂)} ≥ min{κ(χ₁), κ(χ₂)}
∃χ₀ ∈ R such that κ(χ₀) = 1, i.e., v is normal
is compact

The set of all fuzzy numbers is represented by the notation E.

Definition 7. The aforementioned number can be written in parametric form as , so that γ ∈ [0, 1] combined with the values

from left is continuous and bounded function increasing over [0, 1]
from right is continuous and bounded function decreasing over [0, 1]
.

3. Main Work with Applications

(11)

with the initial fuzzy condition

(12)

In this case, we use the Laplace transform on (12) as

(13)

with initial condition using, and we get

(14)

Suppose that the result as

, then (15) defines

(15)

On both sides terms comparisons, we get

(16)

Using inverse Laplace transformation, we get

(17)

As a consequence, the needed series result is obtained by

(18)

3.1. Examples

Example 1. Consider fuzzy fractional homogeneous Helmholtz equation with x-space with the fuzzy initial condition

(19)

where

. Using the abovementioned procedure as described in (18), we obtain the following results.

(20)

and so forth, and more terms can be determined in this manner. As a result of (19), we can write the needed series result as an infinite series.

(21)

such that

(22)

In general, we can write as follows:

(23)

The exact result is

(24)

Figure 1 shows the fuzzy result comparison for lower and upper branches of Example 1 by Laplace decomposition method. The red color shows that the exact solution of lower and upper branch of fuzzy solution at integer order and second cure shows the analytical solution of example 1. In Figure 1, second graph shows two dimensional figure of fuzzy result at four other various fractional order of ρ of Example 1. The two similar color legends represent lower and upper portions of fuzzy solution, respectively.

Example 2. Consider fuzzy fractional homogeneous Helmholtz equation with x-space with the fuzzy initial condition

(25)

where

. Using the abovementioned procedure as described in (18), we obtain the following results:

(26)

and so forth, and more terms can be determined in this manner. As a result of (19), we can write the needed series result as an infinite series.

(27)

such that

(28)

In general, we can write as follows:

(29)

The exact result is

(30)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The first graph depicts a two-dimensional fuzzy upper and bottom branch graph of an analytic series result, while the second depicts various fractional of ρ.

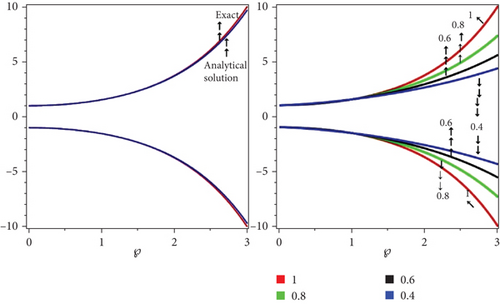
Figure 2 shows the fuzzy result comparison for lower and upper branches of Example 1 by Laplace decomposition method. The red color shows that the exact solution of lower and upper branch of fuzzy solution at integer order and second cure shows the analytical solution of Example 2. In Figure 2, second graph shows two dimensional figure of fuzzy result at four other various fractional order of ρ of Example 2. The two similar color legends represent lower and upper portions of fuzzy solution, respectively.

Example 3. Consider fuzzy fractional homogeneous Helmholtz equation with x-space with the fuzzy initial condition

(31)

where

. Using the abovementioned procedure as described in (18), we obtain the following results:

(32)

and so forth, and more terms can be determined in this manner. As a result of (19), we can write the needed series result as an infinite series.

(33)

such that

(34)

In general, we can write as follows:

(35)

The exact result is

(36)

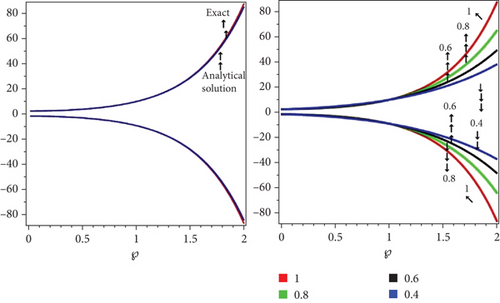
Figure 3 shows the fuzzy result comparison for lower and upper branches of Example 1 by the Laplace decomposition method. The red color shows that the exact solution of lower and upper branch of fuzzy solution at integer order and second cure shows the analytical solution of Example 3. In Figure 3, second graph shows two dimensional figure of fuzzy result at four other various fractional order of ρ of Example 3. The two similar color legends represent lower and upper portions of fuzzy solution, respectively.

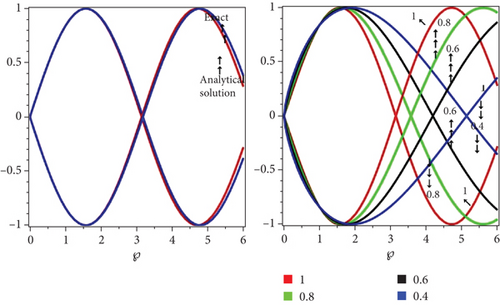
4. Conclusion

The aim of this paper was to propose a semianalytic solution to the fractional fuzzy Helmholtz equations using the Caputo derivative. An significant example has verified the solution achieved. We have also included plots of the analytical solution at various fractional orders. As seen in the graphs, when the fractional order nu approachs its integer value, the graphs will similar with the curve at integer order 1. Our study has shown that fractional calculus can identify the global nature of equations that are associated with fuzzy concepts. As future research continues, we will apply this approach to models with more dynamic features. In the future, this technique can be used to derive analytic and approximation solutions to perturbed fractional differential equations with fractional and classical initial conditions in the sense of the Caputo operator.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this article.

Open Research

Data Availability

The numerical data used to support the findings of this study are included within the article.

References

1 Alesemi M., Iqbal N., and Botmart T., Novel analysis of the fractional-order system of non-linear partial differential equations with the exponential-decay kernel, Mathematics. (2022) 10, no. 4, https://doi.org/10.3390/math10040615.
10.3390/math10040615
Web of Science® Google Scholar
2 Naeem M., Rezazadeh H., Khammash A. A., Shah R., and Zaland S., Analysis of the fuzzy fractional-order solitary wave solutions for the KdV equation in the sense of Caputo-Fabrizio derivative, Journal of Mathematics. (2022) 2022, 12, https://doi.org/10.1155/2022/3688916, 3688916.
10.1155/2022/3688916
Web of Science® Google Scholar
3 Iqbal N., Niazi A. U. K., Shafqat R., and Zaland S., Existence and uniqueness of mild solution for fractional-order controlled fuzzy evolution equation, Journal of Function Spaces. (2021) 2021, 8, https://doi.org/10.1155/2021/5795065, 5795065.
10.1155/2021/5795065
Web of Science® Google Scholar
4 Shah N. A., Alyousef H. A., El-Tantawy S. A., Shah R., and Chung J. D., Analytical investigation of fractional-order Korteweg-De-Vries-type equations under Atangana-Baleanu-Caputo operator: modeling nonlinear waves in a plasma and fluid, Symmetry. (2022) 14, no. 4, https://doi.org/10.3390/sym14040739.
10.3390/sym14040739
Google Scholar
5 Agarwal R. P., Lakshmikantham V., and Nieto J. J., On the concept of solution for fractional differential equations with uncertainty, Nonlinear Analysis: Theory Methods & Applications. (2010) 72, no. 6, 2859–2862, https://doi.org/10.1016/j.na.2009.11.029, 2-s2.0-73249139676.
10.1016/j.na.2009.11.029
Web of Science® Google Scholar
6 Mohammed W. W., Iqbal N., and Botmart T., Additive noise effects on the stabilization of fractional-space diffusion equation solutions, Mathematics. (2022) 10, no. 1, https://doi.org/10.3390/math10010130.
10.3390/math10010130
Web of Science® Google Scholar
7 Iqbal N., Niazi A. U. K., Khan I. U., Shah R., and Botmart T., Cauchy problem for non-autonomous fractional evolution equations with nonlocal conditions of order (1, 2), AIMS Mathematics. (2022) 7, no. 5, 8891–8913, https://doi.org/10.3934/math.2022496.
10.3934/math.2022496
Web of Science® Google Scholar
8 Almatroud A. O., Matouk A. E., Mohammed W. W., Iqbal N., and Alshammari S., Self-excited and hidden chaotic attractors in Matouk’s hyperchaotic systems, 2022, 2022, 1–14, https://doi.org/10.1155/2022/6458027, 6458027.
10.1155/2022/6458027
Google Scholar
9 Sunthrayuth P., Zidan A. M., Yao S. W., Shah R., and Inc M., The comparative study for solving fractional-order Fornberg–Whitham equation via ρ-Laplace transform, Symmetry. (2021) 13, no. 5, https://doi.org/10.3390/sym13050784.
10.3390/sym13050784
Web of Science® Google Scholar
10 Kilbas A. A., Srivastava M. H., and Trujillo J. J., Theory and application of fractional differential equations, 2006, 204, Elsevier, Amsterdam, The Netherlands.
Google Scholar
11 Naeem M., Zidan A. M., Nonlaopon K., Syam M. I., Al-Zhour Z., and Shah R., A new analysis of fractional-order equal-width equations via novel techniques, Symmetry. (2021) 13, no. 5, https://doi.org/10.3390/sym13050886.
10.3390/sym13050886
Web of Science® Google Scholar
12 Nonlaopon K., Alsharif A. M., Zidan A. M., Khan A., Hamed Y. S., and Shah R., Numerical investigation of fractional-order Swift-Hohenberg equations via a novel transform, Symmetry. (2021) 13, no. 7, https://doi.org/10.3390/sym13071263.
10.3390/sym13071263
Web of Science® Google Scholar
13 Ngo V. H., Fuzzy fractional functional integral and differential equations, Fuzzy Sets and Systems. (2015) 280, 58–90, https://doi.org/10.1016/j.fss.2015.01.009, 2-s2.0-84941878741.
10.1016/j.fss.2015.01.009
Web of Science® Google Scholar
14 Iqbal N., Akgul A., Shah R., Bariq A., Mossa Al-Sawalha M., and Ali A., On solutions of fractional-order gas dynamics equation by effective techniques, Journal of Function Spaces. (2022) 2022, 14, https://doi.org/10.1155/2022/3341754, 3341754.
10.1155/2022/3341754
Web of Science® Google Scholar
15 Allahviranloo T., Gouyandeh Z., and Armand A., A full fuzzy method for solving differential equation based on Taylor expansion, Journal of Intelligent Fuzzy Systems. (2015) 29, no. 3, 1039–1055, https://doi.org/10.3233/IFS-151713, 2-s2.0-84944533871.
10.3233/IFS-151713
Web of Science® Google Scholar
16 Chehlabi M. and Allahviranloo T., Concreted solutions to fuzzy linear fractional differential equations, Applied Soft Computing. (2016) 44, 108–116, https://doi.org/10.1016/j.asoc.2016.03.011, 2-s2.0-84963540035.
10.1016/j.asoc.2016.03.011
Web of Science® Google Scholar
17 Hoa N. V., Fuzzy fractional functional differential equations under Caputo gH- differentiability, Communications in Nonlinear Science and Numerical Simulation. (2015) 22, no. 1-3, 1134–1157, https://doi.org/10.1016/j.cnsns.2014.08.006, 2-s2.0-84916631378.
10.1016/j.cnsns.2014.08.006
Web of Science® Google Scholar
18 Agarwal R. P., Baleanu D., Nieto J. J., Torres D. F. M., and Zhou Y., A survey on fuzzy fractional differential and optimal control nonlocal evolution equations, Journal of Computational and Applied Mathematics. (2018) 339, 3–29, https://doi.org/10.1016/j.cam.2017.09.039, 2-s2.0-85031405471.
10.1016/j.cam.2017.09.039
Web of Science® Google Scholar
19 Niazi A. U. K., Iqbal N., Shah R., Wannalookkhee F., and Nonlaopon K., Controllability for fuzzy fractional evolution equations in credibility space, Fractal and Fractional. (2021) 5, no. 3, https://doi.org/10.3390/fractalfract5030112.
10.3390/fractalfract5030112
PubMed Web of Science® Google Scholar
20 Salahshour S., Allahviranloo T., and Abbasbandy S., Solving fuzzy fractional differential equations by fuzzy Laplace transforms, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 3, 1372–1381, https://doi.org/10.1016/j.cnsns.2011.07.005, 2-s2.0-80053384834.
10.1016/j.cnsns.2011.07.005
Web of Science® Google Scholar
21 Ali R. and Pan K., The new iteration methods for solving absolute value equations, Applications of Mathematics. (2021) 1–14, https://doi.org/10.21136/AM.2021.0055-21.
10.21136/AM.2021.0055-21
Web of Science® Google Scholar
22 Shah N. A., Yook S. J., and Tosin O., Analytic simulation of thermophoretic second grade fluid flow past a vertical surface with variable fluid characteristics and convective heating, Scientific Reports. (2022) 12, no. 1, 1–17, https://doi.org/10.1038/s41598-022-09301-x.
10.1038/s41598-022-09301-x
PubMed Web of Science® Google Scholar
23 Ali R. and Pan K., The solution of the absolute value equations using two generalized accelerated overrelaxation methods, Asian-European Journal of Mathematics. (2021) no. article 2250154, https://doi.org/10.1142/S1793557122501546.
10.1142/S1793557122501546
Web of Science® Google Scholar
24 Ali R., Khan I., Ali A., and Mohamed A., Two new generalized iteration methods for solving absolute value equations using M -matrix, AIMS Mathematics. (2022) 7, no. 5, 8176–8187, https://doi.org/10.3934/math.2022455.
10.3934/math.2022455
Web of Science® Google Scholar
25 Shah N. A., Dassios I., El-Zahar E. R., and Chung J. D., An Efficient Technique of Fractional-Order Physical Models Involving ρ-Laplace Transform, Mathematics. (2022) 10, no. 5, https://doi.org/10.3390/math10050816.
10.3390/math10050816
Web of Science® Google Scholar
26 Zheng Q., Xie F., and Lin W., Solution of two-dimensional Helmholtz equation by multipole theory method, Journal of electromagnetic waves and applications. (1999) 13, no. 2, 205–220, https://doi.org/10.1163/156939399X00835, 2-s2.0-0032624952.
10.1163/156939399X00835
Web of Science® Google Scholar
27 Thompson L. L. and Pinsky P. M., A Galerkin least-squares finite element method for the two-dimensional Helmholtz equation, International Journal for Numerical Methods in Engineering. (1995) 38, no. 3, 371–397, https://doi.org/10.1002/nme.1620380303, 2-s2.0-0029239896.
10.1002/nme.1620380303
Web of Science® Google Scholar
28 Zhang W. and Dai Y., Finite-difference solution of the Helmholtz equation based on two domain decomposition algorithms, Journal of Applied Mathematics and Physics. (2013) 1, no. 4, 18–24, https://doi.org/10.4236/jamp.2013.14004.
10.4236/jamp.2013.14004
Google Scholar
29 Samuel M. and Thomas A., On fractional Helmholtz equations, Fractional Calculus and Applied Analysis. (2010) 13, no. 3, 295p–308p.
Google Scholar
30 Baleanu D., Jassim H. K., and Al Qurashi M., Solving Helmholtz equation with local fractional derivative operators, Fractal and Fractional. (2019) 3, no. 3, https://doi.org/10.3390/fractalfract3030043.
10.3390/fractalfract3030043
Web of Science® Google Scholar
31 Gupta P. K., Yildirim A. H. M. E. T., and Rai K. N., Application of He’s homotopy perturbation method for multi-dimensional fractional Helmholtz equation, International Journal of Numerical Methods for Heat and Fluid Flow. (2012) 22, no. 4, 424–435, https://doi.org/10.1108/09615531211215738, 2-s2.0-84862079256.
10.1108/09615531211215738
Web of Science® Google Scholar
32 Iqbal N., Yasmin H., Rezaiguia A., Kafle J., Almatroud A. O., and Hassan T. S., Analysis of the fractional-order kaup–kupershmidt equation via novel transforms, Journal of Mathematics. (2021) 2021, 13, 2567927, https://doi.org/10.1155/2021/2567927.
10.1155/2021/2567927
Web of Science® Google Scholar
33 Abuasad S., Moaddy K., and Hashim I., Analytical treatment of two-dimensional fractional Helmholtz equations, Journal of King Saud University-Science. (2019) 31, no. 4, 659–666, https://doi.org/10.1016/j.jksus.2018.02.002, 2-s2.0-85042907238.
10.1016/j.jksus.2018.02.002
Web of Science® Google Scholar
34 Momani S. and Abuasad S., Application of He's variational iteration method to Helmholtz equation, Chaos, Solitons & Fractals. (2006) 27, no. 5, 1119–1123, https://doi.org/10.1016/j.chaos.2005.04.113, 2-s2.0-24944474278.
10.1016/j.chaos.2005.04.113
Web of Science® Google Scholar
35 Prakash A., Goyal M., and Gupta S., Numerical simulation of space-fractional Helmholtz equation arising in seismic wave propagation, imaging and inversion, Pramana. (2019) 93, no. 2, https://doi.org/10.1007/s12043-019-1773-8, 2-s2.0-85066155555.
10.1007/s12043-019-1773-8
Web of Science® Google Scholar
36 Jan R., Khan H., Kumam P., Tchier F., Shah R., and Bin Jebreen H., The investigation of the fractional-view dynamics of Helmholtz equations within Caputo operator, CMC-COMPUTERS MATERIALS & CONTINUA. (2021) 68, no. 3, 3185–3201, https://doi.org/10.32604/cmc.2021.015252.
10.32604/cmc.2021.015252
Web of Science® Google Scholar
37 Srivastava H. M., Shah R., Khan H., and Arif M., Some analytical and numerical investigation of a family of fractional-order Helmholtz equations in two space dimensions, Mathematical Methods in the Applied Sciences. (2020) 43, no. 1, 199–212, https://doi.org/10.1002/mma.5846.
10.1002/mma.5846
Web of Science® Google Scholar

Citing Literature

All articles

Novel Evaluation of Fuzzy Fractional Helmholtz Equations

Abstract

1. Introduction

2. Basic Definition

3. Main Work with Applications

3.1. Examples

4. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Novel Evaluation of Fuzzy Fractional Helmholtz Equations

Abstract

1. Introduction

2. Basic Definition

3. Main Work with Applications

3.1. Examples

4. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information