Volume 2022, Issue 1 7773659

Review Article

Open Access

A Review for Retrieving Wind Fields by Spaceborne Synthetic Aperture Radar

Baowei Zhang

orcid.org/0000-0001-6247-2298

PLA Strategic Support Force Information Engineering University, No. 62, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Jianzhong Guo,

Corresponding Author

Jianzhong Guo

[email protected]

orcid.org/0000-0002-0662-1508

The College of Environment and Planning of Henan University, North Section of Jinming Avenue, Longting District, Kaifeng, Henan Province 475000, China henu.edu.cn

Search for more papers by this author

Ziwei Li,

Ziwei Li

orcid.org/0000-0003-3840-4601

The School of Water Science and Engineering of Zhengzhou University, No. 100, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Yi Cheng,

Yi Cheng

orcid.org/0000-0003-2774-4168

PLA Strategic Support Force Information Engineering University, No. 62, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Yao Zhao,

Yao Zhao

orcid.org/0000-0001-5402-8533

PLA Strategic Support Force Information Engineering University, No. 62, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Feng Yao,

Feng Yao

orcid.org/0000-0003-4179-6407

Henan Surveying and Mapping Geographic Information Technology Center, No. 10, Weier Road, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Muhammad Waseem Boota,

Muhammad Waseem Boota

orcid.org/0000-0003-0770-0715

The School of Water Science and Engineering of Zhengzhou University, No. 100, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Baowei Zhang,

Baowei Zhang

orcid.org/0000-0001-6247-2298

PLA Strategic Support Force Information Engineering University, No. 62, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Jianzhong Guo,

Corresponding Author

Jianzhong Guo

[email protected]

orcid.org/0000-0002-0662-1508

The College of Environment and Planning of Henan University, North Section of Jinming Avenue, Longting District, Kaifeng, Henan Province 475000, China henu.edu.cn

Search for more papers by this author

Ziwei Li,

Ziwei Li

orcid.org/0000-0003-3840-4601

The School of Water Science and Engineering of Zhengzhou University, No. 100, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Yi Cheng,

Yi Cheng

orcid.org/0000-0003-2774-4168

PLA Strategic Support Force Information Engineering University, No. 62, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Yao Zhao,

Yao Zhao

orcid.org/0000-0001-5402-8533

PLA Strategic Support Force Information Engineering University, No. 62, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Feng Yao,

Feng Yao

orcid.org/0000-0003-4179-6407

Henan Surveying and Mapping Geographic Information Technology Center, No. 10, Weier Road, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

Muhammad Waseem Boota,

Muhammad Waseem Boota

orcid.org/0000-0003-0770-0715

The School of Water Science and Engineering of Zhengzhou University, No. 100, Science Avenue, Zhengzhou, Henan Province 450001, China zzu.edu.cn

Search for more papers by this author

First published: 21 February 2022

https://doi.org/10.1155/2022/7773659

Academic Editor: Romeo Bernini

Share a link

Email
Wechat
Bluesky

Abstract

A high-resolution sea surface wind field (SSWF) has high application requirements, such as weather forecast, wind energy evaluation, and oil spill monitoring. The models for retrieving SSWFs based on spaceborne synthetic aperture radar (SAR) are important methods for obtaining high-resolution SSWFs. These models are continuously updated and improved from the prototype to the model to achieve high-resolution and high-precision SSWF retrieval. With the development of SAR technology and the gradual maturation of global ocean observations, SSWF quantitative estimation using SAR has developed from scientific research to operational monitoring. This study summarises the principles and methods of SSWF with multipolarized SAR. Finally, research suggestions and future development directions are put forward.

1. Introduction

Sea surface wind fields (SSWFs) are the main power source for upper ocean movement and an important factor affecting wave generation, water mass formation, and ocean current movement [1]. High-resolution SSWFs retrieved using spaceborne SAR play an important role in numerical weather prediction, maritime transportation, maritime rescue, marine oil spill monitoring, sea ice trajectory prediction, typhoon intensity monitoring, offshore wind energy resource assessment, and more [2]. The estimation of the wind speed (WS) is an important parameter for offshore wind resource assessment, and it can serve the marine fishing and mariculture industries in the “blue breadbasket”-related industries, especially offshore fishing and deep-sea farming, which are closely related to China food security [3, 4].

Traditional SSWF monitoring methods such as on ships, buoys, and land stations cannot meet the increasing demand. These methods can only provide limited space and time coverage data [3]. Spaceborne microwave radiometers and scatterometers provide global-scale SSWF observations [5] with relatively low resolution (about 25 km), which makes it difficult to meet the needs of high-resolution SSWFs [6]. Using spaceborne SAR with a high resolution, a finer-scale SSWF can be retrieved [4]. Additionally, the retrieval of SSWF-based SAR has become a research hotspot [7, 8].

Spaceborne SAR has been widely used in SSWF inversion, and it has achieved fruitful results [9]. In wind direction (WD) inversion research, Gerling [10] found that the linear structural features of SEASAT SAR images were related to the WD, and the WD was estimated based on the image frequency spectrum with a Fourier transform. Subsequently, Fourier transforms, local gradients (LG), and wavelet analysis have been used to retrieve WD. In WS inversion, Jones et al. used SEASAT SAR data and found that there was a certain relationship between the normalised radar cross-section (NRCS) of the SAR and WS [11]. Then, the geophysical model function (GMF) based on the NRCS of copolarized SAR was proposed and continually updated to form a series of empirical models [12, 13]. However, the phenomenon of saturation exists in WS inversion with copolarized SAR when the WS exceeds 25 m/s [14–16]. It was found that C-band cross-polarized SAR could be used to retrieve high WS and was not sensitive to the WD or the radar incidence angle (RIA) [17, 18]. Furthermore, many models have been constructed based on cross-polarized SAR [19, 20].

Therefore, this paper discusses the methods for retrieving SSWF from spaceborne SAR and comprehensively summarises the research status in order to promote the research on SSWF.

2. The Potential and Drawback for SSWF Estimation Using SAR

Compared with other SSWF acquisition methods, such as ships, scatterometers, or radiometers, the potential applications of SAR-based imagery for an SSWF include the following [9]: (1) all-day, all-weather observation capability as well as higher resolution [4]; (2) high-resolution SSWF data obtained for near-shore waters to meet the demand for research on small-scale and medium-scale SSWFs; (3) long-term observations of near-shore SSWFs helping deepen the understanding of the dynamics of the SSWF processes at the sea surface and strengthen the high-resolution SSWF prediction capability of numerical models [20]; (4) in-depth research on the dynamics of small-scale and medium-scale SSWF processes at the surface of the sea, especially in the near-shore region, which can help improve climate models and enhance the ability of climate models to predict small-scale and medium-scale phenomena near the coast [21]; (5) real-time monitoring of disasters. Information on the internal structures of extreme weather events such as tropical cyclones and even typhoons can be obtained, which can aid the in-depth research and dynamic monitoring of typhoons and other disaster events [22]; and (6) SAR inversion of sea surface SSWFs with high resolution but slightly less coverage. The fusion of SSWF data from scatterometers, radiometers, altimeters, SAR, and other sensors to take advantage of the benefits of different sensors and complement each other is more conducive to obtaining more comprehensive and accurate global sea surface SSWF data [9].

The disadvantages include the following aspects: (1) The temporal resolution of the SAR data needs to be further improved. (2) Models concerning the wind speed inversion are mostly based on empirical (EP) fitting models, such as the GMF [23, 24], and research on the physical methods needs to be further improved. In general, wind speeds based on the EP and electromagnetic (EM) models are quite similar for an RIA below 40° since they deliver close NRCS values. Above 40°, wind speeds based on the EM models tend to be overestimated, since the NRCS is smaller. The reason for this is that the contribution of wave breaking and foam to the NRCS has not been considered in the description of EM models. This should be considered in the next steps to improve radar scattering calculation with the EM models [23]. (3) Regarding the inversion of the wind direction, most algorithms are based on the presence of wind streaks, but this feature is not present in every SAR image [9].

The GMF is one of the most important ways to perform the inversion of SSWFs based on SAR data, which is achieved empirically. The advantages of this method are that the model is reliably stable and widely applicable, and the accuracy of the inversion is further improved by the continuous optimisation of the model [23]. There are, of course, shortcomings in the model. The model requires wind direction as an input parameter, which is generally obtained with the inversion of SAR images or from other SSWF data. The former is subject to inaccuracies in the inversion process that may lead to errors in wind speed estimation, while the latter is difficult to reconcile with SAR images for both spatial and temporal scales [25].

3. Wind Direction Retrieval

A precise and accurate estimation of the WDs is one of the main issues for the SSWF retrieval from SAR images [26]. The inferred WDs are typically used as inputs to the GMFs [27]. The lower the estimation errors of the retrieved WDs, the higher the quality of the SAR-derived WSs and consequently the SSWFs.

3.1. Methodology

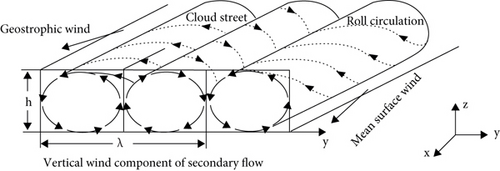
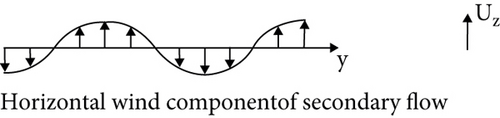
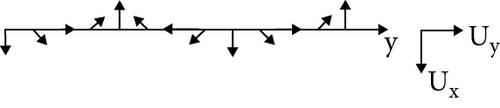
Boundary layer rolls (BLRs) are atmospheric roll vortices generated by thermal instabilities developing within the marine atmospheric boundary layer (MABL) [28, 29], and they are typically associated with unstable or neutral boundary layer conditions [30, 31]. They appear as black and white linear texture features on the SAR image, that is, wind streaks (or wind rows) [32, 33]. The direction of the streak has a parallel relationship with the sea surface WD [34, 35]. The WD is obtained by determining the direction of the wind streaks in the SAR image [36, 37], laying the foundation for WD inversion [38–40]. When reaching a certain intensity, which for GMFs [41] is WS in the range of 2.4-20 m/s with the error within 2 m/s [5, 40, 42], an SSWF will destroy the stability of the MABL, and a secondary flow pattern (spiral atmospheric boundary layer vortex) will be formed above the primary flow (average SSWF) (Figure 1). The secondary flow acts on the sea surface, resulting in convergence or divergence of the sea surface. When the secondary flow direction acts downward on the sea surface, it forms convergence points that appear as bright spots in the image. When the secondary flow direction acts upward on the sea surface, it forms divergence points that appear as dark spots in the image, resulting in bright and dark stripes on the SAR images. The wind stripes mentioned above are periodic, which provides the basis for wind inversion based on SAR images [43, 44].

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Illustration of the secondary flow pattern related to atmospheric BLRs. (a) Perspective of the three-dimensional flow. The roll axes are oriented between the directions of the mean surface wind and the geostrophic wind above the boundary layer [33]; (b) variation of the vertical component u_z of WS along the y direction; (c) variation of the horizontal components (in the x, y plane) [30, 33].

3.2. Method

SAR is a side-looking radar with a fixed observation angle. It cannot measure multiple azimuth angles, which makes it impossible to directly retrieve WS and direction information [9]. Based on the typical features of wind streaks, many methods have been proposed, such as Fourier transform [45–47], LG [38, 48], and wavelet analysis [49, 50]. LG has been widely exploited because the result of the WD has higher resolution and precision. This paper is focused on LG, optimised LG method, wavelet analysis method, and other methods.

3.2.1. Local Gradient

In the SAR image with streaks, the gradient shows the maximum value perpendicular to the streak direction, the main gradient direction of the image is obtained, and the direction perpendicular to this is the WD [38]. The general steps are as follows.

(1) Reducing the Image Size. The convolution kernel B⁴ is used for the smoothing processing for the ROIs (regions of interest), and then, the resolution is halved by operator A₂. Finally, the convolution kernel B² is used again for smoothing, which can be expressed as R = B²A₂B⁴:

(1)

(2) Computing LGs. For all points in the ROIs processed by R, the optimised Sobel operator S is used to calculate the gradient G:

(2)

where i indicates the imaginary part and ROIs_1/2 represents the ROIs processed by R.

(3) Unusable Points. After calculating all the LGs, the values of the first two rows and the last two columns of the image have to be discarded.

(4) Main Directions. For the gradient G, the histogram of the gradient direction is calculated by using the modulus of the gradient and the consistency parameter C as the weight. The angle corresponds to the position of the maximum in the smoothed histogram of the weighted usable LGs, that is, the main direction of the LG [51]:

(3)

The direction perpendicular to this is the WD, and the obtained WD is blurred in the 180° direction.

3.2.2. Optimised Local Gradient Method

(1) Modified LG (LG-Mod). The LG-Mod method [52] directly extracts the main LG direction (and then the predominant local WD) within the ROIs by using a specific unbiased estimator, avoiding histogram analysis [26]. Figure 2 shows the flowchart of the LG and LG-Mod.

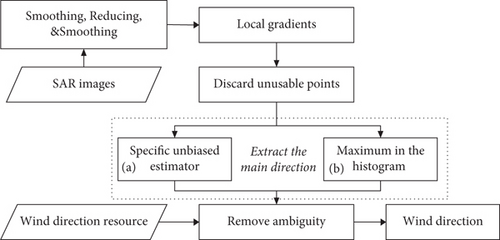
The main difference between the two is the part of the main gradient extraction. The following section introduces the part of the LG-Mod.

Specifically, the main gradient direction of each selected ROI is determined as the maximum point of the following function:

(4)

where α, N, and β_i are a generic direction, the number of ROI pixels, and the LG direction of the ith pixel, respectively. The function f (α, {β_i}) represents a mean collinearity index between α and {β_i}. Assuming a single dominant actual WD within the ROI, the LG direction maximises the collinearity index.

For each ROI, the predominant direction is directly obtained with the direct retrieval of the entire set of the directions previously estimated, provided by the following halved phase:

(5)

where

, and R^′ are the usable LG direction, the mean angle, and the related accuracy, respectively.

Each direction estimate can be assigned as follows:

(6)

where u_α is the upper (1/2) α standard normal distribution quartile and

is the second central trigonometric moment in the local direction of the ROI’s doubling.

LG-Mod eliminates the noise by setting appropriate thresholds. Different thresholding selections and errors are shown in Table 1:

(7)

Table 1. Different thresholding selections to LG-Mod directions.

Thresholding	RMSE (°)	MBE (°)
No	26.3	8.2
α = 0.05; ME^TH = 15^°	21.1	6.4
α = 0.05; ME^TH = 10^°	16.5	3.8
α = 0.05; ME^TH = 5^°	7.7	-0.4

(2) Improved LG (ILG). For the ILG [53], the calculation process is as shown in Figure 3(a). The difference between the ILG and the LG is that the former combines the smoothing and calculation of the LGs to avoid the difference approximation error effect of the noise.

The smoothing of the ILG is achieved by the Gaussian function as follows:

(8)

where s^′(x^′, y^′), s(x, y), and f(·, ·) are the image after smoothing, the original image, and the Gaussian function for smoothing, respectively:

(9)

where σ determines the smoothing window width and is an empirical parameter. The gradients of the image can be expressed as

(10)

where

and

are the unit vectors in the x and y directions, respectively:

(11)

where ∗ denotes the convolution and h_x(x, y) = ∂/∂xf(x, y):

(12)

where F(·) denotes the 2D Fourier transform.

(13)

Therefore, S_x is

(14)

Similarly, S_y is

(15)

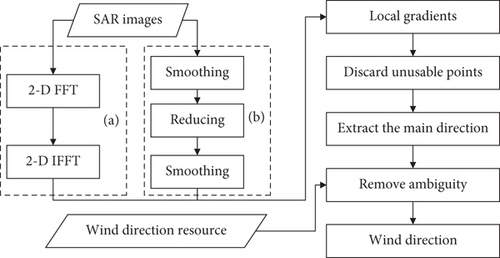
The other steps are the same as those in Koch’s method [38].

3.2.3. Wavelet Analysis Method

The WD based on the wavelet analysis method [54, 55] can quantitatively describe the stripes, through the standard deviation of the mean cross-section of the vertical detail within a wavelet decomposition. The process is shown in Figure 4.

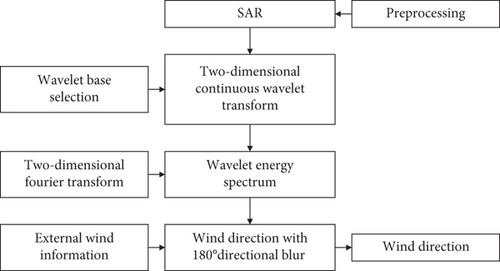
The original SAR image is preprocessed to eliminate the influence of the speckle noise, and then, the image size is reduced.

A two-dimensional continuous wavelet transform was performed (e.g., Daubechies wavelet [49] and Mexican hat [50]) on the SAR image, to obtain the low-frequency wavelet coefficients for the second layer of subdivision.

A two-dimensional FFT is performed on the energy spectrum image to calculate the wave number spectrum of wind streaks in the SAR image, and the two-dimensional FFT [45] can be expressed as

(16)

where Y is the wave number spectrum of wind streaks in the SAR image, X is the image gray value, m = 1, 2, ⋯, n, and l = 1, 2, ⋯, n.

WD with 180° directional blurring can be obtained by plumbing the line of the two-dimensional wave number spectrum peaks [50].

Finally, the external SSWF data is used to defuzzify the WD, i.e., to obtain the WD.

3.2.4. Other Methods

Since Gerling [10] discovered that there are wind streaks on SAR images that can be exploited to retrieve the WD, other methods, such as detection of the maximum variance direction method [56], the regular method [57, 58], and the method of the gray-level cooccurrence matrix (GLCM) [59, 60], have been proposed.

In terms of the regular method [57, 58], the gradient is solved with numerical differentiation, which can effectively suppress the noise in the image while ensuring a minimum error between the gradient and the “real” image intensity. The method solves the gradient in the following way.

The exact function u(x, y) is known to be measured at point (x_i, y_i) as

, and δ is the observation error:

(17)

where Ω is a subimage of the SAR image.

Then, the function f(x, y) satisfying the following is found:

(18)

The Green [61, 62] function is used to reconstruct f(x, y):

(19)

where

and AC = B:

(20)

When a = δ², a unique solution exists [61]. Further, f(x, y) and the gradient can be solved. The rest of the steps are the same as those of the local gradient method [38] for finding the wind direction.

Due to the complexity of SAR imaging and the variability of the atmosphere and the marine environment, not all SAR images contain features of wind streaks, which limits the universal applicability of such methods.

An algorithm of simultaneous WS and WD retrieval (hereinafter called Z-Model1), using CMOD5.N [63] and C-2PO [14], the NRCS of the VV and VH polarizations, and RIA, was proposed [64]. The flowchart for the method is shown in Figure 5(a). The directional ambiguities were resolved by using the different symmetric characteristics of the polarimetric correlation coefficient (PCC) between the VV and VH channels and the NRCS values in quad-polarization. They had odd symmetry and even symmetry with respect to the WD.

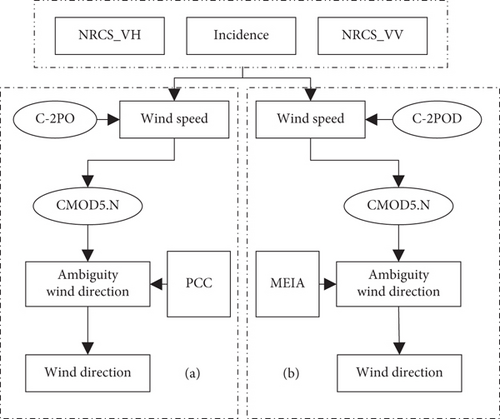
Then, a new model (hereinafter called Z-Model2) was proposed [65], which also achieved the simultaneous inversion of the wind speed and the wind direction by minimizing the cost function constructed by CMOD5.N [63] and C-2POD [65]. Unlike Z-Model1, a parametric two-dimensional sea surface inflow angle model, the model-estimated inflow angle (MEIA) [66, 67], was used to solve the directional ambiguities. The flowchart is shown in Figure 5(b).

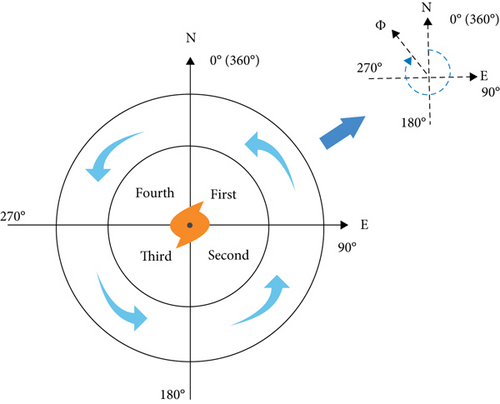
Recently, another new approach [22] (hereinafter called the F-Model) has been proposed regarding extreme weather conditions. This approach uses the local gradient method [38] to estimate tropical cyclone (TC) wind directions, and it removes wind direction ambiguities according to TC SSWFs in the northern direction. The procedure of deblurring the WD is shown in Figure 6, as follows: (1) determine the eye centre position of the TC according to [68], (2) ascertain the quadrant of the proper subimage based on the eye centre positions and the specific subimage position, and (3) derive the unique WD according to the criteria in Table 2.

Table 2. The criteria to derive WD.

Quadrant	The first	The second	The third	The fourth
Φ	(270°, 360°)	(0°, 90°)	(90°, 180°)	(180°, 270°)

Note: where Φ is WD. When the subimage is in the first quadrant, Φ is greater than 270° and less than 360°, and other quadrants and so on.

3.3. Accuracy Verification

The error statistical results of the SAR WD inversion are listed in Table 3. Compared with the SSWF products of the buoy, the numerical model reanalysis data, and the microwave scatterometer, it can be found that the results have good consistency, and the root mean square difference or standard deviation between the data meets the requirements of WD operational accuracy.

Table 3. SAR WS retrieval statistics.

Method	Reference data	Error (°)	SAR data	180° blur	Reference
LG	Situ	26.54 ^∗	Sentinel-1	Yes	La et al. [25]

LG-Mod	Situ	9.4 ^∗	Sentinel-1	Yes	Rana et al. [69]

ILG	ECMWF	21.57 ^∗∗	RADARSAT-2	Yes	Zhou et al. [53]
ILG	CCMP	21.61 ^∗∗	Envisat ASAR	Yes	Zhou et al. [53]

GLCM	ECMWF	39.49 ^∗∗	ENVISAT and RADARSAT-2	Yes	Zheng et al. [59]
GLCM	CCMP	38.90 ^∗∗	ENVISAT and RADARSAT-2	Yes	Zheng et al. [59]

Z-Model1	Situ	22.5 ^∗	RADARSAT-2 fully polarimetric	No	Zhang et al. [64]

Z-Model2	QuikSCAT	19.37 ^∗	RADARSAT-2 dual-polarized	No	Zhang et al. [65]
Z-Model2	Situ	22.22 ^∗	Gaofen-3	No	Wang et al. [60]

F-Model	Buoy	13.3 ^∗	RADARSAT-2 and Sentinel-1A dual-polarized	No	Fan et al. [22]

Note: ∗ and ∗∗ indicate RMSE and root mean square, respectively.

4. Wind Speed Retrieval

WS is the main driving force of upper ocean movement, and it is an important factor affecting wave generation, water mass formation, and ocean current movement [70]. Additionally, WS data have important applications for many areas, such as typhoon intensity monitoring and ocean wind energy resource evaluation [71].

4.1. Methodology

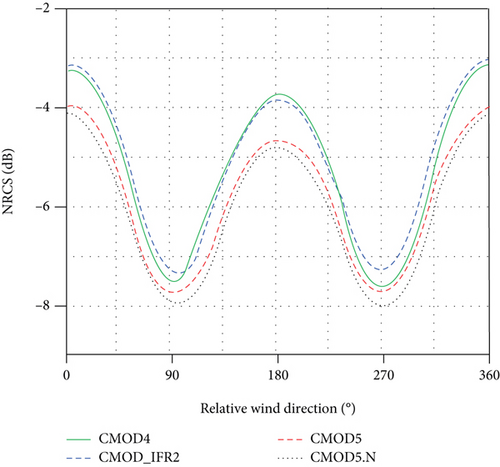
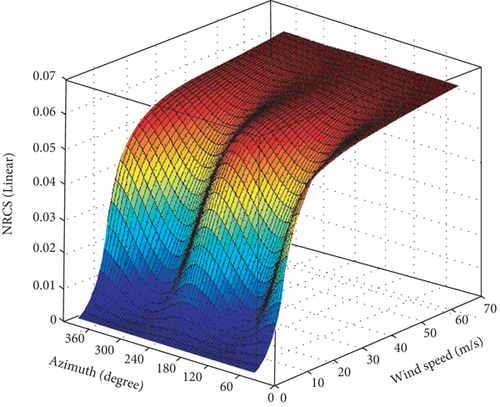
In the microwave band, there is an obvious positive correlation between the intensity of the microwave backscattered signal on the sea surface and the intensity of the WS. For no-WS or extremely low-WS conditions, the sea surface can be regarded as a quasimirror surface. The sea surface echo signal received by the SAR as a side-looking radar is very small. As the WS increases, the sea surface roughness becomes larger, and the sea surface signal is gradually enhanced [27], as shown in Figure 7. The backscattered signal reaches its maximum value when the incident direction of the radar is parallel to the WD, and the intensity of the echo signal when the wind blows toward the radar is slightly stronger than the intensity of the wind away from the radar. The NRCS as a function of the WD relative to the radar observation direction based on different GMFs is shown in Figure 8. The SAR echo signal changes regularly with the WS, which lays the foundation for WS inversion [72, 73].

4.2. Method

In order to quantitatively retrieve the SSWF from the radar backscatter signal, a forward model between the SSWF and the radar backscatter must be established [73, 74]. Models can be divided into two categories: empirical (EP) and electromagnetic (EM) approaches [23]. At present, it is difficult to accurately model the interaction between radar electromagnetic waves and a complicated and rough sea surface, resulting in the accuracy of the microwave remote sensing model of the SSWF based on the physical mechanism being lower than that for the empirical model based on statistics [75–77]. Therefore, studies related to the inversion of an SSWF based on SAR data are mostly based on EP models [4, 11, 27, 78]. EPs based on different polarized modes are introduced in Sections 3.2.1–3.2.3, and EMs are introduced in Section 3.2.4.

4.2.1. Geophysical Model Function

The empirical model describing the quantitative relationship between the radar backscatter signal and the SSWF is called the “geophysical model function (GMF).” The model function must meet the following conditions:

(1)
The corresponding WS and the direction can be calculated from the observations of the spaceborne radar system
(2)
The functions can be tabulated or in the form of functions
(3)
The GMF does not rely on additional meteorological and marine data that is difficult to obtain in real time in business operations. The general form of the GMF is

(21)

where σ⁰, ϕ, and

are the VV NRCS (dB), the included angle (degree) between the WDs, and the radar incident direction, respectively. B₀, B₁, and B₂ are constants determined by the WS, incidence angle, polarized mode, and frequency, and Z is a constant corresponding to the function. The CMOD5 GMF at a 42° incident angle is shown in Figure 9.

GMFs were originally designed to be used in the SSWF inversion of a microwave scatterometer. Then, they underwent long-term operational optimisation. Because the characteristics of the sea surface backscattering signals obtained by a scatterometer and SAR are similar, they are suitable for the SAR SSWF inversion if the SAR has the same radar wave frequency, polarized mode, and incidence angle distribution range as the scatterometer. Commonly used models are CMOD4 [79], CMOD_IFR2 [80], CMOD 5 [81], CMOD 5.N [63], and CMOD 7 [41].

With the accumulation of SAR data, Mouche and Chapron [82] used ENVISAT-ASAR data and the SSWF of ASCAT, and they established the C-band VV-polarized SAR WS GMF, called C_SARMOD. The comparison with the in situ buoy experiments showed that the RMSE was 1.63 m/s [83]. Lu et al. used RADARSAT-2 and Sentinel-1A VV-polarized SAR images and buoy WS observations to establish the model, called C_SARMOD2, which was verified with buoy observation. Its RMSE was 1.84 m/s [24].

It was necessary to convert the HH-polarized SAR data into VV-polarized backscatter coefficients and then use the GMFs (other empirical models for HH-polarized SAR data are introduced in Section 3.2.2). In order to minimize the possible errors caused by the polarized model, Zhang et al. [84] used Envisat ASAR images and ASACT SSWF data to establish the new model called CMODH. The model was available for HH- and VV-polarized SAR without the need for the polarized ratio model. According to the verification with the WS observed by the buoy, its RMSE was 1.66 m/s [85].

4.2.2. Model for HH-Polarized SAR

For the HH-polarized SAR data, the polarized ratio (PR) model and GMFs are generally used for WS inversion [86, 87]. Other methods are used for HH-polarized SAR, such as Komarov’s model [88].

(1) Polarization Ratio Model. For the HH polarimetric SAR, if using CMOD, PR is first used to convert the NRCS from HH polarization to VV polarization, and then, the GMF is used [89]. These models can be divided into two categories: empirical and theoretical models.

(1)1. Empirical PR. The empirical PR contains three categories.

(a)
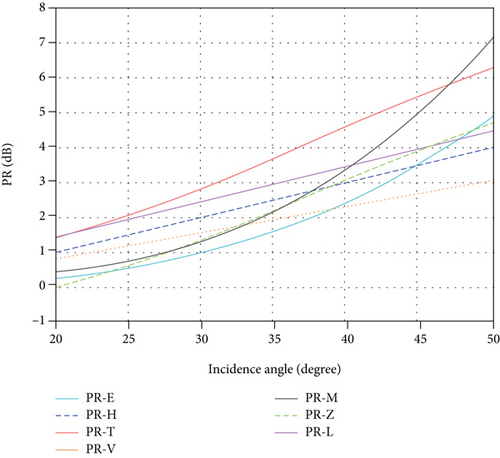
Only Related to the RIA, as shown inTable4. The relationship between the PR and the incident angle for this kind of model is shown in Figure 10.

(b)
PR Depends on the Incidence Angle and the Azimuth Angle [87]. The general expression is as follows:

(22)

(c)
PR Models Related to the WS. For example, Biao and Perrie [18] proposed a PR model considering the influence of the WS:

(23)

where

and Q(θ) = Q₁∗θ + Q₂ (P₁, P₂, Q₁, and Q₁ are constants).

Table 4. PR formula related to incidence angle (θ) only.

PR model	Formula	Coefficient values
PR^T [86]		α = 0.6
PR^H [90]		α = 1.0
PR^V [91]		α = 1.2

PR^E [92]		—

PR^M1 [87]	PR = Aexp(Bθ) + C	A = 0.00799793, B = 0.125465, C = 0.997379
PR^Z1 [18]		A = 0.2828, B = 0.0451, C = 0.2891
PR^L [89]		A = 0.453041, B = 0.0324573, C = 0.524303

(1)2. Theoretical PR. With the widespread applications of spaceborne SAR in the ocean, physical models for the interaction between the ocean surface and radar scattering have been proposed [89], such as the generalised curvature model (GCM) and the two-scale Bragg model [93]. Then, the model should consider the contribution of the wave breaking related to the statistical description of the sea surface [94]. A new physical PR model has extended the improved GCM model [95]. The PRs described above depend on the RIA, WS, and WD [89]. However, the accuracy of the model needs to be further improved, and the application of this kind of PR is rare [96, 97].

(2) Komarov’s Model for HH-Polarized SAR. When estimating the WS using the CMOD and PR for the HH-polarized SAR, the approximate value of the co-PR may introduce a large error. Additionally, the WD provided by the numerical forecast model may introduce new errors. Therefore, Komarov et al. [88] proposed the new model (hereinafter called “Komarov’s model”) based on HH-polarized SAR data without an input WD. The limitation of Komarov’s model is that it is only applicable when the WS < 16 m/s [25]. The general formula can be expressed as

(24)

where V, θ, and

are the WS (m/s), the incidence angle (degree), and the HH NRCS (dB), respectively. The coefficients a₀, a₁, a₂, a₃, a₄, and a₅ are -16.50189, 0.81709, 1.365899, 0.06022, 0.00333, and 0.06981, respectively. The model simulation diagram is shown in Figure 11.

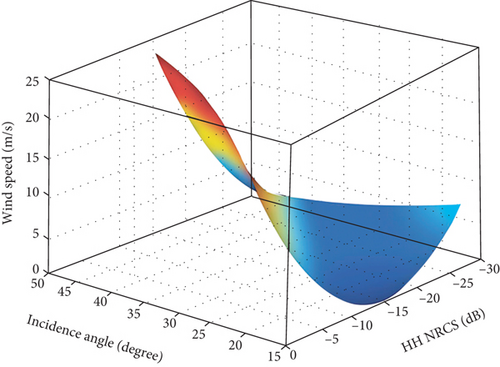
The research [25] shows that (1) for HH-polarized SAR data, Komarov’s model produces better WS estimates than CMOD5.N, which has also been reported in [88], and (2) for VV-polarized SAR data, CMOD5.N produces better WS estimates than Komarov’s model. Additionally, in view of the importance of the wind direction to the GMF, Komarov’s model’s WS inversion effect for the model without consideration of the WD can demonstrate better accuracy.

4.2.3. Model for Cross-Polarized SAR

Cross-polarized SAR has a unique advantage for polarimetric synthetic aperture radar. In 2011, Vachon and Wolfe [17] and Zhang et al. [64] found that the sea surface backscattering signal of C-band cross-polarized SAR was not sensitive to the WD and RIA but rather a linear function of the WS, which could be directly used for WS inversion for the first time [18]. Subsequently, Biao and William [14] found that the cross-polarized SAR echo signal could not easily be saturated for the condition of high WS, and they proposed a model called C-2PO that was suitable for high WS inversion. Zhang et al. [19] found that the sea surface echo signal of C-band cross-polarized SAR was dependent on the incident angle by considering the contribution of the cross-polarized band non-Bragg scattering. Using the observation data for the RADARSAT-2 satellite and a hurricane, an improved C-3PO model function was proposed. Zhu et al. [98] proposed a semiempirical algorithm that considered the influence of the WS and the incident angle on a cross-polarized NRCS. The introduction of cross-polarized SAR observation significantly improved the accuracy of the C-band SAR inversion of an SSWF for a high WS [99–105]. Some representative cross-polarized models are shown in Table 5, and the relationship between WS and VH is shown in Figure 12.

Table 5. GMFs developed for C-band cross-polarized SAR.

Name	Data	Speed (m/s)	Reference
Model-V	RADARSAT-2	<25	Vachon and Wolfe [17]
C-2PO		<25	Zhang et al. [64]
C-2POD		<40	Zhang et al. [14]

Model-H	RADARSAT-2 ScanSAR		Horstmann et al. [15]

Model-Z1-S	RADARSAT-2		Van Zadelhoff et al. [102]
Model-Z1-E			Van Zadelhoff et al. [102]
Model-Z2

S-C2PO	Sentinel-1	<25	Zhang et al. [3]

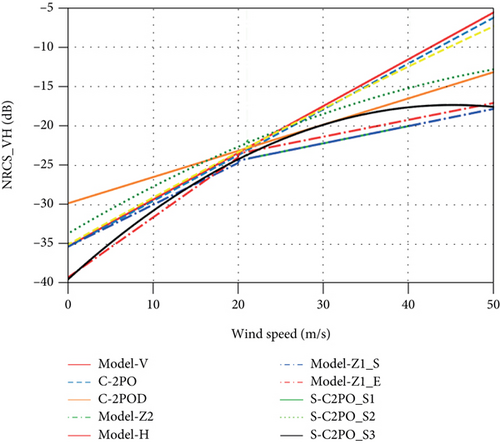
The cross-polarized backscatter coefficients do not saturate at WSs up to 60 m/s [106, 107], and the WS inversion using cross-polarized SAR has higher accuracy than that of the copolarized SAR at wind speeds above 20 m/s [14, 15]. Given that the cross-polarized backscatter coefficients are more suitable than the copolarized backscatter coefficients for SSWF inversion under high WS conditions, the utilisation of cross-polarized SAR data is a new frontier for SAR SSWF inversion [9]. However, the high noise equivalent sigma zero [3] leads to large uncertainty in the WS inversion for low to moderate WS conditions, and thus, there are certain limitations that hinder cross-polarized SAR current use.

4.2.4. Electromagnetic Approach

The physical approach attempts to reveal the relationship between radar scattering and an SSWF based on the principle of electromagnetism (EM) [23]. The EM models are constructed based on quasiexact calculations or the asymptotic method. The former includes the method of moment [108] and the forward-backward method [109] and the latter the composite two-scale model [110], the small slope approximation [111], and the Resonant Curvature Approximation (RCA) [112]. When the range of the RIA is from 20° to 60°, the EM models based on asymptotic calculations are more widely used, since their descriptions are much simpler and they work more rapidly, with similar results. Among the EM models based on the asymptotic method, the NRCS calculated with the approximation models is closer to the EP approach [23, 113].

4.3. Accuracy Verification

The authenticity test of an SSWF retrieved with SAR is the premise of its quantitative application [5, 23]. Table 6 shows the error statistical results of some representative SAR SSWF remote sensing products. After comparison with the fixed buoy, numerical model reanalysis data, and microwave scatterometer SSWF remote sensing products, it can be found that the SAR remote sensing SSWF products have good consistency with the other SSWF data, and the root mean square difference or standard deviation between the data is less than 2.0 m/s. However, the inversion accuracy obtained from different satellites or different polarized data for the same satellite is still different, which is associated with the data quality of the satellite load, calibration accuracy, mode function, and the use of external auxiliary data. Overall, for the conditions of low and medium WSs (<20 m/s), the retrieval accuracy of SAR can be similar to or the same as that of other remote sensing methods. However, for the condition of high WSs, the retrieval of an SSWF by SAR still faces challenges.

Table 6. C-band SAR WS retrieval statistics.

Data	Polarization	Reference data	Error	Speed	Reference
RADARSAT-1	HH	Buoy	1.76	<20	Monaldo et al. [114]
RADARSAT-1	HH	QuikSCAT	1.54	<20	Thompson et al. [115]

ENVISAT/ASAR	VV	Buoy	1.41	<15	Yang et al. [42]
	VV	ASCAT	1.77	<15
	VV	NOGAPS	1.61	<15

Sentinel-1	VV	ASCAT	1.42	<20	Monaldo et al. [40]
	HH	ASCAT	1.48	<25	Monaldo et al. [40]
	VV+VH	SMAP	2.59	<50	Mouche et al. [116]

Gaofen-3	VV	ASCAT	2.04	<20	Ren et al. [117]
	VV	HY2A/SCAT	1.93	<20
	HH	ASCAT	1.85	<20
	HH	HY2A/SCAT	1.73	<20
	HV	NDBC buoys	2.02	<20	Zhu et al. [98]
	VH	NDBC buoys	1.96	<20	Zhu et al. [98]

RADARSAT-2	VH	QuikSCAT	3.63	<40	Zhang et al. [65]
RADARSAT-2	VH	SFMR	2.81	<40	Zhang et al. [104]

Note: the error is the standard deviation or root mean square error, and the units of the error and speed are m/s.

5. Conclusion and Outlook

The WD inversion for the SAR image data is based on the wind streak features in the SAR data. Due to the complexity of the SAR imaging and the variability of the sea and air environment, not all of the SAR images contain clear wind streak features [118, 119]. There are certain limitations in obtaining the WD with this method [64, 120]. Hence, scholars have proposed the inversion of the WD based on numerical calculation methods [121, 122] in view of the fact that there are not many applications of this type of algorithm.

In the WS inversion research, the GMF model has undergone a series of updates and improvements, and the accuracy of the model has been improved. This model is the most widely used. However, at high WSs, there is saturation based on the copolarized data [19, 123]. The cross-polarized model is more suitable for the inversion of the WS in extreme weather (such as hurricanes) [124, 125], but in terms of the applicability and accuracy of the model, there is still a large amount of room for improvement.

Overall, however, the SSWFs retrieved based on SAR data already have similar accuracy to those for other microwave remote sensors, as well as high resolution and strong observation capabilities in coastal waters. This type of retrieval has been operationalized in the meteorological and oceanographic departments of many countries.

With the development of SAR technology, the spatial coverage and continuous observation capabilities of SAR SSWF data will be further improved, and the dynamic and continuous observation of global seas is expected to be achieved.

In terms of SAR wind farm technology, there are still some problems that need to be resolved:

(1)
The WD inversion method based on the features of wind stripes in SAR images still has a lot of room for research
(2)
The inversion of high WS (>35 m/s) still has large uncertainties
(3)
There are few studies considering the interference of rain with the radar backscattered signal on the sea surface
(4)
The method of combining multiplatform and multisource data is used to obtain SSWF information with higher spatial and temporal resolution
(5)
The research on ocean SSWF inversion based on machine learning and deep learning has broad prospects
(6)
For an SSWF, the wave field and the current field are mutually coupled, and the new system of radar satellites provides new opportunities and challenges for sea surface dynamic parameter inversion

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This work was jointly supported by the project of Major scientific and technological innovation in Shandong Province (Y9338301).

References

1 Zhang L., Shi H. Q., Long Z. Y., Du H. D., and Zhang Z. Y., Overview of the ocean wind retrieval from space-borne SAR images, Marine Science Bulletin. (2012) 31, no. 6, 713–720.
Google Scholar
2 Guo Q., Xu X., Zhang K., Li Z., Huang W., Mansaray L. R., Liu W., Wang X., Gao J., and Huang J., Assessing global ocean wind energy resources using multiple satellite data, Remote Sensing. (2018) 10, no. 2, https://doi.org/10.3390/rs10010100, 2-s2.0-85040706713.
10.3390/rs10010100
Web of Science® Google Scholar
3 Zhang K., Huang J., Mansaray L. R., Guo Q., and Wang X., Developing a subswath-based wind speed retrieval model for Sentinel-1 VH-polarized SAR data over the ocean surface, IEEE Transactions on Geoscience and Remote Sensing. (2018) 57, no. 3, 1561–1572.
10.1109/TGRS.2018.2867438
Web of Science® Google Scholar
4 Zhengquan L., Lili S., Hao M., Tao F., and Kuo W., Review of methodologies for offshore wind resource obserrvation and assessment, Advances in Earth Science. (2016) 31, no. 8, 800–810.
Google Scholar
5 Comparison of ocean-surface winds retrieved from QuikSCAT scatterometer and RADARSAT-1 SAR in offshore waters of the U.S. West Coast, IEEE Geoscience and Remote Sensing Letters. (2011) 8, no. 1, 163–167, https://doi.org/10.1109/LGRS.2010.2053345, 2-s2.0-78650928748.
10.1109/LGRS.2010.2053345
Web of Science® Google Scholar
6 Min H., Runyuan K., Lihua W., and Yaoxin Z., Retrieval of sea surface wind field of SAR based on BP neural network-taking the Yangtze River estuary with its adjacent seas as an example, Transactions of Oceanology and Limnology. (2020) 173, no. 2, 37–44.
Google Scholar
7 Zhou X., Yang X., Li Z., Yu Y., Bi H., Ma S., and Li X., Estimation of tropical cyclone parameters and wind fields from SAR images, Science China Earth Sciences. (2013) 56, no. 11, 1977–1987, https://doi.org/10.1007/s11430-013-4633-2, 2-s2.0-84886747799.
10.1007/s11430-013-4633-2
Web of Science® Google Scholar
8 He F., Juzhen C., Yue H., Rui X., Yuhui Z., Xiaowei Z., Zhonghua H., Jingjing X., and Tao X., Ocean surface wind speed retrieve from RADARSAT-2 quad-polarized SAR images, Marine Forecasts. (2021) 38, no. 2, 42–44.
Google Scholar
9 Xiaofeng L., Biao Z., and Xiaofeng Y., Remote sensing of sea surface wind and wave from spaceborne synthetic aperture radar, Journal of Radars. (2020) 9, no. 3, 425–443.
Google Scholar
10 Gerling T. W., Structure of the surface wind field from the Seasat SAR, Journal of Geophysical Research, Oceans. (1986) 91, no. C2, 2308–2320, https://doi.org/10.1029/JC091iC02p02308, 2-s2.0-0022858211.
10.1029/JC091iC02p02308
Google Scholar
11 Jones W. L., Bracalente E. M., and Delnore V. E., The Study of Mesoscale Ocean Winds, 1981, NASA Technical Reports Server.
Google Scholar
12 Zhang W., Jiang Z., Xiang J., and Shi H., Optimal interpolation model for synthetic aperture radar wind retrieval, Frontiers in Earth Science. (2020) 8, 1–16, https://doi.org/10.3389/feart.2020.552833.
10.3389/feart.2020.552833
Web of Science® Google Scholar
13 Lin Z., Ting X., Yiren W., Pingli H., and Xupu G., Wind energy asssessment analysis of Fujian coastal area based on Sentinel-1 synthetic aperture radar images, Journal of Xiamen University. (2020) 3, no. 22, 1–13.
Google Scholar
14 Zhang B. and Perrie W., Cross-polarized synthetic aperture radar: a new potential measurement technique for hurricanes, Bulletin of the American Meteorological Society. (2012) 93, no. 4, 531–541, https://doi.org/10.1175/BAMS-D-11-00001.1, 2-s2.0-84860697372.
10.1175/BAMS-D-11-00001.1
Web of Science® Google Scholar
15 Horstmann J., Falchetti S., Wackerman C., Maresca S., Caruso M. J., and Graber H. C., Tropical cyclone winds retrieved from C-band cross-polarized synthetic aperture radar, IEEE Transactions on Geoscience and Remote Sensing. (2015) 53, no. 5, 2887–2898, https://doi.org/10.1109/TGRS.2014.2366433, 2-s2.0-84921027434.
10.1109/TGRS.2014.2366433
Web of Science® Google Scholar
16 Zhang K., Xu X., Han B., Mansaray L. R., Guo Q., and Huang J., The influence of different spatial resolutions on the retrieval accuracy of sea surface wind speed with C-2PO models using full polarization C-band SAR, IEEE Transactions on Geoscience and Remote Sensing. (2017) 55, no. 9, 5015–5025, https://doi.org/10.1109/TGRS.2017.2700942, 2-s2.0-85028856073.
10.1109/TGRS.2017.2700942
Web of Science® Google Scholar
17 Vachon W. and Wolfe J., C-band cross-polarization wind speed retrieval, Geoscience and Remote Sensing Letters. (2011) 8, no. 3, 456–459, https://doi.org/10.1109/LGRS.2010.2085417, 2-s2.0-79955521849.
10.1109/LGRS.2010.2085417
Web of Science® Google Scholar
18 Biao Z. and Perrie W., Wind speed retrieval from RADARSAT-2 quad-polarization images using a new polarization ratio model, Journal of Geophysical Research, Oceans. (2011) 116, no. C8, https://doi.org/10.1029/2010JC006522, 2-s2.0-80051677832.
10.1029/2010JC006522
Google Scholar
19 Zhang G., Li X., Perrie W., Hwang P. A., Zhang B., and Yang X., A hurricane wind speed retrieval model for C-band RADARSAT-2 cross-polarization ScanSAR images, IEEE Transactions on Geoscience and Remote Sensing. (2017) 55, no. 8, 4766–4774, https://doi.org/10.1109/TGRS.2017.2699622, 2-s2.0-85019851424.
10.1109/TGRS.2017.2699622
Web of Science® Google Scholar
20 Biao Z. and Perrie W., Recent progress on high wind-speed retrieval from multi-polarization SAR imagery: a review, International Journal of Remote Sensing. (2014) 35, no. 11-12, 4031–4045, https://doi.org/10.1080/01431161.2014.916451, 2-s2.0-84902842615.
10.1080/01431161.2014.916451
Web of Science® Google Scholar
21 Zhang B., Guo J., Li Z., Cheng Y., Zhao Y., Boota M. W., Zhang Y., and Feng L., Identifying the spatio-temporal variations of ulva proliferadisasters in all life cycle, Journal of Water and Climate Change. (2021) no. article jwc2021424, https://doi.org/10.2166/wcc.2021.424.
10.2166/wcc.2021.424
Web of Science® Google Scholar
22 Fan S., Zhang B., Mouche A. A., Perrie W., Zhang J. A., and Zhang G., Estimation of wind direction in tropical cyclones using C band dual-polarization synthetic aperture radar, IEEE Transactions on Geoscience and Remote Sensing. (2020) 58, no. 2, 1450–1462, https://doi.org/10.1109/TGRS.2019.2946885.
10.1109/TGRS.2019.2946885
Web of Science® Google Scholar
23 La TV K. A., Comblet F., and Nahum C., Overview of surface wind speed retrieval from C-band SAR images: empirical and electromagnetic approaches, 2017 International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), 2017, Fez, Morocco, 1–4.
Google Scholar
24 Lu Y., Zhang B., Perrie W., Mouche A. A., Li X., and Wang H., A C-band geophysical model function for determining coastal wind speed using synthetic aperture radar, IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing. (2018) 11, no. 7, 2417–2428, https://doi.org/10.1109/JSTARS.2018.2836661, 2-s2.0-85047816062.
10.1109/JSTARS.2018.2836661
Web of Science® Google Scholar
25 La TV K. A., Comblet F., and Nahum C., Exploitation of C-band Sentinel-1 images for high-resolution wind field retrieval in coastal zones (Iroise Coast, France), IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing. (2017) 10, no. 12, 5458–5471, https://doi.org/10.1109/JSTARS.2017.2746349, 2-s2.0-85030788763.
10.1109/JSTARS.2017.2746349
Web of Science® Google Scholar
26 Rana F. M., Adamo M., Pasquariello G., De Carolis G., Morelli S., and Bovenga F., A simplified local gradient method for the retrieval of SAR derived sea surface wind directions, 10th European Conference on Synthetic Aperture Radar (10), 2014, Berlin, Germany, 1–4.
Google Scholar
27 Li X., Zhang J. A., Yang X., Pichel W. G., DeMaria M., Long D., and Li Z., Tropical cyclone morphology from spaceborne synthetic aperture radar, Bulletin of the American Meteorological Society. (2013) 94, no. 2, 215–230, https://doi.org/10.1175/BAMS-D-11-00211.1, 2-s2.0-84875276627.
10.1175/BAMS-D-11-00211.1
Web of Science® Google Scholar
28 Gerling T., Partitioning sequences and arrays of directional ocean wave spectra into component wave systems, Journal of Atmospheric and Oceanic Technology. (1992) 9, no. 4, 444–458, https://doi.org/10.1175/1520-0426(1992)009<0444:PSAAOD>2.0.CO;2.
10.1175/1520-0426(1992)009<0444:PSAAOD>2.0.CO;2
Web of Science® Google Scholar
29 Alpers W. and Brummer B., Atmospheric boundary layer rolls observed by the synthetic aperture radar aboard the ERS-1 satellite, Geoscience and Remote Sensing Symposium. (1994) 99, no. C6, article 12613, https://doi.org/10.1029/94JC00421.
10.1029/94JC00421
Google Scholar
30 Drobinski P. and Foster R. C., On the origin of near-surface streaks in the neutrally-stratified planetary boundary layer, Boundary-Layer Meteorology. Boundary-Layer Meteorology. (2003) 108, no. 2, 247–256, https://doi.org/10.1023/A:1024100125735, 2-s2.0-0038007435.
10.1023/A:1024100125735
Web of Science® Google Scholar
31 Brown D., Roll vortices in the planetary boundary layer: a review, Boundary-Layer Meteorology. (1993) 65, no. 3, 215–248, https://doi.org/10.1007/BF00705527, 2-s2.0-0027790313.
10.1007/BF00705527
Web of Science® Google Scholar
32 Weissman D. E., King D. B., and Thompson T. W., Relationship between hurricane surface winds and L-band radar backscatter from the sea surface, Journal of Applied Meteorology. (1979) 18, no. 8, 1023–1034, https://doi.org/10.1175/1520-0450(1979)018<1023:RBHSWA>2.0.CO;2.
10.1175/1520-0450(1979)018<1023:RBHSWA>2.0.CO;2
Google Scholar
33 Alpers W. and Brummer B., Atmospheric boundary layer rolls observed by the synthetic aperture radar aboard the ERS-1 satellite, Journal of Geophysical Research, Oceans. (1994) 99, no. C6, 12613–12621, https://doi.org/10.1029/94JC00421.
10.1029/94JC00421
Web of Science® Google Scholar
34 Fu L. and Holt B., SEASAT Views Oceans and Sea Ice with Synthetic Aperture Radar, 1982, JPL Publication.
Google Scholar
35 Khanna S. and Brasseur J. G., Three-dimensional buoyancy- and shear-induced local structure of the atmospheric boundary layer, Journal of the Atmospheric Sciences. (1998) 55, no. 5, 710–743, https://doi.org/10.1175/1520-0469(1998)055<0710:TDBASI>2.0.CO;2.
10.1175/1520-0469(1998)055<0710:TDBASI>2.0.CO;2
Web of Science® Google Scholar
36 Weckwerth T. M., Wilson J. W., Wakimoto R. M., and Crook N. A., Horizontal convective rolls: determining the environmental conditions supporting their existence and characteristics, Monthly Weather Review. (1997) 125, no. 4.
10.1175/1520-0493(1997)125<0505:HCRDTE>2.0.CO;2
Web of Science® Google Scholar
37 Tammy M., An observational study of the evolution of horizontal convective rolls, Monthly Weather Review. (1999) 127, no. 9, 2160–2179, https://doi.org/10.1175/1520-0493(1999)127<2160:AOSOTE>2.0.CO;2.
10.1175/1520-0493(1999)127<2160:AOSOTE>2.0.CO;2
Web of Science® Google Scholar
38 Wolfgang K., Directional analysis of SAR images aiming at wind direction, IEEE Transactions on Geoscience and Remote Sensing. (2004) 42, no. 4, 702–710, https://doi.org/10.1109/TGRS.2003.818811, 2-s2.0-2442593185.
10.1109/TGRS.2003.818811
Web of Science® Google Scholar
39 Koch W. and Feser F., Relationship between SAR-derived wind vectors and wind at 10-m height represented by a mesoscale model, Monthly Weather Review. (2006) 134, no. 5, 1505–1517, https://doi.org/10.1175/MWR3134.1, 2-s2.0-33744773858.
10.1175/MWR3134.1
Web of Science® Google Scholar
40 Monaldo F., Jackson C., Li X., and Pichel W. G., Preliminary evaluation of sentinel-1A wind speed retrievals, IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing. (2016) 9, no. 6, 2638–2642, https://doi.org/10.1109/JSTARS.2015.2504324, 2-s2.0-84954048417.
10.1109/JSTARS.2015.2504324
Web of Science® Google Scholar
41 Stoffelen A., Verspeek J., Vogelzang J., and Verhoef A., The CMOD7 geophysical model function for ASCAT and ERS wind retrievals, Journal of Selected Topics in Applied Earth Observations and Remote Sensing. (2017) 10, no. 5, 2123–2134, https://doi.org/10.1109/JSTARS.2017.2681806, 2-s2.0-85017100851.
10.1109/JSTARS.2017.2681806
Web of Science® Google Scholar
42 Yang X., Li X., Pichel W. G., and Li Z., Comparison of ocean surface winds from ENVISAT ASAR, MetOp ASCAT scatterometer, buoy measurements, and NOGAPS model, IEEE Transactions on Geoscience and Remote Sensing. (2011) 49, no. 12, 4743–4750, https://doi.org/10.1109/TGRS.2011.2159802, 2-s2.0-82155167671.
10.1109/TGRS.2011.2159802
Web of Science® Google Scholar
43 Brown R. A., A secondary flow model for the planetary boundary layer, Journal of Atmospheric Sciences. (1970) 27, no. 5, 742–757, https://doi.org/10.1175/1520-0469(1970)027<0742:ASFMFT>2.0.CO;2.
10.1175/1520-0469(1970)027<0742:ASFMFT>2.0.CO;2
Web of Science® Google Scholar
44 Deardorff J. W., Numerical investigation of neutral and unstable planetary boundary layers, Journal of the Atmospheric Sciences. (1972) 29, no. 1, 91–115, https://doi.org/10.1175/1520-0469(1972)029<0091:NIONAU>2.0.CO;2.
10.1175/1520-0469(1972)029<0091:NIONAU>2.0.CO;2
Web of Science® Google Scholar
45 Fetterer F., Gineris D., and Wackerman C. C., Validating a scatterometer wind algorithm for ERS-1 SAR, IEEE Transactions on Geoscience and Remote Sensing. (2002) 36, no. 2, 479–492, https://doi.org/10.1109/36.662731, 2-s2.0-0032026220.
10.1109/36.662731
Google Scholar
46 Tian S., Huang X., Li H., Wang H., Li X., and Cheng P., Wind field retrieval of South China Sea based on Gaussian-FFT method, Journal of Geo-information Science. (2016) 18, no. 11, 1544–1550.
Google Scholar
47 Xian-yun Q. I., Yun-xuan Z. H., Bo T. I., and Peng Y. U., Sea surface wind vector retrieval of off the Yangtze estuary based on Sentinel-1A, Journal of East China Normal University (Natural Science). (2017) 6, no. 12, 126–136, https://doi.org/10.3969/j.issn.1000-5641.2017.06.012.
10.3969/j.issn.1000-5641.2017.06.012
Google Scholar
48 Rana F. M. and Adamo M., Multi-scale LG-mod analysis for a more reliable SAR sea surface wind directions retrieval, Remote Sensing. (2021) 13, no. 3, 410–424, https://doi.org/10.3390/rs13030410.
10.3390/rs13030410
Web of Science® Google Scholar
49 Zhang L., Shi H., Du H., Chen X., and Du H., Estimation of sea surface wind direction using spaceborne SAR images and wavelet analysis, Journal of Remote Sensing. (2014) 18, no. 1, 215–230.
Google Scholar
50 Guanyu C., Weihua A., Yuxin C., Shurui Y., and Lingfeng Y., Research on ocean wind variational fusion method based on space-borne SAR and model data, Journal of Marine Meteorology. (2017) 37, no. 4, 65–74.
Google Scholar
51 He Y., Perrie W., Zou Q., and Vachon P. W., A new wind vector algorithm for C-band SAR, IEEE Transactions on Geoscience and Remote Sensing. (2005) 43, no. 7, 1453–1458, https://doi.org/10.1109/TGRS.2005.848411, 2-s2.0-23844457277.
10.1109/TGRS.2005.848411
Web of Science® Google Scholar
52 Rana F. M., Adamo M., Pasquariello G., De Carolis G., and Morelli S., LG-Mod: a modified local gradient (LG) method to retrieve SAR sea surface wind directions in marine coastal areas, Journal of Sensors. (2016) 2016, no. 7, 9565208, https://doi.org/10.1155/2016/9565208, 2-s2.0-84954149309.
10.1155/2016/9565208
Web of Science® Google Scholar
53 Zhou L., Zheng G., Li X., Yang J., Ren L., Chen P., Zhang H., and Lou X., An improved local gradient method for sea surface wind direction retrieval from SAR imagery, Remote Sensing. (2017) 9, no. 7, 1–17, https://doi.org/10.3390/rs9070671, 2-s2.0-85022329077.
10.3390/rs9070671
Web of Science® Google Scholar
54 Yong D., Wind direction estimation from SAR images of the ocean using wavelet analysis, Canadian Journal of Remote Sensing. (2002) 28, no. 3, 498–509, https://doi.org/10.5589/m02-029, 2-s2.0-0142054252.
10.5589/m02-029
Web of Science® Google Scholar
55 Fichaux N. and Ranchin T., Combined extraction of high spatial resolution wind speed and wind direction from SAR images : a new approach using wavelet transform, Canadian Journal of Remote Sensing. (2002) 28, no. 3, 510–516, https://doi.org/10.5589/m02-038, 2-s2.0-0242491195.
10.5589/m02-038
Web of Science® Google Scholar
56 Wackerman C., Horstmann J., and Koch W., Operational estimation of coastal wind vectors from RADARSAT SAR imagery, IEEE International Geoscience and Remote Sensing Symposium. (2003) 2, no. 3CH37477, 1270–1272, https://doi.org/10.1109/IGARSS.2003.1294079.
10.1109/IGARSS.2003.1294079
Google Scholar
57 Zhuhui J., Sixun H., Rang H., and Chengteng Z., Reguilarization method to retrieve synthetic aperture redar sea surface wind, Acta Physica Sinica. (2011) 60, no. 6, 1–8.
Web of Science® Google Scholar
58 Zhu-Hui J., Si-Xun H., Han-Qing S., Wei Z., and Biao W., A new research on sea surface wind direction retrieval of synthetic aperture radar image, Acta Physica Sinica. (2011) 60, no. 10, 108402–108408, https://doi.org/10.7498/aps.60.108402.
10.7498/aps.60.108402
Web of Science® Google Scholar
59 Zheng G., Li X., Zhou L., Yang J., Ren L., Chen P., Zhang H., and Lou X., Development of a gray-level co-occurrence matrix-based texture orientation estimation method and its application in sea surface wind direction retrieval from SAR imagery, IEEE Transactions on Geoscience and Remote Sensing. (2018) 56, no. 9, 5244–5260, https://doi.org/10.1109/TGRS.2018.2812778, 2-s2.0-85045221782.
10.1109/TGRS.2018.2812778
Web of Science® Google Scholar
60 Wang H., Yang J., Mouche A., Shao W., Zhu J., Ren L., and Xie C., GF-3 SAR ocean wind retrieval: the first view and preliminary assessment, Remote Sensing. (2017) 9, no. 7, 1–12, https://doi.org/10.3390/rs9070694, 2-s2.0-85022328435.
10.3390/rs9070694
Web of Science® Google Scholar
61 Wang Y. B. and Wei T., Numerical differentiation for two-dimensional scattered data, Journal of Mathematical Analysis and Applications. (2005) 312, no. 1, 121–137, https://doi.org/10.1016/j.jmaa.2005.03.025, 2-s2.0-27644587566.
10.1016/j.jmaa.2005.03.025
Web of Science® Google Scholar
62 Yegui W., Qifa C., and Sixun H., A new method for calculating the derivation of meteorological observational data, Acta Physica Sinica. (2010) 59, no. 6, 4359–4368, https://doi.org/10.7498/aps.59.4359.
10.7498/aps.59.4359
Web of Science® Google Scholar
63 Hersbach H., Comparison of C-band scatterometer CMOD5.N equivalent neutral winds with ECMWF, journal of Atmopheric and Oceanic Technology. (2010) 27, no. 4, 721–736, https://doi.org/10.1175/2009JTECHO698.1, 2-s2.0-77953491253.
10.1175/2009JTECHO698.1
Web of Science® Google Scholar
64 Zhang B., Perrie W., Vachon P. W., Li X., Pichel W. G., Guo J., and He Y., Ocean vector winds retrieval from C-band fully polarimetric SAR measurements, IEEE Transactions on Geoscience and Remote Sensing. (2012) 50, no. 11, 4252–4261, https://doi.org/10.1109/TGRS.2012.2194157, 2-s2.0-84869509831.
10.1109/TGRS.2012.2194157
Web of Science® Google Scholar
65 Zhang B., Perrie W., Zhang J. A., Uhlhorn E. W., and He Y., High-resolution hurricane vector winds from C-band dualpolarization SAR observations, Journal of Atmospheric and Oceanic Technology. (2014) 31, no. 2, 272–286, https://doi.org/10.1175/JTECH-D-13-00006.1, 2-s2.0-84893954027.
10.1175/JTECH-D-13-00006.1
CAS Web of Science® Google Scholar
66 Du Y. and Vachon P. W., Characterization of hurricane eyes in RADARSAT-1 images with wavelet analysis, Canadian Journal of Remote Sensing. (2003) 29, no. 4, 491–498, https://doi.org/10.5589/m03-020, 2-s2.0-0142028012.
10.5589/m03-020
Web of Science® Google Scholar
67 Zhang J. A. and Uhlhorn E. W., Hurricane Sea surface inflow angle and an observation-based parametric model, Monthly Weather Review. (2012) 140, no. 11, 3587–3605, https://doi.org/10.1175/MWR-D-11-00339.1, 2-s2.0-84871909127.
10.1175/MWR-D-11-00339.1
Web of Science® Google Scholar
68 Zhang G., Zhang B., Perrie W., Xu Q., and He Y., A hurricane tangential wind profile estimation method for C-band crosspolarization SAR, IEEE Transactions on Geoscience and Remote Sensing. (2014) 52, no. 11, 7186–7194, https://doi.org/10.1109/TGRS.2014.2308839, 2-s2.0-84902117829.
10.1109/TGRS.2014.2308839
Web of Science® Google Scholar
69 Rana F. M., Adamo M., Lucas R., and Blonda P., Sea surface wind retrieval in coastal areas by means of Sentinel-1 and numerical weather prediction model data, Remote Sensing of Environment. (2019) 225, 379–391, https://doi.org/10.1016/j.rse.2019.03.019, 2-s2.0-85063392503.
10.1016/j.rse.2019.03.019
Web of Science® Google Scholar
70 Keramea P., Spanoudaki K., Zodiatis G., Gikas G., and Sylaios G., Oil spill modeling: a critical review on current trends, perspectives, and challenges, Journal of Marine Science and Engineering. (2021) 9, no. 2, https://doi.org/10.3390/jmse9020181.
10.3390/jmse9020181
Web of Science® Google Scholar
71 Bryant K. M. and Akbar M., An exploration of wind stress calculation techniques in hurricane storm surge modeling, Journal of Marine Science and Engineering. (2016) 4, no. 3, https://doi.org/10.3390/jmse4030058, 2-s2.0-85019912688.
10.3390/jmse4030058
PubMed Web of Science® Google Scholar
72 Apel J. R., An improved model of the ocean surface wave vector spectrum and its effects on radar backscatter, Journal of Geophysical Research, Oceans. (1994) 99, no. C8, https://doi.org/10.1029/94JC00846.
10.1029/94JC00846
Google Scholar
73 Du Y., Yang X., Chen K. S., Ma W., and Li Z., An improved spectrum model for sea surface radar backscattering at L-band, Remote Sensing. (2017) 9, no. 8, https://doi.org/10.3390/rs9080776, 2-s2.0-85028346334.
10.3390/rs9080776
Web of Science® Google Scholar
74 Chen K. S., Fung A. K., and Weissman D. A., A backscattering model for ocean surface, IEEE Transactions on Geoscience and Remote Sensing. (1992) 30, no. 4, 811–817, https://doi.org/10.1109/36.158877, 2-s2.0-0026896985.
10.1109/36.158877
CAS PubMed Web of Science® Google Scholar
75 Hwang P. A. and Plant W. J., An analysis of the effects of swell and surface roughness spectra on microwave backscatter from the ocean, Journal of Geophysical Research, Oceans. (2010) 115, no. C4, https://doi.org/10.1029/2009JC005558, 2-s2.0-77953548257.
10.1029/2009JC005558
Google Scholar
76 Romeiser R., Alpers W., and Wismann V., An improved composite surface model for the radar backscattering cross section of the ocean surface: 1. Theory of the model and optimization/validation by scatterometer data, Journal of Geophysical Research, Oceans. (1997) 102, no. C11, 25237–25250, https://doi.org/10.1029/97JC00190, 2-s2.0-1642310554.
10.1029/97JC00190
Web of Science® Google Scholar
77 Dengfeng X., Kunshan C., and Xiaofeng Y., Effects of wind wave spectra on radar backscatter from sea surface at different microwave bands: a numerical study, IEEE Transactions on Geoscience and Remote Sensing. (2019) 57, no. 9, 6325–6334, https://doi.org/10.1109/TGRS.2019.2905558, 2-s2.0-85072023971.
10.1109/TGRS.2019.2905558
Web of Science® Google Scholar
78 Portabella M., Stoffelen A., and Johannessen J. A., Toward an optimal inversion method for synthetic aperture radar wind retrieval, Journal of Geophysical Research-Atmospheres. (2002) 107, no. C8, 1–13, https://doi.org/10.1029/2001JC000925.
10.1029/2001JC000925
Web of Science® Google Scholar
79 Stoffelen B. A. and Anderson D., Ambiguity removal and assimilation of scatterometer data, Quarterly Journal of the Royal Meteorological Society. (1997) 123, no. 538, 491–518.
10.1002/qj.49712353812
Web of Science® Google Scholar
80 Quilfen Y., Chapron B., Elfouhaily T., Katsaros K., and Tournadre J., Observation of tropical cyclones by high-resolution scatterometry, Journal of Geophysical Research, Oceans. (1998) 103, no. C4, 7767–7786, https://doi.org/10.1029/97JC01911.
10.1029/97JC01911
Google Scholar
81 Hersbach H., Stoffelen A., and Haan S. D., CMOD5: an improved geophysical model function for ERS C-band scatterometry, Journal of Geophysical Research, Oceans. (2003) 112, no. C03006, 1–18.
Google Scholar
82 Mouche A. and Chapron B., GlobalC-bandEnvisat,RADARSAT-2 andSentinel-1SARmeasurements in copolarization and cross-polarization, Journal of Geophysical Research, Oceans. (2015) 120, no. 11, 7195–7207, https://doi.org/10.1002/2015JC011149, 2-s2.0-84956757427.
10.1002/2015JC011149
Web of Science® Google Scholar
83 Lin B., Shao W., Li X., Li H., Du X., Ji Q., and Cai L., Development and validation of an ocean wave retrieval algorithm for VV-polarization Sentinel-1 SAR data, Acta Oceanologica Sinica. (2017) 36, no. 7, 95–101, https://doi.org/10.1007/s13131-017-1089-9, 2-s2.0-85021625158.
10.1007/s13131-017-1089-9
CAS Web of Science® Google Scholar
84 Zhang B., Mouche A., Lu Y., Perrie W., Zhang G., and Wang H., A geophysical model function for wind speed retrieval from C-band HHpolarized synthetic aperture radar, IEEE Geoscience and Remote Sensing Letters. (2019) 16, no. 10, 1521–1525, https://doi.org/10.1109/LGRS.2019.2905578.
10.1109/LGRS.2019.2905578
Web of Science® Google Scholar
85 Lu Y., Zhang B., Perrie W., Mouche A., and Zhang G., CMODH validation for C-band synthetic aperture radar HH polarization wind retrieval over the ocean, IEEE Geoscience and Remote Sensing Letters. (2020) 99, no. 10, 1–5, https://doi.org/10.1109/LGRS.2020.2967811.
10.1109/LGRS.2020.2967811
Google Scholar
86 Thompson D. R., Elfouhaily T. M., and Chaoron B., Polarization ratio for microwave backscattering from the ocean surface at low to moderate incidence angles, Proceedings of the 1998 Geoscience and Remote Sensing Symposium Proceedings, 1998, Seattle, WA, USA, 1671–1673.
Google Scholar
87 Mouche A. A., Hauser D., Daloze J. F., and Guerin C., Dual-polarization measurements at C-band over the ocean: results from airborne radar observations and comparison with ENVISAT ASAR data, IEEE Transactions on Geoscience and Remote Sensing. (2005) 43, no. 4, 753–769, https://doi.org/10.1109/TGRS.2005.843951, 2-s2.0-16444372776.
10.1109/TGRS.2005.843951
Web of Science® Google Scholar
88 Komarov A. S., Zabeline V., and Barber D. G., Ocean surface wind speed retrieval from C-band SAR images without wind direction input, IEEE Transactions on Geoscience and Remote Sensing. (2014) 52, no. 2, 980–990, https://doi.org/10.1109/TGRS.2013.2246171, 2-s2.0-84890965408.
10.1109/TGRS.2013.2246171
Web of Science® Google Scholar
89 Liu G., Yang X., Li X., Zhang B., Pichel W., Li Z., and Zhou X., A systematic comparison of the effect of polarization ratio models on sea surface wind retrieval from C-band synthetic aperture radar, IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing. (2013) 6, no. 3, 1100–1108, https://doi.org/10.1109/JSTARS.2013.2242848, 2-s2.0-84880284536.
10.1109/JSTARS.2013.2242848
Web of Science® Google Scholar
90 Horstmann J., Koch W., Lehner S., and Tonboe R., Wind retrieval over the ocean using synthetic aperture radar with C-band HH polarization, IEEE Transactions on Geoscience and Remote Sensing. (2000) 38, no. 5, 2122–2131, https://doi.org/10.1109/36.868871, 2-s2.0-0034271449.
10.1109/36.868871
Web of Science® Google Scholar
91 Vachon P. W. and Dobson F. W., Wind retrieval from RADARSAT SAR images: selection of a suitable C-band HH polarization wind retrieval model, Canadian Journal of Remote Sensing. (2000) 26, no. 4, 306–313, https://doi.org/10.1080/07038992.2000.10874781, 2-s2.0-0034239834.
10.1080/07038992.2000.10874781
Google Scholar
92 Elfouhaily T., Physical Modeling of Electromagnetic Backscatter from the Ocean Surface; Application to Retrieval of Wind Fields and Wind Stress by Remote Sensing of the Marine Atmospheric Boundary Layer, 1996, University Paris VII, France.
Google Scholar
93 Engen G., Friestad-Pedersen I., Johnsen H., and Elfouhaily T., Curvature effects in ocean surface scattering, IEEE International Geoscience and Remote Sensing Symposium. (2003) 1, no. 3CH37477, 224–226, https://doi.org/10.1109/TAP.2006.874309, 2-s2.0-33646502638.
10.1109/TAP.2006.874309
Google Scholar
94 Phillips O. M., Spectral and statistical properties of the equilibrium range in wind-generated gravity-waves, Journal of Fluid Mechanics. (1985) 156, 505–531, https://doi.org/10.1017/S0022112085002221, 2-s2.0-0021830430.
10.1017/S0022112085002221
Web of Science® Google Scholar
95 Johnsen H., Engen G., and Guitton G., Sea-surface polarization ratio from Envisat ASAR AP data, IEEE Transactions on Geoscience and Remote Sensing. (2008) 46, no. 11, 3637–3646, https://doi.org/10.1109/TGRS.2008.2001061, 2-s2.0-56849122888.
10.1109/TGRS.2008.2001061
Web of Science® Google Scholar
96 Kudryavtsev V., Hauser D., Caudal G., and Chapron B., A semiempirical model of the normalized radar cross-section of the sea surface-1. Background model, Journal of Geophysical Research, Oceans. (2003) 108, no. C3, 2–24, https://doi.org/10.1029/2001JC001003.
10.1029/2001JC001003
Google Scholar
97 Mouche A., Hauser D., and Kudryavtsev V., Radar scattering of the ocean surface and sea-roughness properties: a combined analysis from dual-polarizations airborne radar observations and models in C band, Journal of Geophysical Research, Oceans. (2006) 111, no. C9, 1–18, https://doi.org/10.1029/2005JC003166, 2-s2.0-34347224801.
10.1029/2005JC003166
Google Scholar
98 Zhu S., Shao W., Marino A., Sun J., and Yuan X., Semi-empirical algorithm for wind speed retrieval from Gaofen-3 quad-polarization strip mode SAR data, Journal of Ocean University of China. (2020) 19, no. 1, 23–35, https://doi.org/10.1007/s11802-020-4215-9, 2-s2.0-85073933777.
10.1007/s11802-020-4215-9
Web of Science® Google Scholar
99 Troitskaya Y., Abramov V., Baidakov G., Ermakova O., Zuikova E., Sergeev D., Ermoshkin A., Kazakov V., Kandaurov A., Rusakov N., and Poplavsky E., Cross-polarization GMF for high wind speed and surface stress retrieval, Journal of Geophysical Research, Oceans. (2018) 123, no. 8, 5842–5855, https://doi.org/10.1029/2018JC014090, 2-s2.0-85052436323.
10.1029/2018JC014090
Web of Science® Google Scholar
100 Hwang P. A., Stoffelen A., van Zadelhoff G. J., Perrie W., Zhang B., Li H., and Shen H., Cross-polarization geophysical model function for C-band radar backscattering from the ocean surface and wind speed retrieval, Journal of Geophysical Research. (2015) 120, no. 2, 893–909, https://doi.org/10.1002/2014JC010439, 2-s2.0-85027956508.
10.1002/2014JC010439
Web of Science® Google Scholar
101 Hwang P. A., Perrie W., and Biao Zhang, Cross-polarization radar backscattering from the ocean surface and its dependence on wind velocity, IEEE Geoscience and Remote Sensing Letters. (2014) 11, no. 12, 2188–2192, https://doi.org/10.1109/LGRS.2014.2324276, 2-s2.0-84903520095.
10.1109/LGRS.2014.2324276
Web of Science® Google Scholar
102 Van Zadelhoff G. J., Stoffelen A., Vachon P. W., Wolfe J., Horstmann J., and Belmonte Rivas M., Retrieving hurricane wind speeds using crosspolarization C-band measurements, Atmospheric Measurement Techniques. (2014) 7, no. 2, 437–449, https://doi.org/10.5194/amt-7-437-2014, 2-s2.0-84893858250.
10.5194/amt-7-437-2014
Web of Science® Google Scholar
103 Ye X., Lin M., Zheng Q., Yuan X., Liang C., Zhang B., and Zhang J., A typhoon wind-field retrieval method for the dualpolarization SAR imagery, IEEE Geoscience and Remote Sensing Letters. (2019) 16, no. 10, 1511–1515, https://doi.org/10.1109/LGRS.2019.2902418.
10.1109/LGRS.2019.2902418
Web of Science® Google Scholar
104 Zhang G., Perrie W., Li X., and Zhang J. A., A hurricane morphology and sea surface wind vector estimation model based on C-band cross-polarization SAR imagery, IEEE Transactions on Geoscience and Remote Sensing. (2017) 55, no. 3, 1743–1751, https://doi.org/10.1109/TGRS.2016.2631663, 2-s2.0-85006887675.
10.1109/TGRS.2016.2631663
Web of Science® Google Scholar
105 Shao W., Yuan X., Sheng Y., Sun J., Zhou W., and Zhang Q., Development of wind speed retrieval from crosspolarization Chinese gaofen-3 synthetic aperture radar in typhoons, Sensors. (2018) 18, no. 2, 1–18.
10.3390/s18020412
CAS Web of Science® Google Scholar
106 Sapp J., Chang P., Jelenak Z., Frasier S., and Hartley T., Cross-polarized C-band sea-surface NRCS observations in extreme winds, IGARSS 2016-2016 IEEE International Geoscience and Remote Sensing Symposium IEEE, 2016, Beijing, China, 2243–2246, https://doi.org/10.1109/IGARSS.2016.7729579, 2-s2.0-85007452815.
10.1109/IGARSS.2016.7729579
Google Scholar
107 Sapp J. W., Alsweiss S. O., Jelenak Z., and Chang P. S., Airborne co-polarization and cross-polarization observations of the ocean-surface NRCS at C-band, IEEE Transactions on Geoscience and Remote Sensing. (2016) 54, no. 10, 5975–5992, https://doi.org/10.1109/TGRS.2016.2578048, 2-s2.0-84979009512.
10.1109/TGRS.2016.2578048
Web of Science® Google Scholar
108 Colliander A. and YlÄ-Oijala P., Electromagnetic scattering from rough surface using single integral equation and adaptive integral method, IEEE Transactions on Geoscience and Remote Sensing. (2007) 55, no. 12, 3639–3646, https://doi.org/10.1109/TAP.2007.910337, 2-s2.0-37249027710.
10.1109/TAP.2007.910337
Google Scholar
109 Holliday D., DeRaad L. L., and St-Cyr G. J., Forward-backward: a new method for computing low-grazing angle scattering, IEEE Transactions on Geoscience and Remote Sensing. (1996) 44, no. 5, https://doi.org/10.1109/8.496263, 2-s2.0-0030150882.
10.1109/8.496263
Google Scholar
110 Khenchaf A., Bistatic scattering and depolarization by randomly rough surfaces: application to the natural rough surfaces in X-band, Waves in Random Media. (2001) 11, no. 2, 61–89, https://doi.org/10.1088/0959-7174/11/2/301, 2-s2.0-0035304327.
10.1088/0959-7174/11/2/301
Google Scholar
111 Voronovich A. G., Small slope approximation in wave scattering from rough surfaces, Societ Physics-JETP. (1985) 62, 65–70.
Google Scholar
112 Mouche A., Chapron B., Reul N., Hauser D., and Quilfen Y., Importance of the sea surface curvature to interpret the normalized radar cross section, Journal of Geophysical Research, Oceans. (2007) 112, no. C10, 1–12, https://doi.org/10.1029/2006JC004010, 2-s2.0-37349122748.
10.1029/2006JC004010
Google Scholar
113 Thompson D. R., Horstmann J., Mouche A., Winstead N. S., Sterner R., and Monaldo F. M., Comparison of high-resolution wind fields extracted from TerraSAR-X SAR imagery with predictions from the WRF mesoscale model, Journal of Geophysical Research, Oceans. (2012) 117, no. C2, https://doi.org/10.1029/2011JC007526, 2-s2.0-84857824165.
10.1029/2011JC007526
Google Scholar
114 Monaldo F. M., Thompson D. R., Beal R. C., Pichel W. G., and Clemente-Colon P., Comparison of SAR-derived wind speed with model predictions and ocean buoy measurements, IEEE Transactions on Geoscience and Remote Sensing. (2001) 39, no. 12, 2587–2600, https://doi.org/10.1109/36.974994, 2-s2.0-0035696814.
10.1109/36.974994
Web of Science® Google Scholar
115 Thompson D. R., Monaldo F. M., Beal R. C., Winstead N. S., Pichel W. G., and Clemente-Colon P., Combined estimates improve high-resolution coastal wind mapping, Eos, Transactions of the American Geophysical Union. (2001) 82, no. 41, 469–474, https://doi.org/10.1029/01EO00278, 2-s2.0-0010787225.
10.1029/01EO00278
Google Scholar
116 Mouche A. A., Chapron B., Zhang B., and Husson R., Combined co- and cross-polarized SAR measurements under extreme wind conditions, IEEE Transactions on Geoscience and Remote Sensing. (2017) 55, no. 12, 6746–6755, https://doi.org/10.1109/TGRS.2017.2732508, 2-s2.0-85028525297.
10.1109/TGRS.2017.2732508
Web of Science® Google Scholar
117 Ren L., Yang J., Mouche A. A., Wang H., Zheng G., Wang J., Zhang H., Lou X., and Chen P., Assessments of ocean wind retrieval schemes used for Chinese gaofen-3 synthetic aperture radar co-polarized data, IEEE Transactions on Geoscience and Remote Sensing. (2019) 57, no. 9, 7075–7085, https://doi.org/10.1109/TGRS.2019.2911325, 2-s2.0-85072052636.
10.1109/TGRS.2019.2911325
Web of Science® Google Scholar
118 Cheng Y. X., Ai W. H., Kong Y., and Zhao X. B., Ocean wind retrieval from spaceborne synthetic aperture radar images based on wind streaks and external wind direction, Marine Sciences. (2015) 39, no. 12, 157–164.
Google Scholar
119 Zhang W., Shi H., Jiang Z., Yang P., Chang S., Xiang J., and Mai Y., Assessment of variational method schemes for synthetic aperture radar wind retrieval, Chinese Journal of Geophysics. (2021) 64, no. 7, 2436–2446.
Web of Science® Google Scholar
120 Isoguchi O. and Shimada M., An L-band ocean geophysical model function derived from PALSAR, IEEE Transactions on Geoscience and Remote Sensing. (2009) 47, no. 7, 1925–1936, https://doi.org/10.1109/TGRS.2008.2010864, 2-s2.0-67651171229.
10.1109/TGRS.2008.2010864
Web of Science® Google Scholar
121 He Y. and Zou Q., Validation of wind vector retrieval from ENVISAT ASAR images, 5, Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), 2004, Anchorage, AK, USA, 3184–3187, https://doi.org/10.1109/IGARSS.2004.1370377.
10.1109/IGARSS.2004.1370377
Google Scholar
122 Song G., Yijun Y., and Qi P., Wind vector retrieval using dual polarization imagery of ASAR, Progress in Natural Sscience. (2006) 16, no. 11, 1183–1187, https://doi.org/10.1080/10020070612330127, 2-s2.0-33846092011.
10.1080/10020070612330127
Web of Science® Google Scholar
123 Li H., Chapron B., Mouche A., and Stopa J. E., A new ocean SAR cross-spectral parameter: definition and directional property using the global Sentinel-1 measurements, Journal of Geophysical Research, Oceans. (2019) 124, 1566–1577, https://doi.org/10.1029/2018JC014638, 2-s2.0-85062727798.
10.1029/2018JC014638
Web of Science® Google Scholar
124 Huang L., Migliaccio M., Nunziata F., Carcione V., Zhang Z., and Yu W., A SAR cross-pol correlation sea surface wind speed study, IEEE International Geoscience and Remote Sensing Symposium IEEE, 2018, Valencia, Spain, 3212–3215, https://doi.org/10.1109/IGARSS.2018.8519536, 2-s2.0-85064259359.
10.1109/IGARSS.2018.8519536
Google Scholar
125 Longépé N., Mouche A. A., Ferro-Famil L., and Husson R., Co-cross-polarization coherence over the sea surface from Sentinel-1 SAR data: perspectives for mission calibration and wind field retrieval, IEEE Transactions on Geoscience and Remote Sensing. (2022) 60, 1–16, https://doi.org/10.1109/TGRS.2021.3055979.
10.1109/TGRS.2021.3055979
Web of Science® Google Scholar

All articles

A Review for Retrieving Wind Fields by Spaceborne Synthetic Aperture Radar

Abstract

1. Introduction

2. The Potential and Drawback for SSWF Estimation Using SAR