Volume 2022, Issue 1 7144991

Research Article

Open Access

Infrared and Visible Image Fusion Based on Iterative Control of Anisotropic Diffusion and Regional Gradient Structure

Jingyu Ji,

Jingyu Ji

orcid.org/0000-0001-6806-7437

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Yuhua Zhang,

Yuhua Zhang

orcid.org/0000-0003-0644-5230

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Zhilong Lin,

Zhilong Lin

orcid.org/0000-0002-3205-4041

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Yongke Li,

Yongke Li

orcid.org/0000-0003-2332-3980

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Changlong Wang,

Changlong Wang

orcid.org/0000-0002-9847-820X

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Yongjiang Hu,

Corresponding Author

Yongjiang Hu

[email protected]

orcid.org/0000-0001-9902-8211

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Jiangyi Yao,

Jiangyi Yao

orcid.org/0000-0002-2340-9066

Equipment Simulation Training Center, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Jingyu Ji,

Jingyu Ji

orcid.org/0000-0001-6806-7437

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Yuhua Zhang,

Yuhua Zhang

orcid.org/0000-0003-0644-5230

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Zhilong Lin,

Zhilong Lin

orcid.org/0000-0002-3205-4041

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Yongke Li,

Yongke Li

orcid.org/0000-0003-2332-3980

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Changlong Wang,

Changlong Wang

orcid.org/0000-0002-9847-820X

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Yongjiang Hu,

Corresponding Author

Yongjiang Hu

[email protected]

orcid.org/0000-0001-9902-8211

Department of UAV, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

Jiangyi Yao,

Jiangyi Yao

orcid.org/0000-0002-2340-9066

Equipment Simulation Training Center, Army Engineering University, Shijiazhuang, Hebei, China ust.com.cn

Search for more papers by this author

First published: 11 April 2022

https://doi.org/10.1155/2022/7144991

Citations: 1

Academic Editor: Ying-Ren Chien

Share a link

Email
Wechat
Bluesky

Abstract

To improve the fusion performance of infrared and visible images and effectively retain the edge structure information of the image, a fusion algorithm based on iterative control of anisotropic diffusion and regional gradient structure is proposed. First, the iterative control operator is introduced into the anisotropic diffusion model to effectively control the number of iterations. Then, the image is decomposed into a structure layer containing detail information and a base layer containing residual energy information. According to the characteristics of different layers, different fusion schemes are utilized. The structure layer is fused by combining the regional structure operator and the structure tensor matrix, and the base layer is fused through the Visual Saliency Map. Finally, the fusion image is obtained by reconstructing the structure layer and the energy layer. Experimental results show that the proposed algorithm can not only effectively deal with the fusion of infrared and visible images but also has high efficiency in calculation.

1. Introduction

In recent years, UAVs have played an increasingly important role in many fields due to their high flexibility, low cost, and easy operation, which are often used for battlefield reconnaissance, battle situation assessment, target recognition, and tracking in the military. Now, image sensors in UAVS can acquire multiple types of images such as multispectral images, visible images, and infrared images [1]. However, due to the limitation of environmental conditions such as light, imaging with only one sensor will be affected by certain factors and cannot meet the requirements of practical applications. The combination of multiple imaging sensors can overcome the shortcomings of a single sensor and obtain more reliable and comprehensive information. The imaging sensors commonly used in UAVs are infrared sensors and visible sensors. The infrared sensors use the principle of thermal radiation to obtain images with larger infrared targets, but the targets are not clear and the edges are blurred [2]. The visible sensors use the principle of light reflection to obtain clear images with clear details, but under low-visibility conditions, the images have limitations. Research has found that the effective combination of infrared images and visible images can result in a more comprehensive and accurate scene or target, which provides strong support for subsequent task processing [3].

The more widely used methods in the field of infrared and visible image fusion can be roughly classified into MST-based methods [4], sparse representation-based methods [5], spatial domain-based methods [6], and deep learning-based methods [7]. At present, the most researched and applied methods are MST-based methods, including wavelet transform [8], Laplacian pyramid transform [9], nonsubsampled shear wave transform [10], and nonsubsampled contourlet transform [11]. These methods decompose the source images in multiple scales, then fuse them separately according to certain fusion rules, and finally get the fusion result through inverse transformation, which can extract the salient information in the images and get better performance. For example, nonsubsampled contourlet transform is utilized by Huang et al. [11] to decompose the source images to obtain precise decomposition. However, due to the lack of spatial consistency in the traditional MST methods, structural or brightness distortion may appear in the result.

In addition, image fusion methods with edge preserving filtering [12] are also receiving attention. Edge-preserving filtering can effectively reduce the halo artifacts around the edges in the fusion results while retaining the edge information of the image contour and has a good visual performance. Popular methods are mean filtering [13], bilateral filtering [14], joint bilateral filtering [15], and guided filtering [16]. These methods complete decomposition according to the spatial structure of the images to achieve spatial consistency, so as to achieve the purpose of smoothing the texture and preserving edge detail information. For example, Zhu et al. [16] proposed a novel fast single-image dehazing algorithm by using guided filtering to decomposition the images, and it obtained good performance. The edge-preserving fusion algorithms maintain spatial consistency and effectively improve the phenomenon of fusion image distortion or artifacts, but there are certain limitations: (1) it will introduce detail “halos” at the edges; (2) when the input images and the guide images are inconsistent, the filtering will be insensitive or even fail; and (3) it is difficult to meet the requirements of fusion performance, time efficiency, and noise robustness simultaneously.

Inspired by the previous research, this article focuses on reducing “halos” at the edges to retain the edge structure information and obtaining better decomposition performance in both noise-free and noise-perturbed images. In this paper, a new infrared and visible image fusion method based on iterative control of anisotropic diffusion and regional gradient structure operator is proposed. Anisotropic diffusion is utilized to deconstruct the source image into a structure layer and a base layer. Then, the structure layer is processed by using the gradient-based structure tensor matrix and the regional structure operator. Due to the weak detail and high energy of the base layer, the Visual Saliency Map (VSM) is utilized to fuse the base layer. By reconstructing the two prefusion components, the final fusion image can be obtained.

The main contributions of the proposed method can be summarized as follows:

(1)
A novel method of infrared and visible image fusion is proposed. The anisotropic diffusion model with a control iteration operator is proposed to adaptively control the number of iterations, so the image is decomposed adaptively into a structure layer with rich edges and detail information and a base layer with pure energy information. Especially, the computational efficiency is greatly improved
(2)
The regional structure operator is proposed into the structure tensor matrix, which can effectively extract information such as image details, contrast, and structure. It can also greatly improve the detection ability of weak structures and obtain structure images with good prefusion performance
(3)
Since anisotropic diffusion can effectively deal with noise, the proposed method also has a good performance on noisy image fusion. In addition, the algorithm is widely used and it is also suitable for other types of image fusion

The paper is organized as follows. Section 2 briefly reviews the anisotropic diffusion and structure tensor theory and introduces new operators. Section 3 describes the proposed infrared and visible image fusion algorithm in detail. Section 4 introduces related experiments and compares with several current advanced algorithms. Finally, the conclusion is discussed in Section 5.

2. Related Theories

2.1. Anisotropic Diffusion Based on Iterative Control

Anisotropic diffusion [17] can be utilized to smooth the image and maintain the image details and edge information. Compared with other filtering methods, it is more suitable for image decomposition processing. The anisotropic diffusion equation is expressed as

(1)

where v(x, y, t) is the flux function or diffusion rate of diffusion, ∇ is the Laplacian operator, Δ is the gradient operator, and t is the time or scale or iteration. Equation (1) can be regarded as a discrete square matrix, and the four nearest neighbor discretizations of Laplacian can be used:

(2)

where

is the coarser resolution image at t + 1 scale, which is influenced by

. μ is a constant with 0 ≤ μ ≤ 1/4. D_N, D_S, D_W, and D_E are the nearest difference values in the four directions of North, South, West, and East, respectively, which can be defined by

(3)

and v_N, v_S, v_W, and v_E are the conduction coefficients or flux functions in the four directions of North, South, West, and East.

(4)

where g(|∙|) is a monotonically decreasing function with g(0) = 1 and g(∙) is the “edge stop” function or the differential coefficient, which has a very important influence on the noise suppression and edge retention ability of anisotropic diffusion. The image format in this paper is obtained by image processing technology.

(5)

The scale space weighed by these two functions is different. The first function is for the abrupt areas with large gradients, namely, the edge and detail areas. The second function is for flat areas with small gradients. Both functions consist of a free parameter k.

The anisotropic diffusion is a differential iterative process, in which the number of iterations is a key issue. If it is overiterated, it will lead to oversmoothing; but if the number of iterations is not enough, the detail components cannot be separated effectively. Moreover, the number of iterations for noisy images and the number of iterations for noise-free images are also uncertain. Therefore, an iterative control operator θ is introduced to control k, thereby adaptively controlling the number of iterations and reasonably separating structural information such as gradients and details. And it can also be improved in computational efficiency.

(6)

where K₀ is the empirical value for controlling the diffusion strength, which usually is set by 30. It can be seen from Equation (6) that the value of k is related to the edge strength of the region boundary, and the value of k is updated through positive and negative excitation by θ to obtain the optimal number of iterations. Get the most effective and accurate separation results.

The anisotropic diffusion of the image I is simply represented by aniso(I). After the image is diffused through anisotropy, since the iterative control operator can precisely control the number of iterations, almost all the vibration and repetitive context can be effectively preserved in the structure layer, while the energy information and weak edges are preserved in the base layer. Figure 1 shows the base layer and structure layer images obtained after anisotropic diffusion decomposition. It can be clearly seen that the images are basically consistent with the theoretical analysis.

Details are in the caption following the image — Open in figure viewer PowerPoint

2.2. Gradient-Based Structure Tensor Matrix

Gradient is the rate of change, which is reflected by the difference between a central pixel and surrounding pixels. It can be used to accurately reflect the texture details, contour features, and structural components in the image. The structure tensor is an effective method to analyse the gradient problem, and it has been applied to a variety of image processing tasks.

The gradient operator [18] is described as follows. For a local window Θ(x, y) of any ε⟶0⁺ in the direction β, the square of the change of the image I(x, y) at the point (x, y) is

(7)

In any direction β at the point (x, y), the change rate C(β) of the local features of the image I(x, y) is

(8)

To make better analysis of gradient features and effectively realize image processing, the structure tensor matrix S is introduced. And C(β) can be expressed as

(9)

where

(10)

The two extreme values of the structure tensor S can be expressed as

(11)

The structural characteristics of the local area of the image are related to the extreme value of the matrix. Generally, if the two extreme values are relatively small, it indicates that the region does not have gradient characteristics; that is, the region is located in the isotropic part. Otherwise, it means that the local area of the area has obvious changes and contains certain structural information, because in the image area saliency measurement, a wide range of structure types are involved. Finally, the structural saliency operator SSO is defined according to [19] as

(12)

3. Fusion Framework

Based on the above theories, a new image fusion framework is constructed, as shown in Figure 2. Different from the traditional decomposition scheme, in order to make better use of the useful information in the original image, first, the iterative control anisotropic diffusion is utilized to decompose the source image into base and structure components. At this time, most of the gradients and edges can be effectively preserved in the structure layer, and the base layer contains the remaining energy information. Then, according to the characteristics of each layer, different fusion rules are introduced to acquire the prefusion of each layer. Among them, for the fusion of the structure layer, the prefusion is effectively realized through the regional gradient structure; for the base layer, the prefusion is performed through the VSM. Finally, the fusion result is obtained by reconstructing the two prefusion layers.

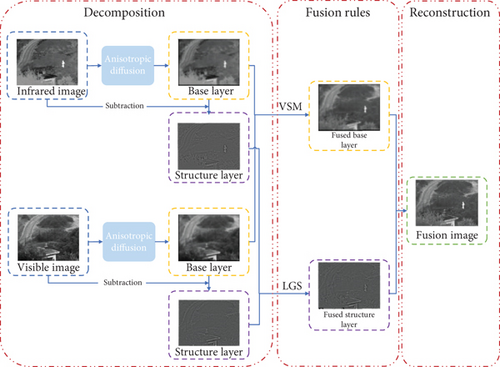
3.1. Anisotropic Decomposition

Let the source images

be all coregistered. The base layer is obtained through the anisotropic diffusion model in the previous section with smooth edges:

(13)

where

is the nth base layer and aniso(I_n(x, y)) represents the anisotropic diffusion process on the nth source image. The structure layer is obtained by subtracting the base layer from the source image.

(14)

After anisotropic decomposition, a structure layer with rich outline and texture details and a base layer with intensity information can be obtained.

3.2. Fusion of Structure Layers

Since the structure saliency operator (SSO) in the previous section can effectively detect the gradient structure information of the images, SSO can be used to prefuse the structure layers. However, due to the lack of intensity variables, SSO cannot accurately detect the weak feature information in the images. In order to improve the structure detection ability, the regional structure operator (RSO) is introduced to improve the performance of SSO. RSO is the regional structural component with (x, y) as the center position; then, the regional gradient structure (RGS) can be expressed as

(15)

where SS_I(x, y) is the salient image produced by SSO, and RS_I(x, y) represents the regional structure feature at position (x, y), which can be expressed as

(16)

where N controls the size of the region and influences the efficiency and effect of fusion. Through comparing the RGS of the input image, the structure saliency map M₁(x, y) of the image

is calculated:

(17)

M₂(x, y) can be obtained in the same way. In addition, M_n(x, y) can be future refined by

(18)

where Θ is a central local area in (x, y) whose size is T × T. Therefore, the prefusion structure layer image

can be expressed by

(19)

3.3. Fusion of Base Layers

Since the base layers contain less details, the weighted average technology based on VSM [20] is used to fuse the base layer .

First, VSM is constructed; let I_P represent the intensity value of a pixel p in the image I. The saliency value V(p) of pixel p is defined as

(20)

where j represents the pixel intensity, M_j represents the number of pixels whose intensity is equal to j, and L represents the number of gray levels (in this case, 256). If two pixels have the same intensity value, their saliency values are equal. Then, normalize V(p) to [0,1].

Let V₁ and V₂ denote the VSM of different source images, and

and

denote the base layer images of different source images, and the final prefusion base layer image is obtained by weighted average

(21)

After obtaining these two prefusion components, the final fusion image F_I is

(22)

4. Experimental Analysis and Results

In order to verify the effectiveness and reliability of the algorithm in this paper, multiple pairs of images are utilized for experimental verification, and the results are analysed through subjective vision and objective quantitative evaluation. After setting the algorithm parameters, the experimental results are displayed and discussed.

4.1. Experimental Setting

As shown in Figure 3, six pairs of source images are employed in the experiment, which can be obtained from the public websitehttp://imagefusion.org/. All the experiments are implemented using MATLAB 2018a on a notebook PC. And five recent methods are compared in the same experimental environment for verification, such as image fusion with ResNet and zero-phase component analysis (ResNet) proposed by Li et al. [21], image fusion with the convolutional neural network (CNN) proposed by Liu et al. [22], gradient transfer and total variation minimization-based image fusion method (GTF) proposed by Ma et al. [23], image fusion through infrared feature extraction and visual information preservation (IFEVIP) proposed by Zhang et al. [24], and multisensor image fusion based on fourth-order partial differential equations (FPDE) proposed by Bavirisetti et al. [25]. In addition, the fusion performance is quantitatively evaluated by six indicators, including entropy (EN) [26], edge information retention (Q_AB/F) [27], Chen-Blum’s index (Q_CB) [28], mutual information (MI) [29], structural similarity (SSIM) [30], and peak signal-to-noise ratio (PSNR) [31].

4.2. Image Fusion and Evaluation

Figures 4 and 5 are six pairs of infrared and visible image fusion examples. Figures 4(a1), 4(b1), and 4(c1) and Figures 5(a1), 5(b1), and 5(c1) are infrared images, and Figures 5(a2), 5(b2), and 5(c2) and Figures 4(a1), 4(b1), and 4(c1) are infrared images. Figures 5(a2), 5(b2), and 5(c2) are visible images; Figures 4(a3)–4(a8), 4(b3)–4(b8), and 4(c3)–4(c8) and Figures 5(a3)–5(a8), 5(b3)–5(b8), and 5(c3)–5(c8) are the fusion results obtained by different methods. The content in the red box in the figure is the part to be emphasized.

4.2.1. Subjective Evaluation

It can be seen from Figures 4 and 5 that the fusion images obtained by the ResNet and GTF methods have lower contrast than the results obtained by the proposed method. Although the structure is better preserved, the details are relatively weakened and lost. The IFEVIP method maintains a good contrast, but the visual effect is too enhanced, especially in the partially enlarged areas, resulting in obvious error in the result. The FPDE method has the phenomenon of blurred internal features. The CNN method has obtained a relatively good fusion result, but its image is somewhat unnatural, and the colour of the result in Figure 5(c4) contains errors. Therefore, the proposed method can effectively separate the component information of different images, preserve the useful information of the source images into the fusion images, and obtain the best visual performance in the aspect of edge and detail preservation.

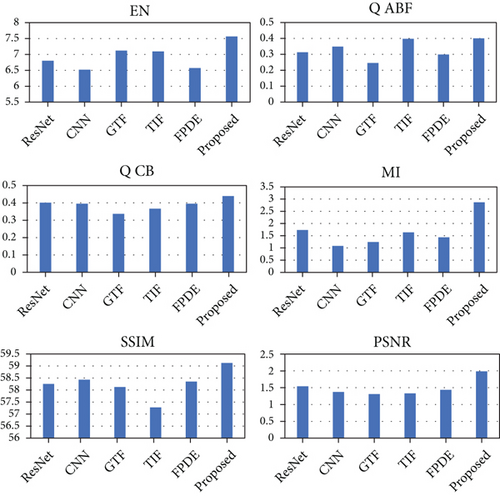
4.2.2. Objective Evaluation

Except for subjective evaluation, the fusion results are quantitatively evaluated, and the results are shown in Table 1, in which the best results are labelled in bold. According to the data in the table, it can be seen that the objective evaluation of the proposed method is significantly higher than other methods. In all quantitative evaluations, only a few places are not optimal, but they do not affect the advantages of the method in this paper. In addition, Figure 6 shows the bar chart comparison of EN, Q_AB/F, Q_CB, MI, SSIM, and PSNR values of various fusion methods for the car example.

1. Quantitative index of image fusion results.

Source images	Index	ResNet	CNN	GTF	TIF	FPDE	Proposed
Car	EN	6.798	6.519	7.119	7.090	6.569	7.564
	Q_ABF	0.313	0.349	0.246	0.398	0.299	0.401
	Q_CB	0.401	0.395	0.337	0.367	0.395	0.439
	MI	1.735	1.082	1.243	1.638	1.432	2.866
	SSIM	1.543	1.372	1.310	1.330	1.435	1.988
	PSNR	58.253	58.430	58.127	57.280	58.349	59.124

House	EN	6.592	6.618	6.952	6.960	6.870	6.998
	Q_ABF	0.375	0.345	0.253	0.402	0.387	0.418
	Q_CB	0.463	0.471	0.338	0.468	0.477	0.490
	MI	1.301	1.251	1.080	1.417	1.222	1.456
	SSIM	1.534	1.436	1.374	1.418	1.305	1.991
	PSNR	58.143	59.462	59.066	58.225	58.356	59.184

Shop	EN	6.275	6.062	6.627	6.266	6.403	6.703
	Q_ABF	0.461	0.205	0.481	0.589	0.328	0.598
	Q_CB	0.478	0.451	0.434	0.481	0.445	0.497
	MI	1.723	0.812	1.746	1.682	1.308	1.896
	SSIM	1.334	1.031	1.221	1.325	1.299	1.993
	PSNR	59.012	59.885	59.466	59.308	59.345	59.936

Snow	EN	7.012	6.818	5.919	6.911	6.918	7.723
	Q_ABF	0.543	0.551	0.498	0.577	0.565	0.579
	Q_CB	0.554	0.483	0.478	0.517	0.612	0.661
	MI	2.045	1.914	1.598	2.368	1.999	2.657
	SSIM	1.367	1.238	1.164	1.222	1.029	1.989
	PSNR	55.034	56.630	56.122	55.237	56.856	57.083

Tree	EN	6.744	6.696	6.696	6.229	6.801	6.962
	Q_ABF	0.301	0.311	0.348	0.341	0.333	0.379
	Q_CB	0.423	0.424	0.417	0.430	0.415	0.469
	MI	1.354	1.109	1.452	1.090	1.027	1.635
	SSIM	1.578	1.512	1.469	1.483	1.496	1.995
	PSNR	58.013	57.641	57.242	57.325	57.934	58.823

Walking Night	EN	6.348	5.734	6.059	6.281	6.786	7.011
	Q_ABF	0.405	0.346	0.309	0.471	0.418	0.474
	Q_CB	0.313	0.353	0.291	0.344	0.350	0.386
	MI	2.019	2.130	2.189	2.139	2.005	2.335
	SSIM	1.346	1.153	1.232	1.208	1.206	1.989
	PSNR	55.999	56.047	55.843	54.825	55.470	56.943

In summary, for infrared and visible fusion, the method in this paper has a good performance both subjectively and objectively.

4.3. Extended Experiment

After experimental verification, the proposed fusion algorithm is equally effective for remote sensing images. To illustrate the effectiveness of this algorithm, two different sets of panchromatic and multispectral satellite remote sensing images are shown in Figure 7.

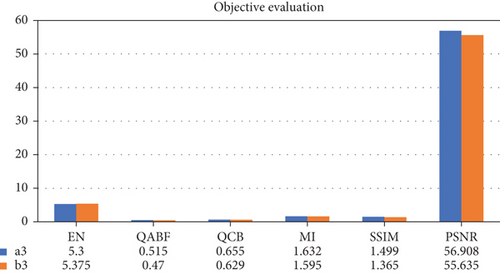
Figures 7(a1) and 7(b1) are multispectral images with high spectral resolution and low spatial resolution. Figures 7(a2) and 7(b2) are panchromatic images with high spatial resolution and low spectral resolution. The corresponding fusion results are shown in Figures 7(a3) and 7(b3). As can be seen from the content in the red box in Figure 7, the fusion results have both high spatial resolution and high spectral resolution, and the fused images have a strong ability to express structure and details. The objective evaluation results are shown in Figure 8. It can be seen from the visual and objective results that this algorithm can effectively retain high-spatial and hyperspectral information and can improve the accuracy of subsequent processing of remote sensing images.

4.4. Computational Efficiency

The methods tested in this paper are all carried out in the same experimental environment. The average implementation time of six pairs of images is compared as shown in Table 2. It can be seen that the calculation efficiency of the proposed algorithm has a considerable advantage over the comparison algorithms.

2. Computational efficiency of different methods.

Method	ResNet	CNN	GTF	IFEVIP	FPDE	Proposed
Time (s)	23.07	23.03	2.91	1.34	5.78	0.78

5. Conclusions

In this paper, an infrared and visible image fusion algorithm based on iterative control of anisotropic diffusion and regional gradient structure is proposed. The algorithm makes full use of the advantages of anisotropic diffusion and improves the decomposition efficiency and effect through iterative control operators. The regional gradient structure operator is introduced to fully extract the detailed information in the structure layer to obtain a better fusion performance. Many experimental results show that this algorithm is significantly better than existing methods in terms of subjective and objective evaluation. In addition, higher calculation efficiency and stronger antinoise performance can be obtained, and the algorithm can be effectively applied to other types of image fusion situations.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This research was funded by the National Natural Science Foundation of China, grant number 61801507, and the National Natural Science Foundation of Hebei Province, grant number F2021506004.

Open Research

Data Availability

The data used to support the findings of this paper are available from http://imagefusion.org/.

References

1 Liu Y., Dong L., Chen Y., and Xu W., An efficient method for infrared and visual images fusion based on visual attention technique, Remote Sensing. (2020) 12, no. 5, https://doi.org/10.3390/rs12050781.
10.3390/rs12050781
Web of Science® Google Scholar
2 Paquin D., Levy D., and Xing L., Hybrid multiscale landmark and deformable image registration, Mathematical Biosciences & Engineering. (2017) 4, no. 4, 711–737.
Google Scholar
3 Zhang X., Zhang A., and Meng X., Automatic fusion of hyperspectral images and laser scans using feature points, Journal of Sensors. (2015) 2015, 9, https://doi.org/10.1155/2015/415361, 2-s2.0-84939188207, 415361.
10.1155/2015/415361
Web of Science® Google Scholar
4 Yan X., Qin H., Li J., Zhou H., Zong J. G., and Zeng Q., Infrared and visible image fusion using multiscale directional nonlocal means filter, Applied Optics. (2015) 54, no. 13, https://doi.org/10.1364/AO.54.004299.
10.1364/AO.54.004299
Web of Science® Google Scholar
5 Zhu Z., Yin H., Chai Y., Li Y., and Qi G., A novel multi-modality image fusion method based on image decomposition and sparse representation, Information Sciences. (2018) 432, 516–529, https://doi.org/10.1016/j.ins.2017.09.010, 2-s2.0-85029232895.
10.1016/j.ins.2017.09.010
Web of Science® Google Scholar
6 Li Y., Li F., Bai B., and Shen Q., Image fusion via nonlocal sparse K-SVD dictionary learning, Applied Optics. (2016) 55, no. 7, 1814–1823, https://doi.org/10.1364/AO.55.001814, 2-s2.0-84963891297, 26974648.
10.1364/AO.55.001814
PubMed Web of Science® Google Scholar
7 Salvetti F., Mazzia V., Khaliq A., and Chiaberge M., Multi-image super resolution of remotely sensed images using residual attention deep neural networks, Remote Sensing. (2020) 12, no. 14, https://doi.org/10.3390/rs12142207.
10.3390/rs12142207
Web of Science® Google Scholar
8 Yehia A., Safy M., and Amein A. S., Fusion of high-resolution SAR and optical imageries based on a wavelet transform and IHS integrated algorithm, International Journal of Engineering Research in Africa. (2021) 52, 62–72, https://doi.org/10.4028/www.scientific.net/JERA.52.62.
10.4028/www.scientific.net/JERA.52.62
Web of Science® Google Scholar
9 Rabie T., Baziyad M., and Kamel I., Enhanced high capacity image steganography using discrete wavelet transform and the Laplacian pyramid, Multimedia Tools and Applications. (2018) 77, no. 18, 23673–23698, https://doi.org/10.1007/s11042-018-5713-2, 2-s2.0-85051624437.
10.1007/s11042-018-5713-2
Web of Science® Google Scholar
10 Zhao M. and Peng Y., A multi-module medical image fusion method based on non-subsampled shear wave transformation and convolutional neural network, Sensing and Imaging. (2021) 22, no. 1, https://doi.org/10.1007/s11220-021-00330-w.
10.1007/s11220-021-00330-w
PubMed Web of Science® Google Scholar
11 Huang X., Qi G., Wei H., Chai Y., and Sim J., A novel infrared and visible image information fusion method based on phase congruency and image entropy, Entropy. (2019) 21, no. 12, https://doi.org/10.3390/e21121135.
10.3390/e21121135
Web of Science® Google Scholar
12 Kang C. Q., Zheng Y., and Liu Y. X., Multi-focus image fusion algorithm based on edge-preserving filtering, Laser & Infrared. (2013) 43, no. 7, 814–817.
Google Scholar
13 Duan J., Long C., and Chen C., Multifocus image fusion using superpixel segmentation and superpixel-based mean filtering, Applied Optics. (2016) 55, no. 36, 10352–10362, https://doi.org/10.1364/AO.55.010352, 2-s2.0-85009260543, 28059263.
10.1364/AO.55.010352
PubMed Web of Science® Google Scholar
14 Bo C., Infrared and visible images fusion based on gradient bilateral filtering, 2016 3rd International Conference on Systems and Informatics (ICSAI), 2016, Shanghai, China, IEEE, https://doi.org/10.1109/ICSAI.2016.7811077, 2-s2.0-85015280631.
10.1109/ICSAI.2016.7811077
Google Scholar
15 Luo T., Liu Z., Pan Z., and Zhang M., A virtual-real occlusion method based on GPU acceleration for MR, 2019 IEEE Conference on Virtual Reality and 3D User Interfaces (VR), 2019, Osaka, Japan, IEEE, https://doi.org/10.1109/VR.2019.8797811, 2-s2.0-85071856820.
10.1109/VR.2019.8797811
Google Scholar
16 Zhu Z., Wei H., Hu G., Li Y., Qi G., and Mazur N., A novel fast single image dehazing algorithm based on artificial multiexposure image fusion, IEEE Transactions on Instrumentation and Measurement. (2021) 70, 1–23, https://doi.org/10.1109/TIM.2020.3024335.
10.1109/TIM.2020.3024335
PubMed Web of Science® Google Scholar
17 Perona P. and Malik J., Scale space and edge detection using anisotropic diffusion, IEEE Computer Society Workshop on Computer Vision. (1990) 12, no. 7, 629–639.
Google Scholar
18 Jin L., Liu H., Xu X., and Song E., Improved direction estimation for Di Zenzo's multichannel image gradient operator, Pattern Recognition. (2012) 45, no. 12, 4300–4311, https://doi.org/10.1016/j.patcog.2012.06.003, 2-s2.0-84864289618.
10.1016/j.patcog.2012.06.003
Web of Science® Google Scholar
19 Zhou Z., Li S., and Wang B., Multi-scale weighted gradient-based fusion for multi-focus images, Information Fusion. (2014) 20, 60–72, https://doi.org/10.1016/j.inffus.2013.11.005, 2-s2.0-84901609240.
10.1016/j.inffus.2013.11.005
Web of Science® Google Scholar
20 Cheng M. M., Mitra N. J., Huang X., Torr P. H., and Hu S. M., Global contrast based salient region detection, IEEE Transactions on Pattern Analysis and Machine Intelligence. (2014) 37, no. 3, 569–582.
10.1109/TPAMI.2014.2345401
Web of Science® Google Scholar
21 Li H., Wu X. J., and Durrani T. S., Infrared and visible image fusion with ResNet and zero-phase component analysis, Infrared Physics & Technology. (2018) 102, article 103039, https://doi.org/10.1016/j.infrared.2019.103039, 2-s2.0-85072573478.
10.1016/j.infrared.2019.103039
Web of Science® Google Scholar
22 Liu Y., Chen X., Cheng J., Peng H., and Wang Z., Infrared and visible image fusion with convolutional neural networks, International Journal of Wavelets, Multiresolution and Information Processing. (2018) 16, no. 3, https://doi.org/10.1142/S0219691318500182, 2-s2.0-85042934953.
10.1142/S0219691318500182
Web of Science® Google Scholar
23 Ma J., Chen C., Li C., and Huang J., Infrared and visible image fusion via gradient transfer and total variation minimization, Information Fusion. (2016) 31, 100–109, https://doi.org/10.1016/j.inffus.2016.02.001, 2-s2.0-84958952372.
10.1016/j.inffus.2016.02.001
Web of Science® Google Scholar
24 Zhang Y., Zhang L., Bai X., and Zhang L., Infrared and visual image fusion through infrared feature extraction and visual information preservation, Infrared Physics & Technology. (2017) 83, 227–237, https://doi.org/10.1016/j.infrared.2017.05.007, 2-s2.0-85018868507.
10.1016/j.infrared.2017.05.007
Web of Science® Google Scholar
25 Bavirisetti D. P., Xiao G., and Liu G., Multi-sensor image fusion based on fourth order partial differential equations, 2017 20th International Conference on Information Fusion (Fusion), 2017, Xi’an, China, IEEE, https://doi.org/10.23919/ICIF.2017.8009719, 2-s2.0-85029413232.
10.23919/ICIF.2017.8009719
Google Scholar
26 Chibani Y., Additive integration of SAR features into multispectral SPOT images by means of the a trous wavelet decomposition, ISPRS Journal of Photogrammetry and Remote Sensing. (2006) 60, no. 5, 306–314, https://doi.org/10.1016/j.isprsjprs.2006.05.001, 2-s2.0-33747126059.
10.1016/j.isprsjprs.2006.05.001
Web of Science® Google Scholar
27 Xydeas C. S. and Pv V., Objective image fusion performance measure, Military Technical Courier. (2000) 56, no. 4, 181–193.
Google Scholar
28 Yin C. and Blum R. S., A new automated quality assessment algorithm for night vision image fusion, 2007 41st Annual Conference on Information Sciences and Systems, 2007, Baltimore, MD, USA, https://doi.org/10.1109/CISS.2007.4298361, 2-s2.0-44049091802.
10.1109/CISS.2007.4298361
Google Scholar
29 Qu G., Zhang D., and Yan P., Information measure for performance of image fusion, Electronics Letters. (2002) 38, no. 7, 313–315, https://doi.org/10.1049/el:20020212, 2-s2.0-0037187687.
10.1049/el:20020212
Web of Science® Google Scholar
30 Zhou W., Bovik A. C., Sheikh H. R., and Simoncelli E. P., Image quality assessment: from error visibility to structural similarity, IEEE Transactions on Image Processing. (2004) 13, no. 4, 600–612, https://doi.org/10.1109/TIP.2003.819861, 2-s2.0-1942436689.
10.1109/TIP.2003.819861
PubMed Web of Science® Google Scholar
31 Jagalingam P. and Hegde A. V., A review of quality metrics for fused image, Aquatic Procedia. (2015) 4, 133–142, https://doi.org/10.1016/j.aqpro.2015.02.019.
10.1016/j.aqpro.2015.02.019
Google Scholar

Citing Literature

All articles

Infrared and Visible Image Fusion Based on Iterative Control of Anisotropic Diffusion and Regional Gradient Structure

Abstract

1. Introduction

2. Related Theories

2.1. Anisotropic Diffusion Based on Iterative Control

2.2. Gradient-Based Structure Tensor Matrix

3. Fusion Framework

3.1. Anisotropic Decomposition

3.2. Fusion of Structure Layers

3.3. Fusion of Base Layers

4. Experimental Analysis and Results

4.1. Experimental Setting

4.2. Image Fusion and Evaluation

4.2.1. Subjective Evaluation

4.2.2. Objective Evaluation

4.3. Extended Experiment

4.4. Computational Efficiency

5. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley