The adjustment method of the fast active reflector of “Chinese heavenly eye” is studied. Firstly, this paper studies the offset characteristics of fast main cable node position, combined with the position of the celestial body to be measured, the follow-up coordinate system is established, and the optimal fitting model of active reflector adjustment based on discrete main cable node is established by using the idea of optimal fitting of the ideal surface. Secondly, the genetic algorithm is used to solve the minimum root mean square error (RMSE). The offset of the triangular reflector is driven by the offset of the main cable node, so that the working area is closer to the ideal paraboloid, and the maximum electromagnetic wave signal receiving ratio is achieved. Finally, rotate the coordinate data of each main cable node according to the known celestial body angle and use the Lagrange operator method to obtain the shortest distance from the actual offset point to the ideal paraboloid as the objective function, with the radial expansion range of the actuator and the variation range of the distance between adjacent points as constraints, and the size of the electromagnetic wave contact area is the basis for judging the amount of information, and a reflector adjustment model for the optimal displacement strategy of discrete main cable nodes is established. Through the test, concluded that the optimal fitting strategy is ideal, the model can accurately obtain the fast active reflector adjustment method under the constraint conditions. Through the test, the conclusion that the optimal fitting strategy is ideal is obtained, and the fast active reflector adjustment method that the model can accurately obtain under the constraints is verified.

1. Introduction

In the early 1990s, since the existing radio telescopes in the world can no longer meet the needs of existing scientific and technological development, the international astronomical community proposed the construction of large-scale radio telescopes to promote further human exploration of the universe (Wu, 1995) [1]. The five-hundred-meter Aperture Spherical radio Telescope (FAST) is a major scientific and technological innovation achievement with independent intellectual property rights in China. As one of the countries with the earliest start and fastest development of celestial literature in the world, many scientists have focused on many cutting-edge and hot topics of astrophysics and creatively proposed to independently develop a new type of large aperture antenna, namely, China’s celestial eye (hereinafter referred to as “fast”), which is a major scientific and technological innovation achievement with independent intellectual property rights in China [2]. The “FAST” telescope is a 500 m-aperture spherical reflector radio telescope with extremely high sensitivity in the world, covering a wide range of astronomical contents, and is engaged in the initial turbidity of the universe, dark matter, dark energy and large-scale structure, the evolution of galaxies and the Milky Way, stellar objects, and even observational research on solar system planets and adjacent space events (Nan and Jiang, 2017) [3]. The “FAST” telescope mainly observes celestial objects through the adjustment of its active reflector, and the active reflector adjustment technology is an important technical means to improve the observation accuracy of radio telescopes (Wang et al., 2022) [4]. Therefore, the active surface adjustment method used in this study drives the offset of the triangular reflection panel and the offset of the main cable node, so that the working area is closer to the ideal paraboloid, so as to achieve the maximum electromagnetic wave signal reception ratio and ensure the safe and efficient operation of the fast telescope, which is of great significance to improve the level of scientific research in China, and also provides a good reference for the research in the same field of the international community.

At present, there are many studies on the “FAST” active reflector [5–8]. As early as 2006, some scholars theoretically and empirically studied the motion of the paraboloid of each unit spherical block during the telescope tracking process [9]. After that, some scholars have analyzed the surface shape accuracy of FAST based on the structure and working principle of FAST active reflector and on the basis of reflector unit dynamics. Also, the fitting accuracy of FAST instantaneous paraboloid was studied [10–12]. Wu and Zhang (2008) fit a paraboloid based on the least squares method and calculated the fitting accuracy of the paraboloid in the FAST reflection surface and found that the surface accuracy is the highest when the paraboloid vertex is at the center of the circle [13]. There are also some scholars who have verified, analyzed, and optimized the FAST project’s active reflector measurement control scheme on the scaled-down radio astronomical telescope model [14–17]. Luo et al. (2011) proposed an integrated astronomical trajectory planning model and carried out the corresponding derivation and analysis to obtain the relationship between the observation trajectory of FAST and the corresponding coordinate of the center point of the cable-net paraboloid with time [18]. Li and Zhu (2012) analyzed the pros and cons of the parabolic deformation strategy based on the premise of the minimum difference between the parabolic arc length and the spherical arc length during the deformation process of the reflecting surface and through the smooth transition between the parabolic edge and the spherical surface [19]. Wang et al. (2022) used the azimuth and elevation angles to determine the positional relationship between the observed object, the origin, the curved surface where the feed cabin is located, and the reference sphere, and based on the limitation of the adjustment range of the reflective panel, the particle swarm algorithm was used to determine the equation of the paraboloid [20]. Based on the research on the “FAST” active reflector, some scholars have established a model to adjust the paraboloid to determine the receiving ratio of the feed cabin to improve the observation accuracy of radio telescopes [21–24]. Li et al. (2020) combined with the joint simulation of kinematics and control, hardware in the loop simulation test and other methods, realized the accurate positioning of the feed source in the feed cabin in the 100 m large-scale space and overcome the effects of high-altitude wind disturbance, steel cable vibration, and its own motion coupling [25]. Li et al. (2022) combined Fermat’s principle to simulate the electromagnetic wave reflection in three-dimensional space, calculate the receiving ratio of the feed cabin, and test the data results, indicating that FAST can freely adjust the autonomous surface in a certain radio frequency band and obtain a higher acceptance ratio [26].

To sum up, the existing extensive research on the “FAST” active reflector, the fitting accuracy of fast instantaneous paraboloid, adjusting paraboloid to determine the receiving ratio of feed cabin, and other aspects has laid a solid theoretical and practical foundation for this paper. However, the existing research also needs to be further deepened, such as the distance between the actual offset point of the main cable node and the ideal paraboloid can still be further reduced, and the electromagnetic wave receiving ratio of the paraboloid reflector still needs to be further improved [27]. By studying the offset characteristics of FAST’s main cable node position, establishing the follow-up coordinate system combined with the position of the celestial body to be measured, and adopting the idea of optimal fitting of the main cable node to the ideal surface, this paper establishes the optimal fitting model of active reflector adjustment based on discrete main cable nodes [28, 29]. On this basis, the genetic algorithm is used to solve the minimum root mean square error, and the offset of the main cable node is used to drive the offset of the triangular reflector. Thus, the working area is better close to the ideal paraboloid to achieve the maximum electromagnetic wave signal reception ratio.

In the following innovation of this paper, the following coordinate system is introduced, which effectively simplifies the geometric operation process, reduces the calculation and model complexity, and adopts the idea of overall deviation distribution, which can make the main cable nodes approach the ideal paraboloid more accurately. At the same time, the optimization model is established by using the known constraints and solved by the genetic algorithm. In the process of solving, the global control variables are added to screen out the bad values.

Firstly, the following coordinate system with the direction of the observed celestial body as the reference is introduced to find the optimal approximation model for the distribution of the mean square deviation of the radial direction. In order to make the expansion distance of the actuator within the adjustable range, take h as the variable to investigate the overall deviation distribution vector and find the h value with the minimum overall offset, that is, the minimum overall RMSE, so as to determine the trajectory equation of the ideal paraboloid. Using the traversal algorithm to search the h value under the restriction of radial expansion, it is obtained that the h value with the smallest RMSE is 300.817 5, and the trajectory equation of the ideal paraboloid is

(1)

The global optimal solution of the offset of each main cable node in the working area is obtained by a genetic algorithm, and the final optimal solution is h = 300.8169, f = 140.6192. The paraboloid trajectory equation (1) of the actual offset in the follow-up coordinate system and the coordinates of the main cable node after the offset are obtained. The coordinates of the main cable node after the offset in the reference coordinate system are obtained through the inverse transformation of the rotation matrix. The mean value of the distance change between adjacent nodes is 0.0633%, and the average length of the radial shrinkage of the main cable node is 0.20343.

2. Basic Assumptions and Index Selection

2.1. Basic Assumptions

In order to facilitate the study of the problem, the following hypotheses are put forward: (i) electromagnetic wave signal and reflected signal are regarded as linear propagation. (ii) The reflecting panel is smooth, and the electromagnetic beam is completely reflected after passing through the reflecting surface. (iii) The electromagnetic beam from the measured celestial body is parallel incidence. (iv) All components of the active reflecting surface are rigid bodies. (v) All data sources involved in this study are true, accurate and scientific.

2.2. Symbol Description

In combination with modeling theory and method, there are 6 variables involved, as shown in Table 1.

Table 1. Symbol description.

Serial number	Symbol	Description
1	R	Reference spherical radius
2	f	Focal length of ideal paraboloid
3	h	Vertex offset
4	d	Deviation value of main cable node
5	D	Overall deviation distribution vector of working area
6	q	The unit vector outward along the normal direction of the sphere at the main cable node

3. Trajectory Equation of Ideal Paraboloid under Nonworking State of Active Reflector of Radio Telescope Based on Ergodic Algorithm

3.1. Research Approach

According to the measurement requirements of the radio telescope, the focus of the ideal paraboloid is in the feed cabin; that is, the coordinates are (0, 0, -0.534R). When the object is directly above the reference sphere, the main cable node of the ideal paraboloid vertex is the easiest to study the offset direction of all nodes; so, the paraboloid trajectory equation can be transformed into a function related to the radial expansion distance h of the vertex. For the convenience of calculation, the following coordinate system with the direction of the observed celestial body as the reference is introduced, and the unit vector outward along the spherical normal direction at the main cable node is introduced to study the radial displacement deviation d. The component of the deviation in the coordinate system forms a functional relationship with the original coordinates of the main cable node, and the objective function only related to the radial expansion distance h can be obtained by substituting the assumed ideal paraboloid equation. The method of RMSE of overall deviation distribution is used to find the most ideal radial displacement of all displaced main cable nodes in the working area. Combined with the constraints of radial shrinkage range, the optimization model of the ideal paraboloid trajectory equation is established. Using the traversal algorithm to calculate the deviation of each node, the h of the optimal solution can be found, and the trajectory equation can be solved [30].

3.2. Displacement Model of Active Reflector

When the active reflector of the radio telescope is in the nonworking state, that is, in the reference state, each main cable node falls on the reference sphere with a radius of 300 meters and a diameter of 500 meters. When observing the celestial body, it is in the working state, and the area of the illumination part of the feed is adjusted to an approximate ideal paraboloid with an aperture of 300 meters. To determine the ideal paraboloid, the benchmark space rectangular coordinate system OXYZ is established with the spherical center of the reference sphere as the origin and the vertical direction as the z-axis, and the spherical trajectory equation of the feed cabin can be obtained as follows:

(2)

Benchmark spherical trajectory equation is as follows:

(3)

At the same time, taking the spherical center of the reference sphere as the origin and the direction pointing to the observed celestial body as the z-axis, we establish the spatial follow-up coordinate system OX^′Y^′Z^′, as shown in Figure 1. The models in the subsequent articles are established and solved based on this follow-up coordinate system OX^′Y^′Z^′.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Rotation diagram of spatial follow-up coordinate system (a) and surface rotation diagram (b).

Assumed that the trajectory equation of the ideal paraboloid in the OX^′Y^′Z^′ coordinate system is as follows:

(4)

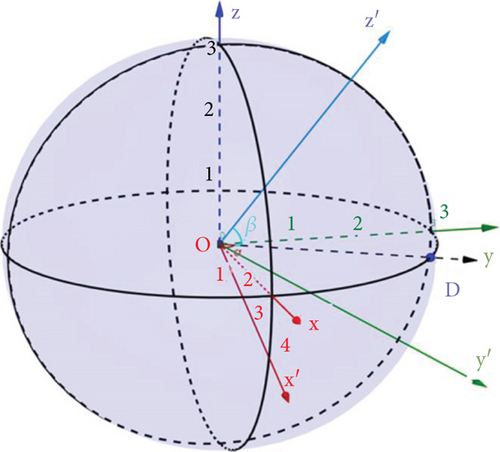
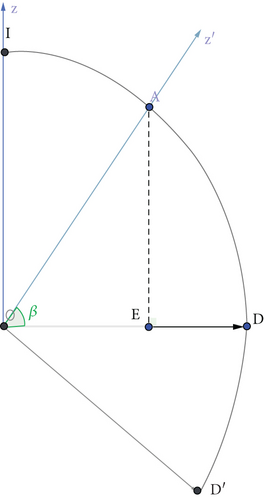
Where variablef is the focal length of the ideal paraboloid, and h is the offset of the paraboloid vertex along the Z^′ axis relative to the reference sphere. Obviously, under the working state, the point with the maximum offset of each main cable node in the working area is the vertex.

Since only each main cable node can be used for paraboloid fitting, the optimal approximation model is found by fitting the distribution of the mean square deviation from the reference sphere center to each point, that is, the radial direction deviation. To make the expansion distance of the actuator within the adjustable range, we take h as the variable to find the h value with the smallest overall offset, that is, the smallest overall RMSE, so as to determine the ideal paraboloid.

3.3. Establishment and Solution of Overall Offset Model

Take a point A(x₀, y₀, z₀) in the above follow-up coordinate system and set it as any main cable node in the lighting area on the ball.

After being pulled by the actuator, point A is offset to point A^′ on the paraboloid. The radial expansion of the actuator is known; so, we can think that the displacement of main cable node A only moves along the normal direction of the sphere, while the displacement along the tangential direction of the sphere is ignored. According to the actual situation, the paraboloid is close to the spherical surface; so, here we think that the vector AA^′ is approximately along the normal direction of the spherical surface, then the line segment AA^′ is parallel to the Z^′ axis A, and its value is set as d. When the point is located on the inner side of the ideal paraboloid, the deviation value d is positive; otherwise, it is negative.

Introduce the unit vector q = (q_x, q_y, q_z) outward along the spherical normal direction at the main cable node A, where A are their projections on the OX^′, OY^′, and OZ^′ axes, respectively, and then point A^′ about point a has parametric equation as follows:

(5)

Then, the coordinates of point A^′ can be obtained as follows:

(6)

Then, we can set the direction for the deviation d of point A. at this time, d is transformed into a deviation vector:

(7)

Known conditions indicated that point A^′ is a point on the ideal paraboloid and satisfies the paraboloid equation. Therefore, substitute it into the coordinate solution equation to obtain the function of deviation d with respect to h:

(8)

Remember γ = −x² + y² − 4fz/2q_xx + 2q_yy − 4q_zf, η = 4f/2q_xx + 2q_yy − 4q_zf. Then,

can be simplified as

(9)

Let

be the overall deviation distribution vector of each main cable node in the working area, where

is the deviation vector of the i − th main cable node. Transformed into a vector formula about h:

(10)

Then, we can get the RMSE calculation formula of the overall deviation distribution D with respect to h:

(11)

where n is the total number of offset main cable nodes. Then, the objective function of the overall offset optimization model is

(12)

If the celestial body to be observed is directly above the reference sphere, the follow-up coordinate system OX^′Y^′Z^′coincides with the reference coordinate system, and the deviation vector is as follows:

(13)

which is downward along the Z − axis. Then, the trajectory equation of the ideal paraboloid in the reference coordinate system is

(14)

and the functional expression of the deviation d with respect to h is obtained:

(15)

Then, the optimization model is

(16)

3.4. Result Analysis

In the case of an ideal paraboloid, the electromagnetic waves reflected by the paraboloid can converge on the feed cabin, then the coordinates of the feed cabin are the focal coordinates of the paraboloid, and the relationship between f and h can be determined according to the formula as follows:

(17)

Since the relationship formula between f and h is determined, the objective function of the optimization model is the univariate variable function about h. Based on the idea of piecewise step size and using the ergodic algorithm, the final optimal solution of h is 300.8175, and the RMSE is 0.19791. Substitute h to obtain the trajectory equation of the ideal paraboloid as follows:

(18)

4. Problem Two Model Establishment and Solution

4.1. Research Approach

A follow-up coordinate system has been established according to the direction of the measured celestial body. When the angle of the celestial body is known, the ideal paraboloid in the reference coordinate system can be transformed into an ideal paraboloid with the vertex on the z-axis in the follow-up coordinate system. To study the coordinate changes of each main cable node, the Lagrange operator method is used to solve the shortest distance from the point to the parabola, which is used as the objective function and added constraints to make the actual offset point approach the ideal paraboloid. The constraint conditions include the expansion amount of radial actuator and the variation range of node spacing. According to this condition, the optimization model is established, and the global variables are defined for the variation range of node spacing.5.1 coordinate rotation and solution of ideal paraboloid trajectory equation.

4.2. Theoretical Derivation

If the object to be observed is located at α = 36.795^°, β = 78.169^°, then in the rotating follow-up coordinate system, the observed object rotates directly above the spherical center, that is, α = 0^°, β = 790^°. We need to discuss the rotation of the coordinate system. The trajectory equation of the ideal paraboloid in the follow-up coordinate system OX^′Y^′Z^′ is solved by MATLAB software as follows:

(19)

The rotation transformation between the reference coordinate system and the follow-up coordinate system is discussed below.

We also choose the follow-up coordinate system to discuss the coordinate offset of each main cable node. Process the coordinates of the main cable node transform it from the reference coordinate system OXYZ to the follow-up coordinate system OX^′Y^′Z^′.

Let the base vector under the reference coordinate system be

and the base vector under the follow-up coordinate system be

. Let the original coordinate of

in the reference coordinate system be

, and there are

(20)

where

can be expressed as

by the original basis vector. Since

is perpendicular to

, there is an angular relationship:

(21)

Take the projection line of the OZ^′ axis on the xOy plane and its unit vector

and use the above formula to obtain the vector

after the rotation of point D. According to the geometric angle relationship, it is known that the rotation angle is the same, that is,

; so, the angle relationship is obtained:

(22)

According to equations (15), (20), and (21), replace the known angle α = 36.795^°, β = 78.169^° to obtain the solution

(23)

The variation of the basis vector is obtained:

(24)

Then, the final coordinate transformation formula is as follows:

(25)

The processed part of the coordinate data is shown in Table 2.

Table 2. Coordinates of each main cable node after rotation.

Node	X	Y	Z	Thea X	Thea Y	Thea Z
A0	49.320 026 47	36.889 381 35	-294.018 482 6	-0.164 181 18	-0.122 800 87	0.978 756 6
B1	55.229 444 59	45.147 999 76	-291.807 329 5	-0.183 874 204	-0.150 286 726	0.971 392 903
C1	59.071 297 35	33.580 077 66	-292.614 262 4	-0.196 623 253	-0.111 766 87	0.974 088 014
D1	49.396 380 8	26.555 491 25	-295.118 526	-0.164 435 398	-0.088 394 798	0.982 419 134
E1	39.575 149 93	33.781 467 71	-295.859 369 1	-0.131 760 932	-0.112 436 88	0.984 884 257
A1	43.180 250 62	45.272 464 75	-293.812 901 1	-0.143 721 369	-0.150 701 494	0.978 076 287
A3	49.071 321 78	53.521 360 38	-291.492 125 4	-0.163 353 742	-0.178 141 503	0.970 351 048
……	……	……	……	……	……	……
E428	-152.060 690 4	187.429 294 9	-178.852 558 8	0.506 172 8	-0.623 929 324	0.595 400 116
E429	-146.547 628 5	195.355 187 4	-174.930 084 6	0.487 849 82	-0.650 329 634	0.582 300 544
E430	-140.771 871 8	203.086 310 4	-170.820 626 6	0.468 615 102	-0.676 066 534	0.568 624 596

Use the rotation coordinate transformation formula of formula (25) to rotate the coordinates of formula (4), that is, the equation of the ideal paraboloid in the follow-up coordinate system, and get the trajectory equation of the ideal paraboloid when the celestial body is at the position of angle α = 36.795^°, β = 78.169^° in the reference coordinate system:

(26)

4.3. Reflector Pane Adjustment Model Based on Discrete Main Cable Node Displacement

To make the main cable node approach the ideal paraboloid as much as possible, a reflector panel adjustment model based on discrete main cable node displacement is established. The first mock exam is the best one in the problem, and the ideal paraboloid is also for the main cable node. The actual paraboloid with triangular panels should have a larger radius of curvature, as shown in Figure 2. Therefore, discrete points to approximate the ideal paraboloid are adopted [31].

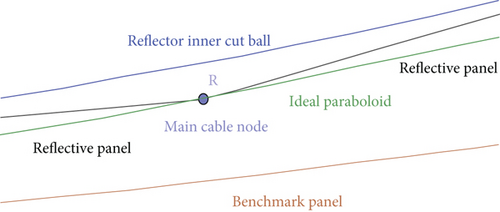
In the follow-up coordinate system, the distance between the actual offset point of the main cable node and the ideal paraboloid is discussed, and the coordinate of the actual offset point closest to the ideal paraboloid under the limiting conditions (i.e., the radial expansion is -0.6 and 0.6, and the change of the distance between adjacent nodes is no more than 0.07%) is found. Therefore, the optimization model is established to find out the adjustment model of the reflection panel based on the displacement of discrete main cable nodes.

In practice, when the actuator pulls the triangular reflector for displacement, there will be a small change in the distance between adjacent nodes, which deviates from the theoretical offset point calculated above, so that the main cable node is not on the ground anchor point and the connecting line of the ball center; that is, the three points cannot be strictly collinear. Therefore, the main cable node and ground anchor point do not move completely along the radial direction in the actual deformation [32, 33].

We take any main cable node A(x₀, y₀, z₀) on the working area of the reference sphere, set the ideal offset point of A point as A^′(x^′, y^′, z^′) point, and the A^′ point is located on the ideal paraboloid x² + y² = 4f(z + h)². Due to the existence of deviation, we set the actual offset point of A point as A^′′(x^′′, y^′′, z^′′) point. Figure 3 shows the geometric relationship between theoretical displacement and actual displacement of main cable node.

The Euclidean distance between point A^′ and point A^′′ is

(27)

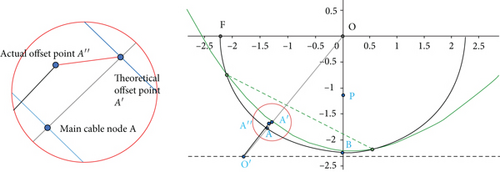
To establish the adjustment model of the main cable node approaching the ideal paraboloid, we use the shortest distance from the actual offset point to the ideal paraboloid as the objective function to establish the optimization model.

The Lagrange operator method is used to calculate the minimum distance between the actual offset point and the ideal paraboloid. For the actual offset point A^′(x^′, y^′, z^′), take the square of Euclidean distance as the objective function, i.e.,

(28)

Lagrangian operator λ with λ ≥ 0 is introduced to construct Lagrangian as follows:

(29)

Calculate the partial derivative of the Lagrangian on x, y, z, λ, respectively, and make it zero, including

(30)

The solution of the equations is obtained

(31)

Replace the x, y, z solved into the original objective function D to obtain

(32)

The objective function gives the minimum value of the distance between any point in space (take the actual offset point here) and the ideal paraboloid. In order to make the objective function reach the minimum value, that is, the actual offset point can best approach the ideal paraboloid, it is necessary to add constraints to it. Obviously, in order to make the actual offset point closer to the ideal paraboloid, the actuator, the main cable node, and the transformed point should be on the same straight line and perpendicular to the reference sphere. The direction vector of the straight line is obtained by using the coordinates:

(33)

The expansion and contraction amount of the actuator tends to the direction of the center of the ball along the radial direction of the reference sphere, and its radial expansion and contraction range are -0.6 ~ +0.6 m. Then, we can solve the radial deviation according to this condition:

(34)

According to the above constraints, we establish the adjustment optimization model of reflective panel based on the displacement of discrete main cable nodes:

(35)

At the same time, the topic shows that the small change range of the spacing between adjacent nodes does not exceed 0.07%. Therefore, we add constraints in the process of solving the optimization model, judge in the global situation, and discard the coordinate sequence with the change range exceeding 0.07%.

4.4. Result Analysis

By changing h and f, the objective function value is minimized. Since this problem is a multivariable optimization function, the ordinary traversal method requires a large amount of computation and is affected by the accuracy of the traversal step size; so, the local optimal solution is often obtained. Therefore, the genetic algorithm is used to find the global optimal solution in this problem, and the specific flow chart is shown in Figure 4.

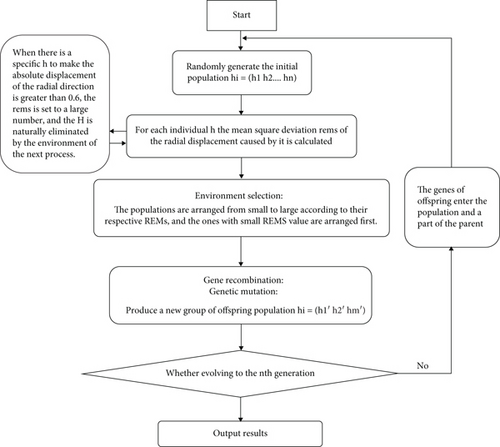
The genetic algorithm steps are roughly as follows:

Step 1. Firstly, the variables are binarized to generate a random initial population, and the fitness value of each individual in the population is calculated.

Step 2. Sort the population individuals according to their fitness and then perform gene recombination and gene mutation in turn to obtain a new population of progeny.

Step 3. Insert the offspring group into the parent group and screen out individuals with excellent fitness values.

Step 4. Enter the next evolution and stop and output the optimal solution when the evolution reaches the formulation of algebra.

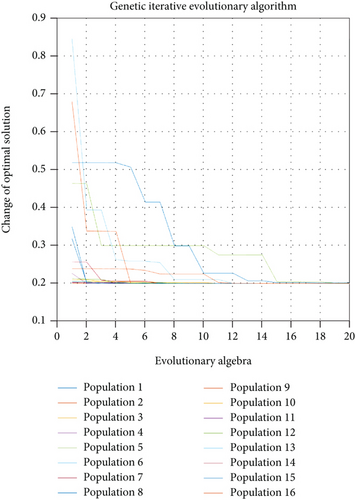
Using the above genetic algorithm and substituting the data in the attachment to solve the optimal offset coordinates of each main cable node, the final optimal solution is h = 300.8169 and f = 140.6192. Substitute h and f into the calculation formula (4) of the deviation d. Since the length does not change with the change of the coordinate system, the value of d is the same as the value in the reference coordinate system. Therefore, it can be obtained that the parabolic trajectory equation of the actual migration is x² + y² = 562.4768(z + 300.8169), the average length of the adjacent nodes is 0.0633%, and the average length of the radial shrinkage of the main cable node is 0.20343. According to the solved main cable node coordinates, perform inverse transformation according to the rotation matrix, solve the transformation coordinates in the reference coordinate system, and adjust the main cable node number, position coordinates, and the expansion and contraction amount of each actuator within the 300-meter diameter of the rear reflection surface. The resulting genetic iterative evolution diagram is shown in Figure 5.

5. Receiving Ratio of Feed Cabin Based on Reflector Adjustment Scheme

5.1. Research Approach

According to the active reflector mediation scheme obtained, in order to calculate the effective amount of information received by the feed cabin, the area contacted by the electromagnetic wave can be used as the basis for judging its amount of information. For each triangular reflector, the projection triangle formed when the electromagnetic wave propagates to the plane of the feed cabin through reflection is considered. Since the effective receiving area of the feed cabin is small, about 0.7854m², it is necessary to judge the area of the projected area. By meshing the plane where the feed cabin is located and decomposing it into a set of points, the effective coverage area of the projection to the feed cabin can be judged according to the distribution of points [34].

5.2. Determination of Receiving Ratio of Feed Cabin after Adjusting Paraboloid

The topic has given that electromagnetic wave signals and reflected signals are regarded as linear propagation; so, their propagation can be considered to obey the optical principle. Since we have rotated the coordinate system, the electromagnetic wave from the observed celestial body can be regarded as a parallel electromagnetic beam of vertical incidence, and its direction vector is set as . We use the size of the area touched by the electromagnetic wave as the basis for judging the amount of information. For each triangular reflecting surface, consider the projection on its plane when the electromagnetic wave received and reflected by its three vertices propagates to the feed cabin located at the ideal parabolic focus. The projection triangle formed by these three projections is the projection area of the electromagnetic wave reflected by the triangular reflective panel, as shown in Figure 6.

Among them,

is the unit normal vector of the triangular panel, and

is the direction vector of the outgoing light after the incident electromagnetic wave is reflected by the reflective panel. Let

be used to calculate the two side length vectors

and

of the triangular panel using the known vertex coordinates of the triangular panel, and then the coordinate expression of the normal vector can be calculated as follows:

(36)

According to the optical principle, the incident ray, the normal line, and the reflected ray are in the same plane; that is, the reflected ray direction vector

satisfies the condition:

(37)

At the same time, the normal is the angle bisector of the incident ray and the reflected ray; that is, the angle between

and

is equal to the angle between

and

. The specific formula is as follows:

(38)

Since

is only used to represent the direction of the reflected light, for the convenience of calculation, we set its component in the x direction to be 1. Combining the above conditions, we get the system of equations:

(39)

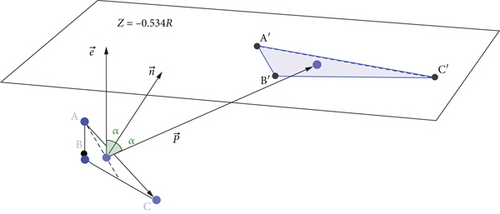
If the normal vector of the triangular unit panel is , then the coordinate expression of is obtained by solving the system of equations as (1, (b/a), (a⁴ + 2a²b² + b⁴ − a²c² − b²c²/2a³c + 2ab²c)).

Combining the reflected light direction vector

and the vertex coordinates of the reflective panel, we can obtain the trajectory equation of the reflected electromagnetic wave projected to the reflective panel as

(40)

Among them, p_x = 1, p_y = b/a, p_z = a⁴ + 2a²b² + b⁴ − a²c² − b²c²/2a³c + 2ab²c. The intersection of the trajectory and the electromagnetic wave receiving plane where the feed cabin is located is the projection point, and the triangle formed by the projection points of the three vertices of the reflective panel is the projected triangle on the plane of the feed cabin. In the follow-up coordinate system, the x-coordinate of the plane where the feed cabin is located is always -0.534R, and using this conditional formula (39), the coordinates of the projection point are solved as follows:

(41)

Similarly, the coordinates of B and C can also be obtained similarly.

Based on the adjustment scheme of the main cable nodes obtained in the second 4, we can find out the projection of the main cable nodes on the plane of the feed cabin according to the position coordinates of each main cable node in the working area, so that the amount of electromagnetic wave information received by the feed cabin can be calculated, as shown in Figure 7.

5.3. Result Analysis

5.3.1. Determination of the Effective Receiving Area of the Circular Surface of the Feed Cabin

It is known that the effective receiving surface of the feed cabin is a central disk with a diameter of 1 m; that is, the effective receiving area of the feed cabin is small, about 0.7854 m²; so, we need to judge the area of the projected area. If the projected area completely covers the central disk, the effective receiving area is 0.7854 m²; if the projected area does not completely cover the central disk, the effective receiving area is the overlapped area; if the projected area does not cover the center disk, the effective receiving area is 0.

Using the finite difference method to decompose the plane where the feed cabin is located into a set of points, for the discretization of the {−1 < x < 1; −1 < y < 1} region on the plane where the feed cabin is located, taking Δ = 0.001 as the step length, use two sets of straight line families parallel to the OX^′ axis and the OY^′ axis to mesh the circular surface and divide it into a square grid, then any point on the circular surface falls on the node of the square grid, and its coordinates are as follows:

(42)

For each point on the circular surface, it is discussed whether it falls inside the projected triangle or on the boundary, and then the problem turns into the problem of whether the point falls inside the triangle. Take any discrete point P as the following discussion [35].

Whether the point P is inside the triangle A^′B^′C^′, the positional relationship between the triangle and the disk can be judged by the barycentric method. The two sides of the projected triangle are used as the direction of a set of two-dimensional basis vectors, and then any point on the plane can be represented by this pair of basis vectors, that is, , Among them, u and v are real numbers, and the positional relationship between point P and triangle A^′B^′C^′ is judged by the values of u and v. The result is shown in Figure 8.

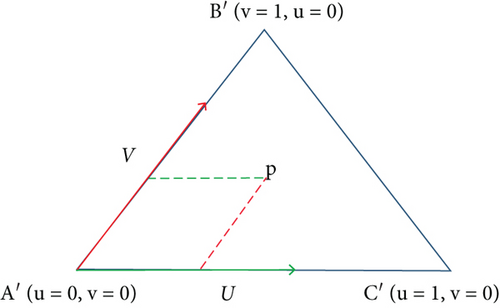
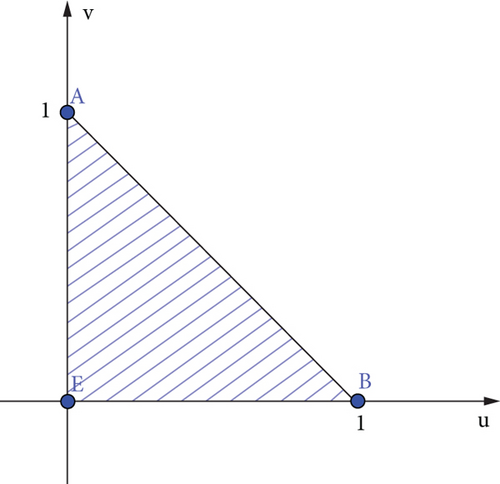
When the value of u and v falls in the shaded part, that is, when the condition is satisfied, the point P falls inside the triangle A^′B^′C^′; otherwise, it is not inside the triangle.

When the point P is inside the triangle A^′B^′C^′, then we think that the point P receives the electromagnetic wave of the panel triangle ABC. It can be seen that N (N = 1290) panels participate in the reflection on the paraboloid with a diameter of 300 meters. Traverse the N panels. Whenever a transmitting panel is mapped to a triangle containing a point on the plane where the feed cabin is located, the number of electromagnetic waves Q received by it increases by 1. When the traversal is completed, the electromagnetic wave reception ratio of this point is λ = Q/N. Then, traverse other discrete points according to the above process. Each discrete point stores the electromagnetic wave reception ratio and draws an image, as shown in Figures 9 and 10.

Then, the total amount of electromagnetic wave radiation received by the feed cabin is λ:

(43)

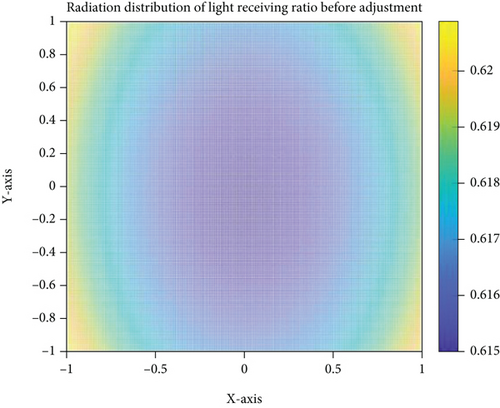
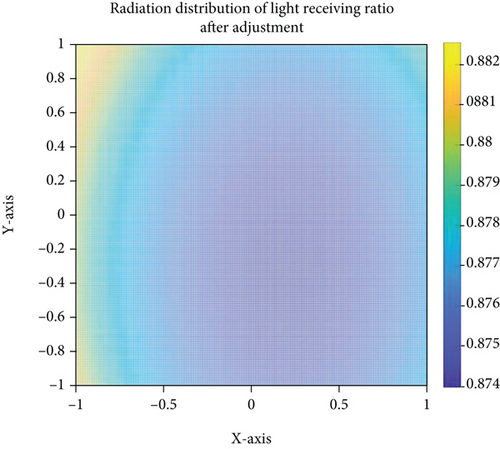
Among them, λ_i is the reception ratio of discrete points in the circular surface of the feed cabin, and Δ = 0.001 is the step size. According to this principle, the feed cabin can receive the information of 61.628% of the total number of panels before adjustment and 87.752% of the total number of panels after adjustment.

5.3.2. Calculation of Receiving Area Ratio of Feed Cabin

It is known that the effective receiving surface of the feed cabin is a central disk with a diameter of 1 m; that is, the effective receiving area of electromagnetic wave is small, about 0.7854m². From the idea of discrete instead of continuous, the formula of the average total electromagnetic wave radiation area of the feed cabin is as follows:

(44)

The formula of the total electromagnetic radiation area provided by the reflection panel is as follows:

(45)

Among them, s_cabin is the shielding area of the feed cabin, and s_i is the area of each reflection panel participating in the reflection within a diameter of 300 meters. The complete data can be found in the supporting material, and some data are shown in Table 3.

Table 3. Area of each reflective panel participating in reflection within 300 m aperture.

Main index node 1	Main index node 2	Main index node 3	Reflector area
A0	B1	C1	51.359 744 99
A0	B1	A1	51.360 016 64
A0	C1	D1	51.357 310 45
A0	D1	E1	51.357 310 45
……	……	……	……
D245	D267	D268	65.874 906 28
D246	D247	D269	62.299 899 98
D246	D268	D269	65.594 604 13

When the reference sphere is not adjusted, the feed cabin can receive the electromagnetic wave signal reflected by about 61.628% of the total panels. The ratio of the area of electromagnetic waves received by the feed cabin to the area of electromagnetic waves received and reflected by the reflector is about 0.636%. After the base sphere is adjusted to a paraboloid, the feed cabin can receive the electromagnetic wave signals reflected by about 87.75% of the total panels. The ratio of the area of electromagnetic waves received by the feed cabin to the area of electromagnetic waves received and reflected by the reflector is about 0.906%.

6. Conclusion and Prospect

In this paper, the following coordinate system is introduced, which effectively simplifies the geometric operation process, reduces the calculation and model complexity, and adopts the idea of overall deviation distribution, which can make the main cable nodes approach the ideal paraboloid more accurately. The optimization model is established with known constraints and solved by genetic algorithm. In the process of solving, global control variables are added to screen out bad values. However, due to the complexity of the optimization algorithm, the large amount of data, the impact of various data, and the long optimization time, the specific details of the change of the distance between the main cable nodes cannot be solved and can only be screened according to the global control variables. The displacement model of the main cable node in the follow-up coordinate system established in this paper can be applied to any angle of the observed celestial body. The active reflector adjustment optimization model can add constraints to it; so, it can be extended to more conventional cases, such as considering the length change after the pull-down force. The specific research conclusions are as follows:

(1)
A follow-up coordinate system with the direction of the observed celestial body as the reference is introduced to find the optimal approximation model for the distribution of the mean square deviation of the radial direction. In order to make the telescopic distance of the actuator within the adjustable range, the overall deviation distribution vector is investigated with h as a variable to find the H value with the minimum overall offset, that is, the minimum overall root mean square error, and the trajectory equation of the ideal paraboloid is determined by the ergodic algorithm
(2)
The coordinate data of each main cable node are rotated according to the known angle of the celestial body, and the shortest distance from the actual offset point to the ideal paraboloid is obtained by using the Lagrange operator method. Taking this as the objective function, the reflective panel adjustment model of the optimal displacement strategy of discrete main cable nodes is established. The global optimal solution of the offset of each main cable node in the working area is obtained by using genetic algorithm. The mean value of the distance variation between adjacent nodes is 0.0633%, and the average length of the radial contraction of the main cable node is 0.20343
(3)
The area contacted by the electromagnetic wave is taken as the basis for judging its information content. For each triangular reflecting surface, considering the projection triangle formed when the electromagnetic wave is reflected and propagated to the plane where the feed cabin is located, the effective coverage area of the projection to the feed cabin is judged by using the finite difference method and the center of gravity method. When the reference sphere is not adjusted, the feed cabin can receive the electromagnetic wave signal reflected by about 61.628% of the total number of panels, and the ratio of the electromagnetic wave area received by the feed cabin to the electromagnetic wave surface product received and reflected by the reflector is about 0.636%. After being adjusted to a paraboloid, the feed cabin can receive about 87.75% of the total number of panels, and the ratio of the electromagnetic wave area received by the feed cabin to the electromagnetic wave area received and reflected by the reflector is about 0.906%

However, there are still some shortcomings, mainly including the following: first, the optimization algorithm is complex, the amount of data is large, there are impacts between various data, and the optimization time is long. Secondly, the change of the distance between the main cable nodes cannot be solved in detail and can only be filtered out according to the global control variables. In order to obtain more accurate results, future research will focus on increasing the constraints of the dynamic reflector adjustment optimization model, so as to extend it to more conventional cases.

Conflicts of Interest

The author declares that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This study was funded by the Natural Science Foundation of the Higher Education Institutions of Anhui Province (KJ2021A0486).

Open Research

Data Availability

The data in this paper come from question A of the 2021 Contemporary Undergraduate Mathematical Contest in Modeling.

References

1 Wu S. Y., A project on the threshold of the 21 century: next generation of radio telescope, Progress in Astronomy. (1995) 13, no. 2, 164–172.
Google Scholar
2 Nan R. D., Five hundred meter aperture spherical radio telescope (FAST), Mechanics & Astronomy. (2006) 49, no. 2, 129–148, https://doi.org/10.1007/s11433-006-0129-9, 2-s2.0-33646497868.
10.1007/s11433-006-0129-9
Web of Science® Google Scholar
3 Han J., Fan D. W., Tao Y. H., Xu Y., Li S., Mi L., Li C., and Cui C., The project management information system for FAST scientific observation, Frontiers of Data & Computing. (2022) 4, no. 1, 20–29.
Google Scholar
4 Wang Y., Deng Q., Niu B. Q., Wei H. B., and Guo X., Design of Active Reflector Adjustment Scheme for ‘FAST’ based on search optimization, Guizhou Science. (2022) 40, no. 1, 93–98.
Google Scholar
5 Xue J. X., Wang Q. M., Gu X. D., Zhao Q., and Gan H. Q., Estimation and improvement for fitting accuracy of instantaneous parabolic reflector in FAST, Optics and Precision Engineering. (2015) 23, no. 7, 2051–2059.
10.3788/OPE.20152307.2051
Google Scholar
6 Li Q. W., Jiang P., and Nan R. D., Initial gap between panels of the reflector of FAST, Journal of Mechanical Engineering. (2022) 53, no. 6, 119–121.
Google Scholar
7 Luo Z. X., Qin X. H., and Chen X., Research of reflector adjustment of FAST: based on OLS model, Technology Innovation and Application. (2022) 12, no. 5, 57–59.
CAS Google Scholar
8 Zhu L. C., Control of the main active reflector of FAST, Frontiers of Data & Computing. (2012) 3, no. 4, 67–75.
Google Scholar
9 Chen Y., Study on Active Main Reflector of 500 Meter Aperture Spherical Radio Telescope (FAST), 2006, Graduate School of Chinese Academy of Sciences, Beijing of China.
Google Scholar
10 Wang Y. A., Research on the FAST Node Displacements Predicting Based on Statistical Regression Analysis Theory, 2015, Northeastern University, Shenyang of China.
Google Scholar
11 Mou M., Kong Y. N., and Guo L., Research on shape adjustment strategy of FAST reflector, Modern Information Technology. (2021) 5, no. 16, 86–92.
Google Scholar
12 Zhu Z. Y., Zhang L., Wang Z., Bai G. B., Liu C. J., Liu F., Wang W., and Li Q. W., Form-finding and structural behavior of cable net of five-hundred-meter aperture spherical radio telescope, Journal of Building Structures. (2021) 42, no. 1, 18–29.
Google Scholar
13 Wu W. and Zhang C., Surface precision analysis of FAST model in MIYUN, Journal of Geomatics. (2008) 6, 21–23.
Google Scholar
14 Luo B., Guo Z. X., and Wang K., Performance optimization analysis of FAST reflector supported cable-net based on initial baseline state, China Civil Engineering Journal. (2015) 48, no. 12, 12–22.
Google Scholar
15 Zhu W. X., Deng L. J., Huang Y., and Ou J. P., Design and process control of cable length with millimeter accuracy of FAST project, Journal of Mechanical Engineering. (2017) 53, no. 17, 17–22, https://doi.org/10.3901/JME.2017.17.017, 2-s2.0-85031040608.
10.3901/JME.2017.17.017
Google Scholar
16 Zheng X. L., Xiong J. M., Zhou J. Z., and Shu Z., Parametrization study of ring expanded symmetrical cable net structure based on ANSYS finite element method, Science Technology and Engineering. (2018) 18, no. 11, 281–286.
Google Scholar
17 Li J. L., Peng B., Li H., Li Q. W., Shen Y. Z., Jiang P., and Luo B., Analysis of collisions of reflector elements of the FAST active reflector, Journal of Xidian University. (2019) 46, no. 5, 148–154.
Google Scholar
18 Luo Y. B., Zheng Y., and Zhu L. C., Astronomical trace layout of FAST, Journal of Geomatics Science and Technology. (2011) 28, no. 2, 105–107.
Google Scholar
19 Li M. H. and Zhu L. C., Optimization analysis of deformation strategy of fast instantaneous parabolic, Journal of Guizhou University (Natural Sciences). (2012) 29, no. 6, 24–28.
Google Scholar
20 Wang W., Duan B. Y., and Ma B. Y., A method for panel adjustment of large reflector antenna surface and its application, Acta Astronomica Sinica. (2008) 36, no. 6, 1114–1118.
10.3724/SP.J.1006.2010.01114
Google Scholar
21 Zhu W. B., Research on Astronomical Planning and Feed Support for FAST, 2006, Graduate University of The Chinese Academy of Science, Beijing.
Google Scholar
22 Wang Q. D. and Luo H. W., The simulation and research on feed’s phase center of rotating parabolic antennas, Journal of Chongqing University. (2013) 36, no. 4, 45–50.
Google Scholar
23 Deng S., Jing F. S., Ling Z. Z., Yang G.-d., and Yu D.-j., Research on pose distribution algorithm of FAST feed support system, Optics and Precision Engineering. (2017) 25, no. 2, 375–384, https://doi.org/10.3788/OPE.20172502.0375.
10.3788/OPE.20172502.0375
Google Scholar
24 Li M. H., Jiang P., Yu D. J. et al., Attitude Kalman filtering to improve position and attitude accuracy by integrated BDS/SINS for the FAST feed cabin, Acta Astronomica Sinica. (2021) 62, no. 3, 113–122.
Google Scholar
25 Li H., Zhu W. B., and Pan G. F., Mechanics in the FEED support of FAST telescope and its research Progress, Advances in Mechanics. (2011) 41, no. 2, 133–154.
Google Scholar
26 Li H., Zhu W. B., and Pan G. F., Equilibrium analysis of FAST rope-drive parallel manipulator based on rope force optimization, Engineering Mechanics. (2015) 37, no. 6, 424–434.
Google Scholar
27 Yu L., Shi F., Wang H., and Hu F., 30 Case Analysis of MATLAB Intelligent Algorithm, 2015, Beihang University Press, Beijing.
Google Scholar
28 Zhu J.-M., Geng Y.-G., Li W.-B., Li X., and He Q.-Z., Fuzzy decision-making analysis of quantitative stock selection in VR industry based on random forest model, Journal of Function Spaces. (2022) 2022, 12, 7556229, https://doi.org/10.1155/2022/7556229.
10.1155/2022/7556229
Web of Science® Google Scholar
29 Zhu J.-M. and Xia W.-Y., The spread pattern on Ebola and the control schemes, International Journal of Innovative Computing and Applications. (2018) 9, no. 2, 77–89, https://doi.org/10.1504/IJICA.2018.092590, 2-s2.0-85049234141.
10.1504/IJICA.2018.092590
Google Scholar
30 Zhang S.-M., Zhan W.-L., Hu H., Liu Y.-S., and Zhu J.-M., Research on Ethanol Coupling to Prepare C4 Olefins Based on BP Neural Network and Cluster Analysis, Journal of Chemistry. (2022) 2022, 10, 5324336, https://doi.org/10.1155/2022/5324336.
10.1155/2022/5324336
Web of Science® Google Scholar
31 Cai X.-W., Bao Y.-Q., Hu M.-F., Liu J.-B., Zhu J.-M., Bao Y.-Q., and Hu M.-F., Simulation and prediction of fungal community evolution based on RBF neural network, Computational and Mathematical Methods in Medicine. (2021) 2021, 13, 7918192, https://doi.org/10.1155/2021/7918192.
10.1155/2021/7918192
PubMed Web of Science® Google Scholar
32 Xu F., Mo L.-Y., Chen H., and Zhu J.-M., Genetic algorithm to optimize the design of high temperature protective clothing based on BP neural network, Frontiers in Physics. (2021) 9, article 600564, https://doi.org/10.3389/fphy.2021.600564.
10.3389/fphy.2021.600564
Web of Science® Google Scholar
33 He Q. Z., Xia P. T., Li B., and Liu J.-B., Evaluating investors’ recognition abilities for risk and profit in online loan markets using nonlinear models and financial big data, Journal of Function Spaces. (2021) 2021, 15, 5178970, https://doi.org/10.1155/2021/5178970.
10.1155/2021/5178970
Web of Science® Google Scholar
34 Liu J.-B., Zhang T., Wang Y. K., and Lin W. S., The Kirchhoff index and spanning trees of Möbius/cylinder octagonal chain, Discrete Applied Mathematics. (2022) 307, 22–31, https://doi.org/10.1016/j.dam.2021.10.004.
10.1016/j.dam.2021.10.004
Web of Science® Google Scholar
35 Liu J.-B., Bao Y., Zheng W. T., and Hayat S., Network coherence analysis on a family of nested weighted n-polygon networks, Fractals. (2021) 29, no. 8, article 2150259, https://doi.org/10.1142/s0218348x21502601.
10.1142/S0218348X21502601
Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] Adjustment Method of “FAST” Active Reflector Based on Optimal Fitting Strategy

Retraction(s) for this article

Retracted: Adjustment Method of “FAST” Active Reflector Based on Optimal Fitting Strategy

Abstract

1. Introduction

2. Basic Assumptions and Index Selection

2.1. Basic Assumptions

2.2. Symbol Description

3. Trajectory Equation of Ideal Paraboloid under Nonworking State of Active Reflector of Radio Telescope Based on Ergodic Algorithm

3.1. Research Approach

3.2. Displacement Model of Active Reflector

3.3. Establishment and Solution of Overall Offset Model

3.4. Result Analysis

4. Problem Two Model Establishment and Solution

4.1. Research Approach

4.2. Theoretical Derivation

4.3. Reflector Pane Adjustment Model Based on Discrete Main Cable Node Displacement

4.4. Result Analysis

5. Receiving Ratio of Feed Cabin Based on Reflector Adjustment Scheme

5.1. Research Approach

5.2. Determination of Receiving Ratio of Feed Cabin after Adjusting Paraboloid

5.3. Result Analysis

5.3.1. Determination of the Effective Receiving Area of the Circular Surface of the Feed Cabin

5.3.2. Calculation of Receiving Area Ratio of Feed Cabin

6. Conclusion and Prospect

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] Adjustment Method of “FAST” Active Reflector Based on Optimal Fitting Strategy

Retraction(s) for this article

Retracted: Adjustment Method of “FAST” Active Reflector Based on Optimal Fitting Strategy

Abstract

1. Introduction

2. Basic Assumptions and Index Selection

2.1. Basic Assumptions

2.2. Symbol Description

3. Trajectory Equation of Ideal Paraboloid under Nonworking State of Active Reflector of Radio Telescope Based on Ergodic Algorithm

3.1. Research Approach

3.2. Displacement Model of Active Reflector

3.3. Establishment and Solution of Overall Offset Model

3.4. Result Analysis

4. Problem Two Model Establishment and Solution

4.1. Research Approach

4.2. Theoretical Derivation

4.3. Reflector Pane Adjustment Model Based on Discrete Main Cable Node Displacement

4.4. Result Analysis

5. Receiving Ratio of Feed Cabin Based on Reflector Adjustment Scheme

5.1. Research Approach

5.2. Determination of Receiving Ratio of Feed Cabin after Adjusting Paraboloid

5.3. Result Analysis

5.3.1. Determination of the Effective Receiving Area of the Circular Surface of the Feed Cabin

5.3.2. Calculation of Receiving Area Ratio of Feed Cabin

6. Conclusion and Prospect

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information