Vibration Characteristics of Shear Thickening Fluid-Based Sandwich Structures
Abstract
The vibration attenuation mechanism of shear thickening fluid- (STF-) filled sandwich structures was investigated in this study. Structural equivalent damping, stiffness, and mass increased simultaneously with the increase in the volume fraction of shear thickening fluid. However, the damping ratio decreased and natural frequency increased with the increase in structural mass. Thus, the damping ratio was not a monotonically increasing function of the volume fraction of STF. A modified shear strain model of the damping layer was developed based on the following conditions: (1) under the condition of small strain, shear thickening fluid was regarded as linear viscoelastic material, and (2) the warpage of the sandwich beam was considered during deformation and the influence of STF on the shear strain of sandwich beam. According to the modified shear strain model of the damping layer, the shear thickening occurred at 1 Hz to 20 Hz during vibration. Therefore, the resonance point of the structure shifted to the left. The predictions were in excellent agreement with the experimental results. The results demonstrated that shear thickening fluid improved the vibration damping performance of the sandwich structure, while the thickening ability was not the higher, the better.
1. Introduction
Viscoelastic damping sandwich structures have not only high stiffness, light weight, and high deformation resistance but also high damping properties. It is a more widely used damping technology in vibration and noise reduction at present [1]. Although the passive control method has the advantages of low cost and design simplicity, it is difficult to give an effective response to external changes. These weaknesses were resolved by the development of smart materials, such as shape memory polymers (SMPs) [2], magnetorheological (MR) [3], and electrorheological (ER) fluids [4]. Sandwich structures with these smart materials need only an external power supply to be activated and have the advantage of better adaptability to external changes [5]. However, long-term use of external power supply damages other devices due to electric breakdown. One approach to avoiding the requirement of an external power supply is to use a material whose characteristics are changed with the loading conditions [6].
Till 2006, the application of shear thickening fluid (STF) in sandwich structures has grown in importance [7]. STF is composed of particulate phase and carrier fluid, demonstrating a significant increase in viscosity when the shear rate exceeded the critical shear rate. The thickening process is quick and reversible [8]. On account of the remarkable properties, STF is applied to body armors [9, 10], dampers [11], polishing operations [12], and machining processes [13]. After integrating STF with sandwich structures, the stiffness [7] and damping properties [14] of STF-filled sandwich structures can be designed by STF with the different rheological properties. Viscoelastic damping sandwich structures consist of a damping layer (viscoelastic damping materials) and a structural layer [15]. The mismatch of stiffness between the structural layer and damping layer led to large shear deformation of the damping layer and then resulted in increased energy dissipation [16]. Therefore, the dynamic properties of sandwich structures change with the shear rheological property of STF. The shear thickening properties of STF have been extensively studied [17]. However, there is little research on the impact of the thickening ability of STF on the vibration performance of sandwich structures [18].
Fischer et al. first explored the effect of STF on the dynamic properties of sandwich structures. The results suggested that the resonant frequency and damping raised as the viscosity of STF increased. The stiffness of sandwich structures increased under better interfacial stress transfer [19]. In a separate study published later, the influence of particle morphology on structural dynamic characteristics was investigated. The results reflected that these parameters can directly affect shear moduli of STF, and therefore, the damping properties of the sandwich structure changed [20]. Based on magnetorheological fluid sandwich beam theory, the influence of thickness ratio of the surface layer to the middle layer, excitation frequency, amplitude, and location on the natural frequency of the sandwich structures integrating STF was analyzed by Wei et al. [21]. Gürgen and Sofuoğlu investigated the effects of STF on vibration performance of tubes under different boundary conditions with vibration tests [22]. Later, dynamic properties of PEG-400 and STF-filled sandwich structures were researched for contrast. The experimental results were consistent with Fischer’s research conclusions [23]. The starting point for previous studies was strain sensitivity of STF [24, 25]. Additionally, the shear strain of the STF interfacial layer was calculated based on classical beam theory [26]. The effects of STF on the dynamic properties of sandwich structures were deduced by the occurrence of shear thickening behavior. The impact of factors influencing STF rheology, vibration conditions, and structure design on sandwich structures was also considered in other studies. Generally, the vibration attenuation mechanism of shear thickening fluid- (STF-) filled sandwich structures was not deeply studied. The shear strain model of Fischer ignored the warpage of the sandwich beam during deformation and the influence of STF on the shear strain of the sandwich beam [27, 28]. Besides, Newtonian fluids and shear-thinning fluids were neglected in these studies, making it difficult to determine whether the thickening characteristics or the viscous properties of fluid played a role.
In this study, the vibration performance of PEG-400, 18 vol.% STF, 49 vol.% STF, and 61 vol.% STF-filled sandwich structures was studied to demonstrate the vibration attenuation mechanism of STF-filled sandwich structures. The shear rheological measurements were performed to reveal shear rheological behavior. Then, the vibration experiment was conducted to research the influence of PEG and STF on the dynamic properties of sandwich structures. The modified shear strain model was developed to analyze the vibration attenuation mechanism of shear thickening fluid on the vibration performance of sandwich structures.
2. Modeling Shear Strain of Damping Layer
The change in the dynamic properties of sandwich structures was correlated with damping layer rheological response under shear deformation. STF was a shear strain-sensitive material, with its damp and rigid performance increasing when the critical shear strain was exceeded. To analyze the effect of STF on the dynamic properties of sandwich structures, the modified shear strain model based on Fischer’s calculation [19] was developed. Previous models ignored the warpage of the sandwich beam during deformation and the influence of STF on the shear strain of the sandwich beam. These conditions were considered when the modified model was established. Shear thickening fluid was regarded as linear viscoelastic material under small strain to simplify the calculation [21].
Figure 1(a) is the schematic diagram of the cantilever sandwich beam filled with STF under external excitation. The sandwich beam consisted of three layers. The lower and upper layers were aluminum alloy with thicknesses of h1 and h3, and the middle layer was STF with a thickness of h2. The length and width of the sandwich beam were a and b, respectively. Based on the classic sandwich plate theory, some assumptions were made about the model. Specifically, (1) the bond of each layer has no slippage during deformation; (2) the transverse displacement w of each layer was equal; (3) the tensile stress along the length direction of the STF layer was ignored; and (4) the section of each layer remained flat after being deformed.
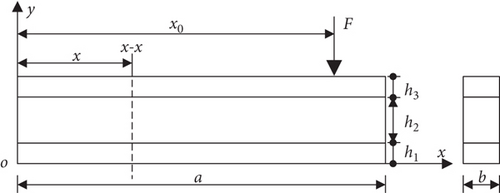
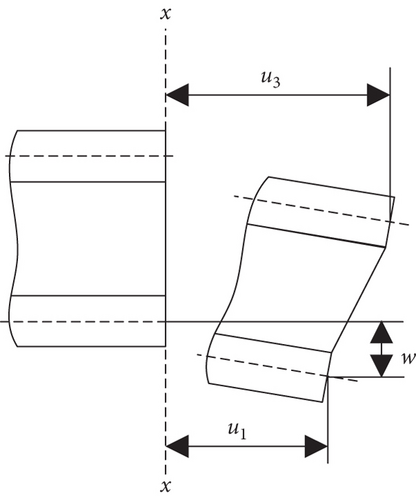
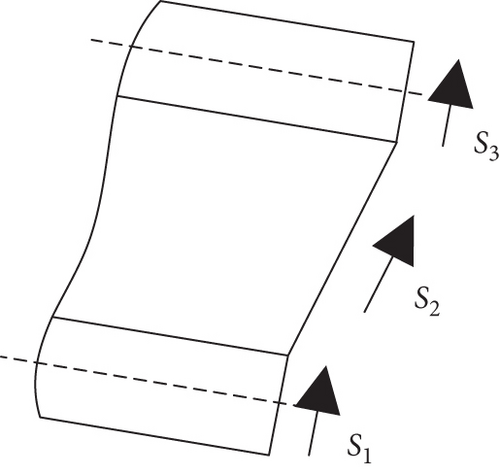
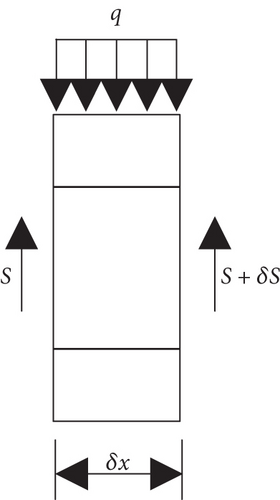
- (1)
The shear strain at the fixed end was 0
- (2)
The shear rate at the fixed end was 0
3. Materials and Method
3.1. Preparation of STFs and STF-Filled Sandwich Structures
STFs were prepared by dispersing silica particles (from Evonik Degussa Co., Ltd.) with a mean particle size of 650 nm into polyethylene glycol medium with Mw values of 400 (PEG-400, from Sinopharm Chemical Reagent Co., Ltd.). Figure 2(a) exhibits the transmission electron microscope (TEM) images of silica particles. The silica particles were monodisperse and spherical. By obtaining a homogeneous suspension, the sample was placed in a vacuum drying oven for 24 hours at 25°C to remove the bubbles. In the study, STFs at the conditions of different concentrations (18 vol.%, 49 vol.%, and 61 vol.% for SiO2) were produced.


STF-filled sandwich structures were prepared by one layer of 3 mm thick STF and two layers of 1 mm thick aluminum alloy (5052 type aluminum alloy). Silicone rubber with a width and a thickness of 3 mm was applied for sealing around the sandwich beams. A bakelite with a length of 30 mm, a width of 10 mm, and a thickness of 3 mm was placed at the clamping end. Figure 2(b) displays STF-filled sandwich structures, with the dimension of 260 × 10 × 5 mm3.
3.2. Method
3.2.1. Rheology Tests
The rheological behavior of PEG and STF was explored by an Anton-Paar Physica MCR 301 rheometer. The steady-shear experiments were performed with 25 mm diameter parallel plates. The frequency sweep and strain amplitude sweep tests were conducted on a cone plate with a diameter of 50 mm and an angle of 1°.
3.2.2. Vibration Tests
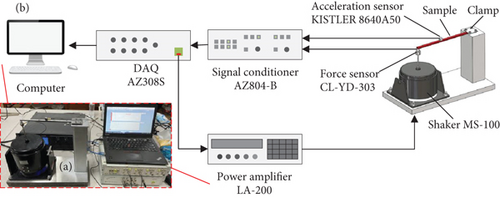
The vibration experiment was conducted by the vibration beam testing (VBT) set-up to investigate the influence of PEG and STF on the dynamic properties of sandwich structures, as illustrated in Figure 3. The boundary conditions of all samples were single-fixed. One end of the sample was clamped, and the other end was excited to generate vibration from a shaker (MS-100). The force signal was collected by a piezoelectric pressure sensor (CL-YD-303). The sandwich beam acceleration signal was measured by the acceleration sensor (KISTLER 8640A50). The power spectrum of the vibration signal was obtained by CRAS modal analysis software. The experimental design is presented in Table 1. The neat sandwich structure is sealed with silicone rubber to ignore the effect of silicone rubber on the damping.
| Specimen code | Specimen design | Average weight (g) |
|---|---|---|
| NSS | Net sandwich structure | 20.39 |
| SSF-PEG | Sandwich structure filled with PEG-400 | 24.83 |
| SSF-STF18 | Sandwich structure filled with 18 vol.% STF | 25.48 |
| SSF-STF49 | Sandwich structure filled with 49 vol.% STF | 26.30 |
| SSF-STF61 | Sandwich structure filled with 61 vol.% STF | 27.25 |
4. Results and Discussion
4.1. Rheological Behavior
4.1.1. Steady-State Rheological
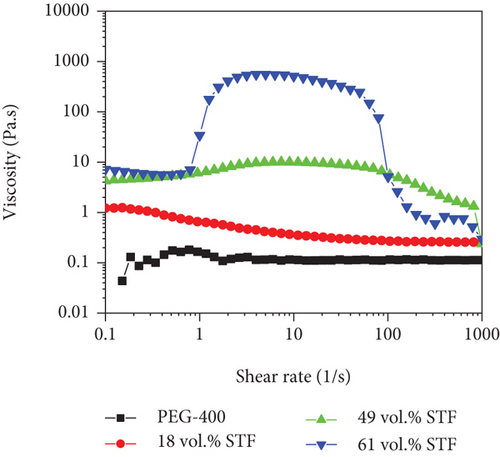
The steady-state shear rheological curve of PEG-400, 18 vol.% STF, 49vol.% STF, and 61 vol.% STF is illustrated in Figure 4. PEG-400 was the dispersion medium of shear thickening fluid. As a Newtonian fluid, the viscosity of PEG-400 did not change with the shear rate. With the addition of silica particles, rheological properties and initial viscosity of PEG-400 solution presented various kinds. Terminal hydroxyl and abundant oxygen atoms in PEG-400 formed a considerable number of hydrogen bonds with the silanol groups of silica particles [29]. Hence, the initial viscosity of STF was greater than that of PEG-400. 18 vol.% STF presented as non-Newtonian shear-thinning fluids. In the initial stages, electrostatic force and Brownian force acted on silica particles. The particles repelled one another and were arranged orderly. With the increasing shear rate, the original aggregates of particles were dispersed. According to the hydrodynamic cluster theory [30], the collisions between particles were neglected when the number of silica particles was small. Therefore, 18 vol.% STF possessed shear-thinning property. Besides, 49 vol.% STF exhibited continuous shear thickening (CST) behavior, and its viscosity slowly increased at the thickening stage. Additionally, 61 vol.% STF had a discontinuous shear thickening (DST) phenomenon, and its viscosity increased rapidly at the transition point. Chen et al. [31] investigated microstructural features of STF. The force between silica particles changed from hydrodynamic forces to contact friction force, resulting in the transition from CST to DST. A stable friction contact network was formed along with the DST phenomenon occurring. The silica particles were subject to compression during the DST stage [25, 32].
4.1.2. Dynamic Rheological
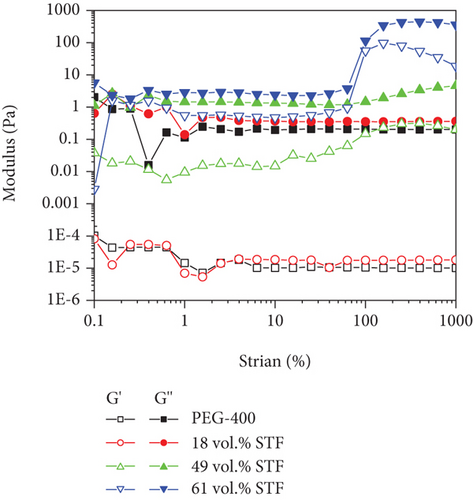
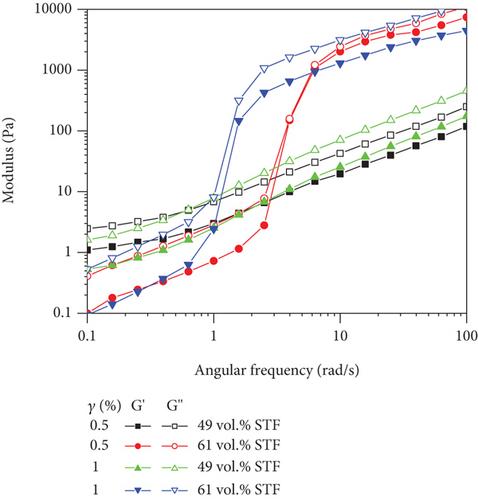
The changes in structure’s damping and stiffness were induced by the STF’s dynamic viscoelastic characteristics [33]. Considering that the frequency and strain varied in vibration, the effects of frequency and strain amplitude on the viscoelasticity of the damping layer were explored. The viscoelastic moduli of PEG-400 and STF versus angular frequency at the strain of 100% are presented in Figure 5(a). The storage and loss modulus of PEG-400 and 18 vol.% STF increased linearly in the range of 0.1-100 rad/s. The viscoelasticity analysis of STF was inconsistent with previous steady-state rheological analysis. This was an artifact due to low torque. PEG-400 mainly exhibited elasticity characteristics because its storage modulus was higher than the loss modulus. After the addition of silica particles, the viscous properties of mixtures were significant since the particle chain breakage resulted in permanent deformation when the angular frequency was high. The modulus of 61 vol.% STF changed suddenly in which significant nonlinear viscoelastic behavior appeared.

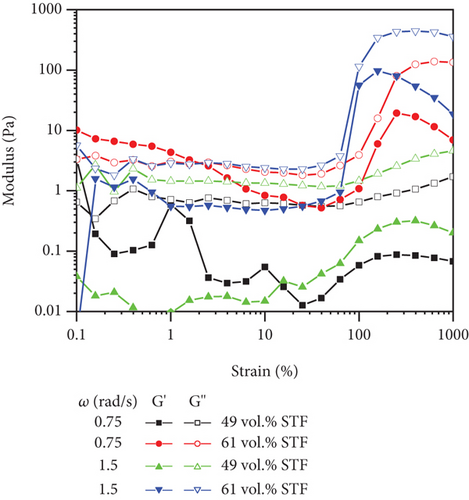
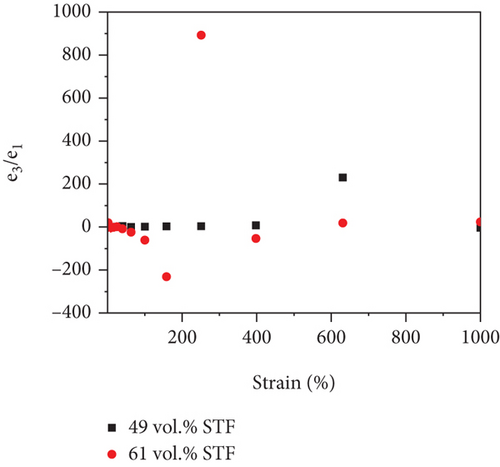
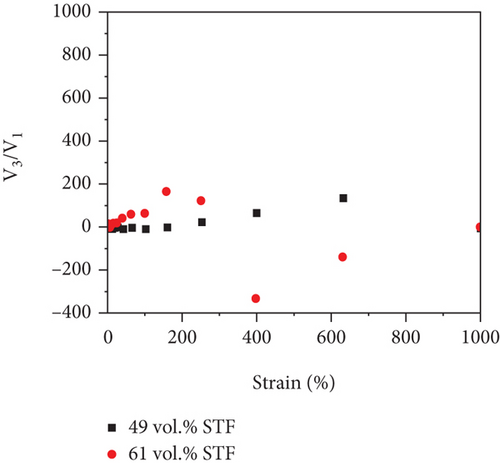
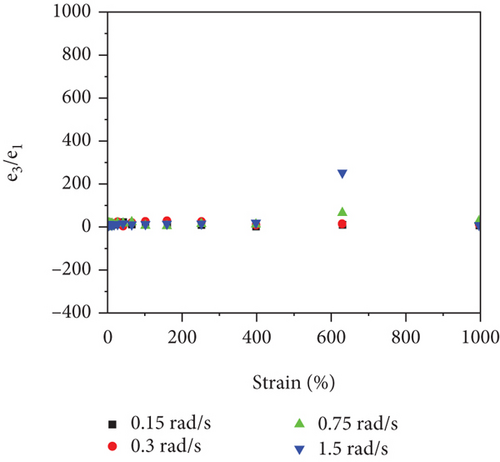
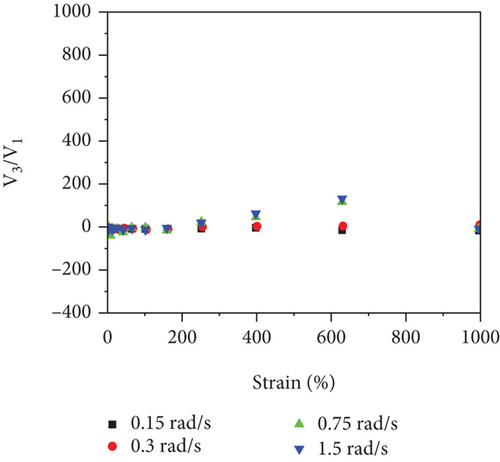
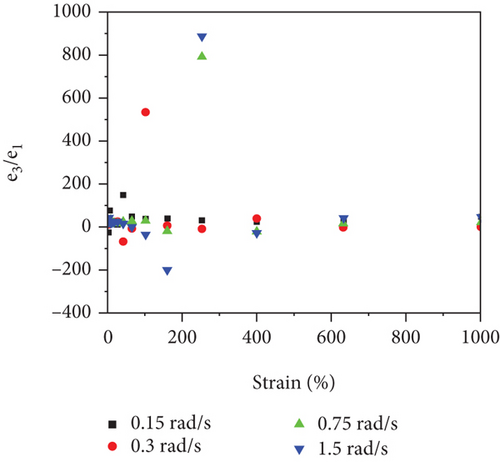
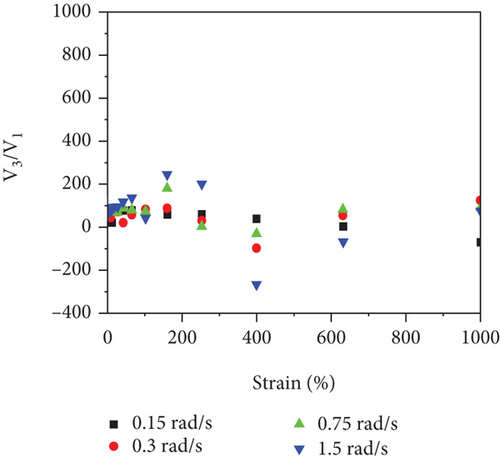
The measured e3/e1 and v3/v1 values from LAOS tests of 49 vol.% STF and 61 vol.% STF with the angular frequency at 1.5 rad/s are presented in Figures 6(a) and 6(b). The results revealed that the elastic nonlinearity of 61 vol.% STF was strain softening (e3 < 0) under a small strain; after that, the strain hardening appeared (e3 > 0). Additionally, 49 vol.% STF first exhibited elastic linearity (e3 = 0). Gradually, the elastic properties changed from linearity to strain hardening. With the increase in STF concentration, the e3/e1 values were added. The reason was that the more the silica particles of STF, the longer the length of particle chains. At the oscillatory shear strain, more particle chains twisted and rotated. Thus, the performance of elasticity of 61 vol.% STF became better. As reflected in Figure 6(b), the viscous nonlinearity of 49 vol.% STF and 61 vol.% STF improved little by little with the increasing strain. The variation trend of the ratio of viscous coefficients was similar to the elastic coefficients’ ratios. More particle chains increased resistance to particle motion. Therefore, the viscous properties of 61 vol.% STF were enhanced. Comparative analysis implied that the e3/e1 values increased and the viscous deformation occurred at small strains with the increase of the volume fraction of STF. Figures 6(c)–6(f) illustrate 49 vol.% STF and 61 vol.% STF elastic and viscous coefficients’ ratios in the angular frequency range from 0.15 to 1.5 rad/s. These data indicated that the e3/e1 values and v3/v1 values rose as the angular frequency increased. Under dynamic conditions, the critical point γmω of STF was a fixed value. Before reaching the critical point, the greater the angular frequency, the higher the viscoelastic moduli. Thus, elastic and viscous coefficients ratios increased [38].
4.2. Dynamic Response of the Sandwich Structure
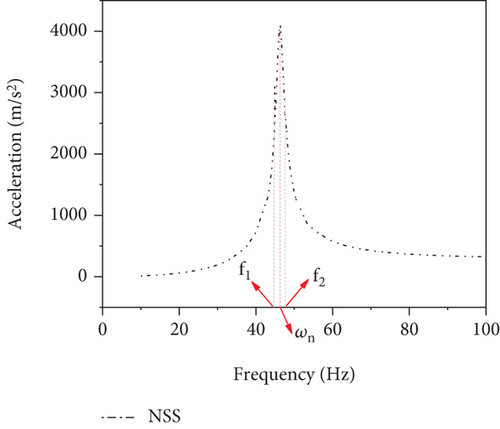
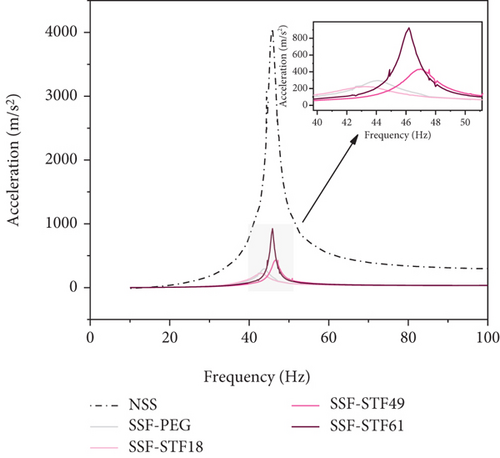
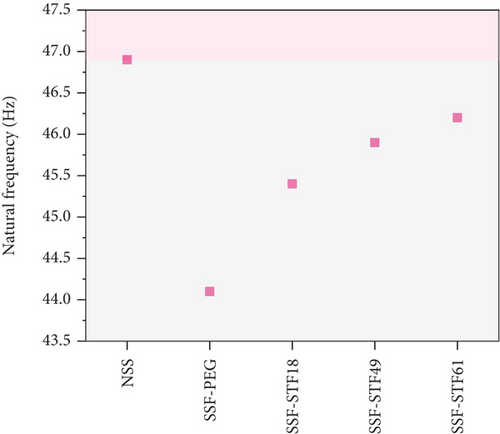
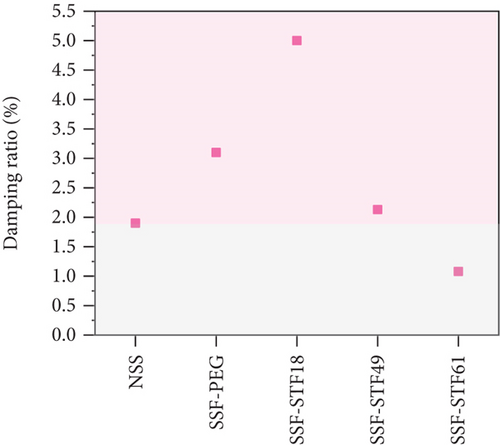
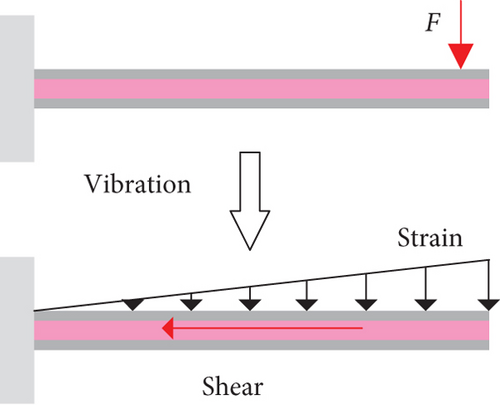
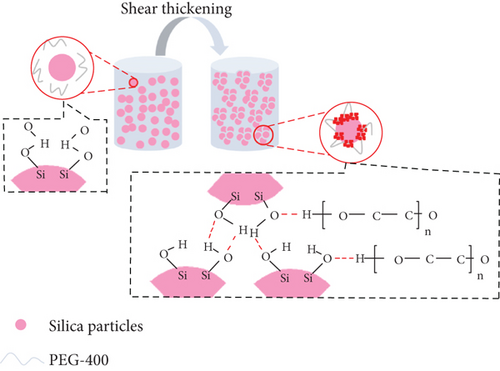
The shear thickening occurred at 1–20 Hz under dynamic conditions. Therefore, the resonance point of the structure shifted to the left after adding STF. The vibration attenuation mechanism of STF-filled sandwich structures is illustrated in Figure 8. Equation (16) indicated that the shear strain of STF was different. As demonstrated by Figure 8(a), the shear strain depended on where STF was. The shear thickening behavior occurred when the shear strain was greater than the critical shear strain, as indicated in Figure 8(b). PEG 400 formed ether hydrogen bonds in multiple positions on the surface of silica particles, or hydrogen bonds might be formed between one end group hydroxyl and surface silanol group. Hydrogen bonds may also be formed between PEG-400 molecules and silica particles. Compared with the one end group hydroxyl, the silanol groups were more acidic. PEG-400 was more likely to bond with silica particles than to form hydrogen bonds between PEG-400 molecules [43]. The formation of particle chain increased E and ceq. Additionally, the natural frequency of the neat sandwich structure was larger than that of the viscous fluid-filled sandwich structure since the maximum E value was smaller than 70 GPa. ζ was proportional to ceq. Nevertheless, keq and m remarkably affected the structural damping ratio. Therefore, ζ was not a monotonically increasing function of silica particles.
5. Conclusions
The vibration characteristics of fluids with different rheological properties filled with sandwich structures were investigated in this study. The results did not demonstrate that the larger the thickening ability, the better the vibration damping performance of the sandwich structure. STF improved the stiffness and damping properties of sandwich structures as a result of its high viscosity. With the increasing content of silica particles, the natural frequency and equivalent damping of STF-filled sandwich structures increased. According to the modified shear strain model of the damping layer, shear thickening behavior occurred under fixed strain amplitudes. Besides, the energy dissipation and stress transfer increased owing to the shear thickening effect. However, STF significantly influenced the mass of the structure, which increased by 33.6% in max. With the increasing mass, the damping ratio decreased, and natural frequency increased. Therefore, the vibrational properties were not monotonically increasing functions of the content of STF. The results demonstrated that after integrating STF with sandwich structures, sandwich structures filled with STF give effective response on external changes without external power supply. Sandwich structures filled with STF can be used for aeronautics, transportation, and buildings. In all these applications, adaptive control of structural vibration is realized by shear rate sensitivity of STF.
Conflicts of Interest
There are no conflicts to declare.
Acknowledgments
This work was supported by the Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX20_1786) and the Fundamental Research Funds for the Central Universities (JUSRP51907A, JUSRP51718A).
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding authors upon request.




