Journal of Function Spaces
Volume 2022, Issue 1 6911654
Research Article
Open Access

[Retracted] Analysis of Eccentricity-Based Topological Invariants with Zero-Divisor Graphs

Zhi-hao Hui, 

Zhi-hao Hui

School of Mathematics and Statistics, Pingdingshan University, Pingdingshan, Henan 467000, China pdsu.edu.cn

International Joint Laboratory for Multidimensional Topology and Carcinogenic Characteristics Analysis of Atmospheric Particulate Matter PM2.5, Henan 467000, China

Search for more papers by this author
Abdul Rauf, 

Abdul Rauf

Air University Multan Campus, Multan, Pakistan aumc.edu.pk

Search for more papers by this author
Muhammad Mohsin Abbas, 

Muhammad Mohsin Abbas

Air University Multan Campus, Multan, Pakistan aumc.edu.pk

Search for more papers by this author
Adnan Aslam, 

Corresponding Author

Adnan Aslam

University of Engineering and Technology, Lahore, Pakistan (RCET), Pakistan uet.edu.pk

Search for more papers by this author
First published: 23 May 2022
https://doi.org/10.1155/2022/6911654
Citations: 2
Academic Editor: Muhammad Gulzar

Abstract

Let be a commutative ring, where ♭1, ♭2, ♭3 are distinct primes, and q is any prime integer. A zero divisor graph J(R) of ring R is a graph with vertex set consist of zero divisors elements of R and any two vertices a, b are adjacent if and only if ab = 0. A topological index is a numerical number associated with the graph and may be helpful to correlate the graph with certain of its physical/chemical properties. In this paper, we have computed some eccentricity based topological indices of J(R), namely, atom-bond connectivity index (ABC5), eccentricity-based harmonic index of fourth type (H4(J)), geometric-arithmetic eccentricity index (GA4(J)), eccentricity-based third Zagreb index, and eccentricity-based first Zagreb index.

1. Introduction

There has been done wide investigation in combinatorics because of their strong ties to number theory and representation theory regarding algebraic structures [1, 2]. Due to their applications, finite rings and finite fields have attracted concentration in coding theory, cryptography along with vast theoretical study in these domains. The important functions known as molecular descriptors treat molecules as actual models as well as convert these molecules into numerals. These numerals are known as topological indices and are graph invariants.

Computing topological indices for different structures have been a study focus of recent work. In mathematical chemistry, the graph structure form of a chemical formula is called molecular graph. The compound’s atoms are considered as vertices, and chemical bonds between the vertices are considered as edges. A topological index can be defined as a numeric number that describes the topological structure of a chemical graph in a chemical graph while being unchanged under graph automorphism. As a result, there are several applications of these indices in nanotube structures, chemistry, and medical sciences [3, 4].

Topological indices are mainly characterized in to three categories: distance-based, degree-based, and counting-related topological indices [5–8]. Atom-bond connectivity index (ABC), Randic connectivity index (R−1/2), geometric-arithmetic index (GA), and harmonic index (H) are some famous degree-based topological indices. The Estrada index, Wiener index, and Hosaya index are the topological indices which are based on distance [9, 10]. The eccentricity-based connectivity atom-bond index [11], eccentricity-based harmonic index of fourth type [12, 13], geometric-arithmetic eccentricity index [14], and Zagreb eccentricity index [15, 16] are few examples of eccentricity-based topological indices. Topological indices may be used to broaden interdisciplinary study through mathematical operations on graphs as well as define conditions under which chemical structures are formed.

These topological indices attached to a molecular graph are useful to predict certain of its physical and chemical properties. For instance, the ABC index is used to study the stability of branched and linear alkanes. This index is utilized to calculate the shear energy of cycloalkanes [17, 18]. The geometric-arithmetic index has strong ability of predict certain physical and chemical properties of chemical structure as compared to the Randic connectivity index [19, 20]. First and second Zagreb indices are were used to estimate the total π-electron energy of alternate hydrocarbons [21]. For investigation of the chemical properties of different molecular structures, degree-based topological indices have great importance. Such application of degree-based indices offers motivation to study eccentricity-based topological indices. Eccentricity-based topological indices can be used to assess a compound’s pharmacological, physicochemical, and toxicological qualities based on its molecular structure [22, 23]. To get more knowledge about topological indices and their applications, see [24–28].

2. Preliminary Definitions

Let G = (V, E) be a graph, where V denotes the vertex set, and E denotes the edge set. Any two vertices x, y ∈ V are adjacent if there is an edge between x and y. The degree of a vertex x is denoted by dx and is defined as the number of vertices adjacent to x. The distance between two vertices x, y ∈ V is the length of the shortest path joining them. Eccentricity of a vertex x is denoted by εx and is the maximum of the distances of all vertices from x. Mathematically εx = max{d(x, y): y ∈ V}. To read more about the basic terminologies related to graph theory, see [29].

Let R be a commutative ring with identity. Any two nonzero elements x, y ∈ R are called zero divisors if x.y = 0. Let Z(R) be set of zero divisors of R. I. Beck [2] established the idea of the zero divisor graph J(R) by considering Z(R) as vertex set, and any two vertices x, y ∈ Z(R) are connected by an edge if and only if x.y = 0. His fundamental goal was to show how a commutative ring can be coloured [2]. Livingston and Anderson [30] proved that J(R) is a connected graph. For more results on this topic, see [24, 31, 32].

In general, any eccentricity-based topological invariant, denoted by T(G), is defined as
(1)
where ∅(εx, εy) is a real function with the property that ∅(εx, εy) = ∅(εy, εx). From Equation (1), we can get some eccentricity based topological indices in the following way:
  • (a)

    Atom-bond connectivity eccentricity index ABC5 if [11]

  • (b)

    Eccentricity-based harmonic index of fourth type H4 if ∅(εx, εy) = 2/εx + εy [12, 13]

  • (c)

    Geometric-arithmetic eccentricity index GA4 if [14].

  • (d)

    First Zagreb eccentricity index if , where β = 1 [15, 16]

  • (e)

    Third Zagreb eccentricity index if , where α = 1 [15, 16]

3. Main Results

In this section, we compute the eccentricity based topological indices of a commutative ring , where ♭1, ♭2, ♭3 are distinct primes, and q is any prime integer.

Theorem 1. Let ♭1, ♭2, ♭3 be distinct prime integers and q be any prime number. Then for the zero divisor graph J(R) of a ring , we have .

Proof. We can partition the vertex set of as follows:

  • (1)

    . The vertices adjacent to x ∈ ϖ1 are of the form (u′, 0) with . Hence, dx = ♭1♭2♭3 − 1 for all x ∈ ϖ1 and |ϖ1| = q2 − q

  • (2)

    ϖ2 = {(0, v) | v = kq, 1 ≤ k ≤ q − 1}. So we have |ϖ2| = q − 1. The vertices adjacent to x ∈ ϖ2 are of the form:

    • (i)

    • (ii)

Hence, for any x ∈ ϖ2, dx = (♭1♭2♭3 − 1) + (♭1♭2♭3 − 1)(q − 1) = ♭1♭2♭3q − q.

  • (3)

    ϖ3 = {(u, 0) | u = k♭1♭2; 1 ≤ k ≤ ♭3 − 1} with |ϖ3| = ♭3 − 1. The vertices adjacent to x ∈ ϖ3 are of the form:

    • (i)

    • (ii)

      (u′, 0): u′ = t1♭3; 1 ≤ t1 ≤ ♭1♭2 − 1

    • (iii)

      (u′, v2): u′ = t1♭3, v2 = t2q; 1 ≤ t1 ≤ ♭1♭2 − 1, 1 ≤ t2 ≤ q − 1

    • (iv)

      (u′, v3): u′ = t1♭3, v3 ≠ t3q; 1 ≤ t1 ≤ ♭1♭2 − 1, 1 ≤ t3 ≤ q − 1

Hence, for any x ∈ ϖ3, dx = q2 − 1 + ♭1♭2 − 1 + (♭1♭2 − 1)(q − 1) + (♭1♭2 − 1)(q2 − q) = ♭1♭2q2 − 1.

  • (4)

    ϖ4 = {(u, 0): u = k♭1♭3; 1 ≤ k ≤ ♭2 − 1}. with |ϖ4| = ♭2 − 1. The vertices adjacent to x ∈ ϖ4 are of the form:

    • (i)

    • (ii)

      (u′, 0): u′ = t1♭2; 1 ≤ t1 ≤ ♭1♭3 − 1

    • (iii)

      (u′, v2): u′ = t1♭2, v2 = t2q; 1 ≤ t1 ≤ ♭1♭3 − 1, 1 ≤ t2 ≤ q − 1

    • (iv)

      (u′, v3): u′ = t1♭2, v3 ≠ t3q; 1 ≤ t1 ≤ ♭1♭3 − 1, 1 ≤ t3 ≤ q − 1

Hence, for any x ∈ ϖ4, dx = q2 − 1 + ♭1♭3 − 1 + (♭1♭3 − 1)(q − 1) + (♭1♭3 − 1)(q2 − q) = ♭1♭3q2 − 1.

  • (5)

    ϖ5 = {(u, 0): u = k1♭1; 1 ≤ k1 ≤ ♭2♭3 − 1; u ≠ k2♭1♭2, 1 ≤ k2 ≤ ♭3 − 1; u ≠ k3♭1♭3, 1 ≤ k3 ≤ ♭2 − 1} with |ϖ5| = (♭2 − 1)(♭3 − 1). The vertices adjacent to x ∈ ϖ5 are of the form:

    • (i)

    • (ii)

      (u′, 0): u′ = t1♭2♭3; 1 ≤ t1 ≤ ♭1 − 1

    • (iii)

      (u′, v2): u′ = t1♭2♭3, v2 = t2q; 1 ≤ t1 ≤ ♭1 − 1, 1 ≤ t2 ≤ q − 1

    • (iv)

      (u′, v3): u′ = t1♭2♭3, v3 ≠ t3q; 1 ≤ t1 ≤ ♭1 − 1, 1 ≤ t3 ≤ q − 1

Hence, for any x ∈ ϖ5, dx = q2 − 1 + ♭1 − 1 + (♭1 − 1)(q − 1) + (♭1 − 1)(q2 − q) = ♭1q2 − 1.

  • (6)

    ϖ6 = {(u, 0); u = k♭2♭3, 1 ≤ k ≤ ♭1 − 1} with |ϖ6| = ♭1 − 1. The vertices adjacent to x ∈ ϖ6 are of the form:

    • (i)

    • (ii)

      (u′, 0): u′ = t1♭1; 1 ≤ t1 ≤ ♭2♭3 − 1

    • (iii)

      (u′, v2): u′ = t1♭1, v2 = t2q; 1 ≤ t1 ≤ ♭2♭3 − 1, 1 ≤ t2 ≤ q − 1

    • (iv)

      (u′, v3): u′ = t1♭1, v3 ≠ t3q; 1 ≤ t1 ≤ ♭2♭3 − 1, 0 ≤ t3 ≤ q − 1

Hence, for any x ∈ ϖ6, dx = q2 − 1 + ♭2♭3 − 1 + (♭2♭3 − 1)(q − 1) + (♭2♭3 − 1)(q2 − q) = ♭2♭3q2 − 1.

  • (7)

    ϖ7 = {(u, 0); u = k1♭2, 1 ≤ k1 ≤ ♭1♭3 − 1; u ≠ k2♭1♭2, 1 ≤ k2 ≤ ♭3 − 1; u ≠ k3♭2♭3, 1 ≤ k3 ≤ ♭1 − 1}. So, |ϖ7)| = (♭1 − 1)(♭3 − 1). The vertices adjacent to x ∈ ϖ7 are of the form:

    • (i)

    • (ii)

      (u′, 0): u′ = t1♭1♭3; 1 ≤ t1 ≤ ♭2 − 1

    • (iii)

      (u′, v2): u′ = t1♭1♭3, v2 = t2q; 1 ≤ t1 ≤ ♭2 − 1, 1 ≤ t2 ≤ q − 1

    • (iv)

      (u′, v3): u′ = t1♭1♭3, v3 ≠ t3q; 1 ≤ t1 ≤ ♭2 − 1, 0 ≤ t3 ≤ q − 1

Hence, for any x ∈ ϖ7, dx = q2 − 1 + ♭2 − 1 + (♭2 − 1)(q − 1) + (♭2 − 1)(q2 − q) = ♭2q2 − 1.

  • (8)

    ϖ8 = {(u, 0); u = k1♭3, 1 ≤ k1 ≤ ♭1♭2 − 1; u ≠ k2♭1♭31 ≤ k2 ≤ ♭2 − 1; u ≠ k3♭2♭3, 1 ≤ k3 ≤ ♭1 − 1}, with |ϖ8| = (♭1 − 1)(♭2 − 1). The vertices adjacent to x ∈ ϖ8 are of the form:

    • (i)

    • (ii)

      (u′, 0): u′ = t1♭1♭2; 1 ≤ t1 ≤ ♭3 − 1

    • (iii)

      (u′, v2): u′ = t1♭1♭2, v2 = t2q; 1 ≤ t1 ≤ ♭3 − 1, 1 ≤ t2 ≤ q − 1

    • (iv)

      (u′, v3): u′ = t1♭1♭2, v3 ≠ t3q; 1 ≤ t1 ≤ ♭3 − 1, 0 ≤ t3 ≤ q − 1

Hence, for any x ∈ ϖ7, dx = q2 − 1 + ♭3 − 1 + (♭3 − 1)(q − 1) + (♭3 − 1)(q2 − q) = ♭3q2 − 1.

  • (9)

    ϖ9 = {(u, 0); u ≠ k1♭1, 1 ≤ k1 ≤ ♭2♭3 − 1; u ≠ k2♭2, 1 ≤ k2 ≤ ♭1♭3 − 1; u ≠ k3♭3, 1 ≤ k3 ≤ ♭1♭2 − 1} with |ϖ9| = (♭1 − 1)(♭2 − 1)(♭3 − 1). In this case dx = q2 − 1 for all x ∈ ϖ9

  • (10)

    ϖ10 = {(u, v) | u = k1♭1♭2, 1 ≤ k1 ≤ ♭3 − 1; v ≠ k2q, 0 ≤ k2 ≤ q − 1} with |ϖ10| = (♭3 − 1)(q2 − q). In this case dx = ♭1♭2 − 1 for all x ∈ ϖ10

  • (11)

    ϖ11 = {(u, v) | u = k1♭1♭3, 1 ≤ k1 ≤ ♭2 − 1; v ≠ k2q, 0 ≤ k2 ≤ q − 1, } with |ϖ11| = (♭2 − 1)(q2 − q). In this case dx = ♭1♭3 − 1 for all x ∈ ϖ11

  • (12)

    ϖ12 = {(u, v) | u = k1♭1, 1 ≤ k1 ≤ ♭2♭3 − 1; u ≠ k2♭1♭2, 1 ≤ k2 ≤ ♭3 − 1; u ≠ k3♭1♭3, 1 ≤ k3 ≤ ♭2 − 1; v ≠ k4q, 0 ≤ k4 ≤ q − 1} with |ϖ12| = (♭2 − 1)(♭3 − 1)(q2 − q). The vertices adjacent to x ∈ ϖ12 are of the form (u′, 0); u′ = t′♭2♭3, 1 ≤ t′ ≤ ♭1 − 1. Hence dx = ♭1 − 1 for all x ∈ ϖ12

  • (13)

    ϖ13 = {(u, v) | u = k1♭2♭3, 1 ≤ k1 ≤ ♭1 − 1; v ≠ k2q, 0 ≤ k2 ≤ q − 1} with |ϖ13| = (♭1 − 1)(q2 − q). The vertices adjacent to x ∈ ϖ12 are of the form (u′, 0); u′ = t′♭1, 1 ≤ t′ ≤ ♭2♭3 − 1. Hence dx = ♭2♭3 − 1 for all x ∈ ϖ13

  • (14)

    ϖ14 = {(u, v); u = k1♭2, 1 ≤ k1 ≤ ♭1♭3 − 1; u ≠ k2♭1♭2, 1 ≤ k2 ≤ ♭3 − 1; u ≠ k3♭2♭3, 1 ≤ k3 ≤ ♭1 − 1; v ≠ k4q, 0 ≤ k4 ≤ q − 1} with |ϖ14)| = (♭1 − 1)(♭3 − 1)(q2 − q). Then, each vertex x = ∈ϖ14 has degree ♭2 − 1

  • (15)

    ϖ15 = {(u, v) | u = k1♭3, 1 ≤ k1 ≤ ♭1♭2 − 1; u ≠ k2♭1♭31 ≤ k2 ≤ ♭2 − 1; u ≠ k3♭2♭3, 1 ≤ k3 ≤ ♭1 − 1; v ≠ k4q, 0 ≤ k4 ≤ q − 1}, with |ϖ15| = (♭1 − 1)(♭2 − 1)(q2 − q). The vertices adjacent to x ∈ ϖ15 are of the form (u′, 0); u′ = t′♭1♭2, 1 ≤ t′ ≤ ♭3 − 1. Then each vertex x = ∈ϖ15 has degree ♭3 − 1

  • (16)

    ϖ16 = {(u, v) | u = k1♭1♭2; 1 ≤ k1 ≤ ♭3 − 1; v = k2q, 1 ≤ k2 ≤ q − 1} with |ϖ16| = (♭3 − 1)(q − 1). The vertices adjacent to x ∈ ϖ16 are of the form:

    • (i)

      (0, v1): v1 = t1q, 1 ≤ t1 ≤ q − 1

    • (ii)

      (u′, 0): u′ = t2♭3; 1 ≤ t2 ≤ ♭1♭2 − 1

    • (iii)

      (u′, v1): u′ = t2♭3, v1 = t1q; 1 ≤ t1 ≤ q − 1, 1 ≤ t2 ≤ ♭1♭2 − 1

Hence, for any x ∈ ϖ16, dx = q − 1 + ♭1♭2 − 1 + (♭1♭2 − 1)(q − 1) = ♭1♭2q − 1.

  • (17)

    ϖ17 = {(u, v) | u = k1♭1♭3, 1 ≤ k1 ≤ ♭2 − 1; v = k2q, 1 ≤ k2 ≤ q − 1} with |ϖ17| = ♭2 − 1. The vertices adjacent to x ∈ ϖ17 are of the form:

    • (i)

      (0, v1): v1 = t1q, 1 ≤ t1 ≤ q − 1

    • (ii)

      (u′, 0): u′ = t2♭2, 1 ≤ t2 ≤ ♭1♭3 − 1

    • (iii)

      (u′, v1): v1 = t1q, u′ = t2♭2 : 1 ≤ t1 ≤ q − 1, 1 ≤ t2 ≤ ♭1♭3 − 1

Hence, for any x ∈ ϖ17, dx = q − 1 + ♭1♭3 − 1 + (♭1♭3 − 1)(q − 1) = ♭1♭3q − 1.

  • (18)

    ϖ18 = {(u, v) | u = k1♭1, 1 ≤ k1 ≤ ♭2♭3 − 1; u ≠ k2♭1♭2, 1 ≤ k2 ≤ ♭3 − 1; u ≠ k3♭1♭3, 1 ≤ k3 ≤ ♭2 − 1; v = k4q, 1 ≤ k4 ≤ q − 1} with |ϖ18| = (♭2 − 1)(♭3 − 1)(q − 1). The vertices adjacent to x ∈ ϖ18 are of the form:

    • (i)

      (u′, v′): u′ = t1♭2♭3, 1 ≤ t1 ≤ ♭1 − 1; v′ = t2q, 0 ≤ t2 ≤ q − 1

    • (ii)

      (0, v1): v1 = t3q, 1 ≤ t3 ≤ q − 1

Hence, for any x ∈ ϖ18, dx = (♭1 − 1)(q2 − q) + q − 1 = (q − 1)(♭1q − q + 1).

  • (19)

    ϖ19 = {(u, v) | u = k1♭2♭3, 1 ≤ k1 ≤ ♭1 − 1; v = k2q, 1 ≤ k2 ≤ q − 1} with |ϖ19| = (♭1 − 1)(q − 1). The vertices adjacent to x ∈ ϖ19 are of the form:

    • (i)

      (0, v1): v1 = t1q, 1 ≤ t1 ≤ q − 1

    • (ii)

      (u′, 0): u′ = t2♭1, 1 ≤ t2 ≤ ♭2♭3 − 1

    • (iii)

      (u′, v1): u′ = t2♭1, v1 = t1q; 1 ≤ t1 ≤ q − 1, 1 ≤ t2 ≤ ♭2♭3 − 1

Hence, for any x ∈ ϖ19, dx = q − 1 + ♭2♭3 − 1 + (♭2♭3 − 1)(q − 1) = ♭2♭3q − 1.

  • (20)

    ϖ20 = {(u, v) | u = k1♭2, 1 ≤ k1 ≤ ♭1♭3 − 1; u ≠ k2♭1♭2, 1 ≤ k2 ≤ ♭3 − 1; u ≠ k3♭2♭3, 1 ≤ k3 ≤ ♭1 − 1; v = k4q, 1 ≤ k4 ≤ q − 1} with |ϖ20)| = (♭1 − 1)(♭3 − 1)(q − 1). The vertices adjacent to x ∈ ϖ20 are of the form:

    • (i)

      (0, v1): v1 = t1q, 1 ≤ t1 ≤ q − 1

    • (ii)

      (u′, 0): u′ = t2♭1♭3; 1 ≤ t2 ≤ ♭2 − 1

    • (iii)

      (u′, v1): u′ = t2♭1♭3, v1 = t1q; 1 ≤ t1 ≤ q − 1, 1 ≤ t2 ≤ ♭2 − 1

Hence, for any x ∈ ϖ20, dx = q − 1 + ♭2 − 1 + (♭2 − 1)(q − 1) = ♭2q − 1.

  • (21)

    ϖ21 = {(u, v); u = k1♭3, 1 ≤ k1 ≤ ♭1♭2 − 1; u ≠ k2♭1♭31 ≤ k2 ≤ ♭2 − 1; u ≠ k3♭2♭3, 1 ≤ k3 ≤ ♭11; v = k4q, 1 ≤ k4 ≤ q − 1} with |ϖ21| = (♭1 − 1)(♭2 − 1)(q − 1). The vertices adjacent to x ∈ ϖ21 are of the form:

    • (i)

      (0, v1): v1 = t1q, 1 ≤ t1 ≤ q − 1

    • (ii)

      (u′, 0): u′ = t2♭1♭2, 1 ≤ t2 ≤ ♭3 − 1

    • (iii)

      (u′, v1): u′ = t2♭1♭2, v1 = t1q; 1 ≤ t1 ≤ q − 1, 1 ≤ t2 ≤ ♭3 − 1

Hence, for any x ∈ ϖ21, dx = q − 1 + ♭3 − 1 + (♭3 − 1)(q − 1) = ♭3q − 1.

  • (22)

    ϖ22 = {(u, v) | u ≠ k1♭1, 1 ≤ k1 ≤ ♭2♭3 − 1; u ≠ k2♭2, 1 ≤ k2 ≤ ♭1♭3 − 1; u ≠ k3♭3, 1 ≤ k3 ≤ ♭1♭2 − 1; v = k4q, 1 ≤ k4 ≤ q − 1}. with |ϖ22| = (♭1 − 1)(♭2 − 1)(♭3 − 1)(q − 1). Then each vertex x = ∈ϖ22 has degree q − 1

Now, the cardinality of vertex set V(JR) can be calculated as .

From the above Theorem, we can compute the number of edges E(JR) by using hand shaking lemma.

(2)

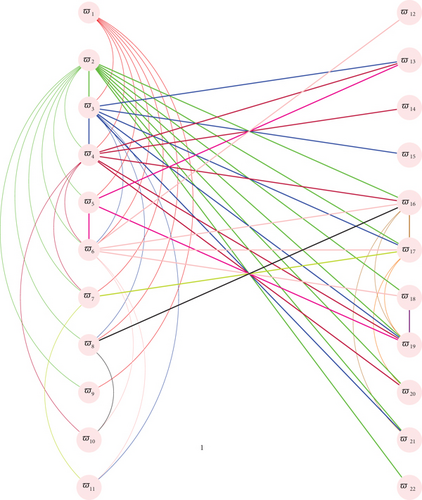
Anderson and Livingston [30] proved that the diameter of the graph J(R) is atmost three. It follows that the eccentricity of any vertex x ∈ V(J(R)) is atmost three. Figure 1 reflects this fact for the case .

Theorem 2 (see [30].)Let , where ♭1, ♭2, ♭3 be distinct prime integers and q is any prime number. Then, eccentricity of a vertex x ∈ V(J(R)) is either 2 or 3.

In the next Theorem, we find the exact expressions for the ABC5, H4, GA4, indices of , where ♭1, ♭2, ♭3 be distinct prime integers and q is any prime number. For simplicity, we fix some notations. Let α = {6 − 3q + (−3 + q)♭3 + ♭2(−3 + q + ♭3) + ♭1(−3 + q + ♭2 + ♭3)},

(3)
(4)
(5)
(6)
(7)

Theorem 3. Let , where ♭1, ♭2, ♭3 be distinct prime integers, and q is any prime number. Then, T(G) has the following expression T(JR) = αϕ(2, 2) + {β + γ + δ}ϕ(2, 3) + {ζ + μ}ϕ(3, 3),

Proof. Let

(8)

Then, from Theorem 1 and Figure 1, we have

(9)
(10)

and

(11)

Finally,

(12)

Theorem 4. Let , where ♭1, ♭2, ♭3 be distinct prime integers and q is any prime number. Then

(13)
(14)
(15)
(16)
(17)

Proof. For the first Zagreb eccentricity index, we have . Then, ∅(2, 2) = 4, ∅(2, 3) = 5, and ∅(3, 3) = 6. Substituting these values in Theorem 3, we get

(18)

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Structure of .
For third Zagreb eccentricity index, we have ∅(εu′, εv′) = εu′ × εv′ and
(19)
For the geometric-arithmetic eccentricity index, we have and
(20)
For atom-bond connectivity eccentricity index, we have and
(21)
For the harmonic index based on eccentricity of fourth type, we have ∅(εu′, εv′) = 2/εu′ + εv′ and
(22)

4. Conclusion

For zero divisor graph of commutative ring , we calculated the eccentricity-based atom-bond index of connectivity, the harmonic index based on eccentricity of fourth type, the geometric-arithmetic eccentricity index, the eccentricity-based third Zagreb index, and the eccentricity-based first Zagreb index. This work is a part of the open problem to calculate the eccentricity based topological indices for zero divisor graph of commutative ring Zm × Zn for m, n ∈ ℤ. In future, similar work can be done for other cases of commutative ring Zm × Zn.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work is partially supported by the National Natural Science Foundation of China (grant no. 61702291) and China Henan International Joint Laboratory for Multidimensional Topology and Carcinogenic Characteristics Analysis of Atmospheric Particulate Matter PM2.5.

    Data Availability

    No data is required to support the study.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.