Metric dimension of a graph is a well-studied concept. Recently, adjacency metric dimension of graph has been introduced. A set Q_a ⊂ V(G) is considered to be an adjacency metric generator for G if u₁, u₂ ∈ V\Q_a (supposing each pair); there must exist a vertex q ∈ Q_a along with the condition that q is indeed adjacent to one of u₁, u₂. The minimum number of elements in adjacency metric generator is the adjacency metric dimension of G, denoted by dim_a(G). In this work, we compute exact values of the adjacency metric dimension of circulant graph C_n(1, 2), Möbius ladder, hexagonal Möbius ladder, and the ladder graph.

1. Introduction

Let G be a simple connected graph with vertex set V and edge set E. Let N be a set of nonnegative integers; we assume a function d_G : V × V⟶N defined as

(1)

Then, (V, d_G) is a metric space. A subset A ⊂ V is called a metric generator for G if it is the generator of the metric space (V, d_G); that is, every point of the space is uniquely determined by its distances from the elements of A. A minimum metric generator is the metric basis, and its cardinality is the metric dimension of G, denoted by dim(G); for further detail of metric and their parameters, see [1–6]. The concept of metric dimension was first introduced by [7] in the problem of uniquely determining the location of an intruder in a network and was named as a locating set instead of metric generators. The same concept of metric generators or locating set was introduced by [8], and this time, they named it as resolving sets. Application of metric dimension to the navigation of robots in networks is studied in [9] and to chemistry in [10, 11]. This concept was further studied by many researchers (for instance, see [12, 13]); different studies of metric and its related parameters are studied in literature; for example, metric dimension of bilinear form graphs is found in [14], distance-regular graph is available in [15], in terms of dominating set [16], study of the corona product is found in [17], and some computer fields are attached to this topic found in [18, 19]. Several metric generators have since been developed and researched, including independent resolving sets [20], resolving dominant sets [21], strong resolving sets [22], and local metric sets [23].

A subset Q_a ⊂ V of the set of vertices is an adjacency metric generator of G if for every two vertices u₁, u₂ ∈ V\Q_a, there exists a vertex q ∈ Q_a such that q is indeed adjacent to one of u₁, u₂. The minimum number of elements in the adjacency metric generator is the adjacency metric dimension of G and symbolized by dim_a(G). The idea of adjacency metric dimension was put forward by [24], and it is closed related to 1-locating dominating set [25]. The goal of this definition is to look at the metric dimension of the lexicographic product of graphs in terms of graph adjacency. For two graphs with n, K-orders, the researchers in [26, 27] had taken the corona product of both graphs; the resulted graph has (local) metric dimension n times the (local) adjacency metric dimension. They demonstrated that calculating the adjacency metric dimension is NP-hard as a result of this tight relationship.

The adjacency metric generator of any graph G can be a metric generator in a correctly selected metric space, as pointed out in [26, 27]. Assume q is a positive number. Assume the d_G,q : V × V⟶N is a distance function, which is defined as

(2)

Then, the metric dimension of (V, d_G,2) is equal to the adjacency metric dimension of G. A subset Q_a ⊂ V is the k adjacency metric generator for a graph G, if for each pair of vertices u₁, u₂ ∈ V, there are at least k vertices v₁, v₂, ⋯, v_k ∈ Q_a as a result d_G,2(u₁, v_i) ≠ d_G,2(u₂, v_i), for each 1 ≤ i ≤ k. For the minimum number (k) of members in the adjacency metric generator, the definition will be called as k adjacency metric dimension of a graph G, and here, it is symbolized by dim_a,j(G).

The adjacency metric dimension is an NP-hard problem [25, 28], and it is very important to determine its exact values for well-known families of graphs. The primary goal of this work is to determine the exact values of the adjacency metric dimension of particular graph families, notably circulant graphs C_n(1, 2), ladder, Möbius ladder, and hexagonal ladder graphs. To compute the adjacency metric dimension of these classes, we need the following proposition by Moreno et al. [29].

Proposition 1 (see [29].)If G is a graph with |G| = n ≥ 2, then dim_a,j(G) = j if and only if j ∈ {1, 2} and G ∈ {P₁, P₂, }.

Remark 2 (see [29].)If G is a graph with |G| = n ≥ 7, then dim_a,1(G) ≥ 3.

2. Construction of Graphs

Circulant graphs are a type of graph that may be utilised in the construction of local area networks. Let v₁, v₂, ⋯, v_zz and n be the nonnegative with given conditions, v_μ ≠ v_ν∀ 1 ≤ μ < ν ≤ z, where 1 ≤ v_μ ≤ ⌊n/2⌋. With the collection of vertices in an undirected graph V = {v₁, v₂, ⋯, v_n} and the set of edges E = {v_μv_μ+vν : 1 ≤ μ ≤ n, 1 ≤ ν ≤ z}, the indices are considered to be taken in modulo n condition, called a circulant graph, and it is symbolized by C_n(v₁, v₂, ⋯, v_z). The generators are v₁, v₂, ⋯, v_z-numbers, and the edge v_μv_μ+vν is of type v_ν. Actually, we can observe that the C_n(v₁, v₂, ⋯, v_z) circulant graph is an r-regular graph, and the r given is

(3)

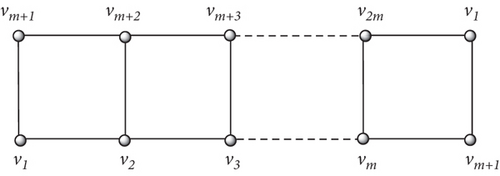
Möbius ladder ML_m is built by a grid of m × 1, and twist this grid at 180°; now, paste the extreme most left and right path of vertices as seen in Figure 1. It contains m-horizontal cycles of order four. For more study on ladder-type networks, see [30, 31]. The metric dimension of ML_m is three [32].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Möbius ladder graph ML_m.

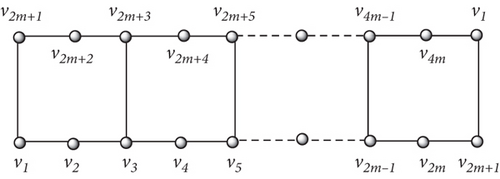
Hexagonal Möbius ladder HML_m is built in [33], it can construct by dividing each horizontal edge of a square grid by inserting a new vertex, and it becomes a grid of m × 1 with each cycle having order six; now, twist this grid at 180° and paste the extreme most left and right path of vertices as shown in Figure 2. This graph contains m-horizontal cycles of order six. The metric dimension of the hexagonal Möbius ladder network is three [33].

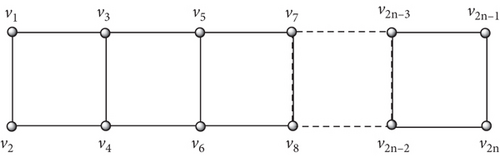
Let L_m be a ladder graph [34], with n ≥ 3. We label the ladder graph as shown in Figure 3. The order and size of the ladder graph are 2n and 3n − 2, respectively.

3. Results on Adjacency Metric Dimension of Graphs

We compute the adjacency metric dimension of certain graph families in this section. Let C_n(1, 2) be a circulant graph obtained from C_n by joining all the vertices at distance 2. Let n ≥ 6; then, |V(C_n(1, 2))| = n and |E(C_n(1, 2))| = 2n. In the next theorem, we compute the exact value of the adjacency metric dimension of the circulant graph C_n(1, 2).

Theorem 3. Let G = C_n(1, 2) be a circulant graph. Then,

(4)

Proof. We divide the proof of the theorem into three parts.

Part A. For the inequality dim_a(G) ≤ 3, when n = 6, 7, 8, let Q_a = {v₁, v₂, v₃} as an adjacency metric generator; then, the representation of v₁, v₂, v₃ are as follows v₁ = (0, 1, 1), v₂ = (1, 0, 1), and v₃ = (1, 1, 0). For any vertex v_k ≠ v₁, v₂, v₃, we have the following representation:

(5)

where a = 2, when k = 4, ⋯, n − 2; otherwise, a = 1. Also, b = 1 when k = 4, n, and c = 1, when k = 4, 5; otherwise, both b, c are 0.

From the above discussion, we can say that dim_a(G) ≤ 3.

Converse: on the contrary, assume that dim_a(G) = 2, for n = 7, 8. Let be a resolving set for adjacency metric dimension. Then, for any , the distance (d(v₁, v), d(v₂, v)) ∈ {(1, 1), (1, 2), (2, 1), (2, 2)}. Given , by the principle of Dirichlet’s box, two or more components of resulted in identical vectors of distance, and further, this implied as a contradiction. Now, for n = 6, let 2 ≤ i ≤ 6; we have the same representations, that is, either or Let the adjacency metric generator 3 ≤ i ≤ 6; then, we have the same representations, that is, either or Let 3 ≤ i ≤ 5, 4 ≤ j ≤ 6; then, we have the same representations, that is, , , or Therefore, dim_a(G) ≥ 3, concluding that dim_a(G) = 3.

Part B. When n ≡ 0, 3, 4, 5(mod6), n ≥ 9, we intend to use the induction method on the order of cycle; set the base step as n = 9, which implies that dim_a(C₉) = 4. Let Q_a = {v₁, v₂, v₃, v₄} be a resolving set for adjacency metric dimension. All vertices have the following representations:

(6)

where a, b, c, d = 0, when k = 1, 2, 3, 4, respectively, and a = 1 when k = 2, 3, 8, 9, b = 1 when k = 1, 3, 4, 9, c = 1 when k = 1, 2, 4, 5, and d = 1 when k = 2, 3, 5, 6; otherwise, all values of a, b, c, d are 2. All the representations are different so

(7)

On the contrary, assume that dim_a(C₉) = 3. On this contradiction, the following are some cases to defend it.

Case 1. Let the adjacency metric generator 1 ≤ i, j, k ≤ 9, taking vertices in with 0-size gap (consecutive vetices). Then, we have the same representations in ; it means that have the same representations with the vertices which are not adjacent to any of the vertex of

Case 2. Let 1 ≤ i ≤ 6, taking vertices in with 1- and 0-size gap, respectively. Then, we have the same representations in ; it means that have the same representations with the vertices which are adjacent to v_i only.

Case 3. Let , 1 ≤ i ≤ 6, taking vertices again in with 0- and 1-size gap, respectively. Then, we have the same representations in v_i+3 ~ {v_i′, v_j′}; it means that have the same representations with the vertices which are adjacent to v_i+3 only.

Case 4. Let , taking vertices in with 1-size gap. Then, we have the same representations in v_i+4 ~ {v_i′, v_j′}; it means that have the same representations with the vertices which are adjacent to v_i+4 only.

Case 5. Let , with 0- and 2-size gap, respectively. Then, we have the same representations in , which simplifies that have the same representations with the vertices which are adjacent to v_i+4 only.

Case 6. Let , taking vertices in with 1- and 2-size gap, respectively. Then, we have the same representations in , which means that have the same representations with the vertices which are adjacent to v_i+5 only.

Due to the nature of the adjacency metric generator with three cardinalities, have the following gap size possibilities:

(i)
The first gap is even, and second is odd
(ii)
The first gap is odd and the next is even
(iii)
Both gaps are even
(iv)
Both gaps are odd

Case 7. Let , taking vertices in above any sizes of gap possibilities. Then, we have the same representations in either or only single vertex of adjacent to both vertices, which have the same representations. From all above cases, dim_a(C₉) ≠ 3. Hence, our base step is true:

(8)

Now, assume that it is also true for n = m, and we have to show that it is also true for n = m + 1 which implies that

(9)

Assume the assertion that

(10)

Putting equations (8) and (9) in equation (10), we have

(11)

where ⌊(n + 3)/6⌋ = ⌊(n + 4)/6⌋.

Part C. Remaining cases when n ≡ 1, 2(mod6), n ≥ 13.

Again, the method of induction can be used, and this implies that the base step becomes true for n = 13 and as well dim_a(C₁₃) = 5; for this purpose, let Q_a = {v₁, v₂, v₅, v₇, v₁₁} be a resolving set for adjacency metric dimension; all the vertices have the following representations:

(12)

where a, b, c, d = 0 when k = 1, 2, 5, 7, 11, respectively, and a = 1 when k = 2, 3, 12, 13, b = 1 when k = 1, 3, 4, 13, c = 1 when k = 3, 4, 6, 7, d = 1 when k = 5, 6, 8, 9, and e = 1 when k = 9,10,12,13; otherwise, all values of a, b, c, d are 2.

(13)

On the contrary, assume that dim_a(C₁₃) = 4. Let be the adjacency metric generator with cardinality 4 having the following gap size possibilities.

(i)
All the gap sizes are even
(ii)
All the gap sizes are odd
(iii)
One gap size is odd, and others are even
(iv)
One gap size is even, and others are odd

Case 1. Let , 1 ≤ i, j, k, l ≤ 13, with any sizes of gap possibilities above defined. Then, we have the same representations in either {v_i, v_j, v_k, v_l}{v_i′, v_j′} or only single vertex of adjacent to both vertices, which have the same representations. From all above cases, dim_a(C₁₃) ≠ 4. Hence,

(14)

Now, assume that it is also true for n = m, and we have to show that it is also true for n = m + 1, which leads to the assertion that

(15)

Assuming that

(16)

Putting equations (14) and (15) in equation (16), we have

(17)

where ⌊(n + 3)/6⌋ = ⌊(n + 4)/6⌋. This completes the proof of the theorem with all possible cases on order of the C_n graph.

Theorem 4. Let ML_m be a Möbius ladder graph. Then,

(18)

Proof. We divide the proof of the theorem into three parts.

Part A. Let Q_a = {v₁, v₂, v₅} be an adjacency metric generator, and those shown in Table 1 are the representations of all vertices for dim_a(ML₄) ≤ 3.

All the vertices have different representations, and it proves that dim_a(ML₄) ≤ 3. On the contrary, suppose that dim_a(ML₄) = 2. By using Proposition 1, it is not possible, concluding that

(19)

Part B. When m = 3, 5, this adjacency metric generator is Q_a = {v₁, v₂, v₄, v_4+⌊m/2⌋} which claims that dim_a(ML_m) ≤ 4. All vertices have the following representations:

(20)

where a, b, c, d = 0 when k = 1, 2, 4, 4 + ⌊m/2⌋, respectively, and a = 1 when k = 2, m + 1, 2m, b = 1 when k = 1, 3, m + 2, c = 1 when k = m − 2, n, 2m − 1, and d = 1 when m − 1, m + 1, 2m; otherwise, all a, b, c, d are 2. It proves the claim that dim_a(ML_m) ≤ 4; on the other hand, suppose that dim_a(ML_m) = 3, when m = 3, 5.

Case 1. Let , 1 ≤ i, j, k ≤ 2m, taking vertices in with 0-size gap. Then, we have the same representations in and m + 2 ≤ l^′ ≤ 2m.

Case 2. Let , with the vertices in with any size of gap discussed in Theorem 3, part 6 Then, we have the same representations in and m + 2 ≤ l^′ ≤ 2m. It means that when choosing the resolving set for adjacency metric dimension with cardinality three and vertices with any gap size, there must exist two vertices with the same representations which have one belonging to l-domain and the second from l^′-domain. From all above cases, dim_a(ML_m) ≠ 3 for the values of m = 3, 5. Hence,

(21)

Part C. Here, we will use the induction method. For the base step, we choose m = 6; the dim_a(ML₆) = 4 having the adjacency metric generator Q_a = {v₁, v₃, v₅, v₇}, and the following are the representations of all vertices:

(22)

where a, b, c, d = 0 when k = 1, 3, 5, 7, respectively, and a = 1 when k = 2, 7, 12, b = 1 when k = 2, 4, 9, c = 1 when k = 4, 6, 11, and d = 1 when k = 1, 6, 8; otherwise, all values of a, b, c, d are 2. It concludes that

(23)

The contradiction side gives us dim_a(ML₆) = 3. For this contradiction, possible cases are discussed in the converse of part b of the theorem. One can evaluate from the discussion that Q_a with cardinality three is not possible which implies that

(24)

Now, assume that it is also true for m = l, and we have to show that m = l + 1 which leads to the inductive step:

(25)

Assume that

(26)

Using equations (24) and (25) in equation (26), we have

(27)

It completes the proof of the theorem with all possible cases on m-cycles of the Möbius ladder graph.

Theorem 5. Let HML_m be a hexagonal Möbius ladder graph. Then,

(28)

Proof. We break the proof of the theorem into four parts according to the adjacency metric dimension.

Part A. In this part, we claim that dim_a(HML₂) = 3. For the case dim_a(HML₂) ≤ 3, let the adjacency metric generator be Q_a = {v₁, v₂, v₆}, and those shown in Table 2 are the representations of all vertices of HML₂ with respect to Q_a.

In Table 2, the given representations are different, and it proves that dim_a(HML₂) ≤ 3; on the reverse, for inequality which is dim_a(HML₂) = 2, using Proposition 1 is not true, concluding that

(29)

Part B. This part contains the adjacency metric dimension of the hexagonal Möbius ladder graph with m = 3; for this, let the adjacency metric generator be Q_a = {v₁, v₃, v₅, v₇}, and those shown in Table 3 are the representations of all vertices according to Q_a, which are again different, and it proves that dim_a(HML₃) ≤ 4; on the reverse, inequality which is dim_a(HML₃) = 3 is not true, and the following are some discussions to this side.

Case 1. Let , taking vertices in with any size of gap discussed in Theorem 3, part 6 Then, we have the same representations in either or and 2m + 2 ≤ l^′ ≤ 4m. It means that when choosing the resolving set of adjacency metric dimension with cardinality three and vertices with any gap size, there must exist two vertices with the same representations which have one belonging to l-domain and the second from l^′-domain. It is also possible that the same representations are in two vertices, and v₁ is one of them, and the second vertex belongs to l^′-domain. From all above cases, dim_a(ML₃) ≠ 3. Hence,

(30)

Part C. For dim_a(HML₄) ≤ 6, let the adjacency metric generator be Q_a = {v₁, v₂, v₅, v₇, v₉, v₁₂}, and representations are shown in Table 4.

Table 1. Representations of vertices with respect to Q_a = {v₁, v₂, v₅}.

v_k	r(v_k \| v₁)	r(v_k \| v₂)	r(v_k \| v₅)	v_k	r(v_k \| v₁)	r(v_k \| v₂)	r(v_k \| v₅)
1	0	1	2	5	1	2	1
2	1	0	1	6	2	1	0
3	2	1	2	7	2	2	1
4	2	2	2	8	1	2	2

Table 2. Representations of vertices with respect to Q_a = {v₁, v₂, v₆}.

v_k	r(v_k \| v₁)	r(v_k \| v₂)	r(v_k \| v₆)	v_k	r(v_k \| v₁)	r(v_k \| v₂)	r(v_k \| v₆)
1	0	1	2	5	1	2	1
2	1	0	2	6	2	1	0
3	2	1	2	7	2	2	1
4	2	2	2	8	1	2	2

Table 3. Representations of vertices with respect to Q_a = {v₁, v₃, v₅, v₇}.

v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)	v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)
1	0	2	2	1	7	1	2	2	0
2	1	1	2	2	8	2	2	2	1
3	2	0	2	2	9	2	1	2	2
4	2	1	1	2	10	2	2	2	2
5	2	2	0	2	11	2	2	1	2
6	2	2	1	1	12	1	2	2	2

Table 4. Representations r(v_k | Q_a) of vertices with respect to Q_a = {v₁, v₂, v₅, v₇, v₉, v₁₂}.

v_k	v₁	v₂	v₅	v₇	v₉	v₁₂	v_k	v₁	v₂	v₅	v₇	v₉	v₁₂
1	0	1	2	2	1	2	9	1	2	2	2	0	2
2	1	0	2	2	2	2	10	2	2	2	2	1	2
3	2	1	2	2	2	2	11	2	2	2	2	2	1
4	2	2	1	2	2	2	12	2	2	2	2	2	0
5	2	2	0	2	2	2	13	2	2	1	2	2	1
6	2	2	1	1	2	2	14	2	2	2	2	2	2
7	2	2	2	0	2	2	15	2	2	2	1	2	2
8	2	2	2	1	1	2	16	1	2	2	2	2	2

The representations given in Table 4 prove that dim_a(HML₄) ≤ 6. On contrary, suppose that dim_a(HML₄) = 5; the following are some discussions to the side of this contradiction.

Case 1. Let , taking vertices in with any size of gap already discussed above in the theorem. Then, we have the same representations in either or and 2m + 2 ≤ l^′ ≤ 4m. It means that when choosing the resolving set for adjacency metric dimension with cardinality five and vertices with any gap size, there must exist two vertices with the same representations which have one belonging to l-domain and the second from l^′-domain. It is also possible that the same representations are in two vertices and v₁ is one of them, and the second vertex belongs to l^′-domain. From all above cases, dim_a(ML₄) ≠ 5. Hence,

(31)

Part D. In this part for the proof of dim_a(HML_m) = m + 3 where m ≥ 5, we will apply the induction method and the base case for m = 5, which implies that dim_a(HML₅) = 8, to prove that dim_a(HML₅) ≤ 8; the following are the representations with respect to the adjacency metric generator Q_a = {v₁, v₂, v₄, v₇, v₉, v₁₁, v₁₃, v₁₆}:

(32)

where a, b, c, d, e, f, g, h = 0 when k = 1, 2, 4, 7, 9,11,13,16, and a = 1 when k = 2,11,20, b = 1 when k = 1, 3, c = 1 when k = 3, 5, d = 1 when k = 6, 8, 17, e = 1 when k = 8,10,19, f = 1 when k = 1,10,12, g = 1 when k = 3,12,14, and h = 1 when k = 15, 17; otherwise, all values of a, b, c, d, e, f, g, h are 2. All the representations show that there are no two vertices with the same representation; hence,

(33)

On the contrary, suppose that dim_a(HML₅) = 7; the following are some discussions to the side of contradiction.

Case 1. Let and 1 ≤ j ≤ 7, taking vertices in with any size of gap discussed in Theorem 3, part 6 Then, we have the same representations in either or or and 2m + 2 ≤ l^′ ≤ 4m. It means that when choosing the resolving set of adjacency metric dimension with cardinality seven and vertices with any gap size, there must exist two vertices with the same representations which have one belonging to l-domain and the second from l^′-domain. It is also possible that the same representations are in two vertices and v₁ is one of them, and the second vertex belongs to l^′-domain. From all above cases, dim_a(HML₅) ≠ 7. Hence,

(34)

Now, assume that the assertion is true for m = l:

(35)

We have to show that it is also true for m = l + 1. Suppose

(36)

Plugging the values of equations (34) and (35) in equation (36), we have

(37)

As a result, the result holds for all positive integers m ≥ 5. It also completes the all possible cases that we assume on the very start of the proof.

Theorem 6. Let L_n be a ladder graph with n ≥ 3. Then,

(38)

Proof. We prove that dim_a(L_n) = n − ⌊(n + 1)/4⌋ with the induction method and the base step is n = 3 which implies that dim_a(L₃) = 2. If we assume on the contrary it is not possible that dim_a(L₃) = 1, for dim_a(L₃) ≤ 2, all vertices have the following representations with respect to Q_a = {v₁, v₅}:

(39)

where a, b = 0 when k = 1, 5, respectively, and a = 1 when k = 2, 3, b = 1 when k = 3, 6; otherwise, all values of a, b are 2. All the representations show that there are no two vertices with the same representation; hence,

(40)

Now, assume that the assertion is true for n = k:

(41)

We have to show that it is also true for n = k + 1. Suppose

(42)

Using equations (40) and (41) in equation (42), we have

(43)

where ⌊(k + 1)/4⌋ = ⌊(k + 2)/4⌋. As a consequence, the result holds for all positive integers for n ≥ 3, which completes the proof.

4. Conclusion

In this article, we studied the adjacency metric dimension of circulant, ladder, Möbius ladder, and hexagonal Möbius ladder graphs. It is known that adjacency metric dimension is a useful parameter in localization, networking, and some robot navigation ideas. Therefore, it is interesting to find adjacency metric generators for generalized classes of graphs. We demonstrated that in adjacency metric generators, all graphs have inconstant numbers of members and that each graph follows the modification of parameters or order.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

There is no data available.

References

1 Alshehri H., Ahmad A., Alqahtani Y., and Azeem M., Vertex metric-based dimension of generalized perimantanes diamondoid structure, IEEE Access. (2022) 10, 43320–43326, https://doi.org/10.1109/ACCESS.2022.3169277.
10.1109/ACCESS.2022.3169277
Web of Science® Google Scholar
2 Koam A. N. A., Ahmad A., Azeem M., and Nadeem M. F., Bounds on the partition dimension of one pentagonal carbon nanocone structure, Arabian Journal of Chemistry. (2022) 15, no. 7, https://doi.org/10.1016/j.arabjc.2022.103923.
10.1016/j.arabjc.2022.103923
Web of Science® Google Scholar
3 Raza H., Waheed M., Jamil M. K., and Azeem M., Structures devised by the generalizations of two graph operations and their topological descriptors, Main Group Metal Chemistry. (2022) 45, no. 1, 44–56, https://doi.org/10.1515/mgmc-2022-0006.
10.1515/mgmc-2022-0006
CAS Web of Science® Google Scholar
4 Ahmad A. N. A. H., Ahmad A., and Azeem M., Computation of edge- and vertex-degree-based topological indices for tetrahedral sheets of clay minerals, Main Group Metal Chemistry. (2022) 45, no. 1, 26–34, https://doi.org/10.1515/mgmc-2022-0007.
10.1515/mgmc-2022-0007
CAS Web of Science® Google Scholar
5 Nadeem M. F., Qu S., Ahmad A., and Azeem M., Metric dimension of some generalized families of Toeplitz graphs, Mathematical Problems in Engineering. (2022) 2022, 10, https://doi.org/10.1155/2022/9155291.
10.1155/2022/9155291
Web of Science® Google Scholar
6 Alatawi M. S., Ahmad A., Koam A. N. A., Husain S., Azeem M., Department of Mathematics Faculty of Sciences, University of Tabuk 71491 Tabuk, Saudi Arabia, College of Computer Science and Information Technology, Jazan University, Jazan, Saudi Arabia, Department of Mathematics, College of Science, Jazan University, New Campus, Jazan 2097, Saudi Arabia, and Department of Mathematics, Riphah Institute of Computing and Applied Sciences, Riphah International University, Lahore, Pakistan, Computing vertex resolvability of benzenoid tripod structure, AIMS-Mathematics. (2022) 7, no. 4, 6971–6983, https://doi.org/10.3934/math.2022387.
10.3934/math.2022387
Web of Science® Google Scholar
7 Slater P. J., Leaves of trees, 1975, 14, Proceeding of the 6th Southeastern Conference on Combinatorics, Graph Theory, and Computing, Congressus Numerantium, 549–559.
Google Scholar
8 Harary F. and Melter R. A., On the metric dimension of a graph, Ars Combinatoria. (1976) 2, 191–195.
Google Scholar
9 Khuller S., Raghavachari B., and Rosenfeld A., Landmarks in graphs, Discrete Applied Mathematics. (1996) 70, no. 3, 217–229, https://doi.org/10.1016/0166-218X(95)00106-2, 2-s2.0-0013510156.
10.1016/0166-218X(95)00106-2
Web of Science® Google Scholar
10 Johnson M., Structure-activity maps for visualizing the graph variables arising in drug design, Journal of Biopharmaceutical Statistics. (1993) 3, no. 2, 203–236, 8220404, https://doi.org/10.1080/10543409308835060, 2-s2.0-0027669150.
10.1080/10543409308835060
CAS PubMed Google Scholar
11 Johnson M. A., Browsable structure-activity datasets, Advances in Molecular Similarity. (1999) 2, 153–170.
10.1016/S1873-9776(98)80014-X
Google Scholar
12 Bailey R. F. and Meagher K., On the metric dimension of Grassmann graphs, Discrete Mathematics and Theoretical Computer Science. (2011) 13, 97–104.
Web of Science® Google Scholar
13 Caceres J., Hernando C., Mora M., Pelayo I. M., Puertas M. L., Seara C., and Wood D. R., On the metric dimension of Cartesian products of graphs, SIAM Journal on Discrete Mathematics. (2007) 21, no. 2, 423–441, https://doi.org/10.1137/050641867, 2-s2.0-38149005958.
10.1137/050641867
Web of Science® Google Scholar
14 Feng M. and Wang K., On the metric dimension of bilinear forms graphs, Discrete Mathematics. (2012) 312, no. 6, 1266–1268, https://doi.org/10.1016/j.disc.2011.11.020, 2-s2.0-84855975294.
10.1016/j.disc.2011.11.020
Web of Science® Google Scholar
15 Guo J., Wang K., and Li F., Metric dimension of some distance-regular graphs, Journal of Combinatorial Optimization. (2013) 26, no. 1, 190–197, https://doi.org/10.1007/s10878-012-9459-x, 2-s2.0-84878376977.
10.1007/s10878-012-9459-x
Web of Science® Google Scholar
16 Haynes T. W., Henning M. A., and Howard J., Locating and total dominating sets in trees, Discrete Applied Mathematics. (2006) 154, no. 8, 1293–1300, https://doi.org/10.1016/j.dam.2006.01.002, 2-s2.0-33645877104.
10.1016/j.dam.2006.01.002
Web of Science® Google Scholar
17 Iswadi H., Baskoro E. T., and Simanjuntak R., On the metric dimension of corona product of graphs, Far East Journal of Mathematical Sciences. (2011) 52, no. 2, 155–170.
Google Scholar
18 Saenpholphat V. and Zhang P., Conditional resolvability in graphs: a survey, International Journal of Mathematics and Mathematical Sciences. (2004) 2004, 2017, https://doi.org/10.1155/S0161171204311403, 2-s2.0-17844386806.
10.1155/S0161171204311403
Google Scholar
19 Yero I. G., Kuziak D., and Rodriquez-Velazquez J. A., On the metric dimension of corona product graphs, Computers and Mathematics with Applications. (2011) 61, no. 9, 2793–2798, https://doi.org/10.1016/j.camwa.2011.03.046, 2-s2.0-79955466115.
10.1016/j.camwa.2011.03.046
Web of Science® Google Scholar
20 Chartrand G., Saenpholphat V., and Zhang P., The independent resolving number of a graph, Mathematica Bohemica. (2003) 128, no. 4, 379–393, https://doi.org/10.21136/MB.2003.134003.
10.21136/MB.2003.134003
Google Scholar
21 Brigham R. C., Chartrand G., Dutton R. D., and Zhang P., Resolving domination in graphs, Mathematica Bohemicam. (2003) 128, no. 1, 25–36, https://doi.org/10.21136/MB.2003.133935.
10.21136/MB.2003.133935
Google Scholar
22 Sebo A. and Tannier E., On metric generators of graphs, Mathematics of Operations Research. (2004) 29, no. 2, 383–393, https://doi.org/10.1287/moor.1030.0070, 2-s2.0-4043098247.
10.1287/moor.1030.0070
Web of Science® Google Scholar
23 Okamoto F., Phinezy B., and Zhang P., The local metric dimension of a graph, Mathematica Bohemica. (2010) 135, no. 3, 239–255, https://doi.org/10.21136/MB.2010.140702.
10.21136/MB.2010.140702
Google Scholar
24 Jannesari M. and Omoomi B., The metric dimension of the lexicographic product of graphs, Discrete Mathematics. (2012) 312, no. 22, 3349–3356, https://doi.org/10.1016/j.disc.2012.07.025, 2-s2.0-84865072850.
10.1016/j.disc.2012.07.025
Web of Science® Google Scholar
25 Chartrand G., Eroh L., Johnson M. A., and Oellermann O. R., Resolvability in graphs and the metric dimension of a graph, Discrete Applied Mathematics. (2000) 105, no. 1-3, 99–113, https://doi.org/10.1016/S0166-218X(00)00198-0, 2-s2.0-0037756351.
10.1016/S0166-218X(00)00198-0
Web of Science® Google Scholar
26 Fernau H. and Rodriguez-Velazquez J. A., On the (adjacency) metric dimension of corona and strong product graphs and their local variants: combinatorial and computational results, http://arxiv.org/abs/1309.2275.
Google Scholar
27 Fernau H. and Rodriguez-Velazquez J. A., Notions of metric dimension of corona products: combinatorial and computational results, International Computer Science Symposium in Russia, 2014, Springer International Publishing, Cham, 153–166, Lecture Notes in Computer Science.
10.1007/978-3-319-06686-8_12
Google Scholar
28 Melter R. A. and Tomescu I., Metric bases in digital geometry, Computer Vision, Graphics, and Image Processing. (1984) 25, no. 1, 113–121, https://doi.org/10.1016/0734-189X(84)90051-3, 2-s2.0-0021643887.
10.1016/0734-189X(84)90051-3
Google Scholar
29 Moreno A. E., Cruz Y. R., and Velazquez J. A. R., On the adjacency dimension of graphs, Applicable Analysis and Discrete Mathematics. (2016) 10, no. 1, 102–127, https://doi.org/10.2298/AADM151109022E, 2-s2.0-84971225698.
10.2298/AADM151109022E
Web of Science® Google Scholar
30 Azeem M., Imran M., and Nadeem M. F., Sharp bounds on partition dimension of hexagonal Mobius ladder, Journal of King Saud University-Science. (2022) 34, 12–25, https://doi.org/10.1016/j.jksus.2021.101779.
10.1016/j.jksus.2021.101779
Web of Science® Google Scholar
31 Deng B., Nadeem M. F., and Azeem M., On the edge metric dimension of different families of Möbius networks, Mathematical Problems in Engineering. (2021) 2020, 9, 6623208, https://doi.org/10.1155/2021/6623208.
10.1155/2021/6623208
Google Scholar
32 Ali M., Ali G., Imran M., Baig A. Q., and Shafiq M. K., On the metric dimension of Móbious ladder, Ars Combinatoria. (2012) 105, 403–410.
Web of Science® Google Scholar
33 Nadeem M. F., Azeem M., and Khalil A., The locating number of hexagonal Möbius ladder network, Journal of Applied Mathematics and Computation. (2021) 66, no. 1-2, 149–165, https://doi.org/10.1007/s12190-020-01430-8.
10.1007/s12190-020-01430-8
Web of Science® Google Scholar
34 Moussa M. I. and Badr E. M., Ladder and subdivision of ladder graphs with pendant edges are odd graceful, International Journal on Applications of Graph Theory in Wireless Ad hoc Networks and Sensor Networks(GRAPH-HOC). (2016) 8, no. 1, 1–8, https://doi.org/10.5121/jgraphoc.2016.8101.
10.5121/jgraphoc.2016.8101
Google Scholar

Citing Literature

All articles

v_k	r(v_k \| v₁)	r(v_k \| v₂)	r(v_k \| v₅)	v_k	r(v_k \| v₁)	r(v_k \| v₂)	r(v_k \| v₅)
1	0	1	2	5	1	2	1
2	1	0	1	6	2	1	0
3	2	1	2	7	2	2	1
4	2	2	2	8	1	2	2

v_k	r(v_k \| v₁)	r(v_k \| v₂)	r(v_k \| v₆)	v_k	r(v_k \| v₁)	r(v_k \| v₂)	r(v_k \| v₆)
1	0	1	2	5	1	2	1
2	1	0	2	6	2	1	0
3	2	1	2	7	2	2	1
4	2	2	2	8	1	2	2

v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)	v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)
1	0	2	2	1	7	1	2	2	0
2	1	1	2	2	8	2	2	2	1
3	2	0	2	2	9	2	1	2	2
4	2	1	1	2	10	2	2	2	2
5	2	2	0	2	11	2	2	1	2
6	2	2	1	1	12	1	2	2	2

[Retracted] On Adjacency Metric Dimension of Some Families of Graph

Retraction(s) for this article

Retracted: On Adjacency Metric Dimension of Some Families of Graph

Abstract

1. Introduction

2. Construction of Graphs

3. Results on Adjacency Metric Dimension of Graphs

4. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)	v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)
1	0	2	2	1	7	1	2	2	0
2	1	1	2	2	8	2	2	2	1
3	2	0	2	2	9	2	1	2	2
4	2	1	1	2	10	2	2	2	2
5	2	2	0	2	11	2	2	1	2
6	2	2	1	1	12	1	2	2	2

v_k	v₁	v₂	v₅	v₇	v₉	v₁₂	v_k	v₁	v₂	v₅	v₇	v₉	v₁₂
1	0	1	2	2	1	2	9	1	2	2	2	0	2
2	1	0	2	2	2	2	10	2	2	2	2	1	2
3	2	1	2	2	2	2	11	2	2	2	2	2	1
4	2	2	1	2	2	2	12	2	2	2	2	2	0
5	2	2	0	2	2	2	13	2	2	1	2	2	1
6	2	2	1	1	2	2	14	2	2	2	2	2	2
7	2	2	2	0	2	2	15	2	2	2	1	2	2
8	2	2	2	1	1	2	16	1	2	2	2	2	2

v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)	v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)
1	0	2	2	1	7	1	2	2	0
2	1	1	2	2	8	2	2	2	1
3	2	0	2	2	9	2	1	2	2
4	2	1	1	2	10	2	2	2	2
5	2	2	0	2	11	2	2	1	2
6	2	2	1	1	12	1	2	2	2

v_k	v₁	v₂	v₅	v₇	v₉	v₁₂	v_k	v₁	v₂	v₅	v₇	v₉	v₁₂
1	0	1	2	2	1	2	9	1	2	2	2	0	2
2	1	0	2	2	2	2	10	2	2	2	2	1	2
3	2	1	2	2	2	2	11	2	2	2	2	2	1
4	2	2	1	2	2	2	12	2	2	2	2	2	0
5	2	2	0	2	2	2	13	2	2	1	2	2	1
6	2	2	1	1	2	2	14	2	2	2	2	2	2
7	2	2	2	0	2	2	15	2	2	2	1	2	2
8	2	2	2	1	1	2	16	1	2	2	2	2	2

[Retracted] On Adjacency Metric Dimension of Some Families of Graph

Retraction(s) for this article

Retracted: On Adjacency Metric Dimension of Some Families of Graph

Abstract

1. Introduction

2. Construction of Graphs

3. Results on Adjacency Metric Dimension of Graphs

4. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)	v_k	r(v_k \| v₁)	r(v_k \| v₃)	r(v_k \| v₅)	r(v_k \| v₇)
1	0	2	2	1	7	1	2	2	0
2	1	1	2	2	8	2	2	2	1
3	2	0	2	2	9	2	1	2	2
4	2	1	1	2	10	2	2	2	2
5	2	2	0	2	11	2	2	1	2
6	2	2	1	1	12	1	2	2	2

v_k	v₁	v₂	v₅	v₇	v₉	v₁₂	v_k	v₁	v₂	v₅	v₇	v₉	v₁₂
1	0	1	2	2	1	2	9	1	2	2	2	0	2
2	1	0	2	2	2	2	10	2	2	2	2	1	2
3	2	1	2	2	2	2	11	2	2	2	2	2	1
4	2	2	1	2	2	2	12	2	2	2	2	2	0
5	2	2	0	2	2	2	13	2	2	1	2	2	1
6	2	2	1	1	2	2	14	2	2	2	2	2	2
7	2	2	2	0	2	2	15	2	2	2	1	2	2
8	2	2	2	1	1	2	16	1	2	2	2	2	2