In order to study the improved genetic algorithm for intelligent grinding trajectory of industrial robot, a trajectory planning method with optimal energy consumption is proposed. Firstly, the trajectory of the robot is regarded as a series of type value points in space, and each adjacent type value point is connected by a quintic B-spline curve to obtain the trajectory function of the robot. Then, the kinetic energy is taken as the target energy consumption function, and the kinematic and dynamic constraints of each joint are considered at the same time. Finally, the genetic algorithm is improved to optimize the objective energy consumption function. The improved genetic algorithm improves the operation efficiency, local search ability, and real-time performance of the algorithm. Front and rear times during handling were 15.034 s and 17.456 s for 2.422 s. The optimal secondary trajectory planning algorithm is called in the single workstation of the welding robot and the robot welding the bucket with spatial straight line and spatial curve, respectively. Through the time difference, the time used in the spatial linear welding is 5.462 s, and the spatial curve welding time is 12.981 s. The proposed algorithm can be applied to the production of various industrial sensor robots such as welding robot, cutting robot, and spraying robot and improves the working efficiency of robot operation. In addition, the genetic method of multichromosome structure also has a certain reference for solving the general GSTP problem.

1. Introduction

With the development of robot technology, the research and application of industrial sensor robot are more and more extensive, which has changed the face of traditional industrial production. Early industrial robots mostly adopted the form of “teaching reproduction,” which had defects such as high production cost, low production efficiency ,and damage to the health of operators caused by harmful working environment, which led to the research on off-line programming technology of industrial robots at home and abroad [1]. Nowadays, industrial robots are widely used in all walks of life. However, they need to consume a lot of electric energy in the working process. How to effectively reduce their energy consumption without reducing their work efficiency becomes very important (Figure 1).Optimizing the movement trajectory of industrial robots can reduce their energy consumed well. One of the industrial robot control problems is optimal grinding trajectory planning, which aims to plan a smooth optimal motion trajectory that interpolates points through a given path and satisfying the boundary constraints. Optimizing the motion trajectory of industrial robots can well reduce their energy consumption [2] The research on the trajectory planning algorithm of the robot can effectively promote the work efficiency of the robot. Therefore, the international scholars who study the subalgorithm keep introducing new algorithms. The trajectory planning of the robot can be carried out in joint space or Cartesian space. If it is carried out in joint space, the joint space conversion of each working path point must be carried out first. These path points can be transformed into the angle value of each joint by inverse kinematic operation. After these working path points are transformed, they form each group of path nodes. One of the optimal control problems of industrial robots is optimal trajectory planning. Its purpose is to plan a smooth optimal trajectory through a given path interpolation point and meet the boundary constraints. The use of industrial robots can not only increase the output and texture of products. At the same time, it can also protect personal safety, improve the working environment, save raw materials, reduce work intensity, and improve labor productivity. Therefore, it is of special significance. It is the development requirement of large-scale production and the basic unit of factory automation and flexible manufacturing system [3]. It integrates many elements such as control, communication, machinery, design, and software. It is a combination of computer science, software engineering, mechanical engineering, control engineering, and other technologies and sciences. In industrial automation or in extremely dangerous situations, it can replace people with boring and repeated long-term work such as welding, coating, stamping, machinery, and devices. Future robots should have high-level capabilities such as perception, planning, and control. Therefore, robot trajectory planning is an important part of the planning module, which has important practical significance in improving the execution efficiency of industrial robots, reducing the errors of industrial robots in actual operation, and making the robot trajectory stable, continuous, and smooth [4].

Details are in the caption following the image — Open in figure viewer PowerPoint

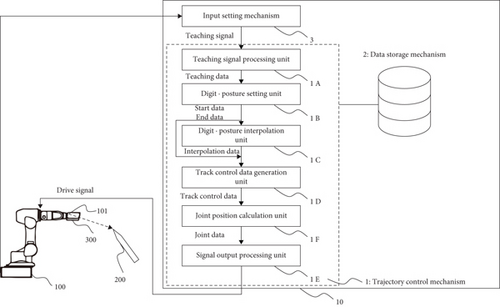
2. Literature Review

Dong, Yang, and others proposed time optimal robot trajectory planning. However, under the same trajectory, the robot action time is minimized, but its motion speed is increased, which may not effectively reduce energy consumption [5]. Dian et al. proposed the trajectory planning with optimal energy consumption, calculated the motion trajectory through spline function, and established the energy consumption model [6]. Batista et al. introduced the robot dynamic planning algorithm. However, the trajectory acceleration and joint torque generated by the above algorithm are not continuous, which will lead to the decline of trajectory accuracy, and the robot may vibrate and damage. At the same time, the controller cannot correct the path error caused by interference or modeling [7]. Therefore, in order to obtain an effective solution, Mohammad and others have made certain restrictions on the acceleration. Although the acceleration is not strictly optimal in time, the robot can effectively execute the expected trajectory [8]. In order to make the robot generate continuous trajectory, smooth trajectory is mostly used in the literature of trajectory planning. Ding et al. interpolated with B-spline curve [9]. Ahmad et al. introduced the optimal time trajectory planning algorithm and connected the important nodes in the joint space of industrial robot with high-order polynomial curve to obtain a satisfactory working trajectory [10]. Sun et al. obtained the joint variables in the joint space according to the inverse kinematics from the pose of the robot end effector and then interpolated according to the expected curve trajectory [11].

In this paper, the trajectory is obtained by B-spline function, the kinetic energy is taken as the target energy consumption, and the optimization results are obtained according to the constraints. In the process of optimization, the improved genetic algorithm is used to overcome its shortcomings such as poor local search ability and premature phenomenon, so that the final optimization result is reliable and practical.

3. Objective Function Optimization Based on the Improved Genetic Algorithm

The genetic algorithm is an evolutionary algorithm that imitates the selection and genetic mechanism of nature. It can overcome the disadvantage of being easy to fall into the trap of local minimum and appear dead cycle. It is a global optimization algorithm. The optimization object is a group of individuals, and the search process is carried out along multiple trajectories, which has implicit parallelism. However, the genetic algorithm has some disadvantages, such as poor local search ability and prone to premature phenomenon. Therefore, it is necessary to improve the algorithm to improve the efficiency and local search ability of the algorithm [12].

3.1. Improved Genetic Algorithm

3.1.1. Coding Method

Instead of using the commonly used binary coding, the binary coding of adjacent integers may have a large hamming distance. The real number coding method is adopted; that is, each gene value of an individual is represented by a real number within a specific range. This method is convenient to deal with the problems of multi-dimensional and high precision and improves the computational complexity and the computational efficiency of the algorithm.

3.1.2. Best Individual Retention

The basic method is to select in proportion according to the size of individual fitness. In this paper, the individuals with the highest fitness in the population are directly copied to the next generation, so that the individuals with the highest fitness; that is, the best individuals do not exchange and mutate in this generation [13]. This method speeds up the search speed and improves the local search ability.

3.1.3. Expected Value Selection Method

The expected value selection method can overcome the random error phenomenon that individuals with high fitness may be eliminated and individuals with low fitness may be selected [14–16] and improve the real-time performance of genetic algorithm. The specific steps are as follows:

(1)
Calculate the expected value of fitness:

(1)

(2)
Calculate the expected value of individual survival:

(2)

(3)
is converted to integer R_i through the rounding principle. If, R_i = O, the individual is eliminated
(4)
Mutation operator

It can restore the population diversity and ensure the global convergence of the algorithm. Therefore, according to the optimal solution retained by the previous generation [17], the variation probability is adjusted as follows:

(3)

where p₀ is the initial mutation probability, 0 < ∂ < 1, ∂ is the adjustment coefficient, H is the algebra maintained by the optimal solution, and C is a constant.

According to different fitness, the variation probability is adjusted as follows:

(4)

where β is the adjustment coefficient determined by the fitness value, 0 < β < 1, K is a constant, and K < P_O.

Equation (3) ensures that when premature occurs and the optimal solution is maintained, the mutation probability increases until it jumps out of the local extreme point, while equation (4) reduces the mutation probability of individuals with large fitness [18], which improves the real-time performance of the algorithm.

3.2. Optimization Results

The EFT 20 kg industrial robot er20-c10 is selected, the parameters are input into the above formula, the appropriate interpolation points are selected, and the trajectory functions of 6 joints are calculated, and substituted into equations (3) and (4) to calculate the objective function. Taking the time interval as the variable and combined with the constraints, the results are optimized by improving the genetic algorithm. Firstly, local optimization and then global optimization improve the efficiency of the algorithm. The specific parameters are set as follows:

3.2.1. Local Optimization

Firstly, a small population of 30 chromosomes is selected, and the evolutionary algebra is set to 20 generations; so, a local optimization time can be obtained quickly.

3.2.2. Global Optimization

Then, expand the population to 100 chromosomes and increase the evolutionary algebra to 60 generations, so as to obtain a global optimization time [19]. The initial value of the time interval is 3 s, each joint trajectory is composed of 5 sections of B-spline curve, and the initial total energy consumption is 30247.56 J. the initial value is optimized for 8 times. The optimization results are shown in Table 1:

1. Optimization results of objective energy consumption function.

Time interval	t₁(s)	t₂(s)	t₃(s)	t₄(s)	t₅(s)	t₅(s)
Initial value	2	3	3	2	3	4
Optimization 1	2.321	2.364	2.361	2.963	2.896	2.456
Optimization 2	2.632	2.369	1.362	2.564	2.786	2.321
Optimization 3	1.963	2.136	2.563	2.213	2.845	2.823
		2.365	2.987	2.364	2.563	2.154

The constraint parameters of robot ER20-C10 are shown in Table 2:

2. Constraint parameters.

Joint	1	2	3	4	5	6
Speed constraint (%/s)	173	165	173	360	361	612
Acceleration constraint (9/S2)	70	70	124	153	153	231
Acceleration constraint (%/3)	100	90	154	165	150	189
Moment constraint (N. m)	420	420	423	46	43	23.6

According to Table 1, the result of the seventh optimization is the best, with a total time of 11.351 s and a total energy consumption of 28447.31 J. The optimal trajectory of the robot can be obtained by substituting the optimization result into the calculated trajectory function [20].

3.3. Joint Space Trajectory Planning

In order to meet the requirements of trajectory in joint space, the inverse kinematics problem is used to transform each path point into joint angle value, and then the smooth function is fitted for each joint to make it pass through each path point in sequence from the starting point to the target point. For each path segment, each joint has a kind of running time to ensure that each joint reaches each path point [17]. Although each joint is the same in each path period, the fitting functions of all joints are independent. The trajectory planning in joint space does not require the trajectory shape as in right angle space; so, the calculation is simple and has no singularity. The trajectory planning of joint space needs to give the position and attitude of the starting point and the ending point under the condition of satisfying a certain constraint (for example, the displacement, velocity, and acceleration of each node are continuous) and interpolate each joint with different functions to obtain the motion trajectory of each joint. This section mainly discusses the application of interpolation method in joint trajectory [21].

If a single joint can move smoothly, θ(t) interpolation function needs to be bound by at least four conditions. There are angle and velocity constraints for both endpoints. The constraint of endpoint angle is the joint angle value of track initial point and track end point [22].

(5)

In order to ensure continuous joint movement speed, it is specified that

(6)

3.4. Rectangular Coordinate Space Straight Line Trajectory Planning

The spatial linear interpolation planning algorithm is a process of solving the position and attitude of each trajectory interpolation point when the position and attitude of the starting point and end point are known. Because in most cases, when the robot moves along a straight line, its end orientation attitude does not change; so, there is no need to interpolate the end attitude [23]. The position and pose of the two points P₁(x₁, y₁, z₁) and P₂(x₂, y₂, z₂) at the beginning and end of the spatial line relative to the global coordinates are known. Find the straight line length L from P₁ to P₂ as follows:

(7)

It is specified that the speed when moving along a straight line is Δt and the interpolation time interval is Δt, then the moving distance a in time Δt and the total number of interpolation N are

(8)

(9)

Then, the displacement increment of each joint of the robot and the coordinate value of each interpolation point are

(10)

3.5. Spatial Arc Interpolation

In three-dimensional space, any three points (not collinear) can determine a circle in any plane. Spatial arc trajectory planning is processed through the following steps:

The first step is to find out the plane where the spatial circle is located and convert the circle in three-dimensional space to two-dimensional plane.

In the second step, the plane arc planning is used to interpolate the arc on the spatial plane.

The third step is to convert the points in the two-dimensional plane in the second step to the base coordinate system.

4. Verification and Implementation of Optimal Trajectory Planning of Industrial Robot

According to the robot 3D simulation environment and project requirements, the design objectives of robot trajectory planning are as follows: (1) verify the real-time and efficiency of the simulation platform, (2) verify and realize the time optimal trajectory planning in the welding transition process of the robot to the bucket; and (3) verify and realize the optimal smooth trajectory planning of straight line and arc in the process of bucket welding. The time optimal and smooth optimal trajectory planning algorithm studied in the previous chapters of this paper has ensured the smoothness and efficiency of the trajectory planning goal of industrial robot. The next research content only needs to verify the trajectory planning problem in the welding process between robot and bucket [24, 25]. The optimal trajectory is obtained from the above optimization results, which is taken as the trajectory of the industrial robot model with degrees of freedom. The kinematic parameter curve is obtained by motion analysis in ADAMS to test whether it meets the constraints. If the constraints are satisfied, the result is optimal. If the constraints are not met, the optimization results will be reselected and simulated again until they meet the constraints. The trajectory planning process between industrial robot and 3D simulation environment is shown in Figure 2.

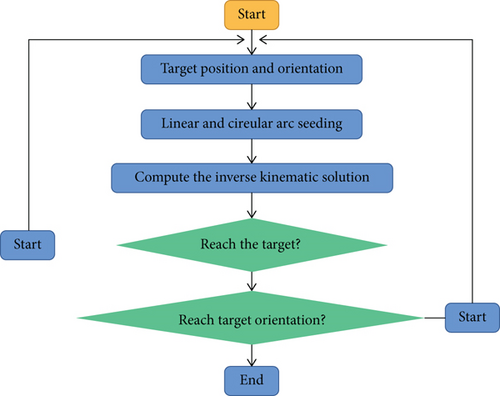
The simulated kinematic parameters include the rotation angle, angular velocity, and angular acceleration of the robot. The change curve during the movement is shown in Figures 3–4 below.

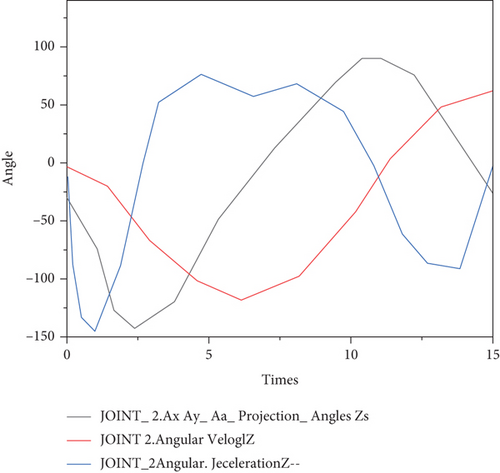
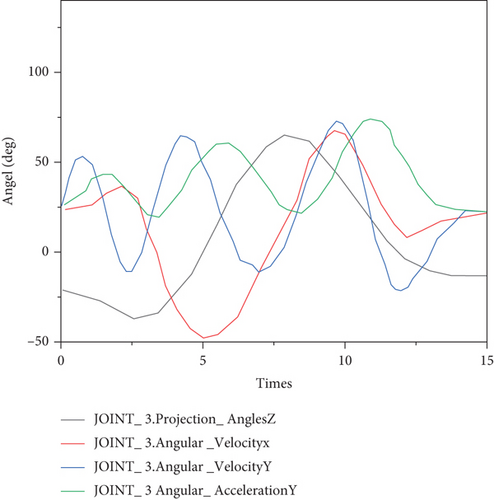
By analyzing Figures 3 and 4, it can be seen that the robot takes the optimized trajectory as the motion trajectory, and the six joints meet the kinematic constraints in the motion process [26, 27]. The maximum amplitude of each curve obtained by simulation is brought into the dynamic equation, and it can be verified that the six joints also meet the dynamic constraints in the process of motion.

The quantitative comparison of the obtained task planning results is shown in Table 3.

3. Comparison of path combination planning methods.

Planning tasks	Planning method	Optimal path length/m	Convergence steps
A	Original method	935.23	249
A	Paper method	931.63	176
B	Original method	223.623.1	43
B	Paper method	203.456.9	21

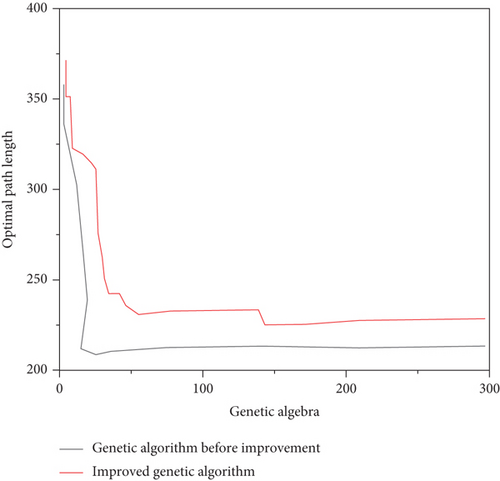
It can be seen from Figure 5 and Table 1 that the improved genetic algorithm can obtain better path combination planning results than the original method. In addition, from the perspective of the speed of evolutionary convergence, the evolutionary algebra required for the improved genetic algorithm to converge to the optimal average path length has been greatly reduced, which further proves the advantages of the method in improving industrial production efficiency by operating the path direction and sequence at the same time.

This paper sets up two scenarios: single workstation of handling robot and single workstation of welding robot. The time optimal trajectory planning algorithm was invoked in the single workstation of the transport robot [28, 29]. The transportation time was 15.034 s and 17.456 s, respectively, and the time was 2.422 s. The second-order trajectory planning algorithm with the best smoothness is called in the single workstation of the welding robot, and the robot welds the space straight line and the space curve, respectively, to the bucket. According to the difference between before and after time, the time for space linear welding is 5.462 s, and the time for space curve welding is 12.981 s. In order to compare with the quadratic smoothing optimization, only the time optimal trajectory planning algorithm is called in the single workstation of the welding robot to make the robot weld the bucket space curve weld. The time is 9.65 s, and the trajectory may produce small jitter, which should be avoided as much as possible in robot welding.

5. Conclusion

In this paper, the trajectory of industrial robot is obtained by quintic B-spline function, and the constraints such as speed, acceleration, acceleration, and torque are given. Then, the kinetic energy of the robot is taken as its target energy consumption function. The genetic algorithm is improved to improve the operation efficiency, local search ability, and real-time performance of the algorithm. The improved genetic algorithm is used to optimize the objective function and obtain the optimal result, so as to obtain the optimal trajectory. This trajectory is used as the motion trajectory of the robot simulation model. The kinematic and dynamic parameters of each joint of the robot are simulated and analyzed in ADAMS to meet the constraint conditions, and the rationality of the optimal trajectory is verified. The optimization strategy has strong practicability and can be used to optimize the trajectory of other types of industrial robots. The simulation results show that the trajectory planning algorithm in this paper can realize the short time and continuous smooth trajectory of the robot in the three-dimensional simulation of industrial robot and ensure the real-time, high efficiency, and smoothness of the robot trajectory in the simulation environment. The algorithms discussed in this paper are carried out in the off-line system, and the real-time trajectory tracking problem is not considered. How to apply the optimized robot trajectory to the practical application of the robot, the real-time tracking of the controller is a further problem to be studied.

Conflicts of Interest

The author declares that he/she has no conflicts of interest.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Luo X., Li S., Liu S., and Liu G., An optimal trajectory planning method for path tracking of industrial robots, Robotica. (2019) 37, no. 3, 502–520, https://doi.org/10.1017/S0263574718001145, 2-s2.0-85056133321.
10.1017/S0263574718001145
Google Scholar
2 Ogbemhe J., Mpofu K., and Tlale N., Optimal trajectory scheme for robotic welding along complex joints using a hybrid multi-objective genetic algorithm, IEEE Access. (2019) 7, 158753–158769, https://doi.org/10.1109/ACCESS.2019.2950561.
10.1109/ACCESS.2019.2950561
Google Scholar
3 Cao J., Song C., Peng S., Xiao F., and Song S., Improved traffic sign detection and recognition algorithm for intelligent vehicles, Sensors. (2019) 19, no. 18, https://doi.org/10.3390/s19184021, 2-s2.0-85072518671, 31540378.
10.3390/s19184021
PubMed Web of Science® Google Scholar
4 Zhou B. and Wu Q., A novel optimal method of robotic weld assembly line balancing problems with changeover times: a case study, Assembly Automation. (2018) 38, no. 4, 376–386, https://doi.org/10.1108/AA-02-2018-026, 2-s2.0-85054584798.
10.1108/AA-02-2018-026
Google Scholar
5 Yang D., Liu Z., Shu T., Yang L., Ouyang J., and Shen Z., An improved genetic algorithm for multiobjective optimization of helical coil electromagnetic launchers, IEEE Transactions on Plasma Science. (2017) 46, no. 1, 127–133.
10.1109/TPS.2017.2773639
Google Scholar
6 Dian S., Fang H., Zhao T., Wu Q., and Li S., Modeling and trajectory tracking control for magnetic wheeled mobile robots based on improved dual-heuristic dynamic programming, Transactions on Industrial Informatics. (2020) 17, no. 2, 1470–1482.
10.1109/TII.2020.2983841
Web of Science® Google Scholar
7 Batista J., Souza D., Silva J., Ramos K., and Braga A., Trajectory planning using artificial potential fields with metaheuristics, IEEE Latin America Transactions. (2020) 18, no. 5, 914–922, https://doi.org/10.1109/TLA.2020.9082920.
10.1109/TLA.2020.9082920
Google Scholar
8 Mohammad A., Hong J., and Wang D., Polishing of uneven surfaces using industrial robots based on neural network and genetic algorithm, International Journal of Advanced Manufacturing Technology. (2017) 93, no. 1, 1–9.
Google Scholar
9 Ding C., Chen L., and Zhong B., Exploration of intelligent computing based on improved hybrid genetic algorithm, Cluster Computing. (2019) 22, no. S4, 9037–9045, https://doi.org/10.1007/s10586-018-2049-7, 2-s2.0-85045071203.
10.1007/s10586-018-2049-7
Web of Science® Google Scholar
10 Ahmad K., Khan K., and Al-Fuqaha A., Intelligent fusion of deep features for improved waste classification, IEEE Access. (2020) 8, 96495–96504, https://doi.org/10.1109/ACCESS.2020.2995681.
10.1109/ACCESS.2020.2995681
Google Scholar
11 Sun W., Huang Y., and Chen H., An improved adaptive genetic algorithm for optimizing pyroshock acceleration synthesis, IEEE Access. (2019) 7, 132682–132693, https://doi.org/10.1109/ACCESS.2019.2941738.
10.1109/ACCESS.2019.2941738
Google Scholar
12 Ma K., Han L., Sun X., Liang C., Zhang S., Shi Y., and Wang X., A path planning method of robotic belt grinding for workpieces with complex surfaces, IEEE/ASME Transactions on Mechatronics. (2020) 25, no. 2, 728–738, https://doi.org/10.1109/TMECH.2020.2974925.
10.1109/TMECH.2020.2974925
Google Scholar
13 Luo G., Zou L., Wang Z., Lv C., and Huang Y., A novel kinematic parameters calibration method for industrial robot based on levenberg-marquardt and differential evolution hybrid algorithm, Robotics and Computer-Integrated Manufacturing. (2021) 71, no. 1, https://doi.org/10.1016/j.rcim.2021.102165.
10.1016/j.rcim.2021.102165
Google Scholar
14 Wang Z., Design and implementation of polishing and polishing flexible workstation based on industrial robot, International Core Journal of Engineering. (2020) 6, no. 4, 193–197.
Google Scholar
15 Wu Z. G., Lin C. Y., Chang H. W., and Lin P. T., Inline inspection with an industrial robot (iiir) for mass-customization production line, Sensors. (2020) 20, no. 11, https://doi.org/10.3390/s20113008, 32466352.
10.3390/s20113008
PubMed Google Scholar
16 Li M., Du Z., Ma X., Gao K., and Gao Y., System design and monitoring method of robot grinding for friction stir weld seam, Applied Sciences. (2020) 10, no. 8, https://doi.org/10.3390/app10082903.
10.3390/app10082903
Google Scholar
17 Lin M., Yang C., Li D., and Zhou G., Intelligent filter-based slam for mobile robots with improved localization performance, IEEE Access. (2019) 7, 113284–113297, https://doi.org/10.1109/ACCESS.2019.2934995.
10.1109/ACCESS.2019.2934995
Google Scholar
18 Shen Y., Improved chaos genetic algorithm based state of charge determination for lithium batteries in electric vehicles, Energy. (2018) 152, 576–585, https://doi.org/10.1016/j.energy.2018.03.174, 2-s2.0-85047598648.
10.1016/j.energy.2018.03.174
Web of Science® Google Scholar
19 Juan Y. and Seok-Bum K., Improved license plate localisation algorithm based on morphological operations, IET Intelligent Transport Systems. (2018) 12, no. 6, 542–549, https://doi.org/10.1049/iet-its.2017.0224, 2-s2.0-85049513138.
10.1049/iet-its.2017.0224
Google Scholar
20 Shan H., Hongjing L., Linlin W., Feng Z., Wang M., Yang L., and Jie G., Economic optimisation of microgrid based on improved quantum genetic algorithm, The Journal of Engineering. (2019) 2019, no. 16, 1167–1174, https://doi.org/10.1049/joe.2018.8849.
10.1049/joe.2018.8849
Web of Science® Google Scholar
21 Zhang R. and Tao J., A nonlinear fuzzy neural network modeling approach using improved genetic algorithm, Transactions on Industrial Electronics. (2017) 65, no. 7, 5882–5892.
10.1109/TIE.2017.2777415
Google Scholar
22 Ren Q., Li M., and Han S., Discrimination and comparison experiments of basalt tectonic setting based on improved genetic algorithm-optimized neural network, Earth Science Frontiers. (2019) 26, no. 4, 117–124.
CAS Google Scholar
23 Yadav G. S. and Ojha A., Improved security in the genetic algorithm-based image steganography scheme using hilbert space-filling curve, The imaging science journal. (2019) 67, no. 3, 148–158, https://doi.org/10.1080/13682199.2019.1570678, 2-s2.0-85060956834.
10.1080/13682199.2019.1570678
Web of Science® Google Scholar
24 Iida T., Anzai D., and Wang J., A three-dimensional em-based implant device localization method improved by genetic algorithm, International Journal of Wireless Information Networks. (2017) 24, no. 2, 180–188, https://doi.org/10.1007/s10776-017-0332-9, 2-s2.0-85011589711.
10.1007/s10776-017-0332-9
Google Scholar
25 Du L., Bo S., Liu Y., Alsaadi F. E., and Alsaedi A., Genetic algorithm-based compliant robot path planning: an improved bi-rrt-based initialization method, Assembly Automation. (2017) 37, no. 3, 261–270.
10.1108/AA-12-2016-173
Google Scholar
26 Wu Y. and Song Q., Improved particle swarm optimization algorithm in power system network reconfiguration, Mathematical Problems in Engineering. (2021) 2021, 10, https://doi.org/10.1155/2021/5574501.
10.1155/2021/5574501
Google Scholar
27 Jie L., Liu W., Sun Z., and Teng S., Hybrid fuzzy clustering methods based on improved self-adaptive cellular genetic algorithm and optimal-selection-based fuzzy c-means, Neurocomputing. (2017) 249, 140–156, https://doi.org/10.1016/j.neucom.2017.03.068, 2-s2.0-85018628965.
10.1016/j.neucom.2017.03.068
Web of Science® Google Scholar
28 Guo X., Huang J., Liu H., and Chen Y., efficient p-cycle combination protection strategy based on improved genetic algorithm in elastic optical networks, IET Optoelectronics. (2018) 12, no. 2, 73–79, https://doi.org/10.1049/iet-opt.2016.0177, 2-s2.0-85042724099.
10.1049/iet-opt.2016.0177
Web of Science® Google Scholar
29 Ponciroli R., Stauff N. E., Ramsey J., Ganda F., and Vilim R. B., An improved genetic algorithm approach to the unit commitment/economic dispatch problem, Transactions on Power Systems. (2020) 35, no. 5, 4005–4013, https://doi.org/10.1109/TPWRS.2020.2986710.
10.1109/TPWRS.2020.2986710
Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] Improved Genetic Algorithm for Intelligent Grinding Trajectory of Industrial Robot Sensor

Retraction(s) for this article

Retracted: Improved Genetic Algorithm for Intelligent Grinding Trajectory of Industrial Robot Sensor

Abstract

1. Introduction

2. Literature Review