Volume 2022, Issue 1 6219155

Research Article

Open Access

Investigation of Atom-Bond Connectivity Indices of Line Graphs Using Subdivision Approach

Corresponding Author

Mohamad Nazri Husin

[email protected]

orcid.org/0000-0003-4196-4984

Special Interest Group on Modelling & Data Analytics (SIGMDA), Faculty of Ocean Engineering Technology & Informatics, Universiti Malaysia Terengganu, Kuala Nerus 21030, Terengganu, Malaysia umt.edu.my

Search for more papers by this author

Sohail Zafar,

Sohail Zafar

University of Management and Technology, Lahore, Pakistan umt.edu.pk

Search for more papers by this author

R. U. Gobithaasan,

R. U. Gobithaasan

orcid.org/0000-0003-3077-8772

Search for more papers by this author

Mohamad Nazri Husin,

Corresponding Author

Mohamad Nazri Husin

[email protected]

orcid.org/0000-0003-4196-4984

Search for more papers by this author

Sohail Zafar,

Sohail Zafar

University of Management and Technology, Lahore, Pakistan umt.edu.pk

Search for more papers by this author

R. U. Gobithaasan,

R. U. Gobithaasan

orcid.org/0000-0003-3077-8772

Search for more papers by this author

First published: 17 June 2022

https://doi.org/10.1155/2022/6219155

Citations: 21

Academic Editor: A. M. Bastos Pereira

Share a link

Email
Wechat
Bluesky

Abstract

A topological index is a numerical measure that characterises the whole structure of a graph. Based on vertex degrees, the idea of an atom-bond connectivity (ABC) index was introduced in chemical graph theory. Later, different versions of the ABC index were created, and some of these indices were recently designed. In this paper, we present the edge version of the atom-bond connectivity (ABC_e) index, edge version of the multiplicative atom-bond connectivity (ABCII_e) index, and atom-bond connectivity temperature (ABCT) index for the line graph of subdivision graph of tadpole graph (T_n,k), ladder graph (L_n), and wheel graph (W_n+1). Numerical simulation has also been shown for some novel families of atom-bond connectivity index comparing the three types of indices which can be useful for QSAR and QSPR studies.

1. Introduction

In this article, we have considered simple graphs, which are unweighted, undirected graphs that have no loops and multiple edges attached. Let G be a simple graph, with vertex set V(G) and edge set E(G). Suppose e is an edge of G, which connects the vertices u and v, then we denote e = uv and state that “u and v are adjacent.” The degree d_u of a vertex u is the number of edges that are incident to it. Topological indices are the mathematical measures that correspond to the structure of any simple finite graph. They are invariant under the graph isomorphism. There are some famous degree-based topological indices, which are introduced and applied in chemical engineering, for instance, the Randic index (refer to Ali & Du [1], Li & Shi [2], and Shi [3] for more details). These indices are also significant in quantitative structure-property relationship (QSPR) and quantitative structure-activity relationship (QSAR) (see [4, 5]).

The subdivision graph [6, 7] S(G) is the graph obtained from G by replacing each of its edge by a path of length 2. In graph G, if the corresponding edges share a vertex in G, the line graph L(G) of a graph G is considered as a graph with vertices of the edges in G. Two vertices e and f are incident if and only if they have a common end vertex in G. Estrada et al. [8] put forward a topological index named atom-bond connectivity index (briefly, ABC) as

(1)

where d_u and d_v represent the degrees of the vertices u and v, respectively. Recent advances on ABC index can be referred to in Das et al. [9], Lin et al. [10], Gao & Shao [11], and Bianchi et al. [12]. Referring to the end vertex degree d_e and d_f of edges e and f in a line graph of G, Farahani [13] proposed the edge version of atom-bond connectivity, ABC_e index. This idea is described in the following:

(2)

where d_e and d_f are the degree of the edge e and f, respectively. The reader can find more information about ABC_e index in References [14–18].

The multiplicative atom-bond connectivity index was introduced by Kulli in 2016 [19]. More information regarding the multiplicative atom-bond connectivity index may be found in references [20, 21]. Later, the edge version of the multiplicative atom-bond connectivity index [22] of a graph G was introduced, and it is defined as

(3)

where d_e is the degree of the edge e in L(G).

The temperature of a vertex u of a connected graph G is defined by Fajtlowicz [23] as

(4)

where d_u is the degree of a vertex u and n is the size of a graph G. Recently, Kahasy et al. [24] introduced a new index, known as the atom-bond connectivity temperature index. This index is defined as follows:

(5)

where T_u and T_v are the temperature of the vertex u and v, respectively.

2. Main Results

In 2011, Ranjini et al. calculated the explicit expression for the Shultz indices of the subdivision graphs of the tadpole, wheel, helm, and ladder graphs [25]. They also studied the Zagreb indices of line graphs of tadpole, wheel, and ladder graphs with subdivision in [26]. In 2015, Su & Xu calculated the general sum-connectivity indices and coindices of line graphs of tadpole, wheel, and ladder graphs with subdivision in [27]. In [28], Nadeem et al. computed ABC₄ and GA₅ indices of the line graphs of these graphs by using the notion of subdivision. They also studied the ABC₄ and GA₅ of these graphs [28]. Other studies on these include Rajasekar & Nagarajan [29] research on the location domination number of the line graph. Recently, Li &. Taylor [30] also studied the first Zagreb index and some Hamilton properties of the line graph.

A tadpole graph T_n,k is the graph obtained by joining a cycle of n vertices with a path of length k. A ladder L_n is obtained by taking the Cartesian product of two paths P_n × P₂. A wheel graph W_n or order n composed of a vertex is called the hub, adjacent to all vertices of a cycle of the order n.

Motivated by the results of [26, 27, 31], we studied the line graph of the subdivision graph T_n,k, L_n, and W_n+1 and derived an expression for the edge version of atom-bond connectivity, multiplicative atom-bond connectivity indices, and atom-bond connectivity temperature index of the graphs L(S(T_n,k)), L(S(W_n+1)), and L(S(L_n)).

Theorem 1. The edge version of the atom-bond connectivity index of L(S(T_n,k)) is

(6)

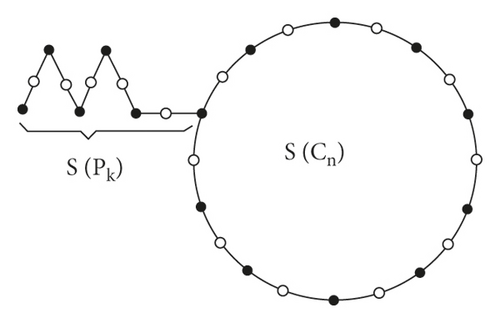
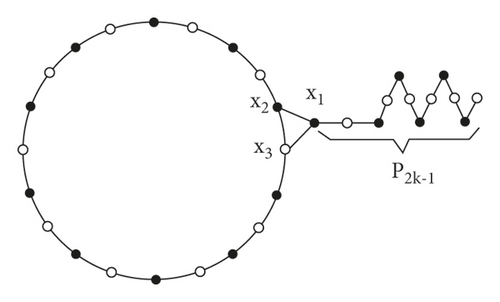
Proof. Let G be the line graph of the subdivision graph L(S(T_n,k)), seeing Figure 1. It contained 2(n + k) edges of the subdivision graph of S(T_n,k), and then, in the graph of G, it contained 2(n + k) vertices. It consists of three types of degree of edge e, such as 1, 2, and 3. Out of which, 3 vertices are of the degree 3, one vertex of degree 1 and the remaining 2(n + k − 2) vertices are of the degree 2. The graph of G contains path of length 2k − 1. Let V₁ be the vertex of degree 3 which is attached to this path. Let and be the neighbor of V₁ which are of degree 3 in the L(G). The vertices and have two neighbors of degree 3 and one neighbor of degree 2 in L(S(C_n) + e), where e is the edge adjacent to S(C_n). The vertex V₁ has 2 adjacent vertices of degree 3 and one vertex of degree 2 in the path. Let we derive an expression for the edge version of topological indices of the graph G, for k = 1. In graph G, it contains a path of length 1 which attached with V₁. Hence, with respect to the path is . For corresponding to the vertices V₁, in L(S(C_n) + e), hence, we have . Since one edge in G is shared between pairs of vertices, . Among the remaining, 2n − 4 vertices, for 2n − 5 vertices, have neighbors of degree 2, and one vertex has neighbor of degree 3. Hence, with respect to 2n − 4 vertices is . Adding all these number together, the edge version of atom-bond connectivity index of G is found as .

If k > 1, then the graph G contains path of length 2k − 1 which attached with V₁. Hence, with respect to the path is . For corresponding to the vertices V₁, in L(S(C_n) + e), hence, we have . Since one edge in G is shared between pairs of vertices, . Out of 2n − 2 vertices, for 2n − 3 vertices have neighbors of degree 2 and one vertex has neighbor of degree 3. Hence, with respect to 2n − 2 vertices is . Adding all these number together, the edge version of atom-bond connectivity index of G is found as . This completes the proof.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

[27] (a) The subdivision graph S(T_n,k) of the tadpole graph T_n,k. (b) The line graph L(S(T_n,k)).

Theorem 2. The edge version of the multiplicative atom-bond connectivity index of L(S(T_n,k)) is

(7)

Proof. After adopting the induction method, it is clear that overall speaking, this line graph of subdivision graph possesses of 2(n + k) vertices and 2(n + k) + 1 edges. If d_e and d_f are the degree of edge e, then there are 1 edge of type d_e = 1, d_f = 3, 2n − 5 edges with d_e = d_f = 2, 2 edges of type d_e = 2, d_f = 3, 3 edges with d_e = d_f = 3. Hence, for graph G with k = 1, we have . For k > 1, we have 1 edge of type d_e = 1, d_f = 2, 2n + 2k − 6 edges with d_e = d_f = 2, 3 edges of type d_e = 2, d_f = 3, 3 edges with d_e = d_f = 3. Hence, we deduce

(8)

This completes the proof.

Theorem 3. The atom-bond connectivity temperature index of L(S(T_n,k)) is

(9)

Proof. In G, there are total 2(n + k) vertices, among which 3 vertices are of the degree 3, one vertex of degree 1 and the remaining 2(n + k − 2) vertices are of the degree 2. The total number of edges of G is 2(n + k) + 1. For k = 1, we have 2(n + 1) vertices, which one vertex of degree 1, 3 vertices of degree 3 and 2(n − 1) vertices of degree 2. Therefore, after adopting the induction trick, we have 4 edge partition based on the temperature. If T_u and T_v are the temperature of the vertex u and v, then there are 1 edge of type T₁ = 1/2n + 1, T₃ = 3/2n − 1, 2n − 5 edges with T₂ = T₂ = 1/n, 2 edges of type T₂ = 1/n, T₃ = 3/2n − 1, 3 edges with T₃ = T₃ = 3/2n − 1. Hence, for graph G with k = 1, we have

(10)

For k > 1, we have 1 edge of type T₁ = 1/2n + 2k − 1, T₂ = 2/2n + 2k − 2, 2n + 2k − 6 edges with T₂ = T₂ = 2/2n + 2k − 2, 3 edges of type T₂ = 2/2n + 2k − 2, T₃ = 3/2n + 2k − 3, 3 edges with T₃ = T₃ = 3/2n + 2k − 3. Therefore, we get

(11)

This completes the proof.

Theorem 4. The edge version of the atom-bond connectivity index of L(S(W_n+1)) is

(12)

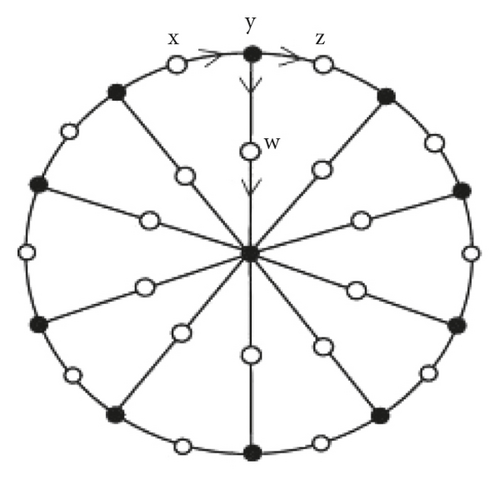
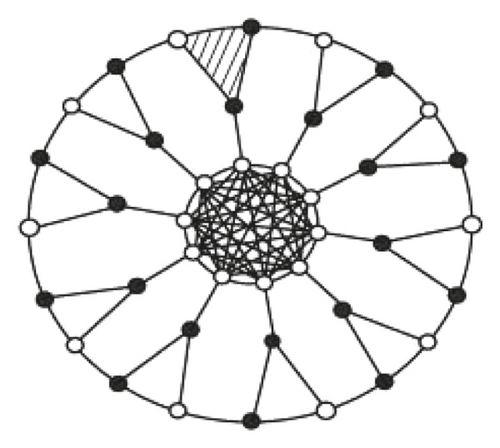
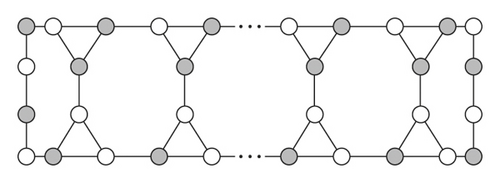
Proof. Let G be the line graph of the subdivision graph L(S(T_n,k)), seeing Figure 2. It contains 4n vertices are of degree 3 and n vertices of degree n. Out of n² + 9n/2 edges, the 4n edges of degree 3 have neighbor of degree 3. Hence, corresponding to these 4n edges which have only neighbor of degree 3 is 8n/3. The remaining n vertices of degree 3 are adjacent to vertices of degree n. Hence, with respect to these n vertices is . Also remaining n(n-1)/2 edges of degree n have neighbor of degree n. Hence, with respect to all these degrees of n is . Adding all these number together, the edge version of atom-bond connectivity index of G is found as . This completes the proof.

Theorem 5. The edge version of the multiplicative atom-bond connectivity index of L(S(W_n+1)) is

(13)

Proof. After adopting the induction technology, it is clear to find that, roughly speaking, this line graph of subdivision graph has contained 4n vertices and n² + 9n/2 edges. Also, there are 4n edges of type d_e = d_f = 3, n edges of type d_e = 3, d_f = n, n(n − 1)/2 edges with d_e = d_f = n. As a result, we infer

(14)

This completes the proof.

Theorem 6. The atom-bond connectivity temperature index of L(S(W_n+1)) is

(15)

Proof. In G, there are total 4n vertices are of degree 3 and n vertices of degree n. The total number of edges of G is n² + 9n/2. After adopting the induction method, we have 3 edge partition based on the temperature. If T_u and T_v are the temperature of the vertex u and v, then there are 4n edge of type T₃ = T₃ = 3/4n − 3, n edges with T₃ = 3/4n − 3, T_n = 1/3 and n(n − 1)/2 edges of type T_n = T_n = 1/3. Hence, we deduce

(16)

This completes the proof.

Theorem 7. The edge version of the atom-bond connectivity index of L(S(L_n)) is

(17)

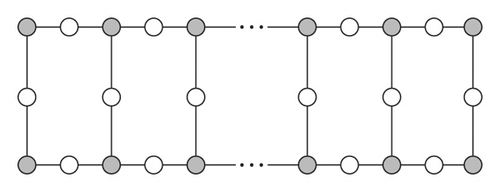
Proof. Let G be the line graph of subdivision graph L(S(L_n)), seeing Figure 3. The number of vertices in G is 6n − 4 among which 8 vertices are of degree 2 and the remaining 6n − 12 vertices are of degree 3. The number of edges in G is 9n − 10 among which 6 edges are of degree 2 with itself, 4 edges are of degree 2 and 3, and the remaining 9n − 20 edges are of degree 3 with itself. Adding all these numbers together, the edge version of the atom-bond connectivity index of G is found as . This completes the proof.

Theorem 8. The edge version of multiplicative atom-bond connectivity index of L(S(L_n)) is

(18)

Proof. After adopting the induction trick, we can find that, in general, this line graph of subdivision graph has 6n − 4 vertices and 9n − 10 edges. At the same, there are 6 edges of type d_e = d_f = 2, 4 edges of type d_e = 2, d_f = 3, 9n − 20 edges with d_e = d_f = 3. Therefore, we get

(19)

This completes the proof.

Theorem 9. The atom-bond connectivity temperature index of L(S(L_n)) is

(20)

Proof. In G, there are total 6n − 4 vertices in which 8 vertices are of degree 2 and the remaining 6n − 12 vertices are of degree 3. The total number of edges of G is 9n − 10. After adopting the induction technology, we have 3 edge partition based on the temperature. If T_u and T_v are the temperature of the vertex u and v, then there are 6 edge of type T₂ = T₂ = 1/3n − 3, 4 edges with T₂ = 1/3n − 3, T₃ = 3/6n − 7 and 9n − 20 edges of type T₃ = T₃ = 3/6n − 7. As a result, we infer

(21)

This completes the proof.

3. Numerical Simulation and Conclusion

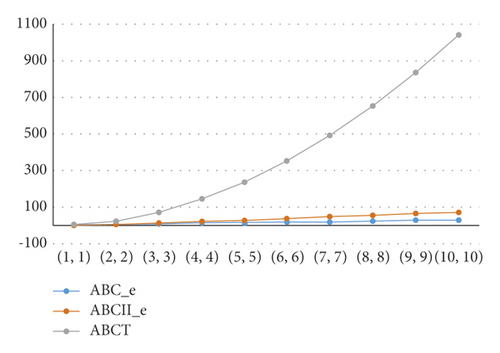
In this paper, we propose some novel families of atom-bond connectivity index. Now, the results of these indices will be compared. The comparison between ABC_e, ABCII_e, and ABCT of L(S(T_n,k)) is shown in Table 1. The graphical representation of Table 1 is illustrated in Figure 4.

Table 1. Comparison between ABC_e, ABC_e, and ABCT of L(S(T_n,k)).

(n, k)	ABC_e	ABCII_e	ABCT
(1, 1)	2.1093898	−4.898979486	4.7876937
(2, 2)	6.242640687	4.242640687	23.98539667
(3, 3)	9.071067812	12.72792206	72.10624376
(4, 4)	11.89949494	21.21320344	142.5586461
(5, 5)	14.72792206	29.69848481	235.5731609
(6, 6)	17.55634919	38.18376618	351.1898721
(7, 7)	20.38477631	46.66904756	489.4215973
(8, 8)	23.21320344	55.15432893	650.2737199
(9, 9)	26.04163056	63.63961031	833.7488996
(10, 10)	28.87005769	72.12489168	1039.848602

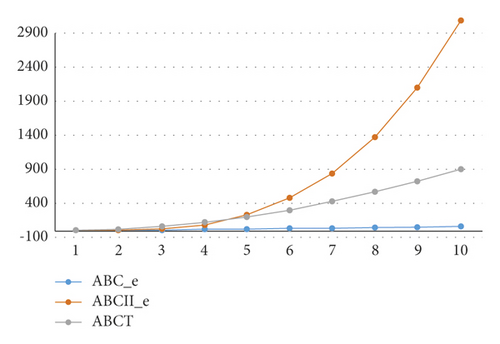
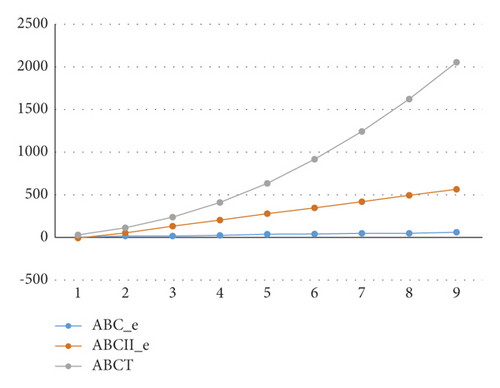
Similarly, the results for ABC_e, ABCII_e, and ABCT of LS(W_n+1) are compared in Table 2. Table 2 is given in Figure 5. Finally, the comparison of ABC_e, ABCII_e, and ABCT of L(S(L_n)) is shown in Table 3. The illustration of the results for ABC_e, ABCII_e, and ABCT is shown as Figure 6.

Table 2. Comparison between ABC_e, ABCII_e, and ABCT of L(S(W_n+1)).

n	ABC_e	ABCII_e	ABCT
1	3.483163248	0	3.821367205
2	7.454653677	5.333333333	20.00859965
3	12	32	62.35382907
4	16.92289018	101.1928851	124.0640009
5	22.15246524	238.5139176	205.2566258
6	27.64735154	473.2863826	305.8662831
7	33.37946531	838.1312546	425.8255499
8	39.32811367	1368.662608	565.0772788
9	45.47722558	2103.254621	723.5738722
10	51.81385047	3082.855819	901.2753388

Table 3. Comparison between ABC_e, ABCII_e, and ABCT of L(S(L_n)).

n	ABC_e	ABCII_e	ABCT
1	−0.2622655215	−88	−8.061498381
2	5.737734479	−16	27.04079003
3	11.73773448	56	100.868826
4	17.73773448	128	225.7405179
5	23.73773448	200	401.5280011
6	29.73773448	272	628.2266894
7	35.73773448	344	905.8363724
8	41.73773448	416	1234.357204
9	47.73773448	488	1613.789329
10	53.73773448	560	2044.132853

In this paper, certain degree-based topological indices, namely, ABC indices, were studied for the case of the line graphs of the subdivision graphs. It is anticipated that this computational study will encourage the researchers to have a firm grasp on the index framework they have chosen. The computational technique presented here can be useful for analysing the physicochemical features of the specified network, as well as being cost-effective and time-efficient. Future work includes the investigation of new classes of line graph of subdivision graphs and their topological indices which is useful in QSAR and QSPR studies.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors acknowledge Universiti Malaysia Terengganu for providing the financial support under Talent and Publication Enhancement-Research Grant (TAPE-RG; vot no. 55330).

Open Research

Data Availability

All data required for this paper are included within these papers.

References

1 Ali A. and Du Z., On the difference between atom-bond connectivity index and Randic index of binary and chemical trees, International Journal of Quantum Chemistry. (2017) 117, https://doi.org/10.1002/qua.25446, 2-s2.0-85031739552.
10.1002/qua.25446
Web of Science® Google Scholar
2 Li X. and Shi Y., A survey on the Randi´c index, MATCH Commun. Math. Comput. Chem.(2008) 59, no. 1, 127–156.
CAS Web of Science® Google Scholar
3 Shi Y., Note on two generalizations of the Randi´c index, Applied Mathematics and Computation. (2015) 265, 1019–1025, https://doi.org/10.1016/j.amc.2015.06.019, 2-s2.0-84933556226.
10.1016/j.amc.2015.06.019
Web of Science® Google Scholar
4 Saheli M., Saati H., and Ashrafi A. R., The eccentric connectivity index of one pentagonal carbon nanocones, Optoelectron. Adv. Mater. Rapid Commun.(2010) 4, no. 6, 896–897.
CAS Web of Science® Google Scholar
5 Javed S., Alanazi Y. F., and Alanazi A. M., Computing correlation among the graphs under Lexicographic product via Zagreb indices, Molecular Topology of Graphs. (2021) 2021, 17, 7465171, https://doi.org/10.1155/2021/7465171.
10.1155/2021/7465171
Google Scholar
6 Rajan M. A., Lokesha V., and Ranjini P. S., A study on series edge graph transformation, Proceedings of the 23rd Joint Congress Iran-South Korea Jangjeon Math. Soc, 2010, Iran.
Google Scholar
7 Saidi N. H. A. M., Husin M. N., and Ismail N. B., Zagreb indices and Zagreb coindices of the line graphs of the subdivision graphs, Journal of Discrete Mathematical Sciences and Cryptography. (2020) 23, no. 6, 1253–1267, https://doi.org/10.1080/09720529.2020.1816695.
10.1080/09720529.2020.1816695
Web of Science® Google Scholar
8 Estrada E., Torres L., Rodriguez L., and Gutman I., An atom-bond connectivity index: modelling the enthalpy of formation of Alkanes, Indian Journal of Chemistry. (1998) 37A, 849–855.
CAS Google Scholar
9 Das K. C., Mohammed M. A., Gutman I., and Atan K. A., Comparison between atom-bond connectivity indices of graphs, MATCH Commun, Math. Comput. Chem.(2016) 76, no. 1, 159–170.
Web of Science® Google Scholar
10 Lin W., Chen J., Ma C., Zhang Y., Chen J., Zhang D., and Jia F., On trees with minimal ABC index among trees with given number of leaves, MATCH Commun, Math. Comput. Chem.(2016) 76, no. 1, 131–140.
Web of Science® Google Scholar
11 Gao Y. and Shao Y., The smallest ABC index of trees with n pendent vertices, MATCH Commun, Math. Comput. Chem.(2016) 76, no. 1, 141–158.
Web of Science® Google Scholar
12 Bianchi M., Cornaro A., Palacios J. L., and Torriero A., New upper bounds for the ABC index, MATCH Commun, Math. Comput. Chem.(2016) 76, no. 1, 117–130.
Web of Science® Google Scholar
13 Farahani M. R., The edge version of atom bond connectivity index of connected graph, Acta Universitatis Apulensis. (2012) 36, 277–284.
Google Scholar
14 Gao W., Farahani M. R., Wang S., and Husin M. N., On the edge-version atom-bond connectivity and geometric arithmetic indices of certain graph operations, Applied Mathematics and Computation. (2017) 308, 11–17, https://doi.org/10.1016/j.amc.2017.02.046, 2-s2.0-85016493822.
10.1016/j.amc.2017.02.046
Web of Science® Google Scholar
15 Husin M. N. and Ariffin A., On the edge version of topological indices for certain networks, Italian Journal of Pure and Applied Mathematics. (2022) 47, 550–564.
Google Scholar
16 Gao W., Husin M. N., Farahani M. R., and Imran M., On the edges version of atom-bond connectivity index of nanotubes, Journal of Computational and Theoretical Nanoscience. (2016) 13, no. 10, 6733–6740, https://doi.org/10.1166/jctn.2016.5621, 2-s2.0-85013650716.
10.1166/jctn.2016.5621
CAS Google Scholar
17 Gao W., Husin M. N., Farahani M. R., and Imran M., On the edges version of atom-bond connectivity and geometric arithmetic indices of nanocones CNC_k[n], Journal of Computational and Theoretical Nanoscience. (2016) 13, no. 10, 6741–6746, https://doi.org/10.1166/jctn.2016.5622, 2-s2.0-85013625776.
10.1166/jctn.2016.5622
CAS Google Scholar
18 Zhang X., Wu X., Akhter S., Jamil M. K., Liu J. B., and Farahani M. R., Edge-version atom-bond connectivity and geometric arithmetic indices of generalized bridge molecular graphs, Symmetry. (2018) 10, no. 12, https://doi.org/10.3390/sym10120751, 2-s2.0-85059034867.
10.3390/sym10120751
PubMed Web of Science® Google Scholar
19 Kulli V. R., Multiplicative connectivity indices of certain nanotubes, Annals of Pure and Applied Mathematics. (2016) 12, no. 2, 169–176, https://doi.org/10.22457/apam.v12n2a8.
10.22457/apam.v12n2a8
Google Scholar
20 Mahboob A., Mahboob S., Jaradat M. M. M., Nigar N., and Siddique I., On some properties of multiplicative topological indices in silicon-carbon, Journal of Mathematics. (2021) 2021, 10, 4611199, https://doi.org/10.1155/2021/4611199.
10.1155/2021/4611199
Web of Science® Google Scholar
21 Kulli V. R., Multiplicative connectivity indices of T U C4C8[m, n] and T U C4[m, n] nanotubes, Journal of Computer and Mathematical Sciences. (2016) 7, no. 11, 599–605.
Google Scholar
22 Kulli V. R., Edge version of multiplicative atom-bond connectivity index of certain nanotubes and nanotorus, International Journal of Mathematics and Applications. (2018) 6, no. 1-E, 977–982.
Google Scholar
23 Fajtlowicz S., On conjectures of graffiti, Discrete Mathematics. (1988) 72, no. 1-3, 113–118, https://doi.org/10.1016/0012-365x(88)90199-9, 2-s2.0-0000251427.
10.1016/0012-365X(88)90199-9
Web of Science® Google Scholar
24 Kahasy A. T., Narayankar K., and Selvan D., Atom bond connectivity temperature index, J. Maths Nanoscienese. (2018) 8, no. 2, 67–75.
CAS Google Scholar
25 Ranjini P. S., Lokesha V., and Cangül I., On the Zagreb indices of the line graphs of the subdivision graphs, Applied Mathematics and Computation. (2011) 218, no. 3, 699–702, https://doi.org/10.1016/j.amc.2011.03.125, 2-s2.0-80051522378.
10.1016/j.amc.2011.03.125
Web of Science® Google Scholar
26 Ranjini P. S., Lokesha V., and Rajan M. A., On the Scultz index of the subdivision graph, Adv. Stud. Contemp. Math.(2011) 21, no. 2, 279–290.
Google Scholar
27 Su G. and Xu L., Topological indices of the line graph of subdivision graphs and their Schur-bounds, Applied Mathematics and Computation. (2015) 253, 395–401, https://doi.org/10.1016/j.amc.2014.10.053, 2-s2.0-84922513899.
10.1016/j.amc.2014.10.053
Web of Science® Google Scholar
28 Nadeem M. F., Zafar S., and Zahid Z., On certain topological indices of the line graph of subdivision graphs, Applied Mathematics and Computation. (2015) 271, 790–794, https://doi.org/10.1016/j.amc.2015.09.061, 2-s2.0-84944197059.
10.1016/j.amc.2015.09.061
Web of Science® Google Scholar
29 Rajasekar G. and Nagarajan K., Location domination number of line graph, Journal of Discrete Mathematical Sciences and Cryptography. (2019) 22, no. 5, 777–786, https://doi.org/10.1080/09720529.2019.1681694.
10.1080/09720529.2019.1681694
Web of Science® Google Scholar
30 Li R. and Taylor M. M., The first zagreb index and some Hamiltonian properties of the line graph of a graph, Journal of Discrete Mathematical Sciences and Cryptography. (2017) 20, no. 2, 445–451, https://doi.org/10.1080/09720529.2015.1103009, 2-s2.0-85020534033.
10.1080/09720529.2015.1103009
Google Scholar
31 Nadeem M. F., Zafar S., and Zahid Z., On topological properties of the line graphs of subdivision graphs of certain nanostructures, Applied Mathematics and Computation. (2016) 273, 125–130, https://doi.org/10.1016/j.amc.2015.10.010, 2-s2.0-84945151432.
10.1016/j.amc.2015.10.010
Web of Science® Google Scholar

Citing Literature

All articles

Investigation of Atom-Bond Connectivity Indices of Line Graphs Using Subdivision Approach

Abstract

1. Introduction

2. Main Results

3. Numerical Simulation and Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Investigation of Atom-Bond Connectivity Indices of Line Graphs Using Subdivision Approach

Abstract

1. Introduction

2. Main Results

3. Numerical Simulation and Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information