Aiming at the shortcomings of traditional genetic algorithms such as premature and insufficient local search ability, a hybrid genetic algorithm combining k-means algorithm and cluster analysis to improve genetic algorithm is proposed. Among them, the selection operation adopts the tournament selection strategy of the elite retention model, the crossover operation adopts the double cut-point crossover, and the variation operator introduces the k-exchange variation operation to ensure the evolution of individuals from generation to generation. Through the selection, crossover, and variation operations, the objective function is minimized, the vehicle travel distance is greatly reduced, and the distribution route is optimized.

1. Introduction

Vehicle path optimization is the central aspect of logistics distribution, which is essential [1]. The traveling salesman problem (TSP) problem is a classical problem of finding the optimal solution from the set of feasible solutions to a combinatorial problem and is an easy to describe but difficult to handle NP problem [2, 3]. With the increase of the number of towns n, the number of paths may grow exponentially, and it is difficult to find the optimal solution to satisfy the condition using the existing conditions [4, 5].

The socialized division of labor is increasingly refined, making supply and production, production and consumption in time and space contradictions, promote logistics in social production and life play a more and more important role, logistics operation level is related to the level of a country’s economic development, governments are vigorously developing their own logistics. In modern logistics, transportation and distribution are an important link directly connected with consumers, which reflects the core competitiveness of enterprises. How to optimize transportation routes has always been a hot issue for scholars, consulting institutions, and enterprises. By optimizing the transportation path, we can improve the operation efficiency of the enterprise, reduce the transportation cost, and realize the scientific logistics. Based on the relevant logistics theory, this paper takes Hainan Xinwei Logistics Company as an example to analyze the problems encountered by enterprises in the transportation path and puts forward the optimal solutions.

At present, the optimization method is mainly used to solve the path problem for logistics distribution center links, and the construction method is the first one proposed to solve the logistics distribution path problem, which is efficient, but the deviation of the solution from the optimal solution is too far [6, 7]. Xie et al., Katoch et al., Vidal et al., Pizzuti, and Arabali et al. proposed to add the points that are not on the current path at minimum cost to form a relatively good initial path and then finally use an improved algorithm to process the initial path to improve the quality of the solution as much as possible [8–12].

2. Mathematical Model of Logistics Distribution Path Optimization

2.1. Problem Description

The scheduling problem of logistics distribution vehicles is described as follows: there is one and only one vehicle to make one delivery and return to the distribution center after completing the delivery task [13–16]. Therefore, the key to the logistics distribution path problem is optimizing the distribution route and allocating the driving route of vehicles so that the total transportation distance is the shortest [17].

2.2. Modeling

Hybrid genetic algorithm is to mix genetic algorithm with other algorithms to take advantage of each other and complement each other’s shortcomings. For example, the combination of genetic algorithm and simulated annealing algorithm is to combine the global search ability of genetic algorithm with the local search ability of simulated annealing algorithm to form a powerful algorithm.

From the above problem description and assumptions, a mathematical model of logistics distribution route optimization is established. The model takes the minimum transportation distance as the objective function and determines the optimal vehicle distribution route to solve the mathematical model, whose objective function and constraints are shown below:

Objective function:

(1)

(2)

(3)

(4)

(5)

(6)

Constraints:

The D indicates the objective function to calculate the shortest travelable path; k indicates that the number of reserved vehicles is calculated; and indicate that each customer is visited once and only once; L indicates that the distance of a vehicle in the distribution process cannot exceed its specified distance L; x_ij is the decision variable of the model.

3. Hybrid Genetic Algorithm for Optimizing Logistics Distribution Path

Since the traditional genetic algorithm has the shortcomings of insufficient local search ability and premature maturity, the K-means algorithm is firstly used to cluster the location coordinates of customers to obtain the local distribution center and the customer points within its distribution range, and then the logistics path is optimized by using the selection, crossover, and variation operations of the improved genetic algorithm.

3.1. K-Means Algorithm

The K-means algorithm definition criterion is as follows:

(7)

where E is the sum of squares of errors of all objects; X is the average of C_i for a given object.

The criterion function attempts to make the generated result clusters as compact and independent as possible.

The calculation steps are as follows:

(1)
Select k objects arbitrarily and then take each data object as the cluster center
(2)
Divide the remaining data objects into the cluster center closest to each data object itself, according to the following equation:
(8)
where C_a, C_b are two clusters which contain m and h elements, respectively. Let element x ∈ C_a, y ∈ C_b, the distance between these two elements is denoted by the intercluster distance and is noted as D(C_a, C_b).
(3)
Recalculate the mean value of the data objects in each cluster center to get a new cluster center, and the mean value is calculated by the formula:
(9)
where C_i is a cluster and x is a data object within C_i, i.e., x ∈ C; n_k is the data object in the kth cluster.

Repeat steps (2) to (3) until the end when the data objects in each cluster no longer change or the objective function converges.

3.2. Improved Genetic Algorithm

The sequential number encoding is used here. Suppose a sequence (1, 2, 3, 4, 7, 6, 5, 9, 8) is randomly generated and let the generated breakpoint matrix be (2, 5, 7), then first add “0” to the 2nd, 5th, and 7th position of the sequence, the sequence becomes (1, 2, 0, 3, 4, 7, 0, 6, 5, 0, 9, 8), and then add “0” to the first and last position of the new sequence, the chromosome becomes (0, 1, 2, 0, 3, 4, 0, 6, 5, 0, 9, 8). Then add “0” at the end of the new sequence, the chromosome will be (0, 1, 2, 0, 3, 4, 7, 0, 6, 5, 0, 9, 8, 0). Where 0 denotes the distribution center and the serial number denotes the customer number, this sequence indicates that the distribution scheme consists of 4 routes. The route of vehicle 1 is (0, 1, 2, 0), which returns to the distribution center after passing the customer, and is subpath 1; similarly, the route of vehicle 2 is (0, 3, 4, 7, 0) and is subpath 2; the route of vehicle 3 is (0, 6, 5, 0) and is subpath 3; the route of vehicle 4 is (0, 9, 8, 0) and is subpath 4, as shown in Figure 1. Figure 1 gives a visual representation of the sub-paths and the order of clients. This chromosome structure can express the solution space of the vehicle path problem very clearly.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Chromosome structure.

The population size M, i.e., the initial population, is reached all the way through the process of coded repetition chromosome generation.

The excellent chromosome is selected by the fitness function, so the fitness function is designed as

(10)

where fitness(x_i) is the fitness of the ith individual; x₀ is the transport distance of the optimal chromosome in the initial population; x_i is the transport distance corresponding to the current chromosome. Then, the fitness function is used to calculate the fitness value, and it is sorted from smallest to largest, and finally, it enters the selection operation.

The new population resulting from the selection operation, in addition to the first chromosome, the other N-1 chromosomes have to be cross-paired according to the crossover probability p_c (p_c taking values between 0 and 1). In traditional genetic algorithms, single-point crossover is used, which makes many chromosomes exchange between the two parents and sometimes destroys the good chromosomes in the population during the exchange process; compared with single-point crossover, few chromosomes are exchanged between the two parents, which helps to retain the good chromosomes. For example, the following two individuals were crossed using the double cut point method, with the cut point at position 2 and position 5, respectively (Table 1).

Table 1. Result of double cut point.

		↓Cut point 1	↓Cut point 2
Chromosomes 1 : 1	0	7 6 9	8 3 2
Chromosomes 2 : 0	1	9 8 7	4 2 3
Then, after the multipoint crossover, the two chromosome individuals become:
Chromosomes 1 : 1	0	9 6 7	8 3 2
Chromosomes 2 : 0	1	7 8 9	4 2 3
That is, only the part between the two cut points is exchanged.

4. Optimization Scheme of Logistics Distribution Path

4.1. Basic Process of Hybrid Genetic Algorithm

Figure 2 shows the flow of the combination of clustering technique and genetic algorithm, because it is important to consider the path optimization problem characteristics comprehensively and also to ensure the feasibility of the compiled code of the solution and chromosome, so how to realize the encoding is its important factor in the process of distribution path optimization. And because the commonly used binary compiled code method has long strings and cannot provide a comprehensive description of the problem properties, this paper uses the natural number encoding method to implement [18–20].

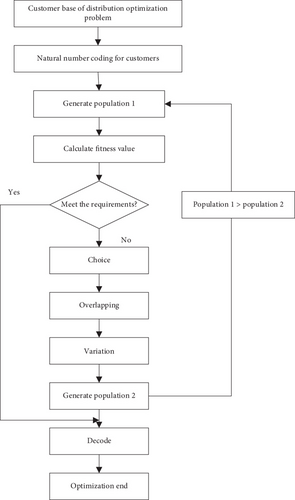
In addition, whether the population size selection is reasonable is the concept of reasonable use of genetic algorithm, if the size of the population is large, then the search time will be longer, if the size of the population is small, then it will fall into the local optimal solution. So, first of all, we have to realize the sorting of distribution vehicles and customers and the statistics of customer demand.

4.2. Optimization of Logistics Distribution Path

First, the coding in the logistics distribution path is determined. In order to achieve a simple description of the most problematic logistics distribution path, this paper uses a direct ordering coding method. For example, if N customers are represented using natural numbers from 1 to n without repetition, then, these arrangements belong to individuals, and individuals are incorporated in the vehicle distribution path according to the constraints of the mathematical model of logistics distribution path optimization [21–24].

Second, the determination of the initial group of logistics distribution path is realized. The arrangement of nonrepeating natural numbers from 1 to n can be generated according to a random way. Assuming that the size of such a logistics distribution path population is denoted k, then k individuals are generated, which is the initial population of the logistics distribution path.

After that, the method of logistics distribution path adaptation evaluation is determined. Using F belonging to the logistics distribution path adaptation, Z denoting the objective function value, and M belonging to the number of distribution paths and the vehicle difference of distribution, then, it is possible to calculate by the following formula.

(11)

The selection of the best individual for the distribution path of the logistics system is realized. The K individuals of the group can be ranked according to their fitness, and the first individual is extracted according to the method from the largest to the smallest, so that it can be the best individual, it is copied to the next one, the sum of the fitness of the individuals of the previous generation group is calculated, and the ratio of the fitness of each individual to the total fitness is used as the probability of being selected, so that the best individual of the logistics distribution path can be effectively determined [23–27].

5. Simulation of the Algorithm

5.1. Arrangement of the Algorithm Simulation

In order to be able to improve the results, it is necessary to realize the settings of different values of the parameters in it. Table 1 shows the levels and factors of the economical genetic algorithm.

According to the situation in Table 2, ten simulation experiments are implemented to realize the simulation of the average shortest path, and Table 3 shows the average shortest path results of ten simulation experiments.

Table 2. Levels and factors of the economical genetic algorithm.

Level	Population size	Crossover probability	Compilation probability
1	50	0.5	0.02
2	100	0.6	0.04
3	200	0.8	0.1

Table 3. Shows the average shortest path results of ten simulations.

Experimental number	Factors			Experimental results
1	50	0.02	0.02	2650.02
2	100	0.04	0.06	2499.35
3	200	0.1	0.1	2448.11
4	50	0.02	0.1	2485.77
5	100	0.04	0.02	2559.22
6	200	0.1	0.06	2552.22
7	50	0.02	0.06	2492.09
8	100	0.04	0.1	2507.33
9	200	0.1	0.02	2533.49

5.2. Effect of the Two Algorithms on the Experimental Results

In order to be able to conduct a comprehensive analysis of the performance of the algorithm designed in this paper and the traditional algorithm, it is necessary to use the visual image method to analyze the advantages of the algorithm in the process of setting different parameters, and the optimization process of the path is detailed in Figures 3–6.

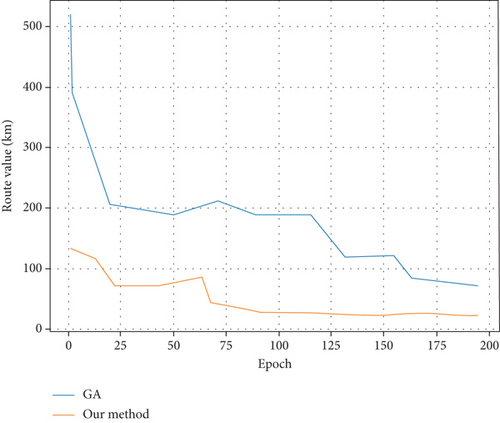
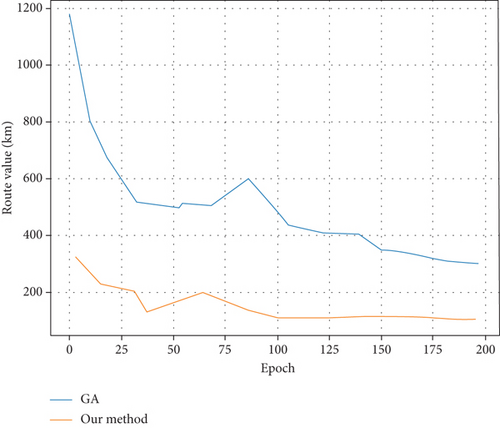
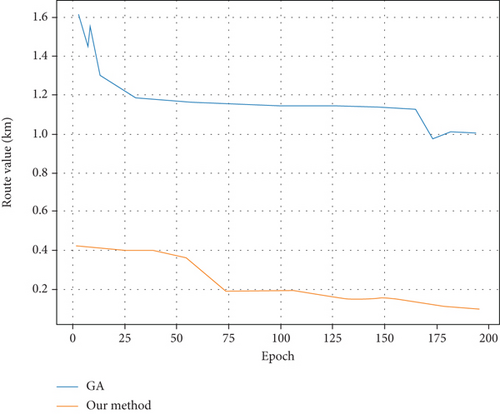
5.3. Effect of the Two Algorithms

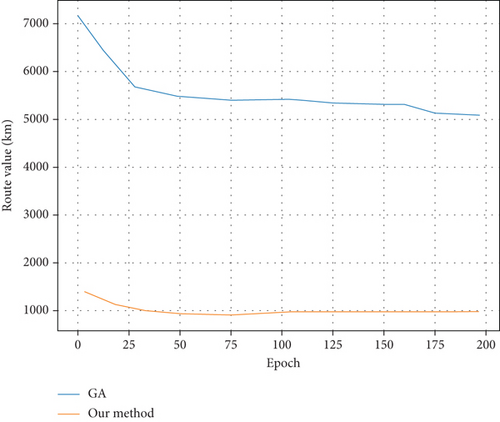
In order to be able to study the effectiveness of the algorithm when the number of customers is large, a hundred customers are randomly selected in the interval range when the vertical and horizontal coordinates are (-8, 8), and the maximum distance of the vehicle is set to achieve the optimal vehicle driving route, Figure 7 is the graph of no distance limitation for the number of customers of 100, and Figure 8 is the graph with distance limitation for the number of customers of 100.

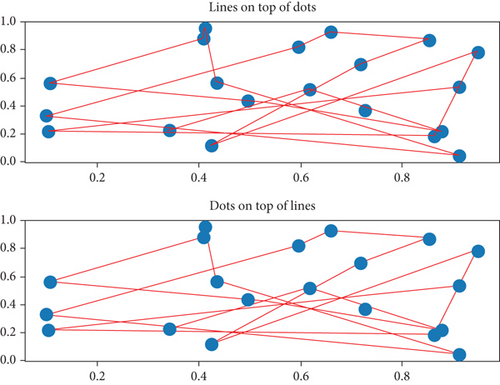
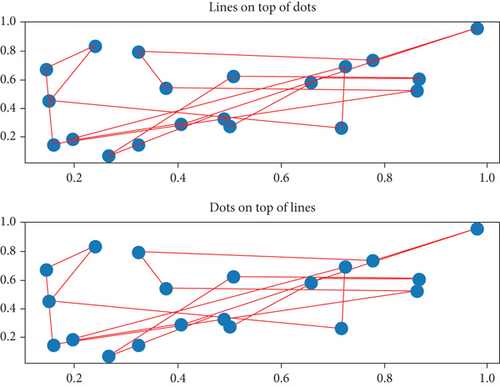
By comparison, the genetic algorithm designed in this paper is more time-saving and convenient, and it has global optimality than the traditional algorithm, which has important practical significance.

6. Conclusion

In this paper, a hybrid algorithm combining clustering technique and genetic hybrid algorithm with each other is used to achieve the optimization of modern logistics distribution paths. Through the research of this paper, it is indicated that the hybrid genetic algorithm’s can realize the optimization of logistics distribution paths, and it can not only realize the global optimal solution but also shorten the search time and improve the efficiency of the algorithm.

Conflicts of Interest

The author declared no conflicts of interest regarding this work.

Open Research

Data Availability

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

References

1 Zhang Y., Li P., and Wang X., Intrusion detection for IoT based on improved genetic algorithm and deep belief network, IEEE Access. (2019) 7, 31711–31722, https://doi.org/10.1109/ACCESS.2019.2903723, 2-s2.0-85064680305.
10.1109/ACCESS.2019.2903723
Web of Science® Google Scholar
2 Zeebaree D. Q., Haron H., Abdulazeez A. M., and Zeebaree S. R., Combination of K-means clustering with genetic algorithm: a review, International Journal of Applied Engineering Research. (2017) 12, no. 24, 14238–14245.
Google Scholar
3 Xie X., Zhang W., Wang H., Li L., Feng Z., Wang Z., Wang Z., and Pan X., Dynamic adaptive residual network for liver CT image segmentation, Computers & Electrical Engineering. (2021) 91, https://doi.org/10.1016/j.compeleceng.2021.107024.
10.1016/j.compeleceng.2021.107024
Web of Science® Google Scholar
4 Keshanchi B., Souri A., and Navimipour N. J., An improved genetic algorithm for task scheduling in the cloud environments using the priority queues: formal verification, simulation, and statistical testing, Journal of Systems and Software. (2017) 124, 1–21, https://doi.org/10.1016/j.jss.2016.07.006, 2-s2.0-84994005147.
10.1016/j.jss.2016.07.006
Web of Science® Google Scholar
5 Hong S. S., Lee W., and Han M. M., The feature selection method based on genetic algorithm for efficient of text clustering and text classification, International Journal of Advances in Soft Computing and its Applications. (2015) 7, no. 1, 2074–8523.
Google Scholar
6 Bahadure N. B., Ray A. K., and Thethi H. P., Comparative approach of MRI-based brain tumor segmentation and classification using genetic algorithm, Journal of Digital Imaging. (2018) 31, no. 4, 477–489, https://doi.org/10.1007/s10278-018-0050-6, 2-s2.0-85040691884, 29344753.
10.1007/s10278-018-0050-6
PubMed Web of Science® Google Scholar
7 Kong L., Pan J. S., Snášel V., Tsai P. W., and Sung T. W., An energy-aware routing protocol for wireless sensor network based on genetic algorithm, Telecommunication Systems. (2018) 67, no. 3, 451–463, https://doi.org/10.1007/s11235-017-0348-6, 2-s2.0-85021107226.
10.1007/s11235-017-0348-6
Web of Science® Google Scholar
8 Xie X., Pan X., Zhang W., and An J., A context hierarchical integrated network for medical image segmentation, Computers and Electrical Engineering. (2022) 101, https://doi.org/10.1016/j.compeleceng.2022.108029.
10.1016/j.compeleceng.2022.108029
Web of Science® Google Scholar
9 Katoch S., Chauhan S. S., and Kumar V., A review on genetic algorithm: past, present, and future, Multimedia Tools and Applications. (2021) 80, no. 5, 8091–8126, https://doi.org/10.1007/s11042-020-10139-6, 33162782.
10.1007/s11042-020-10139-6
PubMed Web of Science® Google Scholar
10 Vidal T., Crainic T. G., Gendreau M., Lahrichi N., and Rei W., A hybrid genetic algorithm for multidepot and periodic vehicle routing problems, Operations Research. (2012) 60, no. 3, 611–624, https://doi.org/10.1287/opre.1120.1048, 2-s2.0-84864700477.
10.1287/opre.1120.1048
Web of Science® Google Scholar
11 Pizzuti C., A multiobjective genetic algorithm to find communities in complex networks, IEEE Transactions on Evolutionary Computation. (2012) 16, no. 3, 418–430, https://doi.org/10.1109/TEVC.2011.2161090, 2-s2.0-84861830467.
10.1109/TEVC.2011.2161090
Web of Science® Google Scholar
12 Arabali A., Ghofrani M., Etezadi-Amoli M., Fadali M. S., and Baghzouz Y., Genetic-algorithm-based optimization approach for energy management, IEEE Transactions on Power Delivery. (2013) 28, no. 1, 162–170, https://doi.org/10.1109/TPWRD.2012.2219598, 2-s2.0-84871735817.
10.1109/TPWRD.2012.2219598
Web of Science® Google Scholar
13 Abualigah L. M., Khader A. T., and Hanandeh E. S., Hybrid clustering analysis using improved krill herd algorithm, Applied Intelligence. (2018) 48, no. 11, 4047–4071, https://doi.org/10.1007/s10489-018-1190-6, 2-s2.0-85047255672.
10.1007/s10489-018-1190-6
Web of Science® Google Scholar
14 Caunhye A. M., Nie X., and Pokharel S., Optimization models in emergency logistics: a literature review, Socio-Economic Planning Sciences. (2012) 46, no. 1, 4–13, https://doi.org/10.1016/j.seps.2011.04.004, 2-s2.0-84155169077.
10.1016/j.seps.2011.04.004
Google Scholar
15 Xu W. and Rong M., Research on optimization of expressway logistics path based on the advantages of multimodal transport in the environment of internet of things, Wireless Personal Communications. (2021) 1–17, https://doi.org/10.1007/s11277-021-08755-y.
10.1007/s11277-021-08755-y
PubMed Web of Science® Google Scholar
16 Subramani N., Mohan P., Alotaibi Y., Alghamdi S., and Khalaf O. I., An efficient metaheuristic-based clustering with routing protocol for underwater wireless sensor networks, Sensors. (2022) 22, no. 2, https://doi.org/10.3390/s22020415, 35062376.
10.3390/s22020415
PubMed Web of Science® Google Scholar
17 Gill H. S., Khalaf O. I., Alotaibi Y., Alghamdi S., and Alassery F., Multi-model CNN-RNN-LSTM based fruit recognition and classification, Intelligent Automation & Soft Computing. (2022) 33, no. 1, 637–650, https://doi.org/10.32604/iasc.2022.022589.
10.32604/iasc.2022.022589
Web of Science® Google Scholar
18 Xie X., Pan X., Shao F., Zhang W., and An J., Mci-net: multi-scale context integrated network for liver ct image segmentation, Computers and Electrical Engineering. (2022) 101, https://doi.org/10.1016/j.compeleceng.2022.108085.
10.1016/j.compeleceng.2022.108085
Web of Science® Google Scholar
19 Lei S., Chen C., Li Y., and Hou Y., Resilient disaster recovery logistics of distribution systems: co-optimize service restoration with repair crew and mobile power source dispatch, IEEE Transactions on Smart Grid. (2019) 10, no. 6, 6187–6202, https://doi.org/10.1109/TSG.2019.2899353.
10.1109/TSG.2019.2899353
Web of Science® Google Scholar
20 Zheng-wan Z., Di W., and Chun-jiong Z., Study of cellular traffic prediction based on multi-channel sparse LSTM, Computer Science. (2021) 48, no. 6, 296–300, https://doi.org/10.11896/jsjkx.210400134.
10.11896/jsjkx.210400134
Google Scholar
21 Lin X., Wu J., Mumtaz S., Garg S., Li J., and Guizani M., Blockchain-based on-demand computing resource trading in IoV-assisted smart city, IEEE Transactions on Emerging Topics in Computing. (2021) 9, no. 3, 1373–1385, https://doi.org/10.1109/TETC.2020.2971831.
10.1109/TETC.2020.2971831
Web of Science® Google Scholar
22 Li J., Zhou Z., Wu J., Li J., Mumtaz S., Lin X., Gacanin H., and Alotaibi S., Decentralized on-demand energy supply for blockchain in internet of things: a microgrids approach, IEEE Transactions on Computational Social Systems. (2019) 6, no. 6, 1395–1406, https://doi.org/10.1109/TCSS.2019.2917335, 2-s2.0-85068142731.
10.1109/TCSS.2019.2917335
Web of Science® Google Scholar
23 Duan W., Gu J., Wen M., Zhang G., Ji Y., and Mumtaz S., Emerging technologies for 5G-IoV networks: applications, trends and opportunities, IEEE Network. (2020) 34, no. 5, 283–289, https://doi.org/10.1109/mnet.001.1900659.
10.1109/MNET.001.1900659
Web of Science® Google Scholar
24 Liu S., Zhang Y., Liu Y., Wang L., and Wang X. V., An 'internet of things' enabled dynamic optimization method for smart vehicles and logistics tasks, Journal of Cleaner Production. (2019) 215, 806–820, https://doi.org/10.1016/j.jclepro.2018.12.254, 2-s2.0-85060923837.
10.1016/j.jclepro.2018.12.254
Web of Science® Google Scholar
25 Hua X., Hu X., and Yuan W., Research optimization on logistics distribution center location based on adaptive particle swarm algorithm, Optik. (2016) 127, no. 20, 8443–8450, https://doi.org/10.1016/j.ijleo.2016.06.032, 2-s2.0-84979763301.
10.1016/j.ijleo.2016.06.032
Web of Science® Google Scholar
26 Bozorgi-Amiri A., Jabalameli M. S., Alinaghian M., and Heydari M., A modified particle swarm optimization for disaster relief logistics under uncertain environment, The International Journal of Advanced Manufacturing Technology. (2012) 60, no. 1-4, 357–371, https://doi.org/10.1007/s00170-011-3596-8, 2-s2.0-84859523532.
10.1007/s00170-011-3596-8
Web of Science® Google Scholar
27 Liberatore F., Ortuño M. T., Tirado G., Vitoriano B., and Scaparra M. P., A hierarchical compromise model for the joint optimization of recovery operations and distribution of emergency goods in humanitarian logistics, Computers & Operations Research. (2014) 42, 3–13, https://doi.org/10.1016/j.cor.2012.03.019, 2-s2.0-84886729980.
10.1016/j.cor.2012.03.019
Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] Multiparty Coordinated Logistics Distribution Route Optimization Based on Data Analysis and Intelligent Algorithm

Retraction(s) for this article

Retracted: Multiparty Coordinated Logistics Distribution Route Optimization Based on Data Analysis and Intelligent Algorithm

Abstract

1. Introduction