Volume 2022, Issue 1 5968496

Research Article

Open Access

Structural and Vibrational Investigation of Benzil-(1,2-Diphenylethane-1,2-Dione): Experimental and Theoretical Studies

N. Kanagathara

orcid.org/0000-0002-3368-3771

Department of Physics, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Thandalam, Chennai 602105, India saveetha.com

Search for more papers by this author

K. Senthilkumar,

K. Senthilkumar

orcid.org/0000-0001-6627-7254

Department of Physics, Rajalakshmi Engineering, Thandalam, Chennai 602105, India

Search for more papers by this author

V. Sabari,

V. Sabari

orcid.org/0000-0001-8549-9530

Department of Physics, Marudhar Kesari Jain College for Women, Vaniyambadi, Tamil Nadu 635751, India

Search for more papers by this author

V. Ragavendran,

V. Ragavendran

orcid.org/0000-0001-6620-4901

Department of Physics, Sri Chandrasekharendra Saraswathi Viswa Mahavidyalaya, Enathur, Kanchipuram 631561, India

Search for more papers by this author

S. Elangovan,

Corresponding Author

S. Elangovan

[email protected]

orcid.org/0000-0002-3045-7701

Department of Physics, College of Natural and Computational Science, Wollega University, Nekemte, Ethiopia 395, wollegauniversity.edu.et

Search for more papers by this author

N. Kanagathara,

N. Kanagathara

orcid.org/0000-0002-3368-3771

Department of Physics, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Thandalam, Chennai 602105, India saveetha.com

Search for more papers by this author

K. Senthilkumar,

K. Senthilkumar

orcid.org/0000-0001-6627-7254

Department of Physics, Rajalakshmi Engineering, Thandalam, Chennai 602105, India

Search for more papers by this author

V. Sabari,

V. Sabari

orcid.org/0000-0001-8549-9530

Department of Physics, Marudhar Kesari Jain College for Women, Vaniyambadi, Tamil Nadu 635751, India

Search for more papers by this author

V. Ragavendran,

V. Ragavendran

orcid.org/0000-0001-6620-4901

Department of Physics, Sri Chandrasekharendra Saraswathi Viswa Mahavidyalaya, Enathur, Kanchipuram 631561, India

Search for more papers by this author

S. Elangovan,

Corresponding Author

S. Elangovan

[email protected]

orcid.org/0000-0002-3045-7701

Department of Physics, College of Natural and Computational Science, Wollega University, Nekemte, Ethiopia 395, wollegauniversity.edu.et

Search for more papers by this author

First published: 15 April 2022

https://doi.org/10.1155/2022/5968496

Citations: 4

Academic Editor: Ajaya Kumar Singh

Share a link

Email
Wechat
Bluesky

Abstract

Single crystals of benzil commonly known as 1,2-diphenylethane-1,2-dione are grown by the slow evaporation method at room temperature. Gaussian 09 program is applied for theoretical calculations with B3LYP/6-311++G(d,p) basis set. The structure is optimized, and the energy, structural parameters, vibrational frequencies, IR, and Raman intensities are determined. Complete natural bonding orbital (NBO) analysis is carried out to analyze the intramolecular electronic interactions and their stabilization energies. From the second-order perturbation theory analysis of the benzil molecule, it is observed that there exists a hyperconjugative intramolecular stabilization energy between 17.45 and 22.76 KJmol^-1. HOMO-LUMO analysis has been performed to identify the charges transferred within the molecule. The energy gap is calculated to be 2.919 eV and thus establishes the soft nature of the molecule. The molecular electrostatic potential (MEP) of the grown crystal was analyzed using the B3LYP method with 6-311++G(d,p) basis set. First-order hyperpolarizability calculations reveal the nonlinear optical microscopic behavior of the benzil molecule with nonzero values. The total value of the first-order hyperpolarizability (β_tot) is of the order of 41.5246 × 10⁻³¹ esu, which is found to be 11.135 times that of urea. Hence, benzil can be referred to as a good material for nonlinear optical applications.

1. Introduction

Benzil-1,2-diphenylethane-1,2-dione(C₆H₅CO)₂) is an organic compound consisting of two phenyl rings, and C-O groups are used as photoinitiators as well as free radicals in polymer chemistry. Benzil has potential applications in biological metabolism and clinical medicine. Benzil derivates exhibit radical scavenging and antibacterial and hypertensive [1], antiprotozoal [2], antiproliferative, and antimitotic [3] activities. Benzil derivatives have versatile applications in the pharmaceutical industry, and various heterocyclic compounds such as triazine, quinoxaline, and imidazole can be synthesized from 1,2-diketones [4–8]. It is also used as a nanocatalyst in the application of imidazole derivatives [9]. Recently, it is reported that benzil derivatives acted as photosensitive agents and photoinitiators due to its antitumor activity [10, 11]. The effective chemoselective synthesis of benzil derivatives was reported by Jadhav et al. [12]. The insect antifeedant activity and growth inhibitory studies on a few benzyl derivatives were reported by Sreelatha et al. [13]. There are few reports available for the benzil-type phosphorescent molecules earlier [14–16]. Wadkins et al. reported the new benzyl (diphenylethane-1,2-dione) analogs as inhibitors of mammalian carboxylesterases [17]. The conductivity property of benzyl derivatives for electronic applications was reported by Stanculescu et al. [18]. Synthesis and antitumor activity of benzil-related natural Z-stilbene was reported by Mousset et al. [19]. Topal et al. reported the computational investigation of benzoin derivatives from benzil compounds [20]. Benzil derivatives are used in a wide range of organic synthesis, especially in the construction of heterocyclic compounds. The structure of benzil was reported earlier [21–23]. Saranraj et al. have grown benzil crystal by unidirectional SR method and reported its structural, optical, electrical as well as dielectric properties [24]. Shankar and Varma have grown this crystal by the Bridgman–Stockbarger method and studied the dielectric dispersion as well as the piezoelectric response of their grown crystal [25]. The benzyl compound and its various derivatives are reported by Chigare et al. [26]. The quantum chemical computational as well as experimental studies of vibrational spectra and structure on benzil and its 18O- and d10-labeled derivatives were reported by Kolev and Stamboliyska [27]. Lopes et al. investigated benzyl for equilibrium conformers using low-temperature matrix-isolation FT-IR spectroscopy with the support of extensive DFT calculations [28]. True computational prediction of material properties before experimentation is needed for finding the new materials for its application. Theoretical computational studies enable us to go well beyond what is known experimentally and can guide future experimentation. In continuation of research on benzil derivatives by the researchers, in this report, we synthesized that benzil (1,2-diphenylethane-1,2-dione), the structure, and vibrational spectrum are reported theoretically by density functional theory. In addition to the above studies, other properties like NBO, NLO, and HOMO-LUMO have also been carried out and explained in this communication.

2. Materials and Methods

The benzil-(1,2-diphenylethane-1,2-dione) compound under investigation was purchased from a Sigma-Aldrich Chemical Company, USA, with a stated purity of 99% and used without further purification. Water is used as the solvent, and the dissolved solution is kept at room temperature for evaporation to get transparent crystals of benzil. The obtained benzil crystals are then subjected to single-crystal XRD. In the present investigation, DFT calculations were performed with a hybrid functional B3LYP at 6-311++G(d,p) basis set using Gaussian 09 program [29]. The structure is optimized with minimum energy. The harmonic frequencies, infrared, and Raman intensities were calculated by the B3LYP method with an identical basis set. All the computed frequencies are scaled by 0.9665. The absence of imaginary values of wavenumbers on the calculated vibrational spectra confirms that the deduced structure corresponds to the minimum energy. The NBO and HOMO-LUMO orbital energies were investigated, and the visual interpretation of the above-mentioned properties was done by using Gauss View 3.1 program [30, 31].

3. Results and Discussion

3.1. Structural Analysis

3.1.1. Data Collection

A good crystal of dimension 0.20 × 0.20 × 0.20 mm was selected for the data collection. Intensity data were measured on Bruker SMART APEX CCD detector diffractometer [32] with graphite monochromatic MoK_α radiation at room temperature. The data collection was covered over a hemisphere of reciprocal space by a combination of three sets of exposures each having a different φ angle for the crystal and exposure of the 30 s covered at 0.3° in ω. The crystal to detector distance was 4 cm, and the detector swing angle was 24°. Coverage of the unique set was 100% complete. Crystal decay was monitored by repeating 30 initial forms at the end of the data collection. The duplicate reflection was found to be negligible. The intensity data were reduced, and Lorentz and polarization corrections were applied.

3.1.2. Structure Solution and Refinement

The structure was solved by direct methods procedures using SHELXS97 [33] program. A total of 4072 reflections (E > 1.2) was available for the phase set with the lowest combined figure of merit (CFOM = 0.0845) revealing that all the 8 nonhydrogen atoms have an initial R-factor of 0.126. The trial structure was first refined isotropically. All H atoms were calculated in the difference Fourier maps. The hydrogen atoms were geometrically fixed and ride on their parent atoms. The final R-value is 0.0443. The structure was refined by full-matrix least-squares on F².

3.1.3. Crystal Structure Analysis

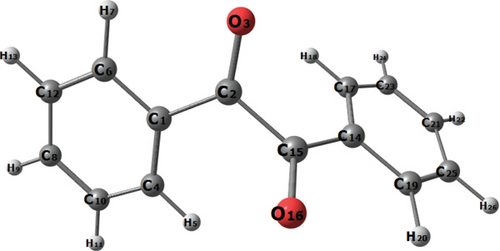
The crystal data and other relevant details are given in Table S1. The atomic coordinates of the nonhydrogen atoms with their equivalent thermal displacement parameters are presented in Table S2. The anisotropic displacement parameters are listed in Table S3. The atomic coordinates and their isotropic displacement parameters involving hydrogen atoms are given in Table S4. The hydrogen bond interactions are presented in Table S5. Figure S1 and Figure S2 show the ORTEP plot and packing diagram of the chosen molecule. Single crystal X-ray diffraction analysis reveals that benzil crystallizes in a trigonal system with noncentrosymmetric space group P3₁21 and the calculated lattice parameters are a = 8.4095(2)Å, b = 8.4095(2)Å, c = 13.6695(4)Å, α = 90^°, β = 90^°, γ = 120^°, and V = 837.19 (Å³). X-ray analysis confirms the molecular structure and atom connectivity for the title compound (Figure 1). The obtained values are listed in Table 1 and are very well matched with the reported structures as well as the literature values [21, 22]. The one-half molecule in the asymmetric unit is located on a twofold rotation axis. The phenyl ring adopts a planer conformation. The crystal packing of the benzil compound is through weak C1-H1···O1 intermolecular interactions and also the crystal packing of the benzil compound C3-H3···O1 hydrogen bonds link molecules to form inversion dimers, with an ring motif. The optimized structure with a global minimum is given in Figure 1. All C-H bond lengths are found to be 0.93Å, and theoretically, this value is found to be 1.084Å. All C-C bond lengths within the phenyl ring are found to be within the range 1.364-1.380Å. However, carbon in the phenyl ring attached to the C-O group has 1.474Å, and the C-C bond that connects the two C-O groups attached to phenyl ring has the highest bond distance of 1.523Å. Theoretically, this value is computed to be 1.543Å. Two C-O bond distances have a bond length of 1.214Å. The small variation between experimental and theoretical values is due to the theoretical calculations are done in the gas phase.

Details are in the caption following the image — Open in figure viewer PowerPoint

1. Geometric parameters of benzil.

Atom	Experimental	B3LYP/6-311++G(d,p)	Atom	Expt	B3LYP/6-311++G(d,p)
Bond distance (Å)			Bond distance (Å)
C(1)-C(2)	1.379	1.388	C(5)-C(4)	1.368 (5)	1.392
C(1)-H(1)	0.930	1.084	C(5)-H(5)	0.93	1.084
C(2)-H(2)	0.930	1.084	C(6)-C(1)	1.380 (4)	1.403
C(3)-C(2)	1.370	1.397	C(6)-C(5)	1.388 (4)	1.402
C(3)-H(3)	0.930	1.084	C(6)-C(7)	1.473 (4)	1.487
C(4)-H(4)	0.930	1.084	C(7)-O(1)	1.213 (3)	1.214
C(3)-C(4)	1.363	1.393	C(7)-C(7) ∗	1.523 (6)	1.543
Bond angle (°)
C(1)-C(6)-C(5)	119.7	119.49	C(2)-C(1)-C(6)	119.7 (3)	120.26
C(1)-C(6)-C(7)	120.9	118.12	C(2)-C(1)-H(1)	120.1	119.94
C(5)-C(6)-C(7)	119.4	122.36	C(6)-C(1)-H(1)	120.1	120.26
O(1)-C(7)-C(6)	123.4	123.46	C(4)-C(5)-C(6)	120.1 (3)	120.08
O(1)-C(7)-C(7) ∗	117.0	117.47	C(4)-C(5)-H(5)	119.9	119.81
C(6)-C(7)-C(7) ∗	119.4	119.29
Torsion angle (°)
C(5)-C(6)-C(7)-O(1)	-3.6 (4)	-4.371	C(7)-C(6)-C(5)-C(4)	178.7 (3)	177.53
C(1)-C(6)-C(7)-C(7)∗	-8.8 (3)	-4.371	C(4)-C(3)-C(2)-C(1)	0.4 (6)	0.0647
C(5)-C(6)-C(7)-C(7)∗	172.4 (2)	177.537	C(6)-C(1)-C(2)-C(3)	-0.6 (6)	-0.1437
C(5)-C(6)-C(1)-C(2)	0.5 (5)	0.115	C(2)-C(3)-C(4)-C(5)	0.0 (6)	0.0422
C(7)-C(6)-C(1)-C(2)	-178.3 (3)	178.262	C(6)-C(5)-C(4)-C(3)	-0.1 (5)	-0.0697
C(1)-C(6)-C(5)-C(4)	-0.2 (4)	-0.008

Symmetry transformations used to generate equivalent atoms: ∗y, x, −z.

(1) Data Collection. SMART [34]; cell refinement: SAINT [34]; and data reduction: SAINT program(s) are used to solve structure: SHELXS97 [33] program(s) are used to refine structure: SHELXL97 [33]; molecular graphics: PLATON [35]; and software are used to prepare material for publication: SHELXL97 and PARST [36].

3.2. Vibrational Analysis

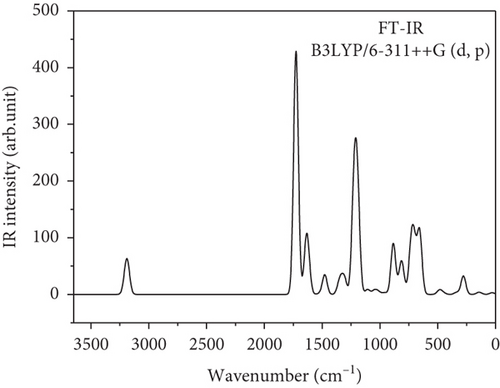
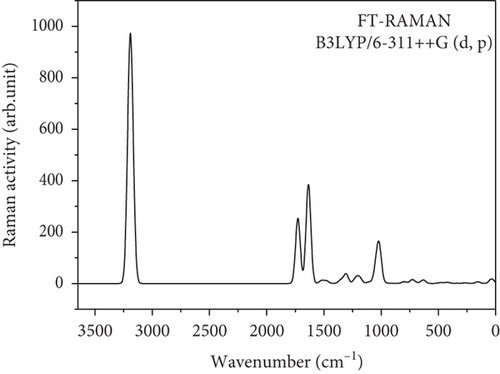
Computational chemistry is used to calculate the structure and properties of the molecule. It seemed to be intuitive to give the theoretical vibrational computation of the benzil molecule to understand the various functional groups present in the system. Normal coordinate vibrational analysis of benzil was reported by Ivanov et al. [37]. Kayadibi et al. reported the theoretical investigation of a few benzyl compounds [38]. There will be 72 modes of vibration (3N-6) which include C-C, C-O, and C-H vibrations in the benzil molecule. There are 25 stretching modes of vibration, 24 bending modes of vibration, and 23 torsion modes of vibration that occur in this benzil molecule. Theoretically obtained FT-IR and FT-Raman vibrational spectrum is given in Figures 2 and 3, respectively. Table 2 list the wavenumbers (cm^-1) and relative intensities of calculated Fourier infrared and Raman spectra of the benzil molecule. C-H stretching modes of vibrational frequencies are usually found in the region 3300–2850 cm^-1 [39–40]. There are 10 such asymmetric and symmetric frequencies computed between 3009 and 3047 cm^-1. The highly intense characteristics vibrations of carboxyl groups occurred in the region 1870-1540 cm^–1. There are two such peaks computed at 1641 and 1640 cm^-1 by the DFT method. The most informative out plane bending vibration of C-H, i.e., H-C-C-C torsion is computed in the region 818–963 cm^-1. Usually, C-C phenyl group ring vibrational modes occurred at 642, 996, 1009, and 1048 cm^-1 is due to the resonance enhancement of the phenyl ring. Those peaks are computed at 662, 995, 1012, and 1052, respectively. C-C stretching and C-C-H vibrational frequencies are computed in the region 1500-800 cm^-1. Usually, C-H, N-H, and O-H vibrations are observed at higher frequencies than C-C and C-O bond vibrations. Bending vibrations of C-C-C are computed in the range 1000–900 cm^-1. At 726 and 624 cm^-1, C-C-O bending mode of vibration is computed. Below 695 cm^-1, torsion modes of C-C-C-C are computed. The possibility of DFT interpretation of the molecule may broaden the application span of vibrational spectroscopy [39–41].

2. Wavenumbers (cm^-1) and relative intensities of calculated Fourier infrared and Raman spectra of benzils.

Unscaled frequency (cm^-1)	Scaled frequency (cm^-1)	IR intensity (arb.unit)	Raman intensity (arb.unit)	Assignment description
3207	3047	2.006	206.277	4C-5H asymmetric stretching
3207	3047	3.768	16.0875	17C-18H asymmetric stretching
3199	3039	0.247	244.675	6C-7H asymmetric stretching
3199	3039	18.27	33.9746	19C-20H asymmetric stretching
3188	3029	4.248	235.243	8C-9H; 10C-11H asymmetric stretching
3188	3029	22.02	61.5706	21C-22H; 23C-24H asymmetric stretching
3179	3020	12.32	90.0344	23C-24H; 25C-26H symmetric stretching
3179	3020	6.23	156.361	23C-24H; 25C-26H symmetric stretching
3167	3009	0.253	78.6184	23C-24H; 25C-26H symmetric stretching
3167	3009	0.343	28.3318	23C-24H; 25C-26H symmetric stretching
1727	1641	132	208.069	3O-2C stretching
1726	1640	297.3	45.2167	16O-15C stretching
1637	1555	68.55	81.8839	6C-12C stretching
1636	1554	21.46	291.67	19C-25C stretching
1617	1536	5.562	12.5458	8C-10C stretching
1617	1536	20.61	5.586	21C-23C stretching
1521	1445	0.817	1.3596	22H-21C-25C bending
1521	1444	0.726	9.7679	22H-21C-25C bending
1479	1405	0.456	10.0279	9H-8C-10C bending
1478	1404	34.11	0.3019	9H-8C-10C bending
1357	1289	8.508	0.2942	7H-6C-12C bending
1357	1289	0.01	10.1592	5H-4C-10C bending
1342	1275	11.54	3.3852	1C-4C; 17C-14C stretching
1337	1270	9.918	0.2745	1C-4C; 17C-14C stretching
1307	1242	26.91	36.8482	2C-1C stretching
1224	1163	175.6	16.7525	14C-15C stretching
1206	1145	1.419	4.8215	2C-1C; 14C-15C stretching
1197	1137	157.2	6.2535	11H-10C-8C bending
1185	1126	0.472	9.4713	26H-25C-21C bending
1184	1125	22.52	5.5839	13H-12C-8C bending
1108	1052	0.216	5.1251	23C-17C stretching
1107	1052	8.46	0.0626	23C-17C stretching
1065	1012	0.744	5.4911	15C-2C stretching; 12C-8C-10C; 25C-21C-23C bending
1048	995	5.853	2.0747	12C-8C stretching
1040	988	0.882	62.6533	12C-8C stretching; 1C-4C-10C bending
1016	966	4.14	6.6288	19C-25C-21C bending
1016	965	0.154	119.219	6C-12C-8C bending
1013	963	0.02	0.1948	13H-12C-8C-10C torsion
1013	963	0.003	0.3665	13H-12C-8C-10C torsion
998.6	949	0.263	0.0184	7H-6C-12C-8C torsion
998.6	949	0.359	0.3017	9H-8C-12C-6C torsion
960	912	1.636	0.0426	5H-4C-10C-8C torsion
955.4	908	1.393	1.5291	11H-10C-8C-12C torsion
884.6	840	89.38	0.3707	9H-8C-12C-6C torsion
860.9	818	0.383	0.2135	5H-4C-10C-8C torsion; 7H-6C-12C-8C torsion;
860.8	818	0.381	0.0109	13H-12C-8C-10C torsion; 24H-23C-25C-21C torsion;
817.2	776	47.64	0.1776	3O-1C-15C-2C torsion
799.2	759	15.58	6.9508	11H-10C-8C-12C torsion
731.8	695	37.37	0.5538	6C-12C-8C-10C torsion
729.9	693	40.62	13.1122	6C-12C-8C-10C torsion
705.1	670	47.32	2.5976	12C-8C-10C; 25C-21C-23C bending
697.6	663	20.14	0.4057	6C-12C-8C-10C torsion
697.3	662	10.99	0.1175	6C-12C-8C-10C torsion
657.1	624	108.4	1.966	3O-2C-15C bending
630.3	599	0.703	6.3203	8C-10C-4C; 23C-17C-14C bending
630.3	599	0.679	6.4854	8C-10C-4C; 23C-17C-14C bending
486.8	463	6.798	2.8116	2C-4C-6C-1C torsion
460	437	3.223	1.4307	25C-21C-23C-17C torsion
433.7	412	0.506	0.5274	25C-21C-23C-17C torsion
421.9	401	1E-04	2.8041	25C-21C-23C-17C torsion
409.2	389	0.016	0.0106	21C-23C-17C-14C torsion
407.3	387	0.001	1.1796	12C-8C-10C-4C torsion
336	319	3.643	0.8309	25C-21C-23C-17C torsion
278.1	264	32.4	0.1769	17C-14C-15C; 2C-1C-6C bending
265.6	252	0.176	2.3752	17C-14C-15C; 2C-1C-6C bending
158.9	151	0.237	3.1713	14C-15C-2C; 15C-2C-1C bending
156	148	0.006	2.9025	2C-4C-6C-1C torsion
147.7	140	2.412	0.2295	2C-4C-6C-1C torsion
129.8	123	1.541	0.4346	14C-15C-2C; 15C-2C-1C bending
40.32	38.3	0.685	6.2676	15C-2C-1C-4C torsion
38	36.1	0.041	5.7474	15C-2C-1C-4C torsion
25.68	24.4	2.34	6.8719	14C-15C-2C-1C torsion

3.3. Natural Bond Orbital Analysis (NBO)

It is an effective method for the analysis of electron density in a molecular orbital. It helps to calculate the hyperconjugative and intermolecular interactions of the compound and gives an idea of the energy transfer between the filled donor state and the empty acceptor state, which is also called as Lewis and non-Lewis type [42–43]. The natural bonding orbital is equal to the number of natural atomic orbitals and also to the number of natural hybrid orbitals. By using the 2nd-order perturbation theory, the following equation is carried out to find the energy of hyperconjugative interactions (E2).

(1)

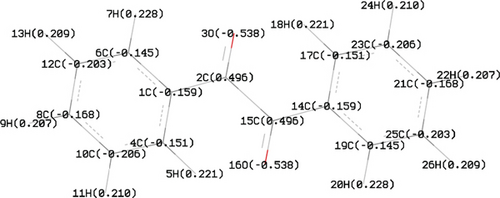
The energy differences between the donor and acceptor are given as E_i and E_j, respectively. Whereas F_ij is the Fock matrix element between i and j orbitals of NBO. Figure 4 shows the natural bonding atomic charges of benzil computed at B3LYP/6-311++G(d,p). The carbon atoms in the phenyl ring have negative charges whereas the carbon atoms attached to oxygen atoms have a positive charge and are found to be a higher value than in the phenyl ring. All the hydrogen atoms have a positive charge of around 0.2e. Several significant interactions are provided in Table 3 which signifies the second-order perturbation theory analysis of the benzil molecule. In this molecule, mainly LP⟶π∗, π⟶π∗ occurs between bonding and antibonding orbitals. NBO analysis shows that hyperconjugative interaction energy has a higher value during π⟶π∗, LP⟶π∗ transitions than σ⟶σ∗ and σ⟶π∗. The π⟶π∗ interactions between bonding and antibonding orbitals are π (C1 − C4)⟶π∗(C6 − C12); π (C6 − C12)⟶π∗(C8 − C10) π(C8 − C10)⟶π∗(C1 − C4); π(C14 − C17)⟶π∗(C19 − C25) 20.05,21.73, 22.76, and 20.05 kJmol^-1, respectively. The strongest interaction LP⟶π∗ involves lone pairs, and nearly vacant antibonding orbitals such as LP(2)O3⟶π∗(C1 − C2) and π∗(C2 − C15) and LP(2)O16⟶π∗(C2 − C15) and π∗(C14 − C15) have high E(2) values of 17.51 and 21.84 kJmol^-1, respectively. These interactions contribute the greatest role to stabilizing the molecule. Thus, it is observed that there exists a hyperconjugative intramolecular stabilization energy between 17.45 and 22.76 KJmol^-1. Similar values are seen due to the mirror reflection of the molecule.

3. Second-order perturbation theory analysis of the Fock matrix in NBO basis calculated at B3LYP/6-311G (d.p) level.

Donor (i)	Acceptor (j)	E⁽²⁾ (Kj.Mol^-1)	E(j)-E(i) (a.u)	F(i.j) (a.u)
BD(2)C1-C4	BD∗(2)C2-O3	19.77	0.28	0.070
BD(2)C1-C4	BD∗(2)C6-C12	20.05	0.29	0.069
BD(2)C1-C4	BD∗(2)C8-C10	17.93	0.28	0.64
BD(2)C6-C12	BD∗(2)C1-C4	18.67	0.28	0.065
BD(2)C6-C12	BD∗(2)C8-C10	21.73	0.28	0.070
BD(2)C8-C10	BD∗(2)C1-C4	22.76	0.28	0.072
BD(2)C8-C10	BD∗(2)C6-C12	17.45	0.29	0.064
BD(2)C14-C17	BD∗(2)C15-O16	19.77	0.28	0.070
BD(2)C14-C17	BD∗(2)C19-C25	20.05	0.29	0.069
BD(2)C14-C17	BD∗(2)C21-C23	17.93	0.28	0.065
BD(2)C19-C25	BD∗(2)C14-C17	18.67	0.28	0.065
BD(2)C19-C25	BD∗(2)C21-C23	21.73	0.28	0.070
BD(2)C21-C23	BD∗(2)C14-C17	22.76	0.28	0.072
BD(2)C21-C23	BD∗(2)C19-C25	17.45	0.29	0.064
LP(2)O3	BD∗(2)C1-C2	17.51	0.71	0.101
LP(2)O3	BD∗(2)C2-C15	21.84	0.62	0.105
LP(2)O16	BD∗(2)C2-C15	21.84	0.62	0.105
LP(2)O16	BD∗(2)C14-C15	17.51	0.71	1.101

3.4. Frontier Molecular Orbital Analysis

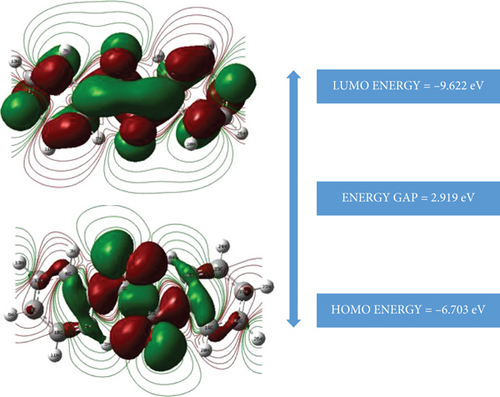
HOMO-LUMO is known as molecular orbitals which are collectively called frontier molecular orbitals. It helps to determine the energy band gap to know the electrical properties of the title compound. Some of the parameters like chemical potential, softness, electronegativity, and electrophilicity can be measured from these studies which in turn give an insight into the chemical reactivity of the compounds. At the time of molecular interactions in HOMO, the molecules donate electrons; thereby, their energies are corresponding to the ionization potential, on another hand, where the LOMO accepts electrons, and it corresponds to the electron affinity. The HOMO-LUMO gap helps to know the stability of the molecule. The value shows that the compound has high kinetic activity when compared to the one with a low value. Figure 5 shows the orbital composition of benzil. The energy value of HOMO is found to be -6.703 eV, and the energy value of LUMO is found to be -9.622 eV. The energy gap is calculated to be 2.919 eV. It shows that the title compound is a soft molecule. HOMO is localized mainly on the carboxyl groups attached to the phenyl ring, whereas LUMO is entirely occupied on the benzil molecule. The chemical descriptors such as hardness (η), chemical potential (μ), softness (S), electronegativity (χ), and electrophilicity index (ω) of benzil is calculated using the energy values of HOMO and LUMO. Based on Koopman’s theorem, the above parameters have been calculated and listed in Table 4 [44–46]. Hardness is the measure of the resistance of the system to change the electron cloud, while softness is the reciprocal of hardness, which is the measure of the ability to undergo electron density distribution. Electronegativity is the inverse of chemical potential. The minimum value of this electronegativity (0.122 eV) indicates the less tendency to gain electrons, and the high value of chemical potential implies the high reactive nature of benzil. Electrophilicity is a measure of the energy stabilization of a molecule when it acquires an additional amount of electron density from the environment. The high value of electrophilicity indicates the strong electrophilic nature of the molecule.

4. HOMO–LUMO energy value and related properties of benzil calculated by B3LYP/6-311++G(d,p) method.

E_HOMO (eV)	-6.703
E_LUMO (eV)	-9.622
Energy gap ΔE (eV)	2.919
Ionization potential (A) eV	+6.703
Electron affinity (I)	+9.622
Global softness (S)	0.343
Global hardness (η)	1.459
Chemical potential (μ)	8.163
Global electrophilicity (ω)	22.835

3.5. First-Order Hyperpolarizability Calculations

Electronic nonlinearities in the most efficient organic materials are based on molecular units with highly delocalized electrons and extra electron donor and acceptor groups on opposite sides of the molecules. For many years, it has been known that certain organic materials have exceptionally large NLO and electrooptic effects. In contrast to inorganic materials, where lattice vibrations occurring in the frequency range of 1 MHz to 100 MHz play a prominent role, the NLO effect of molecular crystals is mostly determined by the polarizability of the electrons in the bonding orbitals. Organic materials are therefore well suited for high-speed applications, such as NLO with ultrashort pulses or high-data-rate electro-optic modulation. Optical frequency doubling, optical sum, difference-frequency generation, optical parametric amplification, linear electrooptic effects (Pockel’s effect), and photorefractive effects all require noncentral symmetry. The first derivative of polarizability (β) measures how the dipole is induced in a molecule in the presence of the electric field. The present crystal belongs to the noncentrosymmetric space group; hence, it is interesting to study the NLO properties. By utilizing the B3YLP/6-311++G(d,p) basis set in Gaussian 09 program, the total molecular dipole moment (m), linear polarizability (α), and first-order hyperpolarizability (b) are calculated in atomic units and are converted into electrostatic units. (α:1a.u = 0.1482 × 10⁻²⁴ esu, β: 1a.u = 8.6393 × 10⁻³⁰ esu). Table 5 lists the calculated parameters of an electric dipole moment μ (D), the average polarizability α_tot (×10^-24 esu), and first-order hyperpolarizability β_tot (×10^-31 esu). The dipole moment in the X and Y direction is computed to be zero, and in the Z direction, it is found to be -3.4881. The calculated total dipole moment is 3.4881 Debye. The biggest value of hyperpolarizability is observed in the β_zzz direction, i.e., electron cloud is more in this particular direction. The total value of the first-order hyperpolarizability (β_tot) is of the order of 41.5246 × 10⁻³¹ esu. Urea is a standard material to study of NLO properties of the compound holding the threshold value of α and β of 3.8312 × 10⁻²⁴ esu and 0.37289 × 10⁻³⁰ esu, respectively. The above computations reveal that the hyperpolarizability of benzil is 11.135 times that of urea and is expected to be a suitable candidate in the development of NLO materials [47–48]. Yadav et al. grew the benzil crystal by Czochralski method which has suitable application in piezoelectric, sensor, and telecommunication fields. Benzil single-crystal exhibits noncentro symmetric structure and has both nonlinear optical and piezoelectric properties. It has a ferroelectric transition at 83.5 K. These properties make its applicability in design of the interface between optical and electrical communication network [49].

5. The electric dipole moment μ (D). The average polarizability α_tot (×10^-24 esu) and first hyperpolarizability β_tot (×10^-31 esu).

Parameters	B3LYP/6-311G(d,p)	Parameters	B3LYP/6-311G(d,p)
μ_x	0	β_xxx	0.0001
μ_y	0	β_xxy	-0.0003
μ_z	-3.4881	β_xyy	-0.0001
μ (D)	3.4881	β_yyy	-0.0005
α_xx	-69.629	β_zxx	-31.1348
α_xy	-0.795	β_xyz	-17.2186
α_yy	-92.195	β_zyy	-15.0123
α_xz	0.000	β_xzz	0.0003
α_yz	-0.0001	β_yzz	0.0002
α_zz	-98.7936	β_zzz	6.8288
α_tot (e.s.u)	−86.873 × 10⁻²⁴	β_tot (e.s.u)	41.5246 × 10⁻³¹

3.6. Molecular Electrostatic Potential Studies

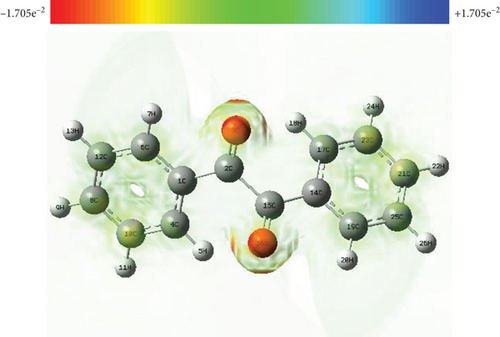
The molecular electrostatic potential (MESP) map is a three-dimensional representation of the charge distribution in molecules that allows the user to see the charge points in the molecule as well as the shape of the potential surface, which aids in the prediction of a variety of chemical properties [50]. With the use of a colour spectrum in the order red > orange > yellow > green > blue, GaussView converts the calculated electrostatic energy into an electron density model derived from the Schrodinger equation. e.s.u. ranges from −1.705 × 10⁻² to +1.705 × 10⁻² electrostatic potential. The colour red denotes an electrophilically active region, while the colour blue denotes a nucleophilically active region. The oxygen atoms at the carbonyls are deep red in colour in the present molecule (Figure 6), indicating that this is the most electrophilic area, where nucleophiles attack after the phenyl rings. The hydrogen atoms have deep blue patches around them, indicating that they are the most nucleophilic region in the molecule susceptible to electrophile attack [51, 52].

4. Conclusion

Single crystals of benzil-1,2-diphenylethane-1,2-dione were grown by slow evaporation method at room temperature and have been taken as the subject for experimental and theoretical investigation. Gaussian 09 program has been applied for theoretical calculations with B3LYP/6-311++G(d,p) basis set to study the vibrational and electronic properties of benzil molecule. The vibrational analysis explores the presence of various functional groups in the benzil molecule. NBO and HOMO-LUMO analysis has been performed and establishes the occurrence of charges transfer within the molecule. HOMO-LUMO energy gap is calculated to be 2.919 eV. First-order hyperpolarizability calculations reveal the nonlinear optical microscopic behavior of the benzil molecule with nonzero values, and it is found to be 11.435 times that of urea. Electrostatic potential establishes the strong electrophilic nature of the grown crystal. Above all the computations, we believe that the benzil compound is a suitable candidate for nonlinear applications as well as device fabrication and will be useful to the scientific community for further research.

Conflicts of Interest

The authors report there are no conflicts of interest.

Open Research

Data Availability

The authors confirm that the data supporting the findings of this study are available within the article and supplementary files.

Supporting Information

References

1 Abd-Alla M. A., Novel synthesis of poly(benzoin) and poly(benzil). Characterization and application as photosensitizer materials, Makromolekulare Chemie. (1991) 192, no. 2, 277–283, https://doi.org/10.1002/macp.1991.021920209.
10.1002/macp.1991.021920209
CAS Google Scholar
2 Ganapaty S., Srilakshmi G. V. K., Pannakal S. T., Rahman H., Laatsch H., and Brun R., Cytotoxic benzil and coumestan derivatives from Tephrosia calophylla, Phytochemistry. (2009) 70, no. 1, 95–99, https://doi.org/10.1016/j.phytochem.2008.10.009, 19062050.
10.1016/j.phytochem.2008.10.009
CAS PubMed Web of Science® Google Scholar
3 Mahabusarakam W., Deachathai S., Phongpaichit S., Jansakul C., and Taylor W. C., A benzil and isoflavone derivatives from Derris scandens Benth, Phytochemistry. (2004) 65, no. 8, 1185–1191, https://doi.org/10.1016/j.phytochem.2004.03.006, 2-s2.0-2142753011.
10.1016/j.phytochem.2004.03.006
CAS PubMed Web of Science® Google Scholar
4 Lindsley C. W., Zhao Z., Leister W. H., Robinson R. G., Barnett S. F., Defeo-Jones D., and Duggan M. E., Allosteric Akt (PKB) inhibitors: discovery and SAR of isozyme selective inhibitors, Bioorganic & Medicinal Chemistry Letters. (2005) 15, no. 3, 761–764, https://doi.org/10.1016/j.bmcl.2004.11.011, 2-s2.0-19944431003, 15664853.
10.1016/j.bmcl.2004.11.011
CAS PubMed Web of Science® Google Scholar
5 Murata K., Okano K., Miyagi M., Iwane H., Noyori R., and Ikariya T., A practical stereoselective synthesis of chiral hydrobenzoins via asymmetric transfer hydrogenation of benzils, Organic Letters. (1999) 1, no. 7, 1119–1121, https://doi.org/10.1021/ol990226a, 2-s2.0-0000759992.
10.1021/ol990226a
CAS Web of Science® Google Scholar
6 Slee D. H., Romano S. J., Yu J., Nguyen T. N., John J. K., Raheja N. K., Axe F. U., Jones T. K., and Ripka W. C., Development of potent non-carbohydrate imidazole-based small molecule selectin inhibitors with antiinflammatory activity, Journal of Medicinal Chemistry. (2001) 44, no. 13, 2094–2107, https://doi.org/10.1021/jm000508c, 2-s2.0-0035927435, 11405647.
10.1021/jm000508c
CAS PubMed Web of Science® Google Scholar
7 Zhao Z., Leister W. H., Strauss K. A., Wisnoski D. D., and Lindsley C. W., Broadening the scope of 1,2,4-triazine synthesis by the application of microwave technology, Tetrahedron Letters. (2003) 44, no. 6, 1123–1127, https://doi.org/10.1016/S0040-4039(02)02845-9, 2-s2.0-0037415505.
10.1016/S0040-4039(02)02845-9
CAS Web of Science® Google Scholar
8 Yu J. W., Mao S., and Wang Y. Q., Copper-catalyzed base-accelerated direct oxidation of C-H bond to synthesize benzils, isatins, and quinoxalines with molecular oxygen as terminal oxidant, Tetrahedron Letters. (2015) 56, no. 12, 1575–1580, https://doi.org/10.1016/j.tetlet.2015.02.019, 2-s2.0-84923768951.
10.1016/j.tetlet.2015.02.019
CAS Web of Science® Google Scholar
9 Maleki A., Alrezvani Z., and Maleki S., Design, preparation and characterization of urea-functionalized Fe₃O₄/SiO₂ magnetic nanocatalyst and application for the one-pot multicomponent synthesis of substituted imidazole derivatives, Catalysis Communications. (2015) 69, 29–33, https://doi.org/10.1016/j.catcom.2015.05.014, 2-s2.0-84930675579.
10.1016/j.catcom.2015.05.014
CAS Web of Science® Google Scholar
10 Kuroiwa K., Ishii H., Matsuno K., Asai A., and Suzuki Y., Synthesis and structure–activity relationship study of 1-phenyl-1-(quinazolin-4-yl) ethanols as anticancer agents, ACS Medicinal Chemistry Letters. (2015) 6, no. 3, 287–291, https://doi.org/10.1021/ml5004684, 2-s2.0-84924679924, 25815147.
10.1021/ml5004684
CAS PubMed Web of Science® Google Scholar
11 Corrales T., Catalina F., Peinado C., and Allen N. S., Free radical macrophotoinitiators: an overview on recent advances, Journal of Photochemistry and Photobiology A: Chemistry. (2003) 159, no. 2, 103–114, https://doi.org/10.1016/S1010-6030(03)00175-8, 2-s2.0-0037533883.
10.1016/S1010-6030(03)00175-8
CAS Web of Science® Google Scholar
12 Jadhav V. G., Sarode S. A., and Nagarkar J. M., Tandem and chemoselective synthesis of benzil derivatives from styrene and arene diazonium salts, Tetrahedron Letters. (2017) 58, no. 19, 1834–1838, https://doi.org/10.1016/j.tetlet.2017.03.076, 2-s2.0-85017168975.
10.1016/j.tetlet.2017.03.076
CAS Web of Science® Google Scholar
13 Sreelatha T., Hymavathi A., Rao V. R. S., Devanand P., Rani P. U., Rao J. M., and Babu K. S., A new benzil derivative from Derris scandens : structure-insecticidal activity study, Bioorganic & Medicinal Chemistry Letters. (2010) 20, no. 2, 549–553, https://doi.org/10.1016/j.bmcl.2009.11.103, 2-s2.0-72249101483, 19969457.
10.1016/j.bmcl.2009.11.103
CAS PubMed Web of Science® Google Scholar
14 Zhao W., He Z., Lam J. W., Peng Q., Ma H., Shuai Z., and Tang B. Z., Rational molecular design for achieving persistent and efficient pure organic room-temperature phosphorescence, Chem. (2016) 1, no. 4, 592–602, https://doi.org/10.1016/j.chempr.2016.08.010, 2-s2.0-85008254093.
10.1016/j.chempr.2016.08.010
CAS Web of Science® Google Scholar
15 Lower S. K. and El-Sayed M. A., The triplet state and molecular electronic processes in organic molecules, Chemical Reviews. (1966) 66, no. 2, 199–241, https://doi.org/10.1021/cr60240a004, 2-s2.0-33947332584.
10.1021/cr60240a004
CAS Web of Science® Google Scholar
16 Gong Y., Tan Y., Li H., Zhang Y., Yuan W., Zhang Y., and Tang B. Z., Crystallization-induced phosphorescence of benzils at room temperature, Science China Chemistry. (2013) 56, no. 9, 1183–1186, https://doi.org/10.1007/s11426-013-4930-9, 2-s2.0-84883447280.
10.1007/s11426-013-4930-9
CAS Web of Science® Google Scholar
17 Wadkins R. M., Hyatt J. L., Wei X., Yoon K. J. P., Wierdl M., Edwards C. C., and Potter P. M., Identification and characterization of novel benzil (diphenylethane-1, 2-dione) analogues as inhibitors of mammalian carboxylesterases, Journal of Medicinal Chemistry. (2005) 48, no. 8, 2906–2915, https://doi.org/10.1021/jm049011j, 2-s2.0-20944443990, 15828829.
10.1021/jm049011j
CAS PubMed Web of Science® Google Scholar
18 Stanculescu A., Stanculescu F., Alexandru H., and Socol M., Doped aromatic derivatives wide-gap crystalline semiconductor structured layers for electronic application, Thin Solid Films. (2006) 495, no. 1-2, 389–393, https://doi.org/10.1016/j.tsf.2005.08.243, 2-s2.0-28044451808.
10.1016/j.tsf.2005.08.243
CAS Web of Science® Google Scholar
19 Mousset C., Giraud A., Provot O., Hamze A., Bignon J., Liu J. M., and Alami M., Synthesis and antitumor activity of benzils related to combretastatin A-4, Bioorganic & Medicinal Chemistry Letters. (2008) 18, no. 11, 3266–3271, https://doi.org/10.1016/j.bmcl.2008.04.053, 2-s2.0-44349096338.
10.1016/j.bmcl.2008.04.053
CAS PubMed Web of Science® Google Scholar
20 Topal K. G., Unaleroglu C., and Aviyente V., Computational study of the synthesis of benzoin derivatives from benzil, International Journal of Quantum Chemistry. (2006) 106, no. 7, 1596–1610, https://doi.org/10.1002/qua.20879, 2-s2.0-33646340159.
10.1002/qua.20879
CAS Web of Science® Google Scholar
21 Brown C. J. and Sadanaga R., The crystal structure of benzil, Acta Crystallographica. (1965) 18, no. 2, 158–164, https://doi.org/10.1107/S0365110X65000403.
10.1107/S0365110X65000403
CAS Web of Science® Google Scholar
22 Gabe E. J., Le Page Y., Lee F. L., and Barclay L. R. C., The structure of 2, 2', 4, 4', 6, 6'-hexa-tert-butylbenzil, Acta Crystallographica Section B: Structural Crystallography and Crystal Chemistry. (1981) 37, no. 1, 197–200, https://doi.org/10.1107/S0567740881002495.
10.1107/S0567740881002495
Web of Science® Google Scholar
23 More M., Odou G., and Lefebvre J., Structure determination of benzil in its two phases, Acta Crystallographica Section B: Structural Science. (1987) 43, no. 4, 398–405, https://doi.org/10.1107/S0108768187097660, 2-s2.0-0001449886.
10.1107/S0108768187097660
Web of Science® Google Scholar
24 Saranraj A., Thirupathy J., Dhas S., Jose M., Vinitha G., and Dhas S. A., Growth and characterization of unidirectional benzil single crystal for photonic applications, Applied Physics B. (2018) 124, no. 6, 1–9, https://doi.org/10.1007/s00340-018-6971-4, 2-s2.0-85046880132.
10.1007/s00340-018-6971-4
CAS Web of Science® Google Scholar
25 Shankar M. V. and Varma K. B. R., Dielectric dispersion and piezoelectric resonance in benzil single crystals grown by Bridgman-Stockbarger technique, Bulletin of Materials Science. (1996) 19, no. 5, 791–798, https://doi.org/10.1007/BF02745199, 2-s2.0-0030263247.
10.1007/BF02745199
CAS Web of Science® Google Scholar
26 Chigare R., Patil J., and Kamat S., Synthesis of Benzil and Its Various Derivatives, International Research Journal of Engineering and Technology. (2020) 7, 3764–3766.
Google Scholar
27 Kolev T. M. and Stamboliyska B. A., Vibrational spectra and structure of benzil and its ¹⁸O- and d₁₀-labelled derivatives: a quantum chemical and experimental study, Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy. (2002) 58, no. 14, 3127–3137, https://doi.org/10.1016/S1386-1425(02)00043-4, 2-s2.0-0036882562, 12511097.
10.1016/S1386-1425(02)00043-4
PubMed Web of Science® Google Scholar
28 Lopes S., Gómez-Zavaglia A., Lapinski L., Chattopadhyay N., and Fausto R., Matrix-isolation FTIR spectroscopy of benzil: probing the flexibility of the C−C torsional coordinate, The Journal of Physical Chemistry A. (2004) 108, no. 40, 8256–8263, https://doi.org/10.1021/jp047116s, 2-s2.0-6344220195.
10.1021/jp047116s
CAS Web of Science® Google Scholar
29 Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., and Petersson G., Gaussian09, R.A gaussian. Inc., Wallingford CT, 2009, 121, 150–166.
Google Scholar
30 Glendening E. D., Reed A. E., Carpenter J. E., Weinhold F., and Version N. B. O., 3.1 Program Manual, 1998, University of Wisconsin, Madison.
Google Scholar
31 Foresman J. and Frish E., Exploring Chemistry, 1996, Gaussian Inc., Pittsburg, USA.
Google Scholar
32 Bruker A. P. E. X. and Saint A. X. S., Inc., Madison, WI, 2004 Search PubMed; a GM Sheldrick. Acta Crystallogr, Sect. A: Fundam. Crystallogr. (2008) 64, article 112.
Google Scholar
33 Sheldrick G. M., A short history of SHELX, Acta Crystallographica Section A: Foundations of Crystallography. (2008) 64, no. 1, 112–122.
10.1107/S0108767307043930
CAS PubMed Google Scholar
34 Smart S., Software Reference Manuals, Versions 6.28 a And 5.625. Bruker Analytical X-Ray SystemsInc, 2001, Bruker Advanced X-Ray Solutions, Madison, Wisconsin, USA.
Google Scholar
35 Spek A. L., Structure validation in chemical crystallography, Acta Crystallographica Section D: Biological Crystallography. (2009) 65, no. 2, 148–155, https://doi.org/10.1107/S090744490804362X, 2-s2.0-58849161857, 19171970.
10.1107/S090744490804362X
CAS PubMed Web of Science® Google Scholar
36 Nardelli M., Ring asymmetry parameters from out-of-plane atomic displacements, Acta Crystallographica Section C: Crystal Structure Communications. (1983) 39, no. 8, 1141–1142, https://doi.org/10.1107/S0108270183007696, 2-s2.0-84906441301.
10.1107/S0108270183007696
Web of Science® Google Scholar
37 Ivanov M. A., Kimasov V. A., and Markov Y. F., Normal vibrational modes in benzil crystals, Physics of the Solid State. (2002) 44, no. 2, 373–378, https://doi.org/10.1134/1.1451031, 2-s2.0-0036003519.
10.1134/1.1451031
CAS Web of Science® Google Scholar
38 Kayadibi F., Sagdinc S. G., and Kara Y. S., Density functional theory studies on the corrosion inhibition of benzoin, benzil, benzoin-(4-phenylthiosemicarbazone) and benzil-(4-phenylthiosemicarbazone) of mild steel in hydrochloric acid, Protection of Metals and Physical Chemistry of Surfaces. (2015) 51, no. 1, 143–154, https://doi.org/10.1134/S2070205115010050, 2-s2.0-84921842756.
10.1134/S2070205115010050
CAS Web of Science® Google Scholar
39 Sheppard N., The historical development of experimental techniques in vibrational spectroscopy, Handbook of Vibrational Spectroscopy. (2006) 1, https://doi.org/10.1002/0470027320.s0101.
10.1002/0470027320.s0101
Google Scholar
40 Kanagathara N., Marchewka M. K., Drozd M., Gunasekaran S., Rajakumar P. R., and Anbalagan G., Structural and vibrational spectroscopic studies on charge transfer and ionic hydrogen bonding interactions of melaminium benzoate dihydrate, Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy. (2015) 145, 394–409, https://doi.org/10.1016/j.saa.2015.03.002, 2-s2.0-84924942052, 25796010.
10.1016/j.saa.2015.03.002
CAS PubMed Web of Science® Google Scholar
41 Sathyanarayana D. N., Vibrational spectroscopy: theory and applications, 2015, New Age International, New Delhi.
Google Scholar
42 Glendening E. D., Badenhoop J. K., Reed A. E., Carpenter J. E., Bohmann J. A., Morales C. M., and Weinhold F., Theoretical Chemistry Institute, 2001, University of Wisconsin, Madison.
Google Scholar
43 Kuruvilla T. K., Prasana J. C., Muthu S., and George J., Vibrational spectroscopic (FT-IR, FT-Raman) and quantum mechanical study of 4-(2-chlorophenyl)-2-ethyl-9-methyl-6H-thieno [3, 2-f][1, 2, 4] triazolo [4, 3-a][1, 4] diazepine, Journal of Molecular Structure. (2018) 1157, 519–529, https://doi.org/10.1016/j.molstruc.2018.01.001, 2-s2.0-85040010335.
10.1016/j.molstruc.2018.01.001
CAS Web of Science® Google Scholar
44 Parr R. G., Szentpály L. V., and Liu S., Electrophilicity index, Journal of the American Chemical Society. (1999) 121, no. 9, 1922–1924, https://doi.org/10.1021/ja983494x, 2-s2.0-0040942563.
10.1021/ja983494x
CAS Web of Science® Google Scholar
45 Pandey M., Muthu S., and Gowda N. N., Quantum mechanical and spectroscopic (FT-IR, FT- Raman,¹H,¹³C NMR, UV-Vis) studies, NBO, NLO, HOMO, LUMO and Fukui function analysis of 5-methoxy-1H-benzo[ d ]imidazole-2(3H)-thione by DFT studies, Journal of Molecular Structure. (2017) 1130, 511–521, https://doi.org/10.1016/j.molstruc.2016.10.064, 2-s2.0-84994029388.
10.1016/j.molstruc.2016.10.064
CAS Web of Science® Google Scholar
46 Kanagathara N., Usha R., Natarajan V., and Marchewka M. K., Molecular geometry, vibrational, NBO, HOMO–LUMO, first order hyper polarizability and electrostatic potential studies on anilinium hydrogen oxalate hemihydrate–an organic crystalline salt, Inorganic and Nano-Metal Chemistry. (2022) 52, no. 2, 226–233, https://doi.org/10.1080/24701556.2021.1891103.
10.1080/24701556.2021.1891103
CAS Web of Science® Google Scholar
47 Muthu S. and Renuga S., Vibrational spectra and normal coordinate analysis of 2-hydroxy-3-(2-methoxyphenoxy) propyl carbamate, Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy. (2014) 132, 313–325, https://doi.org/10.1016/j.saa.2014.05.009, 2-s2.0-84901639228, 24878438.
10.1016/j.saa.2014.05.009
CAS PubMed Web of Science® Google Scholar
48 Gunasekaran S., Kumaresan S., Arunbalaji R., Anand G., Seshadri S., and Muthu S., Vibrational assignments and electronic structure calculations for 6-thioguanine, Journal of Raman Spectroscopy: An International Journal for Original Work in all Aspects of Raman Spectroscopy, Including Higher Order Processes, and also Brillouin and Rayleigh Scattering. (2009) 40, no. 11, 1675–1681, https://doi.org/10.1002/jrs.2318, 2-s2.0-70450169599.
10.1002/jrs.2318
CAS Google Scholar
49 Yadav H., Sinha N., and Kumar B., Growth and characterization of piezoelectric benzil single crystals and its application in microstrip patch antenna, CrystEngComm. (2014) 16, no. 46, 10700–10710, https://doi.org/10.1039/C4CE01846J, 2-s2.0-84908632269.
10.1039/C4CE01846J
CAS Web of Science® Google Scholar
50 Politzer P., Laurence P. R., and Jayasuriya K., Molecular electrostatic potentials: an effective tool for the elucidation of biochemical phenomena, Environmental Health Perspectives. (1985) 61, 191–202, https://doi.org/10.1289/ehp.8561191, 2866089.
10.1289/ehp.8561191
CAS PubMed Web of Science® Google Scholar
51 Thomas R., Mary Y. S., Resmi K. S., Narayana B., Sarojini S. B. K., Armaković S., and Mohan B. J., Synthesis and spectroscopic study of two new pyrazole derivatives with detailed computational evaluation of their reactivity and pharmaceutical potential, Journal of Molecular Structure. (2019) 1181, 599–612, https://doi.org/10.1016/j.molstruc.2019.01.014, 2-s2.0-85060335408.
10.1016/j.molstruc.2019.01.014
CAS Web of Science® Google Scholar
52 Thomas R., Mary Y. S., Resmi K. S., Narayana B., Sarojini B. K., Vijayakumar G., and Van Alsenoy C., Two neoteric pyrazole compounds as potential anti-cancer agents: synthesis, electronic structure, physico-chemical properties and docking analysis, Journal of Molecular Structure. (2019) 1181, 455–466, https://doi.org/10.1016/j.molstruc.2019.01.003, 2-s2.0-85060051270.
10.1016/j.molstruc.2019.01.003
CAS Web of Science® Google Scholar

Citing Literature

All articles

Structural and Vibrational Investigation of Benzil-(1,2-Diphenylethane-1,2-Dione): Experimental and Theoretical Studies

Abstract

1. Introduction

2. Materials and Methods