[Retracted] A Study on the Fuzzy Rule Hunting Strategy of Multiple Unmanned Vehicles Based on the Improved Artificial Potential Field Method
Abstract
A multiple unmanned vehicle hunting strategy based on the improved artificial potential field method is designed to solve the multiple unmanned vehicle cooperative hunting problem in complex environments. First, the decision layer is designed based on the fuzzy inference system to achieve the stage division and selection of the corresponding strategies. Subsequently, the improved repulsive field function for variable safety distance is designed according to the relative velocity and angle between the unmanned vehicle and the obstacle, to achieve efficient obstacle avoidance of the unmanned vehicle during hunting. Then, a hunting strategy comprising the consistent state, obstacle avoidance, and control costs is designed to obtain the time-optimal path of the unmanned vehicle and achieve fast target hunting by minimizing this cost function. Finally, the effectiveness of the designed hunting strategy is verified via simulations and experiments and then compared with other hunting strategies. Accordingly, it is inferred that the hunting strategy designed in this study improves the efficiency of hunting by 12.97%, in addition to ensuring the obstacle avoidance effect.
1. Introduction
Recently, the unmanned cooperative combat system technology has experienced rapid developments. With characteristics including being unmanned, intelligent, efficient, and low cost, it satisfies the demand for future warfare; hence, the cooperative combat model is expected to subvert the combat mode of future warfare. Consequently, the unmanned cooperation technology has also become an important bargaining chip in military games around the world [1–3].
Cooperative robot hunting [4, 5] is an important part of cooperative multi-intelligence control, which focuses on the study of how multiple robots with limited individual capabilities can coordinate, collaborate, and cooperate, to capture or control highly flexible and relatively dangerous targets. Recently, several studies have been conducted on swarm robot hunting. Among them, the artificial potential field method is widely used in the motion control of multiple robots because of its advantages of simple calculation and easy real-time control. Zhang et al. [6, 7] proposed an obstacle avoidance and hunting strategy based on a simplified virtual force model to enable swarm robots to perform both hounding and obstacle avoidance in unknown, complex environments. Liang and Wei [8] designed a hunting method based on artificial physical forces, in which the swarm robot completes hunting under the action of artificial forces. However, there are limitations to this strategy in complex environments.
Considering the limitations of existing hunting strategies in complex environments, a hunting strategy based on an improved artificial potential field method was designed in this study to enable unmanned vehicles to perform both hunting and obstacle avoidance in complex environments. Simulation and experimental results demonstrated that the hunting strategy proposed in this study can achieve effective hunting and obstacle avoidance while being more time effective.
2. Mathematical Model of Unmanned Vehicle Formations
2.1. Kinematic Model for Unmanned Vehicles
The subject of the study presented in this paper was a two-wheeled differential speed unmanned vehicle, as illustrated in Figure 1. The motion of the vehicle was controlled by controlling the rotation of the left and right drive wheels at the rear of the vehicle body.

The center of the line connecting the drive wheels was set as the center of gravity, which is denoted as the base point C. The coordinates of the base point under the geodetic coordinate system xoy were set as (x, y). The instantaneous linear velocity of the unmanned vehicle was vc, the instantaneous angular velocity was ωc, and the attitude angle θ was defined as the angle between the linear velocity and the x axis. Here, the attitude information of the unmanned vehicle was represented by the vector P = [x, y, θ]T.
The distance between the two wheels of the unmanned vehicle was set to l, the instantaneous center of rotation was set to Oc, and the radius of rotation was set to R. When the unmanned vehicle was in coaxial circular motion, the radii of the left and right drive wheels, including the base position to the center of rotation, were different; however, they had the same angular velocity ωl = ωr = ωc.
2.2. Unmanned Vehicle Formation Communication Topology
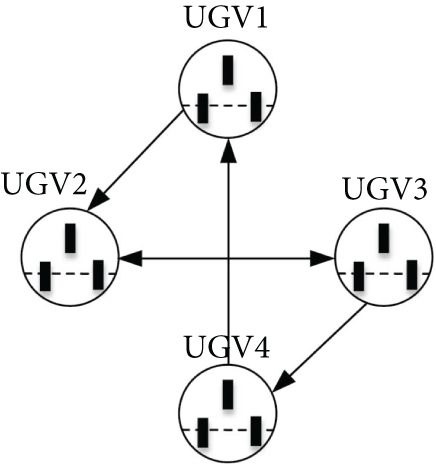
Multiple unmanned vehicles were connected to each other via communication topologies, to form a formation system using the theory of the knowledge graph. A directed graph was adopted to represent the communication network topology of multiple unmanned vehicle systems. A time-delay communication-type communication topology was adopted in this paper, as illustrated in Figure 2. The time-delayed communication-type communication topology was reduced, and the undirected path between nodes was increased, which prevented the nodes from being too homogeneous in terms of their information sources. The information feedback between unmanned vehicles was increased on the basis of forming a strong linkage-type structure, to achieve a reduction in the time transmission delay during formation. This communication topology provided a certain level of protection to each individual unmanned vehicle.
3. Virtual Force Design Based on the Improved Artificial Potential Field Method
- (1)
The unmanned vehicle is far from the target point. In this case, the target point exerts high gravitational force on the unmanned vehicle; hence, if there were obstacles appearing ahead, the unmanned vehicle would be unable to slow down in time and would inevitably collide with the obstacles
- (2)
An obstacle exists near the target point. In this case, the obstacle exerts high repulsive force on the unmanned vehicle and the target will become unreachable
To address the aforementioned cases, suggestions for improvement are provided in this section.
3.1. Gravitational Force of the Target Point on the Unmanned Vehicle
Within the space, the positions of the unmanned vehicle, target point, and obstacle were denoted by , , and , respectively.
3.2. Repulsive Force of External Obstacles on Unmanned Vehicles
Current unmanned vehicles with improved intelligence usually carry LIDAR sensors, which can sense obstacles within a certain range around them while sharing information with other unmanned vehicles in the formation. Considering the instability of information interaction, safety radius of the unmanned vehicle driving, and relative speed and angle between the detected obstacles and unmanned vehicle, the safety distance of avoiding obstacles was then reconfigured, as illustrated in Figure 3.
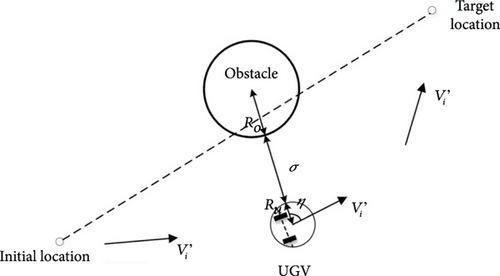
In Figure 3, Ro denotes the radius that can be influenced by the obstacle, which is primarily determined by the diameter of the circle that can surround the obstacle; in addition, σ, Ru, and η denote the safety zone reserved for the avoidance of safety hazards caused by information uncertainty, safety radius of the unmanned vehicle driving, and state clip angle of the unmanned vehicle, respectively. The speed influences the obstacle avoidance effect, as illustrated in Figure 4.
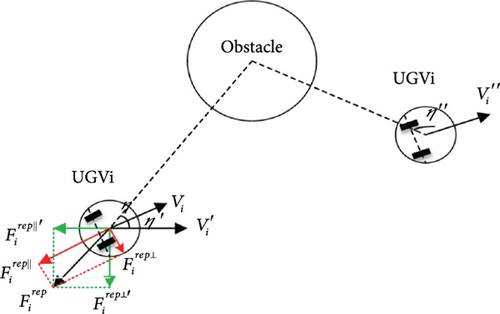
The safety distance was set considering the motion state of the unmanned vehicle with the improved repulsive field function. Although the repulsive force continued to increase when the unmanned vehicle approached the target location near the obstacle, it was not too large. Moreover, the target also exerted a certain amount of gravitational force on the unmanned vehicle, which could enable the unmanned vehicle to draw closer to the target site.
3.3. Virtual Forces between Multiple Unmanned Vehicles
In equation (7), k, dsafe, nij, and rij denote the gain coefficient, unit vector, safety distance between unmanned vehicles, and the distance between unmanned vehicles i and j expectation formation, respectively. When the distance between the unmanned vehicles was greater than the safety distance and rij > dsafe was satisfied, then, the force generated between the unmanned vehicles i and j was gravitational and denoted as . When the distance between the unmanned vehicles was smaller than the safety distance, then, the repulsive force generated by the unmanned vehicles i and j for internal collision avoidance was .
4. Mathematical Model of Unmanned Vehicle Formations
4.1. Coordinated Decision Making Based on Fuzzy Inference Systems
For the accurate identification of the task state of the unmanned vehicle and selection of the corresponding strategy to realize hunting by multiple unmanned vehicles, a fuzzy inference system was adopted as the decision layer. The fuzzy inference system is a system with the ability to process fuzzy information based on the fuzzy set theory and fuzzy inference method [11–13]. The design of the fuzzy rules in the decision layer was fuzzified by the affiliation function in Figure 5 based on the distance Lim between the four hunting unmanned vehicles and the target unmanned vehicle as the input.
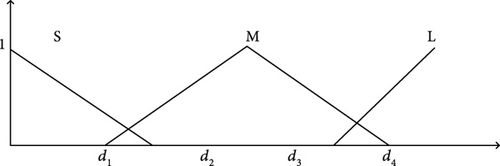
The inference process of the fuzzy inference system began with the calculation of the affiliation degree from zero to one on the corresponding fuzzy set, using the trapezoidal affiliation function according to the preconditions of each rule. The four input variables were fuzzified by the affiliation function to obtain the affiliation degree of μ1m, μ2m, μ3m, μ4m. The affiliation degree of the fuzzy rule obtained by matching the rules was the minimum value of the affiliation degree of the input variables. Finally, the output of each rule was superimposed according to the fuzzy rule affiliation, to derive the output strategies including the search, approach, and hunting strategies. For example, when the distance Lim between all the unmanned hunting vehicles and unmanned target vehicle reached L, the decision layer would output a search strategy and the unmanned hunting vehicles would move randomly to search and sense the target unmanned vehicle. When a certain unmanned hunting vehicle has sensed a target within range, i.e., when the distance Lim between a certain unmanned vehicle and the target reached M, the target location is shared among the unmanned hunting vehicles via a communication link. When a certain hunting unmanned vehicle senses a target within range, i.e., when the distance x between a certain unmanned vehicle and the target is M, the target location is also shared between the unmanned hunting vehicles via a communication link. At this point, the decision layer would output the approach strategy and the hunting vehicles would be subjected to the virtual gravitational force from the target and they would approach the target. When the distance between the hunting party and the target Lim reached S, the unmanned vehicle would execute the hunting strategy.
4.2. Hunting Strategy Design Based on the Improved Artificial Potential Field Method
When outputting a hunting strategy based on the decision layer of the fuzzy inference system, the unmanned hunting vehicle adopted a hunting strategy based on the improved artificial potential field method and regarded the hunting problem as a consistency problem relative to the hunting target, which was then transformed into an optimal control problem. An inverse optimal control method was then adopted to derive a hunting strategy for multiple unmanned vehicles in a closed form, which could perform obstacle avoidance in the state of the perceived hunting target. The strategy is a linear functional form of (L ⊗ Im)X, where ⊗ represents the Kronecker product to extend the matrix dimension and I represents the matrix of dimension m.
The final consistent state XCS would become a constant, and the control input given by the control strategy would also become zero when multiple intelligences reach consistency.
When asymptotic stability was achieved in equation (11), the hunting of the target by multiple unmanned vehicles would succeed.
Theorem 1. For a multi-intelligent system that satisfies equation (12) and all three of its constraints, there exist control algorithms for parameters wp and wc as follows:
It is an optimal control for the consistent hunting problem as expressed in equation (15) and can be expressed as follows:
5. Unmanned Vehicle Formation Simulation and Experimental Verification
5.1. Simulation of the Hunting Control Strategy without Being within the Obstacle Potential Field
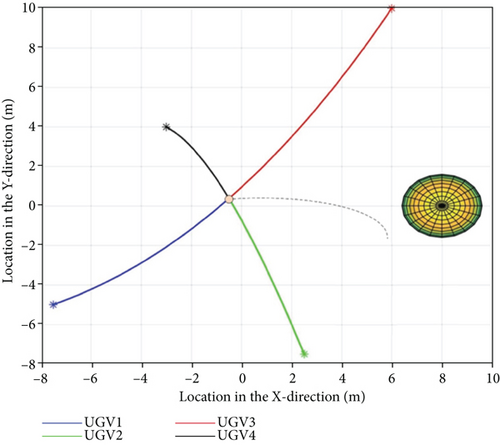
The four unmanned vehicles were employed to simulate a dynamic target point for hunting strategy experiments, and the communication topology adopted between the unmanned vehicles is illustrated in Figure 2. The initial position, travel speed, and directional angle of multiple unmanned vehicles were all set randomly. The initial positions were (−7.5, −5), (2.5, −7.5), (6, 10), and (−3, 4), respectively. In addition, wp = 0.8 in the hunting control strategy and wc = 4. In the simulation case of this subsection, it is assumed that an obstacle appears on (8, 0), which is not on the trajectory of any unmanned vehicle.
It can be deduced in Figure 6 that by using the hunting control strategy, hunting of dynamic targets could ultimately be achieved by four unmanned vehicles with different initial positions. The circle, dotted line, stars, and solid lines of different colors in the figure depict the hunting target, motion trajectory, initial position of the unmanned vehicles, and the motion trajectory, respectively. It can be observed that the motion trajectory of the unmanned vehicle on the hunting target outside the range of the obstacle potential field is smooth and the specific position and control information diagram are presented as follows.
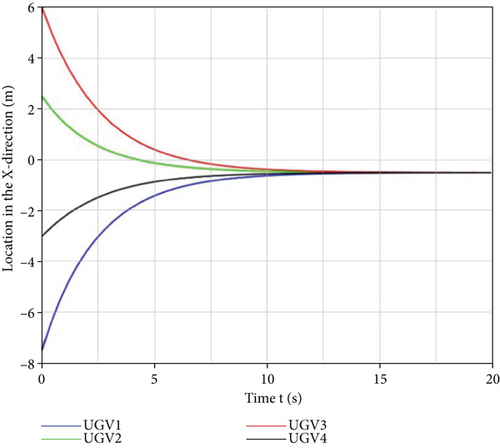
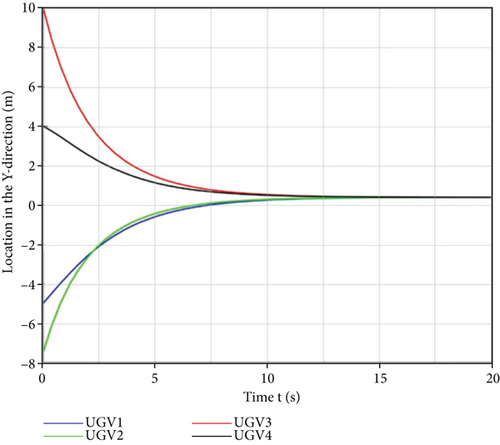
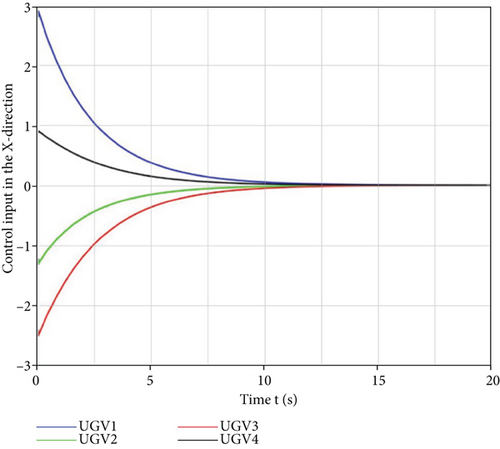
In Figures 7 and 8, it can be observed that the effective hunting of the target could eventually be performed by the four unmanned vehicles with different initial positions at different initial moments in a limited time, using the hunting control strategy. The individual unmanned vehicles eventually converged to consistent values at the positions in the x and y directions, i.e., the target was hunted successfully. It can be observed in Figures 9 and 10 that the control inputs to the unmanned vehicle in the x and y directions were smooth and convergent, which is consistent with the trend of position changes in the x and y directions, and that the control inputs became zero after hunting was achieved, i.e., the hunting was successful. To verify that the designed hunting strategy is superior to others, a comparative test was conducted using the parallel guidance rate-based hunting strategy from the literature [14] and the obtained test results are presented in Table 1.
| Hunting strategy | Number of successful hunting | Average number of cycles required |
|---|---|---|
| Based on the improved artificial potential field method | 99/100 | 12.34 |
| Based on parallel guidance rates [14] | 98/100 | 15.02 |
In an obstacle free environment, the artificial potential field method is attracted by the obstacle, and the closer it is, the faster it is. Therefore, it takes less time. However, it may occur that the surrounding unmanned vehicles are on the same side of the obstacle and the surrounding fails. From the data presented in Table 1, it can be inferred that the success rate of hunting dynamic targets using the improved artificial potential field-based hunting control strategy proposed in this study is as high as 99% and the average time taken is 21.7% less than that of the parallel guidance rate-based hunting strategy. Therefore, this algorithm is better than the others, as it has a higher hunting success rate and requires less time.
5.2. Simulation of the Hunting Control Strategy within the Obstacle Potential Field
Further simulation experiments on the hunting control of hunting targets using four unmanned vehicles will be presented in this section. The communication topology used has the structure illustrated in Figure 2. The initial positions, velocities, and directional angles of multiple unmanned vehicles were all set randomly under the actual motion performance constraints. The initial state values were (−7.5, −5), (2.5, −7.5), (10, 10), and (−3, 4). In addition, wp = 0.8 in the hunting control strategy and wc = 4. Compared to the previous subsection, changes have been made, such that the unmanned vehicle would be affected by the obstacle potential field in the process of hunting the target. The locations of the two obstacles were (−1, −1) and (7, 7) in the environment, and the radii of the obstacles and detection area were 0.5 and 2.5, respectively. The specific simulation results are presented in Figure 11.
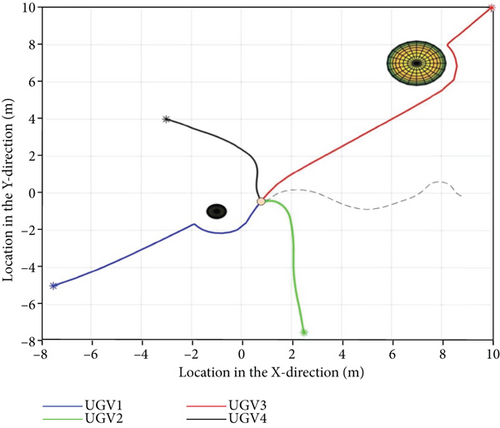
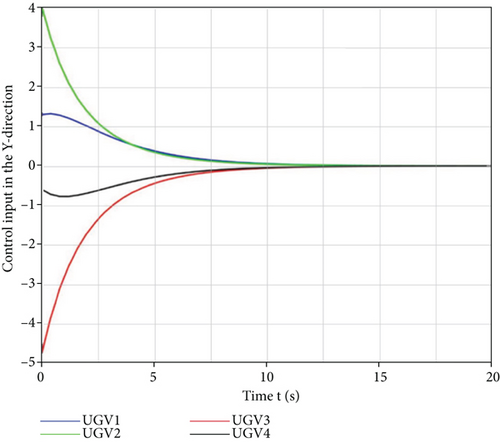
In Figure 11, it can be observed that in the environment with obstacles, the four unmanned vehicles can bypass the obstacles safely and achieve the hunting of the target by applying the siege control strategy based on the improved artificial potential field method, although they had different initial positions. In addition, their motion trajectories were also smooth. The specific state information and control inputs are presented in Figures 12–15.
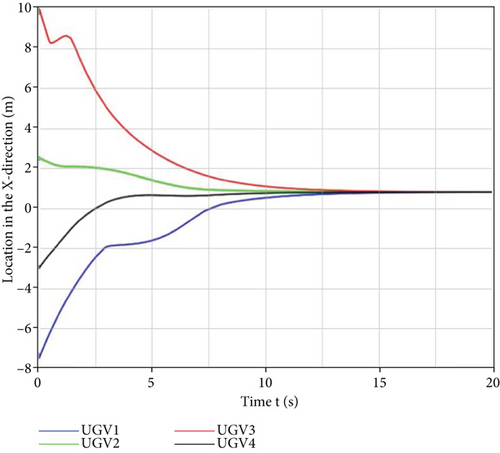
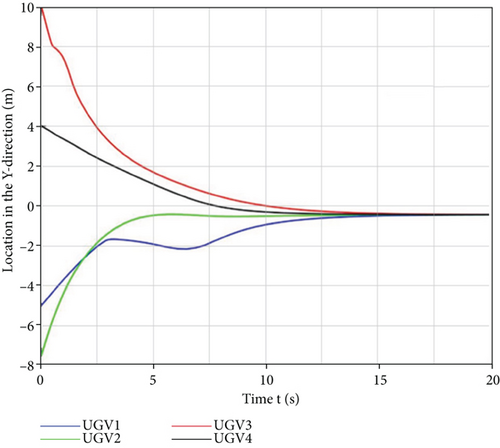
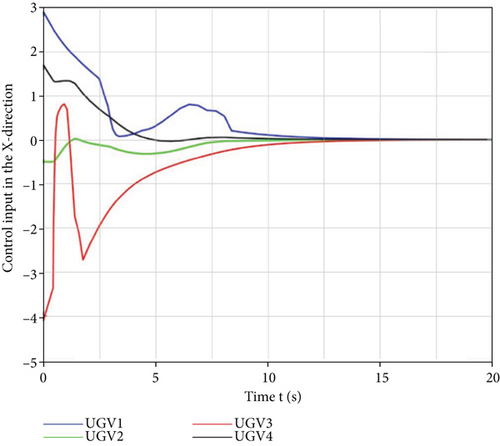
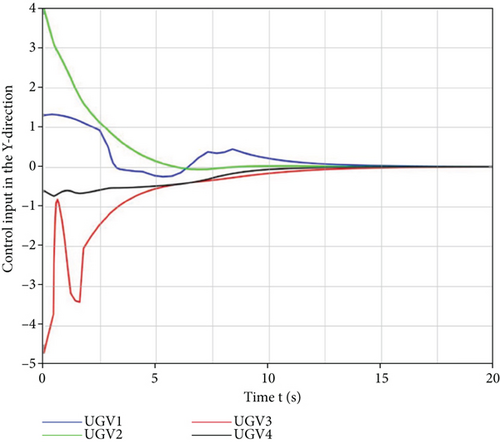
It can be inferred in Figures 12 and 13 that the four unmanned vehicles from different initial positions could eventually achieve the hunting of the target optimally, even under the influence of the obstacles in a limited time. Their trajectories in the x and y directions also reflected the avoidance of obstacles by the hunting control strategy. It can be observed in Figures 14 and 15 that the control inputs to the unmanned vehicle in the x and y directions change with the influence of the obstacle potential field, thus indicating that the designed hunting control strategy can effectively handle the obstacle environment and eventually converge. The changes in the control inputs are consistent and in line with the trend of position changes in the x and y directions for obstacle avoidance. To verify that the designed hunting strategy is better than others, a comparison simulation experiment with the dynamic alliance hunting strategy based on the improved contract network protocol given in the literature [15] was conducted in the environment with obstacles and the obtained results are presented in Table 2.
| Hunting strategy | Number of successful hunting | Average time taken (s) |
|---|---|---|
| Based on the improved artificial potential field method | 99/100 | 15.31 |
| Based on improved contract network protocols [16] | 100/100 | 17.82 |
Under the potential field of obstacles, when the artificial potential field method is adopted in the process of encircling, the unmanned vehicle will be attracted by the target and repulsed by the obstacles, and the encircling may fail due to the long time. From the data presented in Table 2, it can be inferred that the success rate of hunting dynamic targets using the improved artificial potential field-based hunting control strategy proposed in this study is as high as 99%. Although the success rate is lower than the strategy presented in the literature [16], there is a 14.09% reduction in the time taken for hunting. Moreover, the algorithm proposed in this study is more flexible with respect to the obstacles. Therefore, this algorithm is better than the others in terms of the time taken.
5.3. Hunting Control Strategy Experiments in an Environment with Obstacles
The platform for the cooperative control of multiple unmanned vehicles comprises four main parts: unmanned vehicle body, positioning module, communication module, and strategy design module. The physical unmanned vehicle used in this experiment was the iClebo Kobuki mobile robot of YuJin Robot, as illustrated in Figure 1. The localization module was primarily used to calculate the position of the unmanned vehicle, while the ultrawide band localization technology was adopted, considering the indoor environment and practical requirements of the laboratory. The communication module adopted Wi-Fi as the communication method, which was used mainly for the communication between unmanned vehicles, as well as between unmanned vehicles and computers.
A total of five unmanned vehicles were employed in the experiment, four of which were adopted as the hunting parties and one as the target party. The target unmanned vehicle was placed in the experimental area and its movement was controlled. A circle with a radius of 0.8 m was set as the target point with the center of the target vehicle as the center, and then, the unmanned hunting vehicle group was placed in the experimental area in a randomly dispersed manner for the hunting experiment, which was conducted in an environment with obstacles. The process of the hunting experiment is illustrated in Figure 16.




Figure 16 illustrates how the target unmanned vehicle was surrounded by the hunting unmanned vehicles in an environment with obstacles. It can be observed from the visual representation that the unmanned vehicle could safely avoid the obstacles to hunt the target. The experimental results presented in Figure 16 achieved the expected experimental results and verified the feasibility of the multiple unmanned vehicle hunting control strategy. The experiments were conducted several times and the experimental data obtained are presented in Table 3.
| Hunting strategy | Number of successful hunting | Number of collisions | Average time taken (s) |
|---|---|---|---|
| Based on the improved artificial potential field method | 10/10 | 0/10 | 38.6 |
| Based on improved contract network protocols [16] | 10/10 | 0/10 | 44.35 |
The difference in data is the difference in the time consumption of encirclement. The main reason is that the attraction of the target to the obstacle in the artificial potential field method makes the unmanned vehicle move faster, so it takes less time. From the data presented in Table 3, it can be observed that after conducting the experiments several times, the unmanned vehicles could achieve fast hunting of the target with no collision during the hunting owing to the hunting strategy based on the improved artificial potential field method. Compared with the hunting strategy of improved contract network protocols, time spent reduced by 12.97% and it was inferred that the proposed hunting strategy is more time efficient than others.
6. Conclusion
In this study, a hunting strategy based on the improved artificial potential field method is designed to solve the hunting problem in the complex environment containing obstacles. Firstly, the mathematical model of the unmanned vehicle formation is established. Then, according to the possible situation of the encirclement task, the fuzzy inference system is used to divide and decide the whole encirclement stage, so as to select the corresponding perception, approach, and encirclement strategies. First, a gravity threshold is added and the gravity field function greater than the threshold is changed to a linear function to reduce the target’s gravity to the unmanned vehicle and prevent collision due to excessive gravity. Then, the variable safety distance is designed to reduce the repulsion force of obstacles to the short-range unmanned vehicle and solve the problem of the target being unreachable. Finally, based on the improved function, an unmanned system is designed, which is composed of consistent state cost, environment obstacle avoidance cost, and control cost function. The effectiveness and rapidity of the rounding strategy are verified by simulation and experiment. The rounding strategy designed in this paper improves the rounding efficiency by 12.97% while ensuring the obstacle avoidance effect.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Acknowledgments
This study is supported by the Fundamental Research Funds for the Central Universities (3072022JC0404).
Open Research
Data Availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.




