1. Introduction

A system of differential equations represents the dynamics of real-life phenomenon. These systems can be applied in the field of physics, chemistry, fluid dynamics, engineering, economics, biological sciences etc. Initially, only temporal systems were used to observe the dynamics of different situations. But, for studying the most general behaviors of such systems, we can include the additional quantities such as advection and diffusion in the systems of differential equations. These systems depict the generic situations of the temporal and spatial models [1–3]. Reaction-diffusion equations are considered as one of the most important equations that are used in the modeling of chemical and biological systems. Certain phenomena such as population densities, concentration of chemical substance, and pressure of fluid are described by the state variables of such systems. Therefore, the positivity of state variables is an important requirement for the discrete scheme and should not produce nonphysical oscillations and negative solutions. There is not much work in the literature for positivity preserving and chaos-free numerical methods for chemical reaction models. In this study, we have designed two operator splitting positivity preserving and chaos-free numerical schemes for various reaction diffusion models arising in chemistry and biology.

In this paper, three different models of reaction diffusion equations in one-space dimension are considered for the study. The main aim of this work is to find the numerical solutions of these models with reliable numerical techniques. These proposed techniques preserve the structure of continuous systems in one dimension.

First of all, among these important models, we consider the Brusselator system that is used in describing the simulations of nonlinear oscillations in chemical reaction-diffusion processes [4–7]. The importance of oscillation in a biochemical system is very significant and was first introduced by Turning et al. [8]. They showed that when some phenomena are considered with diffusion term, a stable spatial pattern is obtained. Also, this system appears in a wide variety of models, such as ozone formation during oxygen atoms collision and enzymatic reactions. The reaction diffusion Brusselator system contains a couple of variables which intervene with reactions, and this process produces chemicals whose concentrations are then controlled. This model has been revealed as the trimolecular model.

Due to the importance of such models, many powerful and efficient techniques have been proposed for solving this system. Such models with nonlinear evolution terms are very hard to solve with the aid of analytical methods. Therefore, numerical methods are needed while dealing with such models. For example, Mittal et al. [9–11] investigated the solution of the one-dimensional Brusselator system using the differential quadrature technique. The behaviour of one-dimensional version of the Brusselator system is studied in [12] with the aid of collocation method based on the radial bases functions. A B-spline approach with a modification was introduced by Jiwari and Yuan in [13] for the Brusselator system with one and two dimensions. Also, a three dimensional form of this system was first solved in [14] using the modified B-spline differential quadrature method. Lin et al. [15] studied the inhomogeneous Brusselator model with cross diffusion process by using a finite volume element approximation and performed the stability analysis for the method and addressed the formation of turning patterns. A new exact solution for this system was driven using the exp-function method in [16]. For more details about the methods for solving the Brusselator model, see [17–20] and references therein.

As discussed earlier that ψ₁(x, t) and ψ₂(x, t) are the concentrations of the chemical substances or species, ϑ₁ and ϑ₂ represent the concentrations’ constants that appear in the reaction process, and $$ are the diffusion constants. The equilibrium point of systems (1) and (2) is $$. The point $$ is stable if $$ and unstable if $$. The solution to the system represented by equations (1) and (2) describes the positivity criteria as ψ₁ and ψ₂ are the concentrations of the two species [21]. Therefore, negative values of the solution of this model are meaningless. The numerical technique applied to find the solution of system by the coupled equation in (1) and (2) must preserve the positivity.

The finite-difference technique is an important tool to solve the nonlinear model involving differential equations. Because finding the analytical solution of such models is not an easy task. Therefore, various authors used finite-difference numerical schemes to solve several mathematical models involving ordinary differential equations or partial differential equations [22–28].

The nonstandard finite difference method (NSFD) is a powerful technique for solving different type of nonlinear continuous models which was first presented by Mickens back in 1993 [29]. Over the years, this method proved that it can treat continuous dynamical models that should preserve positivity property. For example, Ahmed et al. [30] adapt the NSFD scheme for solving different types of such models including the SEIR reaction diffusion model. Detailed discussion regarding NSFD and positivity preserving techniques can be found in [31–37].

The paper is organized as follows: in Section 2, four numerical techniques are presented for solving the Brusselator model. In Section 3, the stability and accuracy of the presented methods are introduced. Section 4 is devoted for illustrating the positivity of the purposed schemes. The applications of various reaction-diffusion systems along with the comparison of the four presented methods are presented in Section 5. Lastly, Section 6 provides conclusion for the study.

2. Numerical Techniques

In this section, we will introduce four techniques for solving systems (1)and(2) subjected to condition (3) and homogeneous Neumann boundary conditions. These numerical methods can be divided into two classical methods named as forward and backward operator splitting methods and two nonclassical methods named as explicit and implicit OS-NSFD methods. Each of these method has its own pros and cons. These methods are explained as follows.

3. Stability and Consistency of Underlying Techniques

In addition, for the Euler OS-FD and implicit NSFD methods, the stability for the diffusion process is found to be stable without any conditions.

Next, we will study the positivity of the solution by considering all of the above schemes.

4. Positivity of the Proposed Schemes

This section is concerned with the validation of positivity of the designed NSFD explicit and implicit techniques. The following theorem verifies that the proposed explicit technique retains the positivity of the solution.

Theorem 1 verifies that the property of positivity of the solution is preserved by the proposed OS-NSFD schemes at the reaction step.

We, then utilize the M-matrix theory [40] which helps in proving the positivity property for the proposed OS-NSFD implicit method (28)-(29).

5. Application

To support our claims regarding the proposed OS-NSFD techniques, we will implement these schemes to several reaction diffusion models along with the famous Brusselator model.

5.1. Brusselator Model

For the application of the proposed and classical methods under study, we chose the following numerical test. The graphical behaviour of the solution for each of the proposed four methods are demonstrated through the following figures for solving systems (1) and (2). As discussed above, systems (1) and (2) have a positive solution and converge toward the equilibrium point if the condition $$ is satisfied and unstable if $$.

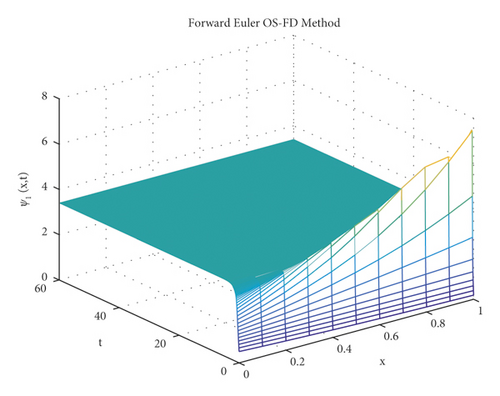
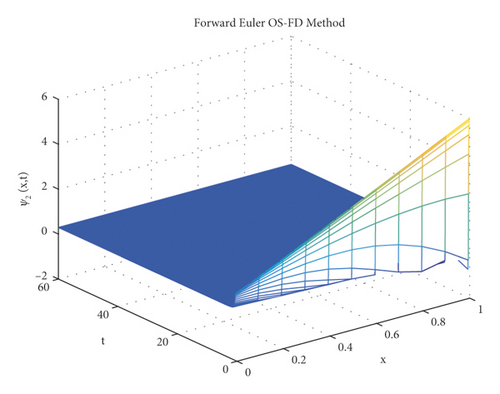
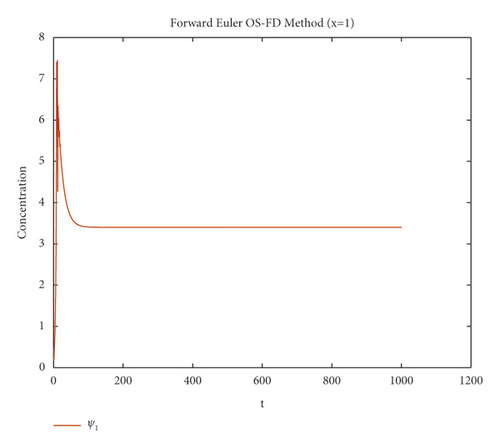
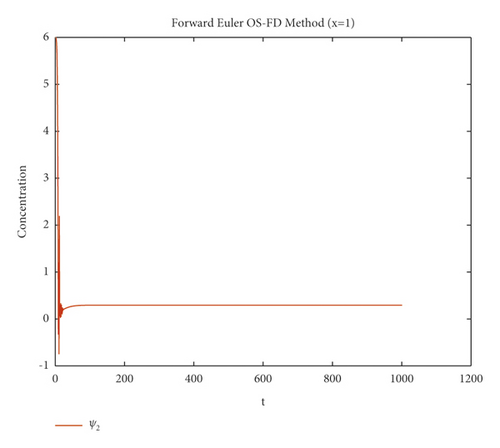
First, Figures 1 and 2 demonstrates the simulated results for the first method which is the forward Euler OS-FD technique at various step sizes. It can be noticed from these figures that this method gives nonconsistent data with systems (1) and (2). This proves that this method gives negative values of the concentrations which is meaningless. Also, the solution diverge from the equilibrium point which contradict with the physical behavior of the solution.

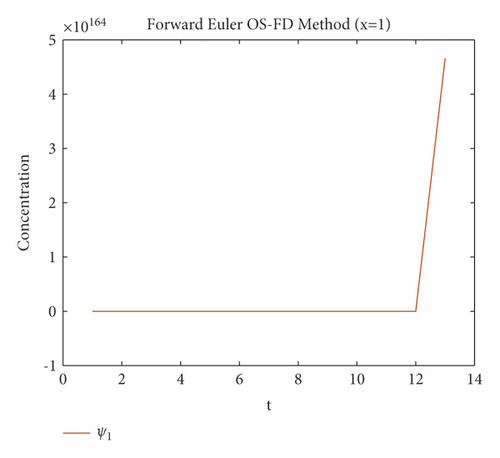
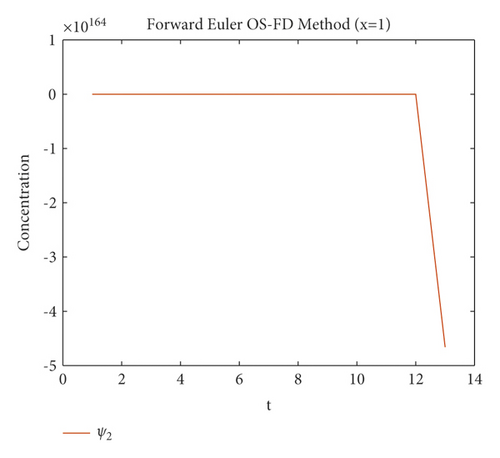
The second method is tested on the same example which is the backward Euler OS-FD method with the same value of parameters as in the first method for the sake of comparison. The behavior of the solution is illustrated in Figures 3 and 4. These figures show that this method, like the first method, fails to preserve the positivity of the solution and also gives divergence.

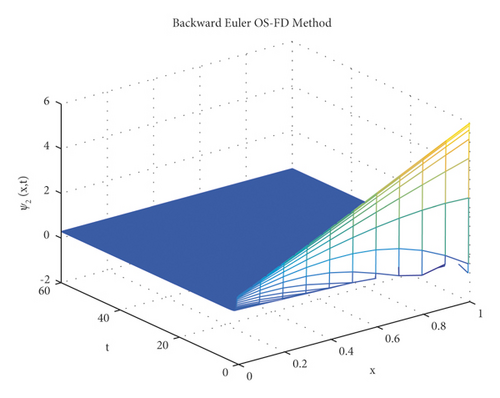
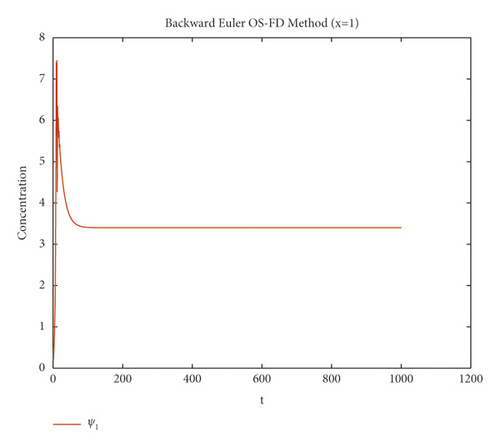
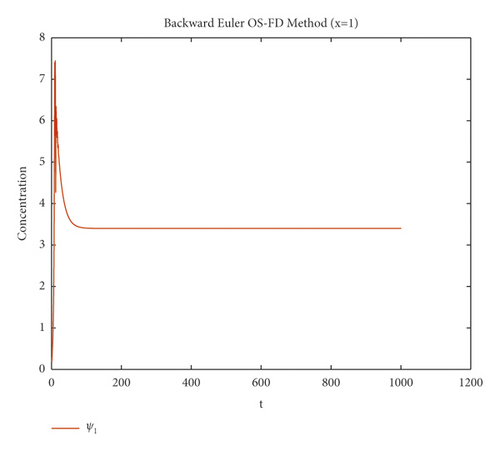
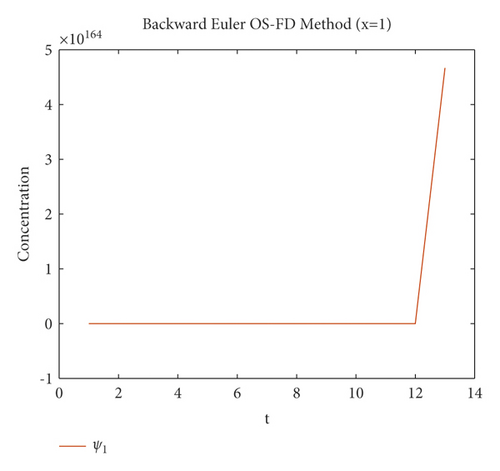
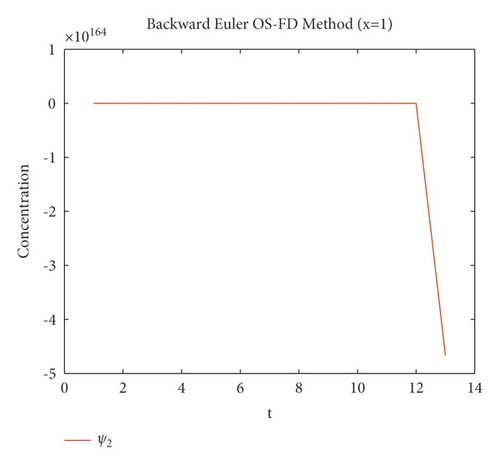
The graphical behaviour of the state variables show that the forward Euler and backward Euler OS-FD method are not the reliable techniques to solve the nonlinear auto-catalytic chemical reaction model. As they provide us with the negative solutions for the small step sizes.

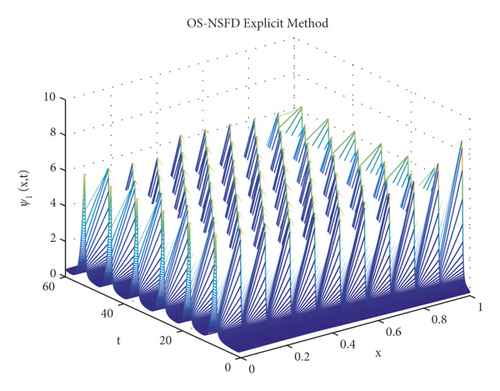
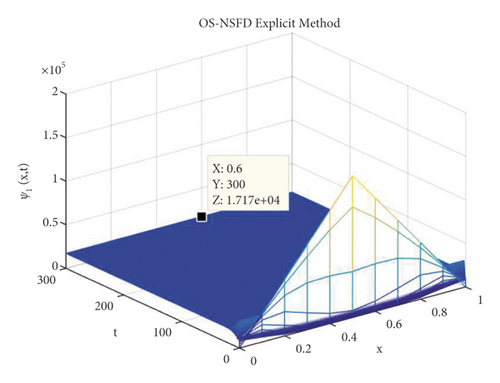
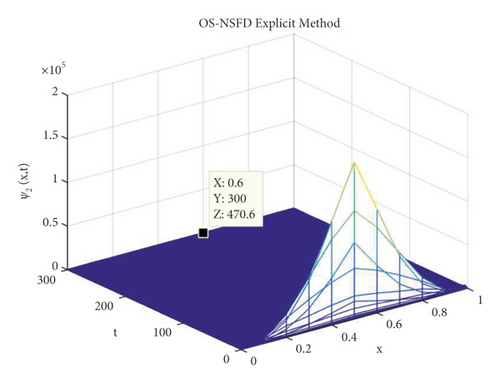
Due to the failure of the two abovementioned methods, the NSFD methods are presented to overcome this issue. Figures 5 and 6 show the graphs of the solution using the explicit OS-NSFD method. For the sake of comparison with the other methods, we use the same values of the parameters which are used in the previous two methods and took the value of ϑ₁ and ϑ₂ such that $$. From these figures, unlike the other methods, we observe that this method preserves the positivity and all the important properties of the glycolysis continuous model and converges toward the equilibrium point.

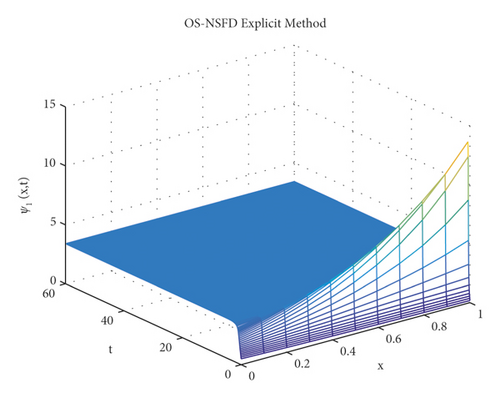
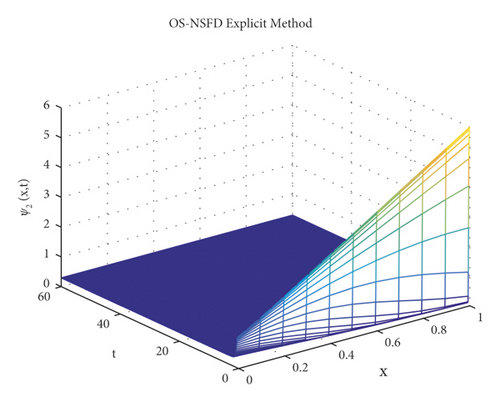
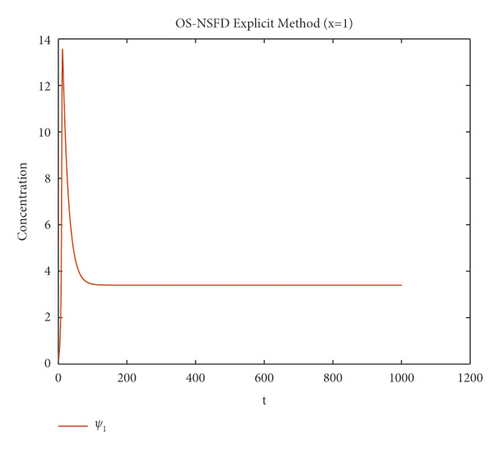
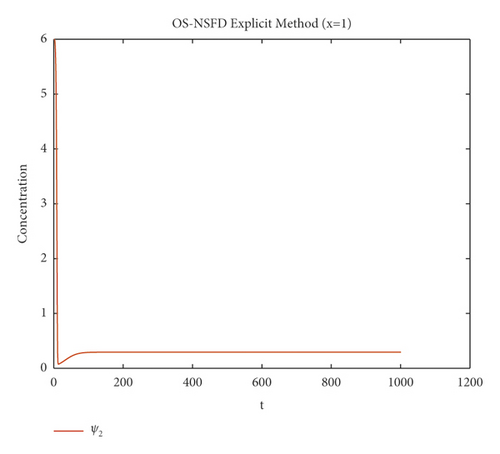
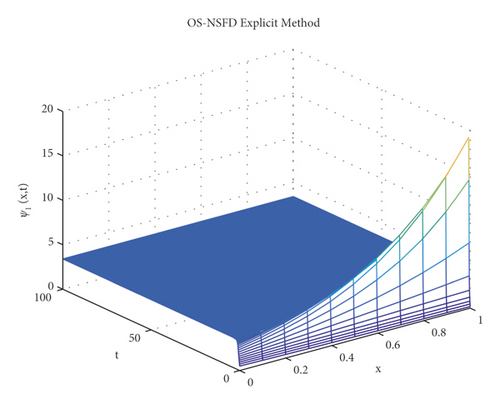
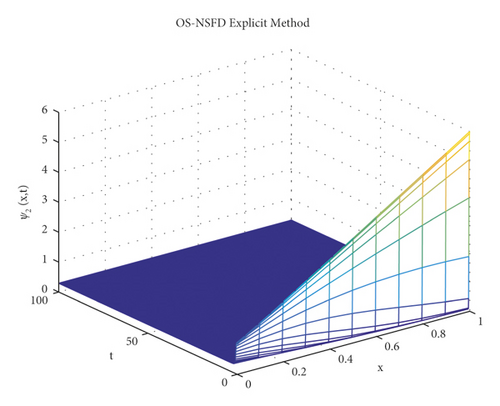
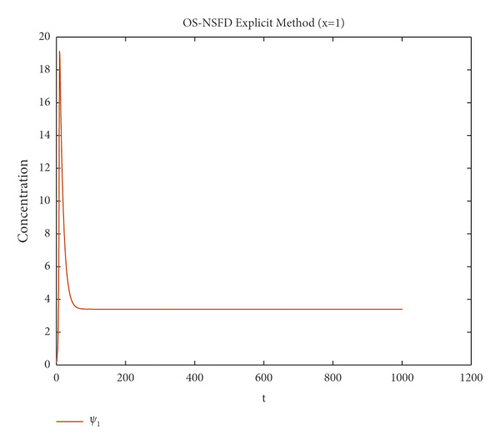
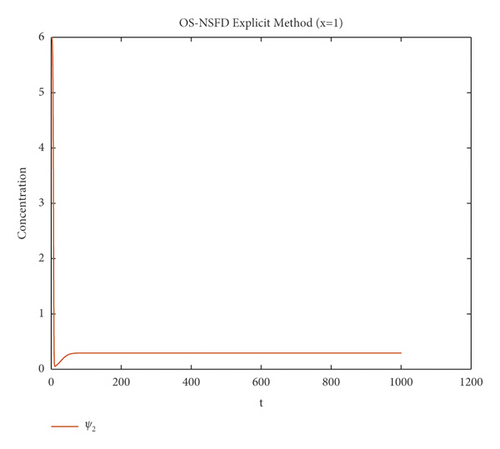
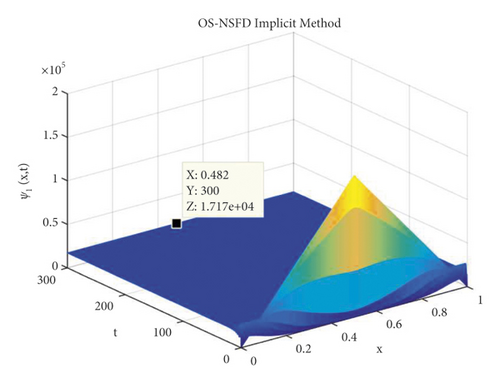
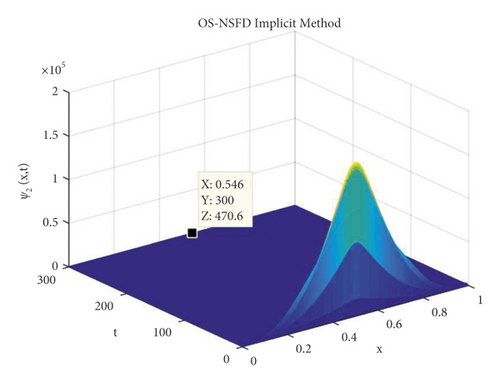
The graphs in Figures 7 and 8 demonstrate the concentrations by using the implicit OS-NSFD method. This behavior is also shown to be consistent with the explicit OS-NSFD method. This method like the previous method also preserves positivity and chaos-free properties and converges towards the equilibrium point which is stable under the condition $$.

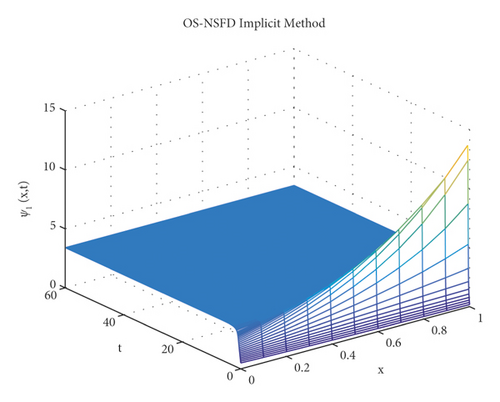
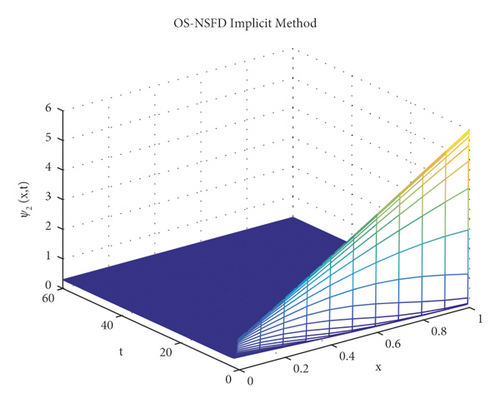
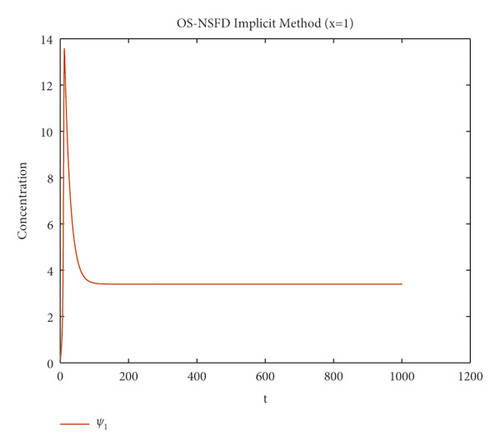
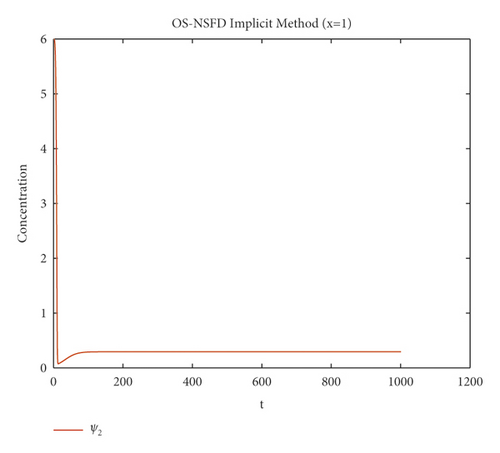
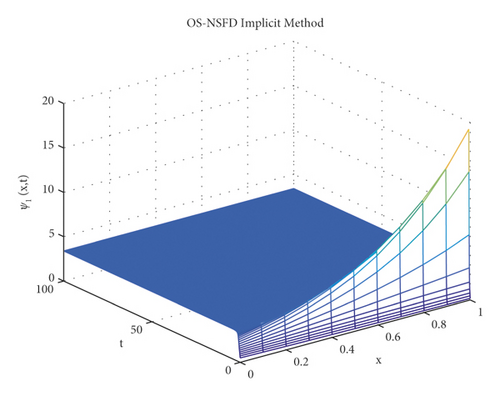
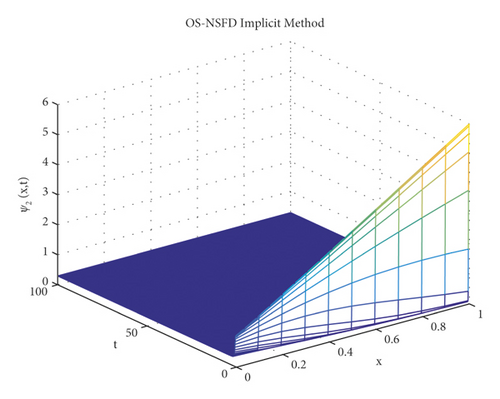
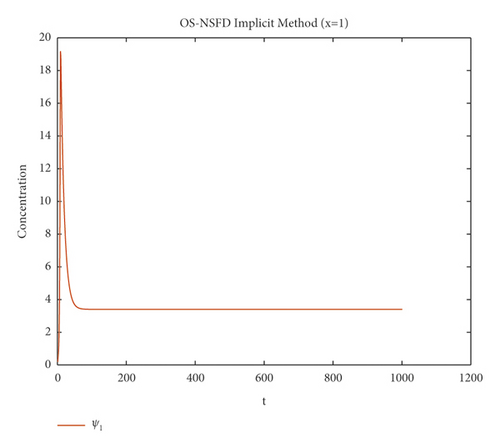
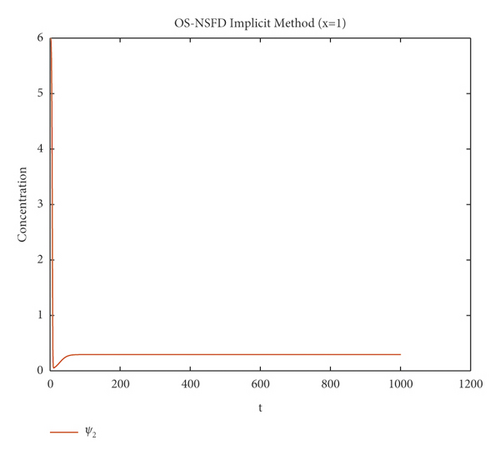
Now, the simulations by using both designed OS-NSFD techniques are given by considering the values of parameters ϑ₁ and ϑ₂ so that $$.

As mentioned before, the stability of the Brusselator system is preserved with the condition $$. Figures 9 and 10 prove this fact that the two new presented OS-NSFD methods are consistent with the continuous model when the stability condition holds and are inconsistent when $$. Figures 9 and 10 reflect the inconsistent behavior when the stability criterion does not hold, while the other while the other parameters and step sizes and kept fixed. This fact has been proven that stability criteria is very important in the stability analysis.

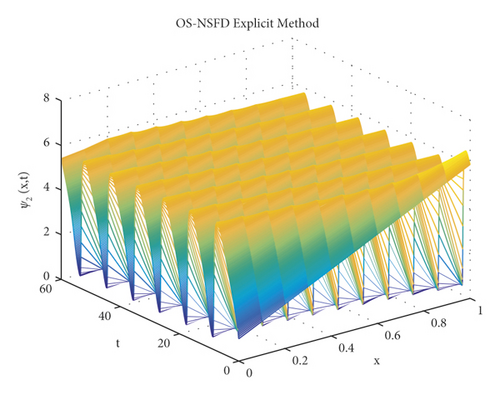
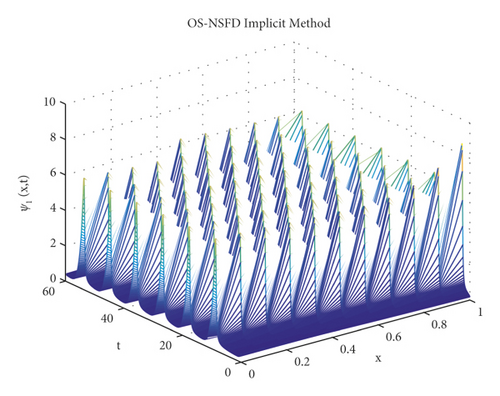
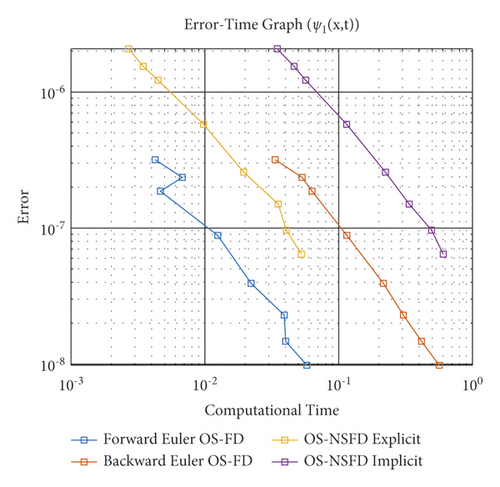
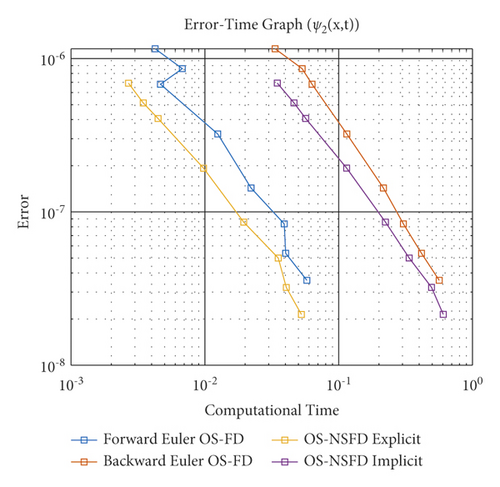
Now, we consider T = 1 and M = 100. Figure 11 depicts log-log graphs of the error versus the computational time. We presented the four schemes, and the graphs correspond to the solutions when we estimate the concentration profiles ψ₁ and ψ₂ of the Brusselator system. The result demonstrates that the OS-NSFD explicit and implicit schemes are approximately as efficient as forward Euler OS-FD and backward Euler OS-FD schemes. Obviously, the former technique stands out in terms of its capability to preserve the structure of the relevant solutions of the Brusselator model under investigation. It is worth pointing out that the approximation to the exact solution was obtained using N = 20000.

Finally, four numerical methods are used to solve the underlying model, namely, the forward Euler operator splitting method, backward Euler operator splitting method, nonstandard finite difference explicit operator splitting method, and nonstandard finite difference implicit operator splitting method. The extensively used numerical Euler methods (backward and forward) are used to solve the underlying models. The obtained solutions are analyzed and compared with the newly developed methods. The failure of the classical methods motivated us to develop new numerical methods. The new techniques are structure-preserving and reliable numerical methods that give positive and bounded solutions. The computed solutions converge towards the exact steady-state. So, the numerical analysis demonstrates that the NSFD methods are the reliable tool to solve the nonlinear models.

5.2. Susceptible-Infected-Recovered Epidemic Model

For the second application, we consider nonlinear reaction-diffusion system of infectious disease dynamics. The system is known as susceptible-infected-recovered (SIR) epidemic [41],

$$ (42)

$$ (43)

with initial conditions

$$ (44)

and homogeneous Neumann boundary conditions. In systems (42) and (43), ψ₁ = ψ₁(x, t) and ψ₂ = ψ₂(x, t) are susceptible and infected population densities. ϑ₁ is the parameter which represents natural birth and death rate. ϑ₂ indicates the rate of recovery from infected to recovered class. The transmission coefficient from susceptibility to disease is denoted by ϑ₃.

The epidemic systems (42) and (43) have two stable fixed points, disease-free point (DFP) and endemic point (EP). DFP is the point when disease eradicates from the population. The DFP of systems (42)and(43) ϵ₀ = (N, 0). The EP is the point when disease persists in the population. The EP of systems (42)and(43) is ϵ_∗ = (ψ_1 ∗, ψ_2 ∗), where ψ_1 ∗ = (ϑ₁ + ϑ₂)/ϑ₃ and ϑ_2 ∗ = (ϑ₁N/(ϑ₁ + ϑ₂)) − (ϑ₁/ϑ₃).

The basic reproductive number of the epidemic system (42)and(43) is ℬ₀ = Nϑ₃/ϑ₁ + ϑ₂ when $$. ℬ₀ is very important quantity which decides whether disease is eradicated or persisted. If ℬ₀ < 1, then disease will wipe out, and the disease is present if ℬ₀ > 1.

In the above experiment, we use the following numerical values of parameters involved in the above system. N = 3 × 10⁻⁰⁵, ϑ₁ = 0.04, ϑ₂ = 24, and $$. First, we depict the simulations of OS-NSFD explicit and implicit schemes at DFP. For the DFP, we take the value ϑ₃ = 9.2 × 10⁻⁰⁷ so that ℬ₀ < 1.

The simulations in the Figures 12 and 13 describe that the proposed splitting methods show positive solution as well as preserves the stability of fixed point DFP ϵ₀ = (N, 0) = (3 × 10⁻⁰⁵) under the condition ℬ₀ < 1. This shows that the designed NSFD splitting techniques do not show the contrived chaos.

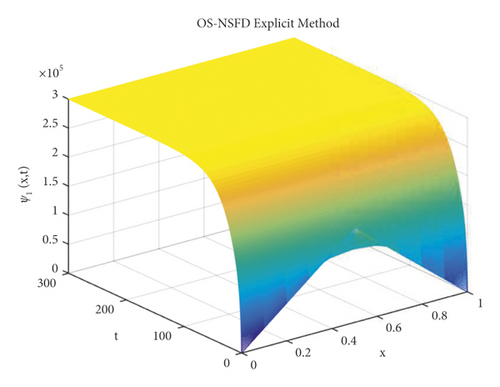
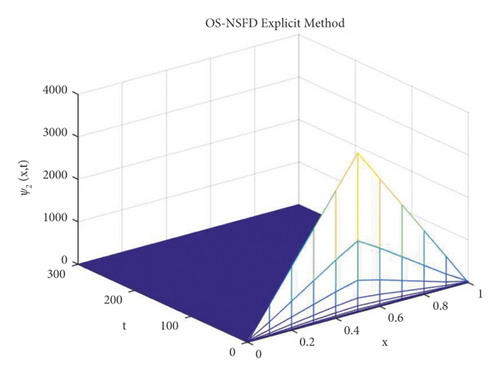
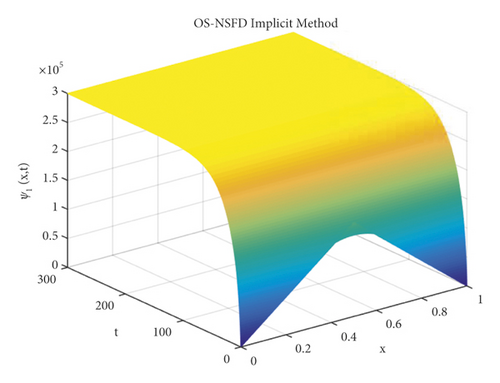
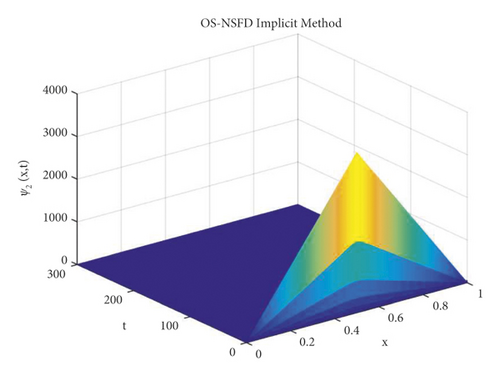
Also, the graphs for susceptible and infected individuals reflect the positive and bounded solutions. It is notable that those graphs converge towards the exact fixed points for the step sizes, and other parameter values are mentioned above.

Next, we present the simulations of OS-NSFD explicit and implicit schemes at EP. For the EP, we use the value ϑ₃ = 1.4 × 10⁻⁰³ so that ℬ₀ > 1.

As we have taken the values of parameters so that ℬ₀ > 1. This implicates that SIR epidemic model converges toward EP ϵ_∗ = (ψ_1∗, ψ_2∗). The simulation executed in Figures 14 and 15 illustrate the positive behavior and convergence to the EP ϵ_∗ = (ψ_1∗, ψ_2∗) of NSFD explicit and implicit splitting schemes. In the light of the above discussion, it can be concluded that OS-NSFD explicit and implicit methods are reliable numerical methods for the solution of reaction diffusion models. Because these methods confine all the important features of reaction diffusion systems like as positivity, boundedness, and stability at equilibrium points.

6. Schnakenberg Model

Here, ψ₁ and ψ₂ demonstrate the chemical concentrations of the two species. ϑ₁ and ϑ₂ are chemical kinetic positive constants, and ϑ₃ is the positive constant for the model which is dimensionless. The equilibrium point of systems (45)and(46) is $$, where $$ and $$. The equilibrium point is stable under the condition $$ [43]. If this condition violates, then the point $$ is unstable.

Now, we present the simulations of the above experiment. First, we take the values of parameters ϑ₁ = 2, ϑ₂ = 3, ϑ₃ = 0.5, and $$ such that the condition $$ satisfies. For these numerical values, the equilibrium point is $$.

The graphs in Figures 16 and 17 show the consistent behavior of both OS-NSFD explicit and implicit schemes. Both schemes show that the graphs converge towards the point $$. We are not presenting the graphical solution with forward Euler and backward Euler splitting schemes, but it is confirmed that the schemes will present the inconsistent behavior for different values of parameters as shown earlier for the Brusselator model.

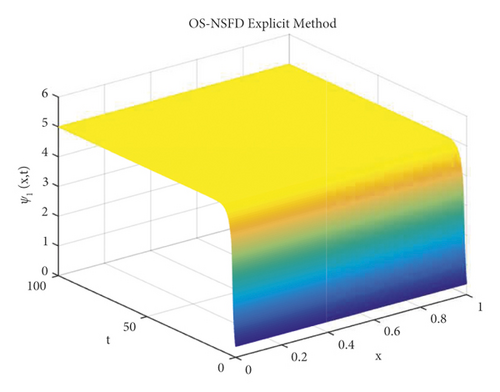
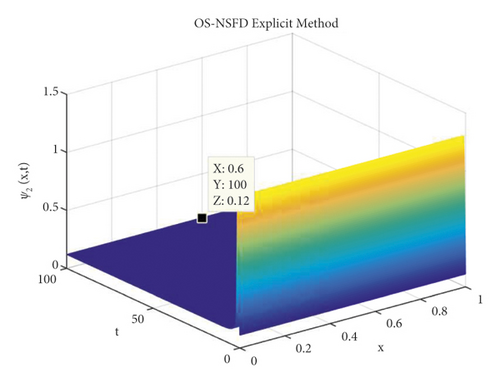
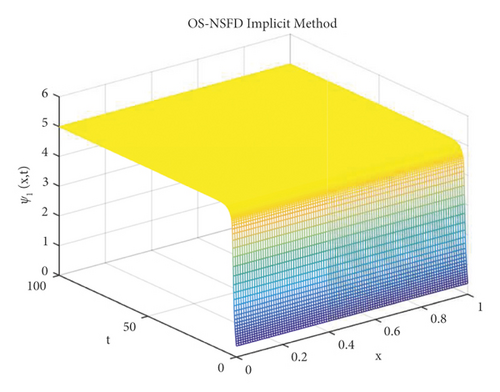
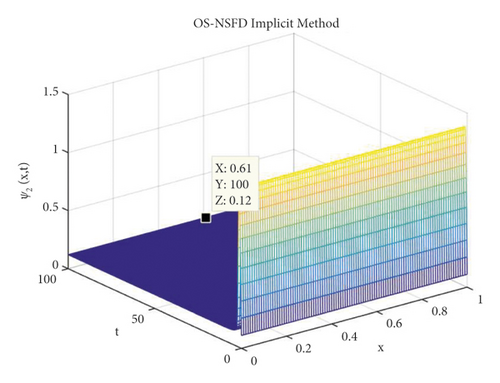
Now, we choose the values of parameters ϑ₁ = 0.1, ϑ₂ = 0.4, ϑ₃ = 0.5, and $$ such that the condition $$ violates.

As we discussed earlier that systems (45) and (46) show the unstable behavior if the condition $$ does not satisfy. The graphs in Figures 18 and 19 clarify that OS-NSFD explicit and implicit schemes also reveal the unstable behavior which is possessed by the continuous system.

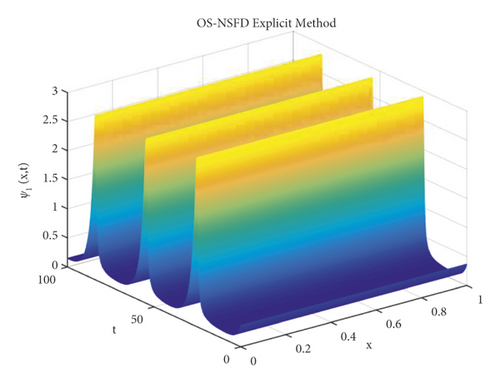
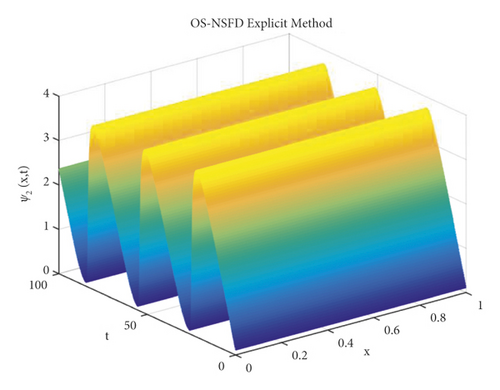
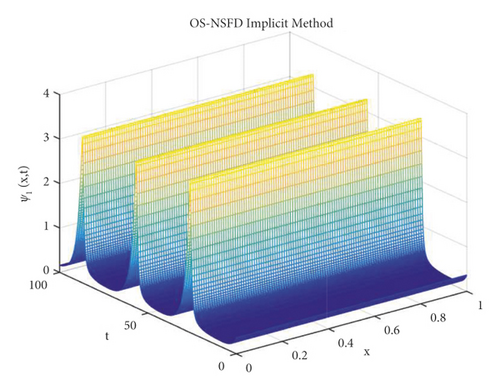
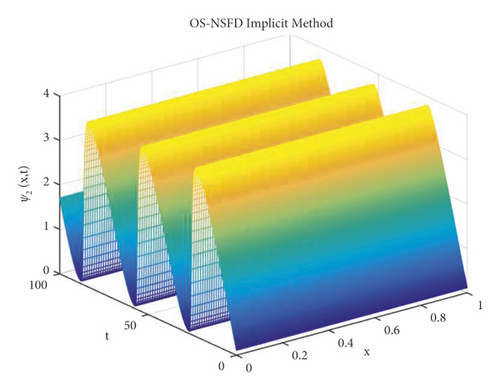
It is important to note that all the parameters and step sizes are kept same during the simulations. It is the stability condition that also plays an important role in describing the stability of the system.

7. Conclusion

In this article, four numerical schemes based on finite difference approximation are presented for solving different reaction-diffusion models in one-space dimension. It has been observed that two classical methods fail to provide accurate solution. Also, these schemes do not hold the positivity condition of the unknown variables in the continuous system. To overcome this issue, two new positivity preserving techniques have been proposed, based on OS-NSFD schemes. Our proposed methods not only provide the positive solution but also retain the essential physical attributes of the state variables. The designed schemes are applied on the Brusselator model, Schnakenberg model, and SIR epidemic model. The simulations are carried out to obtain the graphical solutions. The numerical results ascertained that the newly designed NSFD splitting schemes have some prominent features of the solution such as positivity of the solutions and stability at equilibrium points of the continuous system. One of the main significance is that the designed schemes do not generate the contrived chaos.

The OS-NSFD methods grant the positive solution irrespective of the step sizes. So, these schemes are unconditionally positivity preserving. Also, these schemes are time efficient and consistent.

The successful implementation of NSFD splitting schemes on three different problems show that our proposed schemes are futuristic and these techniques can be applied on various physical reaction diffusion problem in the fields of physical science, engineering, fluid mechanics, economics, and many more.

Conflicts of Interest

The authors declare no conflicts of interest.