Volume 2022, Issue 1 5095966

Research Article

Open Access

Research on Bridge Structural Damage Identification

Yi Sun

Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China kmust.edu.cn

Institute of Civil Engineering, Southwest Forestry University, Kunming 650224, China swfc.edu.cn

Search for more papers by this author

Kun Ma,

Corresponding Author

Kun Ma

[email protected]

orcid.org/0000-0002-9649-5073

Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China kmust.edu.cn

Search for more papers by this author

Dongfa Sheng,

Dongfa Sheng

Institute of Civil Engineering, Southwest Forestry University, Kunming 650224, China swfc.edu.cn

Search for more papers by this author

Dewen Liu,

Dewen Liu

Institute of Civil Engineering, Southwest Forestry University, Kunming 650224, China swfc.edu.cn

Search for more papers by this author

Bihui Dai,

Bihui Dai

Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China kmust.edu.cn

Institute of Civil Engineering, Southwest Forestry University, Kunming 650224, China swfc.edu.cn

Search for more papers by this author

Yi Sun,

Yi Sun

Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China kmust.edu.cn

Institute of Civil Engineering, Southwest Forestry University, Kunming 650224, China swfc.edu.cn

Search for more papers by this author

Kun Ma,

Corresponding Author

Kun Ma

[email protected]

orcid.org/0000-0002-9649-5073

Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China kmust.edu.cn

Search for more papers by this author

Dongfa Sheng,

Dongfa Sheng

Institute of Civil Engineering, Southwest Forestry University, Kunming 650224, China swfc.edu.cn

Search for more papers by this author

Dewen Liu,

Dewen Liu

Institute of Civil Engineering, Southwest Forestry University, Kunming 650224, China swfc.edu.cn

Search for more papers by this author

Bihui Dai,

Bihui Dai

Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China kmust.edu.cn

Institute of Civil Engineering, Southwest Forestry University, Kunming 650224, China swfc.edu.cn

Search for more papers by this author

First published: 2022

https://doi.org/10.1155/2022/5095966

Academic Editor: Le Sun

Share a link

Email
Wechat
Bluesky

Abstract

The traditional identification methods have limited ability to identify damage location of bridge structures. Therefore, a bridge structural damage location identification method based on deep learning is proposed. In addition, the sigmoid function is the activation function, and the cross entropy is the cost function. Meanwhile, take the Gaussian noise as the addition method and take the softmax as the classifier. So the constructed SDAE deep learning model can realize damage location identification of the simply supported the continuous beam bridges. Compared with the traditional identification methods of bridge structures, namely BP network and SVM, the proposed method shows higher identification accuracy and antinoise performance. Here, the average identification accuracy of the method for continuous beam bridge is 99.8%. As can be seen that the proposed method is more suitable for practical bridge structure damage location identification.

1. Intoduction

The development of social economy is inseparable from transportation. Bridge, as an important part of transportation, plays an important role in connecting the north and south. The safety of its structure is related to the safety of transportation, and it affects people's life. Once the bridge structure is seriously damaged, it will inevitably cause traffic accidents. In order to ensure the safe operation of bridges, it is of great significance to identify the damage of bridge structures. With the development of data transmission and processing technology, the nondestructive detection of bridge structures has been widely used. At present, the nondestructive detection and identification methods of bridge structures are mainly based on vibration identification methods, including the method based on modal domain data, the method based on time domain data, the method based on time-frequency domain data, and the method based on intelligent algorithm. For example, Xijun Ye and Boscato et al. proposed an adaptive signal denoising method based on genetic algorithm and singular value decomposition. By selecting SNR as fitness function, the genetic algorithm is introduced to automatically optimize p and r parameters. Then the inverse singular value decomposition is performed to obtain the denoised signal[1, 2]. This method is helpful to improve the identification accuracy of bridge structural damage location. Considering that the long-term effect of vehicle load is an important cause of fatigue, local damage, aging, reliability reduction, and so on, Jihwan Kim and Lili Li et al. proposed a bridge vehicle load model and carrying capacity evaluation method based on dynamic weighing system [3, 4]. Xiao-qin Li and Shiqiang Qin et al. discussed the strategy and scheme of multiscale finite element simulation of long-span bridge structures with the goal of structural damage diagnosis and safety assessment[5, 6]. Based on the analysis of the error sources of the finite element model, an error hierarchical correction method for the long-span bridges structure model is proposed. In addition, based on the finite element modeling and model modification process of cable-stayed bridge of the Runyang Yangtze River Bridge, a multiscale finite element simulation method for damage diagnosis and safety assessment of long-span cable-stayed bridge is proposed. Xianzheng Yu and Marco Furinghetti et al. established and modified the finite element model of the bridge structure to accurately simulate the behavior and working state of the bridge structure [7, 8]. On this basis, combining the finite element forward analysis with the signal inverse identification to evaluate the daily work of the bridge and the impact of various disasters on the structure. To a certain extent, the above research methods have realized the location of damage parts to different bridge structures, but the positioning accuracy and antinoise performance need to be improved. Therefore, in order to improve the identification accuracy and antinoise performance of the algorithm for bridge structure damage location, and based on deep learning model, this paper proposes a bridge structure damage location identification method based on stacked denoising autoencoder.

1.1. Introduction to SDAE Model

SDAE is a common model in deep learning, it is formed by stacking several denoising autoencoders. However, on the basis of autoencoder, the denoising autoencoder is a network. First, it can add noise to the training data and randomly mask part of training data. Subsequently, it forces the model to learn denoising and restore the input data. Therefore, to understand the principle of SDAE, the first is to understand the structure and training mode of autoencoder and denoising autoencoder.

1.2. Introduction to Autoencoder

Autoencoder consists of encoder and decoder, including input layer, hidden layer, and output layer, as shown in Figure 1. Wherein, the encoder is responsible for mapping the input vector to the hidden layer through the activation function, so as to obtain the feature expression of a higher level, as shown in formula (1) [9]. The decoder is responsible for mapping the hidden layer feature representation to the original input, and its function expression is shown in formula (2) [10].

\begin{matrix} z = f (x) = s (W^{(1)} x + b^{(1)}), \end{matrix}

(1)

\begin{matrix} x^{'} = g (z) = s (W^{(2)} x + b^{(2)}) . \end{matrix}

(2)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram of autoencoder structure.

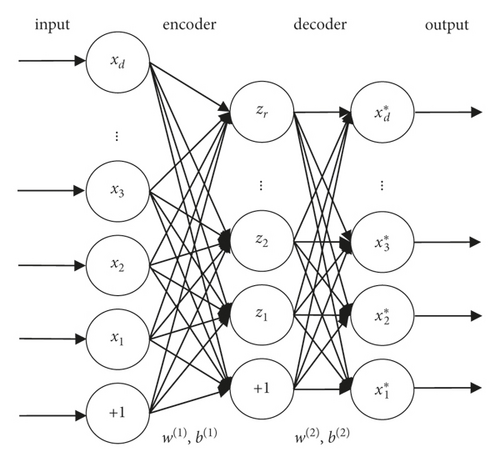
Formula (1) shows that x represents the input vector, z represents the encoder output vector, W⁽¹⁾ represents the input weight of the hidden layer, b⁽¹⁾ represents the input bias of the hidden layer, and s represents the activation function.

Formula (2) shows that x ^′ represents the output matrix, W⁽²⁾ represents the input weight of the output layer, and b⁽²⁾ represents the input bias of the output layer.

The training method of the autoencoder is unsupervised learning, and the network parameter θ = {W⁽¹⁾, W⁽²⁾b⁽¹⁾, b⁽²⁾} is adjusted to make the final output X^∗ as close as possible to the original input X. Its error function is defined as square error, as shown in

\begin{matrix} L = {‖x - g (f (x))‖}^{2} . \end{matrix}

(3)

The weight and bias can be updated according to the error back propagation and gradient descent algorithm, and the optimal parameter θ can be obtained.

1.3. Denoising Autoencoder

Denoising autoencoder takes the data with added noise as input and outputs the predicted original data without noise through training. Its denoising principle is shown in Figure 2. In the figure, x represents the original data, x₁ represents the data with noise, and y represents the feature obtained by encoding x₁ in the hidden layer of the denoising autoencoder, Z represents the original data restored by decoding y, andL_D (x,z) represents the error function.

The training of denoising autoencoder makes the error function L_D minimum. Since random noise is added to the denoising autoencoder, formula (3) can be rewritten as

\begin{matrix} L_{D} = {‖X - g (f (X I))‖}^{2} . \end{matrix}

(4)

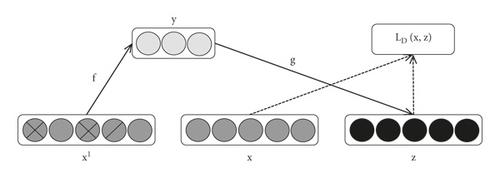
The weight and bias can also be updated by using error back propagation and gradient descent algorithm, and the optimal parameter θ can be obtained.

For SDAE, the training method is that initially determine the parameters of a single denoising autoencoder through unsupervised learning, then use the BP algorithm to conduct supervised learning for all denoising autoencoders, and fine-tune the global parameters.

1.4. BP Algorithm Parameter Tuning

BP algorithm includes two stages, namely information forward calculation and error back propagation, and its common activation function is shown in the following formula[11].

\begin{matrix} f (u) = \frac{1}{1 + e^{- λ u}} . \end{matrix}

(5)

In the information forward calculation stage, the input and output of neuron j in network k layer can be expressed as formula (6). The weight of update method in the error back propagation stage is shown in formula (7).

\begin{matrix} y_{j}^{(k)} = f_{j}^{(k)} (\sum_{i = 1}^{N_{t - 1}} ω_{i j}^{(k - 1)} y_{i}^{(k - 1)} - θ_{j}^{(k)}), k = 1,21,2, \dots, M; j =, \dots N_{k}, \end{matrix}

(6)

\begin{matrix} ω_{i j}^{(k - 1)} (t + 1) = ω_{i j}^{k - 1} (t) + η \sum_{h = 1}^{I} δ_{h j}^{(k)} y_{h k}^{(k - 1)} . \end{matrix}

(7)

Formula (6) shows that M represents the total number of layers; N_k represents the total number of neurons in k layer; $ω_{i j}^{(k - 1)}$ represents the connection weight between neuron i of k-1 layer and this neuron; $θ_{j}^{(k)}$ represents the neuron offset value; and $y_{j}^{(k)}$ represents the output of neuron i of k-1 layer.

Formula (7) shows that 0 < η < 1 represents the learning step and δ represents the error transmission term. For the output layer, it can be calculated by formula (8), and the other layers can be calculated by formula (9).

\begin{matrix} δ_{h j}^{(M)} = ({\overset{\land}{y}}_{h j}^{(M)} - y_{h j}^{(M)}) f_{j} (y_{h j}^{(M)}), \end{matrix}

(8)

\begin{matrix} δ_{h j}^{(k)} = f_{j} (y_{h j}^{(k)}) \sum_{i = 1}^{N_{k + 1}} δ_{h j}^{(k + 1)} ω_{i j}^{(k)} (t) . \end{matrix}

(9)

where

{\overset{\land}{y}}_{h j}^{(M)}

and

y_{h j}^{(M)}

are the actual output and expected output values of BP algorithm, respectively.

Finally, the output error of BP algorithm can be expressed as [12]

\begin{matrix} ε = {\sum_{h = 1}^{I} \sum_{j = 1}^{N_{M}} ({\overset{\land}{y}}_{h j}^{(M)} - y_{h j}^{(M)})}^{2} . \end{matrix}

(10)

It can be seen from the above analysis that SDAE can obtain the most representative features of the original samples from the input samples with noise through multiple stacked denoising autoencoders, which is conducive to enhancing the robustness of the model. Considering the possibility of distortion in the data collection of the bridge structure, which is similar to adding noise data to the real data, SDAE can be used to analyze the data of the bridge structure. Therefore, this paper proposes an identification method of bridge structural damage location based on SDAE.

2. Bridge Structural Damage Location Identification Based on SDAE

2.1. SDAE Model Construction

2.1.1. Activation Function Selection

The activation function can satisfy the nonlinear arbitrary function mapping between input and output information, and it can make the model have the ability of learning complex data. Therefore, the selection of activation function is particularly important. At present, the common activation functions in deep learning models mainly include Tanh, ReLu, and Sigmoid functions. The Tanh function expression is shown in formula (11) [13], and the derivative function expression is shown in formula (12) [14]. There is advantage of improving model training efficiency, but it is prone to zigzag phenomenon. Therefore, the optimal value is difficult to be obtained in the training [15]. The ReLu function expression is shown in formula (13) [16], and the derivative function expression is shown in formula (14) [17]. Here, the problem of gradient disappearance can be effectively solved. However, the point will never be activated when the input value is negative, which results that the training data lack diversity [18]. Sigmoid function can fit the function well, but there is the problem of gradient disappearance, which can be solved by pretraining and BP algorithm fine-tuning [19]. So this paper selects Sigmoid function as the activation function.

\begin{matrix} f (x) = 2 s i g m o i d (2 x), \\ - 1 = \frac{2}{1 + e^{- 2 x}}, \\ - 1 = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}} . \end{matrix}

(11)

\begin{matrix} f^{'} (x) = 1 - {(f (x))}^{2}, \end{matrix}

(12)

\begin{matrix} f (x) = \max (0, x), \end{matrix}

(13)

\begin{matrix} f' (x) = \{\begin{cases} 0 & x < 0, \\ 1 & x \geq 0, \end{cases} \end{matrix}

(14)

Sigmoid function is a nonlinear transformation function, whose mathematical description is shown in formula (15). Its output range is between (0, 1). Since the function is continuously derivable, its derivative function can be expressed as formula (16).

\begin{matrix} f (x) = \frac{1}{1 + e^{- x}}, \end{matrix}

(15)

\begin{matrix} f' (x) = f (x) (1 - f (x)) . \end{matrix}

(16)

2.1.2. Cost Function Selection

The cost function is a function that measures the error between the predicted value and the real value of the model. The cost function is used to calculate the partial derivative for the weight and applied to the gradient descent algorithm to update the weight of each layer. And the deep learning model with learning ability can be obtained. Therefore, the cost function of SDAE needs to be determined. At present, cost functions used in deep learning models are mainly cross entropy cost functions, as shown in formula (17) [20]. In addition, the mean square cost function is shown in formula (18) [21]. Compared with the mean cost function, the cross entropy cost function is more suitable for classification tasks [22]. Because the bridge structural damage location identification is actually a classification task, the cross entropy cost function is selected as the SDAE cost function in this paper.

\begin{matrix} C = - \frac{1}{n} \sum_{i = 1}^{n} [x_{i} I n (x_{i}^{*}) + (1 - x_{i}) I n (1 - x_{i}^{*})], \end{matrix}

(17)

\begin{matrix} C = \frac{1}{2 n} {\sum_{i = 1}^{n} ‖x_{i}^{*} - x_{i}‖}^{2} . \end{matrix}

(18)

Among them, $x_{i}^{*}$ and x_i represent the predicted value and the true value, respectively. N represents the total number of training samples.

2.1.3. Selection of Noise Adding Method

The data of bridge structure usually include the damage data, so the data of bridge structure can be simulated by adding noise. The methods of adding noise mainly include salt and pepper noise and Gaussian noise. Among them, salt-and-pepper noise is usually used in image processing [23]. Since the identification of bridge structural damage location does not involve image processing, the Gaussian noise is selected as the method to add noise. Gaussian noise means that the probability density function of noise obeys normal distribution, as shown in formula (19).

\begin{matrix} P (x) = \sqrt{\frac{1}{2 π σ^{2}} \exp} (- \frac{1}{2 σ^{2}} {(x - μ)}^{2}) . \end{matrix}

(19)

where μ and σ² represent the mean and variance of the Gaussian distribution, respectively.

Add Gaussian noise to the input vector and obtain

\begin{matrix} x_{i}^{*} = x_{i} \cdot η \cdot n o r m m d (0,1) . \end{matrix}

(20)

Here, x_i and $x_{i}^{*}$ represent the input data before and after processing noise i, respectively, η represents noise level; and normrnd(0,1) represents Gaussian noise with mean value 0 and variance 1.

2.1.4. Classifier Selection

Classifiers are used to classify the test samples. And classifiers are an essential part of deep learning models. At present, the common classifiers for deep learning models mainly include SVM, BP network, and Softmax. Among them, the SVM is mainly used to deal with linear separable classification problems. The classification form of BP network is regression value. And the Softmax conducts classification through probability expression, which is closer to the identification of bridge structural damage location in this paper [24]. Therefore, softmax classifier is selected as SDAE classifier. For softmax classifier, if the input is x, the output is k-dimensional vector, and k represents the total number of categories, and its mathematical expression is [25]:

\begin{matrix} h_{ω} (x) = [\begin{matrix} p (y^{(i)} = 1 | x^{(i)}; ω) \\ p (y^{(i)} = 2 | x^{(i)}; ω) \\ ⋮ \\ p (y^{(i)} = k | x^{(i)}; ω) \end{matrix}] = \frac{1}{\sum_{j = 1}^{k} e^{ω_{j}^{T} x^{(i)}}} [\begin{matrix} e^{ω_{1}^{T} x^{(i)}} \\ e^{ω_{2}^{T} x^{(i)}} \\ ⋮ \\ e^{ω_{k}^{T} x^{(i)}} \end{matrix}] . \end{matrix}

(21)

where ω represents the weight parameter.

On the basis of the above analysis, the SDAE model constructed in this paper is shown in Table 1.

Table 1. SDAE model settings.

Deep learning model	Activation function	Cost function	Noise adding mode	Classifier
SDAE	Sigomid	Cross entropy cost function	Gaussian noise	Saftmaxclassifier

2.2. Identification Process

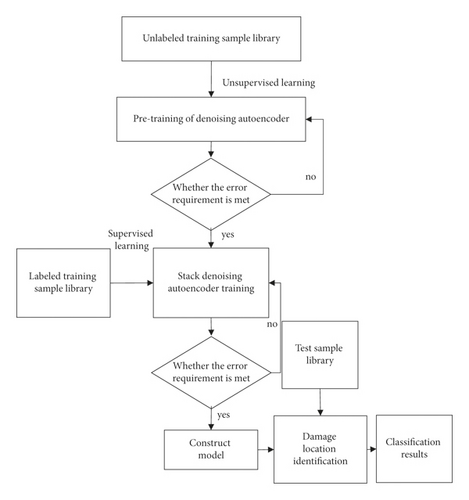
According to the constructed SDAE model, the identification method of bridge structural damage position is designed as Figure 3. First of all, the bridge structure sample data are divided into unlabeled sample and labeled sample data set. Then, the denoising autoencoder is used to conduct unsupervised learning and pretraining for unlabeled data, and the samples meeting the error requirements are input into SDAE for training. Meanwhile, the labeled samples are trained by SDAE for supervised learning and pretraining. When the training results meet the error, the SDAE model is constructed. At last, the constructed SDAE model is adopted to identify the damage locations of test samples and output the results. It can be seen that the bridge structural damage location identification based on SDAE is realized.

3. Simulation Experiment

3.1. Experimental Environment

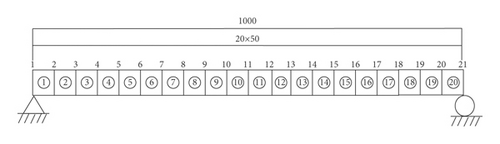
This experiment is simulated on ANSYS finite element analysis software and MATLAB platform. The net span of the simply supported beam bridge model is 10 m, the concrete grade is C50, the beam cross-sectional area is 0.2 m², the inertia moment of unit section is 0.0042 m⁴, the beam height is 0.5 m, the density is ρ = 2500kg/m³, and the elastic modulus is 3.5 × 104 MPa[26–29]. Its unit division and plate-beam interface are shown in Figure 4. As can be seen from the figure, the simply supported beam bridge model is divided into 20 units and 21 nodes. Node 1 and node 21 are end nodes of the bridge, which are fixed hinge supports and sliding supports, respectively. Among them, the main beam is simulated by Bean3 unit, the horizontal and vertical displacements are used for node 1 constraint, and the vertical displacements are used for node 21 constraint.

The continuous beam bridge model is a two-span continuous beam bridge. The net span is (24 + 24) m, the concrete grade is C50, the beam sectional area is 0.18 m², the inertia moment of unit section is 0.0054 m⁴, the beam height is 0.6 m, the density is ρ = 2500kg/m³, and the elastic modulus is 3.5 × 104 MPa. The unit division and plate-beam interface are shown in Figure 5. As can be seen from the figure, the continuous beam bridge model was divided into 24 units and 25 nodes. The length of each unit is 2m. Node 1, node 13, and node 25 are end nodes of the bridge, which are interactive supports, fixed hinge supports, and sliding supports, respectively. Among them, the main beam is simulated by Bean3 unit. The node 1 and node 25 are constrained by displacement cross the bridge, vertical angle along the bridge, and vertical displacement. The node 13 is constrained by displacement cross the bridge, displacement along the bridge, vertical displacement, and vertical angle along the bridge.

3.2. Damage Samples of Bridge Structures

3.2.1. Damage Index and Training Sample Database Determination

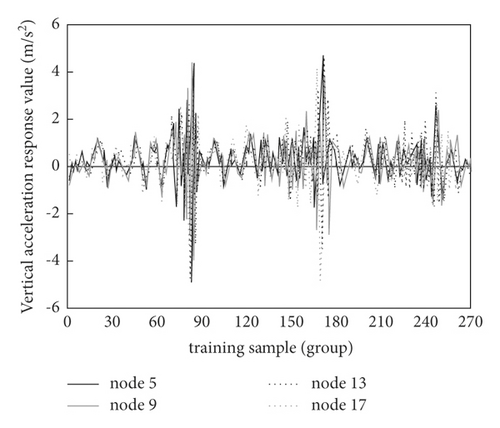
Combining the various literature, the acceleration response value of the measuring point is selected as the damage index of the bridge structure position identification. Totally, 270 groups of measuring point accelerations are used as a training sample database for damage location identification of simply supported beam bridges. In total, 12600 groups of measuring point accelerations are selected as a training sample database for damage location identification of continuous beam bridges.

3.2.2. Simply Supported Beam Bridge

Damage Condition. A moving load with a directional speed of 18 km/h is placed on the bridge, and the reduction of elastic modulus of material is defined as the damage degree. If the elastic modulus is reduced by 10%, the damage degree is 10% and substituted by the concentrated force F = 100 kN. Finally, there are seven damage conditions in this experiment, including no damage state and certain damage degree of a damage unit. The corresponding damage labels are shown in Table 2.

Table 2. Damage labels of simply supported bridge samples.

Damage condition number	Loading condition					Damage unit	Damage degree	Label
Damage condition number	Boundary conditions	Concentration force size (kN)	Movement speed	Start	End	Damage unit	Damage degree	Label
JZLQ1	Boundary conditions of simply supported beam	100	18 km/h	Node 1	Node 21	No	No	1st category
JZLQ2	Boundary conditions of simply supported beam	100	18 km/h	Node 1	Node 21	No. 3	45%	2nd category
JZLQ3	Boundary conditions of simply supported beam	100	18 km/h	Node 1	Node 21	No. 3	55%	2nd category
JZLQ4	Boundary conditions of simply supported beam	100	18 km/h	Node 1	Node 21	No. 7	5%	3rd category
JZLQ5	Boundary conditions of simply supported beam	100	18 km/h	Node 1	Node 21	No. 7	95%	3rd category
JZLQ6	Boundary conditions of simply supported beam	100	18 km/h	Node 1	Node 21	No. 11	25%	4th category
JZLQ7	Boundary conditions of simply supported beam	100	18 km/h	Node 1	Node 21	No. 11	55%	4th category

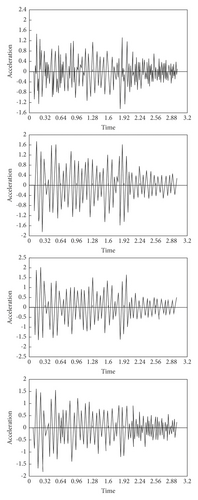
Sample Preprocessing. Under the action of moving load, the vertical acceleration values of nodes 5, 9, 13, and 17 in the 3 s of the simple beam bridge are randomly selected as the damage index [30]. Among them, the corresponding acceleration-time curve to each node in nondamage state is shown in Figure 6.

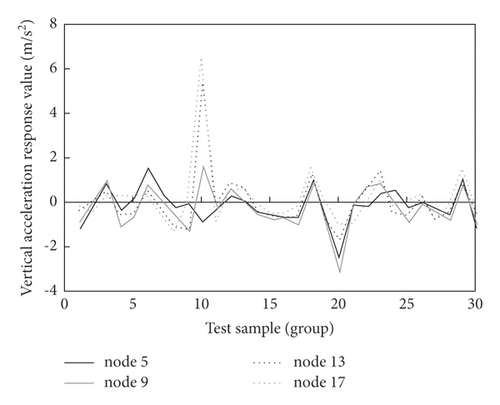
Z-score is used to conduct standardized preprocessing for the training samples and test samples, and sample I for SDAE training and test can be obtained, as shown in Figure 7.

3.2.3. Continuous Beam Bridge

Damage Condition. A moving load with a directional speed of 18 km/h is placed on the bridge, and the reduction of elastic modulus of material is defined as the damage degree. If the elastic modulus is reduced by 10%, the damage degree is 10%, and substituted by the concentrated force F = 100 kN. In order to be different from simply supported beam bridge, multiple unit damage is added in the experiment. Finally, the damage label database of the set test samples is shown in Table 3.

Table 3. Damage labels of continuous beam bridge samples.

Damage condition number	Loading condition					Damage unit	Damage degree	Label
Damage condition number	Boundary conditions	Concentration force size (kN)	Movement speed	Start	End	Damage unit	Damage degree	Label
LXLQ1	Continuous beam bridge boundary conditions	100	18 km/h	Node 1	Node 25	3	40%	1st category
LXLQ2	Continuous beam bridge boundary conditions	100	18 km/h	Node 1	Node 25	10	15%	2nd category
LXLQ3	Continuous beam bridge boundary conditions	100	18 km/h	Node 1	Node 25	21	55%	3rd category
LXLQ4	Continuous beam bridge boundary conditions	100	18 km/h	Node 1	Node 25	6.9	30%, 30%	4th category
LXLQ5	Continuous beam bridge boundary conditions	100	18 km/h	Node 1	Node 25	11, 19	15%, 15%	5th category
LXLQ6	Continuous beam bridge boundary conditions	100	18 km/h	Node 1	Node 25	5, 22	30%, 60%	6th category
LXLQ7	Continuous beam bridge boundary conditions	100	18 km/h	Node 1	Node 25	4, 8, 11	10%, 10%, 10%	7th category
LXLQ8	Continuous beam bridge boundary conditions	100	18 km/h	Node 1	Node 25	9, 15, 20	45%, 45%, 45%	8th category
LXLQ9	Continuous beam bridge boundary conditions	100	18 km/h	Node 1	Node 25	5, 15, 20	60%, 60%, 60%	9th category

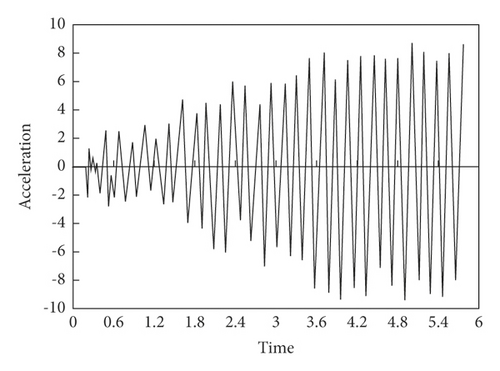
Sample Preprocessing. Under the action of moving load, all the vertical acceleration response values of nodes 4, 7, 10, 11, 19, and 22 within 5.8 s of continuous girder bridge are randomly selected as the training sample database. Among them, the damage degree is 40%, and the damage unite is No. 3. The corresponding acceleration-time curve of each node at this unit state is shown in Figure 8.

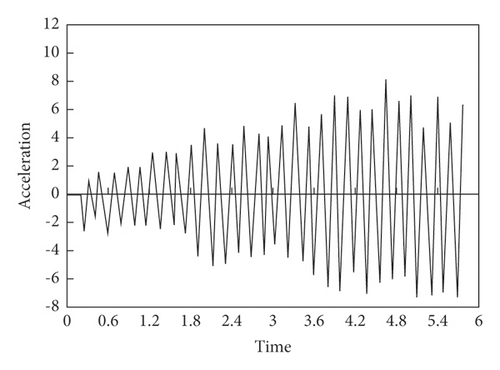
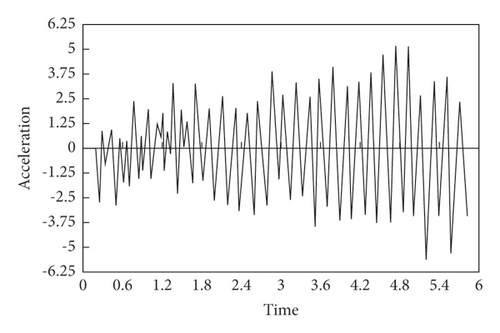
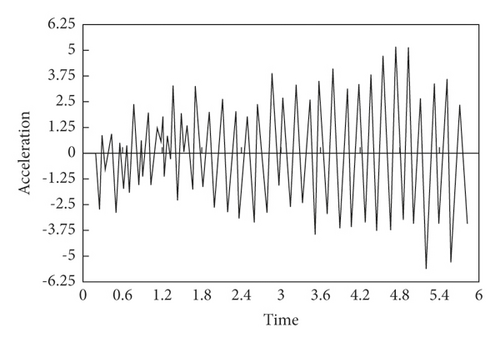
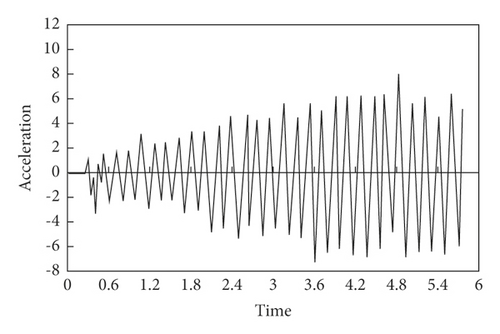
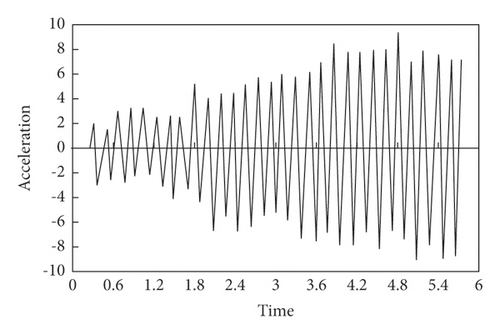
Z-score is adopted to perform standardized preprocessing for training samples and test samples, and sample II for SDAE training and test can be obtained, as shown in Figure 9.

3.3. Results and Analysis

3.3.1. Damage Location Identification of Simply Supported Beam Bridges

Analysis of Recognition Results. The test sample of preprocessed sample I is used as the input data of SDAE, and the recognition results of deep learning model are shown in Table 4. In the table, the first category represents nondamaged unit, the second category represents the No. 3 damaged unit, the third category represents the No. 7 damaged unit, and the fourth category represents the No. 11 damaged unit. As can be seen from the table, the identification accuracy of the proposed method for all damage categories has been reached 93.3%. Among them, the recognition accuracy of undamaged unit and No. 7 damaged unit is 100%, the recognition accuracy of No. 3 damaged unit is 90%, and the recognition accuracy of No. 11 damaged unit is 88.9%. Therefore, the proposed method for the each damage unit location identification of simply supported beam bridge has certain effectiveness.

Table 4. Damage location identification results of simply supported beam bridges.

Damage category	Total number of actual categories	The number of accurate classifications	Accuracy (%)
1st category	1	1	93.33
2nd category	10	9
3rd category	10	10
4th category	9	8

In order to verify the effectiveness of the proposed method for damage location identification of simply supported beam bridges with noise data, 5%, 10%, and 15% Gaussian noise are added to the input data of training data and test data in sample I, respectively. Meanwhile, the proposed method is adopted to identify, and the results are obtained as shown in Table 5. As can be seen from the table, under different noise conditions, the proposed method has a high recognition accuracy, which reaches 93.3%. Therefore, the SDAE proposed in this paper can effectively identify the location of each damage unit of a simply supported beam bridge.

Table 5. Damage location identification results of simply supported beam bridges under different noise conditions.

Project	The number of actual categories	Correct classification at 0% noise	Correct classification at 5% noise	Correct classification at 10% noise	Correct classification at 15% noise
1st category	1	1	1	1	1
2nd category	10	9	9	9	9
3rd category	10	10	10	10	10
4th category	9	8	8	S	8
Accuracy	——	93.33%	93.33%	93.33%	93.33%

Performance Comparison. In order to verify the identification performance of the proposed method, the proposed method and the traditional damage location identification methods of simply supported beam bridges, such as BP network and SVM, are used to identify sample I under the condition of no noise. The results are shown in Table 6. As can be seen from the table, compared with BP network and SVM comparative identification methods, the proposed identification method based on SDAE has the highest identification accuracy and a certain advantages.

Table 6. Recognition results comparison of different recognition methods without noise.

Project	The number of actual categories	The SDAE algorithm is correct	The BP neural network algorithm is correct	The SVM algorithm is correct
1st category	1	1	0	0
2nd category	10	9	1	6
3rd category	10	10	7	3
4th category	9	8	3	3
Accuracy	——	93.33%	36.67%	40.00%

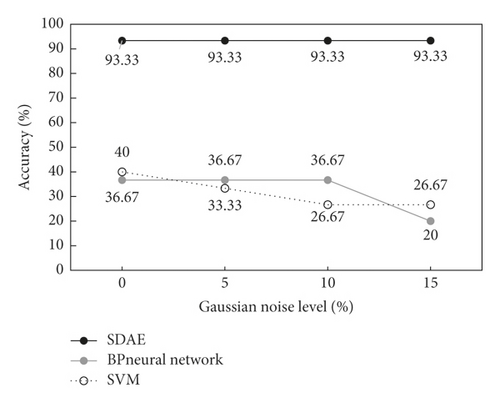
Under different Gaussian noise conditions, the recognition results of BP network, SVM, and the proposed method are shown in Figure 10. As can be seen from the figure, compared with the traditional identification methods BP network and SVM, the proposed method has obvious advantages in recognition accuracy. With the increase of noise level, the recognition accuracy of both BP network and SVM shows a decreasing trend, and the recognition accuracy of the proposed method remains stable. Therefore, the identification performance of the proposed method is better than that of traditional identification methods for simply supported beam bridges, and it has certain practical application value.

3.3.2. Damage Location Identification of Continuous Beam Bridges

Analysis of Recognition Results. The test samples of preprocessed sample II are used as the input data of SDAE, and the recognition results of deep learning model are obtained as shown in Table 7. As can be seen from the table, the average identification accuracy of the method proposed for multiple damage units of continuous beam bridges is higher, which reaches 99.8%. Among them, when the damage unit is No. 3, the recognition accuracy of the first damage category is 98.2%. When the damage unit is No. 10, the recognition accuracy of the second damage category is 98.2%. The recognition accuracy of other damage categories containing multiple damage units is 100%. Therefore, compared with a single damage unit, the method proposed in this paper has a higher identification accuracy for the damage position of continuous girder bridges with multiple damage units simultaneously. The reason is that the more the damage units are, the greater the impact on the carrying capacity of the bridge structure is, and the more obvious the topological relationship between the damage category and the acceleration response value of the monitoring point is. It can be seen that it is conducive to SDAE classification, so as to improve the identification accuracy of the algorithm.

Table 7. Damage location identification results of continuous beam bridges.

Damage category	Total number of actual categories	The number of accurate classifications	Accuracy (%)
1st category	280	275	99.76
2nd category	280	279
3rd category	280	280
4th category	280	280
5th category	280	280
6th category	280	280
7th category	280	280
8th category	280	280
9th category	280	280

In order to verify the effectiveness of the proposed method in identifying the damage position of continuous beam bridges with noise data, the 5%, 10%, and 15% Gaussian noise are added to the input data of training data and test data in sample II. And the proposed method is used to identify the damage position, and the results are obtained as shown in Table 8. It can be seen from the table that under different noise conditions, the method proposed in this paper has high recognition accuracy, with an average recognition accuracy of 99.8%. Therefore, the proposed SDAE can effectively identify the location of each damage unit of continuous beam bridges, and it has certain practical application value.

Table 8. Damage location identification results of continuous beam bridges under different noise conditions.

Project	The number of actual categories	Correct classification at 0% noise	Correct classification at 5% noise	Correct classification at 10% noise	Correct classification at 15% noise
1st category	280	275	275	275	275
2nd category	280	279	279	279	279
3rd category	280	280	280	2S0	280
4th category	280	280	280	280	280
5th category	280	280	280	280	280
6th category	280	280	280	280	280
7th category	280	280	280	280	280
8th category	280	280	280	280	280
9th category	280	280	280	280	2S0
Accuracy	—	99.76%	99.76%	99.76%	99.76%

Performance Comparison. In order to verify the identification performance of the proposed method, the proposed method and the traditional damage location identification methods of continuous beam bridges, such as BP network and SVM, are used to identify sample I under the condition of no noise. The results are shown in Table 9. As can be seen from the table, compared with BP network and SVM comparative identification methods, the proposed identification method based on SDAE has the highest identification accuracy, which has certain advantages.

Table 9. Recognition results comparison of different recognition methods without noise.

Project	The number of actual categories	The SDAE algorithm is correct	The BP neural network algorithm is correct	The SVM algorithm is correct
1st category	2S0	275	0	0
2nd category	280	279	50	34
3rd category	280	280	0	0
4th category	280	280	19	2
5th category	280	280	17	1
6th category	2S0	280	24	0
7th category	2S0	280	48	6
8th category	280	280	63	0
9th category	280	280	43	223
Accuracy	—	99.76%	10.48%	10.56%

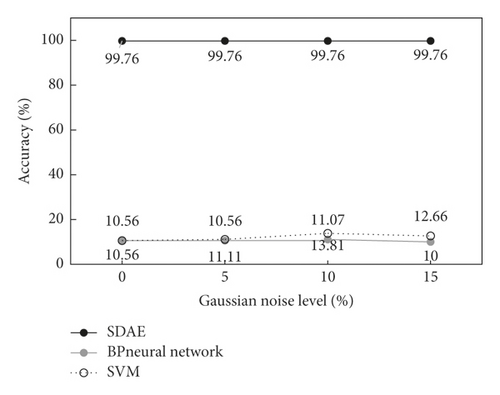
Under different Gaussian noise conditions, the recognition results of BP network, SVM, and the proposed method are shown in Figure 11. As can be seen from the figure, compared with the traditional identification methods BP network and SVM, the proposed method has obvious advantages in recognition accuracy. With the increase of noise level, the recognition accuracy of both BP network and SVM method shows small fluctuation, while the recognition accuracy of the proposed method always maintains a high recognition accuracy, which is up to 99.8%. Therefore, the identification performance of the proposed method is better than that of traditional identification methods for continuous beam bridges, and it has a certain practical application value.

4. Conclusion

To sum up, the damage location identification method of bridge structure based on deep learning proposed in this paper can effectively identify the damage location of simply supported and continuous beam bridges by using SDAE. Compared with the traditional bridge structure recognition method BP network and the SVM method, the proposed method shows a higher recognition accuracy and antinoise performance. And the average identification accuracy for continuous beam bridge of multiple damage unit reaches 99.8%. It can be seen that the proposed method has obvious advantage on the damage location identification of actual bridge structures. Although there are some achievements, all the conclusions are based on software simulation, namely theory. Obviously, it lack of practical test support, so the proposed method has certain limitations. What is more, the constructed damage index is relatively single. In the practical application, the damage index of bridge structure is complex and diverse, so the selection of damage index needs to be further strengthened. Meanwhile, the practicality and persuasiveness of the proposed method also need to be improved.

Conflicts of Interest

The authors declare that they have no conflicts of interest regarding this work.

Open Research

Data Availability

The experimental are available from the corresponding author upon request.

References

1 Ye X., Sun Z., and Chen B., Research on modal parameters identification of bridge structure based on adaptive signal de-noising method, Cluster Computing. (2019) 22, no. 6, 14377, https://doi.org/10.1007/s10586-018-2301-1, 2-s2.0-85045051345.
10.1007/s10586-018-2301-1
Web of Science® Google Scholar
2 Marco F., Pavese A., Lunghi F., and Silvestri D., Strategies of structural health monitoring for bridges based on cloud computing, Journal of Civil Structural Health Monitoring. (2019) 9, no. 5, 607–616, https://doi.org/10.1007/s13349-019-00356-5, 2-s2.0-85073995154.
10.1007/s13349-019-00356-5
Web of Science® Google Scholar
3 Kim J. and Song J., A comprehensive probabilistic model of traffic loads based on weigh-in-motion data for applications to bridge structures, KSCE Journal of Civil Engineering. (2019) 23, no. 8, 3628–3643, https://doi.org/10.1007/s12205-019-2432-9, 2-s2.0-85068230736.
10.1007/s12205-019-2432-9
Web of Science® Google Scholar
4 Li L., Zhang L., Liu G., Li Q., and An X., Sensor fault localization with accumulated residual contribution rate for bridge SHM, Cluster Computing. (2019) 22, no. S4, 7821–7829, https://doi.org/10.1007/s10586-017-1456-5, 2-s2.0-85038104007.
10.1007/s10586-017-1456-5
Web of Science® Google Scholar
5 Li X.-Q., Chen Q.-J., and Ding Z.-D., Structural damage diagnosis and fine scale finite element intelligence simulation of long span cable stayed bridges, Cluster Computing. (2019) 22, no. 2, 4101–4107, https://doi.org/10.1007/s10586-017-1515-y, 2-s2.0-85041907520.
10.1007/s10586-017-1515-y
Web of Science® Google Scholar
6 Qin S., Zhou Y., Cao H., and Wahab M. A., Model updating in complex bridge structures using kriging model ensemble with genetic algorithm, KSCE Journal of Civil Engineering. (2018) 22, no. 9, 3567–3578, https://doi.org/10.1007/s12205-017-1107-7, 2-s2.0-85034853456.
10.1007/s12205-017-1107-7
Web of Science® Google Scholar
7 Yu X., Chen J., Xu Q., and Zhou Z., Research on the influence factors of thermal cracking in mass concrete by model experiments, KSCE Journal of Civil Engineering. (2018) 22, no. 8, 2906–2915, https://doi.org/10.1007/s12205-017-2711-2, 2-s2.0-85033501574.
10.1007/s12205-017-2711-2
Web of Science® Google Scholar
8 Boscato G. and Dal Cin A., Experimental and numerical evaluation of structural dynamic behavior of Rialto Bridge in Venice, Journal of Civil Structural Health Monitoring. (2017) 7, no. 4, 557–572, https://doi.org/10.1007/s13349-017-0242-7, 2-s2.0-85031490291.
10.1007/s13349-017-0242-7
Web of Science® Google Scholar
9 Meng W., Zelin W., Xiaoyu W., Jialuo P., and Yu S., Prediction of TBM penetration rate based on Monte Carlo-BP neural network, Neural Computing & Applications. (2020) 33, 1–9, https://doi.org/10.1007/s00521-020-04993-6.
10.1007/s00521-020-04993-6
Google Scholar
10 Li J., Men C., Qi J., Yang B., and Liu R., Impact factor analysis, prediction, and mapping of soil corrosion of carbon steel across China based on MIV-BP artificial neural network and GIS, Journal of Soils and Sediments. (2020) 20, 1–13, https://doi.org/10.1007/s11368-020-02649-5.
10.1007/s11368-020-02649-5
Web of Science® Google Scholar
11 Feifei Y., Mou J., Sun K., and Chu R., Lossless image compression-encryption algorithm based on BP neural network and chaotic system, Multimedia Tools and Applications. (2020) 79, 1–30, https://doi.org/10.1007/s11042-020-08821-w.
10.1007/s11042-020-08821-w
Web of Science® Google Scholar
12 Xiwen C., Xiaoqian L., and Ruiqing L., Ultrasonic power load forecasting based on BP neural network, Journal of the Institution of Engineers: Series C: Mechanical, Production, Aerospace and Marine Engineering. (2020) 101, no. 23, 383–390, https://doi.org/10.1007/s40032-019-00549-3.
10.1007/s40032-019-00549-3
Google Scholar
13 Linying K., Wenyao Z., and Gab-Geun Y., VR design of public facilities in historical blocks based on BP neural network, Neural Processing Letters. (2020) 53, 1–10, https://doi.org/10.1007/s11063-020-10207-w.
10.1007/s11063-020-10207-w
Web of Science® Google Scholar
14 Ge Q., Jiang H., He M., and Zhu Y., Power load forecast based on fuzzy BP neural networks with dynamical estimation of weights, International Journal of Fuzzy Systems. (2020) 22, 956–969, https://doi.org/10.1007/s40815-019-00796-7.
10.1007/s40815-019-00796-7
Web of Science® Google Scholar
15 Wang S., Multisensor data fusion of motion monitoring system based on BP neural network, The Journal of Supercomputing: An International Journal of High-Performance Computer Design, Analysis, and Use. (2020) 76, no. 2, 1642–1656, https://doi.org/10.1007/s11227-019-03015-0.
10.1007/s11227-019-03015-0
Google Scholar
16 You H., Yu L., Tian S., Ma X., Xing Y., Xin N., and Cai W., MC-Net: multiple max-pooling integration module and cross multi-scale deconvolution network, Knowledge-Based Systems. (2021) 231, https://doi.org/10.1016/j.knosys.2021.107456.
10.1016/j.knosys.2021.107456
PubMed Web of Science® Google Scholar
17 Jin W., Marco A., and Gwanggil J., Reconstruction of missing color-channel data using a three-step back propagation neural network, International Journal of Machine Learning and Cybernetics. (2019) 10, no. 10, 2631–2642, https://doi.org/10.1007/s13042-018-0850-5, 2-s2.0-85072030130.
10.1007/s13042-018-0850-5
Web of Science® Google Scholar
18 Wang J. and Xia L., Abnormal behavior detection in videos using deep learning, Cluster Computing: The Journal of Networks, Software Tools and Applications. (2019) 22, no. 11, 9229–9239, https://doi.org/10.1007/s10586-018-2114-2, 2-s2.0-85045040162.
10.1007/s10586-018-2114-2
Web of Science® Google Scholar
19 Krzysztof Ś., Paweł K., and Jacek K., Autoencoder-based image processing framework for object appearance modifications, Neural Computing & Applications. (2020) 22, 1–12, https://doi.org/10.1007/s00521-020-04976-7.
10.1007/s00521-020-04976-7
Google Scholar
20 Choi J. and Chae H., methCancer-gen: a DNA methylome dataset generator for user-specified cancer type based on conditional variational autoencoder, BMC Bioinformatics. (2020) 21, no. 4, 766–304, https://doi.org/10.1186/s12859-020-3516-8.
10.1186/s12859-020-3516-8
Web of Science® Google Scholar
21 Rong F., Sha J., Xu Q., and Hu B., A new deep sparse autoencoder for community detection in complex networks, EURASIP Journal on Wireless Communications and Networking. (2020) 2020, no. 8, 75–174, https://doi.org/10.1186/s13638-020-01706-4.
10.1186/s13638-020-01706-4
Web of Science® Google Scholar
22 Gourav B., Himanshu A., and Rinkle R., AutoTrustRec: recommender system with social trust and deep learning using AutoEncoder, Multimedia Tools and Applications. (2020) 79, 1–16, https://doi.org/10.1007/s11042-020-08932-4.
10.1007/s11042-020-08932-4
Web of Science® Google Scholar
23 Shotaro A., Asaoka R., Yamashita T., Aoki S., Matsuura M., Fujino Y., Murata H., Nakakura S., Nakao Y., and Kiuchi Y., Visualizing the dynamic change of Ocular Response Analyzer waveform using Variational Autoencoder in association with the peripapillary retinal arteries angle, Scientific Reports. (2020) 10, no. 1, 1739–1748, https://doi.org/10.1038/s41598-020-63601-8.
10.1038/s41598-020-63601-8
PubMed Web of Science® Google Scholar
24 Amina L., Salima O., and Holger F., PathME: pathway based multi-modal sparse autoencoders for clustering of patient-level multi-omics data, BMC Bioinformatics. (2020) 21, no. 8, 747–752.
Web of Science® Google Scholar
25 Hong-Gui H., Hui-Juan Z., and Jun-Fei Q., Robust deep neural network using fuzzy denoising autoencoder, International Journal of Fuzzy Systems. (2020) 22, 1–20, https://doi.org/10.1007/s40815-020-00845-6.
10.1007/s40815-020-00845-6
Web of Science® Google Scholar
26 Zerkouk M. and Chikhaoui B., Spatio-temporal abnormal behavior prediction in elderly persons using deep learning models, Sensors. (2020) 20, no. 8, https://doi.org/10.3390/s20082359.
10.3390/s20082359
Web of Science® Google Scholar
27 Fu H., Liang F., Lei B., Bian N., Zhang Q., Akbari M., Liang J., and Tu C., Improved hybrid layered image compression using deep learning and traditional codecs, Signal Processing: Image Communication. (2020) 82, 115774, https://doi.org/10.1016/j.image.2019.115774.
10.1016/j.image.2019.115774
Web of Science® Google Scholar
28 Yoonhee K. I. M., Yun D., and Lee H., A non-intrusive speech intelligibility estimation method based on deep learning using autoencoder features, IEICE - Transactions on Info and Systems. (2020) E103.D, 714–715.
10.1587/transinf.2019EDL8150
Google Scholar
29 Gracewell J. and John M., Dynamic background modeling using deep learning autoencoder network, Multimedia Tools and Applications: International Journal. (2020) 79, no. 9, 4639–4659, https://doi.org/10.1007/s11042-019-7411-0, 2-s2.0-85062864761.
10.1007/s11042-019-7411-0
Web of Science® Google Scholar
30 Faming H., Zhang J., Zhou C., Wang Y., Huang J., and Zhu L., A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction, Landslides: Journal of the International Consortium on Landslides. (2020) 17, no. 5, 217–229, https://doi.org/10.1007/s10346-019-01274-9, 2-s2.0-85072386403.
10.1007/s10346-019-01274-9
Web of Science® Google Scholar

All articles

Research on Bridge Structural Damage Identification

Abstract